Comprehensive Spectroscopic Study of Competing Recombination Channels and Thermal Quenching Mechanisms in β-Ga₂O₃ Single Crystals

Abstract

This work investigates a comprehensive temperature-dependent photoluminescence (PL) study (7–300 K) of β-Ga₂O₃ single crystals under 250 nm excitation. The emission consists of three competing bands at ~3.55 eV (J₁), ~3.37 eV (J₂), and ~3.07 eV (J₃), exhibiting a redshift, band broadening, and a crossover near ~140 K with increasing temperature. The novelty of this study lies in the first quantitative investigation of the temperature-dependent photoluminescence of undoped β-Ga₂O₃ single crystals, revealing activation, trap-release, and phonon-coupling parameters that define the competition between STE (Self-trapped exciton)- and DAP-related emission channels. A two-channel Arrhenius analysis of global thermal quenching at E_max (at maximum PL), J₁, and J₂ reveals a common shallow barrier (E₁ = 7–12 meV) alongside deeper, band-specific barriers (E₂ = 27 meV for J₁ and 125 meV for J₂). The J₃ band shows non-monotonic intensity (dip–peak–quench) reproduced by a trap-assisted generation model with a release energy E_rel = 50 meV. Linewidth analysis yields effective phonon energies (E_ph ≈ 40–46 meV), indicating strong electron–phonon coupling and a transition to multi-phonon broadening at higher temperatures. These results establish a coherent picture of thermally driven redistribution from near-edge STE-like states to deeper defect centers and provide quantitative targets (activation and phonon energies) for defect engineering in β-Ga₂O₃-based optoelectronic and scintillation materials.

1. Introduction

Gallium oxide in its thermodynamically stable monoclinic phase (β-Ga₂O₃) is a wide-bandgap semiconductor (E_g ≈ 4.5–4.9 eV) that has attracted considerable attention for its potential applications in power electronics [1,2,3,4], solar-blind UV photodetectors [2,5,6,7,8,9,10], luminescence detectors and scintillators [11,12,13,14,15,16,17,18,19,20], catalysts [21,22,23,24] and related sensors [25,26,27,28] and devices for micro- and nanoelectronics [29,30,31,32,33,34,35,36,37,38]. Its unique optical and electrical properties [39,40,41] are largely governed by a complex defect structure, and luminescence under various excitation methods (photoluminescence, cathodoluminescence, X-ray-excited luminescence, etc.) serves as a powerful tool to probe these defects [42]. Unlike classical semiconductors, β-Ga₂O₃ exhibits virtually no band-to-band (near-band-edge) emission; instead, its luminescence spectra consist of several broad bands in the UV, blue, and green spectral regions [43,44]. These emission bands are associated with intrinsic and extrinsic defect centers within the bandgap. Commonly observed are a UV or ultraviolet luminescence (UVL) band (often around 3.2–3.8 eV), a blue luminescence (BL) band (~2.8–3.0 eV), and sometimes green (GL) or other visible bands, depending on sample composition and defects [42].

Studying the temperature dependence of luminescence is a key approach to understanding the recombination mechanisms, the stability of luminescence centers, and the role of nonradiative processes in β-Ga₂O₃. In general, thermal quenching, i.e., the reduction in luminescence intensity with increasing temperature, is universally observed, but its specific characteristics (activation energies, quenching stages) depend on the type of luminescence (UVL, BL, etc.) and the defect makeup of the sample.

Many previous studies have examined these dependencies under various excitation conditions:

Photoluminescence (PL): Early photoluminescence studies on β-Ga₂O₃ single crystals showed that the blue emission band quenches in two steps: an initial quenching with a low activation energy of ~0.05 eV (attributed to thermal release of electrons from shallow donors), and a second quenching stage at higher temperatures with activation energy ~0.42 eV (attributed to release of holes from deep acceptors) [42]. Studies on Li-doped β-Ga₂O₃ nanostructures observed that as temperature is lowered from 300 K to 10 K, the overall luminescence intensity increases (due to suppression of thermal quenching) and a broad red-infrared emission band splits into several sharp peaks, revealing a fine structure of defect-related emission centers [45]. Temperature-resolved photoluminescence excitation (PLE) spectroscopy from 5 K to 350 K has been used to track the shift in optical transition energies in β-Ga₂O₃; the temperature dependence of these transitions can be described by the Varshni model, allowing extraction of fundamental parameters like the average phonon energies (17–27 meV) and the strength of electron–phonon coupling in the material [46]. In Eu-doped Ga₂O₃ ceramics (β-Ga₂O₃:Eu), a dominant “matrix” luminescence band at 300–550 nm (peaking ~440 nm) is observed at low temperatures, arising from Ga–O defect donor–acceptor pair recombination; this band rapidly loses intensity above ~100 K. Its thermal quenching follows a two-barrier behavior with activation energies E₁ ≈ 45 meV and E₂ ≈ 187 meV [47].

Cathodoluminescence (CL): Electron-beam excitation has provided detailed insight into temperature quenching associated with both intrinsic and impurity centers. CL studies on β-Ga₂O₃ nanowires (80–300 K) revealed that below ~220 K, in addition to the usual UVL band, a higher-energy deep-UV band (DUVL) emerges. Both the DUVL and UVL bands exhibit thermal quenching with similar activation energies of ~74–77 meV [48]. In Si-doped β-Ga₂O₃, cathodoluminescence over 4.5–310 K showed a two-step quenching for the UV emission band: the first stage with activation energy ~31–34 meV was attributed to thermal ionization of Si donors, and the second stage (dominant at higher T) with activation energy ~63–75 meV was attributed to the activation of a nonradiative recombination center [49]. Furthermore, analysis of CL in Si- and N-doped samples indicated two quenching components for the UVL band with activation energies of ~8.5 meV (associated with self-trapped exciton processes) and ~71 meV (associated with donor–acceptor-pair recombination), confirming the presence of multiple competing quenching pathways [50].

X-ray-excited luminescence (XEL): XEL studies (50–290 K) reinforce the general thermal quenching trends and relate them to defect migration and scintillation behavior. In β-Ga₂O₃ single crystals, the UV luminescence band quenches with an activation energy of ~72–90 meV. A key finding was a proposed quenching mechanism involving thermally activated migration of self-trapped holes (STH) to nonradiative recombination centers, specifically gallium vacancies (V_Ga⁻³) [51]. In crystals with different electrical conductivities, XEL revealed distinct quenching mechanisms for the blue luminescence band: in conductive samples, a quenching activation energy of ~0.48 eV was found (attributed to thermal delocalization of holes from acceptors), whereas in highly resistive samples the quenching energy was only ~0.08 eV (attributed to delocalization of electrons from donors) [52]. Using XEL to study scintillation properties, it was shown that the light yield of β-Ga₂O₃ can increase significantly upon cooling, reaching a maximum at ~50 K about twice the value at room temperature, demonstrating the potential of β-Ga₂O₃ as a cryogenic scintillator [53].

Significance of Temperature-Dependent Luminescence Studies: Both fundamentally and practically, understanding the luminescence behavior of β-Ga₂O₃ as a function of temperature is highly important. From a fundamental perspective, analysis of thermal quenching curves and spectral line broadening provides direct access to parameters such as activation energies of nonradiative processes, binding energies of excitons or carrier traps at defects, and effective phonon energies and electron–phonon coupling strengths. These data are critical for developing and validating theoretical models of the electronic and defect states in the material [54,55,56,57,58]. From an application standpoint, the thermal stability of luminescence directly impacts the performance and reliability of β-Ga₂O₃-based optoelectronic devices. For high-power transistors and diodes operating at elevated temperatures, understanding degradation mechanisms related to defect activation is key. In scintillation detectors, knowledge of the temperature dependence of light yield and decay times is essential for optimizing devices, especially for low-temperature applications (such as rare-event detection experiments) [53,59,60,61,62,63]. Thus, controlling and comprehending the temperature behavior of luminescence is a necessary step for further progress in deploying gallium oxide in advanced applications.

Among the available literature, the temperature dependence of photoluminescence has been investigated only for β-Ga₂O₃ single crystals by [42] and for Eu-doped ceramics by [47], whereas other works addressed temperature effects mainly under cathodoluminescence [48,49,50] or X-ray excitation [51,52,53]. In contrast, this study presents the first detailed quantitative investigation of temperature-dependent photoluminescence in undoped β-Ga₂O₃ single crystals over a wide range of 7–300 K using UV laser excitation. The steady-state spectral evolution is analyzed to reveal radiative recombination channels and their thermal quenching behavior. Multi-Gaussian spectral decomposition combined with Mott and Arrhenius modeling is applied to quantify activation energies and thermal quenching processes. Furthermore, the temperature-dependent broadening of emission bands is analyzed to determine the effective phonon energies coupled with excited electronic states. The results provide new insights into the competition between STE and DAP recombination channels and are compared with previously reported data.

2. Materials and Methods

Bulk UID (unintentionally doped) β-Ga₂O₃ single-crystal samples with surface orientation (–201) were used in this study. The crystals (10 × 15 × 0.65 mm in size) were purchased from Novel Crystal Technology (Tamura Corp., Tokyo, Japan) and grown by the edge-defined film-fed growth (EFG) melt method [64]. The crystals are nominally undoped (intrinsic) and high-resistivity. Unit cell shown in Figure 1 and

Table 1. Basic physical characteristics of β-Ga₂O₃ single crystal [64].

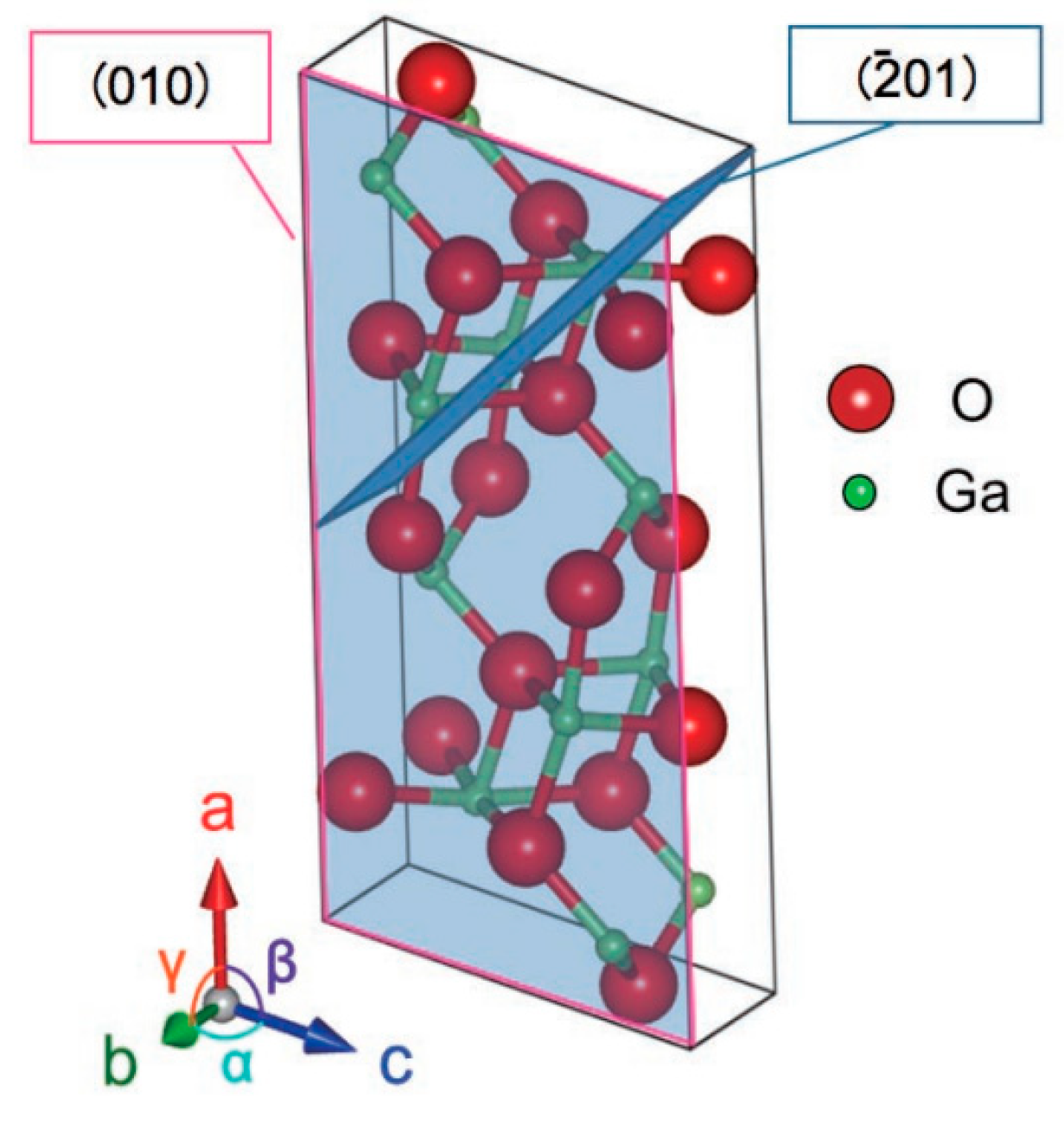
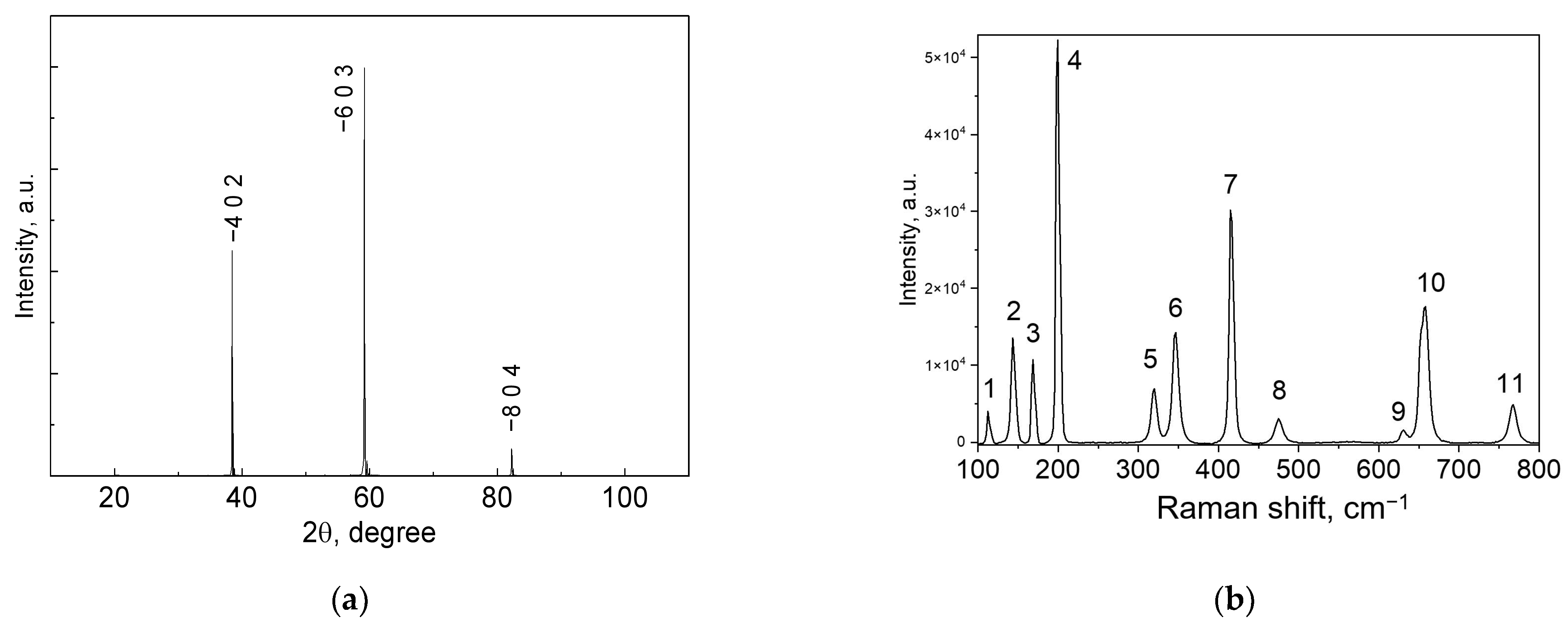
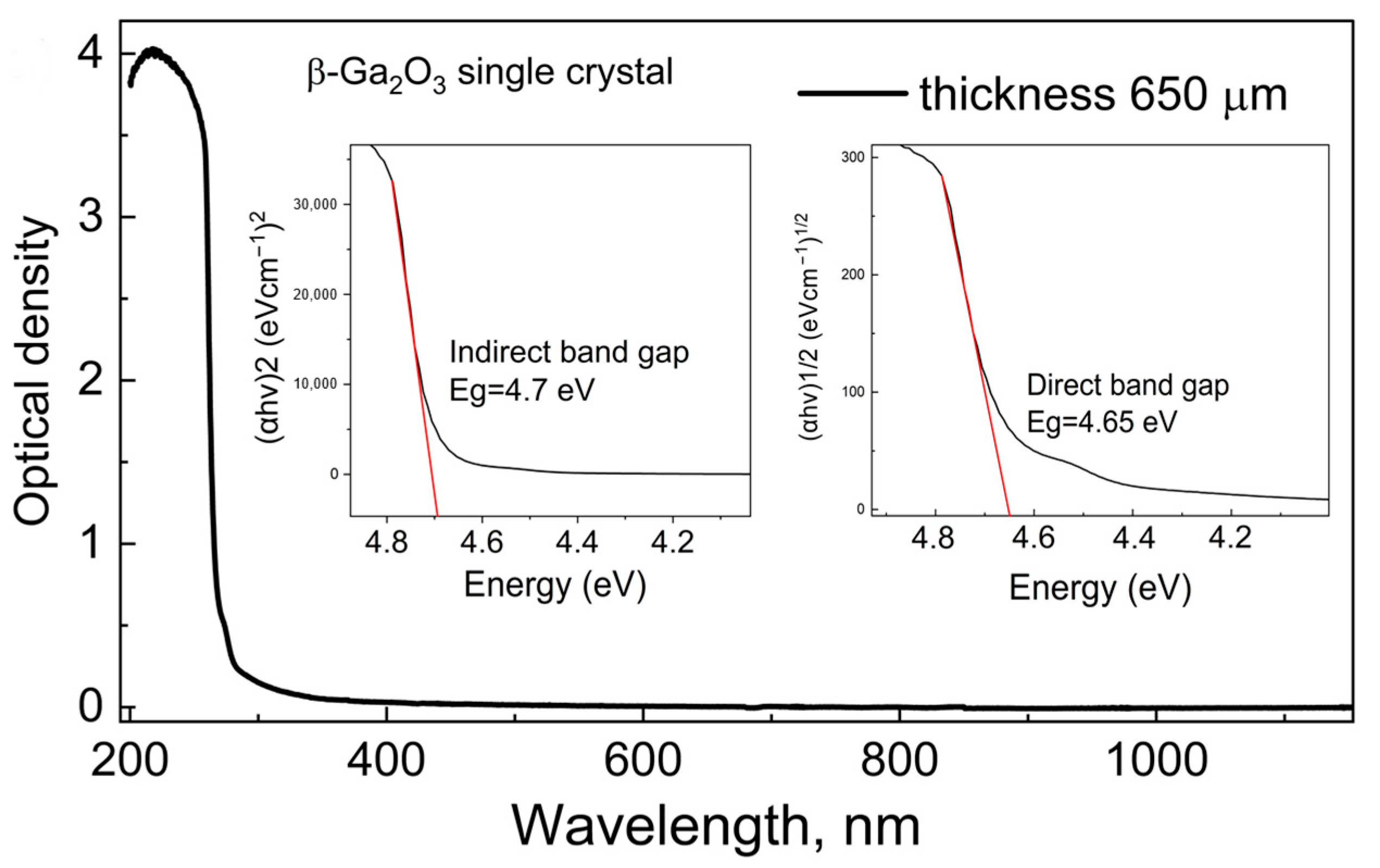
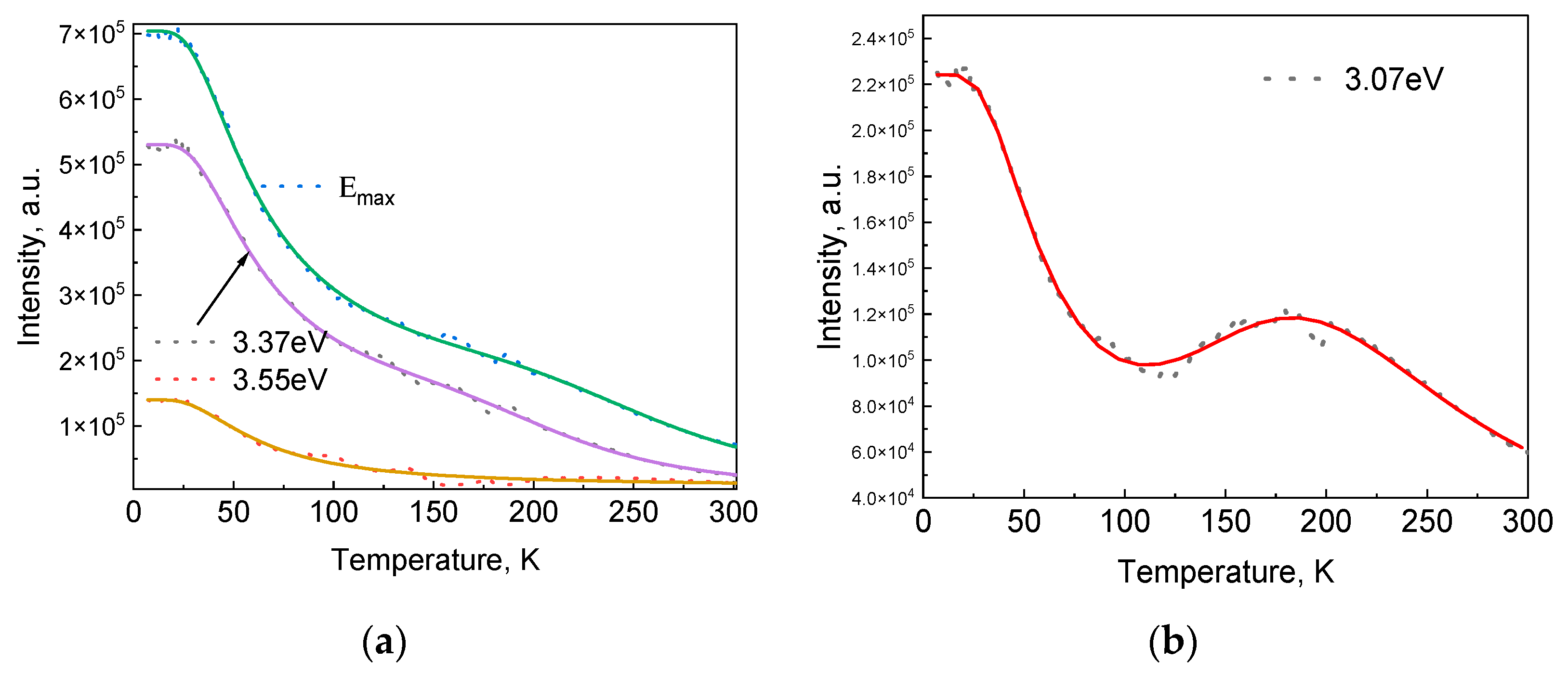
Property	Value (β-Ga2O3)
Crystal structure	Monoclinic; a = 12.23 Å, b = 3.04 Å, c = 5.80 Å; α = γ = 90°, β = 103.7°
Melting point	1725 °C
Density	5.95 × 103 kg/m3
Vickers hardness	(100) face: 9.7 GPa; (201) face: 12.5 Ga
Young’s modulus	230 GPa
Thermal conductivity	(100) direction: 13.6 W/(m·K); (010): 22.8 W/(m·K)
Specific heat capacity	0.49 × 103 J/(kg·K)
Refractive index (450 nm)	1.97
Thermal expansion coeff.	(100): 5.3 × 10−6 K−1; (010): 8.9 × 10−6 K−1; (001): 8.2 × 10−6 K−1 (300–1300 K range)

summarizes the key physical characteristics of the β-Ga₂O₃ crystal as provided by the manufacturer. These include the monoclinic crystal structure parameters, mechanical properties, and thermal and optical constants relevant to the material.

Optical absorption measurements were performed on the β-Ga₂O₃ crystal (thickness 0.65 mm) at room temperature using a UV–Vis spectrophotometer Agilent Cary 7000 UMS (Agilent, Santa Clara, CA, USA). The absorption edge was analyzed using Tauc plots for both indirect and direct bandgap transitions. Photoluminescence (PL) spectra were recorded using a pulsed ultraviolet laser at 250 nm (4.96 eV photon energy, above the bandgap) as the excitation source a tunable pulsed solid-state laser (Ekspla NT342/3UV, Vilnius, Lithuania). The luminescence was detected with an Andor SR-303i-B (Oxford Instruments, Belfast, UK) spectrometer coupled to an Andor iStar DH734 CCD camera(Oxford Instruments, Belfast, UK). Low-temperature experiments were carried out in an Advanced Research Systems DE202 N (Advanced Research Systems, Macungie, PA, USA) helium cold-finger cryostat. The sample was mounted in a temperature-controlled cryostat, allowing measurements from 7 K (liquid helium temperature) up to 300 K. X-ray diffraction measurements were carried out on a D8 ADVANCE ECO diffractometer (Bruker, Karlsruhe, Germany) to analyze the crystal structure. Raman spectra of the crystal were measured using a TriVista CRS Raman (S&I Spectroscopy & Imaging GmbH, Anröchte, Germany) spectrometer equipped with a 532 nm excitation laser, a triple monochromator, and a CCD detector, providing a spectral resolution better than 0.1 cm⁻¹.

To analyze the composite emission bands, the spectra were deconvolved into Gaussian components using a least-squares fitting routine. This allowed identification of sub-band contributions and their evolution with temperature. The temperature dependence of the integrated luminescence intensity was analyzed using a multi-level Arrhenius model. Specifically, we assume the luminescence intensity I(T) follows an expression of the form:

$$I\left(T\right)={\displaystyle \frac{I_0}{1+{\sum }_i{B}_i\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{E_i}{k_{B}T}\right)}},$$

(1)

where I₀ is the intensity in the limit of very low temperature (when thermal quenching is negligible), E_i are the activation energies of nonradiative (quenching) processes, B_i are pre-exponential constants, and k_B is the Boltzmann constant [65,66,67]. Equation (1) accounts for multiple nonradiative recombination channels i that compete with the radiative luminescence. Fitting the experimental I(T) data to this model yields the characteristic E_i and B_i parameters for thermal quenching.

The broadening of the luminescence bands with temperature was analyzed by tracking the full width at half maximum (FWHM) of each emission component as a function of T. We employed a one-phonon coupling model to describe the homogeneous broadening, given by the expression [66,67]:

$$\Gamma \left(T\right)={\Gamma }_0+A\left[\mathrm{c}\mathrm{o}\mathrm{t}\mathrm{h}\left({\displaystyle \frac{E_{ph}}{2k_{B}T}}\right)-1\right]$$

(2)

Here $\Gamma \left(T\right)$ is the FWHM of an emission line at temperature T, ${\Gamma }_0$ is the residual (inhomogeneous) linewidth at low temperature, $E_{ph}$ is an effective phonon energy associated with the dominant phonon mode coupling to the electronic transition, and A is a coupling strength parameter proportional to the Stokes shift (related to the Huang–Rhys factor). Equation (2), which originates from the theory of temperature-dependent broadening of optical transitions in semiconductors [66,67], assumes coupling to a single effective optical phonon mode. By fitting the measured FWHM vs. T data for each luminescence band, we obtained the parameters ${\Gamma }_0$, A, and $E_{ph}$, as well as the fit residuals (RMSE) as a measure of goodness of fit.

3. Results

3.1. Structural Study

X-ray diffraction (XRD) analysis of β-Ga₂O₃ shows a typical diffractogram of the monoclinic phase (space group C2/m) for an oriented crystal: due to Bragg’s condition being satisfied for a limited set of (hkl) planes and pronounced texture, only a small number of intense reflections is observed (Figure 2a). In the presented scan, peaks indexed as (−402), (−603), and (−804) are clearly visible in the 2θ ≈ 38–85° range, consistent with reference data for β-Ga₂O₃. The refined lattice parameters (a ≈ 12.23 Å, b ≈ 3.04 Å, c ≈ 5.80 Å, α = γ = 90°, β ≈ 103.7°) match literature values for the monoclinic polymorph (Table 1). Narrow peak widths indicate high crystallinity and a low level of microstrain. Importantly, no additional peaks associated with other Ga₂O₃ polymorphs (α, γ, etc.) or foreign phases/oxides are observed in the diffractogram, demonstrating the sample’s phase purity. Thus, the XRD data confirm that the specimen is β-Ga₂O₃ with a monoclinic lattice and no impurity phases are detected within the sensitivity of the method.

Raman spectroscopy of β-Ga₂O₃ at room temperature reveals the full set of Ag and Bg modes expected for the monoclinic C2/m phase (Figure 2b). Eleven bands are resolved at 113.1 (A_g, FWHM 2.5), 143.9 (B_g, 5.0), 168.8 (A_g, 3.8), 199.2 (A_g, 4.5), 319.5 (A_g, 6.6), 346.4 (A_g, 7.6), 416.0 (A_g, 5.5), 475.3 (A_g, 8.7), 629.8 (A_g, 1.7), 656.6 (B_g, 10.9) and 767.3 cm⁻¹ (A_g, 9.6). The measured positions and widths closely match the benchmark single-crystal, ceramics [44] datasets and nanocrystals [45] of β-Ga₂O₃ exhibit the same characteristic mode set within experimental tolerance, reinforcing the mode assignments to bending and stretching of Ga_IO₄ tetrahedra and Ga_IIO₆ octahedra with only minor deviations attributable to experimental uncertainty and residual strain, the spectral consistency across literature and our measurements confirms high crystalline quality. No impurity phases were detected: only the main β-Ga₂O₃ phase is observed within the method’s sensitivity.

3.2. Optical Absorption and Band Gap

The β-Ga₂O₃ crystal shows a sharp absorption onset in the ultraviolet region. The optical density rises steeply for wavelengths shorter than 280 nm, indicating the fundamental band edge of the material in the UV range. In the visible and near-infrared range, the crystal exhibits high transparency (very low absorption), confirming the absence of significant mid-gap defect absorption bands and indicating the high crystalline quality of the sample (Figure 3). The synthesis and purity of this single crystal were previously demonstrated [64], and these results are further confirmed by our structural studies presented above. Tauc analysis of the absorption edge was performed for both indirect and direct allowed transitions. The high-energy portion of the absorption spectrum was fitted to (αhν)^1/2 vs. hν (photon energy) for the indirect transition model, and to (αhν)² vs. hν for the direct transition model, where α is the absorption coefficient and hν the photon energy. From these fits, the indirect bandgap energy $E_g^{ind}$ was determined to be approximately 4.7 eV, while the direct bandgap $E_g^{dir}$ was estimated to be about 4.65 eV. This slight difference between $E_g^{ind}$ and $E_g^{dir}$ (with the indirect gap being 0.05 eV larger) indicates that β-Ga₂O₃ is essentially an indirect-gap semiconductor, wherein the conduction band minimum and valence band maximum occur at different k-points in the Brillouin zone. On the same sample discussed in the study, the bandgap width was evaluated using the Tauc plot method for the UID (unintentionally doped) sample with a (−201) orientation, the direct bandgap values were approximately 4.85 eV with parallel polarization (0°) and 4.55 eV with perpendicular polarization (90°) [68]. For the UID sample with a (001) orientation, these values were about 4.88 eV and 4.7 eV, respectively. The obtained bandgap values are in good agreement with literature reports and electronic band structure calculations for β-Ga₂O₃, affirming the validity of our absorption analysis [69,70,71,72,73,74,75,76,77,78,79].

3.3. Temperature Dependence Luminescence Spectra

The luminescent properties were investigated over a wide temperature range from 7 to 300 K (Figure 4) under pulsed laser excitation at a wavelength of 250 nm (4.96 eV), which exceeds the band gap estimated for this crystal. At low temperatures (Figure 4a–c), an intense broad emission band is observed in the UV–blue region with a maximum at ~3.4–3.6 eV (345–365 nm) and a pronounced asymmetric “long-tail” extension toward lower energies down to ~3.0 eV (≈410 nm and beyond).

With increasing temperature (Figure 4a), the overall emission intensity monotonically decreases (thermal quenching), while the maximum of the composite band shifts toward lower energies (longer wavelengths) and the band noticeably broadens. Normalized spectra (Figure 4b) emphasize two key features of the spectral evolution: (1) the persistence of an almost “isosbestic” crossing point within a narrow wavelength interval, indicative of a thermally driven redistribution of populations among a fixed set of emission channels without the emergence of new bands; and (2) a progressive enhancement of the long-wavelength tail accompanied by depletion on the short-wavelength side, reflecting the growing contribution of the low-energy channel concurrent with suppression of the UV component.

Gaussian decomposition at 7 K (Figure 4c) reveals that the spectrum is composed of at least three contributions, are well described by the sum of at least three separate bands, which will be further designated as J₁, J₂ and J₃, with centered at energies of approximately 3.55 eV, 3.37 eV and 3.07 eV, respectively. This corresponds to the well-established emission pattern of β-Ga₂O₃ involving competing radiative channels: (i) a UV component at ~3.5 eV, attributed to recombination from weakly localized states (e.g., near-band-edge transitions or STE-like centers); (ii) an intermediate contribution at ~3.3–3.4 eV; and (iii) a lower-energy “blue” channel at ~3.0–3.1 eV, commonly assigned to more deeply localized defect complexes or donor–acceptor pair (DAP) recombination. At 7 K, the UV component provides a substantial share of the total emission, while the low-energy channel is present but not dominant.

Spectral fitting at 300 K (Figure 4d) quantitatively confirms this behavior: the ~3.07 eV component becomes dominant, the ~3.37 eV contribution decreases, and the high-energy ~3.55 eV component is almost completely quenched. Such spectral reshaping is consistent with a scenario of competing centers differing in localization degree and in the activation barriers for non-radiative pathways. For the more strongly localized blue centers, the radiative probability decreases only weakly with increasing temperature, whereas for high-energy channels (near-band-edge or STE-like), two thermally activated processes become significant: (i) carrier delocalization followed by trapping at non-radiative centers, and (ii) energy transfer to lower-energy defect states, which simultaneously reduces their own UV emission and channels carriers into the blue band. The additional broadening of the emission with heating reflects the strengthening of electron–phonon coupling.

From a kinetic perspective, under pulsed excitation at 250 nm (with photon energy exceeding the band gap of β-Ga₂O₃, the primary process involves interband transitions and excitation of strong defect-related absorption bands. This is followed by rapid carrier relaxation, which populates a set of localized states that compete with one another. Upon heating, the system enters a regime characterized by two (or more) distinct thermally activated quenching energies. Qualitatively, this manifests as a more pronounced decrease in emission intensity above ~120–150 K, accompanied by an additional enhancement of quenching toward room temperature, typical for the activation of successive nonradiative channels. Collectively, this results in (i) overall thermal quenching, (ii) a redshift of the emission maximum, (iii) an increased relative contribution of the low-energy channel, and (iv) broadening of the emission band.

Analysis of the temperature-dependent spectra indicates that around 140 K a transition point emerges, where both the spectral shape and the integral intensity begin to change simultaneously. In this region, pronounced spectral broadening becomes evident for the first time, with the long-wavelength tail strongly developing and the emission maximum gradually shifting to lower energies. Thus, 140 K can be regarded as a characteristic boundary between the low-temperature regime, dominated by near-band-edge and weakly localized radiative centers, and the high-temperature regime, where more deeply localized defects prevail and thermal quenching dominates.

3.4. Activation Energy of Thermal Quenching

The temperature dependences at the intensity maximum (E_max) of the total spectrum, as well as for each of the three resolved bands (J₁, J₂, and J₃), are shown in Figure 5a. For the E_max position, as well as for bands J₁ and J₂, the quenching curves clearly exhibit a two-step character, with a distinct change in slope around 140 K. This indicates the presence of at least two different nonradiative channels that become active at different temperatures. In contrast, band J₃ shows a smoother and less pronounced quenching behavior over the entire investigated temperature range.

The results of fitting (Figure 5) the experimental data using a two-channel thermal quenching model obtained by the expression (1) are summarized in

Table 2. Thermal quenching parameters obtained by Equation (1).

Band	B1	E1, meV	B2	E2, meV
Emax	4.92	11.6	2357.81	154
3.55 eV (J1)	5.44	11	18.44	27
3.37 eV (J2)	5.32	12.3	2110.23	125
3.07 (J3)	4.35	10.6 (up to 120 K)	-	-

. The analysis reveals the presence of two characteristic activation energies. The low-temperature quenching channel is characterized by an activation energy of E₁ ≈ 7–12 meV and is observed for all three bands. This process becomes effective at temperatures above ~140 K. The high-temperature channel is described by an activation energy E₂, which varies significantly for the different bands: 27 meV for J₁ and 125 meV for J₂.

Experimental data show that the intensity of the 3.07 eV band initially decreases, then exhibits a rise in the 120–180 K range, and subsequently undergoes an accelerated decrease above 200 K. Such a dip followed by a peak cannot be explained solely by the two-channel quenching model (Equation (1)). We attribute the observed enhancement to the release of carriers from shallow traps and their subsequent capture by radiative centers. To account for this effect, we introduce a model that explicitly incorporates the contribution of traps.

Let N_t denote the density of trapped carriers in shallow traps, S the attempt frequency for their release, and E_rel the energy required for transition into the conduction band or directly to a radiative center. The probability of carrier release per unit time follows the Arrhenius law:

$$W(T)=s\hspace{0.17em}\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\displaystyle \frac{E_{\mathrm{rel}}}{k_{B}T}}\right),$$

(3)

In the stationary regime, the released carriers increase the generation flux G by an amount ΔG(T) proportional to the exponential term. The effective generation rate therefore becomes:

$$G_{eff}\left(T\right)=G+S\hspace{0.17em}\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\displaystyle \frac{E_{\mathrm{rel}}}{k_{B}T}}\right),$$

(4)

where S depends on both the trap density and the attempt frequency. Substituting G_eff(T) into the intensity Expression (1) yields the modified form:

$$I\left(T\right)={\displaystyle \frac{I_0+S\hspace{0.17em}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{E_{\mathrm{rel}}}{k_{B}T}\right)}{1+B_1\hspace{0.17em}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{E_1}{k_{B}T}\right)+B_2\hspace{0.17em}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{E_2}{k_{B}T}\right)}}.$$

(5)

Physical meaning of the modification: E_rel—the thermal release energy of carriers from shallow traps; for β-Ga₂O₃, analysis of the 100–200 K region yields values of ~10–13 meV, in good agreement with the experimental transition; I₀—the intensity at zero temperature, determined by the concentration of radiative centers; S—the amplitude of the “trap feeding” contribution, reflecting the number of carriers that can be released.

At low temperatures (T << E_rel/k_B), the term $s\hspace{0.17em}\mathrm{e}\mathrm{x}\mathrm{p}\left({-E}_{\mathrm{rel}}/k_{B}T\right)$ is negligible, and Equation (2) reduces to the classical two-channel form (Equation (1)). In the temperature range near E_rel/k_B, this term enhances the numerator, leading to an increase in intensity. At sufficiently high temperatures, quenching via the high-energy channel (E₂) dominates; the numerator essentially saturates, and the intensity decreases. Thermal quenching parameters obtained by using the Expression (4) shown in Figure 4b and

Table 3. Thermal quenching parameters obtained by Equation (5) at J₃ (3.07 eV) band.

Parameters	Value
I0	224,246.9
S	8,261,267.7
Erel (eV)	50 meV
B1	6.51
E1 (eV)	12.6 meV
B2	2097.64
E2 (eV)	122.4 meV

.

For the J₃ band (3.07 eV), two characteristic activation barriers were identified: E₁ = 12.6 meV (shallow quenching channel) and E₂ ≈ 122.4 meV (deep channel), along with an additional energy E_rel = 50 meV associated with carrier release from traps. The latter accounts for the local increase in intensity observed around ≈170 K. The model does not take into account minor oscillations in intensity, which may arise from specific crystallographic trapping sites or experimental uncertainties. Nevertheless, it satisfactorily reproduces the main features of the behavior—namely, the initial decrease up to 100 K, the subsequent minimum, the intermediate maximum, and the final quenching at higher temperatures.

3.5. Broadening of Emission Lines

The temperature dependence of the FWHM for the integral spectrum and for the three individual components is shown in Figure 6. Overall, the width of all bands increases with temperature, which is a typical consequence of the strengthening of electron–phonon coupling. Similarly to the intensity behavior, a change in the FWHM trend is observed around 140 K, where the rate of broadening increases, particularly for the integral spectrum and for band J₃.

For quantitative analysis of this broadening, a single-optical-phonon interaction model was applied according to Equation (3) (

Table 4. Parameters obtained from fitting the temperature dependence of FWHM obtained by Equation (2).

Band	Γ0 (eV)	A (eV)	Eph (meV)	RMSE (meV)
Integral spectra	0.611	0.505	40.2	12
3.07 eV (J3)	0.611	0.369	45.7	65
3.37 eV (J2)	0.487	−0.47	64.0	54
3.55 eV (J1)	0.264	1.351	123.9	25

.). The results of fitting the FWHM data are summarized in Table 3. The model adequately describes the behavior of the integral spectrum and band J₃, for which physically reasonable values of the effective phonon energy E_ph ≈ 40–46 meV were obtained. However, for bands J₁ and J₂, the simple single-phonon model proves insufficient. For band J₂, the fitting yields an unphysical negative value of the coupling constant A, while for band J₁, considerable deviations between the model and the experimental data are observed, indicating a more complex nature of their temperature evolution.

4. Discussion

The temperature-dependent photoluminescence (PL) spectra of the β-Ga₂O₃ single crystals reveal a complex emission profile dominated by a broad UV-blue band that evolves significantly from 7 K to 300 K. Gaussian decomposition identifies three primary components: J₁ at ~3.55 eV, J₂ at ~3.37 eV, and J₃ at ~3.07 eV. These bands align with the established luminescence mechanisms in β-Ga₂O₃, where ultraviolet luminescence (UVL) arises from self-trapped excitons (STE) or recombination of free electrons with self-trapped holes (STH), while blue luminescence (BL) is attributed to donor-acceptor pair (DAP) recombination [42,43,51]. The high-energy J₁ band (~3.55 eV) corresponds to UVL associated with weakly localized states, such as near-band-edge transitions or STE-like centers, consistent with reports of DUVL (~3.9 eV) and UVL (~3.25 eV) components linked to distinct STH configurations at different oxygen sites [18,25]. The intermediate J₂ band (~3.37 eV) may represent a transitional state between STE and DAP processes, while the low-energy J₃ band (~3.07 eV) is characteristic of BL from DAP involving intrinsic defects like oxygen vacancies (V_O) as donors and gallium vacancies (V_Ga) or their complexes (V_O-V_Ga) as acceptors [42,43,80].

The observed redshift of the emission maximum with increasing temperature, accompanied by enhanced contribution from the low-energy tail, indicates thermally driven carrier redistribution among these centers. At low temperatures, the UV component (J₁) dominates due to suppressed nonradiative processes, but as temperature rises, carriers delocalize from shallow traps and transfer to deeper defect states, boosting the BL (J₃) while quenching UVL. This is evidenced by the “isosbestic” point in normalized spectra, suggesting a fixed set of competing channels without new bands emerging [45]. Polarization-dependent PL studies further support this, showing anisotropic excitation of STH states that influence spectral shifts [46,81,82,83,84,85].

Thermal quenching analysis using the multi-channel Mott model (Equation (1)) yields activation energies E₁ ≈ 7–12 meV (low-temperature channel) for all bands and E₂ varying from 27 meV (J₁) to 125 meV (J₂ and λ_max). For J₃, an extended model (Equation (4)) incorporating trap release (E_rel ≈ 50 meV) explains the intensity rise around 120–180 K, attributed to carrier detrapping and subsequent capture by radiative centers. These values compare favorably with literature: UVL quenching energies of 70–90 meV in CL and XEL studies, linked to STE migration over barriers to nonradiative centers like V_Ga⁻³ rather than full delocalization (binding energy ~0.5–0.9 eV) [49,50,51,65]. For BL, the higher E₂ ≈ 122 meV in J₃ aligns with ~0.42–0.48 eV in conductive samples (hole delocalization from acceptors) or ~0.08 eV in resistive ones (electron delocalization from donors), reflecting sample resistivity and defect makeup [42,52]. The two-step quenching in J₁ and J₂ mirrors reports in Si-doped samples (~31–34 meV for donor ionization, ~63–75 meV for nonradiative centers) [49,50].

The temperature-dependent FWHM broadening, fitted to the single-phonon model (Equation (2)), provides effective phonon energies E_ph ≈ 40–46 meV for the integral spectrum and J₃, consistent with Raman modes (~20–100 meV) and strong electron–phonon coupling (Huang-Rhys factor S ~9–39) in β-Ga₂O₃ [45,51,66,67]. The model’s limitations for J₁ and J₂ (unphysical A for J₂, high RMSE for J₁ with E_ph ≈ 124 meV) suggest additional inhomogeneous broadening or multi-phonon contributions, as seen in nanowires and doped ceramics [47,48]. The ~140 K transition in both intensity and FWHM trends marks a shift from low-T dominance of weakly localized centers to high-T prevalence of deep defects and phonon-driven processes.

These findings underscore the role of intrinsic defects in governing luminescence efficiency, with implications for optimizing β-Ga₂O₃ for optoelectronics and scintillators.

5. Conclusions

This comprehensive study of temperature-dependent photoluminescence in β-Ga₂O₃ single crystals elucidates key recombination mechanisms and thermal quenching pathways. The emission spectra decompose into three Gaussian bands (3.55 eV, 3.37 eV, 3.07 eV) attributed to STE/UVL and DAP/BL processes, with thermal redistribution favoring deeper defect states at higher temperatures. Activation energies of 7–12 meV (shallow quenching) and up to 125 meV (deep channels), plus a 50 meV trap release for the blue band, align with defect migration and delocalization models. Phonon energies of ~40–46 meV from FWHM analysis confirm strong electron–phonon interactions driving spectral broadening. These insights advance understanding of defect dynamics in β-Ga₂O₃, paving the way for improved device performance in high-temperature and radiation environments.