Optimization and Prediction of Mass Loss During Adhesive Wear of Nitrided AISI 4140 Steel Parts
Abstract
1. Introduction
2. Materials and Methods
2.1. Material and Treatments
2.2. Methodology
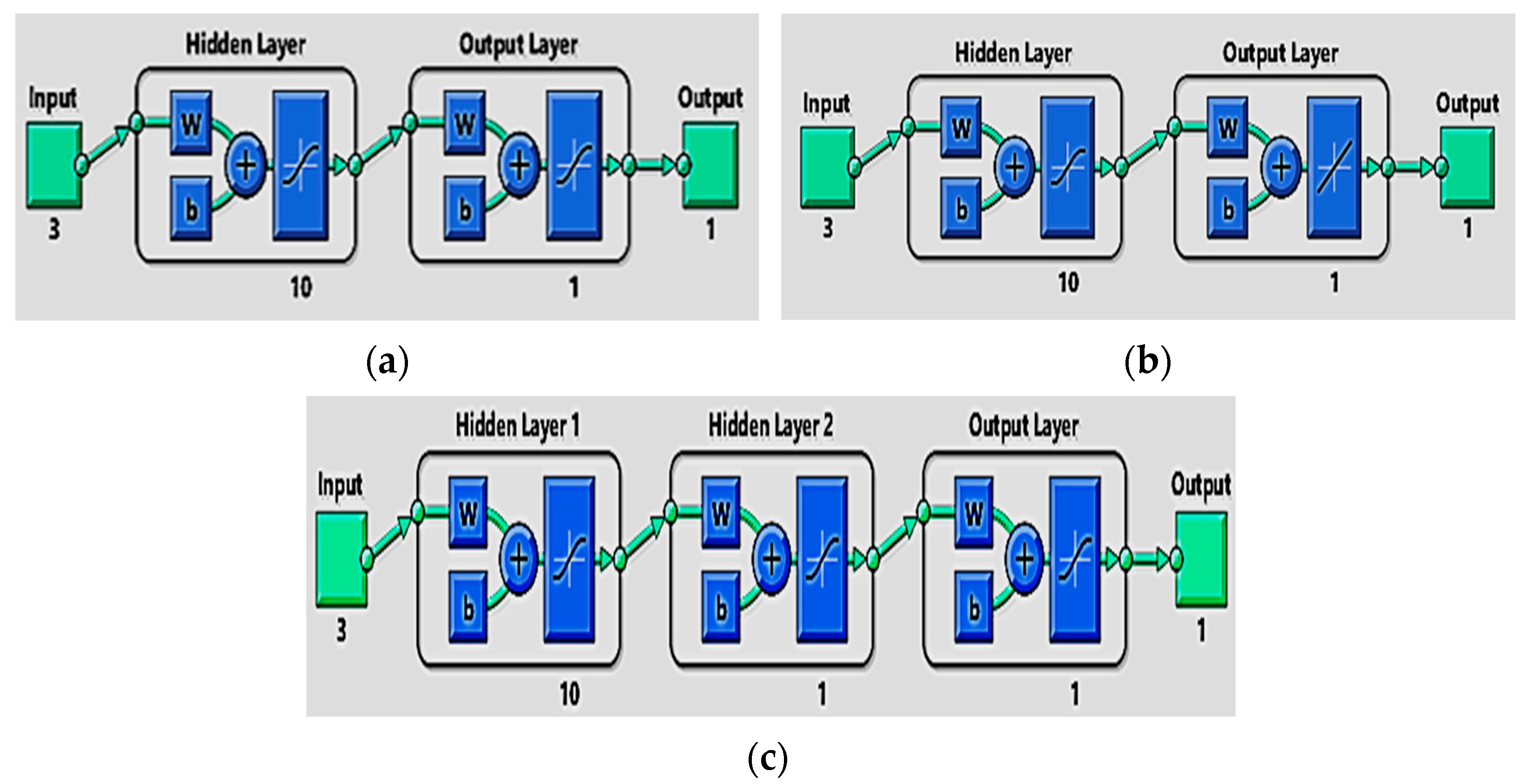
2.3. Prediction by Neural Network
- -
- Hyperbolic: an S-shaped mathematical function, takes real values as input and returns values between −1 and 1, it improves data symmetry and often accelerates convergence.
- -
- Sigmoid: also S-shaped, takes real values as input and returns values between 0 and 1, chosen for its ability to model nonlinear relationships and compress values into the [0, 1] range, which facilitates convergence and stabilizes the learning process.
- -
- Linear: returns the same value that it receives as input and is often used in the last layer of a neural network for regression tasks. it allows the network to reproduce quasi-linear relationships and serves as a benchmark against nonlinear functions.
- -
- TRAINLM: learning by the Levenberg–Marquardt algorithm (quasi-Newton method), known for its speed and accuracy in nonlinear regression problems, particularly suitable for medium-sized networks.
- -
- TRAINSCG: learning by scaled conjugate gradient (SCG) that is more memory-efficient and suitable for larger or more complex networks,
- -
- TRAINBR: version of trainlm but with automatic weight moderation, that incorporates automatic weight regularization, reducing the risk of over fitting and improving generalization capability. The architecture and details of the neural network are illustrated in Table 5. The internal architecture of the three layers is illustrated in Figure 2.
3. Results
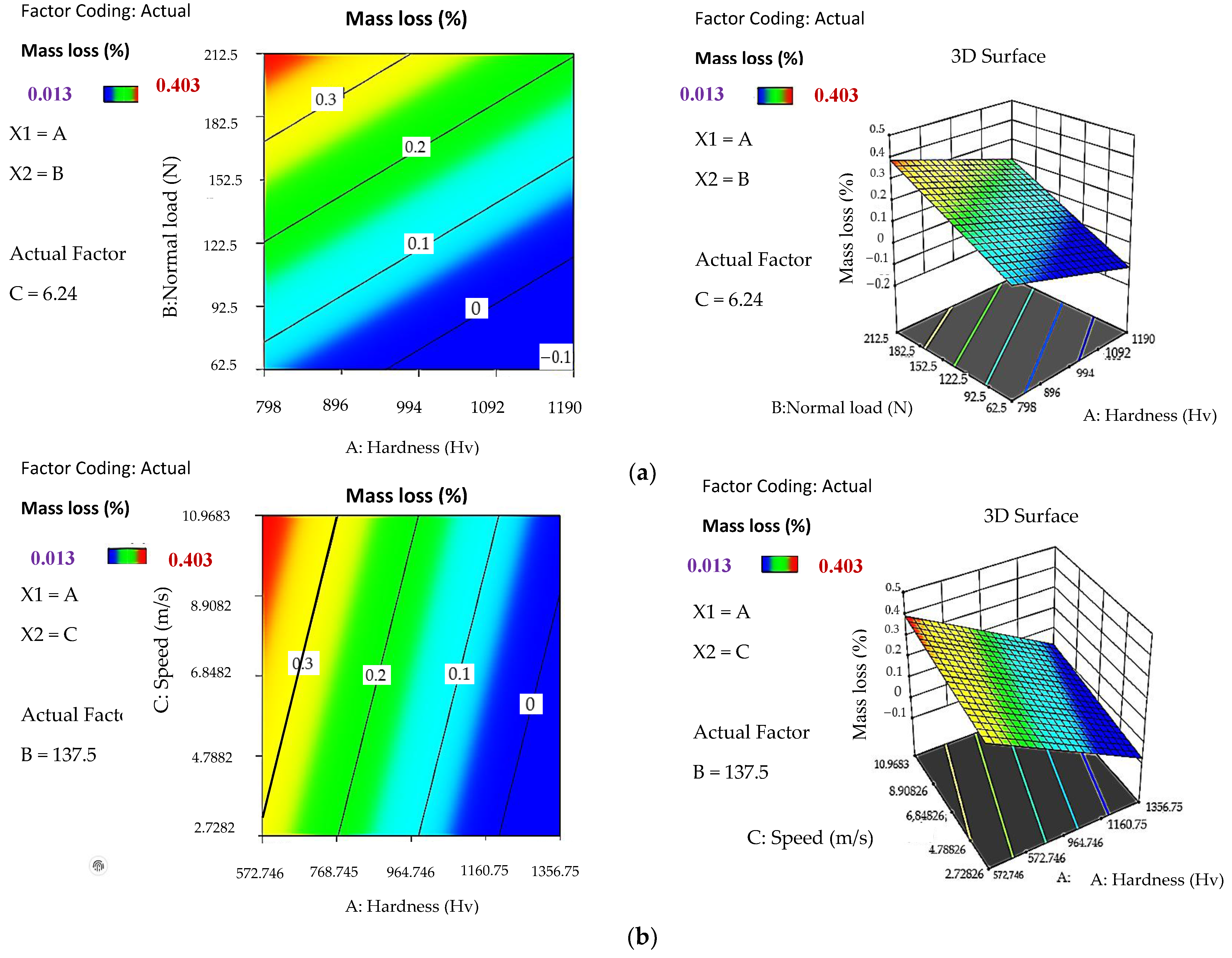
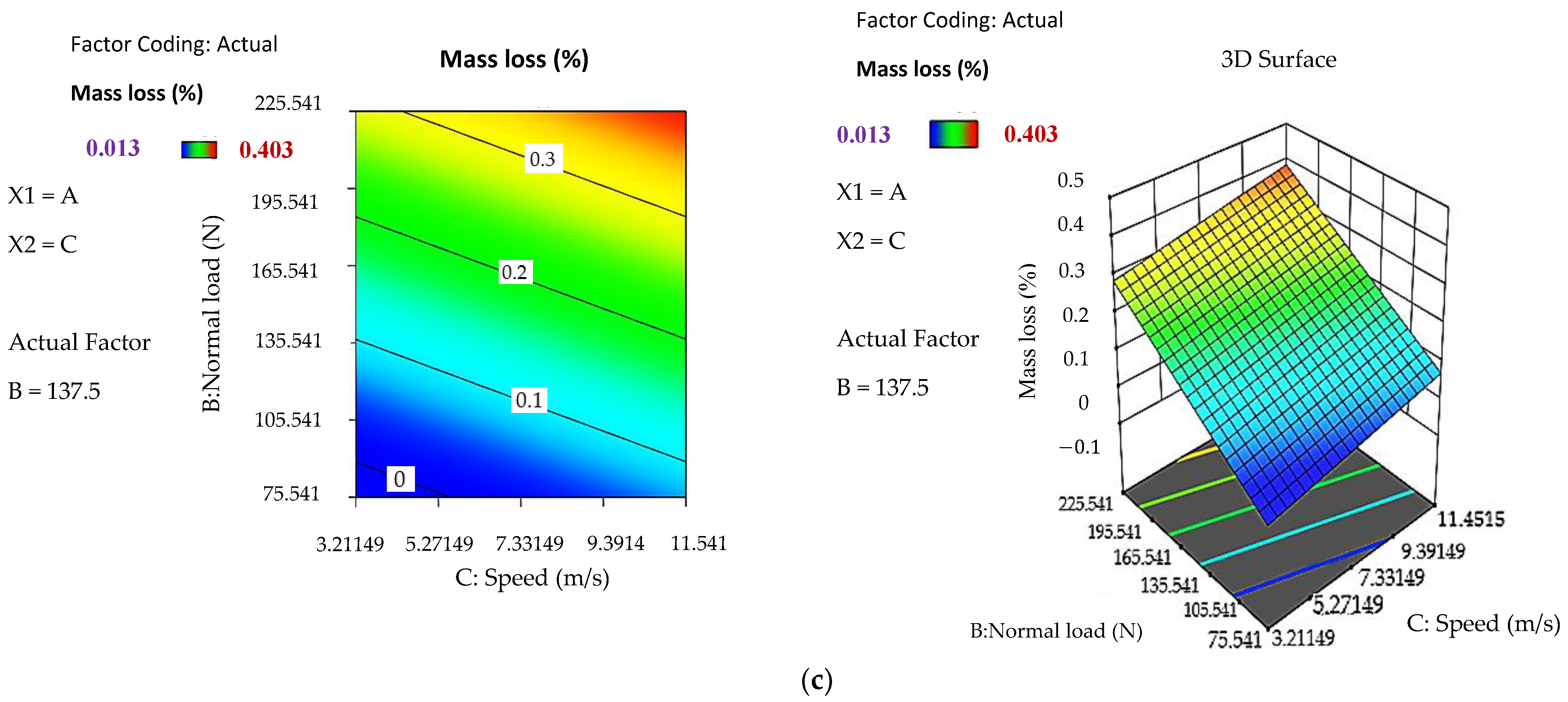
3.1. Surfaces Responses
3.2. Regression Equation
3.3. RSM Method
3.3.1. Regression Models
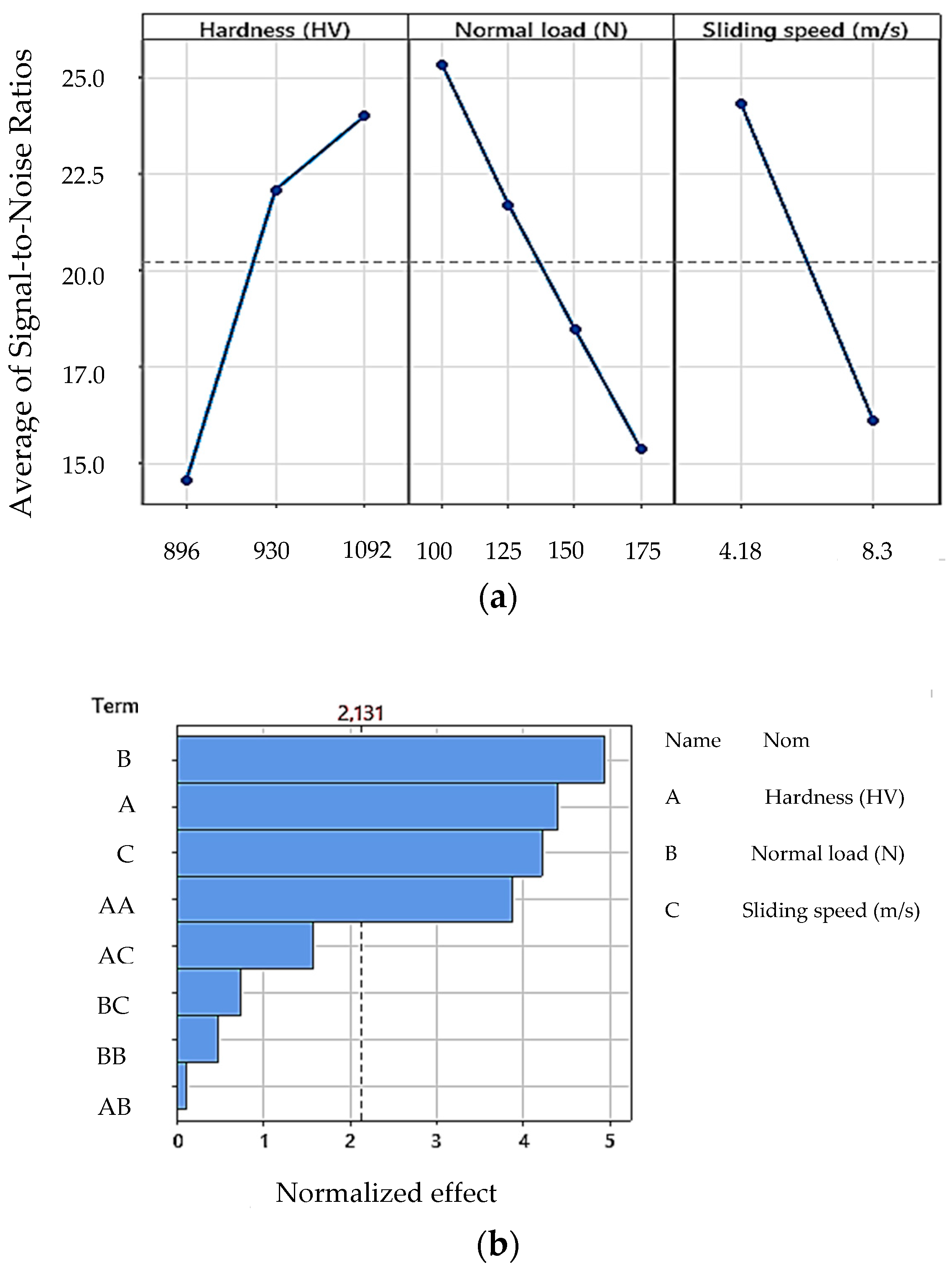
3.3.2. Effect of Independent Variables on Mass Loss
3.4. Artificial Neural Network Models
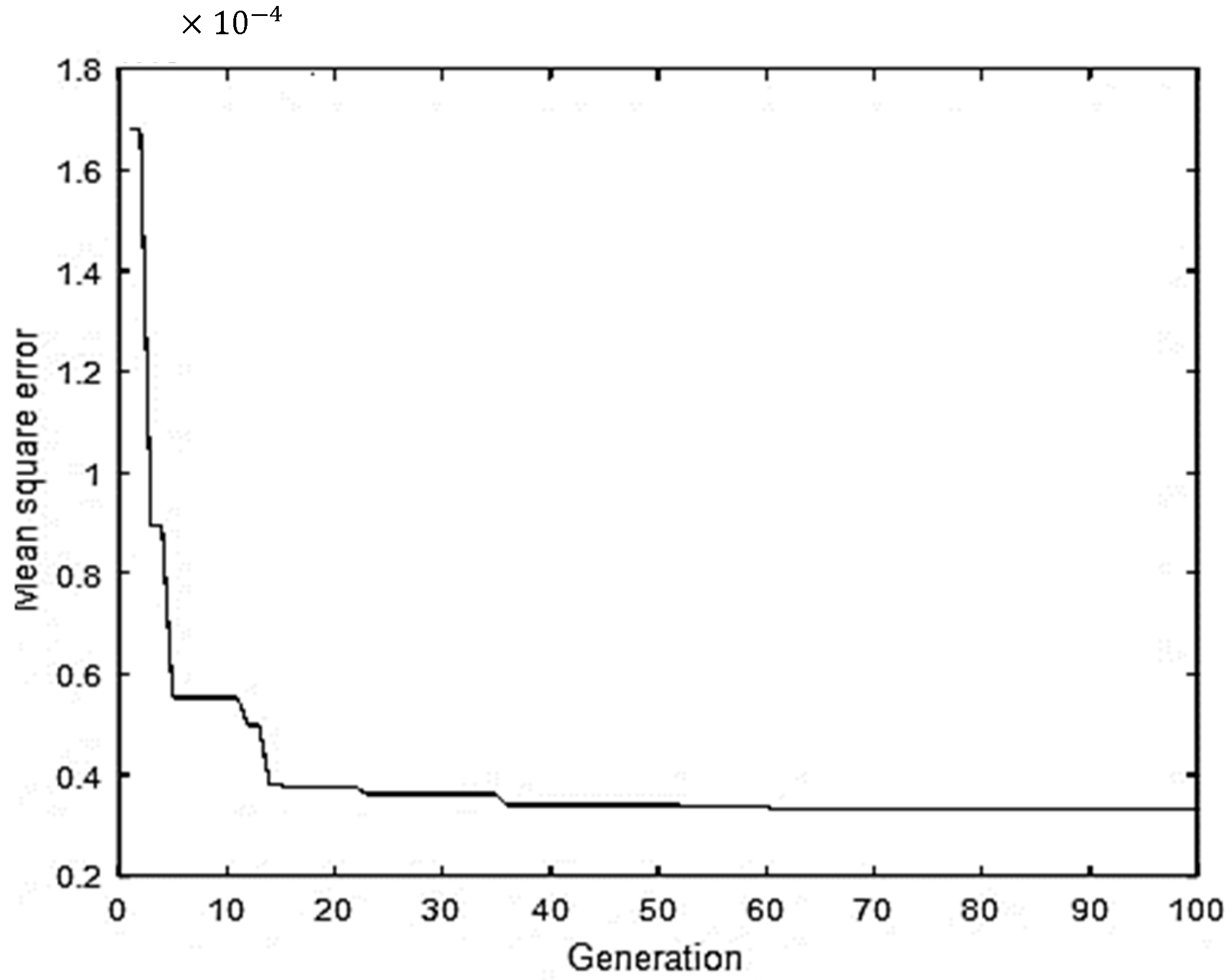
3.4.1. Prediction
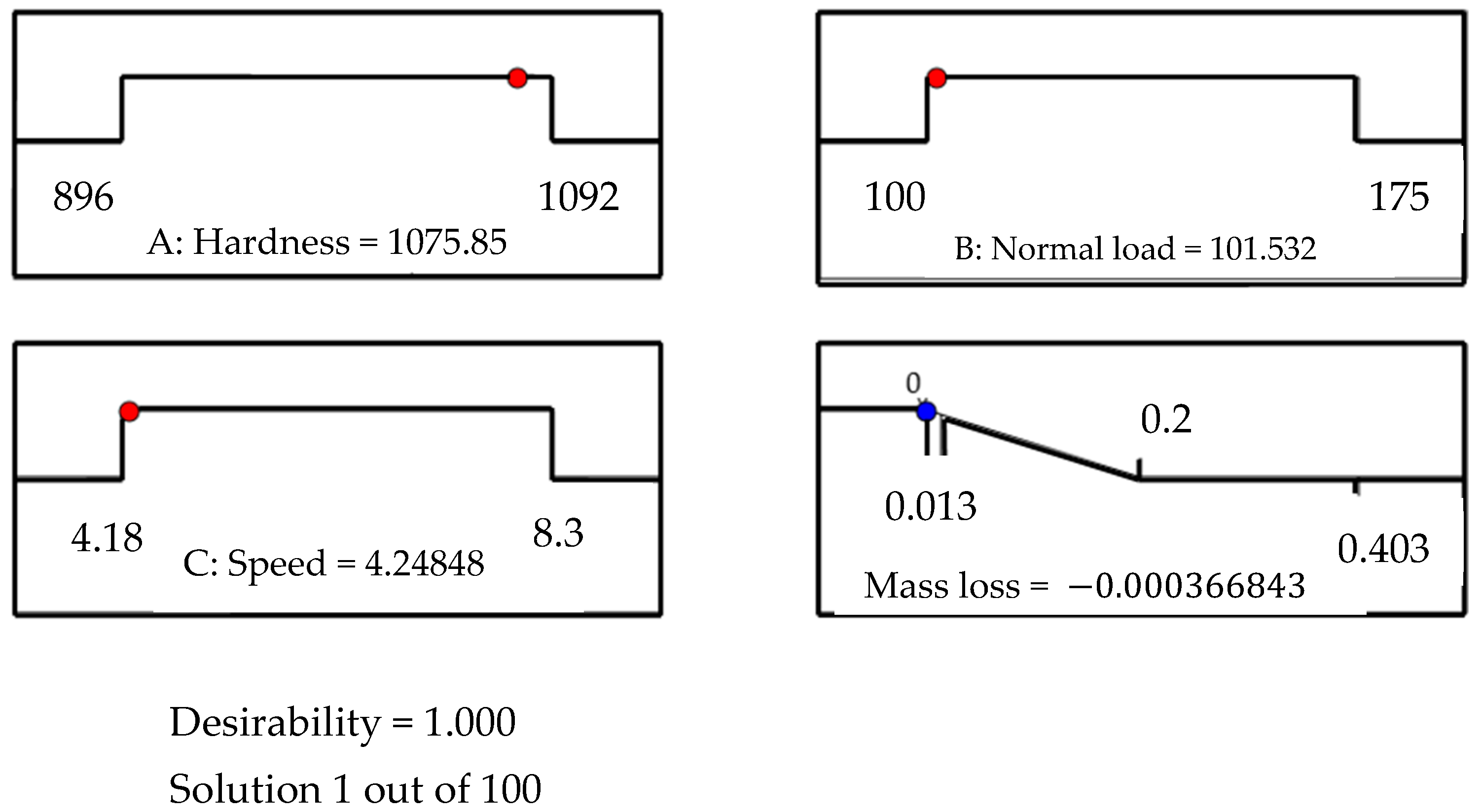
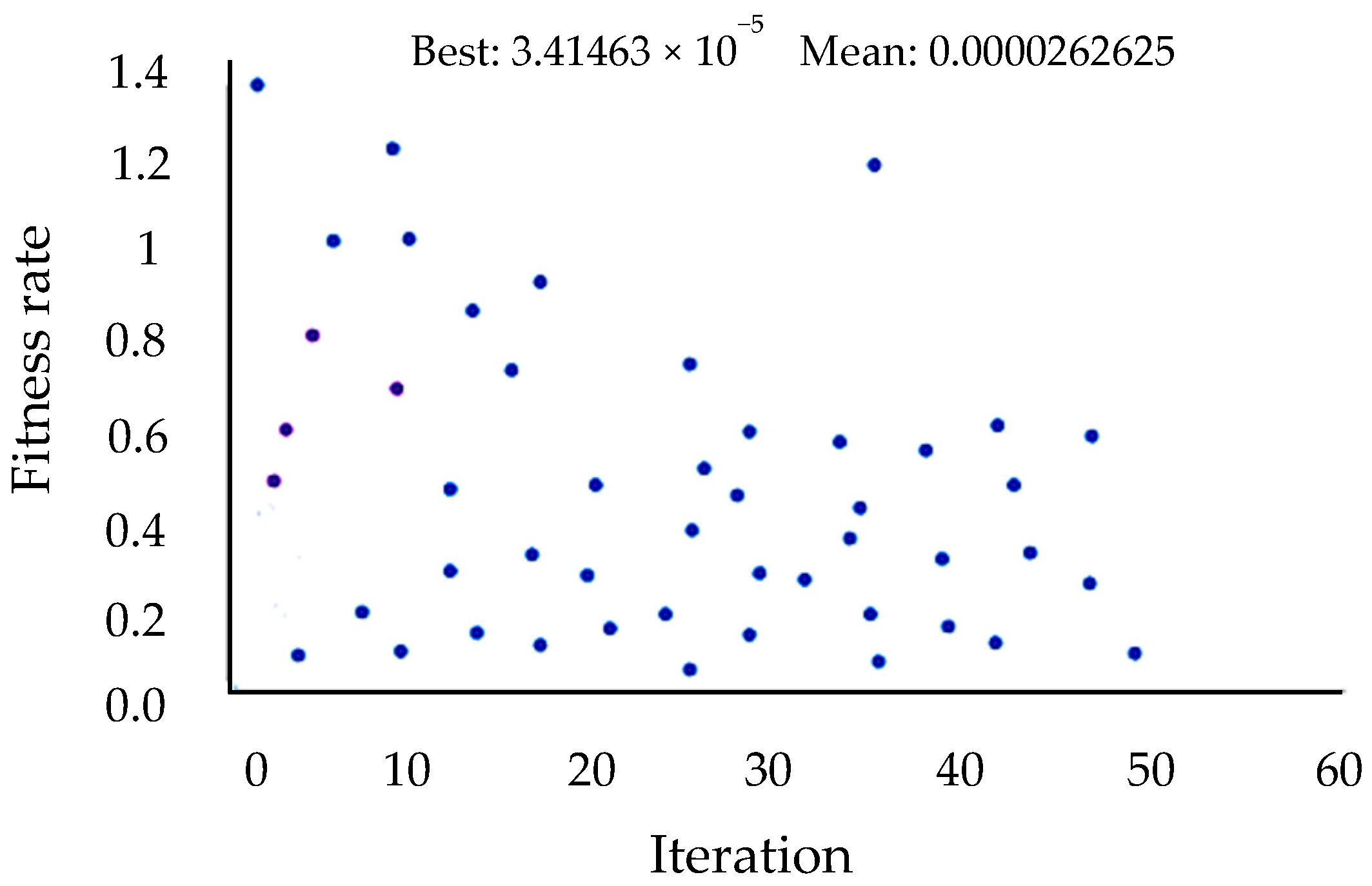
3.4.2. Optimization of the Prediction by Neural Network
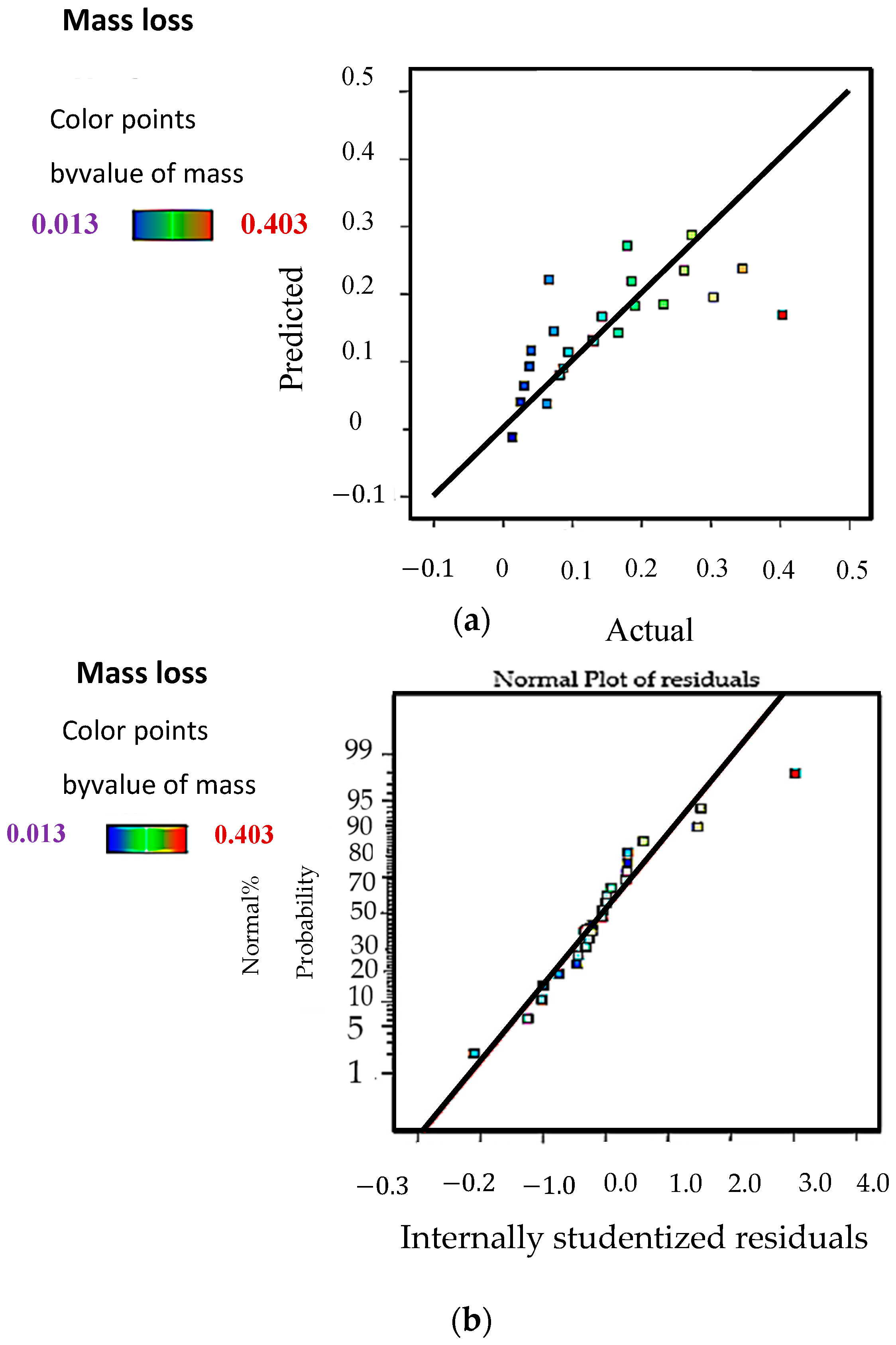
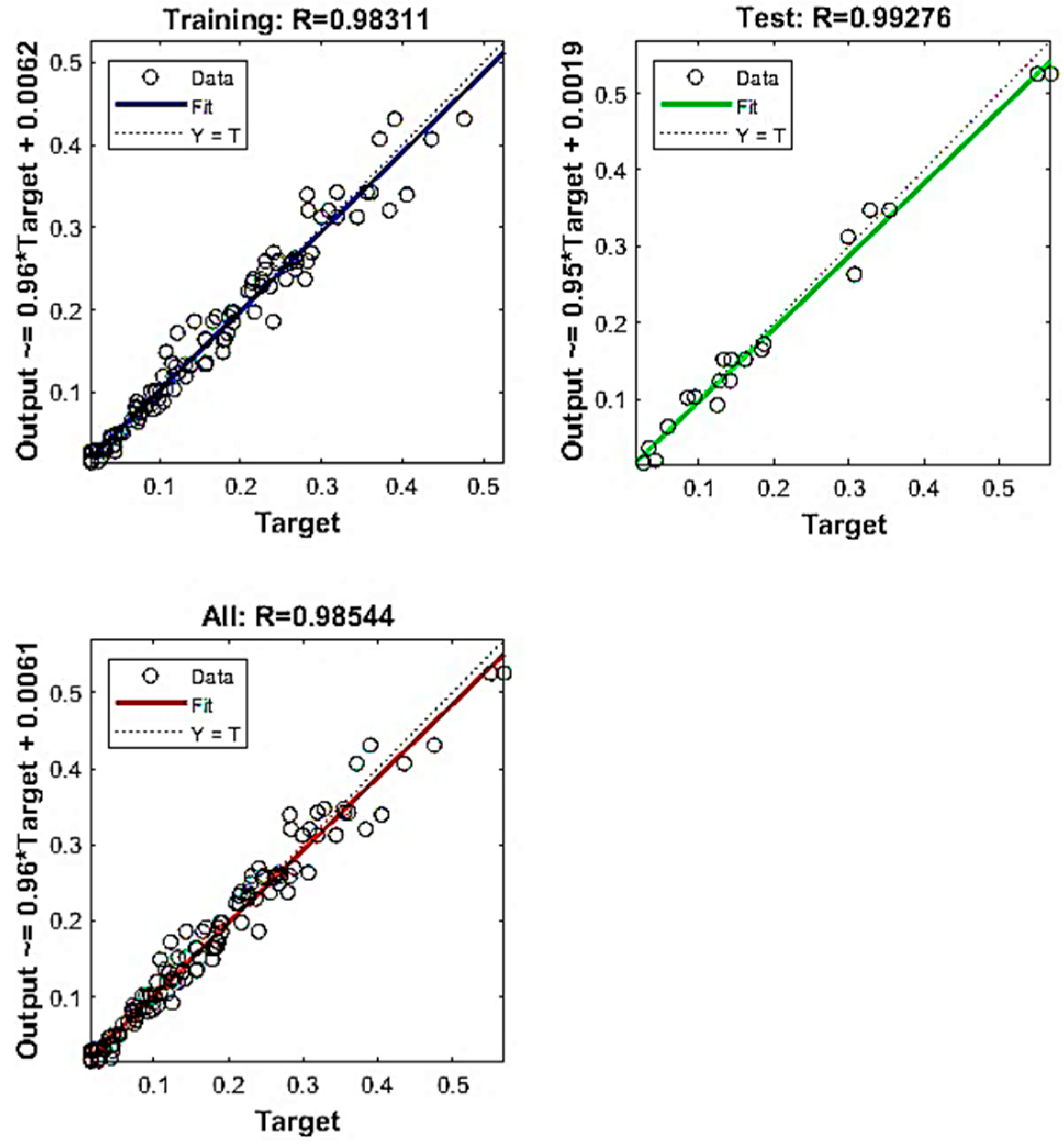
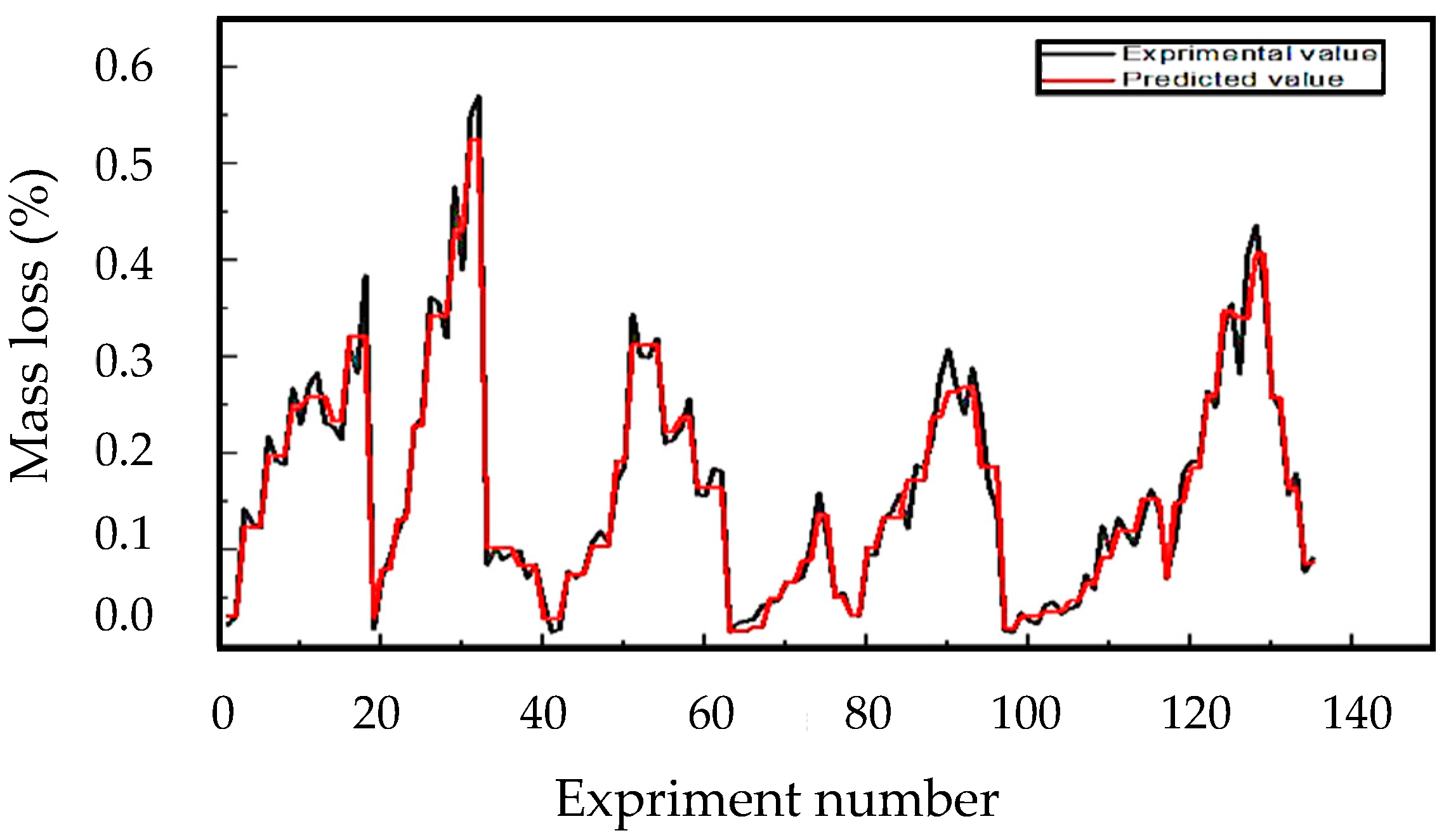
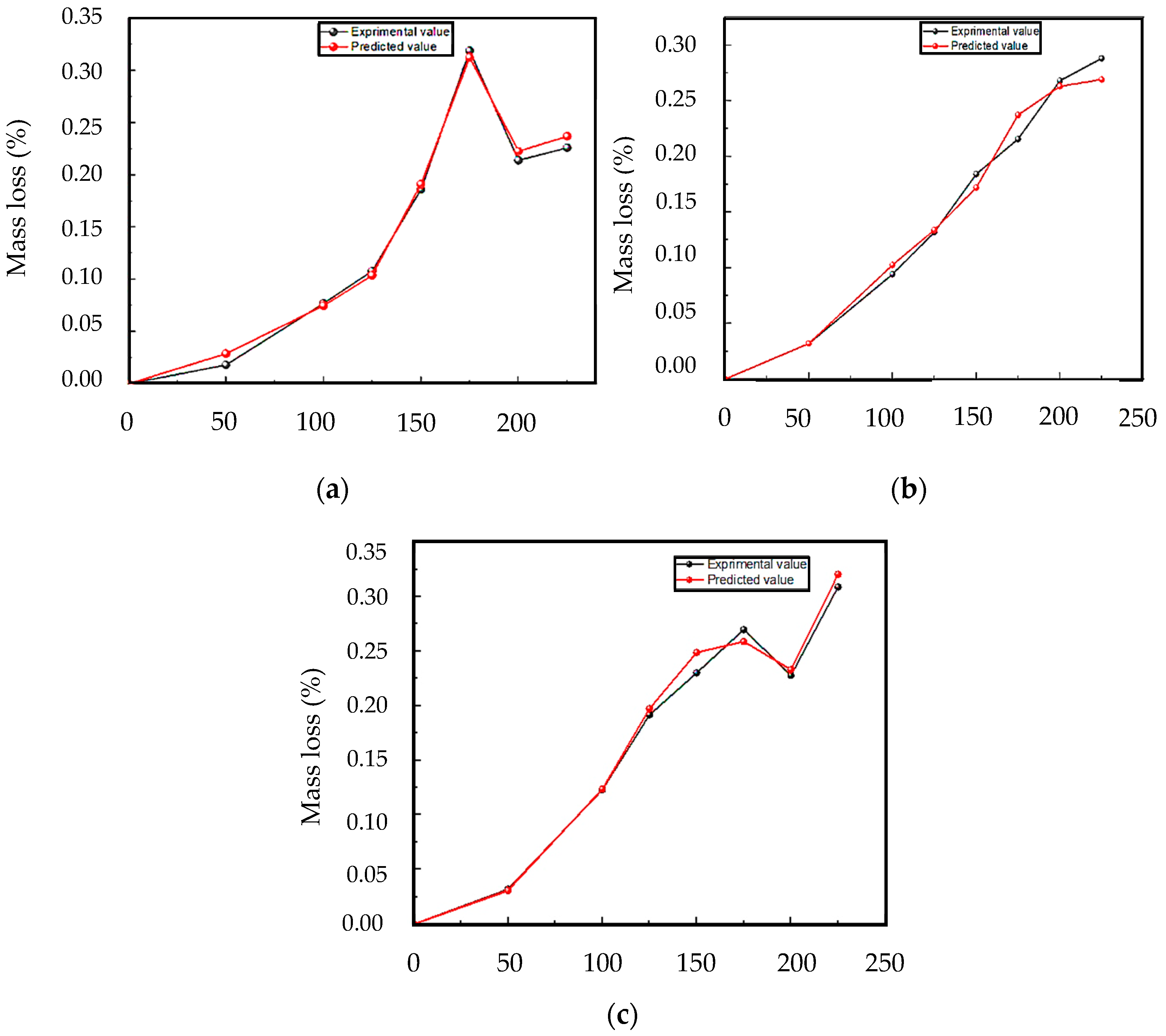
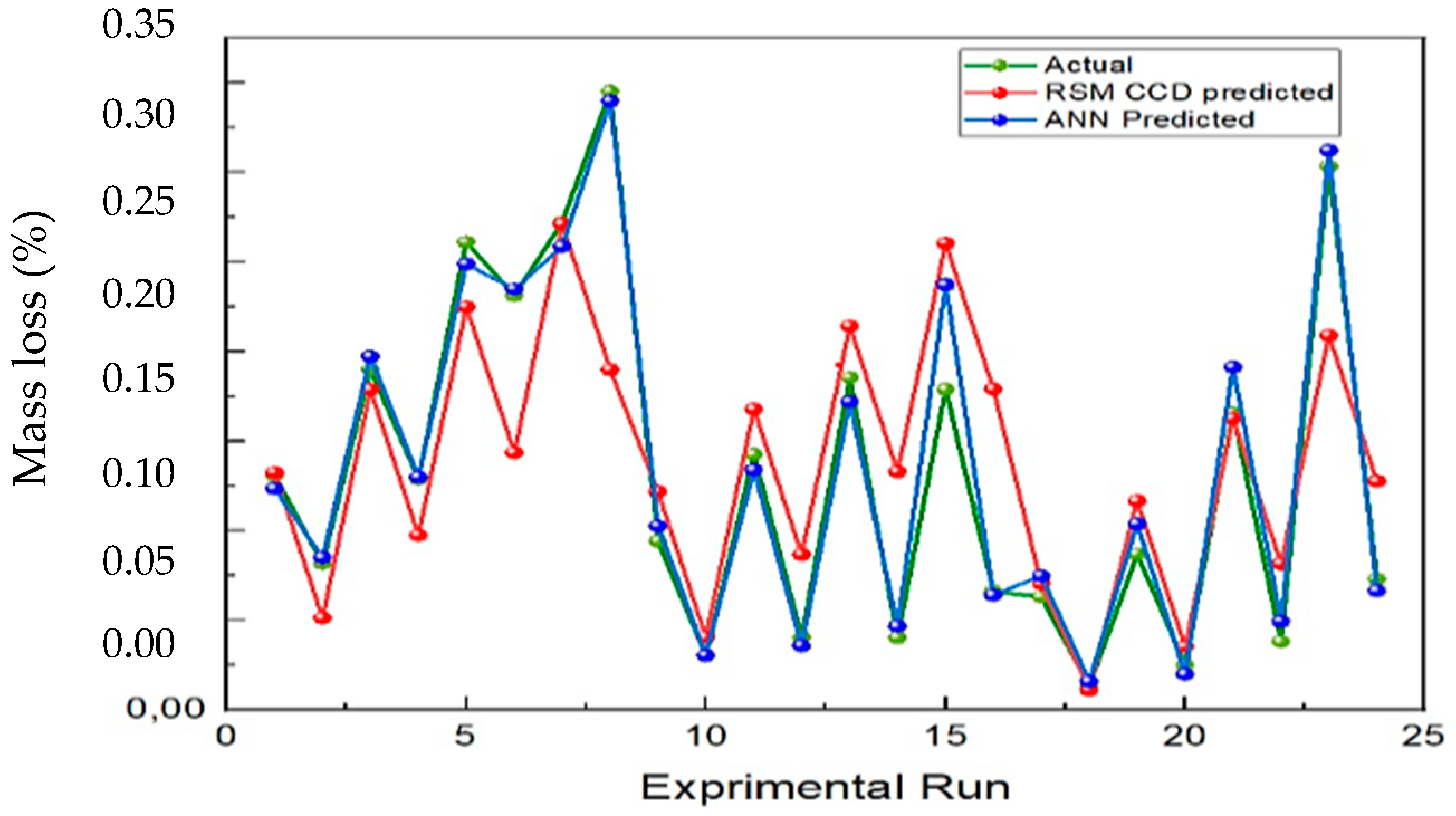
3.4.3. Comparison of Predicted and Experimental Values
4. Conclusions
- The objective of this study was to analyze the effect of normal load, hardness, and sliding speed on mass loss during the adhesive wear of AISI 4140 steel. The experimental method was based on a design of experiments, while the numerical approach relied on artificial neural networks. The analysis demonstrated that all three parameters were found to be significant. The normal load was identified as the most influential factor, followed by hardness and speed. The maximum mass loss was observed at a load of 175 N, whereas the minimum mass loss was obtained at a hardness of 895 HV.
- The significance of hardness was highlighted by the observation that gas nitriding for 24 h enabled the attainment of an optimal hardness level, thereby minimizing mass loss while ensuring satisfactory resistance and durability. Conversely, excessive nitriding (930 HV for 36 h) resulted in nitrogen saturation, leading to the inefficient use of time and resources. These findings emphasize the importance of meticulously controlling nitriding parameters to circumvent inefficient and costly treatments.
- In the initial phase, the quadratic regression equation was obtained by employing the Central Composite Design Response Surface Methodology (CCD RSM). However, the initial results did not achieve an acceptable level of accuracy. In order to enhance the efficacy of the aforementioned equation, a novel approach was adopted. This entailed the utilization of a genetic algorithm, a sophisticated computational methodology, to randomly vary the equation’s variables through a multitude of iterations, numbering in the hundreds. This optimization had a substantial impact on the robustness of the regression model, enabling it to attain a satisfactory level of precision.
- The predictive analysis employing artificial neural networks (ANN) demonstrated that optimal outcomes were attained with a hyperbolic activation function, the trainbr algorithm, three hidden layers, and 11 neurons at epoch 27. The ANN method yielded highly accurate results, demonstrating excellent agreement with the experimental data. Conversely, the genetic algorithm, when utilized as a standalone predictive instrument, was determined to possess a reduced degree of accuracy in the context of modeling adhesive wear.
- From an industrial perspective, the present study proposes a predictive tool capable of anticipating mass loss without the necessity for systematic experimental testing. This will result in time and cost savings for precision engineering industries. The findings can be directly applied to optimize nitriding conditions and wear parameters in real applications, particularly for gears, shafts, and components operating under dry sliding conditions.
- In terms of future research, it would be valuable to extend this approach to other wear mechanisms (abrasive, corrosive), to different alloyed steels, and to integrate more advanced neural network architectures (deep learning, convolutional networks) to further improve predictive accuracy. Furthermore, experimental validation under real industrial conditions would enhance the transferability and practical relevance of the proposed methodology.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, B.; Zhao, X.; Li, W.; Qin, M.; Gu, J. Effect of nitrided-layer microstructure control on wear behavior of AISI H13 hot work die steel. Appl. Surf. Sci. 2017, 431, 39–43. [Google Scholar] [CrossRef]
- Kumar, A.; Kaur, M.; Joseph, A.; Jhala, G.; Nanda, T.; Singh, S. High-Temperature Wear and Frictional Performance of Plasma-Nitrided AISI H13 Die Steel. Lubricants 2023, 11, 448. [Google Scholar] [CrossRef]
- Zambrano, O.A.; Aguilar, Y.; Valdés, J.; Rodríguez, S.A.; Coronado, J.J. Effect of Normal Load on Adhesive Wear Resistance and Wear Micro-mechanisms in FeMnAlC. Alloy and Other Austenitic Steels. Wear 2016, 348–349, 61–68. [Google Scholar] [CrossRef]
- González-Pociño, A.; Alvarez-Antolin, F.; Peral-Martinez, L.B. Effects of Nitriding and Thermal Processing on Wear and Corrosion Resistance of Vanadis 8 Steel. Coatings 2024, 14, 1066. [Google Scholar] [CrossRef]
- Straffelini, G.; Avi, G.; Pellizzari, M. Effect of three nitriding treatments on tribological performance of 42CrAlMo7 steel in boundary lubrication. Wear 2002, 252, 870–879. [Google Scholar] [CrossRef]
- Panfil-Pryka, D.; Kulka, M.; Kotkowiak, M.; Michalski, J.; Grochalski, K. Tribological Behavior of Gas-Nitrided 42CrMo4 Steel at Elevated Temperatures. Coatings 2025, 15, 18. [Google Scholar] [CrossRef]
- Terres, M.A.; Bechouel, R.; Ben Mohamed, S. Low Cycle Fatigue Behavior of Nitrided Layer of 42CrMo4 Steel. Int. J. Mater. Sci. 2017, 6, 18–27. [Google Scholar]
- Pérez, H.; Vargas, G.; Magdaleno, C.; Silva, R. Oxy-Nitriding AISI 304 Stainless Steel by Plasma Electrolytic Surface Saturation to Increase Wear Resistance. Metals 2023, 13, 309. [Google Scholar] [CrossRef]
- Terres, M.A.; Sidhom, H.; Larbi, A.B.C.; Ouali, S.; Lieurade, H.P. Influence de la résistance à la fissuration de la couche de combinaison sur la tenue en fatigue des composants nitrurés. Matériaux Tech. 2001, 89, 23–36. [Google Scholar] [CrossRef]
- Özkan, D.; Yilmaz, M.A.; Karakurt, D.; Szala, M.; Walczak, M.; Bakdemir, S.A.; Türküz, C.; Sulukan, E. Effect of AISI H13 Steel Substrate Nitriding on AlCrN, ZrN, TiSiN, and TiCrN Multilayer PVD Coatings Wear and Friction Behaviors at a Different Temperature Level. Materials 2023, 16, 1594. [Google Scholar] [CrossRef]
- Lu, X.; Jia, Z.; Wangand, H.; Liang, S.Y. The Effect of Cutting Parameters on Microhardness and the Prediction of Vickers Hardness Based on a Response Surface Methodology for Micro-milling Inconel 718. Measurement 2019, 140, 56–62. [Google Scholar] [CrossRef]
- Vikram, S.; Pradhan, S.K. Optimisation des paramètres WEDM à l’aide de la technique Taguchi et de la méthodologie de surface de réponse dans l’usinage de l’acier AISI D2. Procedia Eng. 2014, 97, 1597–1608. [Google Scholar]
- Singh, V.; Pradhan, S.K. Optimization of WEDM parameters using Taguchi technique and Response Surface Methodology in machining of AISI D2 Steel. Procedia Eng. 2017, 97, 1597–1608. [Google Scholar] [CrossRef]
- Singh, A.P.; Singh, D.K. SinghMulti response optimization for micro-EDM machining of AISI D2 die steel using RSM and neural network. Mater. Today Proc. 2023, 43, 1449–1455. [Google Scholar] [CrossRef]
- Shebani, A.; Iwnicki, S. Prediction of wheel and rail wear under different contact conditions using artificial neural networks. Wear 2018, 406–407, 173–184. [Google Scholar] [CrossRef]
- Palavar, O.; Özyürek, D.; Kalyon, A. Artificial neural network prediction of aging effects on the wear behavior of IN706 superalloy. J. Mater. Res. Technol. 2018, 7, 456–467. [Google Scholar] [CrossRef]
- Ebrahimi, M.; Mahboubi, F.; Naimi-jamal, M.R. RSM Base Study of the Effect of Deposition Temperature and Hydrogen Flow on the Wear Behavior of DLC Films; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar] [CrossRef]
- Segu, D.Z.; Kim, J.-H.; Choi, S.G.; Jung, Y.-S.; Kim, S.S. Application of Taguchi Techniques to Study Friction and Wear Properties of MoS2 Coatings Deposited on Laser Textured Surface. Surf. Coat. Technol. 2013, 232, 504–514. [Google Scholar] [CrossRef]
- Ravikumar, K.S.; Chethan, Y.D.; Likith, C.; Chethan, S.P. Prediction of wear characteristics for Al-MnO2 nanocomposites using artificial neural network (ANN). J. Mater. Res. Technol. 2023, 12, 456–467. [Google Scholar] [CrossRef]
- Laouissi, A.; Nouioua, M.; Yallese, M.A.; Abderazek, H.; Maouche, H.; Bouhalais, M.L. Machinability study and ANN-MOALO-based multi-response optimization during Eco-Friendly machining of EN-GJL-250 cast iron. Int. J. Advan. Man. Technol. 2021, 117, 1179–1192. [Google Scholar] [CrossRef]
- Laouissi, A.; Yallese, M.A.; Belbah, A.; Belhadi, S.; Haddad, A. Investigation, modeling, and optimization of cutting parameters in turning of gray cast iron using coated and uncoated silicon nitride ceramic tools. Based on ANN, RSM, and GA optimization. Int. J. Advan. Man. Techol. 2019, 101, 523–548. [Google Scholar] [CrossRef]
- Sada, S.O. Improving the predictive accuracy of artificial neural network (ANN) approach in a mild steel turning operation. Int. J. Advan. Man. Techol. 2021, 112, 2389–2398. [Google Scholar] [CrossRef]
- Souid, A.; Jomaa, W.; Terres, M.A. Artificial neural network-based modeling and prediction of white layer formation during hard turning of steels. Matériaux Tech. 2024, 112, 304. [Google Scholar]
- Long, R.; Hou, J.; Zhang, Y.; Shang, Q.; Ma, C.; Pape, F.; Marian, M. From Experimentation to Optimization: Surface Micro-Texturing for Low-Friction and Durable PTFE–Steel Interfaces under Full-Film Lubrication. Polymers 2024, 16, 3505. [Google Scholar] [CrossRef]
- Huang, Q.; Shi, X.; Xue, Y.; Zhang, K.; Wu, C. Optimization of bionic textured parameters to improve the tribological performance of self-lubricating AISI 4140 composite using response surface methodology. Tribol. Int. 2021, 161, 107104. [Google Scholar] [CrossRef]
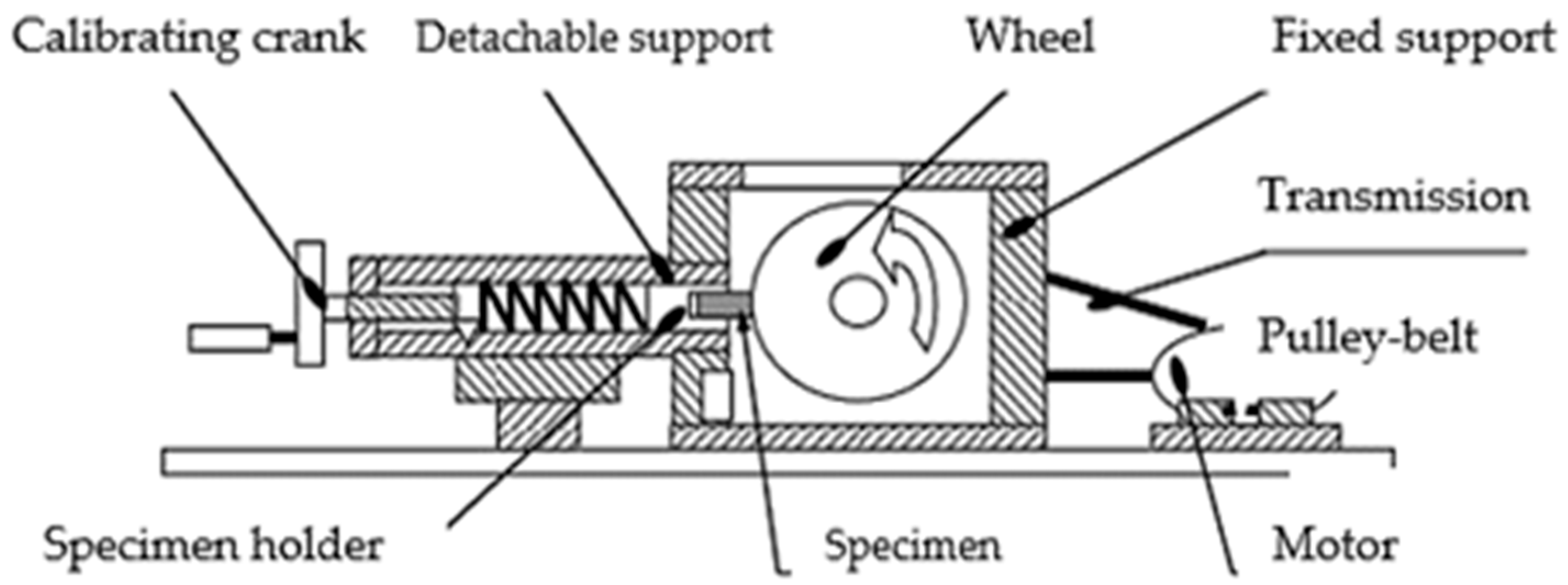
| Elements | Cr | Mn | C | Si | Cu | Mo | Ni | S | P | Fe |
|---|---|---|---|---|---|---|---|---|---|---|
| (%) | 1.02 | 0.77 | 0.41 | 0.28 | 0.25 | 0.16 | 0.16 | 0.026 | 0.019 | Bal. |
| State | Treatment Conditions | Microhardness | ||
|---|---|---|---|---|
| θn (°C) | t (h) | τ (%) | HV | |
| NG12 | 525 | 12 | 35 | 895 |
| NG24 | 24 | 1090 | ||
| NG36 | 36 | 930 | ||
| Factors | Type | Levels | Values |
|---|---|---|---|
| Normal load (N) | Continuous | 4 | 100–125–150–175 |
| Hardness (HV) | Continuous | 3 | 895–930–1092 |
| Speed (m/s) | Continuous | 2 | 4.18–8.30 |
| Parameter | Tested Values | Mean (g) | Std. Dev. | 95% Confidence Interval | Pooled Std. Dev. |
|---|---|---|---|---|---|
| Hardness (HV) | 896 | 0.2052 | 0.0885 | (0.1434; 0.2670) | 0.0840 |
| 930 | 0.0973 | 0.0638 | (0.0355; 0.1591) | ||
| 1092 | 0.0961 | 0.0963 | (0.0343; 0.1578) | ||
| Normal load (N) | 100 | 0.0688 | 0.0431 | (−0.0038; 0.1415) | 0.0853 |
| 125 | 0.1024 | 0.0634 | (0.0297; 0.1750) | ||
| 150 | 0.1537 | 0.0948 | (0.0811; 0.2792) | ||
| 175 | 0.2065 | 0.1194 | (0.1338; 0.2792) | ||
| Speed (m/s) | 4.18 | 0.0928 | 0.0995 | (0.0398; 0.1458) | 0.0885 |
| Factors | Hardness (HV)–Normal Load (N)–Speed (m/s) |
|---|---|
| Response | Mass loss (%) |
| Activation function | Sigmoid–Hyperbolic–Linear |
| Learning algorithms | Trainlm–Trainbr–Trainscg |
| Number of layers | 1–2–3 |
| Number of neurons | 10–11–12 |
| Data report | 70–15–15 |
| Tool | Matlab 2019a |
| Level | Hardness (HV) | Normal Load (N) | Speed (m/s) |
|---|---|---|---|
| 1 | 14.57 | 25.34 | 24.34 |
| 2 | 22.10 | 21.71 | 16.10 |
| 3 | 24.01 | 18.48 | - |
| 4 | - | 15.36 | - |
| Delta | 9.44 | 9.98 | 8.24 |
| Rank | 2 | 1 | 3 |
| Source | Sum of Square | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 0.1367 | 3 | 0.0456 | 6.84 | 0.0024 |
| A-Hardness | 0.0391 | 1 | 0.0391 | 5.87 | 0.0251 |
| B-Normal load | 0.0827 | 1 | 0.0827 | 12.40 | 0.0021 |
| C-Speed | 0.0149 | 1 | 0.0149 | 2.24 | 0.1498 |
| Residual | 0.1333 | 20 | |||
| Cor total | 0.2699 | 23 |
| Configuration | Results | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Activation Function | Algorithms | Number of Layers | Number of Neurons | Training | Test | Validation | R | MSE | RMSE |
| Sigmoid | Trainlm | 1 | 12 | 0.9720 | 0.9805 | 0.9730 | 0.9721 | 0.0007 | 0.0275 |
| Trainlm | 2 | 12 | 0.9827 | 0.9816 | 0.9822 | 0.9814 | 0.0005 | 0.0022 | |
| Trainlm | 3 | 10 | 0.9854 | 0.9949 | 0.9835 | 0.9878 | 0.0004 | 0.02 | |
| Sigmoid | Trainscg | 1 | 11 | 0.9336 | 0.9795 | 0.9533 | 0.9419 | 0.0015 | 0.0398 |
| Trainscg | 2 | 10 | 0.9609 | 0.9870 | 0.9720 | 0.9649 | 0.0009 | 0.0308 | |
| Trainscg | 3 | 12 | 0.9540 | 0.9525 | 0.9818 | 0.9750 | 0.0015 | 0.0039 | |
| Sigmoid | Trainbr | 1 | 10 | 0.9836 | 0.9759 | - | 0.9843 | 0.0004 | 0.0213 |
| Trainbr | 2 | 12 | 0.9831 | 0.9927 | - | 0.9878 | 0.0003 | 0.0179 | |
| Trainbr | 3 | 10 | 0.9867 | 0.9845 | - | 0.9859 | 0.0003 | 0.0195 | |
| Hyperbolic | Trainlm | 1 | 10 | 0.9887 | 0.9810 | 0.9757 | 0.9842 | 0.0004 | 0.2147 |
| Trainlm | 2 | 12 | 0.9825 | 0.9938 | 0.9904 | 0.9839 | 0.0005 | 0.0229 | |
| Trainlm | 3 | 10 | 0.9810 | 0.9973 | 0.9947 | 0.9859 | 0.0004 | 0.0219 | |
| Hyperbolic | Trainscg | 1 | 10 | 0.9660 | 0.9573 | 0.9652 | 0.9616 | 0.0010 | 0.0318 |
| Trainscg | 2 | 12 | 0.9539 | 0.9869 | 0.9701 | 0.9596 | 0.0011 | 0.0336 | |
| Trainscg | 3 | 10 | 0.9547 | 0.9808 | 0.9815 | 0.9583 | 0.0010 | 0.0327 | |
| Hyperbolic | Trainbr | 1 | 12 | 0.9814 | 0.9731 | - | 0.9842 | 0.0004 | 0.0214 |
| Trainbr | 2 | 12 | 0.9877 | 0.9889 | - | 0.9854 | 0.0004 | 0.0200 | |
| Trainbr | 3 | 11 | 0.9852 | 0.9903 | - | 0.9859 | 0.0003 | 0.0196 | |
| Linear | Trainlm | 1 | 11 | 0.8033 | 0.8033 | 0.8033 | 0.8247 | 0.0044 | 0.02 |
| Trainlm | 2 | 11 | 0.9335 | 0.9335 | 0.9335 | 0.8433 | 0.0038 | 0.0620 | |
| Trainlm | 3 | 12 | 0.8811 | 0.8811 | 0.8811 | 0.8245 | 0.0044 | 0.0663 | |
| Linear | Trainscg | 1 | 12 | 0.8018 | 0.8018 | 0.8018 | 0.8245 | 0.0044 | 0.0039 |
| Trainscg | 2 | 12 | 0.9080 | 0.9080 | 0.9080 | 0.8345 | 0.0042 | 0.0653 | |
| Trainscg | 3 | 11 | 0.9483 | 0.9483 | 0.9483 | 0.8246 | 0.0044 | 0.0663 | |
| Linear | Trainbr | 1 | 12 | 0.8249 | 0.8249 | - | 0.8246 | 0.0044 | 0.0211 |
| Trainbr | 2 | 12 | 0.9334 | 0.9334 | - | 0.8521 | 0.0034 | 0.0529 | |
| Trainbr | 3 | 11 | 0.8249 | 0.8249 | - | 0.8501 | 0.0031 | 0.0559 | |
| Order | Activation Function | Algorithms | Number of Layers | Number of Neuron | R |
|---|---|---|---|---|---|
| 1 | Sigmoid | Trainlm | 1 | 10 | 0.9800 |
| 2 | Sigmoid | Trainlm | 1 | 10 | 0.9820 |
| 3 | Sigmoid | Trainlm | 1 | 10 | 0.9842 |
| 4 | Sigmoid | Trainbr | 2 | 11 | 0.9817 |
| 5 | Sigmoid | Trainbr | 2 | 11 | 0.9835 |
| 6 | Sigmoid | Trainbr | 2 | 11 | 0.9862 |
| 7 | Sigmoid | Trainscg | 3 | 12 | 0.9382 |
| 8 | Sigmoid | Trainscg | 3 | 12 | 0.9417 |
| 9 | Sigmoid | Trainscg | 3 | 12 | 0.9636 |
| 10 | Hyperbolic | Trainlm | 2 | 12 | 0.9788 |
| 11 | Hyperbolic | Trainlm | 2 | 12 | 0.9808 |
| 12 | Hyperbolic | Trainlm | 2 | 12 | 0.9814 |
| 13 | Hyperbolic | Trainbr | 3 | 10 | 0.9822 |
| 14 | Hyperbolic | Trainbr | 3 | 10 | 0.9842 |
| 15 | Hyperbolic | Trainbr | 3 | 10 | 0.9859 |
| 16 | Hyperbolic | Trainscg | 1 | 11 | 0.9215 |
| 17 | Hyperbolic | Trainscg | 1 | 11 | 0.9331 |
| 18 | Hyperbolic | Trainscg | 1 | 11 | 0.9419 |
| 19 | Linear | Trainlm | 3 | 11 | 0.8219 |
| 20 | Linear | Trainlm | 3 | 11 | 0.8232 |
| 21 | Linear | Trainlm | 3 | 11 | 0.8246 |
| 22 | Linear | Trainbr | 1 | 12 | 0.8411 |
| 23 | Linear | Trainbr | 1 | 12 | 0.8475 |
| 24 | Linear | Trainbr | 1 | 12 | 0.8495 |
| 25 | Linear | Trainscg | 2 | 10 | 0.8014 |
| 26 | Linear | Trainscg | 2 | 10 | 0.8183 |
| 27 | Linear | Trainscg | 2 | 10 | 0.8213 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daghbouch, A.; Louhichi, B.; Terres, M.A. Optimization and Prediction of Mass Loss During Adhesive Wear of Nitrided AISI 4140 Steel Parts. Crystals 2025, 15, 875. https://doi.org/10.3390/cryst15100875
Daghbouch A, Louhichi B, Terres MA. Optimization and Prediction of Mass Loss During Adhesive Wear of Nitrided AISI 4140 Steel Parts. Crystals. 2025; 15(10):875. https://doi.org/10.3390/cryst15100875
Chicago/Turabian StyleDaghbouch, Ahmed, Borhen Louhichi, and Mohamed Ali Terres. 2025. "Optimization and Prediction of Mass Loss During Adhesive Wear of Nitrided AISI 4140 Steel Parts" Crystals 15, no. 10: 875. https://doi.org/10.3390/cryst15100875
APA StyleDaghbouch, A., Louhichi, B., & Terres, M. A. (2025). Optimization and Prediction of Mass Loss During Adhesive Wear of Nitrided AISI 4140 Steel Parts. Crystals, 15(10), 875. https://doi.org/10.3390/cryst15100875






