Design and Synthesis of Crystalline Al-Doped TiO₂ Buffer Layers for Enhancing Energy Conversion Efficiency of New Photovoltaic Devices

Abstract

Perovskite solar cells (PSCs) characterized by high energy conversion efficiency (ECE) and low manufacturing costs, exhibit promising potential for commercialization in the near term. For commercialization, it is very important to prevent the decomposition of perovskite by ultraviolet (UV) radiation in the air environment. Also, the mesoscopic architecture of PSCs presents considerable opportunities for the solar cell industry, offering potential for recycling of spent photocatalytic materials such as TiO₂, and exploration of new energy resources. To solve these problems, therefore, this study introduces a strategy to mitigate these challenges using a crystalline Al-doped TiO₂ buffer layer as the electron transport layer (ETL) in conjunction with a mesoporous TiO₂ layer in the fabrication of PSCs. Among various Al concentrations in the crystalline Al-doped TiO₂ buffer layer fabricated via spin-coating, an optimum concentration of 7 mol% Al yielded the highest cell performance in the specific perovskite solar cell structure. These solar cells exhibited an impressive ECE of 11.87%, representing a substantial enhancement of nearly double the ECE (6.37%) achieved with the conventional ETL. This remarkable improvement can be attributed to the passivation effect of the newly developed ETL, which combines a crystalline Al-doped TiO₂ buffer layer with a mesoporousTiO₂ layer. Electrochemical impedance spectroscopy (EIS) analysis was performed in conjunction with theoretical calculations of charge transport parameters to substantiate this claim.

1. Introduction

Perovskite solar cells (PSCs) have emerged as a promising technology owing to their potential to meet the desired characteristics of existing silicon solar cells such as eco-friendly, abundant materials, high cell efficiency, low cost, and large-scale solution manufacturing process. PSCs have also attracted considerable attention owing to their simple and cost-effective manufacturing, coupled with their high solar cell performance. While most research efforts have focused on the development of perovskite materials. Moreover, studies on glass electrodes, electron transport layers (ETLs), and hole transport layers (HTLs) are equally crucial for optimizing PSCs and enabling their application in various devices. The pioneering work on the liquid-state PSCs was initiated by the Miyasaka group [1]. However, the liquid-state PSCs using a liquid electrolyte can lead to the decomposition of the perovskite (CH₃NH₃PbI₃, MAPbI₃) structure, resulting in a drop in energy conversion efficiency (ECE). To address this issue, solid-state PSCs were developed, achieving an efficiency of 9.7%. While the MAPbI₃ crystals formed from their precursors exhibited a very fast reaction, challenges arose in producing large crystals and uniform film. In order to enhance the crystal sizes of MAPbI₃, subsequent research explored the use of TiO₂ with a mesoporous (MP) structure [2], giving rise to the concept of a mesoscopic structure [3]. Moreover, PSCs using Al₂O₃ as the electron transport layer (ETL), despite its lack of conductivity compared to MP-TiO₂, achieved an ECE of 12% [4]. By refining the solar cell design, researchers have been able to produce highly efficient PSCs. Various PSC architectures, including mesoscopic [5,6], planar [7,8], bilayer, and inverted PSCs [9,10], have demonstrated efficiency exceeding 20% (now the world record is 34.6% obtained with perovskite/silicon tandem solar cell).

To further enhance the efficiency of PCSs, various techniques have been developed to fabricate high-quality MAPbI₃ films, including solution processes [11,12], and vacuum flash-assisted solution processes [13]. However, in mesoscopic PSCs using MP-TiO₂ with pore sizes below 50 nm, the separated charges exhibit different electrode arrival carrier mobilities owing to electron transfer from MAPbI₃ to MP-TiO₂.This leads to charge trapping and detrapping in the mesoscopic structure, resulting in I-V hysteresis. Consequently, considerable efforts have been devoted to achieving high performance and stability, including optimizing the scan direction and speed to minimize the hysteresis of the I-V curve and overcome this challenge. Therefore, low trap density, high conductivity, and mobility are highly sought-after properties for ETLs, which can be achieved by modifying their surface morphology. To address these challenges, research efforts have been directed toward exploring various ETL architectures, including nanorods [14], nanowires [15], nanotubes [16], and inverse opals [17]. Additionally, the introduction of a passivation layer between the transport layer and perovskite layer as well as the surface modification of the perovskite thin film with hydrophobic groups have been used to enhance PSC efficiency and stability. Furthermore, researchers have explored modifying the ETL properties by incorporating other metal ions, such as NiO [18], CuO [19], and SnO₂ [20], as well as doping metal oxides with hetero metal ions, including Zn-doped TiO₂ [21], Nb-doped TiO₂ [22], and Sm-doped TiO₂ [23]. Metal ions and metal oxides are particularly promising materials owing to their large bandgap, high conductivity, and reduced sensitivity to ultraviolet (UV) light. These modifications have demonstrated the potential to reduce the hysteresis of the I-V response, leading to improved PSC efficiency.

Incorporating aluminum (Al) into TiO₂ materials introduces novel energy levels that influence charge transport characteristics in semiconductors. During the Al doping process, Al³⁺ ions substitute into TiO₂, modifying its electronic structure [24]. Based on the density functional theory (DFT) calculations, it is well known that the holes are strongly localized in the O2p nonbonding orbital of three-coordinated O²⁻ ions. Consequently, dopants hinder carrier mobility by trapping photogenerated carriers at extrinsic defects [25]. We carried out preliminary work for the test of a passivation effect with an Al-doped TiO₂ layer as ETL in the various architecture of PSCs and found that the Al-TiO₂ layer in a specific cell structure can play an important role as a buffer layer, enhancing the ECE [26]. Replacing the mesoporous TiO₂ (MP-TiO₂) layer with an insulating material such as Al₂O₃, led to an increase in open-circuit voltage (V_oc). This improvement can be attributed to a reduction in the quasi-Fermi level splitting. Non-stoichiometric TiO₂ contains deep electron trap sites, which facilitate charge recombination. By reducing the recombination rate through passivation, the efficiency of PSCs can be enhanced. This indicates that passivation strategies can effectively minimize charge recombination of MAPbI₃ and improve device performance, requesting a systematic study about the exact role of the buffer layer.

In this study, therefore, we fabricated the PSCs by incorporating a crystalline Al-doped TiO₂ thin film as a buffer layer in a mesoscopic structure to achieve a passivation effect. We hypothesized that this specific PSC design would reduce carrier recombination at the buffer layer/MAPbI₃ interface by increasing the HOMO-energy level of the ETL. Consequently, V_oc would improve owing to the wider band gap and enhanced conduction band energy level of crystalline Al-doped TiO₂ buffer layer, reflecting improvement of charge carrier transport characteristics with different Al-contents. Experimental and theoretical analyses confirmed our hypothesis, with the optimal cell performance obtained using a MAPbI₃ layer deposited on a combination of MP-TiO₂ and 7 mol% crystalline Al-doped TiO₂ buffer layer as the new ETL.

2. Materials and Methods

2.1. Synthesis of Crystalline Al-Doped TiO₂ Buffer Layer and Fabrication of PSCs

The detailed synthesis of crystalline Al-doped TiO₂ buffer layers and fabrication of PSCs have been previously reported [26]. Briefly, a Ti precursor sol (0.15 M titanium diisopropoxidebis(acetylacetonate) solution) was spin-coated onto a fluorine-doped thin oxide (FTO) substrate to form a compact TiO₂ layer (cp-TiO₂), which was then dried at 155 °C. Subsequently, a mesoporous TiO₂ (MP-TiO₂) layer was deposited onto the cp-TiO₂/FTO substrate using a TiO₂ powder paste. To create crystalline Al-doped TiO₂ buffer layers with varying Al-contents, 3, 5, 7, and 10 mol% aluminum isopropoxide (Sigma-Aldrich, Burlington, NJ, USA, 98.00%) precursors were added to the Ti precursor sol solution. After stirring for 3 h, the buffer layers were synthesized using a spin-coating method. The layers were then dried at 125 °C and annealed at 500 °C for 1 h. To obtain the perovskite (MAPbI₃) active layer, 1 M PbI₂ (476 mg/mL in dimethylformamide (DMF) and CH₃NH₃I (7mg/mL in isopropanol (IPA)) were sequentially deposited onto the MP-TiO₂ layer. The perovskite layer was subsequently dried at 100 °C. The hole transport layer (HTL) was prepared by mixing 28.8 μL of Spiro-MeOTAD (Lumtec) (72.3 mg/mL in chlorobenzene) with 4-tert-butylpyridine (Sigma-Aldrich, 96%). The TSFI stock solution (Sigma-Aldrich, 99.8%) was stirred for 24 h before being deposited onto the perovskite layer. Finally, a gold (Au) electrode was thermally evaporated onto the HTL. The detailed structures of the fabricated PSCs are shown in Figure 1.

2.2. Characterization

To characterize the crystallinity, structure, and crystal phase of the thin films, X-ray diffraction (XRD) measurements were performed using Cu Kα radiation (λ = 1.5416 Å) with a 40 kV beam voltage and a 30 mA beam current. The optical absorbance of the buffer layers was measured in the wavelength range of 300–500 nm using a UV-Vis-NIR spectrometer (Shimadzu, Kyoto, Japan, UV-3600). X-ray photoelectron spectroscopy (XPS) and Raman spectroscopy were subsequently used to analyze the surface species, atomic composition, and functionality. To evaluate the photovoltaic performance of the solar cell devices, photocurrent density–voltage (I-V) curves (SUN 2000, Huawei, Shenzhen, China) were measured using a xenon lamp under an AM 1.5 filter at 100 mW/cm² illumination in open circuit conditions. The analysis of electrochemical impedance spectroscopy (EIS) was subsequently performed in a frequency range from 1 MHz to 100 mHz using SUN 2000 Instruments under AC voltage with a perturbation amplitude of 10 mV applied during the EIS measurement.

3. Results and Discussion

Four different types of PSCs were designed and fabricated, each incorporating a different combination ofnonporous TiO₂, MP-TiO₂, and a buffer layer between the active layer and ETL. The detailed fabrication processes and characteristics of these PSCs have been previously reported [26]. As illustrated in Figure 1, this study focuses on the preparation of mesoscopic PSCs with various selective contacts. These architectures demonstrate the selective collection of electrons, which exhibit different mobilities as they traverse the ETL owing to variations in trap sites introduced by the nonporous TiO₂, MP-TiO₂, and buffer layer. Among the four different device structures depicted in Figure 1, Cell (b) exhibited the highest efficiency owing to relatively high current density (J_sc), open circuit voltage (V_oc), and fill factor (FF) (refer to Figure 2a and

Table 1. Summary of photovoltaic performance parameters obtained from J–V curves of Figure 2a with 4 different solar cell devices shown in Figure 1 [26].

Sample Name	Jsc (mA/cm2)	Voc (V)	FF (%)	PCE (%)
Cell (a)	14.66	0.898	65.66	8.64
Cell (b)	15.12	0.916	66.65	9.24
Cell (c)	12.84	0.908	54.62	6.37
Cell (d)	12.64	0.913	64.72	8.06

). Notably, the J_sc and FF were considerably enhanced compared to the other cells, leading to an improvement in overall solar cell efficiency [26]. In contrast, the performance of Cell (c) and Cell (d) was reduced. Specifically, Cell (c) exhibited a decrease in FF of approximately 20% compared to the other devices, indicating lower stability. The motivation of this study was to understand why the characteristics of solar cells differed considerably.

Upon illumination of the perovskite (MAPbI₃) material with sunlight, electron–hole pairs are generated in the material and subsequently injected carriers into the charge transport layer (refer to Figure 3a). Charge separation and injection can occur via two primary pathways: (1) injection of electrons into the ETL [(e⁻---h⁺) MAPbI₃ perovskite → e_cb⁻(ETL) + h⁺(MAPbI₃ perovskite) (step 1)] and (2) injection of holes into the HTL [(e⁻---h⁺) MAPbI₃ perovskite → h⁺(HTL) + e⁻(MAPbI₃ perovskite) (step 2)]. The carriers injected into the charge transport layers can undergo various processes, including exciton annihilation through photoluminescence [(e⁻---h⁺) MAPbI₃ perovskite → photoluminescence (step 3)] or non-radiative recombination [(e⁻---h⁺) MAPbI₃ perovskite → non-radiative recombination (step 4)]. Additionally, back charge transfer can occur at the ETL/MAPbI₃ layer interface [e_cb⁻(ETL) + h⁺(MAPbI₃ perovskite) → recombination (step 5)] and the MAPbI₃ layer/HTL interface [h⁺(HTL) + e⁻(MAPbI₃ perovskite) → recombination (step 6)]. Finally, charge recombination can take place through the recombination of electrons in the ETL and holes in the HTL [e_cb⁻(ETL) + h⁺(HTL) → recombination (step 7)]. Owing to the above-mentioned processes [steps (3), (4), (5), (6), and (7)], which can reduce the efficiency of PSCs, it is desirable for the carrier lifetime of MAPbI₃ to be prolonged. The implementation of a buffer layer, as depicted in Figure 3b, can decrease the charge recombination rate and enhance the efficiency of PSCs. To mitigate charge recombination in MAPbI₃, we used a passivation effect by incorporating an Al-doped TiO₂ buffer layer between the CP-TiO₂(ETL)/MP-TiO₂ interface. The carrier lifetime (or simply the lifetime) generally refers to the duration during which a charge carrier remains free to move, thereby contributing to electrical conduction. Charge carrier lifetime (or effective electron lifetime, τ_eff) refers to the duration that charge carriers (electrons in the conduction band and holes in the valence band) remain in a free state. It is defined as the average time taken for a minority carrier to recombine and can vary considerably depending on the materials and construction of the semiconductor. The energy released during recombination can manifest as heat or photons (optical recombination, used in LEDs and semiconductor lasers). Consequently, charge carrier lifetime is a critical factor in bipolar transistors and solar cells. The recombination lifetime (τ_r) especially refers to the time frame for the recombination of injected or photogenerated electrons and holes. It serves as a fundamental parameter in the analysis of semiconductor optoelectronic devices, particularly solar cells. Surface recombination occurs at the top of the solar cell, emphasizing the importance of using material layers with superior surface passivation properties to minimize the impact of light exposure over periods. As illustrated in Figure 1, MAPbI₃ possesses two distinct interfaces: the ETL/MAPbI₃ interface and the MAPbI₃/HTL interface. Minimizing the recombination rate of electrons and holes at each of these interfaces is crucial. Furthermore, it is essential to modulate the energy levels of the conduction and valence bands through techniques such as self-passivation, doping, and interlayer passivation, to enhance device performance.

In this study, our primary objective was to investigate the impact of various ETLs on the electron transfer ability of carriers generated in the active layer. Building upon our previous PL analysis [26], which revealed a reduction in the PL area for Cell (b) compared to other cells, we hypothesized that the rate of carrier recombination was influenced by the material properties, structure, and characteristics of the ETL. These factors can affect both the generation of excitons and the mobility of charge carriers. Our findings suggest that the presence of a buffer layer, such as Al-doped TiO₂, at the MAPbI₃/ETL interface facilitates the transfer of generated electrons to the electrode. This indicates an increase in carrier lifetime owing to enhanced recombination resistance. Consequently, the electron acceptor ability was enhanced when the PSC was fabricated using an Al-doped TiO₂ buffer layer. Conversely, in the Cell (c) and Cell (d) structures, the hindered generation of electrons impedes proper crystal growth. This suggests that in poorly formed crystals, these paration of electrons and holes is compromised, hindering charge injection [steps (1) and (2)], back charge transfer [steps (5) and (6)], and charge recombination [step (7)]. Instead, exciton annihilation [steps (3) and (4)] occurs at a considerably higher rate. These effects adversely impact the recombination rate, ETL functionality, and overall solar cell performance. To check this kind of passivation effect systematically, we first prepared the crystalline Al-doped TiO₂ buffer layers with different Al-doping concentrations based on Cell (b). Then, the analysis of X-ray diffraction (XRD), Raman spectroscopy, and X-ray photoelectron spectroscopy (XPS) were sequentially utilized to prove the passivation effect as well as to understand the charge transfer behavior of the PSCs. For the analysis of XRD, we made all structures of perovskite without HTL, and the thickness of whole ETLs was fixed to 100 nm for both pure TiO₂ and Al-TiO₂ thin films.

Figure 4a shows XRD patterns of both pure crystalline TiO₂ and crystalline Al-doped TiO₂ thin films with different Al-doping concentrations. All observed peaks corresponding to TiO₂ can be attributed to the anatase (A) and rutile (R) phases of TiO₂, which were preserved upon the incorporation of Al precursor up to 10 mol%. No additional peaks associated with TiO₂ material were detected during the Al precursor doping process. The ionic radii of the Ti⁴⁺, Ti³⁺, and Al³⁺ ions are 0.61, 0.64, and 0.53 nm, respectively. As Ti³⁺ ions are replaced with Al³⁺ ions, the unit cell size of crystalline Al-doped TiO₂ decreases compared to TiO₂. As we can see from the right-hand side figure of Figure 4a, both the (101) anatase peak and the (110) rutile peak move slightly towards a higher degree as doping proceeds gradually, indicating that the unit cell is to expand its original size. In addition, the (110) rutile peak at 26.8 degreess harpens with increasing Al-doping concentrations up to 10 mol%, while the (101) anatase peak at 25.5 degrees broadens. The crystallite size of Al-doped TiO₂, calculated using the Scherrer equation, increases with the Al-doping concentration. Consequently, the incorporation of Al ions introduces stress into the TiO₂ lattice during the doping process, resulting in a slight shift in the peak positions toward higher degrees, indicating unit cell expansion. Figure 4b shows the UV-Vis absorption spectra, which exhibit a shift toward shorter wavelengths with increasing Al-doping, a phenomenon known as blue shift. This observation suggests the possibility of an increase in the conduction band energy level of the ETL owing to the blue shift effect. Consequently, the Fermi level in the device may be increased, leading to an enhancement in either V_oc or FF. Based on the Tauc-plots, which can be obtained from Figure 4b, moreover, we observed a variation in reducing optical bandgap from 3.20 to 2.24 eV with increasing Al-doping concentration (mol% Al) between 0 and 7.Then, there will be further decreasing the optical bandgap up to 2.07 eV when 10 mol% Al is doped. This means that the conduction band (i.e., HOMO-energy level) of ETLs will be changeable as the Al-doping concentration is changed. In this study, we observed that the HOMO-energy levels of the ETLs gradually increase as the Al-doping content increases.

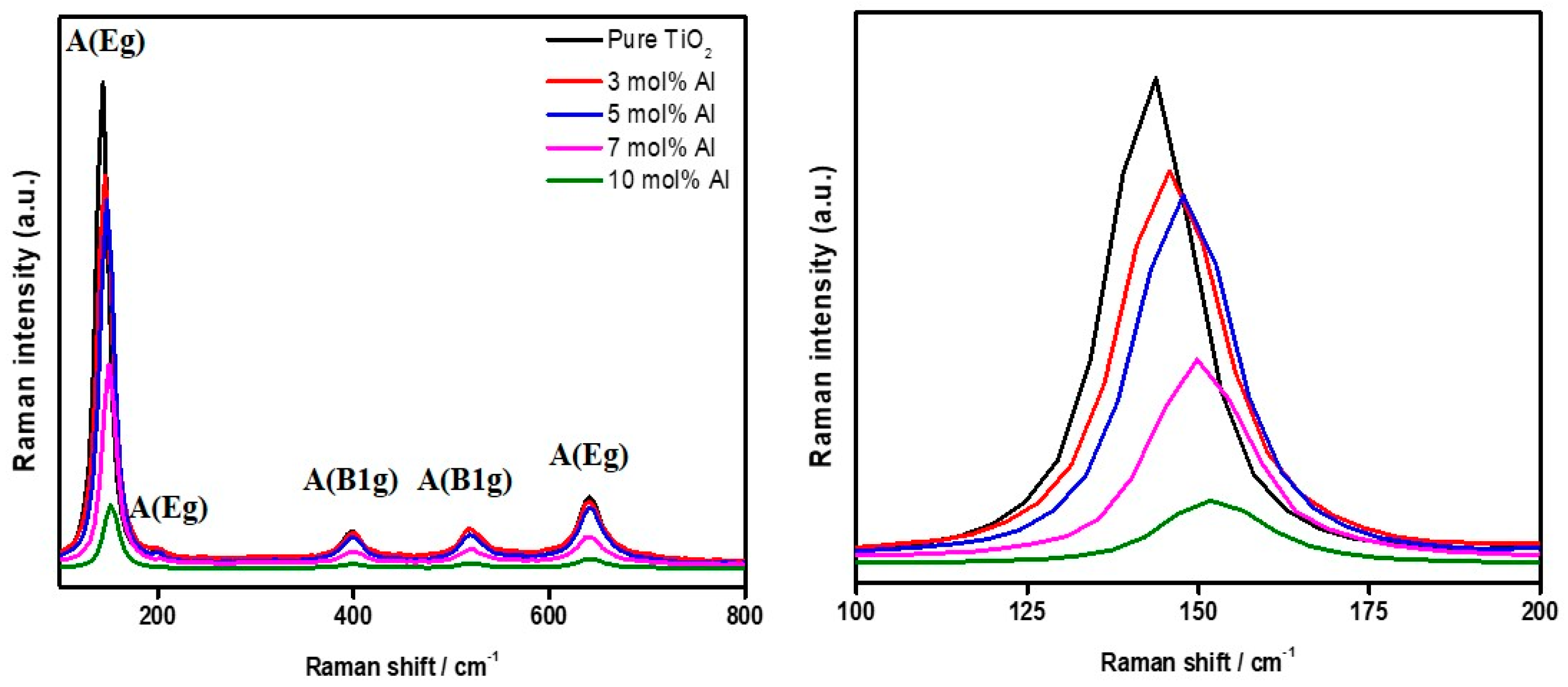
Figure 5 shows the Raman spectra of the crystalline Al-doped TiO₂ samples. Rutile and anatase phases were determined: Rutile peaks at 143 cm⁻¹ (B_1g), 447 cm⁻¹ (E_g), 611 cm⁻¹ (A_1g); Anatase peaks at 144 cm⁻¹ (E_g), 197 and 640 cm⁻¹ (E_g), 398 and 515 cm⁻¹ (B_1g), respectively. Notably, the primary active Raman mode (E_g) of the anatase phase was observed at 144 cm⁻¹, which corresponds to -Ti-Ti vibrations in the octahedral chains [27]. Meanwhile, the active Raman modes reported for aluminum oxide at 384 and 417 cm⁻¹ were not detected, confirming the substitutional incorporation of Al into the TiO₂ crystalline structure [27]. Another noteworthy observation is the decrease in the Raman intensity of TiO₂ associated with the vibrational modes of both anatase and rutile as the Al-dopant concentrations increase. Upon zooming in on the A(E_g) vibrational mode, the Raman peak intensities exhibit a decreasing trend with the following sequence of Al mol% contents: 0, 3, 5, 7, and 10 mol%, respectively (refer to the enlarged figures on the right-hand side). Additionally, the peak positions shift toward higher wavelengths (similar to the UV-visible result), indicating a relative decrease in bond length in the lattice for both anatase and rutile phases [27]. Furthermore, the effects of Al-dopant incorporation into the TiO₂ crystalline structure can be observed through the changing trends of the primary active Raman mode (E_g) in Figure 5. The decrease in peak intensity and shift toward higher wavenumbers (namely bathochromic shift) signify the grain boundary disorder of TiO₂ induced by Al-doping [28]. Notably, despite the increasing Al-doping concentration, all Raman peaks associated with the anatase phase persist, while the rutile phase peaks gradually diminish. This suggests that the remaining peak may be attributed to the insertion of Al³⁺ ions into the TiO₂ lattice. Liu et al. obtained similar results and identified a new Raman vibrational peak at approximately 317 cm⁻¹ in their Al-doped TiO₂ crystalline materials [28].

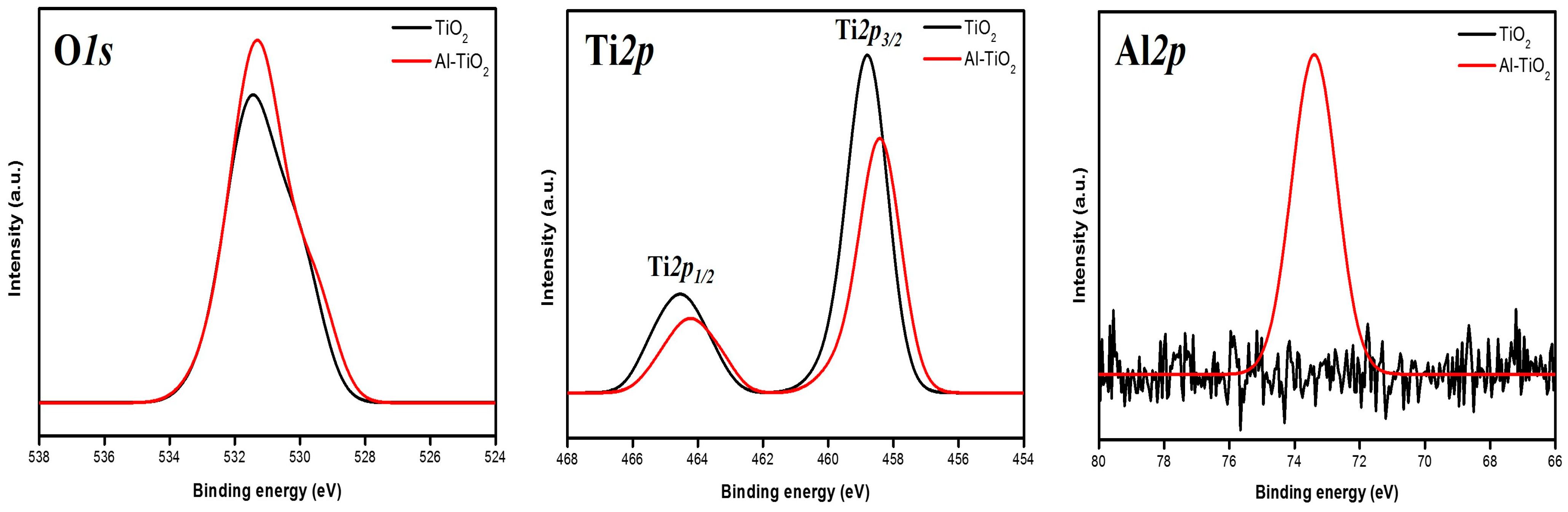
Al-doping was further corroborated by XPS. XPS was measured to confirm the changes in the oxidation number of O1s, Ti2p, and Al2s in TiO₂ during the 7 mol% Al-doping process. Figure 6 shows high-resolution XP spectra of O1s, Ti2p, and Al2p for doped (red color) and undoped (black color) samples. The Al2p peak (refer to the right-hand side figure) increases peak intensity in the Al (7 mol%)-doped TiO₂. However, no Al2p peak was detected in the pure TiO₂ sample. In the pure TiO₂, the Ti2p_3/2 and Ti2p_1/2 peaks (refer to the middle figure) are located at binding energies of 458.8 and 464.5 eV, respectively. Upon the incorporation of Al into the TiO₂ crystalline lattice, the Ti2p peaks exhibit a slight shift toward lower binding energy, indicating a reduced oxidation state compared toTi⁴⁺ in pure TiO₂. The primary O1s peak (refer to the left-hand side figure), with an asymmetric shape, is located at a binding energy of 529.0 eV and may correspond to bonding with both Ti and Al. Additionally, an O1s peak with an asymmetric shape at 531.0 eV was identified and attributed to oxygen species in the Al-doped TiO₂ buffer layers. Only a minor shift toward a lower O1s binding energy was observed, potentially resulting from the change in electronegativity of the Ti bond from -O-Ti to Al-O-Ti in the crystal structure of the buffer layer. Consistent with previous studies [28,29], the O1s peak observed at approximately 529.0 eV exhibits an asymmetric shape for both pure and doped TiO₂, suggesting the presence of defect sites and/or potential surface contamination. This indicates that all our samples may have experienced a degree of contamination during the measurement process (or surface oxidation owing to exposure to air), leading to a chemical shift of up to 0.6 eV in the O1s binding energy.

To check the detailed passivation effect of buffer layers with different Al-doping concentrations, the characteristics of solar cell devices, photocurrent density–voltage (I-V) curves shown in Figure 2b were measured and their measured parameters are summarized in

Table 2. Summary of photovoltaic performance parameters obtained from J–V curves of Figure 2b with PSCs fabricated by the Cell (b)-based structure with different crystalline Al-doped TiO₂ buffer layers (0, 3, 5, 7, and 10 mol% Al).

Sample Name	Jsc (mA/cm2)	Voc (V)	FF (%)	ECE (%)
Pure TiO2	15.12	0.916	66.65	9.24
3 mol% Al	15.63	0.919	67.68	9.722
5 mol% Al	16.93	0.927	67.84	10.66
7 mol% Al	18.79	0.941	67.14	11.87
10 mol% Al	17.50	0.934	67.30	11.00

. As shown in Table 2 and Figure 2b, the J_sc, V_oc, and FF parameters exhibit a gradual increase up to an Al-doping concentration of 7 mol%, contributing to an improvement in cell performance from 9.24% to 11.87%. This enhancement can be attributed to the smoother transfer of electrons from the MAPbI₃ layer to the electrode through the ETL. In the 7 mol% Al-doping range, the ECE shows a consistent increase, primarily owing to the increase in current density (J_sc). However, beyond 7 mol% Al-doping, the ECE increases. These observations suggest that the electron acceptor ability is enhanced by the Al-doping process below 7 mol%, indicating a reduction in the recombination rate and an increase in the Fermi-energy level with an appropriate amount of Al-doping. 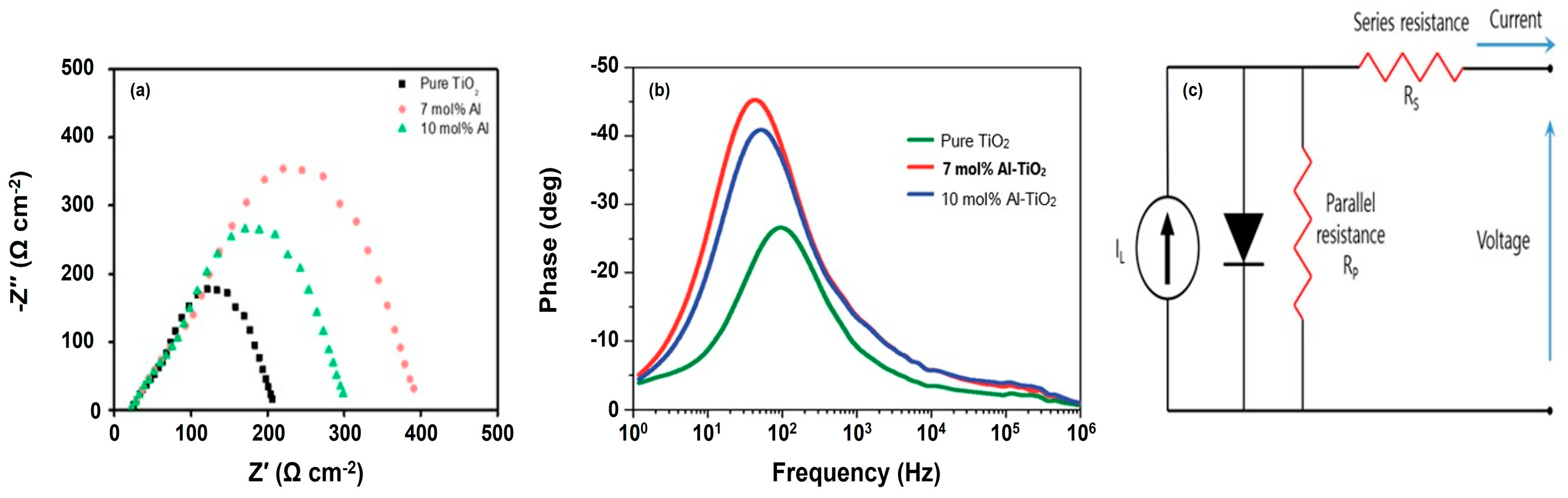Consequently, the crystalline Al-doped TiO₂ buffer layer contributes to an improvement in recombination resistance. In general, photovoltaic performance parameters such as short-circuit current density, open-circuit voltage, and photon current conversion efficiency can be extracted from J-V measurements. While J-V measurements provide insights into the photovoltaic performance of solar cells, they do not offer information about photoelectrochemical behavior such as series and charge transfer resistance, electron lifetime, and charge collection efficiency. These parameters can be obtained using EIS. EIS measurements generate the Nyquist plot (see Figure 7a) as well as the Bode plot [refer to Figure 7b], which depict the charge transfer resistance (R_r or R_ct) and angular frequency (ω_rec) for the solar cell under study.

To prove this, therefore, the EIS analysis for the three fabricated PSCs without and with buffer layers was performed. As we can see in Figure 7a, the EI spectra of PSCs contain two RC arcs. One is related to the contact resistance of the interfaces at high frequency with the same area. The other is attributed to recombination resistance and chemical capacitance (C_μ) of the device at low frequencies [30]. Thus, EIS results can give the values of both charge transfer resistance that can induce with C_μ and recombination resistance at the ETL/MAPbI₃ interfaces and MAPbI₃/counter electrode in the field of PSC. For example, the reduction in frequency in the EIS measurement generated a higher electron lifetime, which is explained in Equation (5) and

Table 3. PSC parameters including charge transfer resistance (R_ct), maximum peak frequency (f_max), effective electron lifetime (τ_eff), effective rate constant (k_eff) for recombination, effective electron chemical diffusion coefficient (D_eff), electrochemical capacitance (C_μ), free electron lifetime (T_t), effective electron diffusion length (L_n),and recombination lifetime (τ_r) extracted from EIS measurements (Figure 6) and voltage decay curves (Figure 7).

Sample Name	Rct (Ω)	fmax (Hz)	τeff (ms)	keff (s−1)	Deff (cm2s−1)	Cμ (μF)	Tt (s)	Ln (µm)	τr (s)
Pure TiO2	124.30	52.79	3.016	331.565	13.98	24.26	0.1054	42.17	1.29
7mol%Al	258.73	21.90	7.271	137.533	11.77	28.10	0.2139	85.61	0.97
10mol%Al	195.20	36.21	4.398	227.376	16.95	22.53	0.1864	74.55	1.12

. In this scenario, the relationship is inversely proportional to the maximum frequency. For the analysis of EIS data, both the Bode plot depicted in Figure 7b and a traditional equivalent circuit model depicted in Figure 7c were also utilized in his study. As shown in Figure 7c, a constant photo-generated current source, a series parasitic resistance (i.e., series resistance, R_s), and a parallel parasitic resistance (i.e., parallel resistance, R_p) are also generally included. When comparing the J-V results with the EIS data presented in Figure 7a, it is evident that the PSC with the 10 mol% crystalline Al-doped TiO₂ layer exhibits higher R_s and lower recombination resistance compared to the PSC with the 7 mol% crystalline Al-doped TiO₂ buffer layer. This indicates a decrease in carrier transport ability owing to a relatively high Fermi-energy level of the ETL, suggesting that electrons encounter difficulty in overcoming the energy barrier. Consequently, exciton annihilation [steps (3) and (4)] and back charge transfer [step (6)] become more likely to occur, while electron injection [step (1)] is hindered. This ultimately leads to electron–hole recombination. As the Al-doping concentration increases, the HOMO-energy level of the ETL gradually increases. The PSC with the 7 mol% crystalline Al-doped TiO₂ buffer layer demonstrates the most efficient charge injection [step (1)] and minimal back charge transfer [step (5)] as a result of the passivation effect. This observation confirms that the solar cell parameters with the 7 mol% crystalline Al-doped TiO₂ buffer layer were improved, leading to the best cell performance (11.87%) in comparison to the non-doping sample (6.37%). However, the solar cell performance declined with the 10 mol% crystalline Al-doped TiO₂ sample. This suggested that the conduction band energy level became excessively high, making it more challenging for electrons to move through the ETL, thereby increasing the recombination rate. To clarify these aspects, we performed theoretical calculations to obtain various electron transport parameters as follows.

Based on the diffusion-recombination transmission line model, the measured impedance in Figure 7a is attributed to the following equations [31,32,33,34].

Z(ω) = [R_tR_r/(1 + i ω/ω_rec)]^1/2coth[(R_t/R_r)^1/2 (1 + i ω/ω_rec)^1/2]

(1)

where Z represents the electrochemical impedance for the photoanode thin film, i = (−1)^1/2, ω denotes the angular frequency, ω_rec signifies the frequency of the charge transfer process, R_t is the transport resistance of the electrons and R_r is the charge transfer resistance associated with the recombination of electrons at the perovskite/HTL interface. R_r can also be referred to as the charge transfer resistance (R_ct) [34]. Additionally, Equation (1) reveals the relationship between two opposing processes that occur in solar cells: electron transfer across the semiconductor layer (ω_d) and carrier loss owing to electron recombination (ω_rec). These processes can be mathematically expressed as follows:

ω_d/ω_rec = R_ct/R_t = (L_n/L)²

(2)

ω_d = 1/R_tC_μ = D_eff/L²

(3)

and ω_rec = 1/R_ctC_μ = D_eff/L_n²

(4)

where D_eff represents the effective electron chemical diffusion coefficient, L is the thickness of the photoanode film layer, L_n is the effective electron diffusion length of the photoanode, and C_μ denotes the chemical capacitance, respectively [31,33]. When R_t ≪ R_ct or ω_rec ≪ ω_d, the parallel connection of R_ct and C_μ results in the formation of a recombination arc, and Equation (1) can be simplified to the following form:

Z(ω) = R_t/3 + [R_ct/(1 + i ω/ω_rec)]

(1A)

The small and large arcs of a conventional Warburg impedance appear at high and low frequencies, respectively, as shown in Figure 7a. A large arc corresponds to a low or slower recombination effect compared to electron diffusion through the TiO₂ layer. Furthermore, R_t ≪ R_ct is a desirable condition for optimal solar cell performance because a large R_ct contributes to reduced electron recombination in the cell. Conversely, when R_t ≫ R_ct or ω_rec ≫ ω_d, a considerable combination effect arises in the solar cell owing to the Gerischer impedance, leading to the impedance curve with a smaller arc at high frequency as observed in Figure 7a. Consequently, the recombination time is shorter than the electron diffusion across the TiO₂ layer. Based on the above-mentioned model theory, various electron transport parameters, such as the effective electron lifetime (τ_eff), maximum peak frequency (f_max), and effective rate constant (k_eff) for recombination, can be extracted from the impedance spectra of solar cells. For instance, τ_eff is derived from the f_max of the impedance spectra [refer to Figure 7b], which corresponds to the photoanode in the medium frequency region [35]. This maximum frequency also represents the effective rate constant (k_eff) for recombination. These three parameters are interrelated as follows:

τ_eff = 1/ω_rec = 1/2πf_max = R_ctC_μ

(5)

ω_rec = k_eff = 1/τ_eff

(6)

This implies that the effective electron lifetime (τ_eff) aligns with the angular frequency at the apex of the arc in Figure 7a, expressed as ω_rec = 2πf_max = τ_eff⁻¹, where ω_rec denotes the angular frequency of the electron recombination reaction [36]. Equation (6) effectively elucidates the separation of a lifetime into two primary components. The separation occurs because R_rec encompasses both a density term, (the chemical capacitance) and a kinetic constant (k_eff). Consequently, the product in Equation (6) isolates the latter. The electrochemical capacitance (C_μ), which is linked to minority carrier accumulation, and the recombination resistances together yield a virtually constant lifetime across varying illumination intensities. In the presence of impurity levels, for instance, lifetimes in silicon exhibit high variability [37], which is evenmore pronounced in amorphous inorganic semiconductors such as Al-TiO₂. It is crucial to emphasize that recombination constitutes an interfacial charge transfer event occurring at the boundary between the semiconductor and ionic/hole carrier. Given that the distance for electron tunneling is typically approximately 1 nm, which is considerably smaller than the average size of nanoparticles in a solar cell, it is beneficial to differentiate between bulk traps. In any transient measurement used to determine lifetime, a modification of the Fermi level entails a change in the occupancy of bulk traps. Consequently, we can derive the free electron lifetime (T_t) by multiplying two experimentally determined quantities: the diffusion coefficient (D_n) and the effective electron lifetime (τ_eff). However, in this study, we used the values of the effective electron chemical diffusion coefficient (D_eff) as obtained theoretically.

T_t = D_n τ_eff/D_o = D_eff τ_eff/D_o

(7)

The denominator of Equation (7) represents a constant estimated to be D₀ = 0.4 cm²s⁻¹ [38]. It has been well established that the mobility–lifetime product corresponds to the free carrier recombination time in amorphous silicon solar cells. Consequently, the electrochemical capacitance (C_μ) was also calculated using Equation (8), utilizing the values of τ_eff and R_ct extracted from the Nyquist plot.

τ_eff = 1/ω_rec = 1/2πf_max = R_ctC_μ = 1/k_eff

(8)

Hence, the effective electron chemical diffusion coefficient (D_eff) and effective electron diffusion length (L_n) of the photoanode can also be derived from Equation (9) [36].

L_n = D_eff τ_eff

(9)

This implies that the electron diffusion length (L_n) can be derived from Equations (3) and (4) and is determined by the product of the diffusion coefficient (D_eff) and the electron lifetime (τ_eff). Based on Equation (9), we observe that L_n increases with increasing electron lifetime, assuming that the diffusion coefficient (D_eff) remains constant at a fixed temperature. It is also noteworthy to examine the observed properties of L_n in our solar cell devices. We initially note that L_n is not a transient quantity, but rather a steady-state parameter; therefore, it can be expressed in terms of the IS resistances as L_n = L(R_rec/R_t)^1/2, where R_t represents the transport resistance [refer to Equation (2)]. Consequently, bulk traps do not interfere with the diffusion length. Notably, the solid hole conductor OMeTAD (HTL) cell exhibits the lowest charge transfer resistance, which considerably impairs performance despite the cell’s attainment of higher photovoltage [39,40]. The model predicts that L_n is proportional to the square root of the free carrier lifetime. In solar cells, the diffusion length typically exhibits a slight increase with increasing bias voltage. For instance, for MP-TiO₂ with MP-TiO₂/Perovskite/HTL interface, the diffusion length is observed to increase with voltage in the absence of illumination, while a contrasting trend is observed under illumination: it decreases with the potential [38,39,40].

In addition, we can determine the recombination lifetimes (τ_r) from a photovoltage (V_oc) decay curve [41] shown in Figure 8. Figure 8 is the photovoltage decay curve plotting 1/V_oc and J_sc as a function of Al-doping amounts in mol%, and realizes a tendency to oppose between τ_r and τ_eff (see Table 3). Table 3 summarizes the experimentally and theoretically obtained PSC parameters, including charge transfer resistance (R_ct), maximum peak frequency (f_max), effective electron lifetime (τ_eff), effective rate constant (k_eff) for recombination, effective electron chemical diffusion coefficient (D_eff), electrochemical capacitance (C_μ), free electron lifetime (T_t), effective electron diffusion length (L_n), and recombination lifetime (τ_r). From Figure 7a,b, we can determine the R_ct and ω_rec values, and by using Equation (6), ω_rec = 2πf_max = τ_eff⁻¹, we could obtain f_max values as well as τ_eff values which are listed in the 2nd and 3rd columns, respectively. As we can see in the 3rd column, the obtained τ_eff values are 3.016 × 10⁻³ s for 0 mol% Al-doping, 7.271 × 10⁻³ s for 7 mol% Al-doping, and 4.398 × 10⁻³ s for 10 mol% Al-doping, respectively. In contrast, the τ_r values are 1.29 (0 mol%), 0.97 (7 mol%), and 1.12 s (10 mol%), respectively. The increase in τ_eff facilitates electron diffusion and transfer owing to the increase in L_n, because τ_r is closely related to both free electron lifetime (T_t) and electron diffusion length (L_n), as well as electrochemical capacitance (C_μ). The response time for recombination, commonly referred to as the “lifetime”, invariably comprises a recombination resistance and a capacitance, and it is directly revealed by IS measurement. However, the time constant of the recombination arc of IS must generally be expressed as τ_r = R_recC_μ [31]. The nature of the electrochemical capacitance (C_μ) is crucial for correctly interpreting τ_r as a lifetime. Under specific conditions, the transient measurement induces charging or discharging of the depletion layer in a Si-based solar cell, resulting in the measured “lifetime” having no correlation with recombination time. In such cases, the τ_r values correspond to depletion capacitance and cannot be associated with the minority carrier lifetime. It is important to emphasize that when determining electron lifetime in solar cell devices, it is essential to verify that the recombination resistance is indeed associated with interfacial charge transfer at the nanostructured metal oxide [42]. Carrier recombination lifetimes are often regarded as indicators of perovskite film quality, with longer decay lifetimes being associated with higher-performing materials. Carrier recombination kinetics has been characterized as a combination of trap-assisted, monomolecular (first-order), and bimolecular (second-order) recombination processes. While most studies agree that radiative bimolecular recombination is dominant at high initial carrier densities (n₀ > 10¹⁷ cm⁻³), reports on kinetics at lower excitation densities (relevant to solar cell operation) vary from single-exponential to bi-exponential and to stretched-exponential functions with varying degrees of accuracy [43].

As evident from Table 2 and Table 3, our highest performing PSC with a 7 mol% crystalline Al-doped TiO₂ buffer layer exhibited the R_ct of 258.73Ω along with a low effective rate constant (k_eff) of 137.533 s⁻¹ for recombination. It also demonstrated a relatively long effective electron lifetime (τ_eff) of 7.271 ms (accompanied by a maximum electrochemical capacitance value of 28.10 μF) among the various solar cell devices. This is potentially attributable to the suppression of recombination, as indicated by the minimal recombination lifetime (0.97 s) and electron chemical diffusion coefficient (11.77 cm²s⁻¹) at the CP-TiO₂(ETL)/Buffer layer(Al-doped TiO₂)/MP-TiO₂/Perovskite/HTL interfaces. Consequently, a relatively long effective electron diffusion length (L_n) of 85.61 μm is achieved. Mahmud et al. observed that halide perovskite-based solar cells using a nano-mesoporous TiO₂ layer exhibited a slower decay rate, which translates to a longer effective electron lifetime, reduced charge recombination with enhanced charge collection efficiency [44]. Similarly, Xiao et al. reported relatively long charge carrier lifetimes under 0.3 sun illumination [45]. Carrier lifetimes in the microsecond range suggest a lack of non-radiative pathways, and such extended carrier lifetimes can fundamentally lead to high V_oc. We speculate that the primary factor contributing to the extended carrier lifetimes is a combination of enhanced perovskite crystal grain size and effective passivation achieved through the crystalline Al-doped TiO₂ layer [46]. Two plausible explanations can be offered for the increased charge carrier lifetime. First, owing to the crystalline Al-doping of the TiO₂ buffer layer located between the pure TiO₂ and perovskite layer, the concentration of deep trap states, which serve as recombination centers, diminishes with increasing Al content. Consequently, the effective charge carrier lifetime is prolonged owing to a reduction in Shockley–Read–Hall (SRH) recombination. Second, the incorporation of Al-TiO₂ into the perovskite MAPbI₃ lattice may introduce additional defects, which are shallow in nature and act as dopants for the MAPbI₃ lattice. Unlike deep trap states located in the middle of the band gap, shallow traps positioned near the conduction or valence band of the semiconductor partially trap charge carriers, which must then be released back into the band prior to recombination. In this scenario, up to a certain doping level, the charge carrier lifetime would be extended because thetrapping-and-release events would decelerate the actual recombination process. Yang et al. reported that the CH₃NH₃Br-treated PSCs exhibited improved charge collection and surface passivation properties, possibly owing to reduced defect states [47].

Based on our comprehensive experimental observations, we propose a plausible mechanism for the Al-doping processes in TiO₂ buffer layers as follows. As depicted in Figure 9, when oxygen vacancies or Ti interstitials arise in the TiO₂ lattice, Ti ions are preferentially substituted by Al ions in substitutional sites rather than interstitial sites. This substitution triggers the transformation of Ti(IV) into both Ti(III) and Ti(IV)⁺ + e⁻ forms owing to the presence of defect [refer to Figure 9a]. Subsequently, Ti(III) is replaced by Al(III), which exhibits enhanced stability, leading to changes in optical and electrical properties [refer to Figure 9b]. In a solar cell, an electrical device, semiconductors such as Si, TiO₂, and perovskite material are subjected to light, which is converted into electricity via the photovoltaic effect. Electrons are either excited through the absorption of light, or if the material’s bandgap energy can be bridged, electron–hole pairs are generated, simultaneously creating a voltage potential. Consequently, charge carrier and electron diffusion, as well as electron recombination events, frequently occur in a solar cell. The charge carriers in the solar cell move through the semiconductor to counteract the voltage potential, which serves as the drifting force for electron movement. Additionally, electrons can be forced to move by diffusion from areas of higher electron concentration to areas of lower electron concentration. Therefore, to optimize the efficiency of a solar cell, it is highly desirable to collect as many charge carriers as possible at the cell’s electrodes. This implies that electron recombination, which can compromise solar cell efficiency, must be minimized. Consequently, we should prioritize increasing carrier lifetime while maintaining minimal electron recombination, suggesting that steps 1 and 5 in Figure 3 are of greater significance than the other steps. By successfully growing higher-quality crystals with minimal defects, we can achieve considerably higher ECE than current levels. This occurs because efficient electron–hole separation is hindered in a defective crystal lattice. Additionally, steps 3 and 4 in Figure 3 will proceed at a faster rate, which can adversely impact the recombination rate, ETL, and overall solar cell performance.

4. Conclusions

In this study, we introduce crystalline Al-doped TiO₂ buffer layers for the fabrication of mesoscopic PSCs with the aim of enhancing photovoltaic performance. Our approach focuses on reducing interfacial resistance and increasing recombination resistance. As a result, the crystalline Al-doped TiO₂ buffer layer increases the energy level of the conduction band, facilitating the efficient transport of electrons to the electrode owing to a passivation effect. We achieved a remarkable solar cell efficiency of 11.87% with a PSC structure of Cell (b) using a 7 mol% crystalline Al-doped TiO₂ buffer layer. The validity of our approach is corroborated by J-V and EIS analysis, as well as theoretical calculations of various electron transport parameters. This is a remarkable achievement because we have obtained a substantial enhancement in power energy conversion efficiency of nearly 50% from 6.37% [obtained from Cell (c)] to 11.87%, by incorporating the newly developed ETL. With the development of new energy sources that can be synthesized from recycled photocatalytic materials (such as TiO₂ powder) at a relatively low cost, the commercialization of PSCs has become a viable prospect.