Quantum Chemical Topological Analysis of [2Fe2S] Core in Novel [FeFe]-Hydrogenase Mimics

Abstract

Synthetic mimics of the active site of [FeFe]-hydrogenase enzymes are important in the context of catalytic hydrogen production for future energetic applications. Providing a detailed quantum chemical description of the catalytic center of such mimics contributes to a better understanding of their behavior in hydrogen production processes. In this work, the analysis of bonds in the butterfly [2Fe2S] core in a series of complexes based on recently synthesized [FeFe]-hydrogenase mimics has been carried out using a wide range of quantum chemical topological methods. This series includes hexacarbonyl diiron dithiolate-bridged complexes with the bridging ligand bearing a five-membered carbon ring functionalized with diverse groups. The quantum theory of atoms in molecules (QTAIM) and the electron localization function (ELF) provided detailed characteristics of Fe–Fe and Fe–S bonds in the [2Fe2S] core of the complexes. A relatively small amount of strongly delocalized electron charge is attributed to the Fe–Fe bond. It was established how the topological parameters of the Fe–Fe and Fe–S bonds are affected by the five-membered carbon ring and its functionalization in the bridging dithiolate ligand. Next, one of the first applications of the interacting quantum atoms (IQA) method to [FeFe]-hydrogenase mimics was presented. The pairwise interaction between the metal centers in the [2Fe2S] core turns out to be destabilizing in contrast to the Fe–S interactions responsible for the stabilization of the entire core.

1. Introduction

Synthetic organometallic complexes inspired by the active site of [FeFe]-hydrogenase enzymes have attracted much attention for the past two decades [1,2,3,4,5,6,7]. [FeFe]-Hydrogenases are well known in nature for their catalytic activity toward the reversible conversion of protons and electrons into dihydrogen with high turnover frequencies [5,6,7], which nowadays is also recognized as a promising approach for H₂ production within green energy solutions [8,9]. In naturally occurring [FeFe]-hydrogenases, this conversion is thought to take place in a dithiolate-bridged diiron subsite [10], whose [2Fe2S] core displays a butterfly geometrical arrangement [1]. The potential of H₂ production processes for future energetic applications has generated a great deal of interest in the design and consequent synthesis of organometallic complexes demonstrating structural and functional resemblance to the catalytic site of [FeFe]-hydrogenase enzymes [6,7,11]. The resulting [FeFe]-hydrogenase mimics are often based on the [2Fe2S] core with its metal centers coordinated by terminally bound CO ligands and by a bridging dithiolate, in which two sulfur atoms may be linked via three carbon atoms (μ-S₂C₃) of a larger substituted moiety [6]. For example, a series of hexacarbonyl diiron dithiolate-bridged complexes with the bridging ligand bearing a five-membered carbon ring functionalized by aryl, hetaryl, and/or ferrocenyl groups have quite recently been synthesized and structurally characterized by X-ray crystallography [12]. However, most [FeFe]-hydrogenase mimics are much less efficient in H₂ production than the naturally occurring enzymes [1,2,3]. What is worse, many mimics tend to form a catalytically inactive μ-hydride complex [13]. Changes in the bridging and terminal ligands of the mimics have an influence on the electronic properties of their Fe centers, and consequently, on the probability of μ-hydride complex formation [14]. Thus, a detailed characterization of the electronic structure features of the [2Fe2S] core in [FeFe]-hydrogenase mimics may help in a better understanding of their behavior in the reduction of protons to dihydrogen [14].

In continuation of our ongoing interest in the reactivity and properties of aromatic thioketones [15,16,17,18], a series of novel [FeFe]-hydrogenase mimics 1, 3–5, and 7 (Figure 1) have recently been synthesized in reactions of α,β-unsaturated aromatic thioketones (that is, thiochalcones) with triiron dodecacarbonyl Fe₃(CO)₁₂ [12]. For 3, 5, and 7, their single crystals suitable for X-ray diffractometry have been obtained [12] and their XRD structures have also been used to benchmark density functional theory (DFT) methods [19]. In the present work, these newly synthesized mimics, their congeners with diverse Ar¹ and Ar² groups (Figure 1), the archetype of the [FeFe]-hydrogenase catalytic site, namely [Fe₂(pdt)(CO)₆] (pdt = propanedithiolate) 10, as well as the by-product 11 from the synthesis of 4, were considered to provide insight into the nature of bonds in their [2Fe2S] core and to establish whether these bonds are affected by the five-membered carbon ring of the dithiolate ligand and its functionalization with Ar¹ and Ar². To that end, the [2Fe2S] core of complexes 1–11 was analyzed from a quantum chemical topology (QCT) perspective.

In general, the computational QCT methods [20] operate on real physical space in which the spatial distributions of scalar fields such as the charge density (ρ) in the quantum theory of atoms in molecules (QTAIM) [21] and the electron localization function (ELF) [22] are studied to provide detailed information on the nature of chemical bonds. As an extension of the long-known QTAIM, the non-covalent interactions (NCI) index [23,24] later introduced an additional scalar field, namely the reduced density gradient (RDG), into the analysis of ρ to identify, in a semi-quantitative fashion, the real-space regions of weak interactions. By modifying the RDG slightly, the interaction region indicator (IRI) [25] was also proposed to visually reveal both strong covalent bonds and weak interactions in chemical systems. The theory of interacting quantum atoms (IQA) [26] is a profound extension of the QTAIM that has lately gained great popularity because it provides an exact partition of total molecular energies into intra- and inter-atomic quantities with clear physical meaning and no external references [27].

The aforementioned QCT methods were employed in this work to shed light on the nature of bonds in the [2Fe2S] core of 1–11. In addition to the metal–metal interaction in this core, we particularly focus on the bonds between the metal centers and the bridging dithiolate of 1–11 because generally much less is known about such metal–ligand bonds in contrast to a wealth of information on transition metal–carbonyl bonds [28,29]. To the best of our knowledge, the use of QCT methods for studying [FeFe]-hydrogenase mimics with the μ-S₂C₃ linker of a dithiolate ligand has been restricted mostly to the QTAIM analysis of archetypical complex 10 so far [30,31,32,33]. This methodological narrowing prompted us to utilize here a wide range of QCT methods.

2. Computational Details

The geometrical structures of complexes 1–11 in the singlet ground state were fully optimized at a spin-unrestricted DFT level of theory. The initial molecular geometries of 3, 5, 7, 10, and 11 were extracted directly from the corresponding XRD crystal structures [12,34]. These structures were also employed to generate the initial geometries of the remaining mimics by replacing Ar¹ and Ar² with the appropriate substituents (Figure 1). The geometry optimizations were carried out at the TPSSh/def2-SVP level of theory [35,36], which is in compliance with the computational methodology of our previous study [12]. Harmonic vibrational frequency calculations were carried out at the same level of theory to verify that each optimized geometrical structure corresponded to a local energy minimum. For comparison, an additional set of geometry optimizations and harmonic vibrational frequency calculations was performed using the B3LYP functional [37,38]. Aside from another functional, a more extended Karlsruhe basis set, that is, def2-TZVP [36], was also used in single-point energy calculations. The charge density generated from the unrestricted wave function at the resulting DFT levels was the starting point for analyses by means of such QCT methods as the IRI, the QTAIM, the source function (SF) [39], and the ELF. Because of its immense computational cost and available implementation, the IQA method was applied to the charge density obtained from the B3LYP/def2-SVP single-point energy calculations. Within the IQA partition of energy, a generalization based on grouping atoms into fragments in an approach referred to as the interacting quantum fragments (IQF) analysis [40] was also taken into account.

Geometry optimizations and harmonic vibrational frequency calculations were carried out using the TURBOMOLE 7.7 program [41]. Extended wavefunction files (.wfx files) were provided by the Gaussian 16 program [42] in a series of single-point energy calculations. The IRI and the ELF were computed with the latest development version of Multiwfn 3.8 [43]. The QTAIM, SF, and IQA implementations available in AIMAll 19.10.12 were used [44]. Graphical representations were generated by means of the VMD 1.9.3 [45] and AIMStudio 19.10.12 [44] programs. Further computational details can be found in Section S1 in Supplementary Materials. A link to the repository of Cartesian coordinates for the optimized structures of 1–11 is provided in Section S2.

3. Results and Discussion

3.1. Molecular Geometries

Before the analysis of QCT results commences, a geometrical characterization of the [2Fe2S] core in complexes 1–11 optimized at the TPSSh/def2-SVP and B3LYP/def2-SVP levels of theory needs to be presented briefly. The bond lengths calculated for the [2Fe2S] core of 1–11 are collected in

Table 1. Calculated and available experimental bond lengths (in pm) for the [2Fe2S] core of complexes 1–11 ^a.

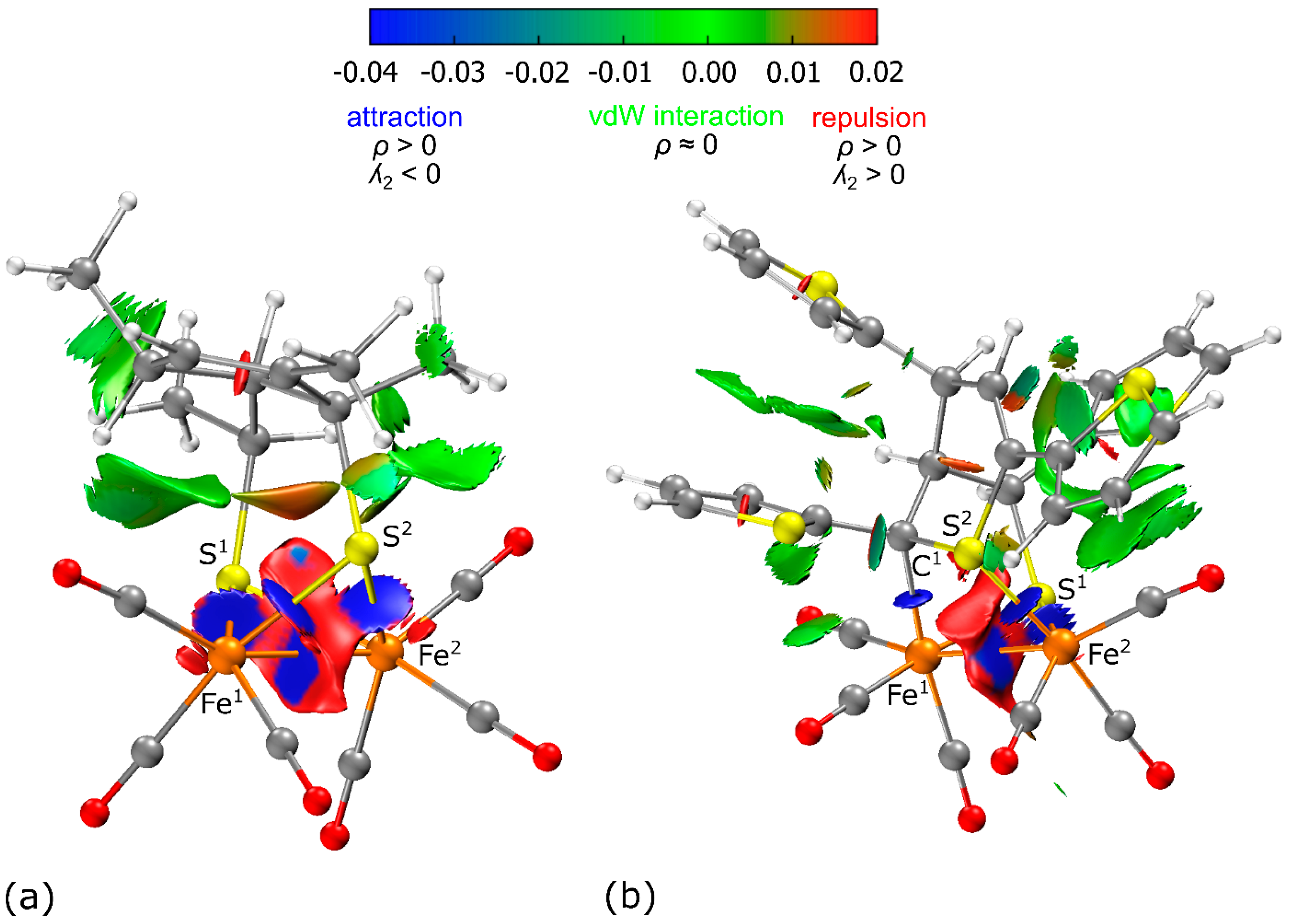
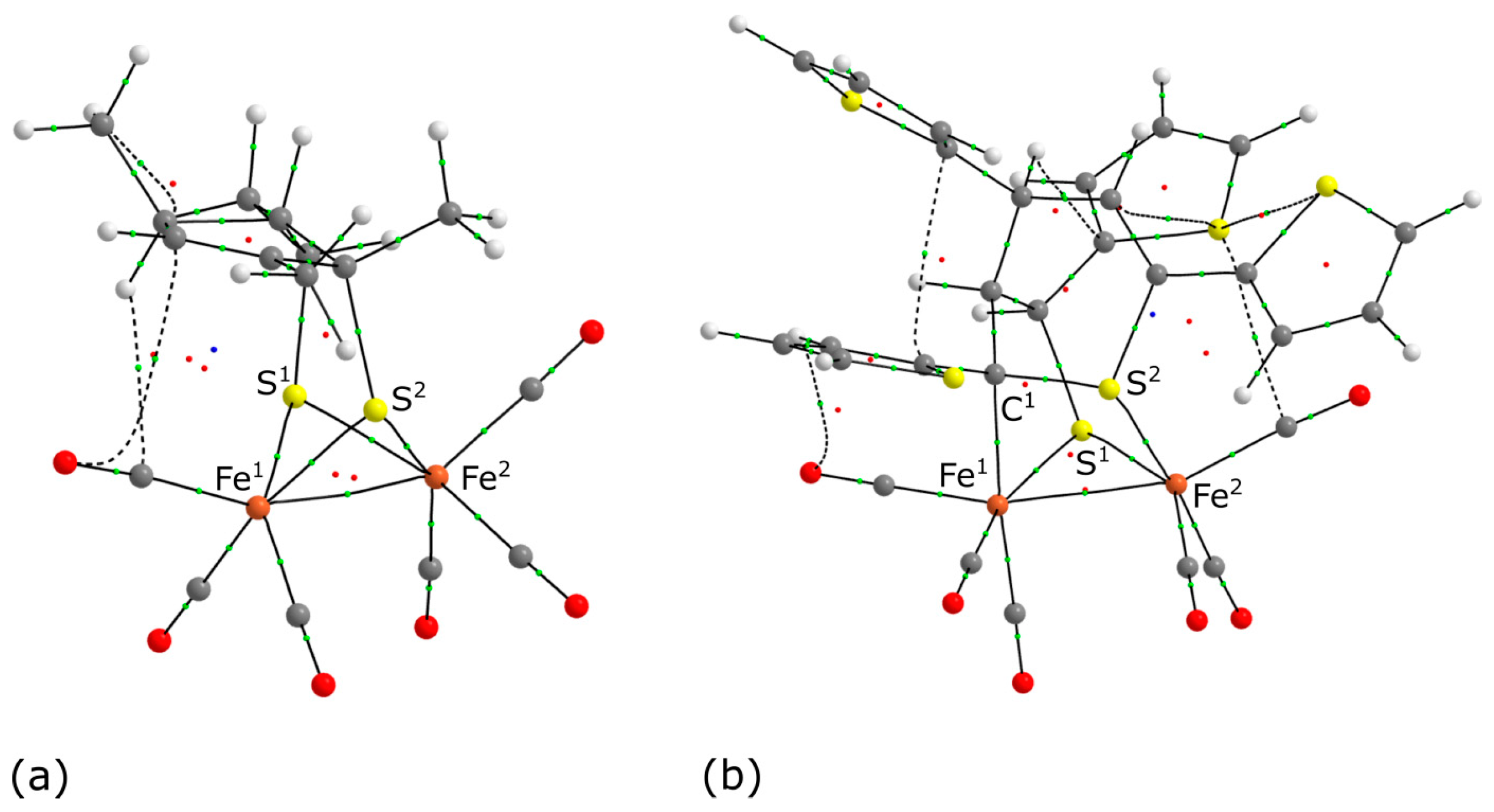
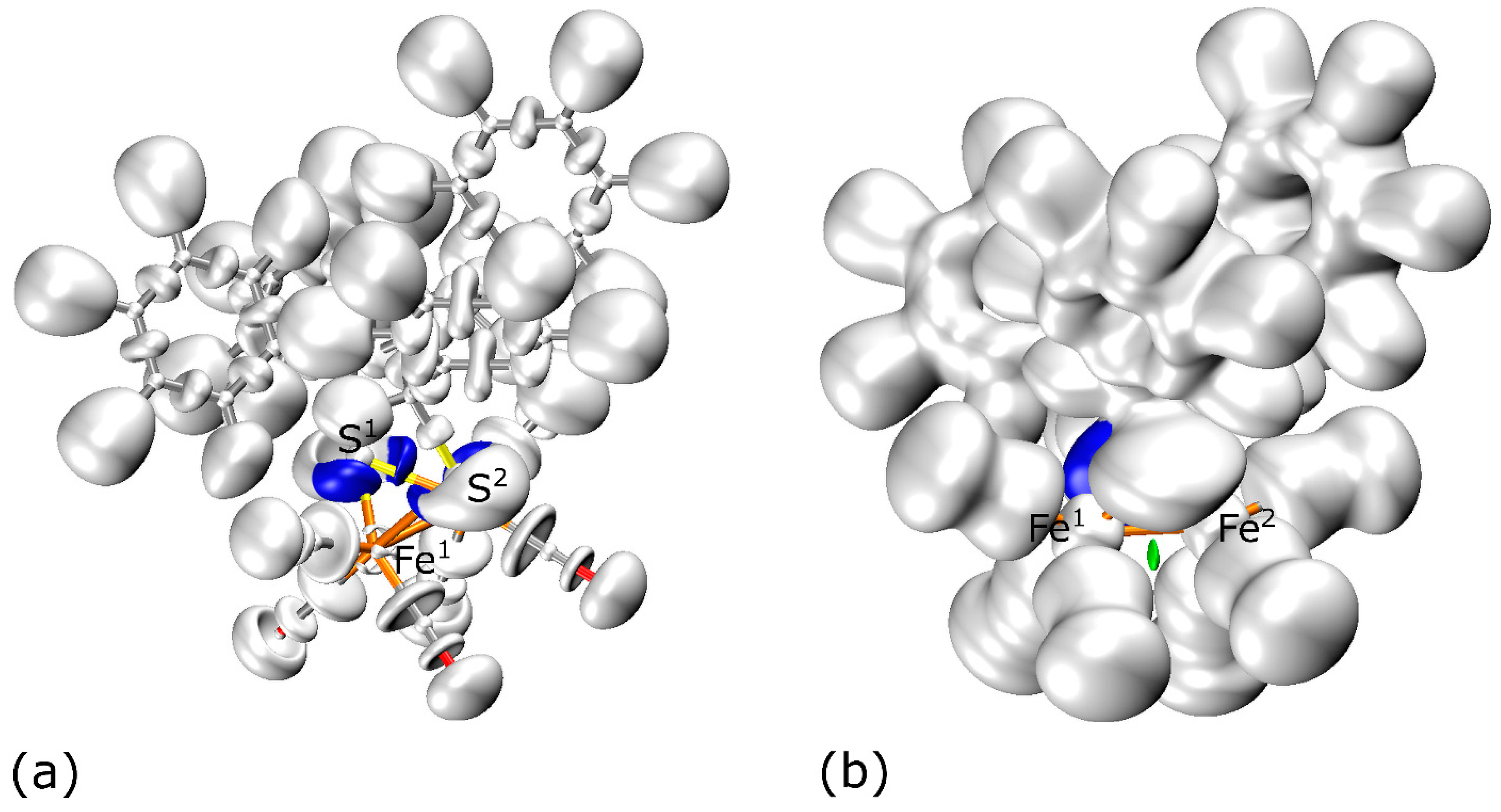
Complex	Fe1–Fe2	Fe1–S1	Fe1–S2	Fe2–S1	Fe2–S2	Average Fe–S
1	247.3 (249.9)	227.9 (230.4)	231.2 (234.0)	231.0 (233.7)	228.4 (230.6)	229.6 (232.2)
2	247.6 (249.9)	227.7 (230.3)	230.7 (233.9)	230.6 (233.5)	228.1 (230.7)	229.3 (232.1)
3	247.6 (250.2) [251.5]	227.5 (230.1) [224.1]	230.7 (233.5) [227.9]	229.8 (232.6) [226.2]	228.4 (230.7) [225.1]	229.1 (231.7)
4	247.8 (250.0)	227.5 (230.2)	230.5 (233.8)	229.5 (232.9)	228.3 (230.8)	229.0 (231.9)
5	248.9 (251.3) [250.8]	227.0 (229.3) [224.1]	229.2 (232.1) [227.3]	227.4 (230.1) [225.3]	228.2 (230.6) [224.9]	228.0 (230.5)
6	248.5 (251.0)	228.2 (230.8)	228.4 (230.8)	227.2 (229.5)	229.5 (232.4)	228.3 (230.9)
7	248.7 (251.3) [251.5]	227.9 (230.3) [223.2]	228.3 (230.7) [224.8]	226.9 (229.2) [225.2]	229.6 (232.2) [225.0]	228.2 (230.6)
8	248.6 (251.1)	228.0 (230.5)	228.2 (230.8)	226.7 (229.2)	229.7 (232.3)	228.2 (230.7)
9	248.2 (250.8)	227.2 (229.7)	229.8 (232.4)	228.3 (230.9)	228.6 (230.9)	228.5 (231.0)
10	248.4 (250.9) [251.0]	228.2 (230.8) [224.9]	228.2 (230.8) [225.4]	228.9 (231.7) [224.9]	228.9 (231.7) [225.4]	228.6 (231.3)
11	260.3 (264.3) [263.7]	223.8 (225.5) [221.4]	286.7 (291.5) [286.5]	227.5 (230.4) [224.3]	229.7 (233.1) [226.4]	241.9 (245.1)

^a Results obtained from the TPSSh/def2-SVP and B3LYP/def2-SVP calculations are shown without and in parentheses, respectively. Experimental results [12,34] are given in square brackets. The numbering of atoms is the same as in Figure 1.

. The [2Fe2S] core of 1–9 and 11 displays a butterfly arrangement with different lengths of its four Fe–S metal–ligand bonds due to the asymmetry of the bridging dithiolate ligand. It is evident that the TPSSh density functional generally yields somewhat shorter metal–metal and metal–ligand bonds in the [2Fe2S] core than those obtained from B3LYP. Comparison with the available experimental results derived from single-crystal X-ray diffraction measurements [12,34] reveals that the structures of the [2Fe2S] core are calculated with an accuracy of several pm, which is typical of DFT optimizations with double-ζ basis sets [46] and the neglect of crystal packing [19,47]. Both TPSSh and B3LYP overestimate the Fe–S bond lengths of 3, 5, 7, 10, and 11, whereas the calculated Fe–Fe bond tends to be too short relative to the experimental results.

The distance between the metal centers in complexes 1–10 is only slightly longer than the typical value of 232 pm for a single Fe–Fe covalent bond [48]. This geometrical prerequisite, along with the attainment of the favored 18-electron metal configuration, suggests the formation of a direct Fe–Fe bond in 1–10. For 9 and 10, their calculated Fe–Fe bond lengths are practically identical, and thus, it can be concluded that the presence of the five-membered carbon ring in the dithiolate bridge of 9 has a marginal effect on the Fe–Fe bond length. On the other hand, the introduction of aryl, hetaryl, and ferrocenyl substituents into the five-membered carbon ring allows us to distinguish certain trends in the length of Fe–Fe. In general, the Fe–Fe bond lengths calculated for 1–8 cluster around the value observed for the simplified (that is, methyl-substituted) analog 9. However, complexes 1–4 demonstrate slightly shorter Fe–Fe bonds than complex 9. By contrast, the presence of ferrocenyl groups in 5–8 results in a minor elongation of Fe–Fe bond as compared to its length in 9.

As for the Fe–S metal–ligand bonds of 1–10, their calculated lengths exceed by 8–15 pm the typical value of 219 pm for a single Fe–S covalent bond [48]. Across the series of 1–10, it is difficult to notice a clear trend in the length between particular Fe and S atoms. Instead, keeping track of changes in the average length of four Fe–S bonds allows us to single out the effect of Ar¹ and Ar² conclusively (Table 1). Then, the Fe–S bonds of 1–4 are longer on average than those calculated for 9. The opposite trend can be observed for the average Fe–S bond lengths of 5–8.

Complex 11 adopts a distorted geometry of its [2Fe2S] core that strikingly stands out from the [2Fe2S] geometries found for 1–10. The Fe–Fe bond of 11 undergoes a noticeable elongation which is accompanied by a rearrangement in the coordination sphere of the Fe¹ center (Figure 1). The S² atom is moved away from the Fe¹ center, while the C¹ atom enters the coordination sphere of Fe¹. As a result, the Fe¹–S² bond is longer by at least 57 pm than the remaining three Fe–S bonds. The calculated Fe¹–C¹ bond length amounts to 213.1 pm and 216.5 pm at the TPSSh/def2-SVP and B3LYP/def2-SVP levels, respectively. The former perfectly reproduces the experimental result.

3.2. IRI Analysis

A preliminary insight into the interactions occurring in the [2Fe2S] core of 1–11 was obtained by means of the IRI topological analysis yielding a visual representation of real-space regions where various kinds of interactions could be identified. In Figure 2, the IRI isosurface is plotted for the [2Fe2S] core of complexes 9 and 11 that were optimized at the TPSSh/def2-SVP level of theory.

The IRI isosurface for the [2Fe2S] core of 9 is essentially identical to those of 1–8 and 10. Within the [2Fe2S] core of 9, each Fe–S interaction is characterized by a blue IRI area that is practically round in shape with its center lying on the axis linking these Fe and S atoms. Such features of the IRI isosurface signal the presence of chemical (covalent) bonds, the metal–ligand bonds in our case. Similarly, a blue area of the IRI isosurface can be observed between Fe¹ and Fe², indicating the region of a covalent interaction involving the metal centers. This area turns into red while moving away from the Fe–Fe bond axis, which in turn signals the appearance of repulsive interactions due to steric congestion inside two three-membered rings formed by one S and two Fe atoms.

Within the [2Fe2S] core of 11, the IRI isosurface delineates a blue disk transversely across the Fe¹–C¹ axis, in addition to three Fe–S blue areas of attractive interactions. This implies the presence of four covalent metal–ligand bonds in complex 11. There is also an attractive interaction between the metal centers. The complex does not exhibit any covalent metal–ligand bond between Fe¹ and S² because no blue IRI area shows up between these atoms.

3.3. QTAIM Analysis

Next, the conventional QTAIM topological analysis of ρ was performed to characterize the properties of bonds in the [2Fe2S] core in 1–11. The QTAIM molecular graphs of 9 and 11 are plotted in Figure 3. With the aim of plotting these molecular graphs, the geometrical structure of the complexes and their ρ distribution were calculated at the TPSSh/def2-SVP level of theory. Again, complex 9 was selected as the representative of 1–10 because its molecular graph depicts the [2Fe2S] core sharing common topological features to the whole series of these complexes. The QTAIM analysis of the [2Fe2S] core in 9 detects a bond path (BP) connecting the metal centers, as well as four BPs associated with the Fe–S metal–ligand bonds. Along each of the BPs, which mark out the lines of concentrated ρ linking pairs of atomic centers, there is a saddle point in ρ, called the bond critical point (BCP). From the QTAIM point of view, the presence of a BP and a BCP between two atoms meets the necessary and sufficient condition that these atoms are bonded to one another [49]. The five BPs within the [2Fe2S] core form two adjacent rings, each of which involves one Fe–Fe and two Fe–S BPs, and thus, they give rise to two ring critical points. These ring critical points are located in the regions earlier encompassed by an IRI isosurface mapped with red color where repulsive interactions were revealed (Figure 2). The QTAIM molecular graph for complex 11 also shows five BPs within its [2Fe2S] core, yet the Fe¹–S² BP is replaced with the Fe¹–C¹ one. Obviously, the different QTAIM topology for the [2Fe2S] core of 11 reflects changes in its geometry and in the coordination of the Fe¹ center.

To obtain more information about the nature of Fe–Fe and Fe–S bonds, the local topological properties of ρ at the corresponding BCPs were examined. The QTAIM characteristics of Fe–Fe bond locally at its BCP are summarized in

Table 2. QTAIM parameters (in atomic units) at the BCP on the path linking Fe¹ and Fe² in complexes 1–11 ^a.

Complex	ρBCP	∇2ρBCP	|VBCP|/GBCP	GBCP/ρBCP	HBCP	δ
1	0.0527 (0.0528)	0.0444 (0.0686)	1.604 (1.443)	0.5312 (0.5833)	−0.0169 (−0.0136)	0.470 (0.477)
2	0.0526 (0.0527)	0.0439 (0.0685)	1.606 (1.442)	0.5297 (0.5826)	−0.0169 (−0.0136)	0.470 (0.477)
3	0.0525 (0.0526)	0.0442 (0.0691)	1.604 (1.439)	0.5313 (0.5849)	−0.0169 (−0.0135)	0.471 (0.477)
4	0.0524 (0.0525)	0.0440 (0.0693)	1.606 (1.437)	0.5313 (0.5858)	−0.0169 (−0.0134)	0.470 (0.476)
5	0.0517 (0.0518)	0.0430 (0.0694)	1.608 (1.429)	0.5298 (0.5862)	−0.0167 (−0.0130)	0.467 (0.474)
6	0.0519 (0.0520)	0.0432 (0.0689)	1.607 (1.434)	0.5295 (0.5842)	−0.0167 (−0.0132)	0.471 (0.478)
7	0.0518 (0.0520)	0.0429 (0.0689)	1.608 (1.433)	0.5289 (0.5841)	−0.0167 (−0.0131)	0.470 (0.477)
8	0.0518 (0.0520)	0.0435 (0.0695)	1.605 (1.430)	0.5311 (0.5868)	−0.0167 (−0.0131)	0.467 (0.474)
9	0.0521 (0.0521)	0.0441 (0.0700)	1.603 (1.429)	0.5331 (0.5888)	−0.0168 (−0.0132)	0.469 (0.475)
10	0.0518 (0.0517)	0.0451 (0.0717)	1.596 (1.418)	0.5383 (0.5954)	−0.0166 (−0.0129)	0.479 (0.484)
11	0.0445 (n/a)	0.0270 (n/a)	1.683 (n/a)	0.4777 (n/a)	−0.0145 (n/a)	0.429 (0.433)

^a Results derived from the TPSSh/def2-SVP and TPSSh/def2-TZVP calculations are shown without and in parentheses, respectively. The numbering of atoms is the same as in Figure 1.

for 1–11 in their geometries optimized at the TPSSh/def2-SVP level of theory. The BCP between the Fe¹ and Fe² atoms of 1–11 is described by relatively low values of ρ_BCP (<0.1 atomic units) and its Laplacian (∇²ρ_BCP < 0.1 atomic units). The latter adopts the plus sign, suggesting a region of charge depletion around the BCP and the closed-shell category of inter-atomic interaction [21]. The magnitudes of ρ_BCP and ∇²ρ_BCP for the BCP of Fe–Fe in 1–11 are quite typical of formally single metal–metal bonds in binuclear complexes [50,51], including those with diiron centers [52]. Moreover, the ρ_BCP and ∇²ρ_BCP values calculated for 10 are in good agreement with earlier theoretical results reported for this archetypical complex [30]. There are also other local QTAIM parameters that are more sensitive to the nature of bonds than the ρ_BCP itself or ∇²ρ_BCP. The total energy density at the BCP of Fe–Fe (H_BCP), which is the sum of the potential energy density (V_BCP) and the kinetic energy density (G_BCP), is negative yet close to zero. Thus, a certain amount of covalency may be assigned to the interaction between Fe¹ and Fe² [53]. The negative value of H_BCP results from the domination of V_BCP over G_BCP; the total amount of kinetic energy (G_BCP/ρ_BCP) is small (<<1). Moreover, the adimensional ratio of energy densities (|V_BCP|/G_BCP) falls into the range between 1.0 and 2.0, and therefore, it categorizes the Fe–Fe interaction as intermediate between pure closed shell (that is, ionic) and pure electron shared (that is, ‘classical’ covalent) [54]. The values of the energy densities at the BCP of Fe–Fe conform with the QTAIM criteria for metallic bonds [54,55]. The calculated values of the delocalization index (δ) [56] between Fe¹ and Fe² in 1–11 also support the conclusion on the partial covalent character of the Fe–Fe bond. These values are slightly smaller than 0.5, which means that approximately half an electron is shared between the metal centers.

Variations in the QTAIM characteristics at the BCP of Fe–Fe can be noticed upon the substitution of Ar¹ and Ar² in 1–8. These variations are rather small in magnitude, yet they disclose important regularities. The ρ_BCP and ∇²ρ_BCP values in 1–4 are larger than in 9, which is associated with the shortening of the Fe–Fe bond in the former. The opposite trend in ρ_BCP and ∇²ρ_BCP pertains to complexes 5–8, in which the elongation of their Fe–Fe bonds is observed. Comparison of the δ values between the metal centers of 1–9 and 10 indicates that the five-membered ring of dithiolate ligands leads to a decrease in the number of electrons shared between the metal centers. The decrease in the delocalization index between Fe¹ and Fe² is more evident for complex 11. The elongated Fe–Fe bond of this complex quenches the electron sharing, and this is accompanied by smaller ρ_BCP and ∇²ρ_BCP values.

In regard to the Fe–S bonds in 1–10, all four BCPs between the Fe and S atoms in each complex show much the same QTAIM characteristics. The following discussion relies on the data gathered in

Table 3. QTAIM parameters (in atomic units) at the BCP on the path linking Fe¹ and S¹ in complexes 1–11 ^a.

Complex	ρBCP	∇2ρBCP	|VBCP|/GBCP	GBCP/ρBCP	HBCP	δ
1	0.0744 (0.0790)	0.2306 (0.1749)	1.159 (1.369)	0.9213 (0.8766)	−0.0109 (−0.0255)	0.688 (0.721)
2	0.0747 (0.0793)	0.2313 (0.1753)	1.160 (1.370)	0.9218 (0.8768)	−0.0110 (−0.0257)	0.688 (0.722)
3	0.0749 (0.0796)	0.2336 (0.1772)	1.159 (1.368)	0.9272 (0.8814)	−0.0111 (−0.0258)	0.689 (0.723)
4	0.0749 (0.0796)	0.2338 (0.1774)	1.159 (1.368)	0.9279 (0.8821)	−0.0110 (−0.0258)	0.687 (0.721)
5	0.0765 (0.0811)	0.2296 (0.1719)	1.174 (1.385)	0.9081 (0.8620)	−0.0121 (−0.0269)	0.698 (0.731)
6	0.0740 (0.0785)	0.2276 (0.1723)	1.163 (1.371)	0.9183 (0.3972)	−0.0110 (−0.0254)	0.678 (0.711)
7	0.0745 (0.0790)	0.2293 (0.1735)	1.164 (1.372)	0.9204 (0.8741)	−0.0112 (−0.0256)	0.679 (0.713)
8	0.0741 (0.0786)	0.2281 (0.1725)	1.162 (1.371)	0.9184 (0.8727)	−0.0110 (−0.0255)	0.680 (0.713)
9	0.0757 (0.0803)	0.2324 (0.1755)	1.165 (1.375)	0.9191 (0.8739)	−0.0115 (−0.0263)	0.697 (0.731)
10	0.0747 (0.0792)	0.2323 (0.1756)	1.159 (1.368)	0.9245 (0.8774)	−0.0110 (−0.0256)	0.687 (0.723)
11	0.0818 (0.0866)	0.2514 (0.1870)	1.180 (1.391)	0.9374 (0.8871)	−0.0138 (−0.0300)	0.713 (0.754)

^a Results derived from the TPSSh/def2-SVP and TPSSh/def2-TZVP calculations are shown without and in parentheses, respectively. The numbering of atoms is the same as in Figure 1.

for the BCP of Fe¹–S¹ in 1–10, but consistent findings come from the analysis of the remaining three BCPs (Tables S1–S3 in Supplementary Materials). The ρ_BCP parameter at the BCP of Fe–S is generally of the same order of magnitude as that at the BCP of Fe–Fe. By contrast, the ∇²ρ_BCP values for the Fe–S bonds are significantly more positive than for the Fe–Fe bond. The negative H_BCP values evidence a certain covalent degree for the Fe–S bonds. Furthermore, the δ values of approximately 0.7 imply that less than one electron is shared (or exchanged) between Fe¹ and S¹. This is in line with the experimental and theoretical findings on the partial covalent character of Fe–S interactions in hydrogenase mimics [57,58]. It is also known that the δ parameter provides an effective way of quantifying Fe–S covalency [58] and its values prove lower Fe–S bond covalency for 1–10 than for biomimetic iron–sulfur clusters containing bridging sulfide and terminal thiolate ligands [58]. Both |V_BCP|/G_BCP and G_BCP/ρ_BCP adopt values that are fairly close to unity for the Fe–S bonds in 1–10. The magnitudes of all these local QTAIM parameters essentially match the QTAIM characteristics of many Fe–S metal–ligand bonds reported previously for iron complexes [52,59,60]. On the basis of the values obtained for these parameters, the Fe–S bonds in 1–10 belong to a transit closed shell class [61], lying between purely ionic and purely covalent limits. More specifically, they can be described as a donor–acceptor kind of bonds [54,55].

The substitution of Ar¹ and Ar² in 1–9 affects the QTAIM parameters at the BCPs of individual Fe–S metal–ligand bonds, and the resulting trends in these parameters essentially follow variations in the lengths of these bonds. Accordingly, longer Fe–S metal–ligand bonds tend to show smaller values of ρ_BCP and δ. The same changes in the topological characteristics of Fe–S bonds in complex 10 are observed upon introducing the five-membered ring into the dithiolate ligand, as occurs in complex 9. For the Fe–S bonds of complex 10, their δ estimations presented in this work agree well with the results of previous calculations [31].

For complex 11, the shortening of its Fe¹–S¹ bond (as well as Fe²–S¹ and Fe²–S²) results in an increase in the absolute values of the local topological parameters describing this bond, but it remains a donor–acceptor character, nonetheless. The QTAIM characteristics of the Fe¹–C¹ bond (Table S4) are essentially similar to that of Fe–S in 11.

The last aspect of the QTAIM analysis that deserves a word of comment is the dependence of the obtained results on the basis sets and DFT functionals used. Extending the basis set from def2-SVP to def2-TZVP usually results in noticeable variations in the values of QTAIM parameters for the [2Fe2S] core of 1–10 (Table 2 and Table 3). This means that the def2-SVP basis set does not suffice to approach the basis set saturation close enough to generate the reasonably converged charge density. Only the ρ_BCP and δ values for Fe¹–Fe² change marginally upon increasing the basis set size. It is worth emphasizing that no BP and the related BCP were found between Fe¹ and Fe² in 11 while using the charge densities obtained from the TPSSh/def2-TZVP and B3LYP/def2-TZVP single-point calculations. This revealed that the topology of the [2Fe2S] core in 11 is close to a catastrophe point relating to the Fe¹−Fe² bond path. In this sense, the QTAIM picture of Fe–Fe in 11 is similar to that reported for Fe₂(μ-S₂)(CO)₆ and Fe₂(CO)₉, in which the presence or absence of an Fe–Fe BCP was also dependent on the basis set used [52,62]. As for the dependence on the density functional used, TPSSh and B3LYP yield quite close values of the QTAIM parameters for the [2Fe2S] core of 1–11 despite differences in the optimized geometries (Tables S5–S9). In consequence, both functionals produce consistent trends in these parameters.

3.4. SF Analysis

We have also involved the SF method to distinguish percentage contributions from individual atoms in the [2Fe2S] core of 1–11 to the accumulation of ρ at the BCPs of Fe–Fe and Fe–S. At the BCP of Fe–Fe in 1–10, two percentage source function (%SF) contributions from the metal centers sum up to merely 8–9%, while the contributions from S¹ and S² amount to 23–24% in total at the TPSSh/def2-SVP level (Table S10). The %SF contribution from the Fe² atom in 11 becomes negative, which means this metal center behaves as a sink, rather than a source, for the ρ_BCP value. The %SF contributions originating from the CO ligands predominate at the BCP of Fe–Fe for all complexes. This seems to construe the Fe–Fe bond in 1–11 as a highly delocalized (non-local, multicenter) interaction that is strikingly different from a typical single covalent bond [63]. As for the ρ_BCP value of each Fe–S metal–ligand bond in 1–11, the S atom forming such a bond provides the leading %SF contribution, and the two linked atoms supply more than half of the ρ_BCP value (Table S11). These relatively high %SF contributions from the bonded atoms speak for a more local character of Fe–S with respect to Fe–Fe. They are also mirrored in the δ values of approximately 0.7 for Fe–S in 1–11.

3.5. ELF Analysis

We move now to the ELF method to inspect an alternative real-space scalar field that can be a valuable indicator of electron localization and the local pairing of electrons. The topology of the ELF for the [2Fe2S] core of 1–11 identifies a disynaptic valence bonding attractor (that is, a local maximum of the ELF) between Fe¹ and Fe². Its essential features are summarized in

Table 4. ELF parameters (in atomic units) for the bonding basin of Fe¹–Fe² in complexes 1–11 ^a.

Complex	ELFmax	$\overline{\mathit{N}}$	λ	$\overline{\mathit{N}}\left({\mathbf{Fe}}^1\right)$	$\overline{\mathit{N}}\left({\mathbf{Fe}}^2\right)$
1	0.469 (0.430)	0.498 (0.457)	0.882 (0.889)	0.241 (0.225)	0.248 (0.230)
2	0.472 (0.433)	0.500 (0.459)	0.881 (0.889)	0.242 (0.225)	0.248 (0.230)
3	0.476 (0.437)	0.505 (0.462)	0.880 (0.888)	0.244 (0.228)	0.251 (0.231)
4	0.476 (0.436)	0.502 (0.457)	0.881 (0.888)	0.245 (0.227)	0.247 (0.228)
5	0.498 (0.456)	0.518 (0.477)	0.876 (0.884)	0.255 (0.237)	0.256 (0.236)
6	0.499 (0.458)	0.521 (0.482)	0.875 (0.883)	0.259 (0.240)	0.256 (0.238)
7	0.500 (0.458)	0.519 (0.482)	0.876 (0.883)	0.256 (0.238)	0.258 (0.240)
8	0.496 (0.455)	0.516 (0.478)	0.876 (0.883)	0.253 (0.237)	0.257 (0.237)
9	0.485 (0.445)	0.509 (0.465)	0.879 (0.887)	0.247 (0.230)	0.253 (0.232)
10	0.510 (0.470)	0.529 (0.489)	0.873 (0.881)	0.263 (0.237)	0.260 (0.247)
11	0.492 (0.451)	0.517 (0.474)	0.880 (0.887)	0.224 (0.207)	0.279 (0.257)

^a Results derived from the TPSSh/def2-SVP and TPSSh/def2-TZVP calculations are shown without and in parentheses, respectively. The numbering of atoms is the same as in Figure 1.

. The localization domain surrounding this attractor in complex 1 calculated at the TPSSh/def2-SVP level of theory is displayed in Figure 4. The Fe–Fe attractor signals a shared electron interaction, yet its small value (ELF_max < 0.5) means a great electron delocalization due to the Pauli repulsion exerted by the charge density concentrated in the core regions of the metal atoms. The basin of this attractor is populated by an average number of electrons ($\overline{N}$) amounting to ca. 0.5e, mainly thanks to the charge density of the atomic basins of Fe¹ and Fe². The contributions from the Fe¹ and Fe² basins are almost equal for each complex except complex 11 for which a greater contribution from Fe² is observed. The relative fluctuation (λ) of the Fe–Fe basin population is high, which in turn confirms that the charge density inside this basin is strongly delocalized. In that regard, the λ values for the Fe–Fe bond in 1–11 are similar to those reported for Fe–Fe in the Fe₄ cluster [64]. The small population and the significant relative fluctuation of ρ for the disynaptic Fe–Fe basin in 1–11 are not typical features of a ‘classical’ covalent bond—rather, they highlight its metallic and essentially delocalized character. This finding agrees with our conclusions yielded by the QTAIM and SF analyses. Moreover, the calculated $\overline{N}$ values of Fe¹–Fe² in 1–10 confirm that the presence of the five-membered carbon ring in the dithiolate ligands decreases the Fe¹–Fe² basin population, which compares with the trend in δ.

The ELF topology of the [2Fe2S] core in 1–10 reveals four valence bonding attractors describing the Fe–S metal–ligand bonds. Not all of them are identified as disynaptic Fe–S attractors: depending on the complex analyzed, at least two are recognized as trisynaptic, corresponding to the basins in which one S atom and two Fe atoms participate. The localization domains connected with the four attractors in complex 1 are marked in color in Figure 4. Several ELF parameters for the Fe¹–S¹ basin of 1–11 as an example of Fe–S metal–ligand bonds in these complexes are collected in

Table 5. ELF parameters (in atomic units) for the bonding basin of Fe¹–S¹ in complexes 1–11 ^a.

Complex	ELFmax	$\overline{\mathit{N}}$	λ	$\overline{\mathit{N}}\left({\mathbf{Fe}}^1\right)$	$\overline{\mathit{N}}\left({\mathbf{S}}^1\right)$
1	0.899 (0.898)	1.615 (1.641)	0.642 (0.640)	0.196 (0.210)	1.405 (1.415)
2	0.900 (0.898)	1.622 (1.646)	0.641 (0.639)	0.197 (0.211)	1.411 (1.420)
3	0.900 (0.898)	1.618 (1.645)	0.642 (0.639)	0.196 (0.210)	1.408 (1.419)
4	0.899 (0.897)	1.593 (1.629)	0.646 (0.642)	0.195 (0.210)	1.384 (1.404)
5	0.896 (0.895)	1.632 (1.650)	0.641 (0.640)	0.204 (0.217)	1.419 (1.423)
6	0.899 (0.898)	1.656 (1.645)	0.634 (0.633)	0.192 (0.201)	1.458 (1.441)
7	0.895 (0.898)	1.632 (1.647)	0.642 (0.634)	0.205 (0.203)	1.419 (1.428)
8	0.895 (0.897)	1.628 (1.650)	0.642 (0.635)	0.203 (0.205)	1.418 (1.438)
9	0.898 (0.896)	1.626 (1.651)	0.642 (0.639)	0.198 (0.213)	1.415 (1.423)
10	0.897 (0.896)	1.540 (1.601)	0.650 (0.644)	0.193 (0.206)	1.339 (1.384)
11	0.891 (0.889)	1.542 (1.587)	0.655 (0.650)	0.206 (0.221)	1.327 (1.357)

^a Results derived from the TPSSh/def2-SVP and TPSSh/def2-TZVP calculations are shown without and in parentheses, respectively. The numbering of atoms is the same as in Figure 1.

. In comparison to the Fe¹–Fe² basin, the Fe¹–S¹ one is characterized by much larger ELF values of its attractor, which suggests a low probability of local parallel spin electron pairing. Instead, finding an antiparallel spin pair may be expected in the region between Fe¹ and S¹. The λ values of the Fe¹–S¹ basin population in 1–11 are still high yet smaller than those of Fe¹–Fe². They reflect a noticeable delocalization of the charge density inside the Fe¹–S¹ basin. Integration of ρ over the Fe¹–S¹ basin yields an $\overline{N}$ value of ca. 1.6e. The population of this basin is determined by the dominant contribution from the atomic basin of S¹, while the contribution from Fe¹ does not exceed 0.25e. The second metal center provides a negligible contribution to the population of the Fe¹–S¹ basin. Even the Fe–S basins that are formally classified as trisynaptic show the contribution from one Fe atom being of one order of magnitude smaller than that from another Fe atom. Nonetheless, the occurrence of the trisynaptic basins suggests a certain degree of electron delocalization across two Fe–S bonds sharing the same sulfur atom. Thus, these bonds tend to become uniform. As a matter of fact, the ELF parameters of four Fe–S metal–ligand bonds in each of complexes 1–10 are very similar (Table 5 and Tables S12–S14) despite the fact that the coordinated sulfur atoms of the dithiolate ligands are formally three-electron donors. According to the ELF analysis, each of these coordinated sulfur atoms possesses a single monosynaptic valence non-bonding attractor corresponding to its lone pair that is not shared with the metal centers. The population of the sulfur lone pair basin is oversaturated by 0.5 to 0.7e, while the Fe–S basins conserve their non-saturated occupations (<2e). Bearing in mind the dominant S-atom contribution to the population of each Fe–S basin, the aforementioned ELF topological features of Fe–S bonds in 1–11 do not match the description of ‘classical’ covalent bonds but rather a donor–acceptor kind of bonds. Such a conclusion drawn from the ELF analysis is in accord with the previous ELF study of Fe–S bonds in iron–oxo porphyrin π-cation radical species [65].

The Fe¹–C¹ bond in complex 11 is characterized by a disynaptic valence bonding attractor between the Fe¹ and C¹ atoms. Similarly to the Fe¹–S¹ bond, the Fe¹–C¹ bond has ELF topological features of a donor–acceptor bond (Table S15). The contribution of ρ from the atomic basin of C¹ predominates in the population of the Fe¹–C¹ valence bonding basin. There is no ELF bonding attractor between Fe¹ and S² in complex 11.

Trends in the ELF description of the Fe–Fe, Fe–S, and Fe–C bonds in the [2Fe2S] core of 1–11 calculated using the TPSSh functional are consistent with those obtained from the B3LYP functional (Tables S16–S20).

3.6. IQA and IQF Analyses

At the last stage of this QCT study, let us turn to the energetics of the Fe–Fe and Fe–S interactions occurring in the [2Fe2S] core of 1–11. The real-space energetic image of these interactions obtained from the IQA method allows us to present a new perspective on their nature and role in the stabilization of 1–11. An insight into this nature rests on the IQA pairwise inter-atomic interaction energy (E_int) partitioned into two components associated with the conventional notions of ionicity and covalency, namely a classical electrostatic component (V_cl) and a purely quantum–mechanical exchange–correlation component (V_xc), respectively. The IQA energies of Fe¹–Fe² and Fe¹–S¹ across the series of complexes 1–11 are collected in

Table 6. Pairwise IQA energies (in atomic units) for Fe¹–Fe², Fe¹–S¹, and four Fe–S bonds in total in complexes 1–11 ^a.

Complex	Fe1–Fe2			Fe1–S1			All Four Fe–S Bonds
	Eint	Vcl	Vxc	Eint	Vcl	Vxc	Eint	Vcl	Vxc
1	0.0304	0.1096	−0.0791	−0.1974	−0.0588	−0.1386	−0.7615	−0.2273	−0.5341
2	0.0306	0.1096	−0.0790	−0.1973	−0.0585	−0.1389	−0.7617	−0.2254	−0.5363
3	0.0304	0.1093	−0.0788	−0.1946	−0.0556	−0.1390	−0.7597	−0.2228	−0.5370
4	0.0306	0.1094	−0.0788	−0.1945	−0.0556	−0.1389	−0.7596	−0.2210	−0.5385
5	0.0288	0.1073	−0.0785	−0.1987	−0.0571	−0.1416	−0.7726	−0.2213	−0.5513
6	0.0285	0.1078	−0.0793	−0.1947	−0.0579	−0.1369	−0.7689	−0.2220	−0.5469
7	0.0287	0.1077	−0.0790	−0.1949	−0.0577	−0.1372	−0.7703	−0.2221	−0.5482
8	0.0293	0.1079	−0.0786	−0.1949	−0.0580	−0.1369	−0.7743	−0.2250	−0.5493
9	0.0296	0.1083	−0.0787	−0.1990	−0.0584	−0.1405	−0.7740	−0.2276	−0.5463
10	0.0260	0.1063	−0.0803	−0.1897	−0.0516	−0.1381	−0.7550	−0.2080	−0.5470
11	0.0326	0.1014	−0.0688	−0.2028	−0.0545	−0.1483	−0.5403	−0.1073	−0.4330

^a Results derived from the B3LYP/def2-SVP single-point energies for the geometries optimized at the TPSSh/def2-SVP level of theory. The numbering of atoms is the same as in Figure 1.

. The IQA results for Fe¹–S¹ share the main features with the remaining three pairs of Fe and S atoms in 1–10 (Table S21).

For each of the studied complexes, the interaction between its metal centers is characterized by a positive value of the E_int energy; thus, this interaction is associated with a destabilization. Its V_cl component adopts a positive value because there is an electrostatic repulsion between the positively charged metal centers (Table S22). The covalent-like V_xc component of Fe¹–Fe² is always stabilizing (i.e., negative) but the electron sharing between the metal centers is too small to compensate for the destabilizing V_cl component. The dominant role of V_cl in the destabilization of Fe–Fe interaction was also observed for a [Fe₂(CO)₈]^2- complex showing a distance of 284.7 pm between its Fe atoms [66]. It is noteworthy that, despite the destabilizing E_int energy, a delocalized multicenter Fe–Fe bond involving carbonyl ligands was found to occur in the [Fe₂(CO)₈]^2- complex. For complex 11, the elongation of its Fe–Fe bond diminishes the electron sharing between the bonded atoms and, in consequence, the E_int energy of Fe–Fe becomes even more positive than for 1–10.

It is instructive to elucidate the destabilizing E_int energy of Fe–Fe in light of the occurrence of the BP linking these atoms, the QTAIM implication being that the two atoms are bonded to one another. According to the IQA interpretation [67], the occurrence of this BP indicates the privileged exchange–correlation channel between the Fe atoms, and it is independent of the overall E_int destabilization due to electrostatic repulsion. The stabilizing V_xc component between the Fe atoms is intense enough to develop a BP linking them.

The pairwise interaction energy of Fe¹–S¹ is always stabilizing for complexes 1–10. The source of this stabilization is the highly negative V_xc component, highlighting the importance of the partial covalent character of the Fe–S bond. Additionally, the V_cl component of Fe¹–S¹ is also energetically favorable due to the electrostatic attraction between the positively charged Fe¹ atom and the negatively charged S¹ atom (Table S22). The IQA description of Fe¹–S¹ in 1–10 can be extended to the Fe¹–S¹ bond of complex 11. Furthermore, the IQA energies of Fe²–S¹ and Fe¹–C¹ in 11 are actually of similar magnitudes to the corresponding energies of Fe¹–S¹ (Tables S21 and S23). However, the negligible charge acquired by the S² atom in 11 (Table S22) diminishes the stabilizing electrostatic interaction of Fe²–S². Bearing in mind that the S² atom is pushed away from the Fe¹ center of 11, their pairwise E_int energy is reduced by one order of magnitude in comparison to the E_int value of Fe¹–S¹. Interestingly, the V_cl value of Fe¹–S² becomes positive due to the destabilizing electrostatic contribution from higher atomic multipole moments (higher than monopoles).

Trends in the E_int energies of Fe–Fe and Fe–S in 1–8 essentially follow the changes in their bond lengths relative to those of the methyl-substituted analog 9. The shortened Fe–Fe bond of 1–4 is associated with the increased destabilization of Fe–Fe, while the elongation of Fe–Fe in 5–8 implies a lesser Fe–Fe destabilization than in 9. The summed E_int energies of all four Fe–S bonds in 1–4 is less stabilizing than that of complex 9, whose Fe–S bonds are shorter. These trends can be simply explained by the distance dependence of the dominant IQA contribution. Growing inter-atomic distances reduce both the electrostatic repulsion between two Fe atoms and the electron sharing between the Fe and S atoms. Compared to complexes 1–9, archetype 10 shows a less destabilizing E_int of Fe–Fe and simultaneously a less stabilizing E_int of all four Fe–S bonds. The introduction of the five-membered carbon ring into the dithiolate ligand of 1–9 results in the growing stabilization of V_cl for all four Fe–S bonds. The V_xc energies of Fe–Fe and Fe–S in 1–11 correlate with the corresponding δ values because both these quantities are a signature of electron sharing.

From the IQA results presented above, it can be inferred that the Fe–S interactions are the main source of [2Fe2S] stabilization in 1–11; even a single Fe–S interaction suffices to compensate the destabilization produced by the interaction between the metal centers. Within the [2Fe2S] core of 1–11, there is also a stabilizing interaction between S¹ and S², but this interaction is extremely weak and thus plays a negligible role in [2Fe2S] stabilization (Table S24).

Finally, the IQF analysis is employed to dissect the interaction between the diiron and dithiolate fragments of complexes 1–11 and thus to establish how the strength and nature of this interaction is affected by the dithiolate ligand as a whole. The calculated IQF E_int energies between these two fragments in 1–11 and their V_cl and V_xc components are listed in

Table 7. IQF energies (in atomic units) between the dithiolate fragment and the diiron Fe¹–Fe² fragment in complexes 1–11 ^a.

Complex	Eint	Vcl	Vxc
1	−0.7397	−0.1836	−0.5561
2	−0.7429	−0.1849	−0.5580
3	−0.7449	−0.1868	−0.5581
4	−0.7468	−0.1874	−0.5594
5	−0.7481	−0.1776	−0.5705
6	−0.7463	−0.1805	−0.5658
7	−0.7469	−0.1795	−0.5674
8	−0.7440	−0.1754	−0.5687
9	−0.7437	−0.1792	−0.5644
10	−0.7374	−0.1739	−0.5635
11	−0.7815	−0.1858	−0.5957

^a Results derived from the B3LYP/def2-SVP single-point energies for the geometries optimized at the TPSSh/def2-SVP level of theory. The numbering of atoms is the same as in Figure 1.

. The IQF E_int energy is stabilizing for all dithiolate ligands and its V_xc component provides the main stabilizing contribution to the interfragment interaction. This stresses again the great relevance of electron sharing to this interaction. From the negative value of the IQF V_cl component, it can be inferred that the interfragment interaction is strengthened by the electrostatic attraction between the positively charged diiron center and the dithiolate ligand, acquiring an ancillary electron charge of ca. –0.5e upon complex formation. A comparison between 9 and 10 reveals that the presence of the five-membered carbon ring in the dithiolate ligand results in an increase in the strength of the interfragment interaction even though the geometry of the [2Fe2S] core remains virtually unchanged (Table 1). Substituting the phenyl groups of 1 with hetaryl and/or ferrocenyl groups leads to more stabilizing IQF E_int energies. Interestingly, the substitution of these phenyl groups with the methyl ones in 9 strengthens the interfragment interaction owing to its greater stabilization from V_xc. The strongest interaction between the diiron center and the dithiolate ligand is observed for the coordination pattern occurring in complex 11.

4. Conclusions

In this work, the nature of bonds formed in the [2Fe2S] core of complexes 1–11 was analyzed from a QCT perspective. The results of the preliminary IRI analysis signals the occurrence of Fe–Fe and Fe–S chemical (that is, covalent) bonds in the [2Fe2S] core, but the subsequent in-depth QTAIM, SF, and ELF analyses agree that both the Fe–Fe and Fe–S bonds are not ‘classical’ covalent bonds.

The Fe–Fe bond in the [2Fe2S] core of 1–11 conforms to the QCT criteria of the metallic kind of bonds, and it is characterized by a relatively small amount of the strongly delocalized electron charge, partly originating from the carbonyl and dithiolate ligands. Four Fe–S bonds in the [2Fe2S] core of 1–10 are recognized as nearly identical and of donor–acceptor type, according to the QCT criteria. The IQA results indicate that the electrostatic repulsion between the positively charged Fe centers in the [2Fe2S] core of 1–11 cannot be counterbalanced by the stabilizing effect of electron sharing between these centers. Notwithstanding the energetically unfavorable IQA interaction between the Fe centers, the stabilization of the [2Fe2S] core is produced by the contributions from the IQA pairwise Fe–S interactions. The QCT results reveal that the effect of the functionalized five-membered carbon ring in the bridging dithiolate ligand on the bonds formed in the [2Fe2S] core of 1–11 is rather small in magnitude but shows regularity. The presence of the five-membered carbon ring decreases the amount of the electron charge shared between the metal centers, which further destabilizes the Fe–Fe interaction. On the other hand, this is accompanied by the growing strength of all four Fe–S interactions, with a regular increase in the stabilizing contribution from the classical electrostatic component. The functionalization of the five-membered carbon ring with ferrocenyl groups exerts an energetically favorable influence on the pairwise inter-atomic interactions in the [2Fe2S] core of complexes 5–8. It obviously means a strengthening of the Fe–S interactions but also a decreased destabilization between the Fe centers. Furthermore, a stronger attractive interaction acts between the entire bridging dithiolate ligand of 5–8 and their diiron center. Similarly, the different coordination pattern observed in complex 11 is associated with a stronger interaction between the dithiolate ligand and the diiron center than in 1–8.

From a practical viewpoint, the QCT perspective provides an insight into the charge density in the catalytic center of [FeFe]-hydrogenase mimics, and therefore, it may aid in determining the dominant site for protonation, which in turn is decisive in efficient hydrogen production processes. In our case, the QCT results for the [2Fe2S] core of complexes 1–11 reveal a relatively small amount of electron charge delocalized between the metal centers bearing highly positive charges. This indicates the occurrence of an electron-poor diiron center which seems to be not readily protonated, thereby affecting the probability of μ-hydride complex formation and the electrocatalytic behavior (redox potentials) of this center in general. It should, however, be stressed that there are also other factors that have not been taken into consideration here (e.g., the nature of terminal ligands), even though they significantly contribute to the electrocatalytic properties of the diiron center [4].

Furthermore, the QCT results show a small effect of dithiolate ligand functionalization on the [2Fe2S] core of 1, 3–5, and 7. This is reflected in their almost identical electrocatalytic behavior, as evidenced by cyclic voltammetry experiments [12].

In light of the above findings, the QCT methods prove to be a useful tool for the analysis of bonds in moderately large organometallic systems such as complexes based on the recently synthesized [FeFe]-hydrogenase mimics [12]. These methods produce a lot of chemically important details supplementing an orbital-based picture of the [2Fe2S] core of [FeFe]-hydrogenase mimics [68,69].