First-Principles-Based Structural and Mechanical Properties of Al3Ni Under High Pressure
Abstract
1. Introduction
2. Methods of Calculation
3. Results and Discussion
3.1. Structural Properties Under High-Pressure Conditions
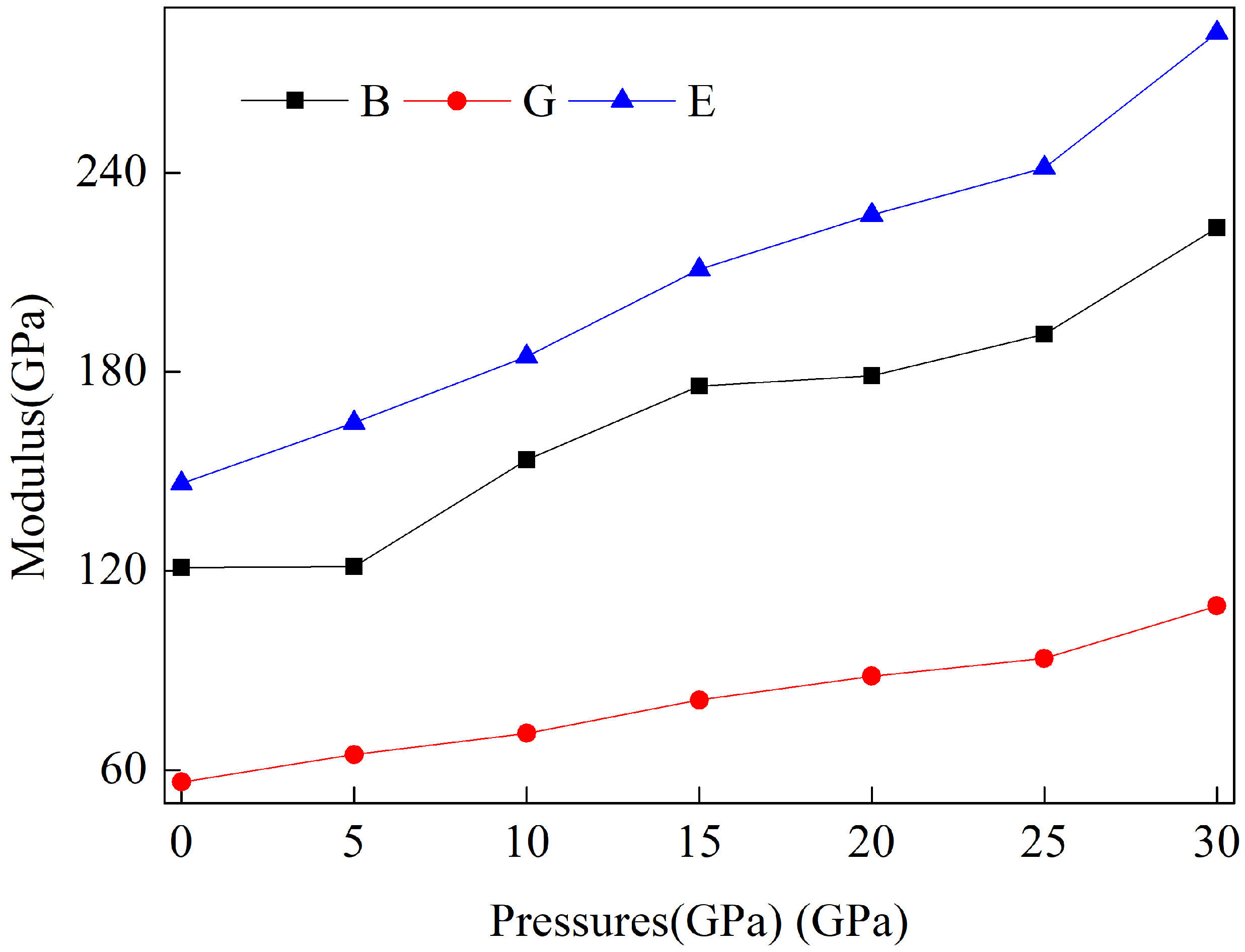
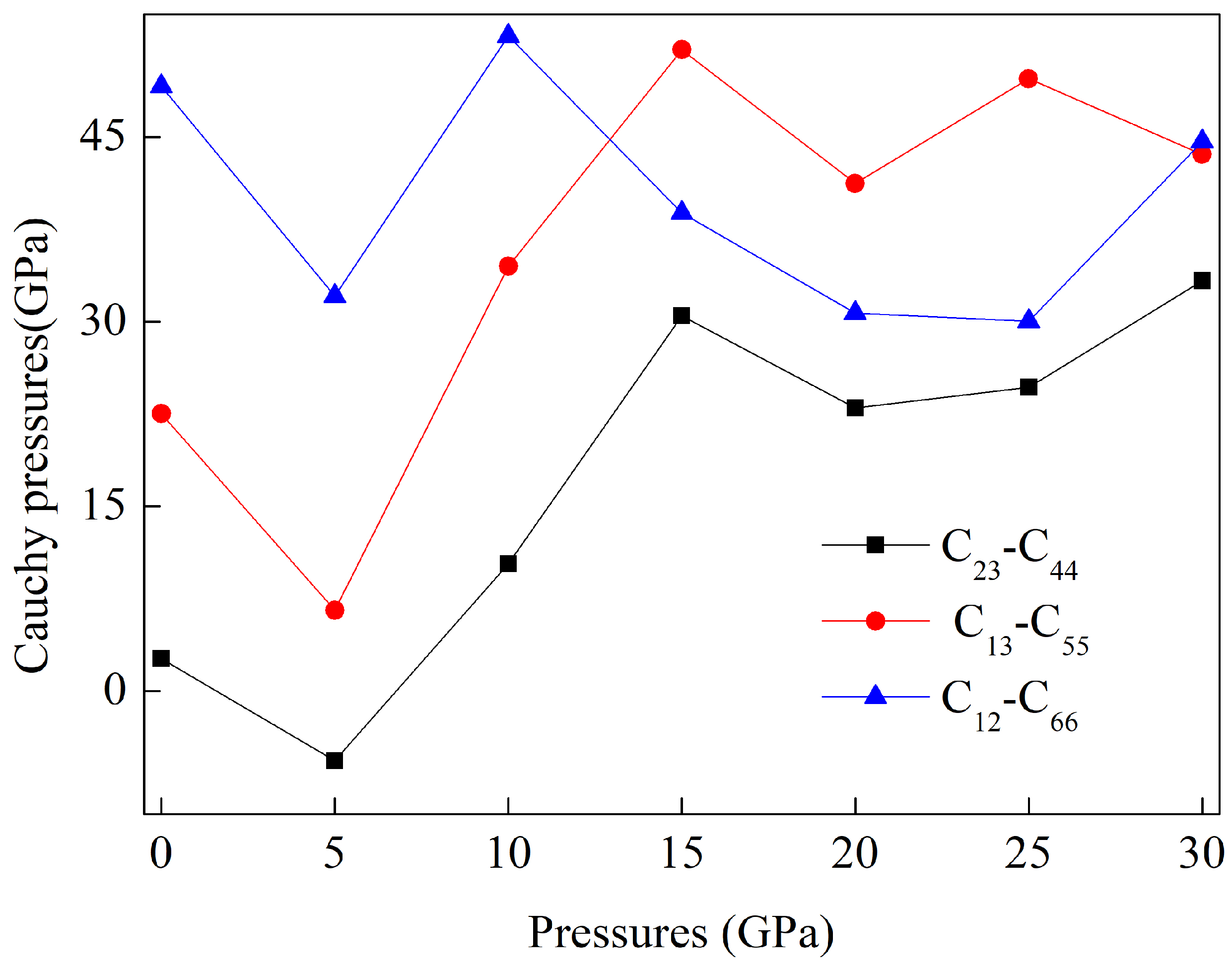
3.2. Elastic Constants Within a Pressurized Environment
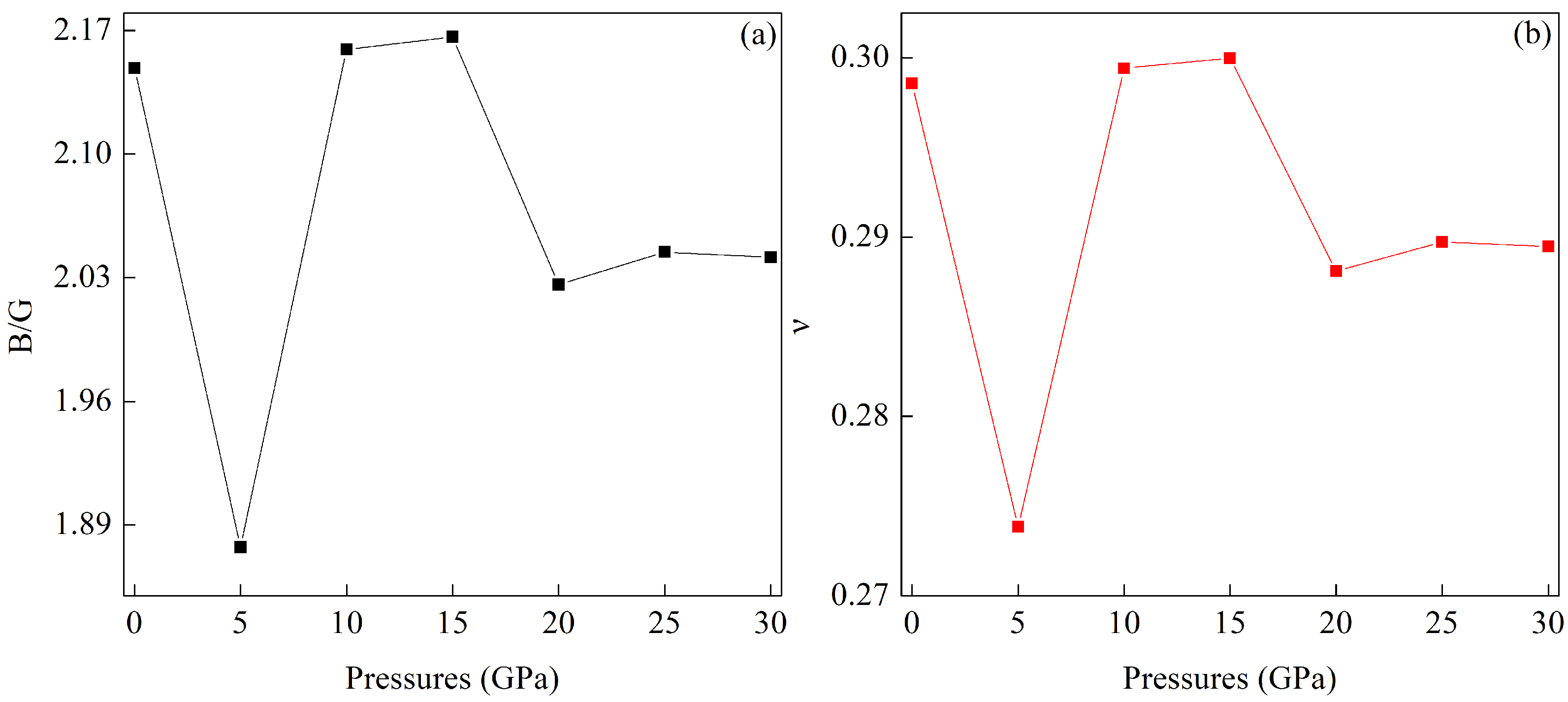
3.3. Pressure-Induced Variations in Elastic Constants and Mechanical Properties
3.4. Elastic Anisotropy Under Pressure
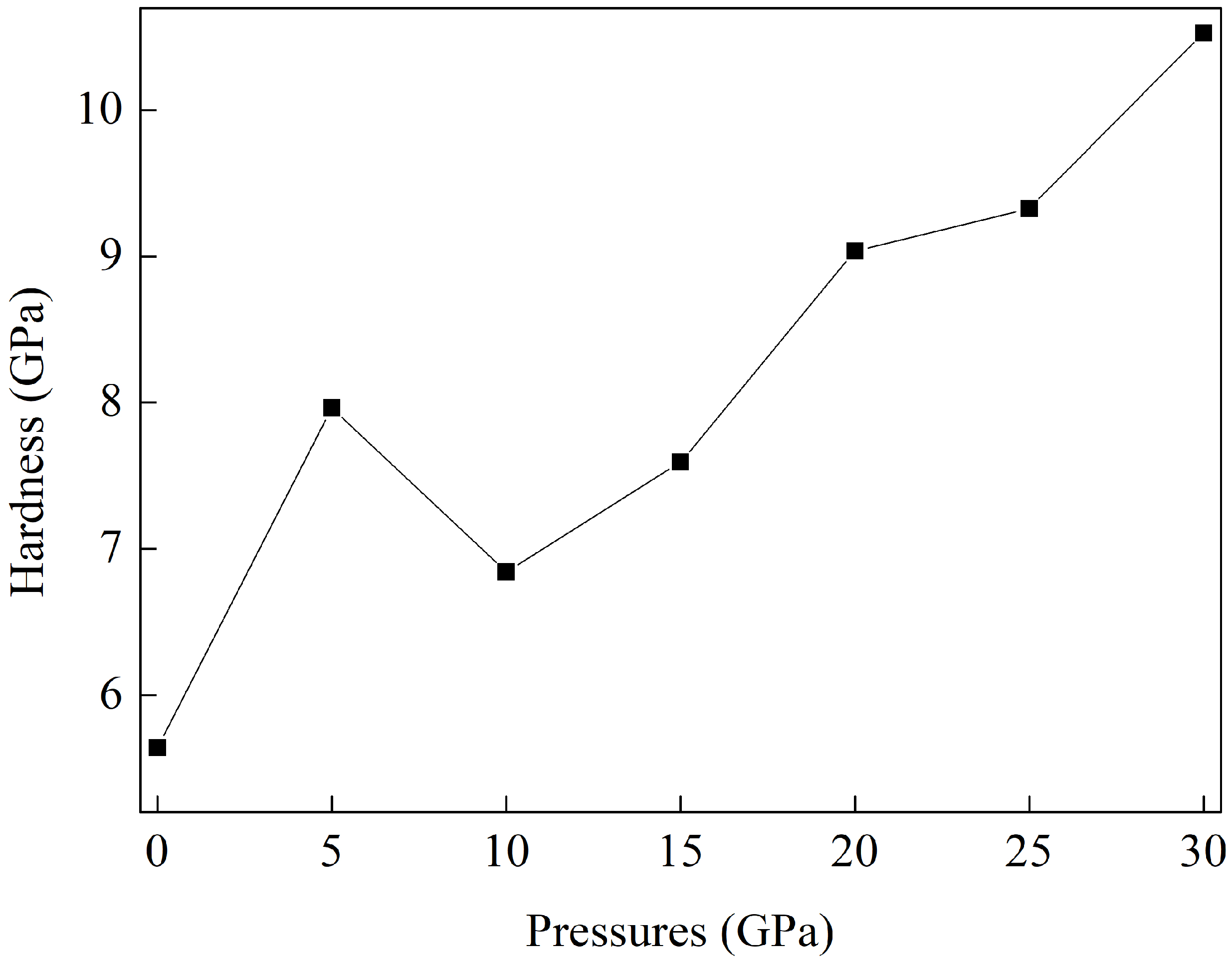
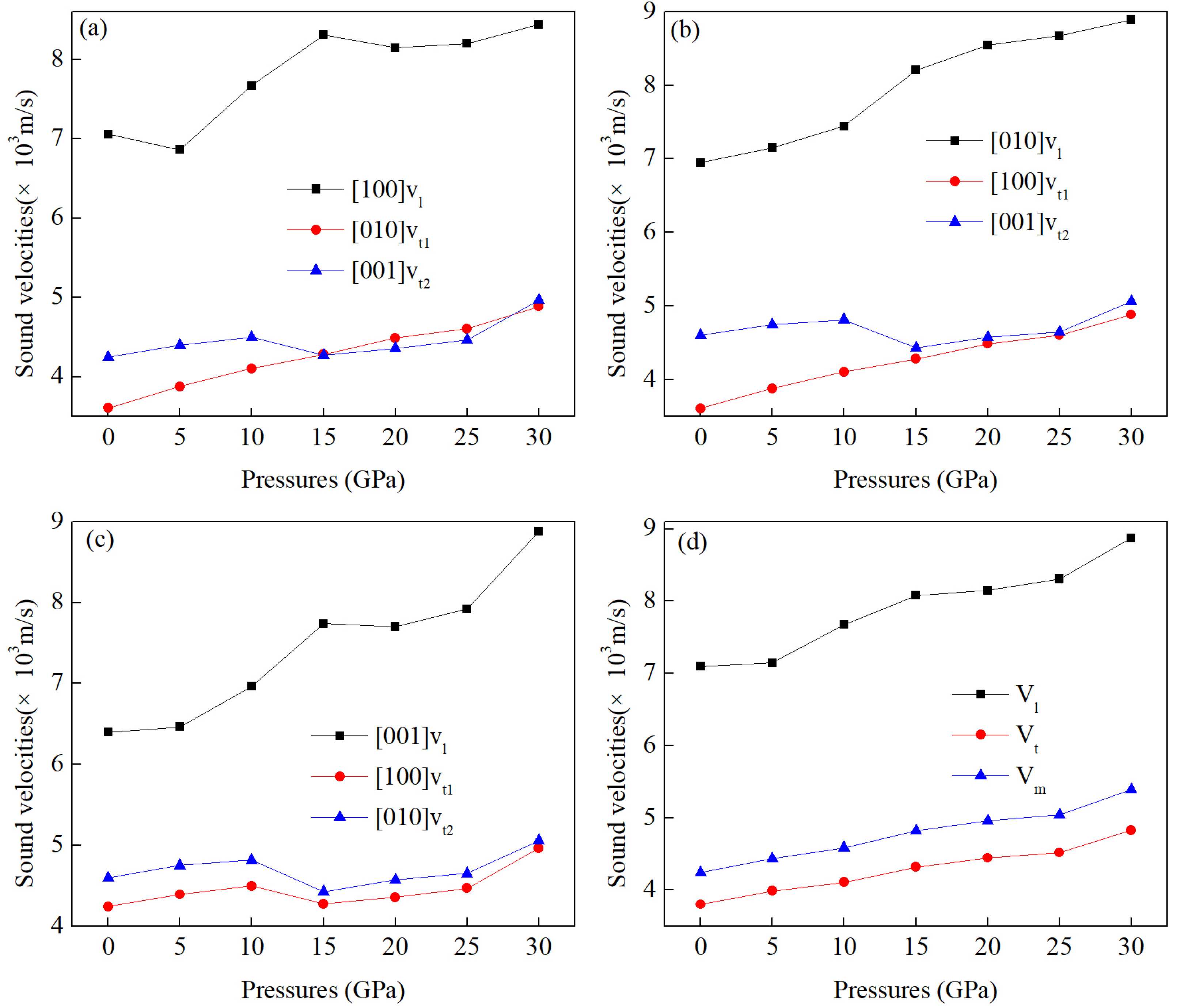
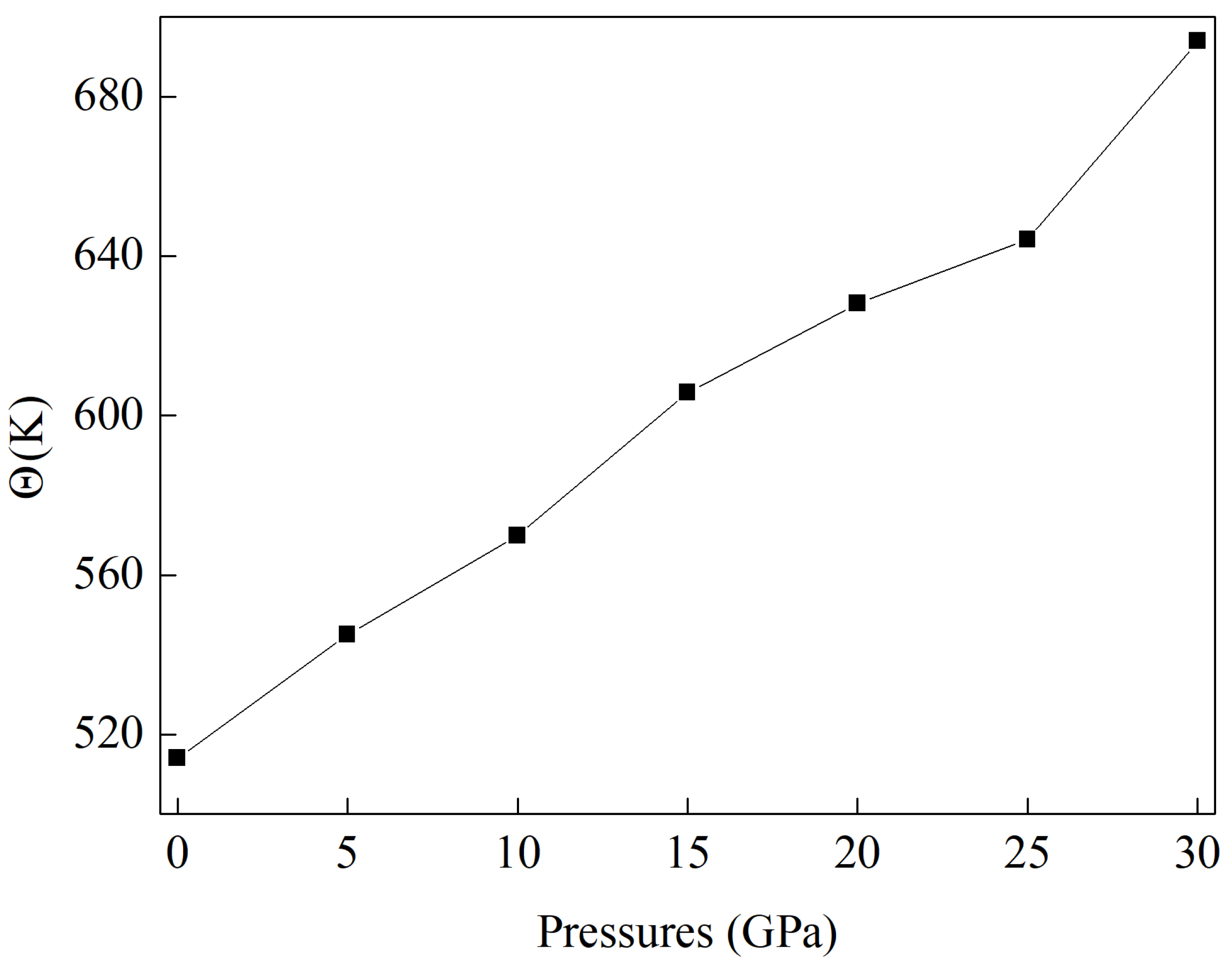
3.5. The Speed of Sound and Thermal Conductivity Under Pressure
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Czerwinski, F. Thermal stability of aluminum alloys. Materials 2020, 13, 3441. [Google Scholar] [CrossRef] [PubMed]
- Czerwinski, F. Thermal stability of aluminum-nickel binary alloys containing the Al-Al3Ni eutectic. Metall. Mater. Trans. 2021, 52, 4342–4356. [Google Scholar] [CrossRef]
- Suwanpreecha, C.; Pandee, P.; Patakham, U.; Limmaneevichitr, C. New generation of eutectic Al-Ni casting alloys for elevated temperature services. Mater. Sci. Eng. A 2018, 709, 46–54. [Google Scholar] [CrossRef]
- Pan, L.; Zhang, S.; Yang, Y.; Gupta, N.; Yang, C.; Zhao, Y.; Hu, Z. High-temperature mechanical properties of aluminum alloy matrix composites reinforced with Zr and Ni trialumnides synthesized by in situ reaction. Metall. Mater. Trans. A 2020, 51, 214–225. [Google Scholar] [CrossRef]
- Michi, R.A.; Toinin, J.P.; Seidman, D.N.; Dunand, D.C. Ambient-and elevated-temperature strengthening by Al3Zr-Nanoprecipitates and Al3Ni-Microfibers in a cast Al-2.9 Ni-0.11 Zr-0.02 Si-0.005 Er (at.%) alloy. Mater. Sci. Eng. A 2019, 759, 78–89. [Google Scholar] [CrossRef]
- Suwanpreecha, C.; Toinin, J.P.; Michi, R.; Pandee, P.; Dunand, D.C.; Limmaneevichitr, C. Strengthening mechanisms in AlNiSc alloys containing Al3Ni microfibers and Al3Sc nanoprecipitates. Acta Mater. 2019, 164, 334–346. [Google Scholar] [CrossRef]
- Pandey, P.; Makineni, S.K.; Gault, B.; Chattopadhyay, K. On the origin of a remarkable increase in the strength and stability of an Al rich Al-Ni eutectic alloy by Zr addition. Acta Mater. 2019, 170, 205–217. [Google Scholar] [CrossRef]
- Michi, R.A.; Plotkowski, A.; Shyam, A.; Dehoff, R.R.; Babu, S.S. Towards high-temperature applications of aluminum alloys enabled by additive manufacturing. Int. Mater. Rev. 2022, 67, 298–345. [Google Scholar] [CrossRef]
- Cantor, B.; Chadwick, G. The growth crystallography of unidirectionally solidified Al-Al3Ni and Al-Al2Cu eutectics. J. Cryst. Growth 1974, 23, 12–20. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, H.; Yuan, H.; Wang, S.; Lin, Y.; Zeng, Q.; Xu, G.; Liu, Z.; Solanki, G.; Patel, K.; et al. Pressure induced metallization with absence of structural transition in layered molybdenum diselenide. Nat. Commun. 2015, 6, 7312. [Google Scholar] [CrossRef] [PubMed]
- Xiao, F.; Lei, W.; Wang, W.; Autieri, C.; Zheng, X.; Ming, X.; Luo, J. Pressure-induced structural transition, metallization, and topological superconductivity in PdSSe. Phys. Rev. B 2022, 105, 115110. [Google Scholar] [CrossRef]
- Ben sadallah, H.; Boulechfar, R.; Meradji, H.; Ghemid, S.; Khenioui, Y.; Lebga, N.; Khenata, R.; Bin-Omran, S.; Haq, B.U.; Kim, S.H. Phase stability and physical behaviour of Fe3Pd, FePd and FePd3 binary intermetallic compounds. Phys. B Condens. Matter 2024, 686, 416074. [Google Scholar]
- Yin, D.; Sahu, B.P.; Tsurkan, P.; Popov, D.; Dongare, A.M.; Velisavljevic, N.; Misra, A. High-pressure phase transitions in a laser directed energy deposited Fe-33Cu Alloy. Acta Mater. 2024, 268, 119797. [Google Scholar] [CrossRef]
- Ciftci, Y.O.; Çatıkkaş, B. Pressure effects on the structural, electronic, elastic, optical, and vibrational properties of YMg intermetallic compounds: A first-principles study. Phys. Scr. 2024, 99, 065981. [Google Scholar] [CrossRef]
- Wang, P.; Wang, Y.; Qu, J.; Zhu, Q.; Yang, W.; Zhu, J.; Wang, L.; Zhang, W.; He, D.; Zhao, Y. Pressure-induced structural and electronic transitions, metallization, and enhanced visible-light responsiveness in layered rhenium disulphide. Phys. Rev. B 2018, 97, 235202. [Google Scholar] [CrossRef]
- Zheng, B.; Zhao, L.; Hu, X.; Dong, S.; Li, H. First-principles studies of Mg17Al12, Mg2Al3, Mg2Sn, MgZn2, Mg2Ni and Al3Ni phases. Phys. B Condens. Matter 2019, 560, 255–260. [Google Scholar] [CrossRef]
- Li, Z.; Graziosi, P.; Neophytou, N. Efficient first-principles electronic transport approach to complex band structure materials: The case of n-type Mg3Sb2. Npj Comput. Mater. 2024, 10, 8. [Google Scholar] [CrossRef]
- Song, J.; Jiang, M.; Li, H.; Wan, C.; Chu, X.; Zhang, Q.; Chen, Y.; Wu, X.; Zhang, X.; Liu, J. First-Principles Computational Insights into Silicon-Based Anode Materials: Recent Progress And Perspectives. Surf. Rev. Lett. 2024, 31, 2430006. [Google Scholar] [CrossRef]
- Peng, J.; Zhao, Y.; Wang, X.; Zeng, X.; Wang, J.; Hou, S. Metal-organic frameworks: Advances in first-principles computational studies on catalysis, adsorption, and energy storage. Mater. Today Commun. 2024, 40, 109780. [Google Scholar] [CrossRef]
- Li, K.; Choudhary, K.; DeCost, B.; Greenwood, M.; Hattrick-Simpers, J. Efficient first principles based modeling via machine learning: From simple representations to high entropy materials. J. Mater. Chem. A 2024, 12, 12412–12422. [Google Scholar] [CrossRef]
- Pimachev, A.K.; Neogi, S. First-principles prediction of electronic transport in fabricated semiconductor heterostructures via physics-aware machine learning. NPJ Comput. Mater. 2021, 7, 93. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, J.; Liu, Y.; Xi, J.; Li, Q.; Xiang, H.; Zhou, Y. Application of high-throughput first-principles calculations in ceramic innovation. J. Mater. Sci. Technol. 2021, 88, 143–157. [Google Scholar] [CrossRef]
- Liu, L.; Wang, M.; Hu, L.; Wen, Y.; Jiang, Y. Structural, elastic, and electronic properties of MgB2 C2 under pressure from first-principles calculations. Int. J. Quantum Chem. 2021, 121, e26442. [Google Scholar] [CrossRef]
- Wan, H.; Yao, W.; Zeng, D.; Zhou, J.; Ruan, W.; Liu, L.; Wen, Y. Structural, Elastic, Electronic, and Magnetic Properties of a New Full-Heusler Alloy Mn2MgGe: First-Principles Calculations. J. Supercond. Nov. Magn. 2019, 32, 3001–3008. [Google Scholar] [CrossRef]
- Wen, Y.; Zeng, X.; Ye, Y.; Gou, Q.; Liu, B.; Lai, Z.; Jiang, D.; Sun, X.; Wu, M. Theoretical Study on the Structural, Elastic, Electronic and Thermodynamic Properties of Long-Period Superstructures h- and r-Al2Ti under High Pressure. Materials 2022, 15, 4236. [Google Scholar] [CrossRef]
- Ciftci, Y.O.; Coban, C.; Evecen, M.; Durukan, İ.K. Pressure effects on structural, electronic and anisotopic elastic properties of Si doped RuGe compound with different concentrations by first-principles calculations. Mater. Chem. Phys. 2022, 291, 126695. [Google Scholar] [CrossRef]
- Chen, C.; Liu, L.; Wen, Y.; Jiang, Y.; Chen, L. Elastic properties of orthorhombic YBa2Cu3O7 under pressure. Crystals 2019, 9, 497. [Google Scholar] [CrossRef]
- Wen, Y.; Yu, X.; Zeng, X.; Ye, Y.; Wu, D.; Gou, Q. Ab initio calculations of the mechanical and acoustic properties of Ti 2-based Heusler alloys under pressures. Eur. Phys. J. B 2018, 91, 1–10. [Google Scholar] [CrossRef]
- Pebdani, Z.H.; Janisch, R.; Pyczak, F. Effect of V-VIB group ternary elements on the properties of Ti2AlM-type O-phases: A first-principles study. Comput. Condens. Matter 2024, 40, e00945. [Google Scholar] [CrossRef]
- Fan, S.; Hou, H.; Zhang, S. Understanding of the crystal structure, mechanical, vibrational properties of α-MgSO4 under pressure. Vacuum 2021, 190, 110280. [Google Scholar] [CrossRef]
- Liu, Z.J.; Sun, X.W.; Zhang, C.R.; Zhang, S.J.; Zhang, Z.R.; Jin, N.Z. First-principles calculations of high-pressure physical properties anisotropy for magnesite. Sci. Rep. 2022, 12, 3691. [Google Scholar] [CrossRef]
- Evecen, M.; Ciftci, Y. Theoretical investigation of the electronic structure, elastic, dynamic properties of intermetallic compound NiBe under pressure. Eur. Phys. J. B 2021, 94, 19. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Krist.-Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Mull, T.; Baumeister, B.; Menges, M.; Freund, H.J.; Weide, D.; Fischer, C.; Andresen, P. Bimodal velocity distributions after ultraviolet-laser-induced desorption of NO from oxide surfaces. Experiments and results of model calculations. J. Chem. Phys. 1992, 96, 7108–7116. [Google Scholar] [CrossRef]
- Hamann, D. Optimized norm-conserving Vanderbilt pseudopotentials. Phys. Rev. B—Condens. Matter Mater. Phys. 2013, 88, 085117. [Google Scholar] [CrossRef]
- Bradley, A.; Taylor, A. XCIX. The crystal structures of Ni2Al3 and NiAl3. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1937, 23, 1049–1067. [Google Scholar] [CrossRef]
- Le Page, Y.; Saxe, P. Symmetry-general least-squares extraction of elastic data for strained materials from ab initio calculations of stress. Phys. Rev. B 2002, 65, 104104. [Google Scholar] [CrossRef]
- Wu, X.; Vanderbilt, D.; Hamann, D. Systematic treatment of displacements, strains, and electric fields in density-functional perturbation theory. Phys. Rev. B—Condens. Matter Mater. Phys. 2005, 72, 035105. [Google Scholar] [CrossRef]
- Gunda, N.H.; Michi, R.A.; Chisholm, M.F.; Shyam, A.; Shin, D. First-principles study of Al/Al3Ni interfaces. Comput. Mater. Sci. 2023, 217, 111896. [Google Scholar] [CrossRef]
- Shi, D.; Wen, B.; Melnik, R.; Yao, S.; Li, T. First-principles studies of Al–Ni intermetallic compounds. J. Solid State Chem. 2009, 182, 2664–2669. [Google Scholar] [CrossRef]
- Cheng, H.C.; Yu, C.F.; Chen, W.H. First-principles density functional calculation of mechanical, thermodynamic and electronic properties of CuIn and Cu2In crystals. J. Alloys Compd. 2013, 546, 286–295. [Google Scholar] [CrossRef]
- Pugh, S. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Frantsevich, I.N. Elastic Constants and Elastic Moduli of Metals and Insulators; Reference book; Naukova Dumka: Kyiv, Ukraine, 1982. [Google Scholar]
- Pettifor, D. Theoretical predictions of structure and related properties of intermetallics. Mater. Sci. Technol. 1992, 8, 345–349. [Google Scholar] [CrossRef]
- Mao, P.; Yu, B.; Liu, Z.; Wang, F.; Ju, Y. First-principles investigation on mechanical, electronic, and thermodynamic properties of Mg2Sr under high pressure. J. Appl. Phys. 2015, 117, 115903. [Google Scholar] [CrossRef]
- Kube, C.M. Elastic anisotropy of crystals. AIP Adv. 2016, 6, 095209. [Google Scholar] [CrossRef]
- Brugger, K. Determination of third-order elastic coefficients in crystals. J. Appl. Phys. 1965, 36, 768–773. [Google Scholar] [CrossRef]
- Zeng, X.; Peng, R.; Yu, Y.; Hu, Z.; Wen, Y.; Song, L. First-Principles Calculations on Structural Property and Anisotropic Elasticity of γ 1-Ti4Nb3Al9 under Pressure. Materials 2018, 11, 2025. [Google Scholar] [CrossRef]
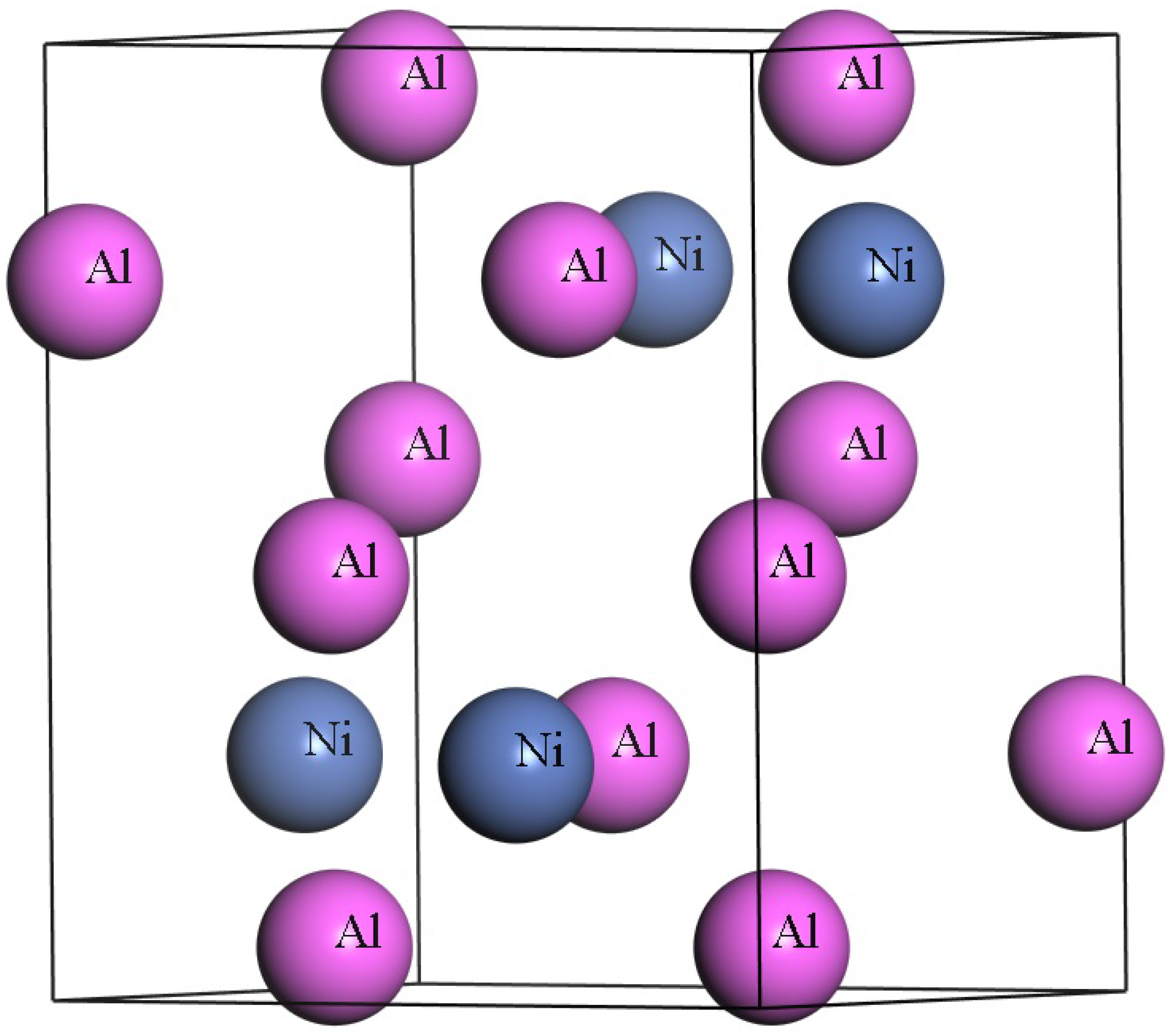


| Method | a | b | c |
|---|---|---|---|
| Present | 6.669 | 7.356 | 4.850 |
| Exp. [38] | 6.589 | 7.352 | 4.80 |
| Theo. [41] | 6.620 | 7.390 | 4.81 |
| Theo. [16] | 6.698 | 7.352 | 4.801 |
| Theo. [42] | 6.565 | 7.257 | 4.75 |
| Pressure | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 194.188 | 99.825 | 92.714 | 188.249 | 85.107 | 159.507 | 82.487 | 70.186 | 50.690 |
| 5 | 191.437 | 93.151 | 85.004 | 207.704 | 86.025 | 169.722 | 91.692 | 78.453 | 61.053 |
| 10 | 247.767 | 124.152 | 119.637 | 233.570 | 108.005 | 204.375 | 97.675 | 85.127 | 70.922 |
| 15 | 299.935 | 118.541 | 131.479 | 292.731 | 115.682 | 260.294 | 85.198 | 79.370 | 79.709 |
| 20 | 296.481 | 120.618 | 126.124 | 326.432 | 116.447 | 264.949 | 93.454 | 84.887 | 89.939 |
| 25 | 308.355 | 127.146 | 141.222 | 344.547 | 123.846 | 287.486 | 99.168 | 91.471 | 97.117 |
| 30 | 333.877 | 156.503 | 159.168 | 370.778 | 153.446 | 369.997 | 120.139 | 115.574 | 111.860 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, C.; Yang, B.; Lai, Z.; Chen, Z.; Yang, H.; Wang, H.; Zhou, Y.; Zeng, X. First-Principles-Based Structural and Mechanical Properties of Al3Ni Under High Pressure. Crystals 2025, 15, 3. https://doi.org/10.3390/cryst15010003
Xiao C, Yang B, Lai Z, Chen Z, Yang H, Wang H, Zhou Y, Zeng X. First-Principles-Based Structural and Mechanical Properties of Al3Ni Under High Pressure. Crystals. 2025; 15(1):3. https://doi.org/10.3390/cryst15010003
Chicago/Turabian StyleXiao, Chuncai, Baiyuan Yang, Zhangli Lai, Zhiquan Chen, Huaiyang Yang, Hui Wang, Yunzhi Zhou, and Xianshi Zeng. 2025. "First-Principles-Based Structural and Mechanical Properties of Al3Ni Under High Pressure" Crystals 15, no. 1: 3. https://doi.org/10.3390/cryst15010003
APA StyleXiao, C., Yang, B., Lai, Z., Chen, Z., Yang, H., Wang, H., Zhou, Y., & Zeng, X. (2025). First-Principles-Based Structural and Mechanical Properties of Al3Ni Under High Pressure. Crystals, 15(1), 3. https://doi.org/10.3390/cryst15010003






