Ab Initio Study of the Crystalline Structure of HgS under Low and High Pressure
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
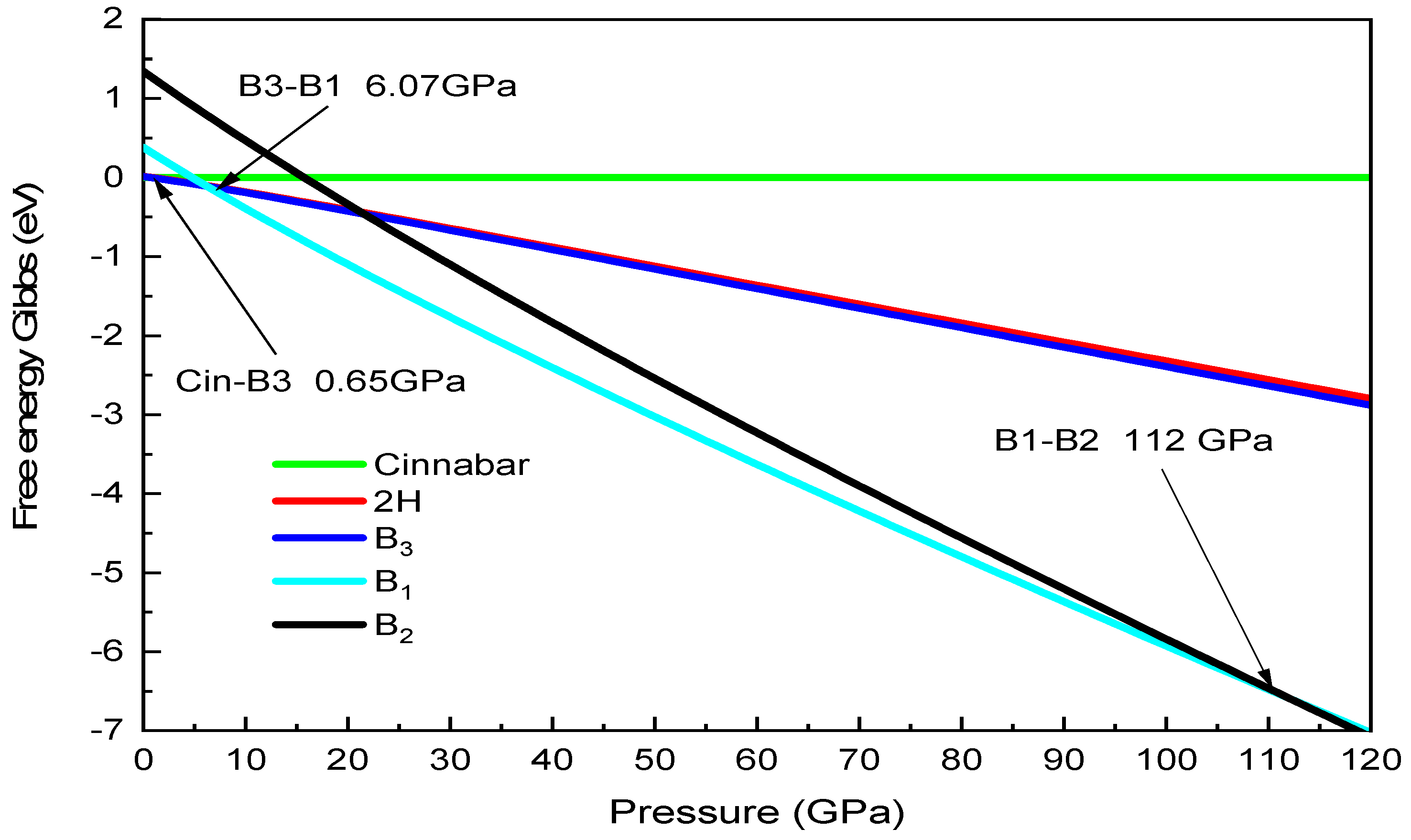
3.1. Structural Properties
3.2. Elastic Properties
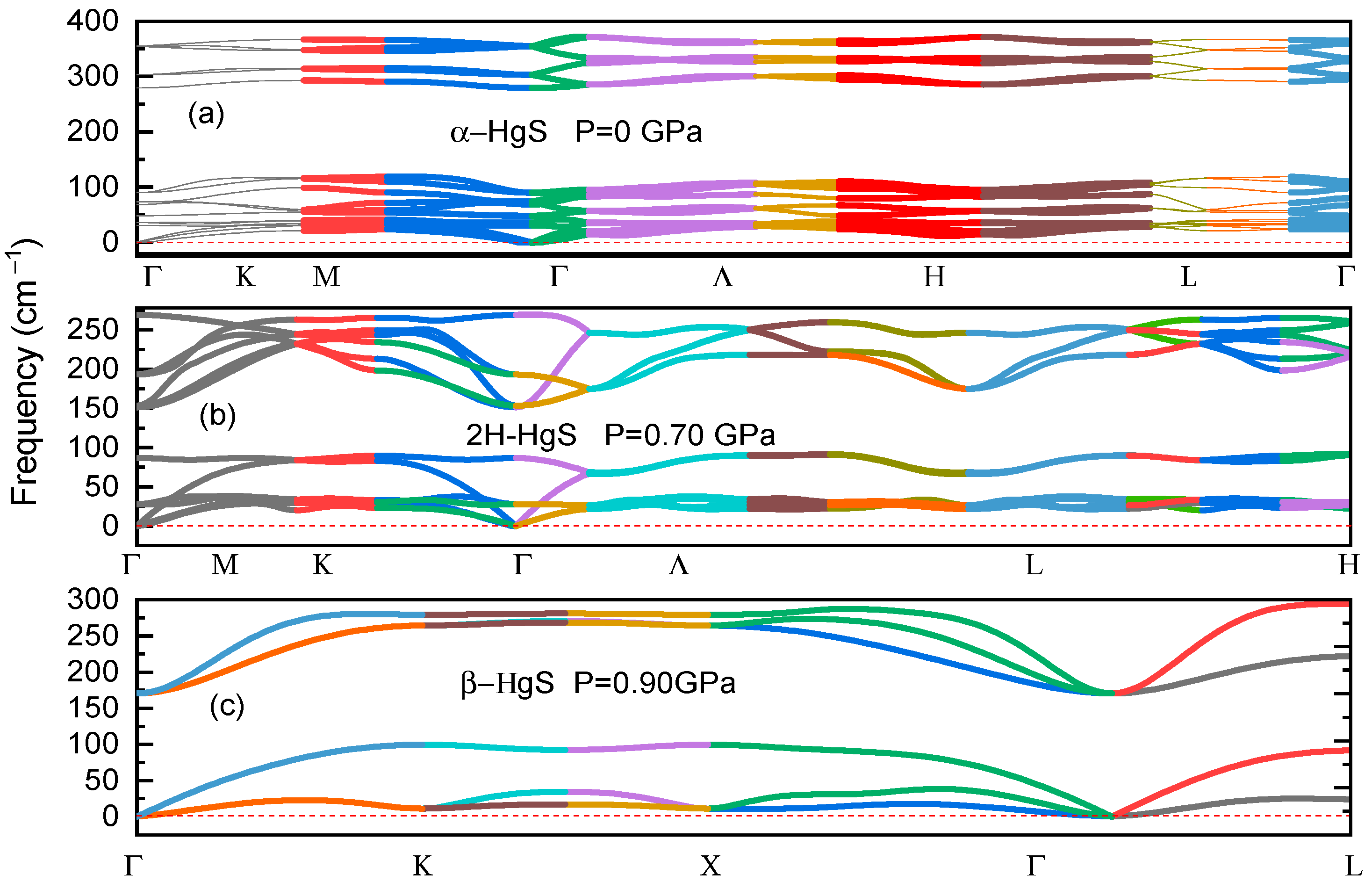
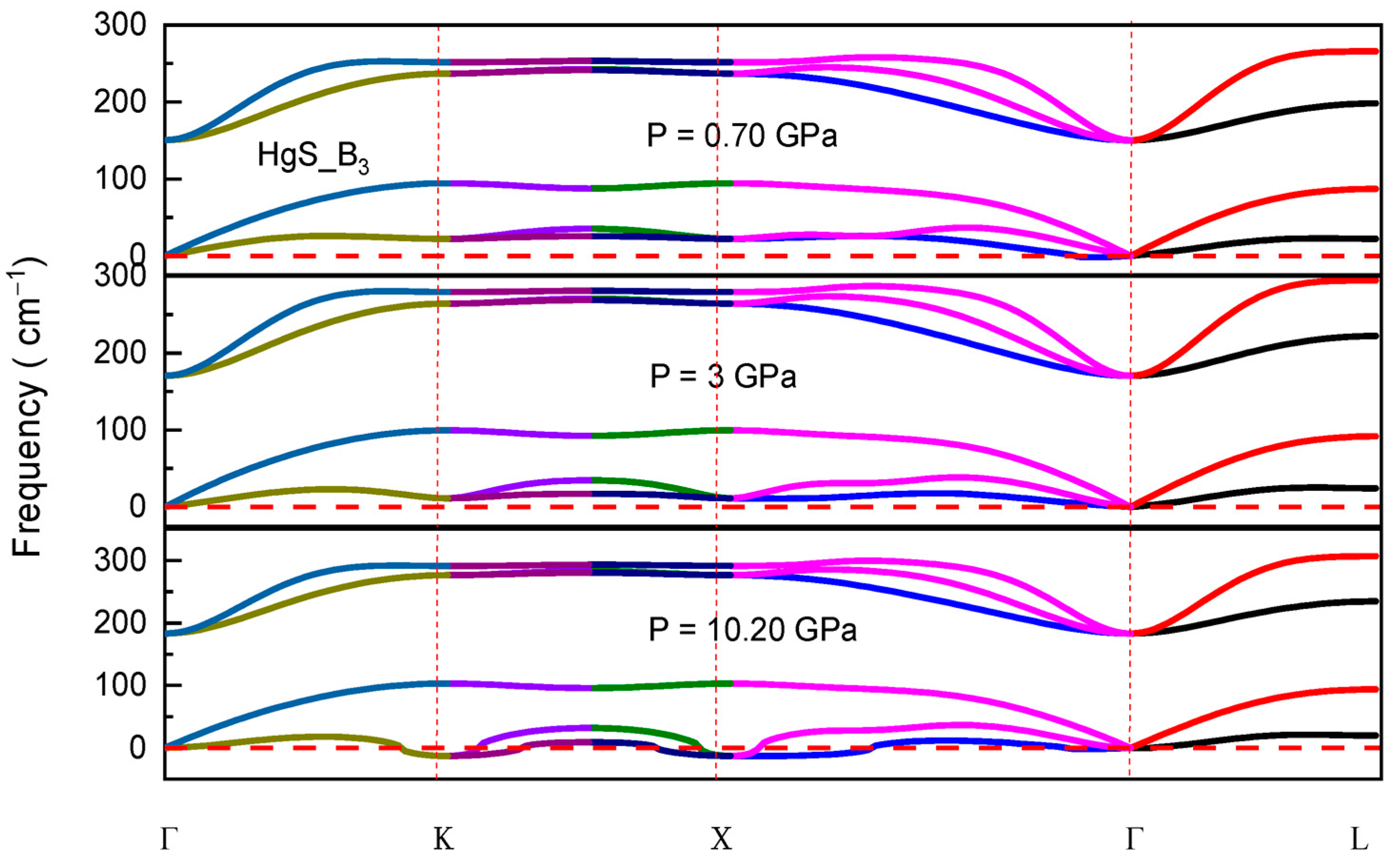
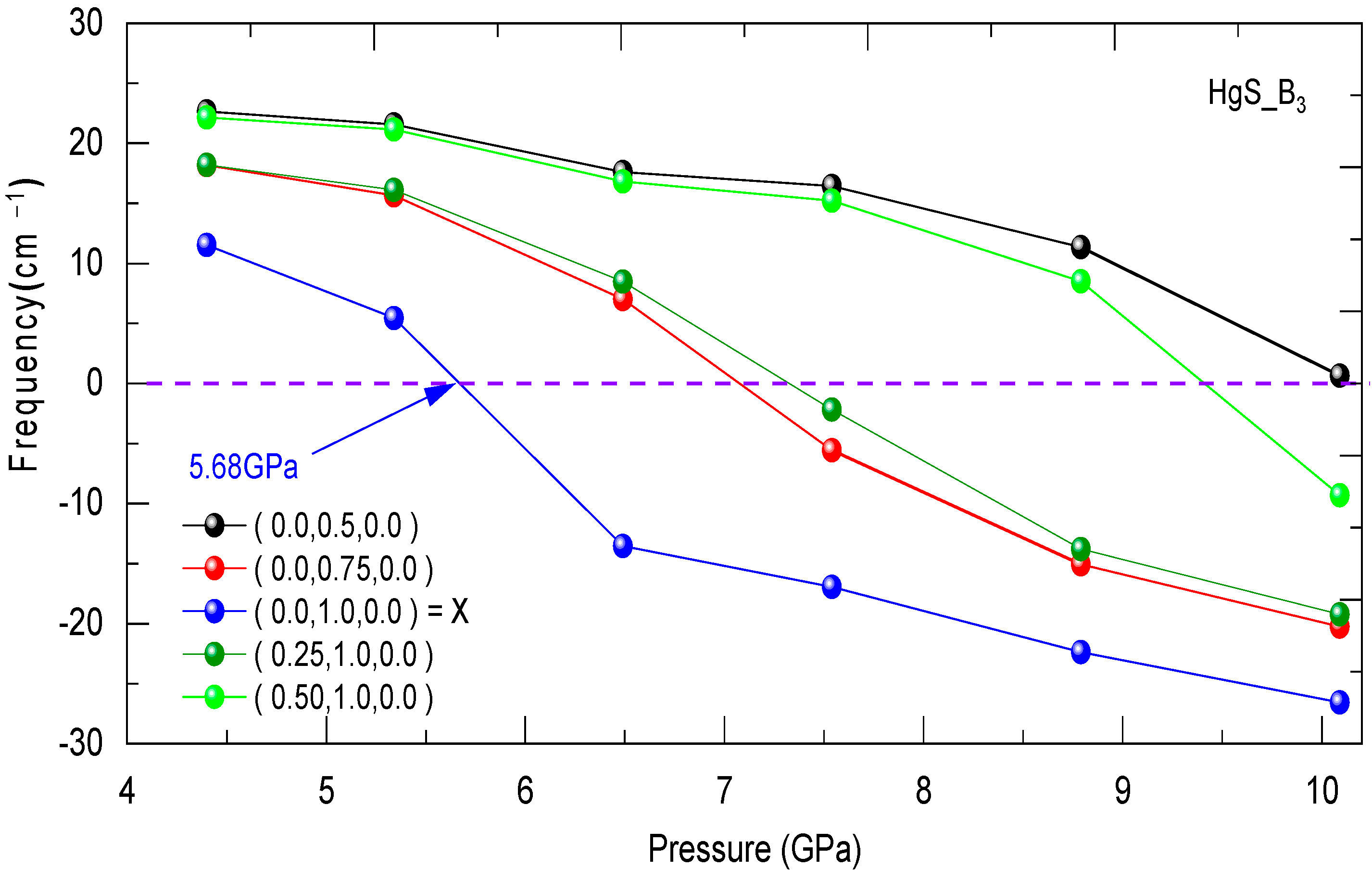
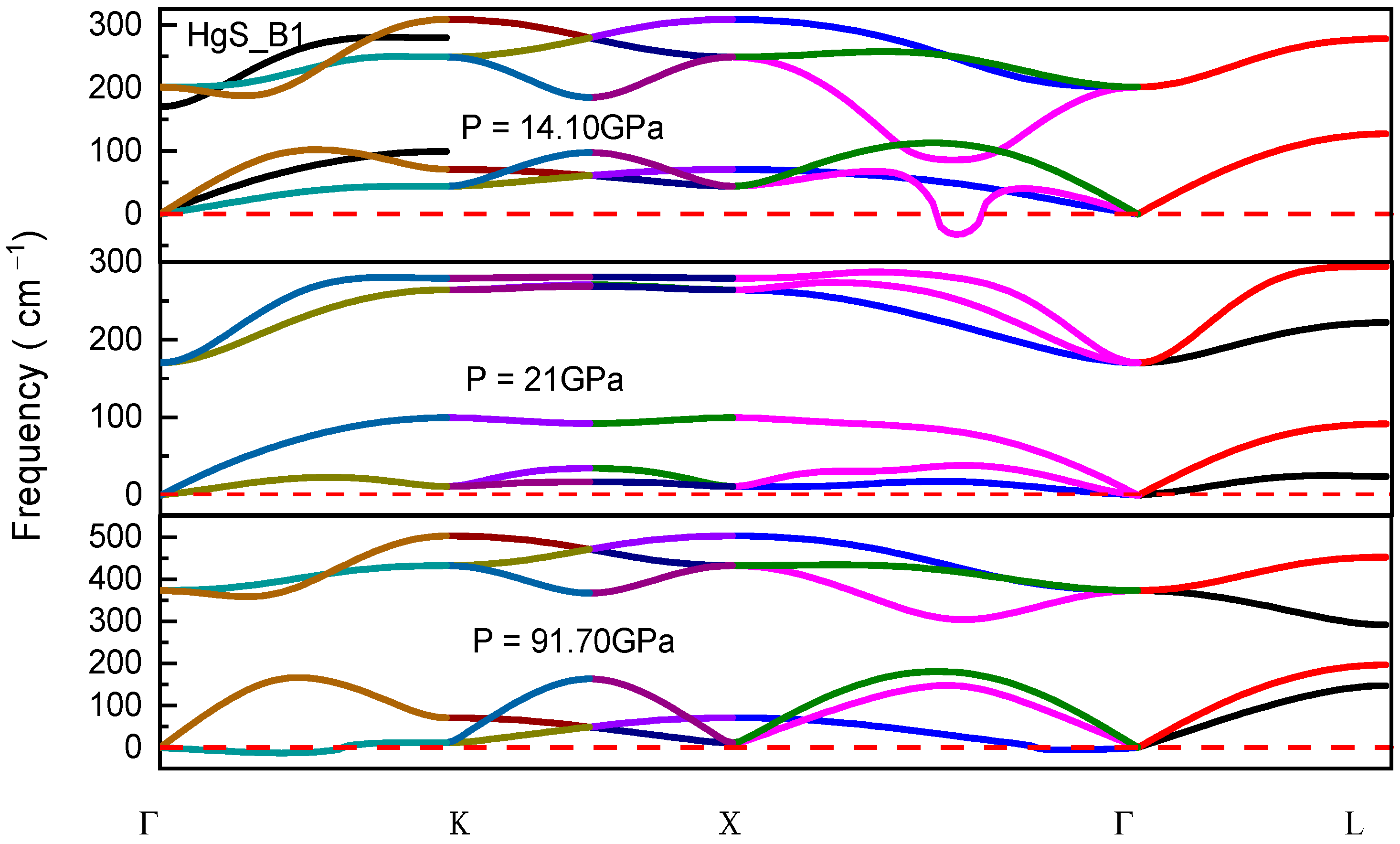
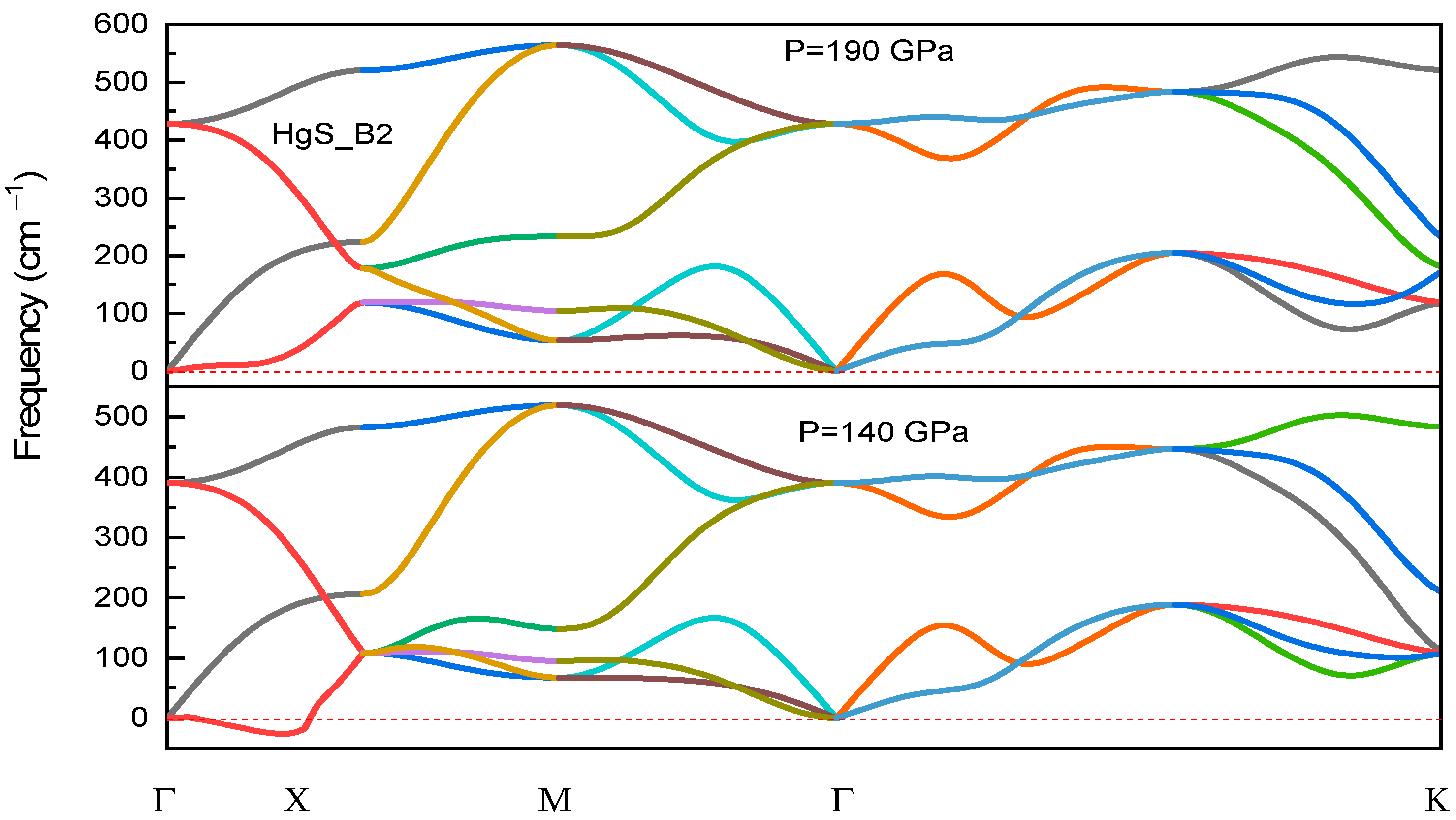
3.3. Dynamical Stability
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wissmann, H.; Anh, T.T.; Rogaschewski, S.; Von Ortenberg, M. Self-organized MBE growth of II–VI epilayer son patterned GaSb substrates. J. Cryst. Growth 1999, 201, 619–622. [Google Scholar] [CrossRef]
- Hu, T.-J.; Cui, X.-Y.; Li, X.-F.; Wang, J.-S.; Yang, J.-H.; Gao, C.-X. In Situ Electrical Resistivity and Hall Effect Measurement of beta-Hg Sunder High Pressure. Chin. Phys. Lett. 2015, 32, 3. [Google Scholar] [CrossRef]
- Ren, T.; Xu, S.; Zhao, W.-B.; Zhu, J.-J. A surfactant-assisted photochemical route to single crystalline HgS nanotubes. J. Photochem. Photobiol. A Chem. 2005, 173, 93–98. [Google Scholar] [CrossRef]
- Kershaw, S.V.; Yiu, W.K.; Sergeev, A.; Rogach, A.L. Development of synthetic methods to grow long-wavelength infrared-emitting HgTe quantum dots in dimethyl form amide. Chem. Mater. 2020, 32, 3930–3943. [Google Scholar] [CrossRef]
- Mews, A.; Kadavanich, A.V.; Banin, U.; Alivisatos, A.P. tructural and spectroscopic investigations of CdS/HgS/CdS quantum-dot quantum wells. Phys. Rev. B 1996, 53, R13242. [Google Scholar] [CrossRef]
- Zallen, R.; Michael, E.S. Plasma edge and band structure of cubic HgS. Solid State Commun. 1970, 8, 1291–1294. [Google Scholar] [CrossRef]
- Szuszkiewicz, W.; Witkowska, B.; Jouanne, M.; Balkanski, M. Raman spectroscopy of cubic Hg1-xFexS. Mater. Sci. Forum. 1995, 182–184, 711–714. [Google Scholar] [CrossRef]
- Kovácskis, V.; Dódony, I. Structural disorder in natural cubic HgS. Acta Mineral. Petrogr. 1999, 40, 3–10. [Google Scholar]
- Chatterjee, P.M.; Pandey, D.; Raval, R.; Dubey, A.K. Coherent Aspects of Multifaceted Eco-friendly Biopolymer-Polyglutamic Acid from the Microbes. J. Pure Appl. Microbiol. 2019, 13, 741–756. [Google Scholar] [CrossRef]
- Werner, A.; Hochheimer, H.D.; Strössner, K.; Jayaraman, A. High-pressure X-ray diffraction studies on HgTe and HgS to 20GPa. Phys. Rev. B 1983, 28, 3330. [Google Scholar] [CrossRef]
- Bridgman, P.W. The Compression of 46 Substances to 50,000 kg/cm2; American Academy of Arts& Sciences: Boston, MA, USA, 1940; pp. 21–51. [Google Scholar]
- Huang, T.; Ruoff, A.L. Pressure induced phase transition of HgS. J. Appl. Phys. 1983, 54, 5459–5461. [Google Scholar] [CrossRef]
- Nelmes, R.J.; McMahon, M.I. Structural transitions in the group IV, III-V, and II-VI semiconductors under pressure. Semicond. Semimet. 1998, 54, 145–246. [Google Scholar]
- Kürkçü, C.; Selgin, A.L.; Merdan, Z.; Yamçiçier, Ç.; Öztürk, H. Investigation of structural and electronic properties of β-HgS: Molecular dynamics simulations. Chin. J. Phys. 2018, 56, 783–792. [Google Scholar] [CrossRef]
- Ullah, N.; Murtaza, G.; Khenata, R.; Wong, K.M. Phase transition, electronic and optical properties of mercury chalcogenides under pressure. Phase Transit. 2014, 87, 571–581. [Google Scholar] [CrossRef]
- Saini, P.K.; Ahlawat, D.S.; Singh, D. Structural, electronic and optical properties of HgS under pressure using FP-LAPW method. Int. Res. J. Eng. Technol. (IRJET) 2017, 4, 1080–1086. [Google Scholar]
- Vodolazov, D.Y.; Peeters, F.M. Superconducting rectifier based on the asymmetric surface barrier effect. Phys. Rev. B 2005, 72, 172508. [Google Scholar] [CrossRef]
- Yang, X.C.; Yang, J.; Zhang, E.-J.; Gao, C.-X. Study of electronic and elastic properties of beta-HgS under high pressure viafirst-principles calculations. Phys. Status Solidi C Curr. Top. Solid State Phys. 2011, 8, 1703–1707. [Google Scholar]
- Cardona, M.; Kremer, R.K.; Lauck, R.; Siegle, G.; Muñoz, A.; Romero, A.H. Electronic, vibrational, and thermodynamic properties of metacinnabar β-HgS, HgSe, and HgTe. Phys.Rev. 2009, B 80, 195204. [Google Scholar] [CrossRef]
- Ozoliņš, V.; Zunger, A. The oryofsy stematicabsence of NaCl-Type(β-Sn–Type)high pressure phases in covalent(ionic) semiconductors. Phys. Rev. Lett. 1999, 82, 767. [Google Scholar] [CrossRef]
- Baroni, S.; de Gironcoli, S.; Stefano; Corso, D. Phonons and related crystal properties from density functional perturbationtheory. Rev. Mod. Phys. 2001, 73, 515–562. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Matthias, Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Andrew, M.R.; Karin, M.R.; Kaxiras, E.; Joannopoulos, J.D. Optimised pseudopotential. Phys. Rev. B 1990, 41, 1227, Erratum in Phys. Rev. 1991, 44, 13175–13176. [Google Scholar]
- Pack, J.D.; Hendrik, M.J. Special points for Brillouin-zone integrations, a reply. Phys. Rev. B 1977, 16, 1748. [Google Scholar] [CrossRef]
- Dominic, F.M. The compressibility of media under extreme pressures. Proc. Natl. Acad. Sci. USA 1944, 30, 244–247. [Google Scholar]
- Madelung, O. Landolt Bornste: Numerical Data and Functional Relationships in Science and Technology; New Series, Group III; Springer: Berlin/Heidelberg, Germany, 1982; Volume 22, pp. 244–247. [Google Scholar]
- Strobel, S.; Schleid, T. Quaternäre Caesium-Kupfer(I)-Lanthanoid (III)-Selenide Vom Typ CsCu3M2Se5(M=Sm, GdLu). Z. Für Anorg. Und Allg. Chem. 2014, 630, 706–711. [Google Scholar] [CrossRef]
- Földvári, M. Hand book of Thermogravimetric System of Minerals and Its Use in Geological Practice; Geological Institute of Hungary: Budapest, Hungary, 2011. [Google Scholar]
- Biering, S.; Schwerdtfeger, P.A. comparative density functional study of the high-pressure phases of solid ZnX, CdX, and HgX (X=S, Se, and Te): Trends and relativistic effects. J. Chem. Phys. 2012, 137, 034705. [Google Scholar] [CrossRef] [PubMed]
- Nelmes, R.J.; Mc Mahon, M.I. High Pressure Semiconductor Physics I; Suski, T., Paul, W., Eds.; Academic Press: Cambridge, MA, USA, 1998; pp. 145–247. [Google Scholar]
- McMahon, M.I.; Nelmes, R.J. Observation of a cinnabar phase in GaAs at high pressure. Phys. Rev. Lett. 1997, 19, 3697. [Google Scholar] [CrossRef]
- Born, M.; Huang, K. Dynamical Theory of Crystal Lattices; Oxford University Press: Oxford, UK, 1954. [Google Scholar]
- Eshelby, J.D. The determination of the elastic field o fan ellipsoidal inclusion, and related problems. Proc. R. Soc. A 1957, 241, 376–396. [Google Scholar]
- Reuss, A. Berechnung Der Fließgrenzen Mischkristallen Aufgrund Der Plastizität Bedingung Für Einkristalle. ZAMM-J. Appl. Math. Mech./Zeitschriftfür Angewandte Mathematik und Mechanik 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Morse, P.M. The elastic constants of isotropic materials. Phys. Rev. 1929, 34, 57–64. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Introduction to Perturbation Techniques; John Wiley&Sons: Hoboken, NJ, USA, 1981. [Google Scholar]


| Structure | Reference | a (Å) | C (Å) | B (GPa) | B0 (GPa) |
|---|---|---|---|---|---|
| α-HgS | This work | 4.28 | 9.71 | 63.96 | 3.73 |
| Exp [28] | 4.15 | 9.50 | - | 4.00 | |
| Cal [19] | 4.36 | 9.70 | 16.00 | 5.40 | |
| Cal [19] | 4.29 | 9.69 | 22.50 | 4.80 | |
| β-HgS | This work | 6.00 | 70.01 | 4.91 | |
| Exp [27] | 5.85 | 68.60 | |||
| Cal [15] | 5.97 | 65.40 | |||
| Cal [14] | 6.04 | 59.08 | 4.69 | ||
| Wurtzite | This work | 4.22 | 6.91 | 50.50 | 4.93 |
| B1 | This work | 5.52 | 92.30 | 3.58 | |
| Cal [14] | 5.59 | 98.90 | 4.65 | ||
| Cal [15] | 5.49 | 86.30 | |||
| B2 | This work | 3.45 | 53.80 | 5.00 | |
| Cal [14] | 3.43 | 94.31 | 5.44 | ||
| Cal [15] | 3.52 | 67.40 | 4.80 |
| Structure | Reference | Pt (GPa) |
|---|---|---|
| α-HgS | Stat | 0 |
| Dyn | 0 | |
| Exp [28] | 0 | |
| Cal [19] | 0 | |
| β-HgS | Stat | 0.65 |
| Dyn | 0 | |
| Exp [28] | 0 | |
| Cal-LDA [19] | 0.70 | |
| Wurtzite | Stat | 0.70 |
| Dyn | 0 | |
| B1 | Stat | 6.07 |
| Dyn | 21 | |
| Exp [12,13] | 13, 20.57 | |
| Cal-GGA [14,15,16,17] | 20, 19.9, 16.1, 26.75 | |
| Cal-LDA [19] | 22.2 | |
| B2 | Dyn | 190 |
| Exp | - | |
| Cal-GGA [14,30] | 28, 210 |
| Ref. | C11 | C12 | C13 | C33 | C44 | E | G | ν | |
|---|---|---|---|---|---|---|---|---|---|
| This work | 82.50 | 71.10 | - | - | 18.20 | 32.70 | 11.40 | 0.42 | 138 |
| [16] | 70.40 | 46.50 | - | - | 43.30 | 76.90 | 30.30 | 0.26 | - |
| [32] | 61.80 | 44.90 | - | - | 25.20 | 44.10 | - | 0.33 | 213 |
| This work | 86.70 | 37.80 | 27.60 | 93.80 | 16.80 | 59.50 | 23.40 | 0.27 | 196 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aidouni, A.A.; Aissat, A.; Ould-Mohamed, M.; Benamar, M.E.A.; Dupont, S.; Vilcot, J.P. Ab Initio Study of the Crystalline Structure of HgS under Low and High Pressure. Crystals 2024, 14, 780. https://doi.org/10.3390/cryst14090780
Aidouni AA, Aissat A, Ould-Mohamed M, Benamar MEA, Dupont S, Vilcot JP. Ab Initio Study of the Crystalline Structure of HgS under Low and High Pressure. Crystals. 2024; 14(9):780. https://doi.org/10.3390/cryst14090780
Chicago/Turabian StyleAidouni, Ahmed Amine, Abdelkader Aissat, Mounir Ould-Mohamed, Mohamed El Amine Benamar, Samuel Dupont, and Jean Pierre Vilcot. 2024. "Ab Initio Study of the Crystalline Structure of HgS under Low and High Pressure" Crystals 14, no. 9: 780. https://doi.org/10.3390/cryst14090780
APA StyleAidouni, A. A., Aissat, A., Ould-Mohamed, M., Benamar, M. E. A., Dupont, S., & Vilcot, J. P. (2024). Ab Initio Study of the Crystalline Structure of HgS under Low and High Pressure. Crystals, 14(9), 780. https://doi.org/10.3390/cryst14090780






