Abstract
The rise of straintronics—the possibility of fine-tuning the electronic properties of nanosystems by applying strain to them—has enhanced the interest in characterizing the mechanical properties of these systems when they are subjected to tensile (or compressive), shear and torsion strains. Four parameters are customarily used to describe the mechanical behavior of a macroscopic solid within the elastic regime: Young’s and shear moduli, the torsion constant and Poisson’s ratio. There are some relations among these quantities valid for elastic continuous isotropic systems that are being used for 2D nanocrystals without taking into account the non-continuous anisotropic nature of these systems. We present in this work computational results on the mechanical properties of six small quasi-square (aspect ratio between 0.9 and 1.1) graphene nanocrystals using the PM7 semiempirical method. We use the results obtained to test the validity of two relations derived for macroscopic homogeneous isotropic systems and sometimes applied to 2D systems. We show they are not suitable for these nanostructures and pinpoint the origin of some discrepancies in the elastic properties and effective thicknesses reported in the literature. In an attempt to recover one of these formulas, we introduce an effective torsional thickness for graphene analogous to the effective bending thickness found in the literature. Our results could be useful for fitting interatomic potentials in molecular mechanics or molecular dynamics models for finite carbon nanostructures, especially near their edges and for twisted systems.
1. Introduction
Strain engineering or “straintronics” has emerged as a way to change the behavior of materials, in particular, 2D nanomaterials, especially graphene [1,2,3,4,5,6,7,8,9]. In this case, straintronics has been considered in recent years as a way to fine-tune, among other properties, its band gap in order to use it in many different applications [10,11,12,13,14,15,16,17,18,19]. In fact, strained graphene nanobubbles have been recently proposed as qubits for quantum computing [20]. It is also possible to take advantage of the changes in properties caused by strain in sensing devices [21]. For instance, a graphene strain sensor that can detect various types of strain induced via stretching, bending and torsion [22] and a graphene-based torsion balance [23] have been constructed. Graphene’s properties make it suitable to be used as an actuator to build artificial muscles [24] and in many other biomedical applications [25].
Material simulation methods can be classified according to, among other criteria, two distinct features. The first one uses classical or quantum mechanics, and the second considers materials as continuous media or takes into account their discrete atomistic nature. Therefore, we can consider four different approaches in the study of carbon nanostructures:
- 1.
- Quantum atomistic calculations, which explicitly treat materials as atoms obeying the rules of quantum mechanics. This category includes methods that solve either full (like quantum chemistry and Density Functional Theory approaches) or approximate quantum equations (like tight-binding and semiempirical methods). See, for instance, [14,26];
- 2.
- Quantum continuous models, in which approximate quantum equation solutions are extrapolated to the continuum limit. See, as an example, [27,28];
- 3.
- Classical atomistic simulations, which consider matter as being built of particles that interact following the equations of classical mechanics with potentials (force fields) that try to mimic experimental properties (or those calculated by quantum methods) using empirical parameters. This category includes static calculations called molecular mechanics (MM), also known as molecular structural mechanics (MSM) or nanoscale continuum modelling (NCM)—in which molecular bonds are considered as springs or beams—as well as classical molecular dynamics (MD). See, for instance, [29,30];
- 4.
- Classical continuous models, traditionally used in engineering. See, as an example, [31,32].
Present computational power precludes using quantum atomistic calculations for very large systems, and multi-scale approaches are employed. In these models, macroscopic parameters for approach 4 are obtained from classical atomistic calculations (approach 3) that, in turn, fit their microscopic parameters using quantum mechanical results (approach 1). Therefore, these multi-scale models need a hierarchy of calculations. Jumping from approach 1 to 3 in the case of deformed graphene is still an open question, and better comprehension of the atomistic mechanisms at work in graphene deformations is needed [33].
There are many studies on the different mechanical properties of both infinite graphene and finite graphene nanostructures [30,34,35,36,37,38,39,40,41,42,43,44]. Nevertheless, there is a lack of a comprehensive study on the three different deformations a graphene nanoflake can be subjected to—stretching, shear and torsion (especially the last one)—and on the validity of the use of macroscopic formulas for isotropic materials [45,46] for this clearly anisotropic system.
We have studied the behavior of six different nearly square graphene nanoflakes of various sizes subjected to the three aforementioned deformations along their two edges (zigzag and armchair) and calculated for each of them Young’s and shear moduli and the torsion constant, as well as Poisson’s ratio. Our results could be useful for fitting interatomic potentials in MM/MSM/NCM or MD models for finite carbon nanostructures, especially near their edges and for twisted carbon systems. We have also tested how well commonly used formulas for calculating the torsion constant for a thin slab, as well as Poisson’s ratio from Young’s and shear moduli, perform.
The structure of the paper is as follows. We present in Section 2 (Materials and Methods) first the theoretical model employed, then the systems studied and, finally, the computational method used. Our results are presented in Section 3 in four different subsections: Young’s Modulus, Shear Modulus, Torsion Constant and Poisson’s Ratio. Finally, the conclusions of the study are summarized in Section 4.
2. Materials and Methods
2.1. Theoretical Model
Hooke’s law states that when a material is loaded within the elastic limit, stress T is proportional to strain q:
The proportionality constant is the so-called elastic constant and can be calculated as the stress/strain ratio associated to a given deformation within the elastic limit.
From a computational point of view, it is easier to adopt a different approach and calculate this constant from the expression for the deformation energy (taking the solid in the absence of any external load as the energy origin) as follows:
Using this energy approach yields values closer to the experimental results than the stress–strain approach since the latter requires an additional process, the differentiation of the energy, which introduces some inaccuracies [47].
Let us consider the elastic homogeneous and isotropic rectangular parallelepiped solid with length l, width w and height h depicted in Figure 1.
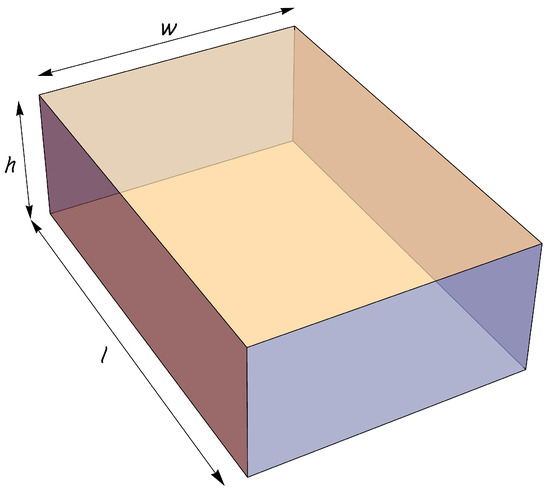
Figure 1.
An elastic homogeneous and isotropic rectangular parallelepiped solid with length l, width w and height h.
We can load the solid in three different ways in order to obtain three small deformations: stretching, shear and torsion. In the case of uniaxial normal stress (either tensile or compressive), the ratio of the stress (force per unit area) applied to the solid, as depicted in Figure 2 (), and the resulting axial strain () is called the (tensile) elastic modulus or Young’s modulus and can be calculated as follows:
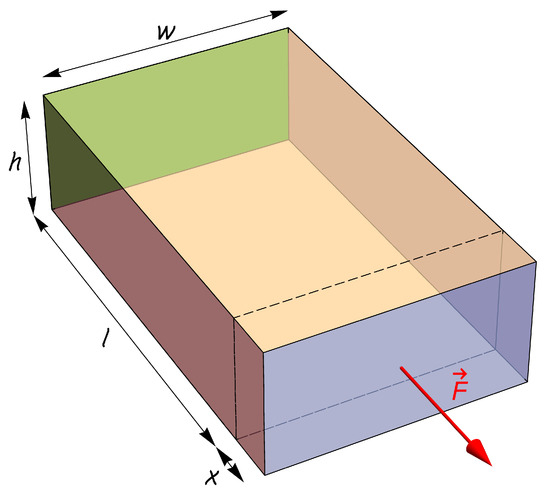
Figure 2.
The solid in Figure 1 subjected to a tensile stress caused by fixing the rear face (colored in green) and pulling with a normal force uniformly distributed over the front face.
It is easy to prove that the elastic energy of the stretched system is given by using a particular case of Equation (2),
where is the volume of the solid.
In the case of uniaxial tangential stress, the ratio of the shear stress (force per unit area) applied to the solid, as depicted in Figure 3 (), and the resulting shear strain () is called the rigidity modulus or shear modulus and can be calculated as follows:
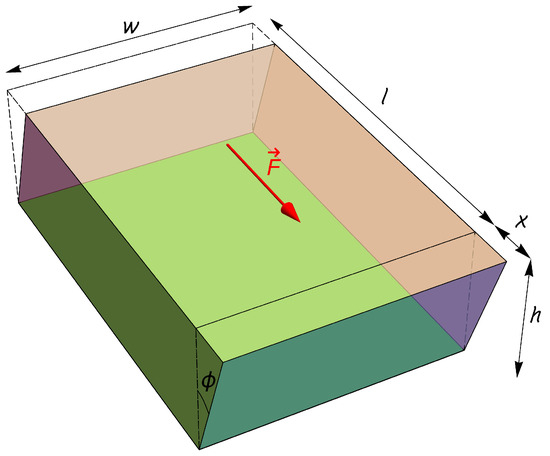
Figure 3.
The solid in Figure 1 subjected to a shear stress caused by fixing the lower face (colored in green) and tearing with a tangential force uniformly distributed over the upper face.
It is straightforward to prove that the elastic energy of the deformed system is given by using another particular case of Equation (2):
Finally, in the case of torsion, shown in Figure 4, the ratio of the applied torque M to the twist angle is known as torsional stiffness, calculated as follows:
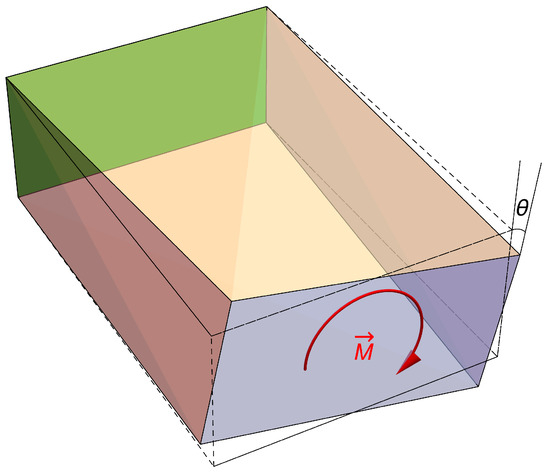
Figure 4.
The solid in Figure 1 subjected to a torsional stress caused by fixing the rear face (colored in green) and twisting with torque on the front face.
Once again, it is easy to prove that the elastic energy of the twisted system is given by using a third particular case of Equation (2):
Torsion can be seen as a special case of shear, and there exists a relationship between their elastic constants. Taking into account this [48,49],
where J is the so-called torsion constant, torsional constant or polar second moment of area (also known as polar moment of inertia). Using this expression and Equation (7),
J can be calculated by reordering this equation as follows:
Graphene is considered as a 2D system. It is, in fact, extremely thin, but it has a small thickness due to the electron cloud surrounding the honeycomb structure of carbon nuclei. The accepted value for this thickness is 3.4 Å [50] (though other values are used by different studies, especially in the case of graphene sheets rolled up to build carbon nanotubes [43,51,52,53,54]). Therefore, in principle, rectangular graphene nanoflakes could be considered as elastic solids of the type shown in Figure 1 with Å. When the thickness of a homogeneous isotropic solid is much smaller that its other two dimensions, there is a formula for calculating the torsion constant [46] that, in our notation, reads:
where, in practice, going up to in the series is enough.
Another consideration to take into account is that the situation depicted in Figure 2 is only a first approximation. When a solid is stretched, its perpendicular cross section usually changes. In most cases, it decreases. This phenomenon can be measured by using the so-called Poisson’s ratio (denoted by ), which is the opposite of the ratio of transverse strain to axial strain. For small deformations, can be calculated as the transversal compression divided by the axial elongation. In our case, for small deformations, the height of the system (i.e., the thickness of the nanoflake) does not change since the breadth of the electron cloud with an appreciable density practically remains constant around the central carbon plane. Therefore,
For homogeneous systems, the following expression links Poisson’s ratio to Young’s and shear moduli:
2.2. Systems Studied
In order to test whether all the equations valid for homogeneous isotropic systems hold for graphene, which is clearly an anisotropic system, we have selected six small quasi-square hydrogen-passivated carbon nanoflakes. The selection criteria were that the aspect ratio must lie between 0.9 and 1.1 and that the electronic ground state has to be a spin singlet. The reason for these rules was the need to be able to analyze the effect of the kind of border (zigzag or armchair) without contamination from changes in aspect ratio or spin state. In order to label the nanoflakes, we have used n × m, where n (m) is the number of hexagons along the zigzag (armchair) edge. Figure 5 presents as an example the 6 × 7 case, while Figure 6 shows all the nanoflakes studied.
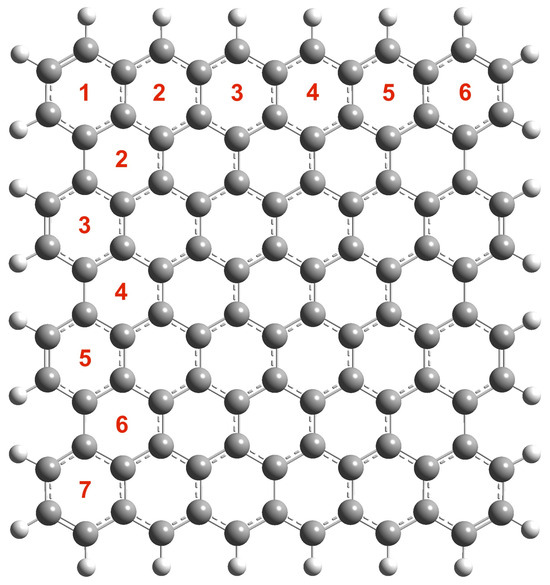
Figure 5.
A 6 × 7 nanoflake with the hexagons along zigzag and armchair edges numbered.
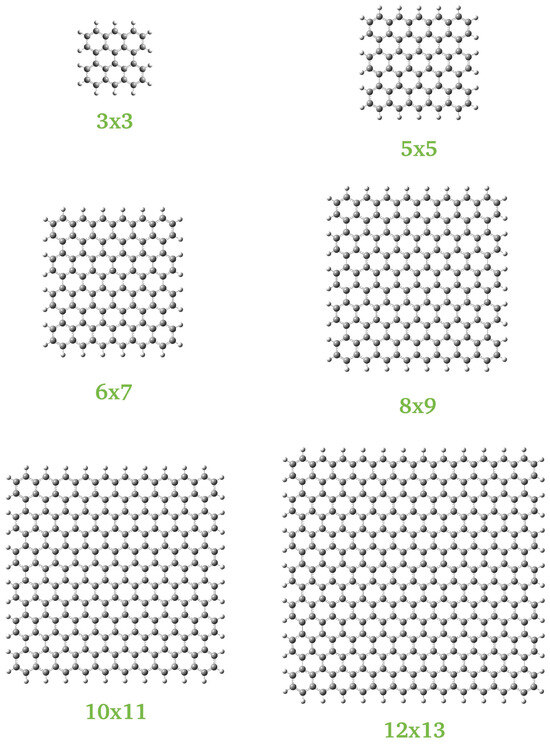
Figure 6.
The six nanoflakes considered in this study.
The six stresses considered in this study are shown in Figure 7 for the 3 × 3 nanoflake.
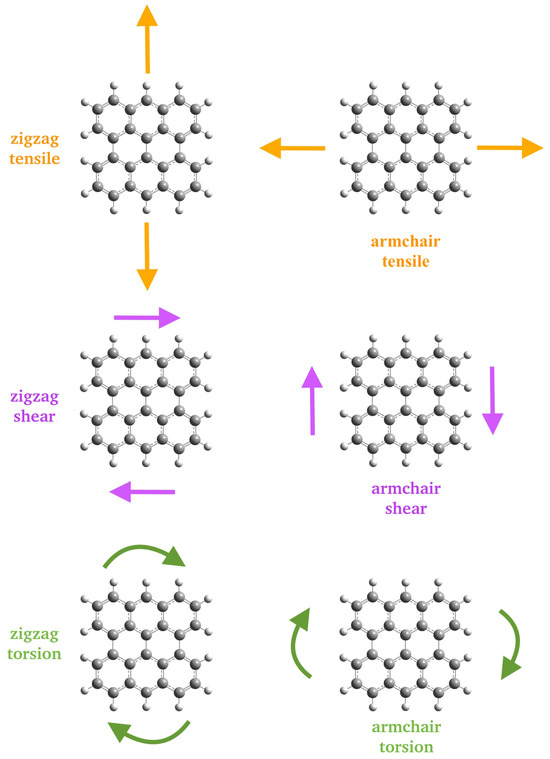
Figure 7.
The six different stresses considered applied on a 3 × 3 nanoflake: tensile (top row), shear (middle row), torsion (bottom row); zigzag (left column), armchair (right column).
2.3. Computational Method
As we pointed out in the Introduction, quantum calculations are needed in order to fit the interatomic potentials used in MM/MSM/NCM and MD methods. Taking into account that these methods only deal with mechanical properties and do not try to explain electronic properties, in order to provide data useful for potential fitting, it is not necessary to use full ab initio quantum mechanics calculations (which would be unavoidable when, for instance, establishing the minimum size for antiferromagnetic ordering to appear in finite graphene nanostructures), and semiempirical approaches (much faster than first-principles calculations) are enough for our purpose.
We have selected the semiempirical PM7 method [55], as implemented in Gaussian16 [56] (i.e., PM7R8 [57]), because it is a fast quantum model that explicitly includes dispersion as well as hydrogen bonding corrections and has been successfully used to analyze interactions in graphene nanostructures [58,59,60,61,62,63,64,65].
We have fully relaxed all atomic positions to obtain the different initial geometries. We have calculated all vibrational frequencies to check for the absence of imaginary values and thus are sure that our initial geometries correspond to minima in the potential energy surface. We have then moved and fixed some boundary atoms in order to deform the nanoflakes and relaxed the positions of the rest of the atoms using the same algorithm to obtain deformation energies. As an example, we present in Figure 8 the final optimized geometries for the six stresses applied to the 3 × 3 nanoflake. The carbon atoms fixed in each case to achieve the desired deformation are highlighted in blue.
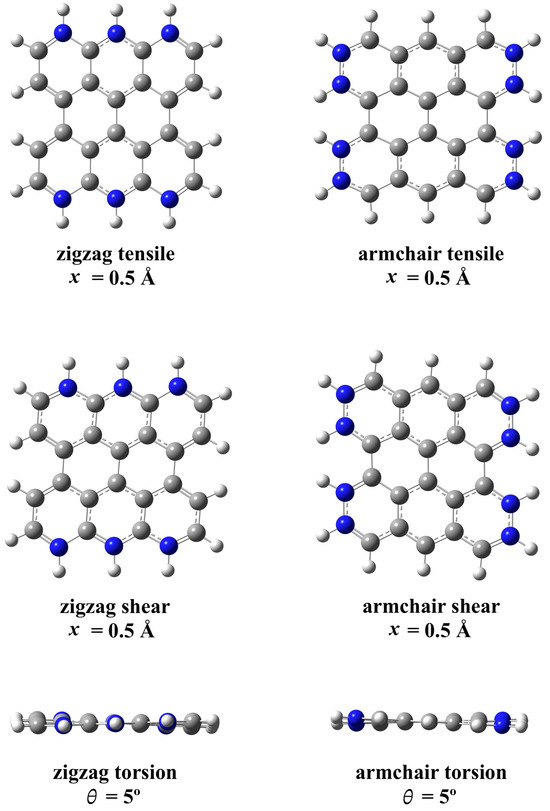
Figure 8.
The six different optimized geometries corresponding to the maximum deformations applied to the 3 × 3 nanoflake: tensile (top row), shear (middle row), torsion (bottom row); zigzag (left column), armchair (right column). The carbon atoms fixed to achieve the desired deformation are highlighted in blue.
3. Results
3.1. Young’s Modulus
We have displaced the carbon atoms on one of the edges along the stretching direction between 0.1 Å and 0.5 Å in 0.1 Å steps, as shown in the upper row of Figure 7, relaxed the rest of the atoms until the new equilibrium geometry depicted in the upper row of Figure 8 is reached and calculated the corresponding strain energies. We have fitted the results to a second-order polynomial and used the quadratic coefficient to calculate E.
As an example of this procedure, we show in Figure 9 the stretching energies corresponding to both armchair and zigzag edges for the 10 × 11 nanoflake. The graphs for other nanoflakes are similar.
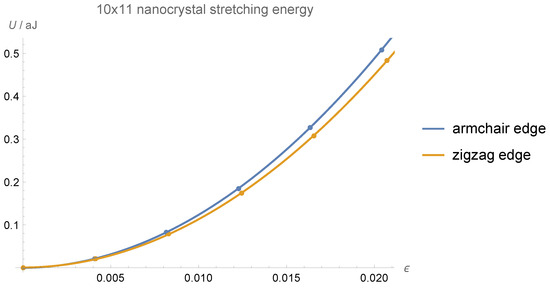
Figure 9.
Stretching energies U as a function of strain for the 10 × 11 nanoflake. Points correspond to calculated energies, while lines show a second-order polynomial fit.
We present in Table 1 the geometrical characteristics of the fully relaxed nanoflakes (the lengths of the two carbon atoms’ edges and the aspect ratio) as well as our results for their Young’s moduli, obtained using Equation (4).

Table 1.
Young’s modulus of square carbon nanoflakes.
For small nanoflakes, the zigzag results are smaller than the armchair ones, but they increase (while armchair Young’s moduli remain practically constant), and both edges show similar E values, for large nanoflakes. Results from other calculations (in ascending order) are presented in Table 2. It can be seen that our results are in the upper part of the interval defined by all of them, excluding Shi et al.’s value, which is very far from the rest. The table also includes the thicknesses (assumed or calculated) when available.

Table 2.
Young’s moduli (E) and thicknesses (h) of graphene found in the literature.
The experimental value for the (infinite) graphene Young’s modulus is 1.0 TPa [76], very similar to the in-plane Young’s modulus in graphite (1.020 TPa [77]). Our results for small nanoflakes are, globally, slightly bigger. This is not surprising since Young’s modulus tends to decrease when the size of the system grows from a few tens to a few hundreds of angstroms [78]. The reason is the edge effect on C–C distances. In infinite graphene, all distances are equal. This is not the case for graphene nanoflakes. To show this, we present in Table 3 a comparison between average C–C distances in the central ring (we have selected the nanoflakes with a central hexagon) and on the edge. C–C distances in the center ring are very close to the experimental infinite graphene value (1.42 Å), but they slightly decrease on the edges. This means C–C bonds are a little bit stronger on the edges of carbon nanoflakes than in graphene, and this translates into an increase in Young’s modulus. As can be seen in the table, the percentage of edge carbon atoms, logically, decreases with the size of the system, but, for our nanoflakes, it is high. For our biggest nanoflake (12 × 13, not shown in the table because it has no central C ring), it is 28%. This explains our values for E being bigger than that for infinite graphene.

Table 3.
Average C–C distance in square carbon nanoflakes and percentage of edge C atoms.
As we have pointed out, graphene is clearly an anisotropic system because the properties in the direction perpendicular to the honeycomb plane are completely different to those in plane. Nevertheless, infinite graphene is transversely isotropic, i.e., its properties are symmetric about an axis normal to the honeycomb plane [79]. This means zigzag and armchair Young’s moduli should be equal. In order to test how far our nanoflakes are from this transverse isotropy, we define their transverse isotropicity as the ratio of their zigzag and armchair Young’s moduli as follows:
With this definition, transverse isotropy corresponds to , and anisotropy can be measured as the absolute deviation from this value . Using the data in Table 1, we have calculated these two quantities for the six nanoflakes studied. The results are presented in Figure 10. For very small flakes (3 × 3 and 5 × 5), aspect ratio is more important than nanoflake size, and the anisotropy increases with size, but, for the rest of the flakes, as expected, the bigger the flake, the smaller the anisotropy.
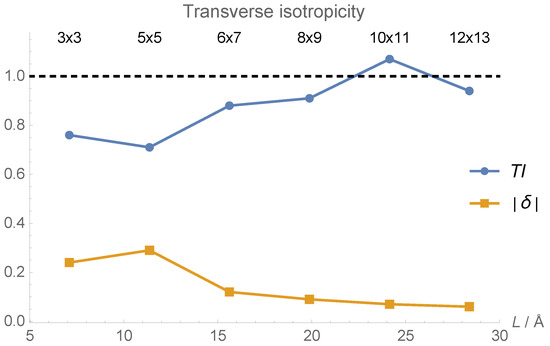
Figure 10.
Transverse isotropicities of the Young’s moduli of the six nanoflakes studied and their anisotropies (absolute deviations from unity) as a function of the zigzag edge length L.
3.2. Shear Modulus
We have displaced the carbon atoms on one of the edges along the shear direction between 0.1 Å and 0.5 Å in 0.1 Å steps, as shown in the middle row of Figure 7, relaxed the rest of the atoms until the new equilibrium geometry depicted in the middle row of Figure 8 is reached and calculated the corresponding strain energies. We have fitted the results to a second-order polynomial and used the quadratic coefficient to calculate G.
As an example of this procedure, we show in Figure 11 the shear energies corresponding to both armchair and zigzag edges for the 8 × 9 nanoflake. The graphs for other nanoflakes are similar.
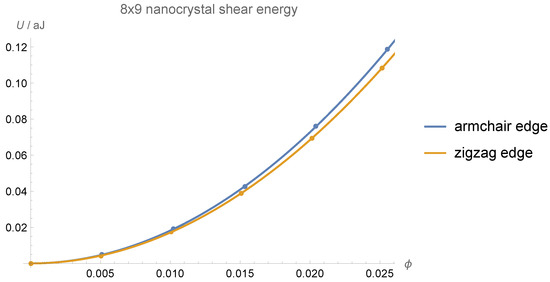
Figure 11.
Shear energies U as a function of the shear angle (in radians) for the 8 × 9 nanoflake. Points correspond to calculated energies, while lines show a second-order polynomial fit.

Table 4.
Shear modulus of square carbon nanoflakes.
Armchair values for G are bigger than zizgzag ones, in agreement with Sakhaee-Pour [37] and Min and Aluru [36].
Results from other calculations (in ascending order) are presented in Table 5. Our results agree very well with most of them and are similar to the experimental value for graphene, which is 280 GPa [80]. It is worth noting that the shear modulus for graphite is 440 GPa [77]. This is proof of the fact that using in-plane graphite properties for isolated graphene is not always valid.

Table 5.
Shear moduli (G) and thicknesses (h) of graphene found in the literature.
3.3. Torsion Constant
We present in Table 6 our results for the torsion constant of the nanoflakes calculated using Equations (11) and (12). In the first case, we have twisted one of the edges between and in steps, as shown in the lower row of Figure 7, relaxed the rest of the atoms until the new equilibrium geometry depicted in the lower row of Figure 8 is reached and calculated the corresponding strain energies. We have fitted the results to a second-order polynomial and used the quadratic coefficient to calculate the torsional stiffness according to Equation (8). We have then used our values for G and l and employed Equation (11) to determine J.

Table 6.
Torsion constant and effective torsional thickness of square carbon nanoflakes.
As an example of this procedure, we show in Figure 12 the torsion energies corresponding to both armchair and zigzag edges for the 6 × 7 nanoflake. The graphs for other nanoflakes are similar.
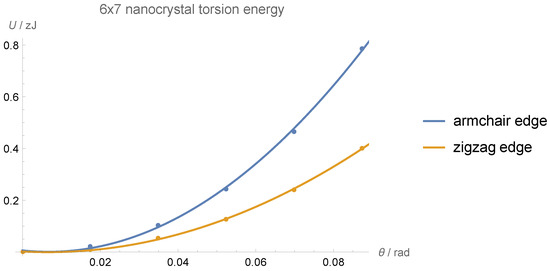
Figure 12.
Torsion energies U as a function of the torsion angle for the 6 × 7 nanoflake. Points correspond to calculated energies, while lines show a second-order polynomial fit.
The first thing to notice is that the direct use of Equation (12) with the standard value for graphene thickness h is not valid. This expression for homogeneous isotropic systems overestimates the value of J by an order of magnitude. The situation is similar to what happens for graphene bending rigidity B. Using continuous mechanics expressions for thin plates leads to a value for B one order of magnitude larger than B values obtained based on atomic-level calculations [84,85,86,87]. In fact, as we have already pointed out, there are several proposals for graphene thickness, and some of them arise precisely from trying to apply equations valid for homogeneous isotropic solids to 2D systems. Values of h determined from calculations on bent graphene sheets and carbon nanotubes (which can be seen as a particular case of bent carbon nanoribbons) are very different from the standard value used in stretched (or compressed) planar graphene (the so-called “Yakobson’s paradox”). Using molecular mechanics calculations, Duan et al. reported 0.52 Å [88], Scarpa et al. 0.84–1 Å [68] and Shi et al. 1.27 Å [51], while Yakobson et al. obtained 0.66 Å using molecular dynamics simulations [29]. From ab initio calculations, Kudin et al. [89] obtained 0.894 Å, Wang et al. 0.665 Å [90] and Shenderova et al. 0.9 Å [91]. Following this idea of an effective bending thickness, we report in the last column of the table the effective torsional thickness defined as the value of h that has to be used in Equation (12) in order to obtain the same value for J as the one obtained directly from torsion data and Equation (11). Our values for the effective torsional thicknesses are similar to these effective bending thicknesses and compatible with the upper limit for the effective single-walled carbon nanotube thickness determined by Pine et al., 1 Å [92].
Focusing on the results obtained using Equation 11, with the exception of in the 5 × 5 case, the torsion constant is greater when the nanoflake is twisted around the armchair edge, and, globally, J increases with the size of the system. Both behaviors are in agreement with results obtained in previous studies [93,94,95]. In this case, we cannot compare our numerical results to those in the literature because we have found neither calculations nor experiments dealing with any of our nanoflakes, and neither torsional stiffness nor torsion constant are intrinsic material properties but depend on the exact geometry of the system. Results for twisting are by far less abundant than those for other deformations, and our results could be useful for fitting interatomic potentials (especially for torsion and out-of-plane hybridization terms in MM/MSM/NCM and MD models) for finite carbon nanostructures.
3.4. Poisson’s Ratio
Table 7 includes our results for the Poison’s ratio of the nanoflakes calculated using Equations (13) and (14). In the first case, we have used the optimized stretched geometries obtained for determining Young’s moduli, measured the transverse compression at the center of the nanoflake and computed .

Table 7.
Poisson’s ratio of square carbon nanoflakes.
It is clear that Equation (14) overestimates the value of and cannot be used for these systems. This fact has been previously found for boron nitride nanoflakes [96,97], which also have a honeycomb structure. Results obtained by applying the definition of Poisson’s ratio given by Equation (13) indicate that is bigger for stretching and pulling on the armchair edges (in agreement with Sakhaee-Pour [37]) but that the difference decreases as the size of the nanoflakes increases.
Results from other calculations are presented (in ascending order) in Table 8. We do not include thicknesses in this case because h is not needed in order to calculate . Poisson’s ratio is strongly dependent on the strain applied (it can even become negative for large strains) [98,99]. In the table, we have selected the values corresponding to the smallest strain possible, but not all cases correspond to the so-called zero-strain limit. That is the reason for the variety of results reported, except for in the last case; Sakhaee-Pour’s results [37] are much higher that those from other calculations because he uses Equation (14) to determine .

Table 8.
Poisson’s ratios () of graphene found in the literature.
Our results should be compared to those from Jiang et al. [98] and Wang et al. [99], which correspond to the zero-strain limit. The agreement with those results is complete. Regarding experiments, the experimental value of for graphite is 0.160 [77] and, for graphene, 0.19 [104], but those papers do not indicate the strain, and it is not possible to know how far they are from the zero-strain limit.
4. Conclusions
We have studied the mechanical properties of six small nearly square graphene nanoflakes using the semiempirical PM7 model. We have considered stretching, shear and torsion deformations along zigzag and armchair edges, calculating Young’s and shear moduli as well as the torsion constant and Poisson’s ratio. Results obtained could be useful for fitting interatomic potentials (especially for torsion and out-of-plane hybridization terms and for near-the-edge bonds in MM/MSM/NCM and MD models) for finite carbon nanostructures. Our results are close to other calculations and to experimental values corresponding to infinite graphene, when these are available. Additionally, by making use of these results, we have tested two formulas valid for macroscopic homogeneous isotropic systems that are sometimes used for 2D nanostructures. We have shown that they do not hold for graphene and explained some strange results reported in the literature. In an attempt to recover one of these formulas, we have introduced an effective torsional thickness for 2D crystals analogous to the effective bending thickness found in the literature. The fast methodology developed in this work can be extended to two other dimensional nanostructures—fully planar and buckled—providing valuable results in order to fit interatomic potentials for faster and more reliable molecular mechanics and molecular dynamics calculations in these systems.
Author Contributions
Conceptualization, N.A.C.; methodology, N.A.C.; software, A.S.-G. and N.A.C.; validation, A.S.-G. and N.A.C.; formal analysis, A.S.-G. and N.A.C.; investigation, A.S.-G.; writing—original draft preparation, N.A.C.; writing—review and editing, A.S.-G. and N.A.C.; visualization, A.S.-G. and N.A.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the European Union NextGenerationEU (PRTR C17.I1).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Bissett, M.A.; Tsuji, M.; Ago, H. Strain engineering the properties of graphene and other two-dimensional crystals. Phys. Chem. Chem. Phys. 2014, 16, 11124–11138. [Google Scholar] [CrossRef]
- Deng, S.; Sumant, A.V.; Berry, V. Strain engineering in two-dimensional nanomaterials beyond graphene. Nano Today 2018, 22, 14–35. [Google Scholar] [CrossRef]
- Peng, Z.; Chen, X.; Fan, Y.; Srolovitz, D.J.; Lei, D. Strain engineering of 2D semiconductors and graphene: From strain fields to band-structure tuning and photonic applications. Light. Sci. Appl. 2020, 9, 190. [Google Scholar] [CrossRef] [PubMed]
- Ge, X.; Zhou, X.; Sun, D.; Chen, X. First-Principles Study of Structural and Electronic Properties of Monolayer PtX2 and Janus PtXY (X, Y = S, Se, and Te) via Strain Engineering. ACS Omega 2023, 8, 5715–5721. [Google Scholar] [CrossRef]
- Qi, Y.; Sadi, M.A.; Hu, D.; Zheng, M.; Wu, Z.; Jiang, Y.; Chen, Y.P. Recent Progress in Strain Engineering on Van der Waals 2D Materials: Tunable Electrical, Electrochemical, Magnetic, and Optical Properties. Adv. Mater. 2023, 35, 2205714. [Google Scholar] [CrossRef]
- Hasani, N.; Rajabi-Maram, A.; Touski, S.B. Strain engineering of electronic and spin properties in SnX (X = P, As, Sb, Bi) monolayers. J. Phys. Chem. Solids 2023, 174, 111131. [Google Scholar] [CrossRef]
- Kim, J.M.; Haque, M.F.; Hsieh, E.Y.; Nahid, S.M.; Zarin, I.; Jeong, K.Y.; So, J.P.; Park, H.G.; Nam, S. Strain Engineering of Low-Dimensional Materials for Emerging Quantum Phenomena and Functionalities. Adv. Mater. 2023, 35, 2107362. [Google Scholar] [CrossRef] [PubMed]
- Pandey, M.; Pandey, C.; Ahuja, R.; Kumar, R. Straining techniques for strain engineering of 2D materials towards flexible straintronic applications. Nano Energy 2023, 109, 108278. [Google Scholar] [CrossRef]
- Fan, W.; Winands, T.; Doltsinis, N.L.; Li, Y.; Wang, Z. A Decatwistacene with an Overall 170° Torsion. Angew. Chem. Int. Ed. 2017, 56, 15373–15377. [Google Scholar] [CrossRef]
- Liu, H.; Lee, M.; Šiškins, M.; van der Zant, H.S.J.; Steeneken, P.G.; Verbiest, G.J. Tuning heat transport in graphene by tension. Phys. Rev. B 2023, 108, L081401. [Google Scholar] [CrossRef]
- He, S.; Zhang, Y.; Gao, J.; Nag, A.; Rahaman, A. Integration of Different Graphene Nanostructures with PDMS to Form Wearable Sensors. Nanomaterials 2022, 12, 950. [Google Scholar] [CrossRef]
- Srimaneepong, V.; Skallevold, H.E.; Khurshid, Z.; Zafar, M.S.; Rokaya, D.; Sapkota, J. Graphene for Antimicrobial and Coating Application. Int. J. Mol. Sci. 2022, 23, 499. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, Y.; Liu, J.; Ren, Q.; Chen, Z.; Zhao, Y.; Zhao, P. Strain engineering of graphene on rigid substrates. Nanoscale Adv. 2022, 4, 5056–5061. [Google Scholar] [CrossRef] [PubMed]
- de-la Huerta-Sainz, S.; Ballesteros, A.; Cordero, N.A. Quantum Revivals in Curved Graphene Nanoflakes. Nanomaterials 2022, 12, 1953. [Google Scholar] [CrossRef]
- Yuan, X.; Zhu, S. Compressive strain engineering of strong and sensitive pseudomagnetic fields in buckled graphene nanobubbles. Phys. Rev. B 2023, 107, 195417. [Google Scholar] [CrossRef]
- De Beule, C.; Phong, V.T.; Mele, E.J. Network model for periodically strained graphene. Phys. Rev. B 2023, 107, 045405. [Google Scholar] [CrossRef]
- Mahmud, M.T.; Zhai, D.; Sandler, N. Topological Flat Bands in Strained Graphene: Substrate Engineering and Optical Control. Nano Lett. 2023, 23, 7725–7732. [Google Scholar] [CrossRef]
- Dawood, O.M.; Thameel, M.N.; Mohammad, J. Unveiling a new Raman active mode in graphene and its implications for band gap formation: A DFT study. Phys. E Low-Dimens. Syst. Nanostruct. 2023, 154, 115810. [Google Scholar] [CrossRef]
- Tepliakov, N.V.; Lischner, J.; Kaxiras, E.; Mostofi, A.A.; Pizzochero, M. Unveiling and Manipulating Hidden Symmetries in Graphene Nanoribbons. Phys. Rev. Lett. 2023, 130, 026401. [Google Scholar] [CrossRef]
- Park, H.C.; Han, J.; Myoung, N. A strain-engineered graphene qubit in a nanobubble. Quantum Sci. Technol. 2023, 8, 025012. [Google Scholar] [CrossRef]
- Lee, H.C.; Hsieh, E.Y.; Yong, K.; Nam, S. Multiaxially-stretchable kirigami-patterned mesh design for graphene sensor devices. Nano Res. 2020, 13, 1406–1412. [Google Scholar] [CrossRef]
- Chun, S.; Choi, Y.; Park, W. All-graphene strain sensor on soft substrate. Carbon 2017, 116, 753–759. [Google Scholar] [CrossRef]
- Cong, L.; Yuan, Z.; Bai, Z.; Wang, X.; Zhao, W.; Gao, X.; Hu, X.; Liu, P.; Guo, W.; Li, Q.; et al. On-chip torsion balances with femtonewton force resolution at room temperature enabled by carbon nanotube and graphene. Sci. Adv. 2021, 7, eabd2358. [Google Scholar] [CrossRef]
- Foroughi, J.; Spinks, G. Carbon nanotube and graphene fiber artificial muscles. Nanoscale Adv. 2019, 1, 4592–4614. [Google Scholar] [CrossRef] [PubMed]
- Malisz, K.; Świeczko Żurek, B. Graphene Production and Biomedical Applications: A Review. Crystals 2023, 13, 1413. [Google Scholar] [CrossRef]
- Cordero, N.A.; Alonso, J.A. Interaction of Surfactants Containing a Sulfuric Group with a (5,5) Carbon Nanotube. J. Phys. Chem. 2010, 114, 17249–17256. [Google Scholar] [CrossRef]
- García, T.; Rodríguez-Bolívar, S.; Cordero, N.A.; Romera, E. Wavepacket revivals in monolayer and bilayer graphene rings. J. Phys. Condens. Matter 2013, 25, 235301. [Google Scholar] [CrossRef]
- García, T.; Cordero, N.A.; Romera, E. Zitterbewegung and quantum revivals in monolayer graphene quantum dots in magnetic fields. Phys. Rev. B 2014, 89, 075416. [Google Scholar] [CrossRef]
- Yakobson, B.I.; Brabec, C.J.; Bernholc, J. Nanomechanics of Carbon Tubes: Instabilities beyond Linear Response. Phys. Rev. Lett. 1996, 76, 2511–2514. [Google Scholar] [CrossRef]
- Reddy, C.D.; Rajendran, S.; Liew, K.M. Equilibrium configuration and continuum elastic properties of finite sized graphene. Nanotechnology 2006, 17, 864. [Google Scholar] [CrossRef]
- Ru, C.Q. Effect of van der Waals forces on axial buckling of a double-walled carbon nanotube. J. Appl. Phys. 2000, 87, 7227–7231. [Google Scholar] [CrossRef]
- El Kass, D.; Monneau, R. Atomic to continuum passage for nanotubes: A discrete Saint-Venant principle and error estimates. Arch. Ration. Mech. Anal. 2014, 213, 25–128. [Google Scholar] [CrossRef]
- Huang, K.; Yin, Y.; Qu, B. Tight-binding theory of graphene mechanical properties. Microsyst. Technol. 2021, 27, 3851–3858. [Google Scholar] [CrossRef]
- Anastasi, A.A.; Ritos, K.; Cassar, G.; Borg, M.K. Mechanical properties of pristine and nanoporous graphene. Mol. Simul. 2016, 42, 1502–1511. [Google Scholar] [CrossRef]
- Cho, J.; Luo, J.; Daniel, I. Mechanical characterization of graphite/epoxy nanocomposites by multi-scale analysis. Compos. Sci. Technol. 2007, 67, 2399–2407. [Google Scholar] [CrossRef]
- Min, K.; Aluru, N.R. Mechanical properties of graphene under shear deformation. Appl. Phys. Lett. 2011, 98, 013113. [Google Scholar] [CrossRef]
- Sakhaee-Pour, A. Elastic properties of single-layered graphene sheet. Solid State Commun. 2009, 149, 91–95. [Google Scholar] [CrossRef]
- Tsai, J.L.; Tu, J.F. Characterizing mechanical properties of graphite using molecular dynamics simulation. Mater. Des. 2010, 31, 194–199. [Google Scholar] [CrossRef]
- Zakharchenko, K.V.; Katsnelson, M.I.; Fasolino, A. Finite Temperature Lattice Properties of Graphene beyond the Quasiharmonic Approximation. Phys. Rev. Lett. 2009, 102, 046808. [Google Scholar] [CrossRef]
- Chandra, Y.; Adhikari, S.; Mukherjee, S.; Mukhopadhyay, T. Unfolding the mechanical properties of buckypaper composites: Nano- to macro-scale coupled atomistic-continuum simulations. Eng. Comput. 2022, 38, 5199–5229. [Google Scholar] [CrossRef]
- Savin, A.; Korznikova, E.; Dmitriev, S. Improving bending rigidity of graphene nanoribbons by twisting. Mech. Mater. 2019, 137, 103123. [Google Scholar] [CrossRef]
- Thakur, R.; Ahluwalia, P.; Kumar, A.; Sharma, M.; Sharma, R. Twisted helical armchair graphene nanoribbons: Mechanical and electronic properties. Eur. Phys. J. 2021, 94, 99. [Google Scholar] [CrossRef]
- Sun, Y.W.; Papageorgiou, D.G.; Humphreys, C.J.; Dunstan, D.J.; Puech, P.; Proctor, J.E.; Bousige, C.; Machon, D.; San-Miguel, A. Mechanical properties of graphene. Appl. Phys. Rev. 2021, 8, 021310. [Google Scholar] [CrossRef]
- Ragab, T.; McDonald, J.; Basaran, C. Aspect ratio effect on shear modulus and ultimate shear strength of graphene nanoribbons. Diam. Relat. Mater. 2017, 74, 9–15. [Google Scholar] [CrossRef]
- Landau, L.; Lifshitz, E. Theory of Elasticity; Pergamon Press: Oxford, UK, 1970. [Google Scholar]
- Timoshenko, S.; Goodier, J. Theory of Elasticity; McGRAW-HILL: New York, NY, USA, 1951. [Google Scholar]
- Shodja, H.M.; Ojaghnezhad, F.; Etehadieh, A.; Tabatabaei, M. Elastic moduli tensors, ideal strength, and morphology of stanene based on an enhanced continuum model and first principles. Mech. Mater. 2017, 110, 1–15. [Google Scholar] [CrossRef]
- Guo, C.; Papangelis, J. Torsion of beams with corrugated webs. In Proceedings of the Ninth International Conference on Advances in Steel Structures (ICASS 2018), Hong Kong, China, 5–7 December 2018; pp. 5–7. [Google Scholar] [CrossRef]
- Trahair, N.; Bradford, M.; Nethercot, D.; Gardner, L. The Behaviour and Design of Steel Structures to EC3, 4th ed.; Taylor & Francis: New York, NY, USA, 2008. [Google Scholar]
- Xia, D.; Li, Q.; Xue, Q.; Liang, C.; Dong, M. Super flexibility and stability of graphene nanoribbons under severe twist. Phys. Chem. Chem. Phys. 2016, 18, 18406–18413. [Google Scholar] [CrossRef]
- Shi, J.X.; Natsuki, T.; Lei, X.W.; Ni, Q.Q. Equivalent Young’s modulus and thickness of graphene sheets for the continuum mechanical models. Appl. Phys. Lett. 2014, 104, 223101. [Google Scholar] [CrossRef]
- Lee, D.H.; Lee, M.J.; Kim, Y.S.; Choi, J.S.; Park, B.H. Sample rotation angle dependence of graphene thickness measured using atomic force microscope. Carbon 2015, 81, 210–215. [Google Scholar] [CrossRef]
- Delfani, M.R.; Shodja, H. Dual ideal shear strengths for chiral single-walled carbon nanotubes. Int. J.-Non-Linear Mech. 2020, 120, 103382. [Google Scholar] [CrossRef]
- Huang, Y.; Wu, J.; Hwang, K.C. Thickness of graphene and single-wall carbon nanotubes. Phys. Rev. B 2006, 74, 245413. [Google Scholar] [CrossRef]
- Stewart, J. Optimization of parameters for semiempirical methods VI: More modifications to the NDDO approximations and re-optimization of parameters. J. Mol. Model. 2013, 19, 1–32. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16; Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2019. [Google Scholar]
- Throssel, K. Evaluating and Improving Approximate LCAO-MO Theory with Restored Overlap and Bond Order Bond Energy Corrections. Ph.D. Thesis, Wesleyan University, Middletown, CT, USA, 2017. Available online: https://digitalcollections.wesleyan.edu/object/ir-2308 (accessed on 24 March 2024).
- Jurkiewicz, K.; Hawelek, L.; Balin, K.; Szade, J.; Braghiroli, F.L.; Fierro, V.; Celzard, A.; Burian, A. Conversion of Natural Tannin to Hydrothermal and Graphene-Like Carbons Studied by Wide-Angle X-ray Scattering. J. Phys. Chem. A 2015, 119, 8692–8701. [Google Scholar] [CrossRef] [PubMed]
- Jaiyong, P.; Bryce, R.A. Approximate quantum chemical methods for modelling carbohydrate conformation and aromatic interactions: β-cyclodextrin and its adsorption on a single-layer graphene sheet. Phys. Chem. Chem. Phys. 2017, 19, 15346–15355. [Google Scholar] [CrossRef] [PubMed]
- Vorontsov, A.V.; Tretyakov, E.V. Determination of graphene’s edge energy using hexagonal graphene quantum dots and PM7 method. Phys. Chem. Chem. Phys. 2018, 20, 14740–14752. [Google Scholar] [CrossRef] [PubMed]
- Hariharan, S.; Majumder, M.; Edel, R.; Grabnic, T.; Sibener, S.J.; Hase, W.L. Exploratory Direct Dynamics Simulations of 3O2 Reaction with Graphene at High Temperatures. J. Phys. Chem. C 2018, 122, 29368–29379. [Google Scholar] [CrossRef]
- Bertorelle, F.; Basu, S.; Fakhouri, H.; Bakulic, M.P.; Mignon, P.; Russier-Antoine, I.; Brevet, P.F.; Thomas, S.; Kalarikkal, N.; Antoine, R. Covalent anchoring of atomically precise glutathione-protected gold nanoclusters on graphene oxide nanosheets. Nano Express 2020, 1, 030005. [Google Scholar] [CrossRef]
- Gun’ko, V. Quantum-chemically computed integral characteristics of complex nanomaterials. Chem. Phys. Technol. Surf./Khimiya Fiz. Tekhnologiya Poverhni 2021, 12, 157–167. Available online: https://www.cpts.com.ua/index.php/cpts/article/download/590/598 (accessed on 24 March 2024). [CrossRef]
- Chi, S.C.; Lee, C.L.; Chang, C.M. Adsorption of Pesticides, Antibiotics and Microcystin-LR by Graphene and Hexagonal Boron Nitride Nano-Systems: A Semiempirical PM7 and Theoretical HSAB Study. Crystals 2022, 12, 1068. [Google Scholar] [CrossRef]
- Tromer, R.M.; Felix, I.M.; Pereira, L.F.C.; da Luz, M.G.E.; Junior, L.A.R.; Galvão, D.S. Lattice thermal conductivity of 2D nanomaterials: A simple semi-empirical approach. Phys. Chem. Chem. Phys. 2023, 25, 28703–28715. [Google Scholar] [CrossRef]
- Lebedeva, I.V.; Minkin, A.S.; Popov, A.M.; Knizhnik, A.A. Elastic constants of graphene: Comparison of empirical potentials and DFT calculations. Phys. E Low-Dimens. Syst. Nanostruct. 2019, 108, 326–338. [Google Scholar] [CrossRef]
- Giannopoulos, G.I. Elastic buckling and flexural rigidity of graphene nanoribbons by using a unique translational spring element per interatomic interaction. Comput. Mater. Sci. 2012, 53, 388–395. [Google Scholar] [CrossRef]
- Scarpa, F.; Adhikari, S.; Phani, A.S. Effective elastic mechanical properties of single layer graphene sheets. Nanotechnology 2009, 20, 065709. [Google Scholar] [CrossRef] [PubMed]
- Polyakova, P.; Galiakhmetova, L.K.; Murzaev, R.; Lisovenko, D.; Baimova, J. Elastic properties of diamane. Lett. Mater. 2023, 13, 171–176. [Google Scholar] [CrossRef]
- Tzeng, S.H.; Tsai, J.L. Characterizing the Mechanical Properties of Graphene and Single Walled Carbon Nanotubes. J. Mech. 2011, 27, 461–467. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, L.; Huang, J. A modified spring finite element model for graphene elastic properties study. Mater. Today Commun. 2023, 34, 105158. [Google Scholar] [CrossRef]
- Sha’bani, F.; Rash-Ahmadi, S. Length scale effect on the buckling behavior of a graphene sheets using modified couple stress theory and molecular dynamics method. Acta Mech. 2022, 233, 943–960. [Google Scholar] [CrossRef]
- Zaeri, M.; Ziaei-Rad, S.; Vahedi, A.; Karimzadeh, F. Mechanical modelling of carbon nanomaterials from nanotubes to buckypaper. Carbon 2010, 48, 3916–3930. [Google Scholar] [CrossRef]
- Tapia, A.; Peón-Escalante, R.; Villanueva, C.; Avilés, F. Influence of vacancies on the elastic properties of a graphene sheet. Comput. Mater. Sci. 2012, 55, 255–262. [Google Scholar] [CrossRef]
- Tahani, M.; Safarian, S. Determination of rigidities, stiffness coefficients and elastic constants of multi-layer graphene sheets by an asymptotic homogenization method. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 1–16. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
- Blakslee, O.L.; Proctor, D.G.; Seldin, E.J.; Spence, G.B.; Weng, T. Elastic Constants of Compression-Annealed Pyrolytic Graphite. J. Appl. Phys. 2003, 41, 3373–3382. [Google Scholar] [CrossRef]
- Lengvarskỳ, P.; Bocko, J. Mechanical Properties and Eigenfrequencies of Graphene Sheets. Acta Mech. Slovaca 2017, 21, 26–32. [Google Scholar] [CrossRef]
- Thomas, S.; Ajith, K.; Lee, S.U.; Valsakumar, M.C. Assessment of the mechanical properties of monolayer graphene using the energy and strain-fluctuation methods. RSC Adv. 2018, 8, 27283–27292. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Metcalf, T.H.; Robinson, J.T.; Houston, B.H.; Scarpa, F. Shear Modulus of Monolayer Graphene Prepared by Chemical Vapor Deposition. Nano Lett. 2012, 12, 1013–1017. [Google Scholar] [CrossRef]
- Mukhopadhyay, T.; Mahata, A.; Adhikari, S.; Asle Zaeem, M. Probing the shear modulus of two-dimensional multiplanar nanostructures and heterostructures. Nanoscale 2018, 10, 5280–5294. [Google Scholar] [CrossRef]
- Georgantzinos, S.; Giannopoulos, G.; Anifantis, N. Numerical investigation of elastic mechanical properties of graphene structures. Mater. Des. 2010, 31, 4646–4654. [Google Scholar] [CrossRef]
- Zheng, W.; Guo, Z.; Wang, Z.; Boay, C.G.; Wang, X.; Li, Y. Modeling analysis of elastic properties of graphene-carbon nanotube (G-C) reinforced composites. Polym. Compos. 2022, 43, 3136–3149. [Google Scholar] [CrossRef]
- Lindahl, N.; Midtvedt, D.; Svensson, J.; Nerushev, O.A.; Lindvall, N.; Isacsson, A.; Campbell, E.E.B. Determination of the Bending Rigidity of Graphene via Electrostatic Actuation of Buckled Membranes. Nano Lett. 2012, 12, 3526–3531. [Google Scholar] [CrossRef]
- Androulidakis, C.; Zhang, K.; Robertson, M.; Tawfick, S. Tailoring the mechanical properties of 2D materials and heterostructures. 2D Mater. 2018, 5, 032005. [Google Scholar] [CrossRef]
- Androulidakis, C.; Koukaras, E.; Hadjinicolaou, M.; Galiotis, C. Non-Eulerian behavior of graphitic materials under compression. Carbon 2018, 138, 227–233. [Google Scholar] [CrossRef]
- Androulidakis, C.; Koukaras, E.N.; Sampathkumar, K.; Rahova, J.; Galiotis, C.; Frank, O. Hierarchy of nanoscale graphene wrinkles on compliant substrate: Theory and experiment. Extrem. Mech. Lett. 2020, 40, 100948. [Google Scholar] [CrossRef]
- Duan, W.H.; Wang, C.M. Nonlinear bending and stretching of a circular graphene sheet under a central point load. Nanotechnology 2009, 20, 075702. [Google Scholar] [CrossRef] [PubMed]
- Kudin, K.N.; Scuseria, G.E.; Yakobson, B.I. C2F, BN, and C nanoshell elasticity from ab initio computations. Phys. Rev. B 2001, 64, 235406. [Google Scholar] [CrossRef]
- Wang, L.; Zheng, Q.; Liu, J.Z.; Jiang, Q. Size Dependence of the Thin-Shell Model for Carbon Nanotubes. Phys. Rev. Lett. 2005, 95, 105501. [Google Scholar] [CrossRef] [PubMed]
- Shenderova, O.A.; Zhirnov, V.V.; Brenner, D.W. Carbon Nanostructures. Crit. Rev. Solid State Mater. Sci. 2002, 27, 227–356. [Google Scholar] [CrossRef]
- Pine, P.; Yaish, Y.E.; Adler, J. Vibrational analysis of thermal oscillations of single-walled carbon nanotubes under axial strain. Phys. Rev. B 2014, 89, 115405. [Google Scholar] [CrossRef]
- Shen, H. Mechanical properties and thermal conductivity of the twisted graphene nanoribbons. Mol. Phys. 2014, 112, 2614–2620. [Google Scholar] [CrossRef]
- Chatzidakis, G.D.; Kalosakas, G.; Fthenakis, Z.G.; Lathiotakis, N.N. A torsional potential for graphene derived from fitting to DFT results. Eur. Phys. J. B 2018, 91, 11. [Google Scholar] [CrossRef]
- Yoneyama, K.; Yamanaka, A.; Okada, S. Energetics and electronic structure of graphene nanoribbons under uniaxial torsional strain. Jpn. J. Appl. Phys. 2019, 58, SDDD05. [Google Scholar] [CrossRef]
- Tapia, A.; Cab, C.; Hernández-Pérez, A.; Villanueva, C.; Peñuñuri, F.; Avilés, F. The bond force constants and elastic properties of boron nitride nanosheets and nanoribbons using a hierarchical modeling approach. Phys. E Low-Dimens. Syst. Nanostruct. 2017, 89, 183–193. [Google Scholar] [CrossRef]
- Sakharova, N.A.; Pereira, A.F.G.; Antunes, J.M. A Study of the Mechanical Behaviour of Boron Nitride Nanosheets Using Numerical Simulation. Nanomaterials 2023, 13, 2759. [Google Scholar] [CrossRef]
- Jiang, J.W.; Chang, T.; Guo, X.; Park, H.S. Intrinsic negative Poisson’s ratio for single-layer graphene. Nano Lett. 2016, 16, 5286–5290. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Lei, J.; Liu, Z. Molecular dynamics study on the anisotropic Poisson’s ratio of the graphene. Diam. Relat. Mater. 2019, 93, 66–74. [Google Scholar] [CrossRef]
- Caillerie, D.; Mourad, A.; Raoult, A. Discrete homogenization in graphene sheet modeling. J. Elast. 2006, 84, 33–68. [Google Scholar] [CrossRef]
- Cadelano, E.; Palla, P.L.; Giordano, S.; Colombo, L. Nonlinear Elasticity of Monolayer Graphene. Phys. Rev. Lett. 2009, 102, 235502. [Google Scholar] [CrossRef] [PubMed]
- Lu, Q.; Huang, R. Nonlinear mechanics of single-atomic-layer graphene sheets. Int. J. Appl. Mech. 2009, 1, 443–467. [Google Scholar] [CrossRef]
- Koberidze, M. Computational Studies of Torsional Properties of Single-Walled Carbon Nanotubes. Master’s Thesis, University of Jyväskylä, Jyväskylä, Findland, 2010. Available online: https://jyx.jyu.fi/handle/123456789/37243 (accessed on 24 March 2024).
- Politano, A.; Marino, A.R.; Campi, D.; Farías, D.; Miranda, R.; Chiarello, G. Elastic properties of a macroscopic graphene sample from phonon dispersion measurements. Carbon 2012, 50, 4903–4910. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).