The Effect of Mn³⁺ Substitution on the Electric Field Gradient in a HoFe_1−xMn_xO₃ (x = 0–0.7) System

Abstract

The effect of the Mn³⁺ ion on the local distortions of FeO₆ octahedra in orthoferrite samples was investigated. Mössbauer spectroscopy measurements for a series of ${\mathrm{HoFe}}_{1-x}{\mathrm{Mn}}_x{\mathrm{O}}_3$ (x = 0–0.7) orthoferrite samples with the space group Pnma were carried out at temperatures above the Néel point (700 K). The electric field gradient (EFG) tensor on Fe ions for these compounds was found using first-principle calculations. The concentration dependence of quadrupole splitting was obtained using experimental and theoretical data. Mn³⁺ cations were found to affect the Mössbauer spectra mainly due to distortions of the crystal lattice. Theoretical calculations show that the values of all electric field gradient components increase significantly with the manganese concentration in the system, and the eigenvectors ${\mathbf{e}}_{\mathbf{xx}}$ and ${\mathbf{e}}_{\mathbf{yy}}$ of the electric field gradient tensor sharply change their direction at concentrations of x > 0.1.

1. Introduction

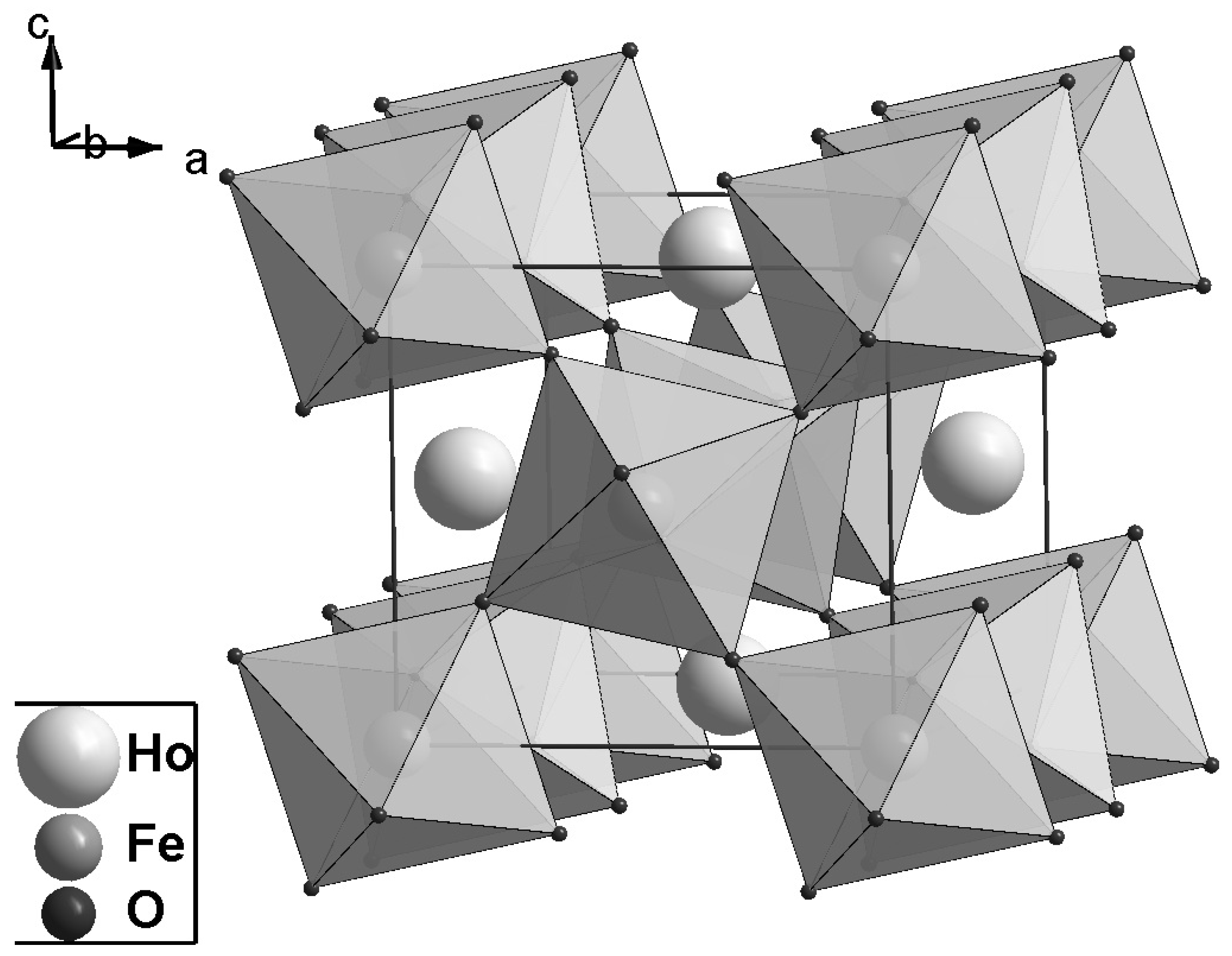
To date, crystals of rare-earth orthoferrites $R{\mathrm{F}\mathrm{e}\mathrm{O}}_3$ (R = La, Pr, …, Lu, and Y) of almost all available compositions have been synthesized and studied [1,2,3]. The $R{\mathrm{F}\mathrm{e}\mathrm{O}}_3$ crystal structure is described by the space group $Pnma$ of the orthorhombic system, and the unit cell contains four formula units (Z = 4). This is the distorted structure of a perfect perovskite, in which distortions are mainly caused by oxygen ion displacements, leading to rotations of FeO₆ octahedra (Figure 1). Briefly, this structure can be described as a frame of vertex-sharing FeO₆ octahedra with rare-earth element atoms in voids between transition ion octahedra.

Orthoferrites undergo magnetic phase transitions of several types, including spontaneous spin-reorientation transitions [4]. The complex magnetic behavior of $R{\mathrm{F}\mathrm{e}\mathrm{O}}_3$ compounds still evokes keen interest from both experimentalists and theoreticians [3]. Over the past few decades, rare-earth orthoferrites have been a focus of research [5,6]. The magnetic structure of the high-temperature orthoferrite phase is a canted antiferromagnet. The relatively small canting of the magnetic moments in the $3d$ subsystem causes a weak ferromagnetic moment in these compounds [7]. Orthoferrite crystals have a high Néel temperature $T_N$, which decreases monotonically as the atomic number of a rare-earth element grows [8].

Below the Néel temperature, $R{\mathrm{F}\mathrm{e}\mathrm{O}}_3$ orthoferrites undergo a spin-reorientation transition, during which the weak ferromagnetic moment changes its direction by 90° [9,10]. The transition temperature varies over a wide range, from units to hundreds of Kelvin, depending on the rare-earth ion type. The highest temperature of the spin-reorientation transition is observed in the ${\mathrm{S}\mathrm{m}\mathrm{F}\mathrm{e}\mathrm{O}}_3$ crystal and amounts to 480 K [11,12]. The task of tuning the temperature of this transition is crucial for possible applications. As was shown previously, one way to control the transition temperature is isovalent substitution in the $3d$ subsystem [13,14]. This substitution, among other things, affects the Néel temperature. As has been shown recently, changes in the angles and distances in (Fe, Mn)O₆ oxygen octahedra play an important role, leading to changes in the electric field gradient (EFG) on $3d$ ions [14,15]. Similar behavior is observed when a rare-earth element in the subsystem is replaced [16,17]. In [14], it was shown that the substitution of Jahn–Teller Mn³⁺ ions for iron ions in the ${\mathrm{H}\mathrm{o}\mathrm{F}\mathrm{e}}_{1-x}{\mathrm{M}\mathrm{n}}_x{\mathrm{O}}_3$ crystals induces additional distortions of the (Fe,Mn)O₆ oxygen octahedron and, consequently, a strong increase in the temperature of the spin-reorientation transition, which can be indicative of the impact of oxygen octahedron distortions on the magnetic properties of orthoferrites.

In this study, a series of the ${\mathrm{H}\mathrm{o}\mathrm{F}\mathrm{e}}_{1-x}{\mathrm{M}\mathrm{n}}_x{\mathrm{O}}_3$ orthoferrites were investigated to establish the effect of substituting manganese ions on the local distortions of the Fe environment. Mössbauer effect measurements and theoretical calculations of the EFG tensor were carried out. The concentration dependence of quadrupole splitting, EFG tensor components, the field asymmetry parameter, and EFG tensor eigenvector directions was found.

2. Materials and Methods

A series of ${\mathrm{H}\mathrm{o}\mathrm{F}\mathrm{e}}_{1-x}{\mathrm{M}\mathrm{n}}_x{\mathrm{O}}_3$ ($0\le x\le 0.7)$ single crystals was synthesized by optical floating zone melting. In the first stage, to obtain the ${\mathrm{H}\mathrm{o}\mathrm{F}\mathrm{e}}_{1-x}{\mathrm{M}\mathrm{n}}_x{\mathrm{O}}_3$ (x = 0, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, and 0.7) samples, powders of the initial ${\mathrm{H}\mathrm{o}}_2{\mathrm{O}}_3$, ${\mathrm{F}\mathrm{e}}_2{\mathrm{O}}_3$, and $\mathrm{M}\mathrm{n}{\mathrm{O}}_2$ oxides (99.9%, Alfa Aesar) were mixed in the desired ratio and annealed at a temperature of 925 °C for 18 h. Due to the volatility of Mn, the added amount of MnO₂ was increased by 2%. The annealed powders were poured into a rubber mold and pressed in a hydrostatic press under a pressure of ≈100 MPa. The obtained cylindrical samples were then annealed in a vertical furnace at a temperature of 1400 °C for 16 h. After annealing, the synthesized polycrystalline ${\mathrm{H}\mathrm{o}\mathrm{F}\mathrm{e}}_{1-x}{\mathrm{M}\mathrm{n}}_x{\mathrm{O}}_3$ ($0\le x\le 0.7)$ samples were placed in an FZ-T-4000-H-VIII-VPO-PC optical floating zone furnace (Crystal Systems Corp., Kobuchisawa, Japan) to grow single crystals. The growth occurred in air under normal pressure at a relative rod rotation speed of 30 rpm. The growth rates varied from 3 to 1 mm/h, depending on the manganese concentration in the samples. The parameters during optical floating zone melting (the feeding rate $V_f$, growth rate $V_g$, rotation rate of the feed $W_f$, rotation rate of the crystal $W_g$, and growth length) are listed in

Table 1. Growth parameters during optical floating zone melting.

Sample	Growth Rate		Rotation Rate		Growth Length	Result
	${\mathit{V}}_{\mathit{f}}$ (mm/h)	${\mathit{V}}_{\mathit{g}}$ (mm/h)	${\mathit{W}}_{\mathit{f}}$ (rpm)	${\mathit{W}}_{\mathit{g}}$ (rpm)	(mm)
HoFeO3	3	3	15	15	80	stable growth
HoFe0.95Mn0.05O3	3	3	15	15	70	stable growth
HoFe0.9Mn0.1O3	3	3	15	15	70	stable growth
HoFe0.8Mn0.2O3	3	3	15	13	70	stable growth
HoFe0.7Mn0.3O3	2.5	2.5	15	12	65	stable growth
HoFe0.6Mn0.4O3	2	2	15	12	65	stable growth
HoFe0.5Mn0.53	1	1	15	10	60	stable growth
HoFe0.4Mn0.6O3	2	2	15	12	60	stable growth
HoFe0.3Mn0.7O3	2.5	2.5	15	12	65	stable growth

.

The uniform distribution of chemical elements on the surface of the samples was controlled using an energy-dispersive spectrometer (Bruker XFlash 630Hc, Bruker Corporation, Billerica, MA, USA). A uniform distribution of Ho, Fe, and Mn over the surface of the samples was realized (see Supplementary Materials).

The synthesized rod-shaped ${\mathrm{H}\mathrm{o}\mathrm{F}\mathrm{e}}_{1-x}{\mathrm{M}\mathrm{n}}_x{\mathrm{O}}_3$ ($0\le x\le 0.7)$ single crystals had a diameter of up to 7 mm and a length of up to 8 cm. The quality of the samples of the entire series and their orientations along the three crystallographic axes were tested by X-ray Laue diffraction. As an example, Figure 2a presents a typical view of a single crystal and Laue patterns for the sample with a manganese concentration of x = 0.3 along different crystallographic directions (Figure 2b–d). For all the samples, one can see narrow symmetrical reflections corresponding to the space group Pnma (♯62).

Samples for the Mössbauer study were prepared by grinding the ${\mathrm{H}\mathrm{o}\mathrm{F}\mathrm{e}}_{1-x}{\mathrm{M}\mathrm{n}}_x{\mathrm{O}}_3$$(0\le x\le 0.5)$ single crystals into a powder. For the samples with manganese concentrations above 0.5, high-temperature Mössbauer measurements require too much time because of the low ${}^{57}\mathrm{Fe}$ concentration and strong absorption by a rare-earth atom. The resulting powder of a 5–10 mg/cm² sample (by iron content) was pressed in aluminum foil tablet with a diameter of 20 mm. Mössbauer spectra of the investigated samples were obtained on an MS-1104Em spectrometer equipped with an MRP-750K furnace (Research Institute of Physics, Southern Federal University) with a ${}^{57}\mathrm{Co}\left(\mathrm{Rh}\right)$ radioactive source in the transmission geometry at a temperature T = 700 K, since the measurements in the paramagnetic state yield information about distortions in the close vicinity of the Mössbauer isotope caused by structural factors [18].

The spectra were processed in two stages. In the first stage, possible nonequivalent states of iron were determined by calculating the quadrupole splitting probability distributions [19]. Using the results obtained, a preliminary model spectrum was formed. In the next stage, the model spectrum was adjusted to the experimental spectrum by varying the entire set of hyperfine parameters using the least squares method in the linear approximation. The chemical shift values are given relative to metallic iron ($\alpha$Fe).

The calculations were carried out with density functional theory using the Perdew–Burke–Ernzerhof exchange-correlation functionals with the generalized gradient approximation (PBE–GGA) implemented in the VASP package [20,21]. The number of plane waves was limited by an energy of 600 eV. The Monkhorst–Pack grid [22] was chosen to be $7\times 5\times 8$. The calculation used the GGA + U method in the Dudarev approximation [23], in which the parameter U for the iron ion was chosen to be 2 eV. The configurations of valence electrons were $5p^{6}5d^{1}6s^2$ for Ho atoms, $3s^{2}3p^{6}3d^{7}4s^1$ for Fe atoms, and $2s^{2}2p^4$ for O atoms. The values of the EFG tensor components were calculated using the technique described in [24] implemented in the VASP package.

3. Results and Discussion

The room-temperature Mössbauer spectra were described in detail in [14]. It should be noted that, with increasing concentrations of ${\mathrm{M}\mathrm{n}}^{3+}$ cations, an increase in the chemical shift of the spectra is observed. In addition, an interplay was suggested between the structural distortions and the magnetic reorientation transition temperature as a result of the substitution of the Jahn–Teller ${\mathrm{M}\mathrm{n}}^{3+}$ cation for the ${\mathrm{F}\mathrm{e}}^{3+}$ cation [14]. Therefore, to thoroughly examine the direct effect of the substitution of the ${\mathrm{M}\mathrm{n}}^{3+}$ cation on the degree of distortion of the nearest environment of iron ions, Mössbauer spectra were recorded above the temperature of magnetic ordering of the $3d$ subsystem at 700 K. 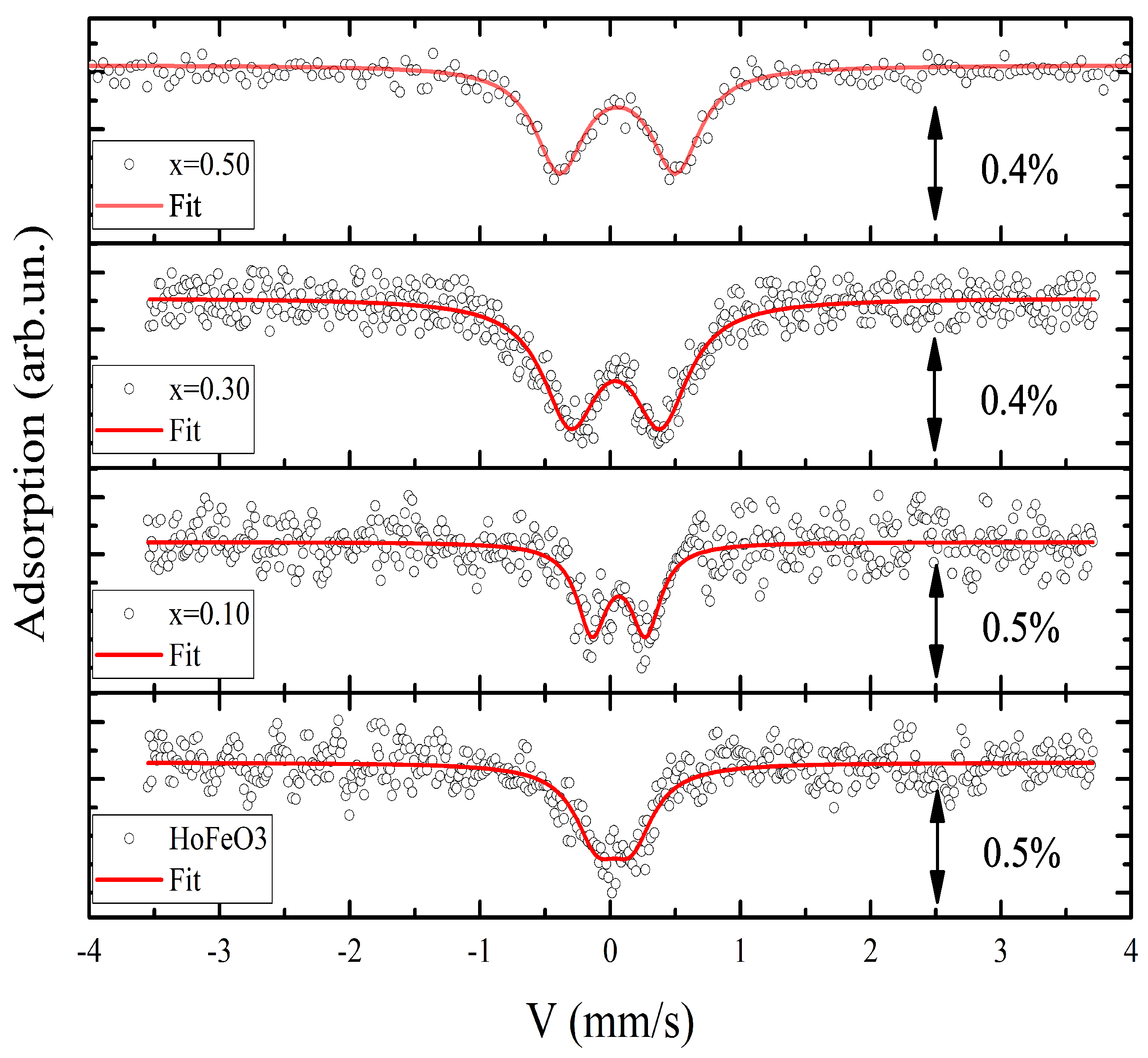The obtained spectra are shown in Figure 3.

At a temperature of 700 K, the spectra for all the samples have the form of quadrupole doublets. Their hyperfine parameters are given in

Table 2. Mössbauer parameters of the ${\mathrm{H}\mathrm{o}\mathrm{F}\mathrm{e}}_{1-x}{\mathrm{M}\mathrm{n}}_x{\mathrm{O}}_3$ (x = 0, 0.1, 0.3, and 0.5) samples at a temperature of 700 K. $\delta$ is the chemical shift with respect to $\alpha$-Fe, $\Delta$ is quadrupole splitting, W is the full width at half maximum of the Mössbauer line, and A is the relative occupancy of sites.

x	$\mathit{\delta }$, ±0.005 mm/s	$\mathbf{\Delta }$, ±0.01 mm/s	W, ±0.01 mm/s	A, ±0.03 arb. un.	Origin
0	0.067	0.28	0.41	1.0	${}^{57}\mathrm{Fe}-octahedral$
0.10	0.098	0.41	0.29	1.0	${}^{57}\mathrm{Fe}-octahedral$
0.30	0.093	0.71	0.31	1.0	${}^{57}\mathrm{Fe}-octahedral$
0.50	0.088	0.92	0.44	1.0	${}^{57}\mathrm{Fe}-octahedral$

. The obtained hyperfine parameters of the $\mathrm{H}\mathrm{o}\mathrm{F}\mathrm{e}{\mathrm{O}}_3$ compound at 700 K correspond to those reported previously in [17]. It is clear that a manganese substitution of x = 0.1 leads to an increase in the isomer shift, $\delta$. This hyperfine parameter indicates a decrease in electronic density on ${}^{57}\mathrm{Fe}$ nuclei in the crystal. It should be noted that the following rise in x does not significantly influence $\delta$. For all Mn-containing samples, $\delta =0.093\pm 0.005$ mm/s. The linewidth W for the sample with x = 0 shows a relatively large value due to the non-full splitting of the excited nuclear level ($I_e=3/2$). This is due to local distortions determined by the crystal structure itself. Then, when the x value rises, the quadrupole doublet shows full-line separation. This leads to a decrease in the linewidth, but the consequent rise in x results in a monotonic increase in the linewidth due to the local distortions induced by Mn³⁺ cations. According to the experimental data obtained here, the quadrupole splitting $\Delta$ has the smallest value for this composition. With an increase in the $\mathrm{M}\mathrm{n}$ concentration, the $\Delta$ value increases in the series ${\mathrm{H}\mathrm{o}\mathrm{F}\mathrm{e}}_{1-x}{\mathrm{M}\mathrm{n}}_x{\mathrm{O}}_3$ ($x=0,0.1,0.3,0.5$). The results obtained show an almost threefold increase in quadrupole splitting on iron atoms already at $x=0.5$, with a tendency for further growth.

A similar situation was observed in the ${\mathrm{S}\mathrm{m}\mathrm{F}\mathrm{e}}_{1-x}{\mathrm{M}\mathrm{n}}_x{\mathrm{O}}_3$ system [25], where the observed $\Delta$ growth was attributed to an increase in the degree of distortion of ${\mathrm{F}\mathrm{e}\mathrm{O}}_6$ octahedra. As a result, the crystal field acting on the nucleus of the Fe atom is significantly changed. Although the nucleus is only sensitive to the second derivative of the crystal field (EFG, $V_{zz}$), there is a direct correlation between the parameters of second-order crystal field splitting and the lattice contribution to quadrupole splitting [26]. At the same time, when replacing ${\mathrm{F}\mathrm{e}}^{3+}$ with ${\mathrm{C}\mathrm{r}}^{3+}$ cations with a spherical $3d$ shell in the series of ${\mathrm{H}\mathrm{o}\mathrm{F}\mathrm{e}}_{1-x}{\mathrm{C}\mathrm{r}}_x{\mathrm{O}}_3$ orthoferrites, the $\Delta$ value barely grows, even with a significant degree of substitution ($x=0.50,0.75$), despite the difference between the ionic radii of $3d$ cations. Thus, one can speak about the decisive role of the cation type in changing the degree of distortion of the nearest environment [15].

Due to the interaction of the quadrupole moment of a nucleus with an EFG on ${}^{57}\mathrm{Fe}$, the effect of cation substitution on the degree of distortions of the FeO₆ octahedron can be directly estimated from the Mössbauer spectra of orthoferrites in the paramagnetic state. In the paramagnetic state, the $\Delta$ value is only determined by the quadrupole transitions (${\mathrm{I}}_e^{\pm 3/2}\to {\mathrm{I}}_g^{\pm 1/2}$ and ${\mathrm{I}}_e^{\pm 1/2}\to {\mathrm{I}}_g^{\pm 1/2}$) of the nucleus of the Mössbauer ${}^{57}\mathrm{Fe}$ atom. In general, the quadrupole splitting of the Mössbauer spectrum has two contributions: (i) from charges of the ions surrounding the Mössbauer nuclei and (ii) from intrinsic electrons, in particular, resulting from the covalent admixture.

To identify the main contribution, first-principle calculations of the electric field gradient tensor within the framework of the method [24] implemented in the VASP package were performed for the iron ion in the ${\mathrm{H}\mathrm{o}\mathrm{F}\mathrm{e}}_{1-x}{\mathrm{M}\mathrm{n}}_x{\mathrm{O}}_3$ compound (x = 0, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7). All calculations were performed using the lattice parameters and relative coordinates of atoms obtained from the X-ray diffraction experiment [14]. Relaxation of the crystal structures of the studied crystals was not carried out. At the same time, calculations for samples with different concentrations of manganese were performed without accounting for the manganese ion. That is, in fact, calculations were performed for the ${\mathrm{H}\mathrm{o}\mathrm{F}\mathrm{e}\mathrm{O}}_3$ crystal using lattice parameters and atomic coordinates corresponding to ${\mathrm{H}\mathrm{o}\mathrm{F}\mathrm{e}}_{1-x}{\mathrm{M}\mathrm{n}}_x{\mathrm{O}}_3$ crystals with specific concentrations of manganese. This approach can be justified for the following reasons: (1) this greatly simplifies the calculation procedure and, as a result, significantly saves calculation time; (2) the experiment demonstrates the effect on iron atoms.

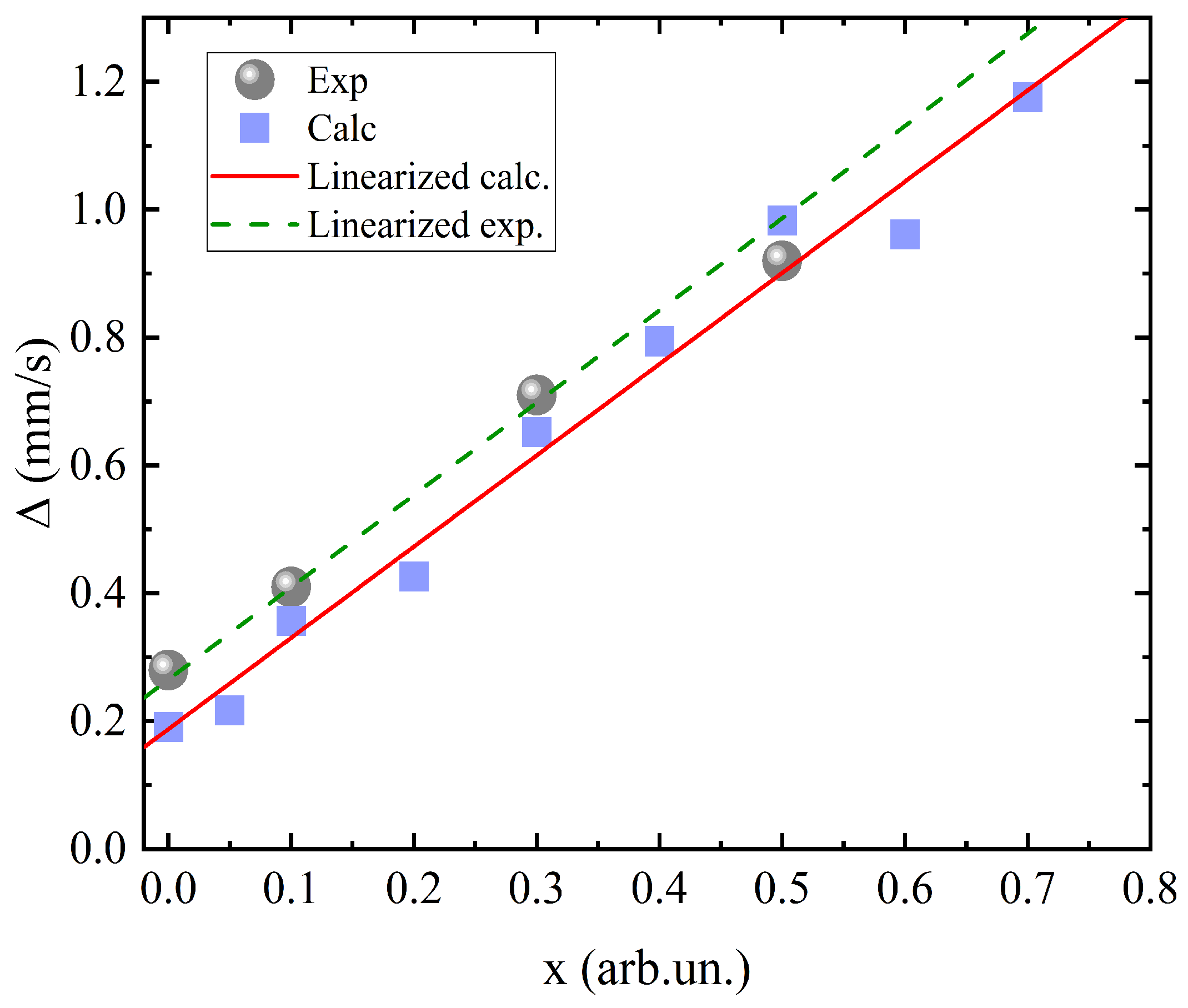
Based on data from the theoretical calculations using Formula (1) [27], the calculated Mössbauer quadrupole splitting values were obtained as a function of the manganese concentration.

$$\Delta =0.5V_{zz}eQ\sqrt{1+{\displaystyle \frac{{\eta }^2}{3}}},$$

(1)

where Q is a nuclear quadrupole moment (Q = 0.16 b for ${}^{57}\mathrm{Fe}$), and $\eta$ is an asymmetry parameter (which will be defined below). The results are presented in Figure 4.

It can be clearly seen that the calculated data are in good agreement with the experiment, and the straight approximation lines have the same slope for both the experimental and theoretical values. Values at all concentrations differ only by a constant value. This means that there are no additional contributions to the shift value depending on the Mn concentration.

The good qualitative and quantitative agreement of the $\Delta$ values confirms the appropriateness of the approach used in the calculations described above. Thus, the most important conclusion can be made, namely that Mn³⁺ cations affect the Mössbauer spectra mainly due to distortions of the crystal lattice. There is no addition of electron density to the iron cations. This is somewhat different from the results of [13].

Using the calculated data, the concentration dependence of the components $V_{xx}$, $V_{yy}$, and $V_{zz}$ (|$V_{zz}$|>|$V_{xx}$|>|$V_{yy}$|) of the diagonalized EFG tensors and the EFG asymmetry parameter $\eta$ (Equation (2)) were plotted [27]. The plots are shown in Figure 5. The linear growth of the field components with increasing concentration is seen. The calculation yielded a value of $V_{zz}=1.2\times {10}^{21}$ V/m² for the principal component of the EFG tensor of the $\mathrm{H}\mathrm{o}\mathrm{F}\mathrm{e}{\mathrm{O}}_3$ compound, which is consistent with the data reported in [16] ($V_{zz}=1.5\times {10}^{21}$ V/m²), where the lattice contribution to the EFG in unsubstituted orthoferrite crystals was thoroughly studied by measuring the perturbed angular correlation spectra.

$$\eta ={\displaystyle \frac{|V_{xx}-V_{yy}|}{|V_{zz}|}}.$$

(2)

The asymmetry parameter $\eta$ abruptly drops in the low-concentration region x = 0.05–0.2 and has a constant value at $x>0.2$. This follows from the change in the EFG symmetry at $x>0.2$, which becomes closer to axial. The EFG in the unsubstituted sample has no axial symmetry, contrary to the assumption in previous work [16].

The relation between $V_{xx}$ and $V_{zz}$ should be closely inspected. The first one is only 1.5 times smaller than the second one for all the considered concentrations of manganese ions. This is a sufficiently large value. Thus, the gradient of the electric field for this series of crystals does not have a pronounced axial symmetry. Therefore, it is necessary to monitor the behavior of both components $V_{zz}$ and $V_{xx}$ of the field gradient.

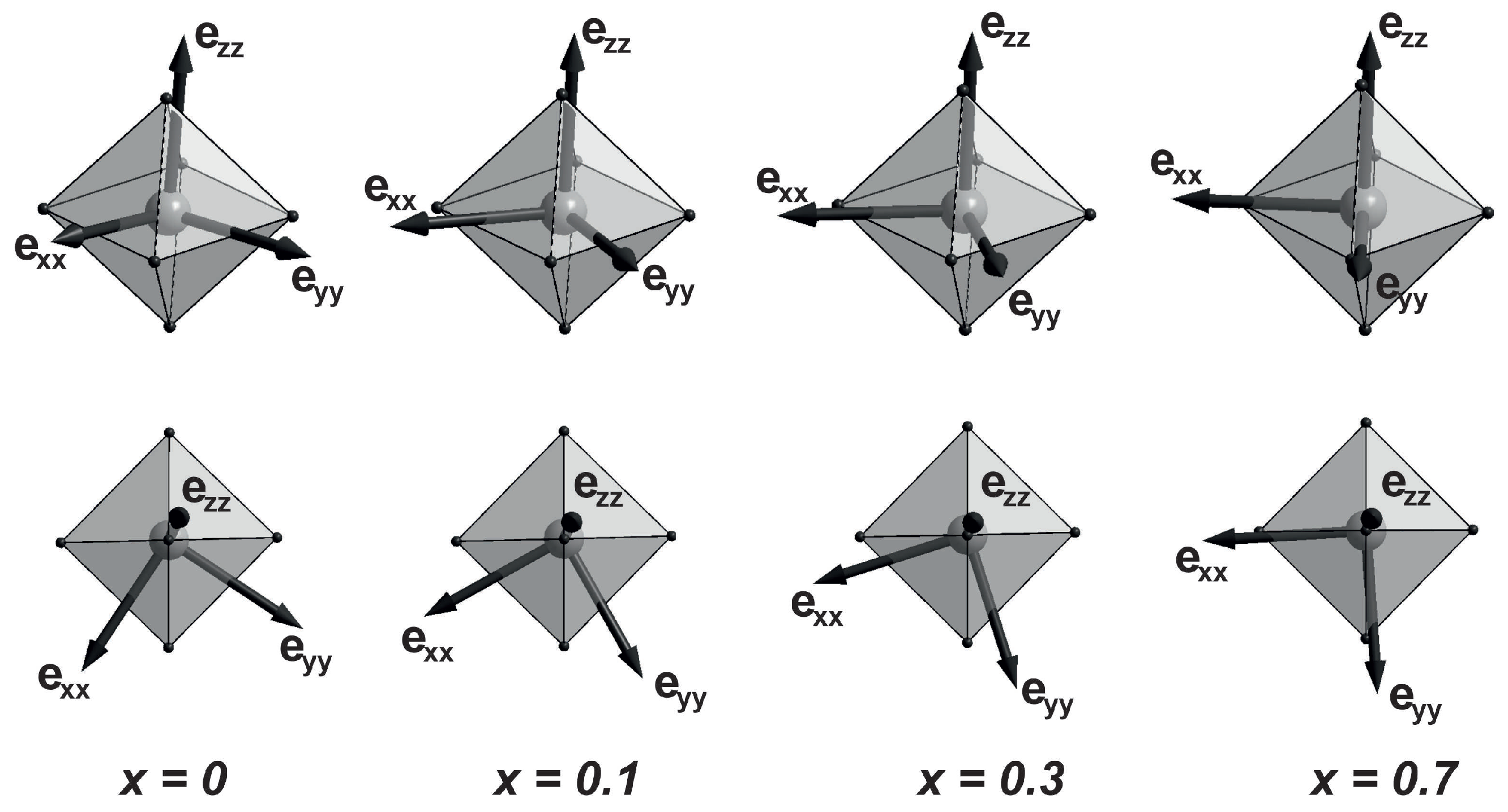
The coordinates of the eigenvectors of the components of the electric field gradient were calculated for structures corresponding to concentrations of manganese ions x = 0–0.7. It should be noted that in the initial $\mathrm{H}\mathrm{o}\mathrm{F}\mathrm{e}{\mathrm{O}}_3$ compound, due to the orthorhombic structural symmetry, the oxygen octahedron FeO₆ is non-perfect and has some distortions. All the Fe–O bonds have different lengths. When manganese is substituted for the iron ion, the degree of distortion of the (Fe,Mn)O₆ octahedron increases, and the two axes of the octahedron decrease.

Figure 6 shows the directions of the calculated EFG eigenvectors ${\mathbf{e}}_{\mathbf{xx}}$, ${\mathbf{e}}_{\mathbf{yy}}$, and ${\mathbf{e}}_{\mathbf{zz}}$ at concentrations of x = 0, 0.1, 0.3, and 0.7. These eigenvectors are unit vectors corresponding to the principal axis system of the EFG. The vector ${\mathbf{e}}_{\mathbf{zz}}$ barely changes its direction at all concentrations and passes close to the longest axis of the FeO₆ octahedron. A bright feature is the behavior of the vector ${\mathbf{e}}_{\mathbf{xx}}$. In the initial compound (x = 0), this vector lies in a plane close to the base of the octahedron, perpendicular to its longest axis, and passes near the middle of the octahedron base edge. At $x=0.1$, the vector ${\mathbf{e}}_{\mathbf{xx}}$ rotates by 27° in the plane close to the octahedron base, shifting closer to one of the oxygen atoms (see Figure 6). At x = 0.3, the angle of rotation of the vector ${\mathbf{e}}_{\mathbf{xx}}$ increases to 39°. At $x=0.7$, the angle of rotation of the vector ${\mathbf{e}}_{\mathbf{xx}}$ is 53°. In this case, its direction almost coincides with the shortest axis of the FeO₆ oxygen octahedron. The direction of the vector ${\mathbf{e}}_{\mathbf{yy}}$ behaves similarly (the field vectors ${\mathbf{e}}_{\mathbf{xx}}$, ${\mathbf{e}}_{\mathbf{yy}}$, and ${\mathbf{e}}_{\mathbf{zz}}$ are mutually perpendicular).

The obtained features of the behavior of EFG on the Fe ion (a significant increase in the values of the field components and a sharp change in the direction of the EFG eigenvectors ${\mathbf{e}}_{\mathbf{xx}}$ and ${\mathbf{e}}_{\mathbf{yy}}$ due to Mn doping), apparently, should lead to a change in the balance of exchange constants in the 3d subsystem of HoFe_1−xMn_xO₃ compounds. This is consistent with the results of [14], where a change in the ground magnetic state at concentrations $x>0.1$, as well as the disappearance of the orientation phase transition at concentrations $x>0.4$, was found.

4. Conclusions

A series of single crystals of the ${\mathrm{H}\mathrm{o}\mathrm{F}\mathrm{e}}_{1-x}{\mathrm{M}\mathrm{n}}_x{\mathrm{O}}_3$ (x = 0–0.7) orthoferrites were grown. The Mössbauer effect was measured at temperatures above the Néel point (700 K) in ${\mathrm{H}\mathrm{o}\mathrm{F}\mathrm{e}}_{1-x}{\mathrm{M}\mathrm{n}}_x{\mathrm{O}}_3$ (x = 0–0.5) orthoferrite samples with sp. gr. Pnma. A monotonic increase in the quadrupole splitting $\Delta$ with increasing manganese concentration in the crystal lattice was found. The density functional theory calculation of the EFG tensor on iron cations for the entire series of ${\mathrm{H}\mathrm{o}\mathrm{F}\mathrm{e}}_{1-x}{\mathrm{M}\mathrm{n}}_x{\mathrm{O}}_3$ samples (x = 0–0.7) showed that the main reason for the observed growth is the crystal lattice distortion by the Jahn–Teller ${\mathrm{M}\mathrm{n}}^{3+}$ cation; an electron contribution to quadrupole splitting caused by the covalent admixture of electrons was absent. At the same time, a significant increase in the values of all EFG tensor components was observed with an increase in the manganese concentration in the ${\mathrm{H}\mathrm{o}\mathrm{F}\mathrm{e}}_{1-x}{\mathrm{M}\mathrm{n}}_x{\mathrm{O}}_3$ crystal lattice, while the crystal field symmetry in the $3d$ subsystem approaches the axial type.

As the calculation of the EFG on the Fe ion demonstrated, a concentration change in the directions of the EFG eigenvectors ${\mathbf{e}}_{\mathbf{xx}}$ and ${\mathbf{e}}_{\mathbf{yy}}$ was detected at $x>0.1$, while the direction of the vector ${\mathbf{e}}_{\mathbf{zz}}$ remains unchanged. In our opinion, such motion of the EFG components with an increase in the concentration of ${\mathrm{M}\mathrm{n}}^{3+}$ cations can lead to an increase in the temperature of the spin-reorientation transition in this system due to a change in the balance of the exchange constants in the $3d$ subsystem of the ${\mathrm{H}\mathrm{o}\mathrm{F}\mathrm{e}}_{1-x}{\mathrm{M}\mathrm{n}}_x{\mathrm{O}}_3$ compounds.