Abstract
Belomarinaite KNaSO4 (space group P3m1, a = 5.6072(3), c = 7.1781(4) Å and Z = 2) has been studied by high-temperature single crystal X-ray diffraction. The K and Na atoms are disordered, and M1(1c) and M2(1b) sites merge into an M1(2d)(K50%/Na50%) site with increasing temperature, and novel translationsgleiche phase transition of belomarinaite KNaSO4 (P3m1 → P-3m1) was revealed at 123 °C. Then, the temperature increase leads to phase transition of -polymorph of KNaSO4 to α-KNaSO4 (P63/mmc) at 446 °C, and sodium and potassium atoms in K1(1a) and Na1(1b) sites merged into an M4(2a)(K50%/Na50%) site. Crystal structures of KNaSO4 were refined at 300, 500 and 750 °C to R1 = 0.057, 0.056 and 0.048, respectively. The BVS maps and bond-valence energy landscape (BVEL) have been calculated, and the probability of the Na+ migration has been predicted using structural data for belomarinaite at 25 °C. The Na+ ion migration can occur at 2.14 eV in the ab plane and 2.80 eV along the c axis at 25 °C.
1. Introduction
Belomarinaite, KNaSO4, is a volcanogenic mineral from the Tolbachic volcano, Kamchatka peninsula, Russia. Belomarinaite crystallizes in a trigonal crystal system (space group P3m1, a = 5.6072(3), c = 7.1781(4) Å and Z = 2). The mineral was reported in [1] as pale-blue to green arborescent aggregates of tabular crystals. It was discovered on the Toludskoe lava field, formed during the Tolbachik Fissure eruption in 2012–2013 (55°45′1.32″ N, 160°19′40.74″ E, altitude 1480 m). The specimen was found in the high part of a lava cave. Data on the Tolbachik Fissure eruption in 2012–2013 are given in [2].
Then, belomarinaite was found in the Arsenatnaya fumarole [3]. These belomarinaite specimens are colorless or white, semitransparent hexagonal tabular or lamellar crystals along with johillerite, nickenichite and calciojohillerite. The most complete list of minerals identified on the Tolbachik volcano is given in the review paper [4].
The thermal behavior of belomarinaite was studied using high temperature X-ray powder diffraction over the temperature range of 30–800 °C and using DSC/TG over the temperature range of 30–1000 °C in [5]. The existence of a high-temperature modification (P63/mmc) of this mineral above 446 °C has been demonstrated. It was determined that the volumetric expansion varies for the low-temperature phase within the range of 80−200 × 10–6 °C−1 and 350–300 × 10−6 °C−1 for the high-temperature phase.
The crystal structure of the synthetic KNaSO4 (space group P3m1, a = 5.6066(7), c = 7.177(1) Å, Z = 2 and R1 = 4.2%) was refined in [6]. The crystal chemistry of related structures has been reviewed in [7,8,9,10,11,12].
The thermal behavior of all compounds of the K2SO4–Na2SO4 system was studied using thermal analysis and powder high-temperature X-ray diffraction, but only the end-members of the series were studied using single crystal high-temperature X-ray diffraction [13,14,15,16,17,18,19]. In the high-temperature phase (P63/mmc), a reorientation of SO4 tetrahedra (dynamic disorder) is observed, which at different temperatures can be described in the apex and edge models. Thus, it will be interesting to know whether a similar reorientation of SO4 tetrahedra will be observed for the mineral belomarinaite KNaSO4, and what model of dynamic disorder will prevail in its crystal structure.
In this study, the thermal behavior of KNaSO4 was investigated using single crystal high-temperature X-ray diffraction. Crystal structures were refined at 300, 500 and 750 °C. New polymorphic modification of KNaSO4 () was discovered.
2. Materials and Methods
2.1. Samples
The studied sample is belomarinaite holotype with empirical formula (K0.95Na0.92Cu0.04)Σ1.91S1.01O4 [1]. The suitable crystal of belomarinaite for single crystal X-ray diffraction (0.05 × 0.04 × 0.03 mm) was selected from holotype sample.
2.2. Single Crystal X-ray Diffraction
The thermal behavior of belomarinaite was studied by high-temperature single crystal X-ray diffraction analysis using a Rigaku XtaLAB Synergy-S diffractometer (Rigaku, Tokyo, Japan) (MoKα radiation, 50 kV and 1.0 mA) equipped with high-speed direct-action detector HyPix-6000HE (Rigaku, Tokyo, Japan). The data were collected at 300, 500 and 750 °C. The heating process was controlled by «Hot Air gas blowers» system (Rigaku, Tokyo, Japan). A single crystal of belomarinaite was placed and fixed in quartz capillaries with approximately 10 micron wall thickness. The hemisphere of diffraction data (frame width 0.5°) was collected for each temperature value. The orientation of the crystals was not changed during all temperature measures. The CrysAlisPro software (version 1.171.39.44) was used for the further processing [20]. An absorption correction was introduced by the SCALE3 ABSPACK algorithm [21]. The crystal structures have been solved and refined using Jana 2006 software [22]. The crystal structure of belomarinaite at 300 °C was initially refined in the P3m1 space group. Due to high correlation between coordinates of M1(1c)(Na/K) and M2(1b)(K/Na) sites, the ADDSYM program within the PLATON software package [23] was used for the checking of missing symmetry operations, which led to the crystal structure refinement in the P-3m1 space group. The crystal structure data and refinement parameters for all modifications are shown in Table 1. Final atomic positional and displacement parameters (Å2) as well as selected bond lengths are given in Table 2, Tables S1 and S2, cifs and checkcifs are in supplementary.

Table 1.
Crystallographic data and refinement parameters for belomarinaite at 25, 300, 500 and 750 °C.

Table 2.
Selected bond lengths for belomarinaite at 25, 300, 500 and 750 °C.
2.3. BVS for Na-Ion Transport
BVS maps were calculated for a preliminary assessment of possible Na-ion pathways. The BVS maps at various bond–valence mismatches Zi − Σsi (Zi = 1 for Na+, si = exp[(R0− R)/b], where R0 and b are empirical constants [24], R is the cation–anion distance, and Σsi is BVS) were calculated using the BondStr program [25] for Na+ sites in grids with steps of Δx, Δy and Δz = 0.1 Å in the unit cell with the fixed sites of other atoms. The calculated data were visualized using VESTA software [26].
2.4. Structural Complexity Calculation
The structural complexity measures of different KNaSO4 modifications were calculated as the amounts of Shannon information per atom (strIG) and per unit cell (strIG,total) using the methodology discussed in [27,28] and the following equations:
Above, k is the multiplicity of a crystallographic orbit, pi is the random choice probability for an atom from the ith crystallographic orbit, that is
where mi is the multiplicity of a crystallographic orbit relative to the reduced unit cell and ν is the number of atoms in the reduced unit cell. TOPOSPro software was used for the calculations [29].
3. Results and Discussion
3.1. Thermal Order–Disorder Phase Transitions
Belomarinaite KNaSO4 crystallizes in the P3m1 space group, and in the crystal structure, there are two symmetrically independent [4]S (S1 and S2), one [6]Na, one [12]K, two [10]K/Na (M1 and M2) and four O (O1, O2, O3, O4) sites (Figure 1 bottom). Belomarinaite is isotypical with the synthetic compound KNaSO4 [6]. In the crystal structure of the synthetic compound, the K and Na atoms are ordered at the M2(1b) and M1(1c) sites. In the belomarinaite crystal structure, Na and K are disordered over M1 and M2 sites. Apparently, this is explained by the high-temperature genesis of the mineral. New data on the belomarinaite crystal structure obtained in this work at 300 °C indicate that with increasing temperature, the belomarinaite crystal structure changes slightly and translationsgleiche phase transition occurs. The belomarinaite crystallizes in the space group at 300 °C. The presence of this transition is confirmed by the DSC data of synthetic KNaSO4, e.g., [10,30,31], and those of belomarinaite [5]; there are three thermal effects at about 123, 446 and 840 °C. It was suggested in [30] for synthetic KNaSO4 that the first broad endothermic peak corresponds to a second-order phase transition. Thus, according to the high-temperature single crystal X-ray diffraction data, the first peak can be attributed to a P3m1↔ P-3m1 phase transition. Apparently, it is caused by the mobility of Na+ and K+ cations with increasing temperature. As a result, they are statistically distributed over M1(1c) and M2(1b) sites, which leads to the appearance of an inversion center and the existence of only the M(2d) site (Figure 1 middle). The second and third peaks are attributed to a → P63/mmc phase transition and congruent melting of the solid solution, respectively, in accordance with the phase diagram [10].
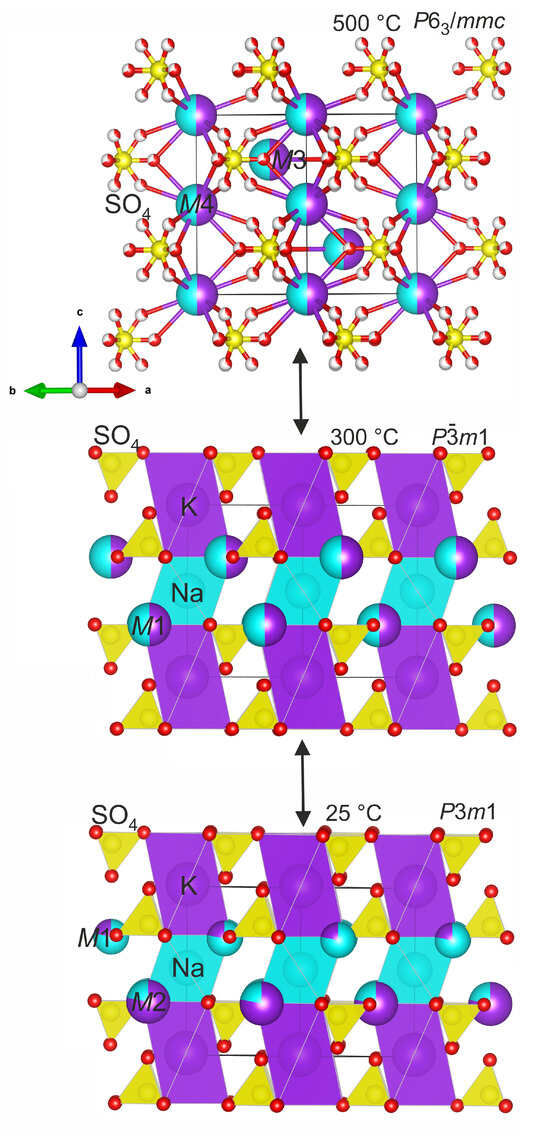
Figure 1.
Thermal evolution of belomarinaite KNaSO4 crystal structure.
In contrast to room temperature, in the crystal structure of belomarinaite at 300 °C, due to the presence of an inversion center, the number of symmetrically independent sites decreases: one for [4]S, one for [6]Na, one [10]K/Na (M1) and two for O. The <Na–O> (NaO6) bond lengths increase from 2.344 Å (25 °C) to 2.405 Å (300 °C), and the <K–O> (KO12) bond lengths increase from 3.056 Å (25 °C) to 3.124 Å (300 °C). The <(Na/K)–O> (M1O10) and <(K/Na)–O> (M2O10) bond lengths are 2.863Å and 2.873Å at 25 °C, respectively (Figure 2). In the -polymorph, there is only an M1(2d) site coordinated by ten oxygen atoms with <M1–O> bond lengths equal to 2.937 Å (Figure 2). Na and K atoms are completely disordered in the M1(2d) site—50%/50%, due to its mobility, in contrast to room temperature, where the M1(1c) site is occupied by 78% Na and 22% K, while the M2(1b) site is occupied by 22% Na and 78% K. The <S–O> bonds in the S1O4 and S2O4 tetrahedra are in the range of 1.378–1.485 Å at 25 °C and 1.42–1.44 Å at 300 °C (Table 2).
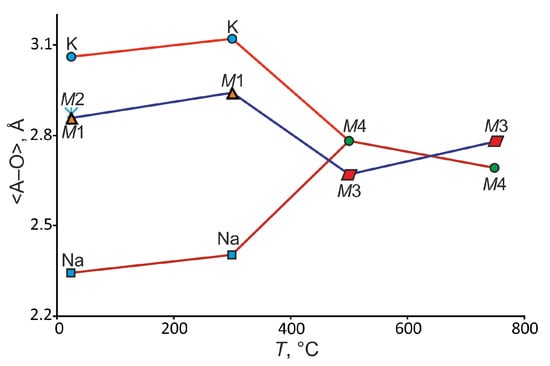
Figure 2.
Average values of bond lengths in the K and Na polyhedra in the crystal structures of different belomarinaite KNaSO4 modifications with an increase in temperature.
The mineral crystallizes in the hexagonal crystal system, space group P63/mmc, Z = 2, at 500 and 750 °C. The process of K and Na disordering occurs in the M3(2d) and M4(2a) sites of the crystal structure without changing the symmetry.
After the → P63/mmc phase transition (446 °C) in the crystal structure of the high-temperature polymorph at 500 °C, the number of independent crystallographic sites decreases again. The M1(2d)(Na/K) site is preserved, and it is designated as M3(2d); there is M4(2a)(Na/K) instead of K1 and Na1 sites (Figure 1 top). In both sites, the K and Na atoms are disordered (M3: 50%/50% and M4: 50%/50%). There are S sites and O1 and O2 sites with occupancies of 0.66 and 0.33 (Figure 1). The M4–O bond lengths vary from 2.724 to 2.84 Å (500 °C) to 2.66–2.75 Å (750 °C), and the M3–O bond lengths vary from 2.50 to 2.848 Å (500 °C) to 2.76–2.83 Å (750 °C) (Figure 2). The S–O bonds in the SO4 tetrahedra are in the range of 1.358–1.50 Å at 500 °C and 1.37–1.48 Å at 750 °C (Table 2). A presence of the short and long S–O bonds can be explained by libration effects, typical for the crystal structures with statistical or dynamical disorder. It is worth noting that the coordinates of oxygen sites differ at temperatures of 500 and 750 °C, which further indicates dynamic disorder.
The temperature dependencies of the unit cell parameters for belomarinaite in the temperature range of 25–800 °C were investigated by our group in [5]. The K and Na atoms are ordered in M1O10 and M2O10 polyhedra in the belomarinaite crystal structure at room temperature. According to [1], the M1O10 and M2O10 polyhedra share faces of 2.4 × 3.4 Å2, and the size of these faces is suitable for Na and K migration at high temperatures. With the temperature increasing, the atoms in the M1O10 and M2O10 polyhedra are disordered, and M1(1c) and M2(1b) sites merge into an M3(2d)(K50%/Na50%) site in the KNaSO4 () crystal structure (Figure 3). Then, the sodium and potassium atoms in K1 and Na1 sites, which form the rods, merged into an M4(2a)(K50%/Na50%) site at 446 °C. Since the value of the c unit cell parameter is determined mainly by the polyhedra forming the rods (cf. 3.2) along the c axis, the disorder of cations in the M3(2d) site leads to a sharp increase in the a unit cell parameter. Then, the disorder of K1(1a) and Na1(1b) sites leads to a sharp increase in the c unit cell parameter (Figure 3). It should be noted that the migration paths of Na and K ions in the high-temperature phase (P63/mmc) pass through both M3(2d) and M4(2a) sites.
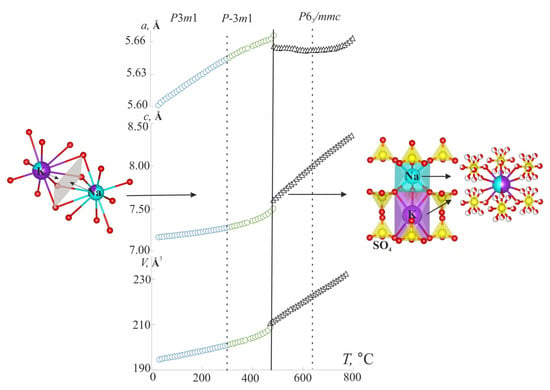
Figure 3.
Interpretation of order–disorder processes in crystal structure of belomarinaite KNaSO4.
3.2. Temperature-Dependent Inheritance of KNaSO4 Structural Transformations
The crystal structure of KNaSO4 under ambient conditions consists of complex columns of the KO12, NaO6, M1O10 and M2O10 (M = K, Na) and SO4 polyhedra [7,8,9,12]. Crystal structures of belomarinaite and similar (aphthitalite-like) minerals can be described as pseudo-close-packed cationic arrays with hexagonal layers parallel to (001) [32,33,34,35,36,37], as well as mixed frameworks consisting of columns formed by octahedral–tetrahedral clusters of MO6 octahedra that share six vertices with six adjacent SO4 tetrahedra [37] (Figure 4).
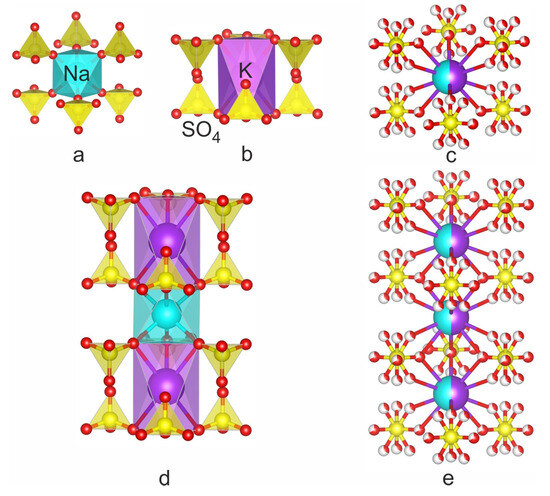
Figure 4.
Structural fragments of belomarinaite KNaSO4 modifications: (a,b)—FBB in KNaSO4 ( and P3m1); (c)—parent FBB in α-KNaSO4; (d)—columns of MO6 octahedra with six adjacent SO4 tetrahedra in KNaSO4 ( and P3m1); (e)—columns of MO6 octahedra that share six vertices with six adjacent disordered SO4 tetrahedra in α-KNaSO4.
If the temperature of the crystal increases, the thermal motion of atoms increases, e.g., [38,39], and the areas of solid solutions’ miscibility increases with increasing temperature. The thermal motion of atoms gradually decreases with a decrease in temperature. Therefore, the degree of atom difference increases, and atoms tend to be ordered through different sites in a crystal structure.
The crystal structures of compounds of the Na2SO4–K2SO4 series were firstly described as consisting of microblocks, including the assumption of the genesis of minerals structurally close to the compounds of this series, as formed from a single type of parent microblock in [40]. The crystal structures of the α-Na2SO4 and α-K2SO4 sulfates contain disordered SO4 tetrahedron and two symmetrically independent sites for alkali cations. The parent FBB consists of a NaO6 or KO6 octahedron surrounded by six disordered SO4 tetrahedra (a tetrahedron with disordered oxygen atoms) (Figure 5). The term microblock was proposed in [41]. A microblock [M(TO4)6] that consisted of an octahedron interlinked by six vertices with six adjacent tetrahedra was considered a structural unit inherited upon cooling from a high-temperature disordered parent unit [40].
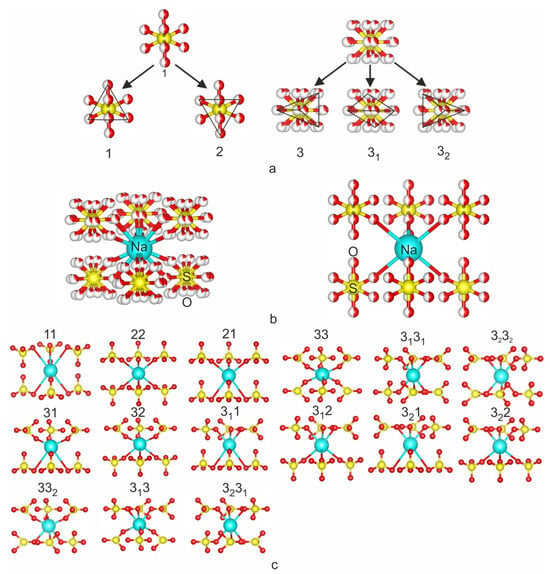
Figure 5.
Crystal structures inherited from parent high-temperature disordered microblocks: (a)—the 5 types of the different orientations of the SO4 tetrahedron in high-temperature KNaSO4 phase; (b)—parent FBB of α-KNaSO4 in edge and apex models, (c)—15 trigonal octahedral–tetrahedral clusters of trigonal symmetry, which can be formed after cooling of parent FBB. Microblock designations are given in accordance with [40].
At high temperatures, dynamic disorder exists in the α-Na2SO4 and α-K2SO4 structures, which leads to the formation of inherited microblocks under cooling. Phase transitions in the Na2SO4–K2SO4 series are reversible, and therefore, we can describe the subsequences of phase transitions upon cooling, since a high-temperature phase crystallizes from the melt.
The disordered SO4 tetrahedron can be represented as the five different orientations of SO4 tetrahedra, and only one is possible at a time [15,16,17,18,19,42] and references terrain (Figure 5). In the trigonal crystal system, 15 types of microblocks were derived that can be obtained by cooling [40] (Figure 5). Some of these microblocks were derived in [41] for heteropolyhedral frameworks, and then, they were described as “elementary bricks” of the mixed octahedral–tetrahedral frameworks [36]. All microblocks derived in 1975 [41] have –3m or 3m symmetry.
All structures in the Na2SO4–K2SO4 system (excluding Na2SO4-Fddd) consist of these microblocks with the SO4 tetrahedra in one of the described orientations [40]. A transition from the parent block to the inherited block occurs upon cooling of the high-temperature modification that is structurally similar to α-Na2SO4. All orientations of the tetrahedra that can be inherited from the parent microblock of the high-temperature phase are in in the crystal structure of dobrovolskyite Na4Ca(SO4)3 [37]. This mineral was found in association with petrovite [43].
The crystal structure of belomarinaite can be described as a three-dimensional framework consisting of K–O, Na–O polyhedra and SO4 tetrahedra. The framework consists of rods elongated along the c axis which formed by NaO6 or KO6 octahedron sharing six corners with six adjacent SO4 tetrahedra (Figure 1 and Figure 2). These microblocks sharing corners with the tetrahedra and faces with the octahedra form rods along the c axis.
The structures of low-temperature modifications ( and P3m1) consist of microblocks 11 and 22, and high-temperature modifications (P63/mmc) are formed by parent FBB—the disordered octahedral MO6 (M = Na, K) site is surrounded by six disordered tetrahedra. Microblock designations are given in accordance with [40].
3.3. Sodium-Ion Migration in KNaSO4 at Different Temperatures
The BVS maps and bond-valence energy landscape (BVEL) have been calculated, and the probability of the Na+ migration has been predicted using structural data for belomarinaite at 25 and 300 °C (Figure 6). The Na+ ion migration can occur at 2.14 eV in the ab plane and 2.80 eV along the c axis at 25 °C, and the Na+ ion migration can occur at 1.85 eV in the ab plane and 2.21 eV along the c axis at 300 °C. Usually, percolation energy of 1.6 eV for Na+ ion migration in compounds is promising for solid-state electrolytes [44]. Previously, experimental studies for this compound showed significant electrical conductivity of the high-temperature phase of KNaSO4 [30].
Figure 6.
The BVS map isosurfaces (1.36) of sodium ions in belomarinaite KNaSO4 at 25 °C (a), the BVS map isosurfaces (1.00) of sodium ions in belomarinaite KNaSO4 at 500 °C (b).
Apparently, the fact that all sites for alkali cations in P3m1 and polymorphs are completely occupied makes it difficult for the movement of ions, which leads to high values of activation energy, as well as to small values of conductivity according to the [30] data.
We also calculated possible migration paths of Na ions at 500 °C. Quantitative estimates of migration barriers are not given, since the bond-valence parameters at such a temperature will differ significantly from room-temperature ones. Nevertheless, in our opinion, such a calculation is capable of qualitatively showing the migration paths of Na and K ions at high temperatures. This allows us to conclude that both M3(2d) and M4(2a) cation sites are involved in the migration path of Na and K ions.
3.4. Structural Complexity
The information-based structural complexity parameters [27,45] for different KNaSO4 modifications are listed in Table 3. Generally, the complexities of the KNaSO4 polymorphs are consistent with the observations that complexity decreases with increasing temperature [28]. A slight increase in structural complexity in the hexagonal modification can be caused by dynamic disorder in the structure, as a result of which, the oxygen sites are split.

Table 3.
The structural complexity of belomarinaite KNaSO4 modifications.
4. Conclusions
The thermal structural evolution of belomarinaite was studied using single-crystal diffraction data. The novel translationsgleiche phase transition of belomarinaite KNaSO4 (P3m1 → ) was investigated. The presence of the → P-3m1 phase transition is confirmed by the existence of a broad peak in the DSC curve, first discovered in [31], where the abrupt change in heat capacity was also studied, indicating a second-order transition. The symmetry increases with the increasing temperature in the trigonal–trigonal P3m1→ P-3m1 and trigonal–hexagonal → P63/mmc transformations, which is in agreement with the well-known tendency [38,46,47,48]. The K and Na atoms in the M1O10 and M2O10 polyhedra are fully disordered with temperature increasing, and M1(1c) and M2(1b) sites merge into an M1(2d)(K50%/Na50%) site in the P-3m1-polymorph of KNaSO4 crystal structure. Then, the Na and K atoms in K1(1a) and Na1(1b) sites merged into an M4(2a) (K50%/Na50%) site at 446 °C and disordered phase or solid solution exists above 446 °C. The calculations of the bond-valence energy landscape (BVEL) show the probability of the Na+ migration at high activation energy of 2.14 eV in the ab plane and 2.80 eV along the c axis at 25 °C. Therefore, only the high-temperature phase of belomarinaite KNaSO4 is suitable as a solid-state electrolyte. It has been shown that the crystal structures of KNaSO4 modifications consist of M(TO4)6 microblocks. The inheritance of microblocks from the parent structural unit may help to clarify the genesis of similar minerals.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/cryst14010027/s1, Table S1: Fractional atomic coordinates and isotropic or equivalent isotropic displacement parameters (Å2) for belomaronaite at 25, 300, 500 and 750 °C. Table S2: Atomic anisotropic displacement parameters for belomarinaite at 25, 300, 500 and 750 °C. Cifs and checkcifs of KNaSO4 at 300, 500 and 750 °C.
Author Contributions
Writing—original draft, A.S. and R.B.; Writing—review and editing, A.S., O.S., S.F., M.K. and R.B.; Investigation, A.S., O.S., M.K. and S.V.; Project administration, A.S., O.S., R.B. and S.F.; Data curation, A.S. and S.F.; Visualization, A.S. and O.S.; Supervision, S.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Russian Science Foundation [grant number 22-13-00317].
Data Availability Statement
CCDC 2312036, 2312037 and 2312041 contain the crystallographic data for this paper.
Acknowledgments
The X-ray diffraction experiments were performed at The Centre for X-ray. Diffraction Studies (Saint Petersburg State University).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Filatov, S.K.; Shablinskii, A.P.; Vergasova, L.P.; Saprykina, O.U.; Bubnova, R.S.; Moskaleva, S.V.; Belousov, A.B. Belomarinaite KNa(SO4): A new sulfate from 2012-2013 Tolbachik Fissure eruption, Kamchatka Peninsule, Russia. Mineral. Mag. 2019, 83, 569–575. [Google Scholar] [CrossRef]
- Belousov, A.B.; Belousova, M.G.; Edwards, B.; Volynets, A.O.; Melnikov, D.V. Overview of the precursors and dynamics of the 2012–13 basaltic fissure eruption of Tolbachik Volcano, Kamchatka, Russia. J. Volcanol. Geotherm. Res. 2015, 307, 22–37. [Google Scholar] [CrossRef]
- Shchipalkina, N.V.; Pekov, I.V.; Chukanov, N.V.; Zubkova, N.V.; Belakovskiy, D.I.; Koshlyakova, N.N.; Britvin, S.N.; Sidorov, E.G.; Vozchikova, S.A. Alkali sulfates with aphthitalite-like structures from fumaroles of the Tolbachik volcano, Kamchatka, Russia. II A new mineral, natroaphthitalite, and new data on belomarinaite. Can. Mineral. 2020, 58, 167–181. [Google Scholar] [CrossRef]
- Pekov, I.V.; Agakhanov, A.A.; Zubkova, N.V.; Koshlyakova, N.N.; Shchipalkina, N.V.; Sandalov, F.D.; Yapaskurt, V.O.; Turchkova, A.G.; Sidorov, E.G. Oxidizing-type fumarolic systems of the Tolbachik volcano—A mineralogical and geochemical unique. Russ. Geol. Geophys. 2020, 61, 675–688. [Google Scholar] [CrossRef]
- Belousova, M.G.; Saprykina, O.Y.; Bubnova, R.S.; Shablinskii, A.P.; Vergasova, L.P.; Belousov, A.B.; Filatov, S.K. A thermal study of the new mineral belomarinaite KNaSO4. J. Volcanol. Seismol. 2021, 15, 51–57. [Google Scholar] [CrossRef]
- Okada, K.; Osaka, J. Structures of potassium sodium sulfate and tripotassium sodium disulphate. Acta Crystallogr. 1980, B36, 919–921. [Google Scholar] [CrossRef]
- Moore, P.B. Bracelets and pinwheels: A topological-geometrical approach to the calcium orthosilicate and alkali sulphate structures. Am. Mineral. 1973, 58, 32–42. [Google Scholar]
- Moore, P.B. The glaserite, K3Na(SO4)2, structure type as a‘super’ densepacked oxide: Evidence for icosahedral geometry and cation-anion mixed layer packings. Neues Jahrb Fur Miner. 1976, 127, 187–196. [Google Scholar]
- Moore, P.B. Complex crystal structures related to glaserite, K3Na(SO4)2: Evidence for very dense packings among oxysalts. Bull Miner. 1981, 104, 536–547. [Google Scholar] [CrossRef]
- Eysel, W. Crystal chemistry of the system Na2SO4–K2SO4–K2CrO4–Na2CrO4 and of the glaserite phase. Am. Mineral. 1973, 58, 736–747. [Google Scholar]
- Egorov-Tismenko, Y.K.; Sokolova, E.V.; Smirnova, N.L.; Yamnova, N.A. Crystal chemical features of minerals related to the glaserite structure type. Mineral. Zhurnal 1984, 6, 3–9. (In Russian) [Google Scholar]
- Hawthorne, F.C.; Krivovichev, S.V.; Burns, P.C. The crystal chemistry of sulfate minerals. Rev. Miner. Geochem 2000, 40, 1–112. [Google Scholar] [CrossRef]
- Fischmeister, H.F. Roentgenkristallographische Ausdehnungsmessungen an einigen Alkalisulfaten. Monatshefte Fuer Chem. 1962, 93, 420–434. [Google Scholar] [CrossRef]
- van den Berg, A.J.; Tuinstra, F. The space group and structure of alpha-K2SO4. Acta Crystallogr. B 1978, 34, 3177–3181. [Google Scholar] [CrossRef]
- Miyake, M.; Morikawa, H.; Iwai, S.I. Structure reinvestigation of the high-temperature form of K2SO4. Acta Crystallogr. B 1980, 36, 532–536. [Google Scholar] [CrossRef]
- Arnold, H.; Kurtz, W.; Richter-Zinnius, A.; Bethke, J. The phase transition of K2SO4 at about 850 K. Acta Crystallogr. B 1981, 37, 1643–1651. [Google Scholar] [CrossRef]
- Eysel, W.; Hoefer, H.H.; Keester, K.L.; Hahn, T. Crystal chemistry and structure of Na2SO4(I) and its solid solutions. Acta Crystallogr. B 1985, 41, 5–11. [Google Scholar] [CrossRef]
- Naruse, H.; Tanaka, K.; Morikawa, H.; Marumo, F. Structure of Na2SO4 at 693 K. Acta Crystallogr. B 1987, 43, 143–146. [Google Scholar] [CrossRef]
- Rasmussen, S.E.; Jorgensen, J.E.; Lundtoft, B. Structures and Phase Transitions of Na2SO4. J. Appl. Crystallogr. 1996, 29, 42–47. [Google Scholar] [CrossRef]
- CRYSALISPRO Software System, version 1.171.39.44; Rigaku Oxford Diffraction: Oxford, UK, 2015.
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. B 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Petricek, V.; Dusek, M.; Palatinus, L. JANA2006; The Crystallographic Computing System; Institute of Physics, Academy of Sciences of the Czech Republic: Staré Město, Czechia, 2006. [Google Scholar]
- Spek, A.L. Single-crystal structure validation with the program PLATON. J. Appl. Crystallogr. 2003, 36, 7–13. [Google Scholar] [CrossRef]
- Brown, I.D.; Altermatt, D. Bond-valence parameters obtained from a systematic analysis of the Inorganic Crystal Structure Database. Acta Crystallogr. 1985, 41, 244–247. [Google Scholar] [CrossRef]
- Rodríguez-Carvajal, J. The Program BondStr (or Bond_Str) and Its GUI GBond_Str Version December 2018. Available online: https://journals.iucr.org/j/issues/2019/01/00/po5136/po5136sup2.pdf (accessed on 4 December 2023).
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Krivovichev, S.V. Structural complexity of minerals: Information storage and processing in the mineral world. Mineral. Mag. 2013, 77, 275–326. [Google Scholar] [CrossRef]
- Krivovichev, S.V.; Krivovichev, V.G.; Hazen, R.M.; Aksenov, S.M.; Avdontceva, M.S.; Banaru, A.M.; Gorelova, L.A.; Ismagilova, R.M.; Kornyakov, I.V.; Kuporev, I.V.; et al. Structural and Chemical Complexity of Minerals: An Update. Mineral. Mag. 2022, 86, 183–204. [Google Scholar] [CrossRef]
- Blatov, V.A.; Shevchenko, A.P.; Proserpio, D.M. Applied topological analysis of crystal structures with the program package ToposPro. Cryst. Growth Des. 2014, 14, 3576–3586. [Google Scholar] [CrossRef]
- Kumari, M.S.; Secco, E.A., II. Electrical conductivity and phase transition studies on pure and doped (Cd2+, Gd3+)KNaSO4 and K3Na(SO4)2. Can. J. Chem. 1983, 61, 599–601. [Google Scholar] [CrossRef]
- Abboudy, S.; Hamed, A.E.; Kassem, M.E.; Abou-El-Nasr, L.I. Stoichiometric ratio and doping effects on the thermal properties of sodium potassium sulphate crystals. J. Therm. Anal. 1993, 39, 301–308. [Google Scholar] [CrossRef]
- O’Keeffe, M.; Hyde, B.G. An alternative approach to non-molecular crystal structures with emphasis on the arrangements of cations. Struct. Bond. 1985, 61, 77–144. [Google Scholar]
- Krivovichev, S.V.; Filatov, S.K. Metal arrays in structural units based on anion-centered metal tetrahedra. Acta Crystallogr. B 1999, 55, 664–676. [Google Scholar] [CrossRef]
- Vegas, A. Cations in Inorganic Solids. Crystallogr. Rev. 2000, 7, 189–283. [Google Scholar] [CrossRef]
- Gorelova, L.A.; Vergasova, L.P.; Krivovichev, S.V.; Avdontseva, E.Y.; Moskaleva, S.V.; Karpov, G.A.; Filatov, S.K. Bubnovaite, K2Na8Ca(SO4)6, a new mineral species with modular structure from the Tolbachik volcano, Kamchatka peninsula, Russia. Eur. J. Miner. 2016, 28, 677–686. [Google Scholar] [CrossRef]
- Krivovichev, S.V. Structure description, interpretation and classification in structural mineralogy. Crystallogr. Rev. 2017, 23, 2–71. [Google Scholar] [CrossRef]
- Shablinskii, A.P.; Filatov, S.K.; Krivovichev, S.V.; Vergasova, L.P.; Moskaleva, S.V.; Avdontseva, E.Y.; Knyazev, A.V.; Bubnova, R.S. Dobrovolskyite, Na4Ca(SO4)3, a new fumarolic sulfate from the Great Tolbachik fissure eruption, Kamchatka Peninsula. Russia. Mineral. Mag. 2021, 85, 233–241. [Google Scholar] [CrossRef]
- Filatov, S.K. High Temperature Crystal Chemistry; Nedra: Leningrad, Russia, 1990; 288p. (In Russian) [Google Scholar]
- Filatov, S.K.; Shablinskii, A.P.; Volkov, S.N.; Bubnova, R.S. Forms of solid solution ordering upon decreasing temperature. J. Struct. Chem. 2017, 58, 135–158. [Google Scholar] [CrossRef]
- Shablinskii, A.P.; Filatov, S.K.; Biryukov, Y.P. Crystal structures inherited from parent high-temperature disordered microblocks: Ca2SiO4, Na2SO4–K2SO4 sulfates, and related minerals (bubnovaite and dobrovolskyite). Phys. Chem. Miner. 2023, 50, 30. [Google Scholar] [CrossRef]
- Voronkov, A.A.; Ilyukhin, V.V.; Belov, N.V. Crystal chemistry of mixed frameworks. Principles of Their Formation. Kristallographia 1975, 20, 556–566. (In Russian) [Google Scholar]
- Pekov, I.V.; Shchipalkina, N.V.; Zubkova, N.V.; Gurzhiy, V.V.; Agakhanov, A.A.; Belakovskiy, D.I.; Chukanov, N.V.; Lykova, I.S.; Vigasina, M.F.; Koshlyakova, N.N.; et al. Alkali sulfates with aphthitalite-like structures from fumaroles of the Tolbachik volcano, Kamchatka, Russia. I. Metathenardite, a natural high-temperature modification of Na2SO4. Can. Mineral. 2019, 57, 885–901. [Google Scholar] [CrossRef]
- Filatov, S.K.; Shablinskii, A.P.; Krivovichev, S.V.; Vergasova, L.P.; Moskaleva, S.V. Petrovite, Na10CaCu2(SO4)8, a new fumarolic sulfate from the Great Tolbachik fissure eruption, Kamchatka Peninsula, Russia. Mineral. Mag. 2020, 84, 691–698. [Google Scholar] [CrossRef]
- Kovrugin, V.M.; Nekrasova, D.O.; Siidra, O.I.; Mentre, O.; Masquelier, C.; Stefanovich, S.Y.; Colmont, M. Mineral-inspired crystal growth and physical properties Na2Cu(SO4)2 and review of Na2M(SO4)2(H2O)x (x = 0–6) Compounds. Cryst. Growth Des. 2019, 19, 1233–1244. [Google Scholar] [CrossRef]
- Krivovichev, S.V. Topological complexity of crystal structures: Quantitative approach. Acta Crystallogr. 2012, A68, 393–398. [Google Scholar] [CrossRef] [PubMed]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics. Course of Theoretical Physics; Pergamon Press Oxford: Oxford, UK, 1980; Volume 5, Part 1; p. 440. [Google Scholar]
- Tröster, A.; Schranz, W.; Ehsan, S.; Belbase, K.; Blaha, P. Symmetry-adapted finite Landau theory applied to KMnF3. Crystals 2020, 10, 124. [Google Scholar] [CrossRef]
- Errandonea, D. Landau theory applied to phase transitions in calcium orthotungstate and isostructural compounds. EPL 2007, 77, 56001. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).