Rayleigh Waves Propagating in the Functionally Graded One-Dimensional Hexagonal Quasicrystal Half-Space
Abstract
1. Introduction
2. Mathematics and Formulation
- (1)
- z-FGQC half-space
- (2)
- x-FGQC half-space
3. Analytical Integration Expression of Laguerre Polynomial Method
4. Numerical Results
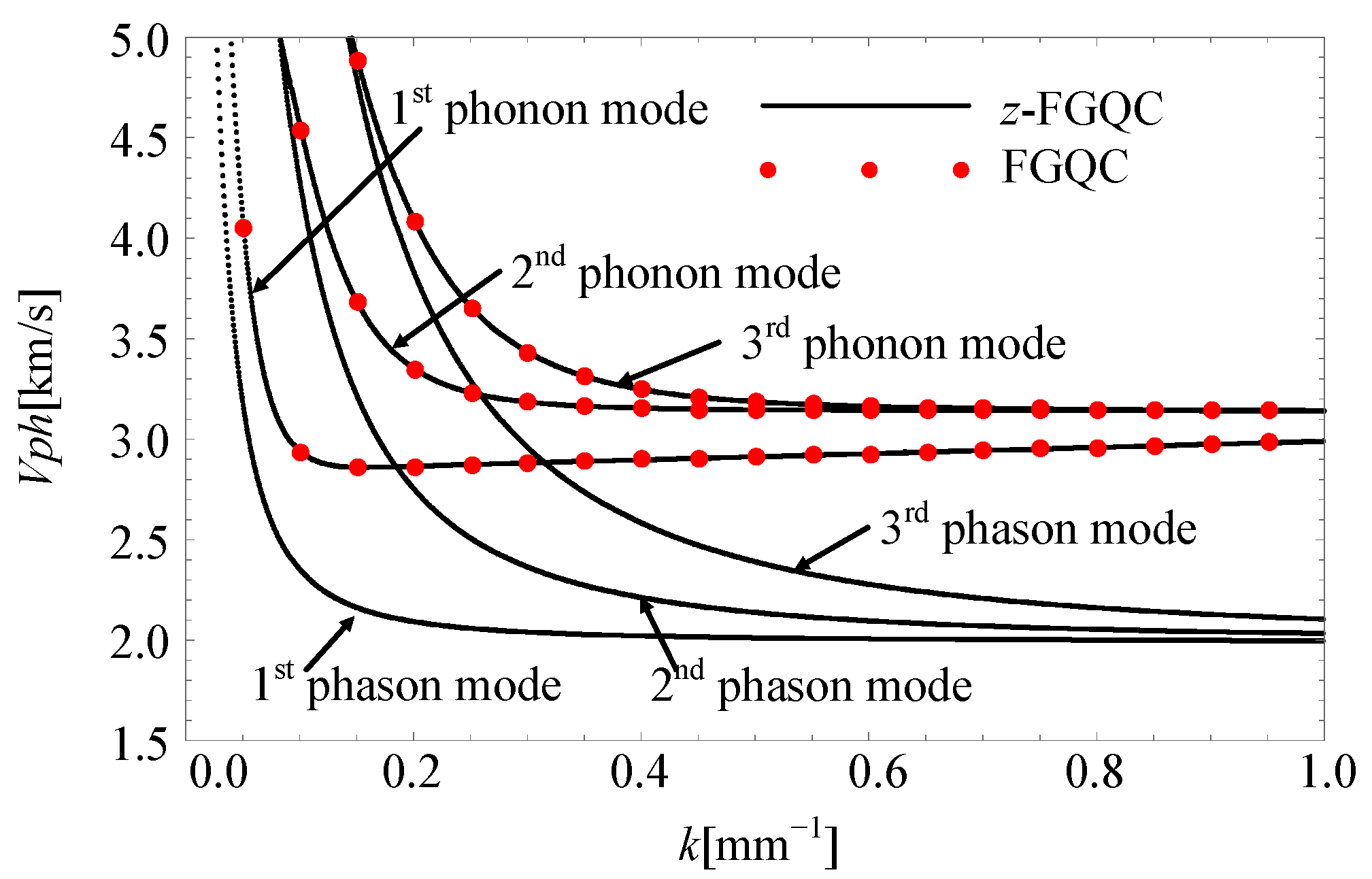
4.1. Method Validation
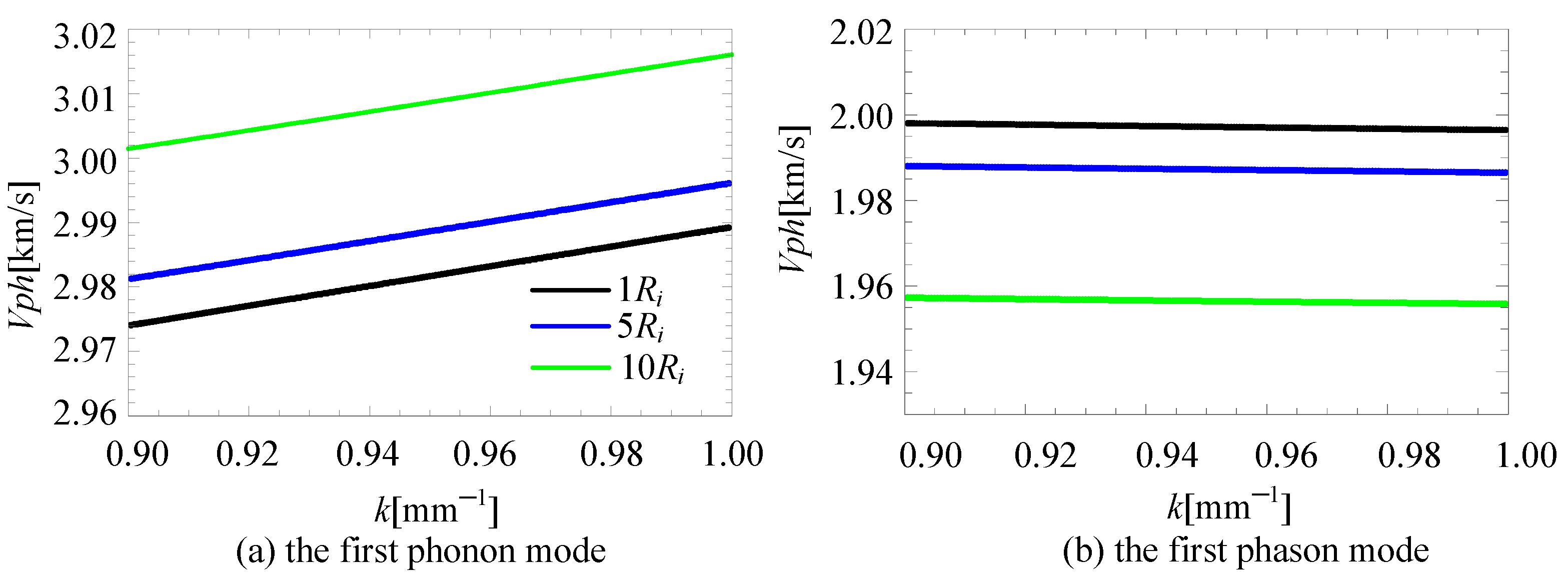
4.2. Convergence and Computational Efficiency Analysis
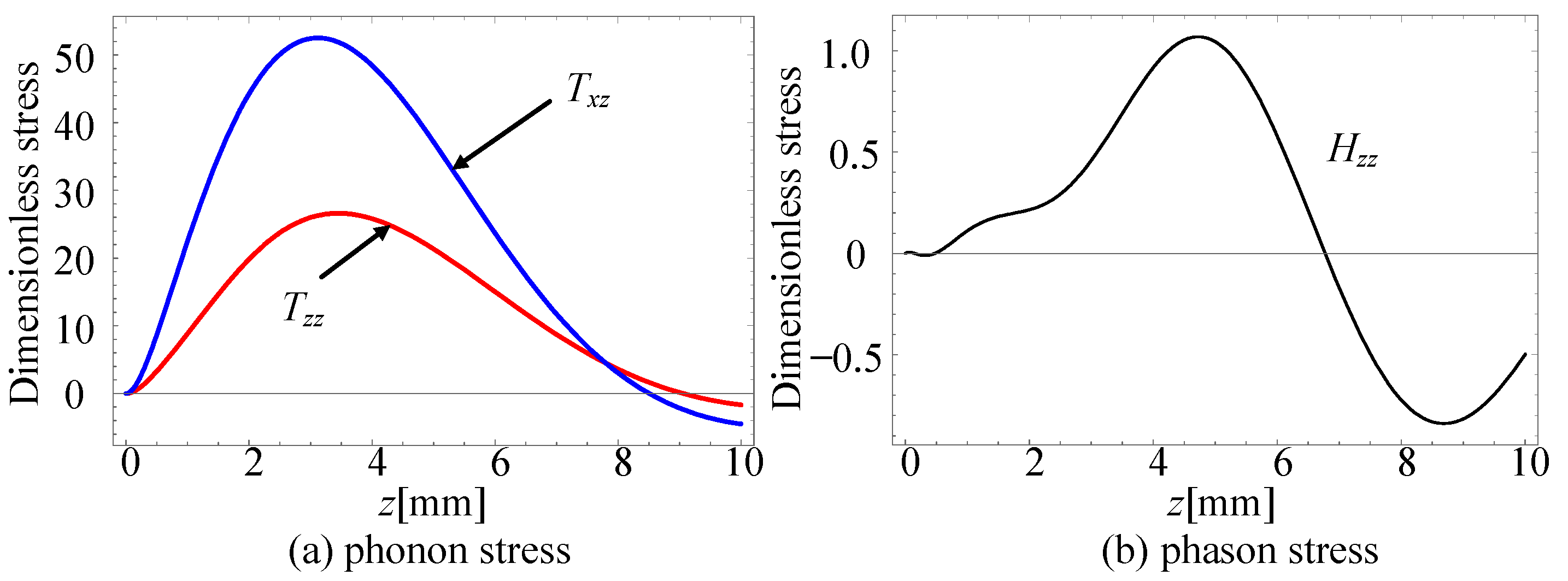
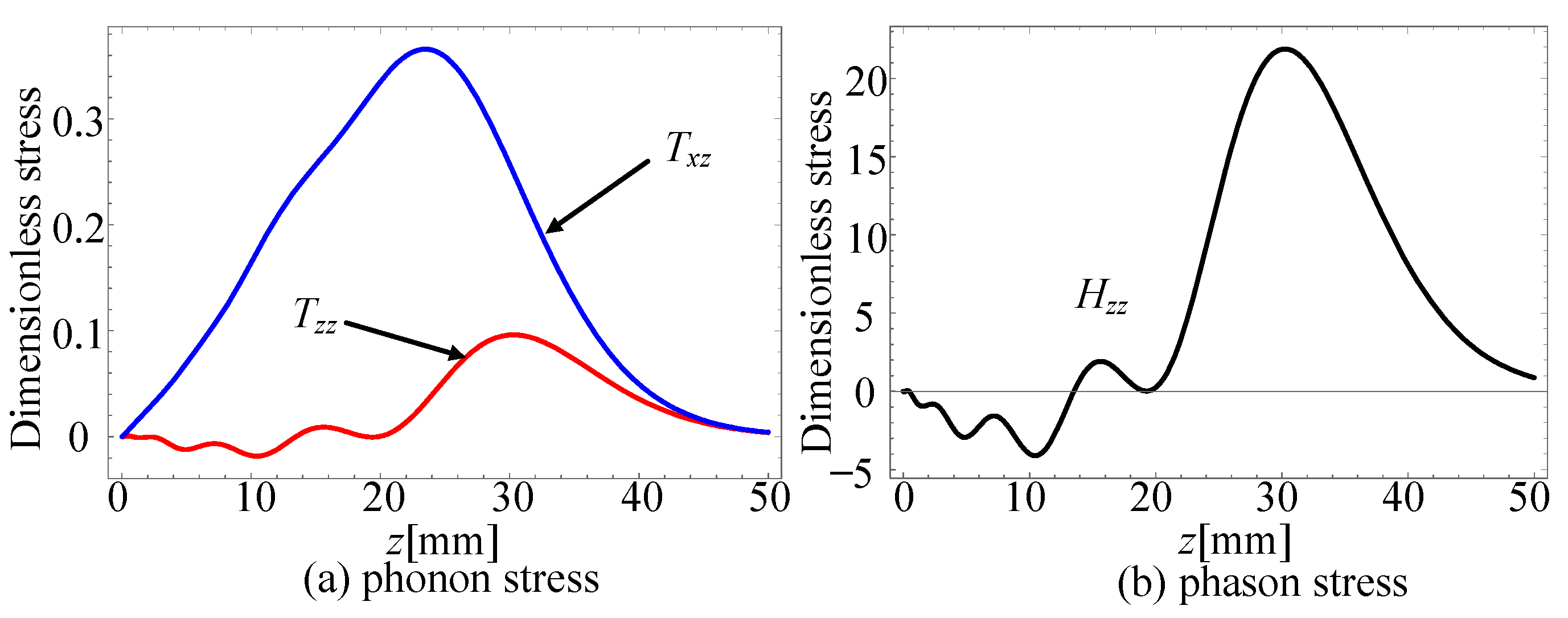
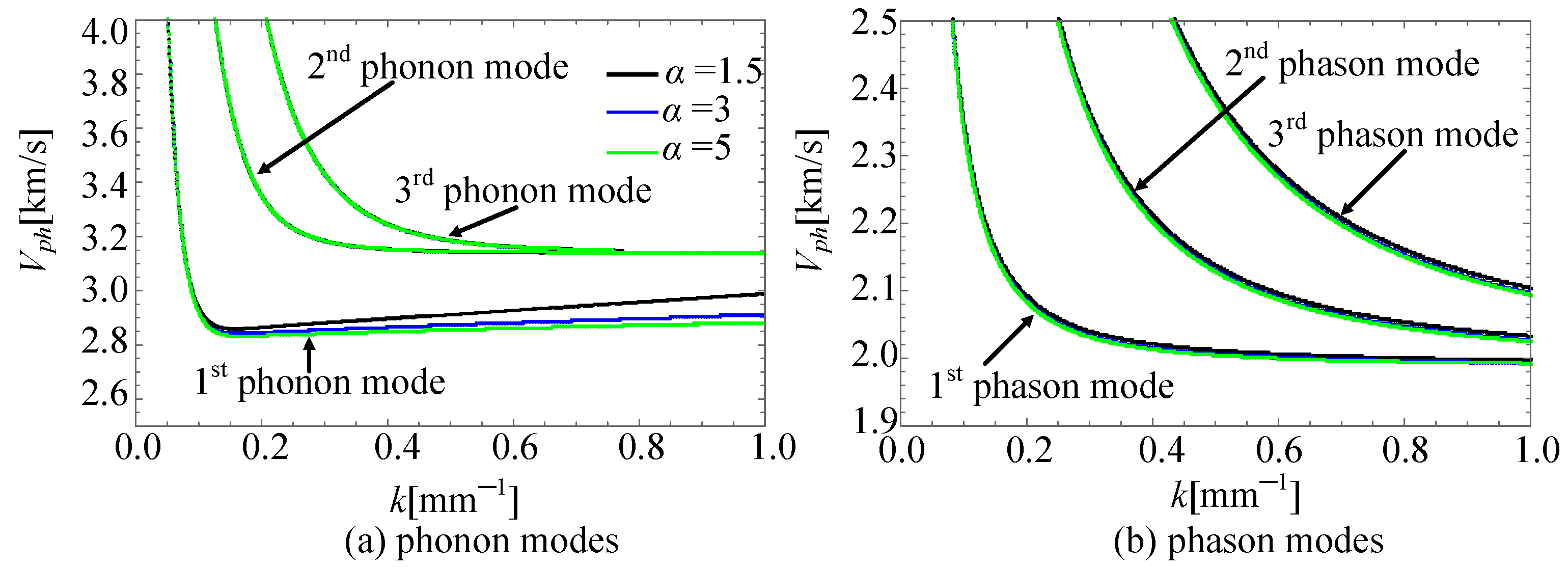
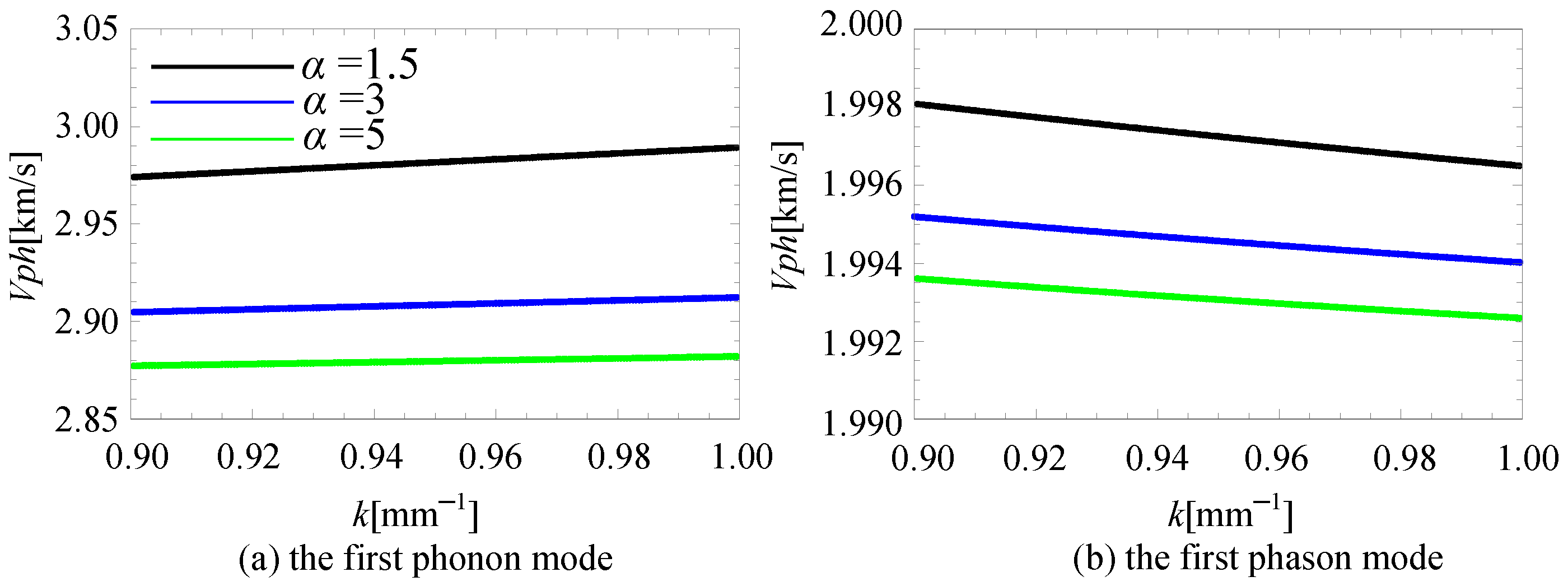
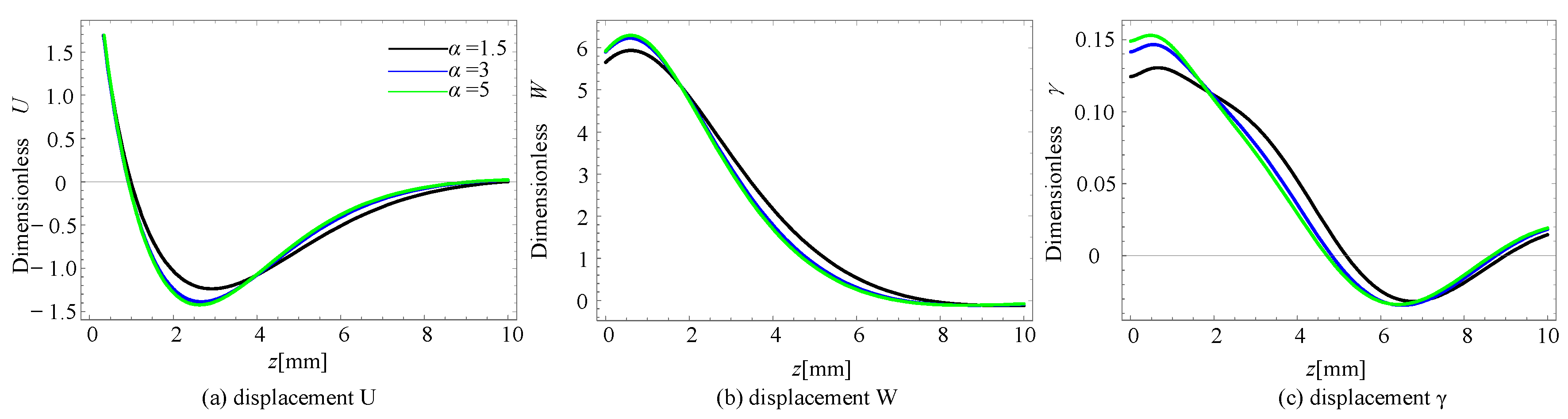
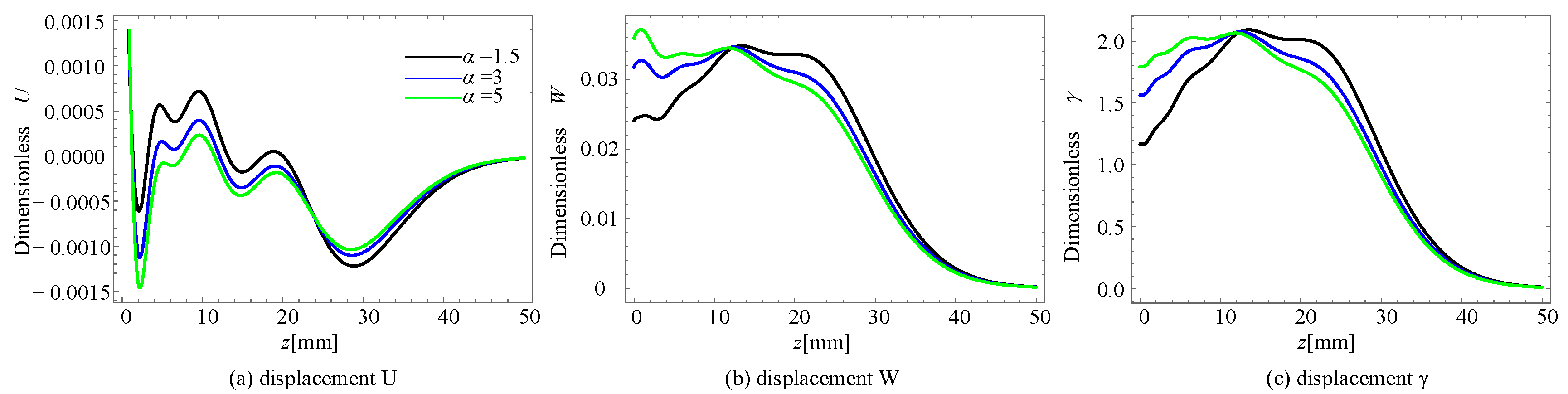
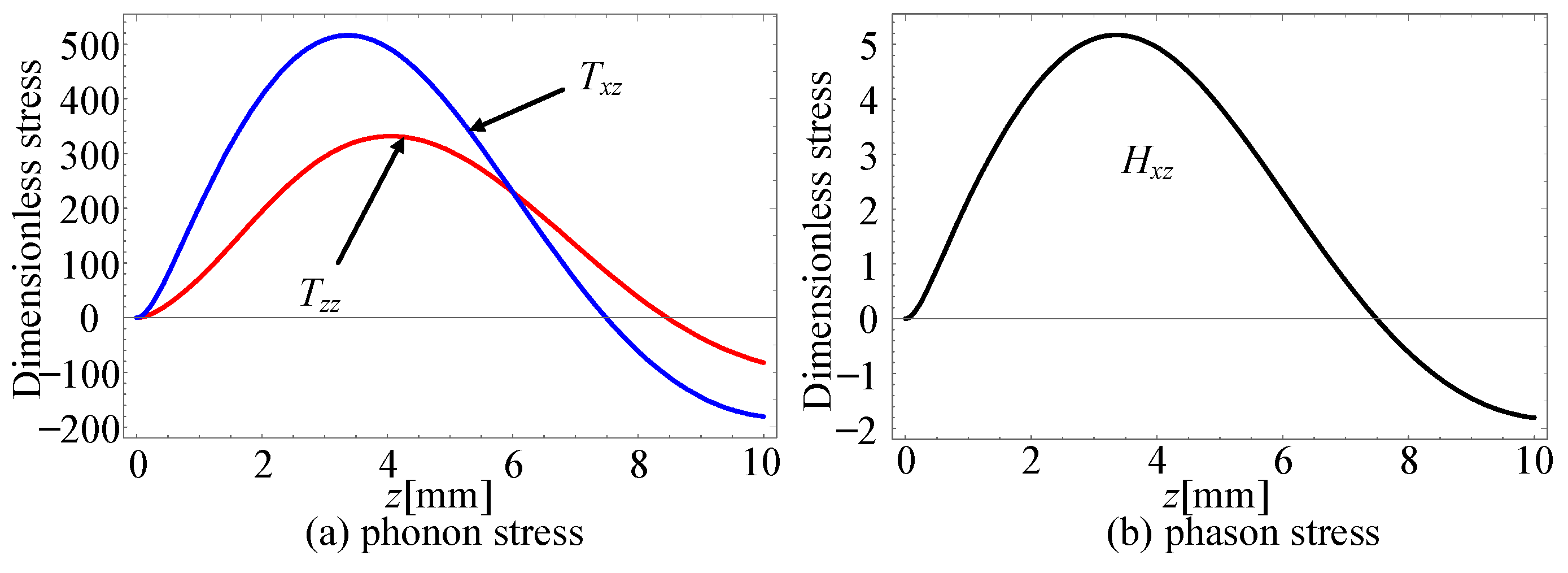
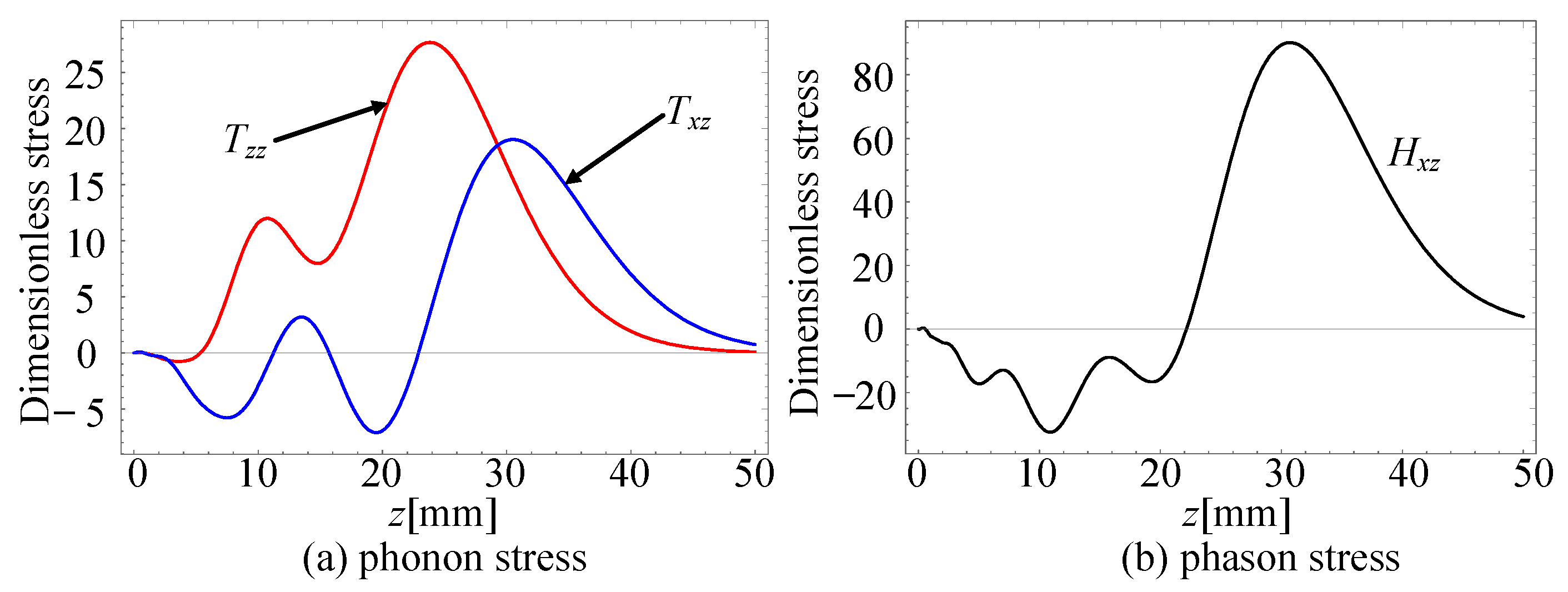
4.3. Phonon–Phason Coupling Effect
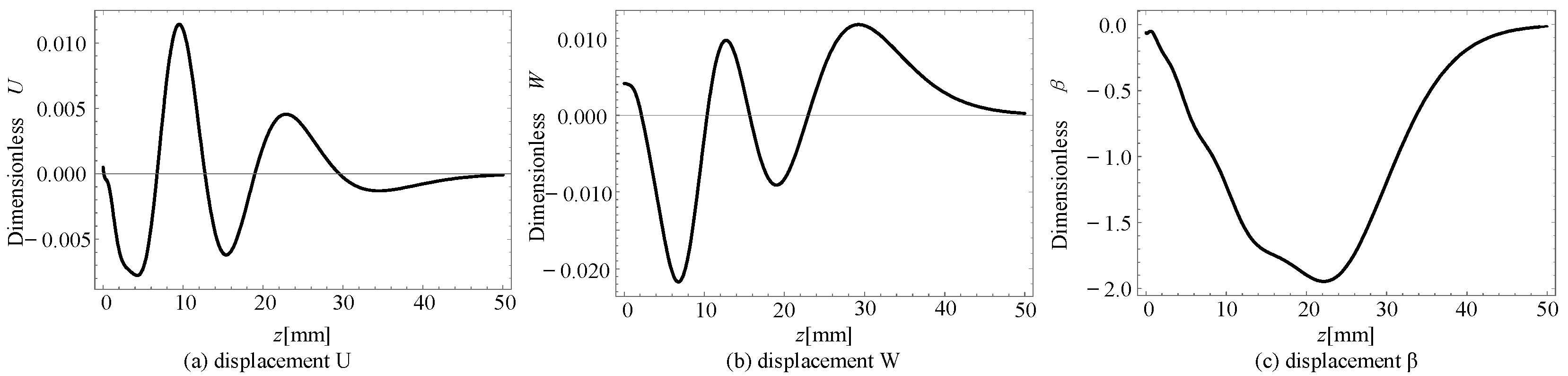
4.4. Inhomogeneity of Material
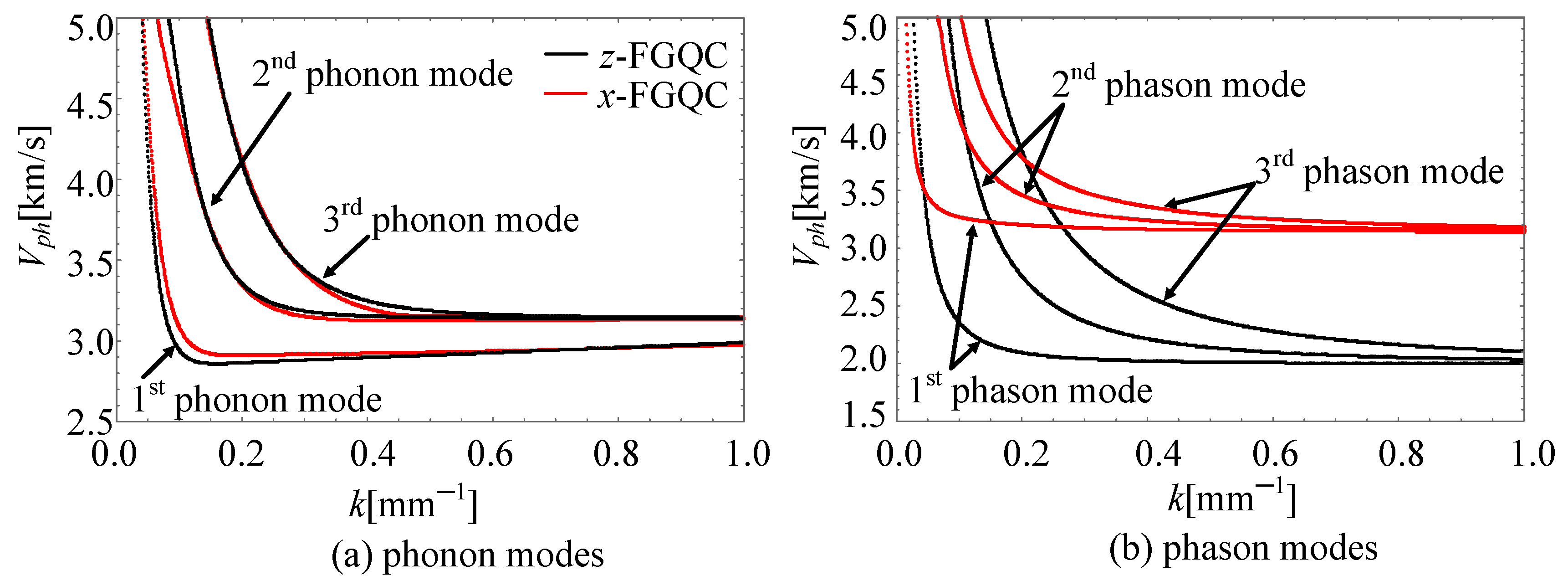
4.5. The Influence of Quasiperiodic Direction on Wave Characteristics
5. Conclusions
- (1)
- Compared with the classical Laguerre polynomial method, the improvement in computational efficiency of the analytical Laguerre polynomial method is more than 99%.
- (2)
- The energy penetration depth of the phason modes for Rayleigh waves is greater than that of the phonon modes.
- (3)
- The variation in the graded function has a considerable influence on the phase velocity and displacement distribution. Therefore, the performance of FGQC half-spaces can be adjustable by changing the graded function.
- (4)
- The phase velocity of Rayleigh waves is higher when the directions of quasiperiodicity and wave propagation coincide.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Stephens, P.W.; Goldman, A.I. Metallic Phase with Long-Range Orientational Order and No Translational Symmetry. Phys. Rev. Lett. 1984, 53, 1951–1953. [Google Scholar]
- Hammock, D.; Fang, F.; Irwin, K. Quasicrystal Tilings in Three Dimensions and Their Empires. Crystals 2018, 8, 370. [Google Scholar] [CrossRef]
- Li, G.; Li, L. An Analysis Method of Symplectic Dual System for Decagonal Quasicrystal Plane Elasticity and Application. Crystals 2022, 12, 636. [Google Scholar] [CrossRef]
- Prekul, A.; Shchegolikhina, N. Two-Level Electron Excitations and Distinctive Physical Properties of Al-Cu-Fe Quasicrystals. Crystals 2016, 6, 119. [Google Scholar] [CrossRef]
- Radi, E.; Mariano, P.M. Steady-State Propagation of Dislocations in Quasi-Crystals. Proc. R. Soc. A 2011, 467, 3490–3508. [Google Scholar] [CrossRef]
- Sathish, S.; Kulik, A.; Gremaud, G. Elastically isotropic Al-Li-Cu quasicrystal. Solid State Commun. 1991, 77, 403–407. [Google Scholar] [CrossRef]
- Farrokh, M.; Taheripur, M.; Carrera, E. Optimum Distribution of Materials for Functionally Graded Rectangular Plates Considering Thermal Buckling. Compos. Struct. 2022, 289, 115401. [Google Scholar] [CrossRef]
- Zhang, R.; Jiang, F.; Xue, L.; Yu, J.Y. Review of Additive Manufacturing Techniques for Large-Scale Metal Functionally Graded Materials. Crystals 2022, 12, 858. [Google Scholar] [CrossRef]
- Raza, A.; Talha, M.; Pathak, H. Influence of Material Uncertainty on Vibration Characteristics of Higher Order Cracked Functionally Gradient Plates Using XFEM. INT J. Appl. Mech. 2021, 13, 2150062. [Google Scholar] [CrossRef]
- Iqbal, M.D.; Birk, C.; Ooi, E.T.; Pramod, A.L.N.; Natarajan, S.; Gravenkamp, H.; Song, C. Thermoelastic Fracture Analysis of Functionally Graded Materials Using the Scaled Boundary Finite Element Method. Eng. Fract. Mech. 2022, 264, 108305. [Google Scholar] [CrossRef]
- Afshar, A.; Abbasi, M.; Eslami, M.R. Two-Dimensional Solution for Coupled Thermoelasticity of Functionally Graded Beams Using Semi-Analytical Finite Element Method. Mech. Adv. Mater. Struct. 2011, 18, 327–336. [Google Scholar] [CrossRef]
- Salah, I.B.; Wali, Y.; Ghozlen, M.H.B. Love Waves in Functionally Graded Piezoelectric Materials by Stiffness Matrix Method. Ultrasonics 2011, 51, 310–316. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, W.Q.; Ye, G.R.; Fu, J.Z. Waves in fluid-filled functionally graded piezoelectric hollow cylinders: A restudy based on the reverberation-ray matrix formulation. Wave Motion 2013, 50, 415–427. [Google Scholar] [CrossRef]
- Liu, H.; Pan, E.; Cai, Y. General Surface Loading over Layered Transversely Isotropic Pavements with Imperfect Interfaces. Adv. Eng. Softw. 2018, 115, 268–282. [Google Scholar] [CrossRef]
- Pan, E. Green’s Functions for Geophysics: A Review. Rep. Prog. Phys. 2019, 82, 106801. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.; Jin, F.; Jeon, I. Calculation of Propagation Properties of Lamb Waves in a Functionally Graded Material (FGM) Plate by Power Series Technique. NDT E Int. 2011, 44, 84–92. [Google Scholar] [CrossRef]
- Zhang, B.; Yu, J.G.; Zhang, X.M.; Ming, P.M. Complex Guided Waves in Functionally Graded Piezoelectric Cylindrical Structures with Sectorial Cross-Section. Appl. Math. Model. 2018, 63, 288–302. [Google Scholar] [CrossRef]
- Ferreira, T.; Koga, G.Y.; Oliveira, I.L.D.; Kiminami, C.S.; Botta, W.J.; Bolfarini, C. Functionally Graded Aluminum Reinforced with Quasicrystal Approximant Phases-Improving the Wear Resistance at High Temperatures. Wear 2020, 462–463, 203507. [Google Scholar] [CrossRef]
- Ferreira, T.; Oliveira, I.L.D.; Zepon, G.; Bolfarini, C. Rotational Outward Solidification Casting: An Innovative Single Step Process to Produce a Functionally Graded Aluminum Reinforced with Quasicrystal Approximant Phases. Mater. Des. 2020, 189, 108544. [Google Scholar] [CrossRef]
- Mu, X.; Xu, W.S.; Zhu, Z.W.; Zhang, L.L.; Gao, Y. Multi-field Coupling Solutions of Functionally Graded Two-Dimensional Piezoelectric Quasicrystal Wedges and Spaces. Appl. Math. Mech. 2022, 109, 251–264. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, J.H.; Xing, Y. Bending Analysis of Functionally Graded One-Dimensional Hexagonal Piezoelectric Quasicrystal Multilayered Simply Supported Nanoplates Based on Nonlocal Strain Gradient Theory. Acta Mech. Solida Sin. 2021, 34, 237–251. [Google Scholar] [CrossRef]
- Yang, J.; Wang, X.; Ding, S.H.; Li, X. Scattering of SH Wave by a Crack in a Functionally Graded One Dimensional Hexagonal Piezoelectric Quasicrystals. ZAMM-Z. Angew. Math. Mech. 2023, 103, 202200071. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Qin, Q.; Yang, L.Z.; Zhang, L.L.; Gao, Y. Axisymmetric Bending Analysis of Functionally Graded One-Dimensional Hexagonal Piezoelectric Quasi-Crystal Circular Plate. Proc. R. Soc. A-Math. Phys. 2020, 476, 2241. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Yu, J.G.; Zhang, X.M. Guided Wave Propagation in Functionally Graded One-Dimensional Hexagonal Quasi-Crystal Plates. J. Mech. 2020, 36, 773–788. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, X.H.; Elmaimouni, L.; Yu, J.G.; Zhang, X.M. Axial Guided Wave Characteristics in Functionally Graded One-Dimensional Hexagonal Piezoelectric Quasi-Crystal Cylinders. Math. Mech. Solids 2022, 27, 125–143. [Google Scholar] [CrossRef]
- Nobili, A.; Radi, E.; Signorini, C. A New Rayleigh-Like Wave in Guided Propagation of Antiplane Waves in Couple Stress Materials. Proc. R. Soc. A 2020, 476, 20190822. [Google Scholar] [CrossRef]
- Xiang, L.; Greenshields, D.; Dixon, S.; Edwards, R.S. Phased Electromagnetic Acoustic Transducer Array for Rayleigh Wave Surface Defect Detection. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2020, 67, 1403–1411. [Google Scholar] [CrossRef]
- Govindarajan, R.S.; Eduardo, R.N.; Kim, D. Surface Acoustic Wave-Based Flexible Piezocomposite Strain Sensor. Crystals 2021, 11, 1576. [Google Scholar] [CrossRef]
- Maradudin, A.A.; Wallis, R.F.; Mills, D.L.; Ballard, R.L. Vibrational Edge Modes in Finite Crystals. Phys. Rev. B 1972, 6, 1106–1111. [Google Scholar] [CrossRef]
- Li, K.; Jing, S.; Yu, J.G.; Zhang, X.M.; Zhang, B. The Complex Rayleigh Waves in a Functionally Graded Piezoelectric Half-Space: An Improvement of the Laguerre Polynomial Approach. Materials 2020, 13, 2320. [Google Scholar] [CrossRef]
- Matar, O.B.; Gasmi, N.; Zhou, H.; Goueygou, M.; Talbi, A. Legendre and Laguerre Polynomial Approach for Modeling of Wave Propagation in Layered Magneto-Electro-Elastic Media. J. Acoust. Soc. Am. 2013, 133, 1415–1424. [Google Scholar] [CrossRef] [PubMed]
- Maradudin, A.A.; Subbaswamy, K.R. Edge Localized Vibration Modes on a Rectangular Ridge. JAP 1977, 48, 3410–3414. [Google Scholar] [CrossRef]
- Zhang, B.; Yu, J.G.; Zhang, X.M. Love Waves in Multilayered Elastic Half-Space: An Improved Orthogonal Polynomials Method. In Proceedings of the 2015 Symposium on Piezoelectricity, Acoustic Waves and Device Applications, Jinan, China, 30 October–2 November 2015; pp. 269–272. [Google Scholar]
- Yu, J.G.; Wang, X.H.; Zhang, X.M. An Analytical Integration Legendre Polynomial Series Approach for Lamb Waves in Fractional Order Thermoelastic Multilayered Plates. Math. Method Appl. Sci. 2022, 45, 7631–7651. [Google Scholar] [CrossRef]
- Waksmanski, N.; Pan, E.; Yang, L.Z.; Gao, Y. Harmonic Response of Multilayered One-Dimensional Quasicrystal Plates Subjected to Patch Loading. J. Sound Vib. 2016, 375, 237–253. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Sladek, J.; Sladek, V. Elastodynamic Analysis of a Hollow Cylinder with Decagonal Quasicrystal Properties: Meshless Implementation of Local Integral Equations. Crystals 2016, 6, 94. [Google Scholar] [CrossRef]
- Lefebvre, J.E.; Yu, J.G.; Ratolojanahary, F.E.; Elmaimouni, L.; Xu, W.J.; Gryba, T. Mapped Orthogonal Functions Method Applied to Acoustic Waves-Based Devices. AIP Adv. 2016, 6, 065307. [Google Scholar] [CrossRef]
- Yu, J.; Guo, J. Analytical Solution for a 1D Hexagonal Quasicrystal Strip with Two Collinear Mode-III Cracks Perpendicular to the Strip Boundaries. Crystals 2023, 13, 661. [Google Scholar] [CrossRef]
- Liu, C.C.; Yu, J.G.; Zhang, B.; Zhang, X.M.; Wang, X.H.; Elmaimouni, L. Size-Dependent and Piezoelectric Effects on SH Wave Propagation in Functionally Graded Plates. Mech. Res. Commun. 2022, 124, 103965. [Google Scholar] [CrossRef]
- Wang, X.H.; Li, F.L.; Zhang, B.; Yu, J.G.; Zhang, X.M. Wave Propagation in Thermoelastic Inhomogeneous Hollow Cylinders by Analytical Integration Orthogonal Polynomial Approach. Appl. Math. Model. 2021, 99, 57–80. [Google Scholar] [CrossRef]
- Graham, R.L.; Knuth, D.E.; Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed.; Addison-Wesley: Reading, MA, USA, 1994. [Google Scholar]
- Vrettos, C. The Boussinesq Problem for Soils with Bounded Non-Homogeneity. Int. J. Numer. Anal. Met. 1998, 22, 655–669. [Google Scholar] [CrossRef]
- Rose, J.L. Ultrasonic Waves in Solid Media; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Chai, H.Y. Surface Wave Theory in Elastic Media and Its Application in Geotechnical Engineering; Science Press: Beijing, China, 2008. [Google Scholar]






| C11 | C12 | C13 | C22 | C23 | C33 | C44 | C55 | |
|---|---|---|---|---|---|---|---|---|
| QC1 | 23.433 | 5.741 | 6.663 | 23.433 | 6.663 | 23.222 | 7.019 | 7.019 |
| QC2 | 20 | 10 | 10 | 20 | 10 | 15 | 5 | 5 |
| C66 | ρ | R1 | R2 | R3 | K1 | K2 | ||
| QC1 | 8.846 | 4.186 | 8.846 | 8.846 | 0.8846 | 12.2 | 2.4 | |
| QC2 | 5 | 5.07 | 0.5 | 0.5 | 0.5 | 5 | 2 |
| C11 | C12 | C44 | ρ | E | σ |
|---|---|---|---|---|---|
| 10.77 | 5.55 | 2.61 | 2.7 | 7 | 0.34 |
| Mode | k | M = 2 | M = 4 | M = 8 | M = 16 | M = 32 |
|---|---|---|---|---|---|---|
| The first phonon mode | 0.5 | 2.922 | 2.913 | 2.912 | 2.912 | 2.912 |
| 1 | 3.010 | 2.993 | 2.989 | 2.989 | 2.989 | |
| 2 | 3.183 | 3.139 | 3.122 | 3.121 | 3.121 | |
| The first phason mode | 0.5 | 2.482 | 2.114 | 2.006 | 2.005 | 2.005 |
| 1 | 2.175 | 2.037 | 1.996 | 1.994 | 1.994 | |
| 2 | 2.088 | 2.008 | 1.990 | 1.988 | 1.988 |
| Method | M = 8 | M = 9 | M = 10 | M = 11 |
|---|---|---|---|---|
| CLPA | 217.391 | 258.969 | 376.578 | 448.281 |
| ALPA | 0.360 | 0.469 | 0.812 | 0.875 |
| Save | 99.83% | 99.82% | 99.78% | 99.80% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Tu, H.; Li, L.; Yu, J.; Dai, J. Rayleigh Waves Propagating in the Functionally Graded One-Dimensional Hexagonal Quasicrystal Half-Space. Crystals 2023, 13, 1205. https://doi.org/10.3390/cryst13081205
Zhang B, Tu H, Li L, Yu J, Dai J. Rayleigh Waves Propagating in the Functionally Graded One-Dimensional Hexagonal Quasicrystal Half-Space. Crystals. 2023; 13(8):1205. https://doi.org/10.3390/cryst13081205
Chicago/Turabian StyleZhang, Bo, Honghang Tu, Liangjuan Li, Jiangong Yu, and Jun Dai. 2023. "Rayleigh Waves Propagating in the Functionally Graded One-Dimensional Hexagonal Quasicrystal Half-Space" Crystals 13, no. 8: 1205. https://doi.org/10.3390/cryst13081205
APA StyleZhang, B., Tu, H., Li, L., Yu, J., & Dai, J. (2023). Rayleigh Waves Propagating in the Functionally Graded One-Dimensional Hexagonal Quasicrystal Half-Space. Crystals, 13(8), 1205. https://doi.org/10.3390/cryst13081205






