Mode-I Plane Elasticity Problem of Two Asymmetrical Edge Cracks Emanating from an Elliptical Hole in Two-Dimensional Decagonal Quasicrystals

Abstract

We consider the plane elasticity problem of two asymmetrical edge cracks emanating from an elliptical hole in two-dimensional decagonal quasicrystals (QCs) under remotely uniform tensile stress. A complex variation method of two-dimensional QCs is developed to solve the plane elasticity problem of two-dimensional decagonal QCs containing complex defects. The analytical solutions for the stress field and the stress intensity factors near the crack tip are expressed by using a conformal mapping technique and complex potential theory. Some special cases of the results are also obtained, such as the T-type crack, cross crack, and Griffith crack. The effects of geometrical parameters of crack configuration on the stress intensity factors are presented graphically.

1. Introduction

Quasicrystals (QCs) are a kind of solid different from the crystal and the glassy solid which were first discovered in 1984 by Shechtman et al. [1]. Different from the regular arrangement of atoms in ideal crystals, which is mainly reflected in the periodicity of atomic arrangement, quasicrystals have long-range quasi-periodic translation symmetry and noncrystallographic rotation symmetry. The discovery of QCs is a significant breakthrough for condensed matter physics in recent years. According to the cutting and projection methods, 3D quasi-lattice points are obtained by selecting projections to the respective 6D periodic lattice points [2,3]. Therefore, there are two kinds of subspace in elasticity, which were called physical space and complement space. Due to the unusual structure of QCs, the materials have a number of different physical properties [4,5,6]. Quasicrystalline materials are brittle [7], and their defects have been observed [8]. When quasicrystalline materials are subjected to mechanical stress in the process of their use, the propagation of cracks generated during their fabrication may cause these materials to fail prematurely. Therefore, it is of great significance to study the crack problem of QCs from the view of theoretical and practical applications.

Experiments show that as a solid material with a special structure, quasicrystalline material has many excellent properties, such as low surface energy, a low friction coefficient, low thermal conductivity, and good oxidation resistance. So quasicrystalline materials can be used as surface-modification materials, structural materials reinforcing phasons, hydrogen-storage materials, semiconductor materials, and thermoelectric-power-generation materials. Specifically, the application of surface-modified materials involves the application of quasicrystalline materials as coatings or thin films over the surface of other materials. The excellent physicochemical properties of quasicrystals are used to change the properties of the material surface as well as to optimize the overall material properties [9], for example, as a surface coating for kitchen cookware such as non-stick pans [10,11] to make them less wearable and long-lasting; as a thermal barrier coating for the aerospace industry, and as an insulating material in automotive engines [12]. Using the optical properties of quasicrystals, quasicrystal materials can be used as thin film materials for the solar industry, infrared detectors, and temperature sensors [13]. Quasicrystals have high hardness and wear resistance and are often used as a reinforcing phase for materials. In addition, quasicrystals are filled in other matrix materials such as metals as a particle-reinforcing phase. Not only can the performance of the matrix be improved, but it is relatively easy to recycle and can be regarded as an environmentally friendly material.

Due to the quasi-periodicity of quasicrystals, quasicrystals have a special elastic degree of freedom called the phonon degree of freedom different from the phase degree of freedom. In other words, the discussion of quasicrystal elasticity involves not only the phonon field but also the phase field. Therefore, the basic equations of quasicrystal elasticity theory are much more complex than those of classical elasticity theory. Hence, the study of quasicrystal elasticity and fracture mechanics has attracted the attention of researchers and carried out extensive research. Linear elastic theory of QCs have been studied by many researchers [14,15,16,17,18,19,20,21,22,23,24]. There are two kinds of displacement fields in elasticity. One is a phonon displacement field $u_i$, which is the same as the displacement field of usual crystals. The other is new and named as a phason displacement field $v_i$, which is diffusive due to the elementary excitation associated with the phason mode and describes the local rearrangements of the unit cells. The complex function method is one of the effective methods to solve the quasicrystal plane elasticity and complex defects. By developing this method, the exact analytical solutions of many quasicrystal elasticity problems can be obtained [25,26,27]. By constructing several new conformal mapping functions and using the method of complex variable function, Guo and his coauthors [28,29,30] solved the antiplane elasticity problem of one-dimensional hexagonal quasicrystals with edges of a hole and other complex defects, including double cracks with an elliptic hole, collinear cracks with an elliptical hole, four cracks with unequal length with an elliptical hole, etc., and obtained the exact solutions of phonon field and phason phase field at the crack tip. Gao and his coauthors [31] applied the Stroh formalism to one-dimensional quasicrystals.

Two-dimensional quasicrystals are three-dimensional solid structures derived from the projection of five-dimensional periodic structures into three-dimensional space. In the rectangular coordinate system, the arrangement of atoms is periodic in one direction, and the arrangement of atoms is quasi-periodic in the plane perpendicular to that direction. The direction of the periodic arrangement is exactly the direction of the axes of the five-fold, eight-fold, ten-fold, and twelve-fold rotational symmetry. Quintic, octagonal, decagonal, and dodecagonal symmetry quasicrystals are also called pentagonal, octagonal, decagonal, and dodecagonal quasicrystals. Two-dimensional quasicrystals contain 10 crystal systems, 18 Laue classes, and 51 kinds of point groups. Decagonal symmetry two-dimensional quasicrystals are two-dimensional quasicrystals with ten-fold rotational symmetry axis. Experiments have shown that two-dimensional quasicrystalline materials have kinds of defects, such as face defects and cracks. The defects such as cracks, holes, and dislocations greatly affect the physical and mechanical properties of solid materials. Effectively preventing and predicting the initiation and propagation of cracks and other defects in quasicrystalline materials is of great significance for analyzing the strength, stiffness, and reliability of quasicrystal materials and structures. The elasticity and fracture problems of two-dimensional quasicrystalline materials have been widely taken into consideration. The general two-dimensional quasicrystals are three-dimensional elastic problems, which are completely different from the classical elastic plane problems. When the defects (including dislocations, cracks, and holes) in two-dimensional quasicrystals penetrate along the periodic direction, all the field variables do not change with this direction. In this case, its elasticity is plane elasticity. Decagonal symmetry two-dimensional quasicrystals are the largest class of two-dimensional quasicrystals found in experiments. Bendersky [32] and Chatopadihyay et al. [33], respectively, found decagonal symmetry two-dimensional quasicrystals with point group 8/mmm in Al–Mn alloy. Fung et al. [34] found decagonal symmetry quasicrystals in the quench-cooled Al–Fe alloy. Therefore, it can be seen that decagonal symmetry two-dimensional quasicrystals are an important class of two-dimensional quasicrystals. It can be seen that decagonal symmetry two-dimensional quasicrystals are a kind of important two-dimensional quasicrystals, so decagonal symmetry two-dimensional quasicrystals are selected as the research object of the quasicrystal fracture problem in this paper.

Li and Fan [35] developed the complex function method for the plane elasticity problem of point group 10 mm two-dimensional quasicrystals and solved the plane elasticity problem of two-dimensional quasicrystals with an elliptical hole. Li and Fan [36,37] have given the complex method for the plane elasticity problem of point group 10 mm two-dimensional quasicrystals, and obtained the analytical solution of the dislocation problem. They also discussed interaction between two parallel dislocations. Using the complex method, Wang and Zhong [38] studied the interaction of a linear dislocation with a semi-infinite crack in decagonal quasicrystals, and obtained stress intensity factors, energy release rate, and expressions of the Peach–Koehler force acting on the linear dislocation. Li [39] developed the Muskhelishvili method of two-dimensional decagonal quasicrystal plane elasticity theory. Based on the complex representation of stress and displacement, the method of determining the complex potential function is discussed and applied to the study of elliptical holes, and the corresponding analytical solution is obtained. In some special cases, the results can be reduced to the existing solution, which fully shows that this method is one of the effective methods to study the plane elasticity theory of two-dimensional decagonal quasicrystals. By using the Stroh formalism, Radi and Mariano [40] investigated the straight cracks in two-dimensional quasicrystals and obtained the closed-form solution of the balance equations in terms of phonon and phason fields. The Stroh formalism for 2D deformations of the icosahedral QC was then studied by Li and Liu [41]. From the above results, it can be seen that the elasticity of two-dimensional quasicrystals has received more attention. Researchers have applied the complex function method, Stroh method, and Muskhelishvili method to the study of two-dimensional quasicrystal elasticity. However, in general, the study of two-dimensional quasicrystals focuses on some defects with relatively simple configurations. For more complex defects, study is also concentrated on Mode-Ⅲ antiplane elasticity problems. Some studies have focused on numerical results. For defects with a complex configuration, it is difficult to obtain analytical results because of the difficulty of calculation. Therefore, the analytical results of the Mode-I plane elasticity problem of the decagonal symmetry two-dimensional quasicrystals with complex defects were considered in this paper. The geometric parameters of complex defects can be reduced to some simple configurations under special conditions. The results obtained in this paper are more general analytic results than other results.

In this paper, the Muskhelishvili method of the decagonal symmetry two-dimensional quasicrystal planar elasticity theory is used. Based on the complex representation of stress and displacement and the determination method of complex potential function, the conformal mapping technique in the complex function method is introduced in the calculation process. With the help of the conformal mapping technique, the complex defect configurations contained in the decagonal symmetry two-dimensional quasicrystals are transformed into circular holes in the mathematical plane. Then, the analytical results of the problem are derived. In some special cases, the results of the analysis can be degraded to some existing simple configurations, indicating that the defects studied are more general.

As a special new solid material, quasicrystals are sensitive to force, heat, electricity, and related effects [42]. The force, electricity, heat, and related physical and chemical properties of quasicrystals are fundamentally different from those of conventional crystals. The theory and criteria of quasicrystal fracture mechanics are fundamentally different from traditional linear elastic materials. Therefore, it will be groundbreaking to study the thermal and electrical effects of quasicrystals. At present, there is little research on the force, heat, electricity, and related effects of two-dimensional quasicrystals. On the basis of this study, it is of great significance for the application of two-dimensional quasicrystals containing complex defects to study the force, heat, electricity, and related effects in the future. Recently, the research of functionally graded materials has also achieved many excellent results [43,44], for example, by using a newly developed simple first-order shear deformation theory to solve the problem of the free vibration of temperature-dependent functionally graded plates resting on a viscoelastic foundation. In view of the excellent properties of functionally graded materials, the mechanical behavior of unequal length cracks at the edge of elliptical holes in functionally graded materials can be studied in the future.

2. Basic Equation

According to the quasicrystalline elasticity theory [14], the basic equations of quasicrystalline materials include deformation equation, equilibrium equation, and generalized Hooke’s law. In the cartesian coordinate system $x_i(i=1,2,3)$, the plane perpendicular to the periodic direction (that is the direction of x₃) in the two-dimensional quasicrystal is the quasi-periodic plane; then, in this coordinate system, the basic equation of the quasicrystals is a geometric equation of deformation

$${\epsilon }_{ij}=\frac{1}{2}(\frac{\mathrm{\partial }{u}_i}{\mathrm{\partial }{x}_j}+\frac{\mathrm{\partial }{u}_j}{\mathrm{\partial }{x}_i}),\hspace{1em}{w}_{ij}=\frac{\mathrm{\partial }{w}_i}{\mathrm{\partial }{x}_j}$$

(1)

an equilibrium equation (if the body force is neglected)

$$\frac{\mathrm{\partial }{\sigma }_{ij}}{\mathrm{\partial }{x}_j}=0,\hspace{1em}\frac{\mathrm{\partial }{H}_{ij}}{\mathrm{\partial }{x}_j}=0$$

(2)

and generalized Hooke’s law

$$\begin{array}{l}{\sigma }_{11}=L({\epsilon }_{11}+{\epsilon }_{22})+2M{\epsilon }_{11}+R(w_{11}+w_{22})\\ {\sigma }_{22}=L({\epsilon }_{11}+{\epsilon }_{22})+2M{\epsilon }_{22}-R(w_{11}+w_{22})\\ {\sigma }_{12}={\sigma }_{21}=2M{\epsilon }_{12}+R(w_{21}-w_{12})\\ H_{11}=K_1{w}_{11}+K_2{w}_{22}+R({\epsilon }_{11}-{\epsilon }_{22})\\ H_{22}=K_1{w}_{22}+K_2{w}_{11}+R({\epsilon }_{11}-{\epsilon }_{22})\\ H_{12}=K_1{w}_{12}-K_2{w}_{21}-2R{\epsilon }_{12}\\ H_{21}=K_1{w}_{21}-K_2{w}_{12}+2R{\epsilon }_{12}\end{array}$$

(3)

where

$$L=C_{12},\hspace{1em}M=(C_{11}-C_{12})/2=C_{66}$$

$C_{ij}$ is the phonon field elastic constants, $K_i$ is the phason field elastic constants, and $R$ is the phonon–phason field coupling elastic constants. ${\sigma }_{ij}$ and $H_{ij}$ are the phonon field stress and phason field stress, respectively, and ${\epsilon }_{ij}$ and $w_{ij}$ are the phonon field strain and phason field strain, respectively.

By introducing a new stress potential function, the basic equation of two-dimensional decagonal quasicrystals elasticity theory can be simplified as a four-fold harmonic equation [45]:

$${\nabla }^2{\nabla }^2{\nabla }^2{\nabla }^{2}G=0$$

(4)

where $G(x,y)$ is the stress potential function. The general solution of Equation (4) is as follows [45]:

$$G=2\mathrm{Re}[g_1(z)+\overline{z}{g}_2(z)+\frac{1}{2}{\overline{z}}^2{g}_3(z)+\frac{1}{6}{\overline{z}}^3{g}_4(z)]$$

(5)

in which $g_i(z),(i=1,2,3,4)$ are arbitrary analytic functions of a complex variable $z=x+iy$. $\overline{z}=x-iy$ denotes the complex conjugate of a complex variable $z$. On this basis, the complex expressions of phonon field stress and phason field stress are obtained as follows [45]:

$$\begin{array}{l}{\sigma }_{xx}=-32c_1\mathrm{Re}(\mathrm{\Omega }(z)-2g_4^{‴}(z))\\ {\sigma }_{yy}=32c_1\mathrm{Re}(\mathrm{\Omega }(z)+2g_4^{‴}(z))\\ {\sigma }_{xy}={\sigma }_{yx}=32c_1\mathrm{Im}\mathrm{\Omega }(z)\\ H_{xx}=32R\mathrm{Re}({\mathrm{\Theta }}^{\prime }(z)-\mathrm{\Omega }(z))\\ H_{xy}=-32R\mathrm{Im}({\mathrm{\Theta }}^{\prime }(z)+\mathrm{\Omega }(z))\\ H_{yx}=-32R\mathrm{Im}({\mathrm{\Theta }}^{\prime }(z)-\mathrm{\Omega }(z))\\ H_{yy}=-32R\mathrm{Re}({\mathrm{\Theta }}^{\prime }(z)+\mathrm{\Omega }(z))\end{array}$$

(6)

The complex representation of phonon displacement and phason displacement are [45]

$$\begin{array}{l}{u}_x+i{u}_y=32(4c_1{c}_2-c_3-c_1{c}_4)g_4^{″}(z)-32(c_1{c}_4-c_3)(\overline{g_3^{‴}(z)}+z\overline{g_4^{‴}(z)})\\ w_x+i{w}_y=\frac{32R}{K_1-K_2}\overline{\mathrm{\Theta }(z)}\end{array}$$

(7)

where

$$c_1=\frac{c}{K_1-K_2}+M,c_2=\frac{c+(L+M)(K_1+K_2)}{4(L+M)c},c_3=\frac{R^2}{c},c_4=\frac{K_1+K_2}{c}$$

$$c=M(K_1+K_2)-R^2$$

and

$$\begin{array}{l}\mathrm{\Theta }(z)=g_2^{(\mathrm{IV})}(z)+\overline{z}{g}_3^{(\mathrm{IV})}(z)+\frac{1}{2}{\overline{z}}^2{g}_4^{(\mathrm{IV})}(z)\\ \mathrm{\Omega }(z)=g_3^{(\mathrm{IV})}(z)+\overline{z}{g}_4^{(\mathrm{IV})}(z)\end{array}$$

In order to simplify the complex representation of stress, we introduce the following new notation:

$$g_2^{(\mathrm{IV})}(z)=h_2(z),g_3^{‴}(z)=h_3(z),g_4^{″}(z)=h_4(z)$$

(8)

Then Equation (6) can be further simplified as

$${\sigma }_{xx}+{\sigma }_{yy}=4\times 32c_1\mathrm{Re}{h}_4^{\prime }(z)\hspace{1em}\hspace{1em}$$

(9)

$${\sigma }_{yy}-{\sigma }_{xx}+2i{\sigma }_{xy}=2\times 32c_1\mathrm{\Omega }(z)=2\times 32c_1[h_3^{\prime }(z)+\overline{z}{h}_4^{″}(z)]$$

(10)

$$H_{xy}-H_{yx}-i(H_{xx}+H_{yy})=2\times 32iR\mathrm{\Omega }(z)$$

(11)

$$H_{xx}-H_{yy}-i(H_{xy}+H_{yx})=2\times 32R{\mathrm{\Theta }}^{\prime }(z)$$

(12)

The certainty of the complex potential function is discussed by means of Equations (9)–(12) in reference [39], and the expression is as follows:

$$\begin{array}{l}{h}_4(z)=d_1(X+iY)\ln z+Bz+h_4^0(z)\\ h_3(z)=d_2(X-iY)\ln z+(B^{\prime }+i{C}^{\prime })z+h_3^0(z)\\ h_2(z)=(B^{″}+i{C}^{″})z+h_2^0(z)\end{array}$$

(13)

where

$$\begin{gathered} d_1=-\frac{1}{-64c_1\pi \times (32(4c_1{c}_2-c_3-c_1{c}_4)+1)},d_2=-\frac{4c_1{c}_2-c_3-c_1{c}_4}{2c_1\pi \times (32(4c_1{c}_2-c_3-c_1{c}_4)+1)} \\ B=\frac{1}{4}({\sigma }_1+{\sigma }_2),B^{\prime }+i{C}^{\prime }=-\frac{1}{2}({\sigma }_1-{\sigma }_2)e^{-2i\alpha },B^{″}+i{C}^{″}=-\frac{1}{2}(H_1-H_2)e^{-2i{\alpha }^{\prime }} \end{gathered}$$

(14)

$B,B^{\prime },C^{\prime },B^{″},C^{″}$ are arbitrary real constants, $h_2^0(z)$ is an analytic function of complex variable $z$.${\sigma }_1,{\sigma }_2$, and $H_1,H_2$ are the principal values of the stresses of the phonon field and the phason field at infinity, respectively. $\alpha$ and ${\alpha }^{\prime }$ are the angles made by the direction of ${\sigma }_1,H_1$ with the positive of the $x$ axis.

3. Complex Expression of the Boundary Conditions

For the two-dimensional quasicrystal plane problem, the stress boundary conditions of phonon field and phason field are [25]

$$\begin{array}{l}{\sigma }_{xx}\cos (n,x)+{\sigma }_{xy}\cos (n,y)=T_x, {\sigma }_{xy}\cos (n,x)+{\sigma }_{yy}\cos (n,y)=T_y\hspace{1em}\\ H_{xx}\cos (n,x)+H_{xy}\cos (n,y)=h_x , H_{xy}\cos (n,x)+H_{yy}\cos (n,y)=h_y\end{array}$$

(15)

$n$ denotes the outer normal vector of any point on the boundary, $T_x, T_y$ denotes the tractions, and $h_x,h_y$ denotes the generalized tractions. Since there are no reports on generalized tractions, we assume $h_x=h_y=0$ for simplicity.

According to Equations (6) and (8), the stress boundary conditions (15) can be simplified as

$$h_4(z)+\overline{h_3(z)}+z\overline{h_4^{\prime }(z)}=\frac{i}{32c_1}{\displaystyle \int (T_x}+i{T}_y)ds$$

(16)

$$h_2(z)+\overline{z}{h}_3^{\prime }(z)+\frac{1}{2}{\overline{z}}^2{h}_4^{″}(z)=0$$

(17)

By introducing the suitable conformal mapping $z=\omega (\zeta )$, the stress function $h_2(z), h_3(z), h_4(z)$ can be expressed as a function of parameters $\zeta$:

$$\begin{array}{l}{\phi }_2(\zeta )=h_2(z)=h_2[\omega (\zeta )]\\ {\phi }_3(\zeta )=h_3(z)=h_3[\omega (\zeta )]\\ {\phi }_4(\zeta )=h_4(z)=h_4[\omega (\zeta )]\end{array}$$

(18)

From Equations (13) and (18), ${\phi }_2(\zeta ), {\phi }_3(\zeta ), {\phi }_4(\zeta )$ can be expressed as follows:

$$\begin{array}{l}{\phi }_2(\zeta )=(B^{″}+i{C}^{″})\omega (\zeta )+{\phi }_{20}(\zeta )\\ {\phi }_3(\zeta )=-d_2(X-iY)\ln \zeta +(B^{\prime }+i{C}^{\prime })\omega (\zeta )+{\phi }_{30}(\zeta )\\ {\phi }_4(\zeta )=-d_1(X+iY)\ln \zeta +B\omega (\zeta )+{\phi }_{40}(\zeta )\end{array}$$

(19)

where $X,Y$ are the tractions component along the $x$ axis and $y$ axis of the inner boundary.

From Equation (18), the conjugate of (18) and (19), and boundary conditions (16) and (17) can be rewritten as

$${\phi }_{40}(\zeta )+\frac{1}{2\pi i}{\displaystyle \int \frac{\omega (\sigma )}{\overline{{\omega }^{\prime }(\sigma )}}\cdot \frac{\overline{{\phi }_{40}^{\prime }(\sigma )}}{\sigma -\zeta }}d\sigma =\frac{1}{2\pi i}{\displaystyle \int \frac{f_0}{\sigma -\zeta }d\sigma }$$

(20)

$${\phi }_{30}(\zeta )+\frac{1}{2\pi i}{\displaystyle \int \frac{\overline{\omega (\sigma )}}{{\omega }^{\prime }(\sigma )}\cdot \frac{{\phi }_{40}^{\prime }(\sigma )}{\sigma -\zeta }}d\sigma =\frac{1}{2\pi i}{\displaystyle \int \frac{\overline{f_0}}{\sigma -\zeta }d\sigma }$$

(21)

$$\begin{array}{l}{\phi }_{20}(\zeta )+\frac{1}{2\pi i}{\displaystyle \int \frac{\overline{\omega (\sigma )}}{{\omega }^{\prime }(\sigma )}\cdot \frac{{\phi }_{30}^{\prime }(\sigma )}{\sigma -\zeta }}d\sigma +\\ \hspace{1em}\hspace{1em}\frac{1}{4\pi i}{\displaystyle \int \left[\frac{{\overline{\omega (\sigma )}}^2{\phi }_{40}^{″}(\sigma )}{{\omega }^{\prime }{(\sigma )}^2}-\frac{{\overline{\omega (\sigma )}}^2{\omega }^{″}(\sigma ){\phi }_{40}^{\prime }(\sigma )}{{\omega }^{\prime }{(\sigma )}^3}\right]}\frac{d\sigma }{\sigma -\zeta }=0\end{array}$$

(22)

where

$$\begin{array}{l}{f}_0=\frac{i}{32c_1}{\displaystyle \int (T_x}+i{T}_y)ds-\frac{X+iY}{2\pi }\ln \sigma -d_1(X-iY)\frac{\omega (\sigma )}{\overline{{\omega }^{\prime }(\sigma )}}\sigma \\ \hspace{1em}\hspace{1em}-2B\omega (\sigma )-(B^{\prime }-i{C}^{\prime })\overline{\omega (\sigma )}\end{array}$$

(23)

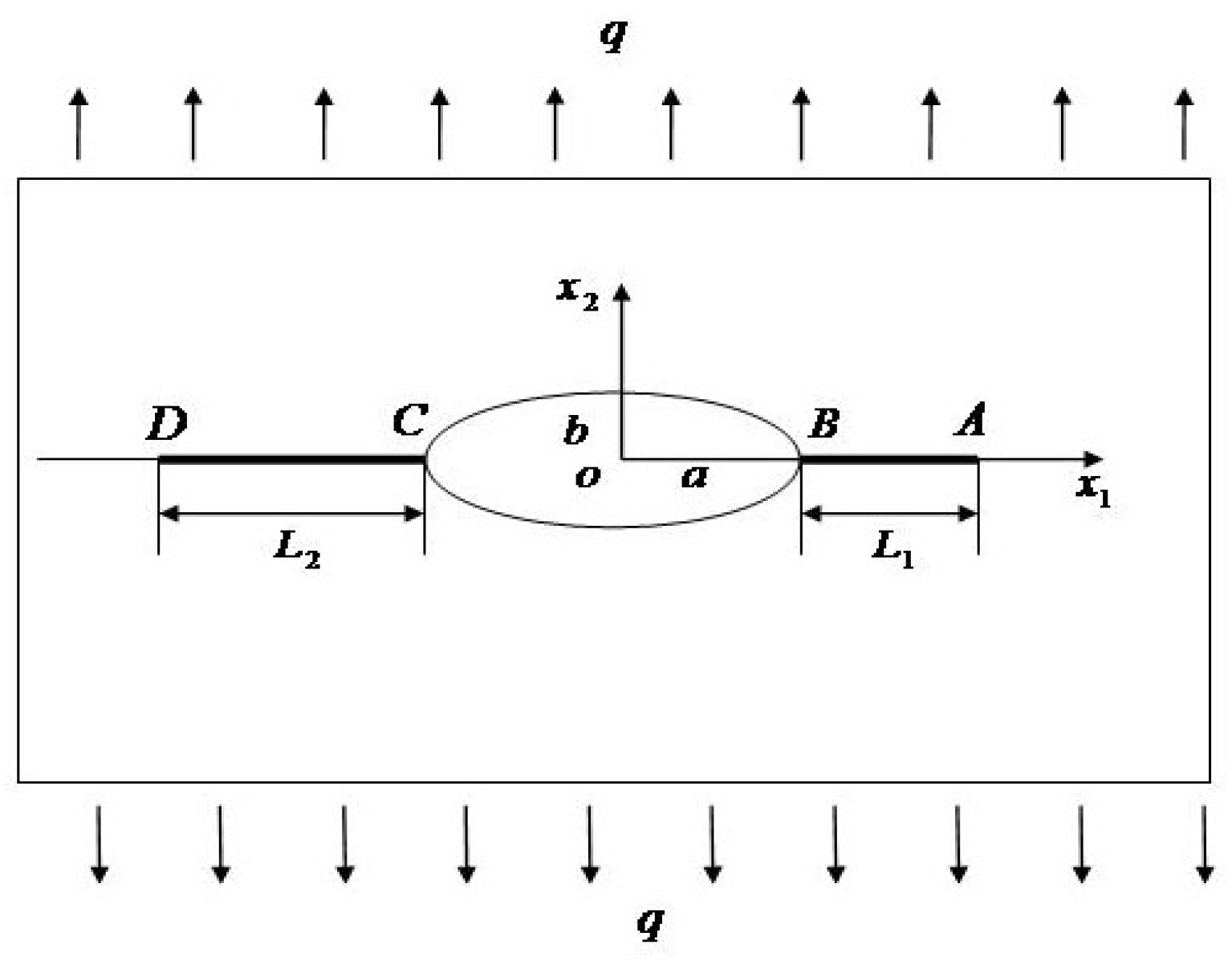
4. Mode-I Plane Elasticity Problem and Exact Solution

We considered the configuration as shown in Figure 1, that is, an elliptical hole with two asymmetrical collinear cracks.

In Figure 1, $a$ and $b$ denote the long semi-axis and the short semi-axis of the ellipse, respectively, and $L_1$ and $L_2$ denote the crack lengths of the two asymmetrical collinear at the edge of the elliptical hole. For two asymmetrical edge cracks emanating from an elliptical hole in two-dimensional decagonal QCs under remotely uniform tensile stress, the tensile stress is $q$.

4.1. Stress Functions

By introducing the conformal mapping function [29], stack-complicated calculation at the $z$-plane was avoided.

$$z=\omega (\zeta )=\frac{a+b}{2}\mu (\zeta )+\frac{a-b}{2}\frac{1}{\mu (\zeta )}$$

(24)

$$\mu (\zeta )=\frac{{\epsilon }_1{(1+\zeta )}^2+{\epsilon }_2{(1-\zeta )}^2}{4\zeta }+\frac{{\left[{({\epsilon }_1{(1+\zeta )}^2+{\epsilon }_2{(1-\zeta )}^2)}^2-16{\zeta }^2\right]}^{1/2}}{4\zeta }$$

(25)

$${\epsilon }_i=\frac{{(a+L_i)}^2+b^2+ab+(a+L_i)\sqrt{L_i^2+2a{L}_i+b^2}}{(a+b)(a+L_i+\sqrt{L_i^2+2a{L}_i+b^2})}$$

(26)

From Equation (24), one can obtain

$${\omega }^{\prime }(\zeta )=-\frac{(1-{\zeta }^2)({\epsilon }_1+{\epsilon }_2)}{4{\zeta }^2}\left\{\frac{b[{\epsilon }_1{(1+\zeta )}^2+{\epsilon }_2{(1-\zeta )}^2]}{\sqrt{{[{\epsilon }_1{(1+\zeta )}^2+{\epsilon }_2{(1-\zeta )}^2]}^2-16{\zeta }^2}}+a\right\}$$

(27)

$$\begin{array}{l}\overline{\omega (\zeta )}=R_0\left[\zeta \cdot \frac{{\epsilon }_1{(1+\zeta )}^2+{\epsilon }_2{(1-\zeta )}^2+\sqrt{{({\epsilon }_1{(1+\zeta )}^2+{\epsilon }_2{(1-\zeta )}^2)}^2-16{\zeta }^2}}{4}\right.\\ \hspace{1em}\hspace{1em}\hspace{1em}\left.+\frac{1}{\zeta }\cdot \frac{4m}{{\epsilon }_1{(1+\zeta )}^2+{\epsilon }_2{(1-\zeta )}^2+\sqrt{{({\epsilon }_1{(1+\zeta )}^2+{\epsilon }_2{(1-\zeta )}^2)}^2-16{\zeta }^2}}\right]\end{array}$$

(28)

where

$$R_0=\frac{a+b}{2},m=\frac{a-b}{a+b}$$

(29)

Under the loading condition as shown in Figure 1, it can be seen that $B=\frac{q}{4},B^{\prime }+i{C}^{\prime }=\frac{q}{2}$ and $T_x=T_y=X=Y=0$; thus, Equations (3)–(23) can be expressed as

$$f_0=-\frac{q}{2}\omega (\sigma )-\frac{q}{2}\overline{\omega (\sigma )}$$

(30)

Substituting Equation (30) into Equation (20), we can obtain

$${\phi }_{40}(\zeta )=\frac{1}{32c_1}\left[\frac{q}{4}\omega (\zeta )-\frac{q{R}_0(1+m)({\epsilon }_1+{\epsilon }_2)}{4}\cdot \zeta \right]$$

(31)

From Equations (30), (31), and (21), one can be obtained by means of the Cauchy integral formula

$${\phi }_{30}(\zeta )=\frac{1}{32c_1}\left\{\frac{q}{2}\omega (\zeta )+\frac{q{R}_0(1+m)({\epsilon }_1+{\epsilon }_2)}{4}\left[\frac{\overline{\omega (\zeta )}}{{\omega }^{\prime }(\zeta )}-\zeta \right]\right\}$$

(32)

Substituting Equations (31) and (32) into Equation (22) yields

$$\begin{array}{l}{\phi }_{20}(\zeta )=\frac{q{R}_0}{32c_1}\cdot \left\{-\frac{f^2}{g^2}\left[t+\frac{-32mhk+8m(8k^2-2lh)\zeta }{h^3}\right]\cdot \right.\\ \hspace{1em}\hspace{1em}\hspace{1em} \left[1+\frac{1}{g}\left(\frac{16mh-32km\zeta }{h^2}-\frac{h-2k\zeta }{{\zeta }^2}\right)-\frac{4}{g}(1+m)({\epsilon }_1+{\epsilon }_2)\right]\\ \hspace{1em}\hspace{1em}\hspace{1em} -\frac{fg}{2}\left[g-2(1+m)({\epsilon }_1+{\epsilon }_2)-\frac{16f}{g^2}(1+m)({\epsilon }_1+{\epsilon }_2)\cdot \right.\\ \hspace{1em}\hspace{1em}\hspace{1em} \left(\frac{-32mhk+64m{k}^2\zeta -161mh\zeta }{h^3}+t\right)\\ \hspace{1em}\hspace{1em}\hspace{1em} \left.\left.+\frac{2}{g}(1+m)({\epsilon }_1+{\epsilon }_2)\left(h+2k\zeta -\frac{16m}{h{\zeta }^2}-\frac{32km}{h^2\zeta }\right)\right]\right\}\end{array}$$

(33)

in which

$$f=\frac{4m}{\zeta h}+\frac{1}{4}\zeta h,\hspace{1em}g=\frac{2k}{\zeta }-\frac{32m\zeta k}{h^2}+\frac{16m}{h}-\frac{h}{{\zeta }^2},\hspace{1em}t=-\frac{2k}{{\zeta }^2}+\frac{1}{\zeta }+\frac{h}{{\zeta }^3}$$

(34)

$$\begin{array}{cc}\hfill k=& {\epsilon }_1(\zeta +1)+{\epsilon }_2(\zeta -1)+\frac{{\epsilon }_1^2(\zeta +1{)}^3+{\epsilon }_2^2(\zeta -1{)}^3+2{\epsilon }_1{\epsilon }_2\zeta ({\zeta }^2-1)-8\zeta }{\sqrt{{({\epsilon }_1(1+\zeta {)}^2+{\epsilon }_2(1-\zeta {)}^2)}^2-16{\zeta }^2}}\hfill \\ \hfill l=& {\epsilon }_1+{\epsilon }_2-\frac{2{[{\epsilon }_1^2(\zeta +1{)}^3+{\epsilon }_2^2(\zeta -1{)}^3+2{\epsilon }_1{\epsilon }_2\zeta ({\zeta }^2-1)]}^2-8\zeta }{{[{({\epsilon }_1(1+\zeta {)}^2+{\epsilon }_2(1-\zeta {)}^2)}^2-16{\zeta }^2]}^{3/2}}\hfill \\ & +\frac{3{\epsilon }_1^2(\zeta +1{)}^2+3{\epsilon }_2^2(\zeta -1{)}^2+2{\epsilon }_1{\epsilon }_2(3{\zeta }^2-1)-8}{\sqrt{{({\epsilon }_1(1+\zeta {)}^2+{\epsilon }_2(1-\zeta {)}^2)}^2-16{\zeta }^2}}\hfill \\ \hfill h=& {\epsilon }_1(\zeta +1{)}^2+{\epsilon }_2(\zeta -1{)}^2+\sqrt{{({\epsilon }_1(1+\zeta {)}^2+{\epsilon }_2(1-\zeta {)}^2)}^2-16{\zeta }^2}\hfill \end{array}$$

(35)

Using the expressions (31), (32), and (33), we can determine the stresses and displacements in the phonon field and the phason field in the $\zeta$-plane.

To change the geometric parameters of two asymmetrical edge cracks emanating from an elliptical hole, the present results can be degraded to the results of other configurations, such as two symmetrical edge cracks emanating from an elliptical hole, single cracks emanating from an elliptical hole, or two symmetrical edge cracks emanating from a circular hole, elliptical hole, cross crack, T-shape crack, and the classical Griffith crack. Due to limited space, only a few special defect configuration results are listed below.

(1)

Elliptical hole. When $L_1=L_2=0$, the two asymmetrical edge cracks emanating from an elliptical hole degenerate into an elliptical hole, which can be obtained by Equations (31), (32), and (33):

$${\phi }_{20}(\zeta )=\frac{q{R}_0}{2\times 32c_1}\frac{({\zeta }^2+m)[1+(1-2m){\zeta }^2+(2+2m^2+m^3){\zeta }^4-m{\zeta }^6]}{\zeta {(m{\zeta }^2-1)}^3}$$

(36)

$${\phi }_{30}(\zeta )=\frac{q{R}_0}{2\times 32c_1}\frac{[{\zeta }^4+{(1+m)}^2{\zeta }^2-1]}{\zeta (m{\zeta }^2-1)}$$

(37)

$${\phi }_{40}(\zeta )=\frac{q{R}_0}{4\times 32c_1}\left[\frac{1}{\zeta }-(2+m)\zeta \right]$$

(38)

which are identical to the results of the reference [34].

(2)

Cross crack. When $a=0$, the two asymmetrical edge cracks emanating from an elliptical hole degenerate into the asymmetrical cross crack, so we have

$$\begin{array}{l}{\phi }_{20}(\zeta )=\frac{qb}{64c_1}\cdot \{-\frac{f_1^2}{g_1^2}\left[t_1+\frac{32h_1{k}_1-(64k_1^2-16l_1{h}_1)\zeta }{h_1^3}\right]\cdot \\ \hspace{1em}\hspace{1em}\hspace{1em} \left.\left[1+\frac{1}{g_1}\left(\frac{-16h_1+32k_1\zeta }{h_1^2}-\frac{h_1-2k_1\zeta }{{\zeta }^2}\right)\right]-\frac{f_1{g}_1^2}{2}\right\}\end{array}$$

(39)

$${\phi }_{30}(\zeta )=\frac{1}{32c_1}\cdot \frac{qb}{4}\left[{\mu }_1(\zeta )+\frac{1}{{\mu }_1(\zeta )}\right]$$

(40)

$${\phi }_{40}(\zeta )=\frac{1}{32c_1}\cdot \frac{qb}{8}\left[{\mu }_1(\zeta )+\frac{1}{{\mu }_1(\zeta )}\right]$$

(41)

where

$$f_1=-\frac{4}{\zeta h_1}+\frac{1}{4}\zeta h_1,\hspace{1em}{g}_1=\frac{2k_1}{\zeta }+\frac{32\zeta k_1}{h_1^2}-\frac{16}{h_1}-\frac{h_1}{{\zeta }^2},\hspace{1em}{t}_1=-\frac{2k_1}{{\zeta }^2}+\frac{1}{\zeta }+\frac{h_1}{{\zeta }^3}$$

(42)

$$\begin{gathered} \begin{array}{l}{k}_1=\frac{\sqrt{L_1^2+b^2}}{b}(\zeta +1)+\frac{\sqrt{L_2^2+b^2}}{b}(\zeta -1)\\ \hspace{1em}\hspace{1em}+\frac{(L_1^2+b^2){(\zeta +1)}^3+(L_2^2+b^2){(\zeta -1)}^3+2\sqrt{(L_1^2+b^2)(L_2^2+b^2}\zeta ({\zeta }^2-1)-8\zeta }{\sqrt{{(b\sqrt{L_1^2+b^2}{(1+\zeta )}^2+b\sqrt{L_2^2+b^2}{(1-\zeta )}^2)}^2-16b^4{\zeta }^2}}\end{array} \\ \begin{array}{l}{l}_1=\frac{\sqrt{L_1^2+b^2}+\sqrt{L_2^2+b^2}}{2b}-\\ \hspace{1em}\hspace{1em}\frac{2b{[(L_1^2+b^2){(\zeta +1)}^3+(L_2^2+b^2){(\zeta -1)}^3+2\sqrt{(L_1^2+b^2)(L_2^2+b^2)}\zeta ({\zeta }^2-1)]}^2-8b\zeta }{{[{(\sqrt{L_1^2+b^2}{(1+\zeta )}^2+\sqrt{L_2^2+b^2}{(1-\zeta )}^2)}^2-16b^2{\zeta }^2]}^{3/2}}\end{array} \\ +\frac{3(L_1^2+b^2){(\zeta +1)}^2+3(L_2^2+b^2){(\zeta -1)}^2+2\sqrt{(L_1^2+b^2)(L_2^2+b^2)}(3{\zeta }^2-1)-8b^2}{\sqrt{{(b\sqrt{L_1^2+b^2}{(1+\zeta )}^2+b\sqrt{L_2^2+b^2}{(1-\zeta )}^2)}^2-16b^4{\zeta }^2}} \\ {h}_1=\frac{\sqrt{L_1^2+b^2}}{b}{(\zeta +1)}^2+\frac{\sqrt{L_2^2+b^2}}{b}{(\zeta -1)}^2+\sqrt{{\left[\frac{\sqrt{L_1^2+b^2}}{b}{(1+\zeta )}^2+\frac{\sqrt{L_2^2+b^2}}{b}{(1-\zeta )}^2\right]}^2-16{\zeta }^2} \end{gathered}$$

(43)

$$\begin{array}{l}{\mu }_1(\zeta )=\frac{\sqrt{L_1^2+b^2}{(1+\zeta )}^2+\sqrt{L_2^2+b^2}{(1-\zeta )}^2}{4b\zeta }\\ \hspace{1em}\hspace{1em}\hspace{1em}+\frac{{\left[{(\sqrt{L_1^2+b^2}{(1+\zeta )}^2+\sqrt{L_2^2+b^2}{(1-\zeta )}^2)}^2-16b^2{\zeta }^2\right]}^{1/2}}{4b\zeta }\end{array}$$

(44)

(3)

T-shape crack. When $a=0,L_2=0$, the two asymmetrical edge cracks emanating from an elliptical hole degenerate into a T-shaped crack, so we have

$$\begin{array}{l}{\phi }_{20}(\zeta )=\frac{qb}{64c_1}\cdot \left\{-\frac{f_2^2}{g_2^2}\left[t_2+\frac{32h_2{k}_2-(64k_2^2-16l_2{h}_2)\zeta }{h_2^3}\right]\cdot \right.\\ \hspace{1em}\hspace{1em}\hspace{1em} \left. \left[1+\frac{1}{g_2}\left(\frac{-16h_2+32k_2\zeta }{h_2^2}-\frac{h_2-2k_2\zeta }{{\zeta }^2}\right)\right]-\frac{f_2{g}_2^2}{2}\right\}\end{array}$$

(45)

$${\phi }_{30}(\zeta )=\frac{1}{32c_1}\cdot \frac{qb}{4}\left[{\mu }_2(\zeta )+\frac{1}{{\mu }_2(\zeta )}\right]$$

(46)

$${\phi }_{40}(\zeta )=\frac{1}{32c_1}\cdot \frac{qb}{8}\left[{\mu }_2(\zeta )+\frac{1}{{\mu }_2(\zeta )}\right]$$

(47)

where

$$f_2=-\frac{4}{\zeta h_2}+\frac{1}{4}\zeta h_2,\hspace{1em}{g}_2=\frac{2k_2}{\zeta }+\frac{32\zeta k_2}{h_2^2}-\frac{16}{h_2}-\frac{h_2}{{\zeta }^2},\hspace{1em}{t}_2=-\frac{2k_2}{{\zeta }^2}+\frac{1}{\zeta }+\frac{h_2}{{\zeta }^3}$$

(48)

$$\begin{gathered} \begin{array}{l}{k}_2=\frac{\sqrt{L_1^2+b^2}}{b}(\zeta +1)+(\zeta -1)\\ \hspace{1em}\hspace{1em}+\frac{(L_1^2+b^2){(\zeta +1)}^3+b^2{(\zeta -1)}^3+2\sqrt{L_1^2+b^2}b\zeta ({\zeta }^2-1)-8\zeta }{\sqrt{{(b\sqrt{L_1^2+b^2}{(1+\zeta )}^2+b^2{(1-\zeta )}^2)}^2-16b^4{\zeta }^2}}\end{array} \\ \begin{array}{l}{l}_2=\frac{\sqrt{L_1^2+b^2}+b}{2b}-\frac{2b{[(L_1^2+b^2){(\zeta +1)}^3+b^2{(\zeta -1)}^3+2b\sqrt{L_1^2+b^2}\zeta ({\zeta }^2-1)]}^2-8b\zeta }{{[{(\sqrt{L_1^2+b^2}{(1+\zeta )}^2+b{(1-\zeta )}^2)}^2-16b^2{\zeta }^2]}^{3/2}}\\ \hspace{1em} +\frac{3(L_1^2+b^2){(\zeta +1)}^2+3b^2{(\zeta -1)}^2+2b\sqrt{L_1^2+b^2}(3{\zeta }^2-1)-8b^2}{\sqrt{{(b\sqrt{L_1^2+b^2}{(1+\zeta )}^2+b\sqrt{L_2^2+b^2}{(1-\zeta )}^2)}^2-16b^4{\zeta }^2}}\end{array} \\ {h}_2=\frac{\sqrt{L_1^2+b^2}}{b}{(\zeta +1)}^2+{(\zeta -1)}^2+\sqrt{{\left(\frac{\sqrt{L_1^2+b^2}}{b}{(1+\zeta )}^2+{(1-\zeta )}^2\right)}^2-16{\zeta }^2} \end{gathered}$$

(49)

$${\mu }_2(\zeta )=\frac{\sqrt{L_1^2+b^2}{(1+\zeta )}^2+b{(1-\zeta )}^2}{4b\zeta }+\frac{{\left[{(\sqrt{L_1^2+b^2}{(1+\zeta )}^2+b{(1-\zeta )}^2)}^2-16b^2{\zeta }^2\right]}^{1/2}}{4b\zeta }$$

(50)

(4)

Griffith crack. When $b=0,L_1=L_2=0$, the two asymmetrical edge cracks emanating from an elliptical hole degenerate into a Griffith crack, so we have

$$\begin{array}{l}{\phi }_{20}(\zeta )=\frac{q{R}_0}{32c_1}\cdot \left\{-{\left(\frac{1}{\zeta }+\zeta \right)}^2\frac{1}{g_0^2}\left[\frac{4-{\zeta }^2}{{\zeta }^3}-2\zeta +\left({\zeta }^2-\frac{-3{\zeta }^6-11{\zeta }^4-{\zeta }^2+\zeta -1}{{(1-{\zeta }^2)}^3}\right)\zeta \right]\cdot \right.\\ \hspace{1em}\hspace{1em}\hspace{1em} \left[1+\frac{1}{g_0}(4-2{\zeta }^2)\left(1-\frac{1}{{\zeta }^2}\right)-\frac{16}{g}\right]-\left(\frac{1}{\zeta }+\zeta \right)\frac{g_0}{2}\left[g_0-8\right.-\frac{2}{g_0^2}\left(\frac{1}{\zeta }+\zeta \right)\cdot \\ \hspace{1em}\hspace{1em}\hspace{1em} \left(-64\zeta +64{\zeta }^3-322\zeta +\frac{2(4-{\zeta }^2)}{{\zeta }^3}\right)\left. \left.+\frac{16}{g_0}\left(1+{\zeta }^2-\frac{2}{{\zeta }^2}\right)\right]\right\}\end{array}$$

(51)

$${\phi }_{30}(\zeta )=\frac{1}{32c_1}\cdot \frac{q{R}_0}{2}\left\{\left(\frac{1}{\zeta }+m\zeta \right)-\frac{(1+m)\zeta \cdot [1+m+(1-m){\zeta }^2]}{1-m{\zeta }^2}\right\}$$

(52)

$${\phi }_{40}(\zeta )=\frac{1}{32c_1}\cdot \frac{q{R}_0}{4}\left[\frac{1}{\zeta }-(2+m)\zeta \right]$$

(53)

$$g_0=2(1-{\zeta }^2)\left(1-\frac{2}{{\zeta }^2}\right)$$

(54)

which are identical to the results of Ref. [35].

It should be shown that the stress distribution is independent of the material constant, which is consistent with classical elastic theory. The stresses and displacements in the two-dimensional decagonal QCs may now be evaluated from Equations (6) and (7). The expressions are omitted because of their verboseness. In order to obtain the stress function on the plane, it is necessary to substitute the inversion of $\zeta ={\omega }^{-1}(z)$ back into Equations (31)–(33).

4.2. Stress Intensity Factors

The stress intensity factor at the crack tip is a very important physical quantity in the plane elasticity problem. For the mixed problem of Mode-I and Mode-II, the stress intensity factor can be expressed as follows [25]:

$$K=K_{{\rm I}}^{\parallel }-i{K}_{\prod }^{\parallel }=32c_1\left[2\sqrt{\pi }\underset{\zeta \to 1}{\lim }\frac{{\phi }_4^{\prime }\left(\zeta \right)}{\sqrt{{\omega }^{″}\left(\zeta \right)}}\right]$$

(55)

Inserting Equations (27) and (31) into Equation (55), one can obtain

$$\left\{\begin{array}{l}{K}_{{\rm I}}^{\parallel }{}^{\left(c,0\right)}=q{R}_0\sqrt{\frac{2\pi \left({\epsilon }_1+{\epsilon }_2\right)\sqrt{{\epsilon }_1^2-1}}{b{\epsilon }_1+a\sqrt{{\epsilon }_1^2-1}}}\\ K_{\prod }^{\parallel }{}^{\left(c,0\right)}=0\end{array}\right.$$

(56)

where $c$ is the coordinate at point A of the crack tip.

Equation (56) shows the Mode-I stress intensity factor at the crack tip of the elliptic hole with two asymmetrical edge cracks in two-dimensional decagonal QCs. This result is further discussed, and the details are as follows:

(1)

When $b\to 0,L_1\to c-a,L_2\to c-a$, Equation (56) becomes

$$K_{{\rm I}}^{\parallel }=q\sqrt{\pi c}$$

(57)

which is the case of a Griffith crack. Clearly, the stress intensity factor is the same as that of shown in Ref. [24].

(2)

When $a\to 0,L_2\to 0,L_2\to 0,$ Equation (56) becomes

$$K_{{\rm I}}^{\parallel }=q\sqrt{\frac{\pi b\left({\epsilon }_{11}+1\right)\sqrt{{\epsilon }_{11}^2-1}}{2{\epsilon }_{11}}}$$

(58)

where ${\epsilon }_{11}=\frac{L_1^2+b^2+L_1\sqrt{L_1^2+b^2}}{b\left(L_1+\sqrt{L_1^2+b^2}\right)}$.

which is the stress intensity factor of a T-shape crack tip.

(3)

When $a\to 0,$ Equation (56) becomes

$$K_{{\rm I}}^{\parallel }=q\sqrt{\frac{\pi b\left({\epsilon }_{11}+{\epsilon }_{21}\right)\sqrt{{\epsilon }_{11}^2-1}}{2{\epsilon }_{11}}}$$

(59)

where ${\epsilon }_{11}=\frac{L_1^2+b^2+L_1\sqrt{L_1^2+b^2}}{b\left(L_1+\sqrt{L_1^2+b^2}\right)},\hspace{1em}{\epsilon }_{21}=\frac{L_2^2+b^2+L_2\sqrt{L_2^2+b^2}}{b\left(L_2+\sqrt{L_2^2+b^2}\right)}$

which is the stress intensity factor of a cross crack tip.

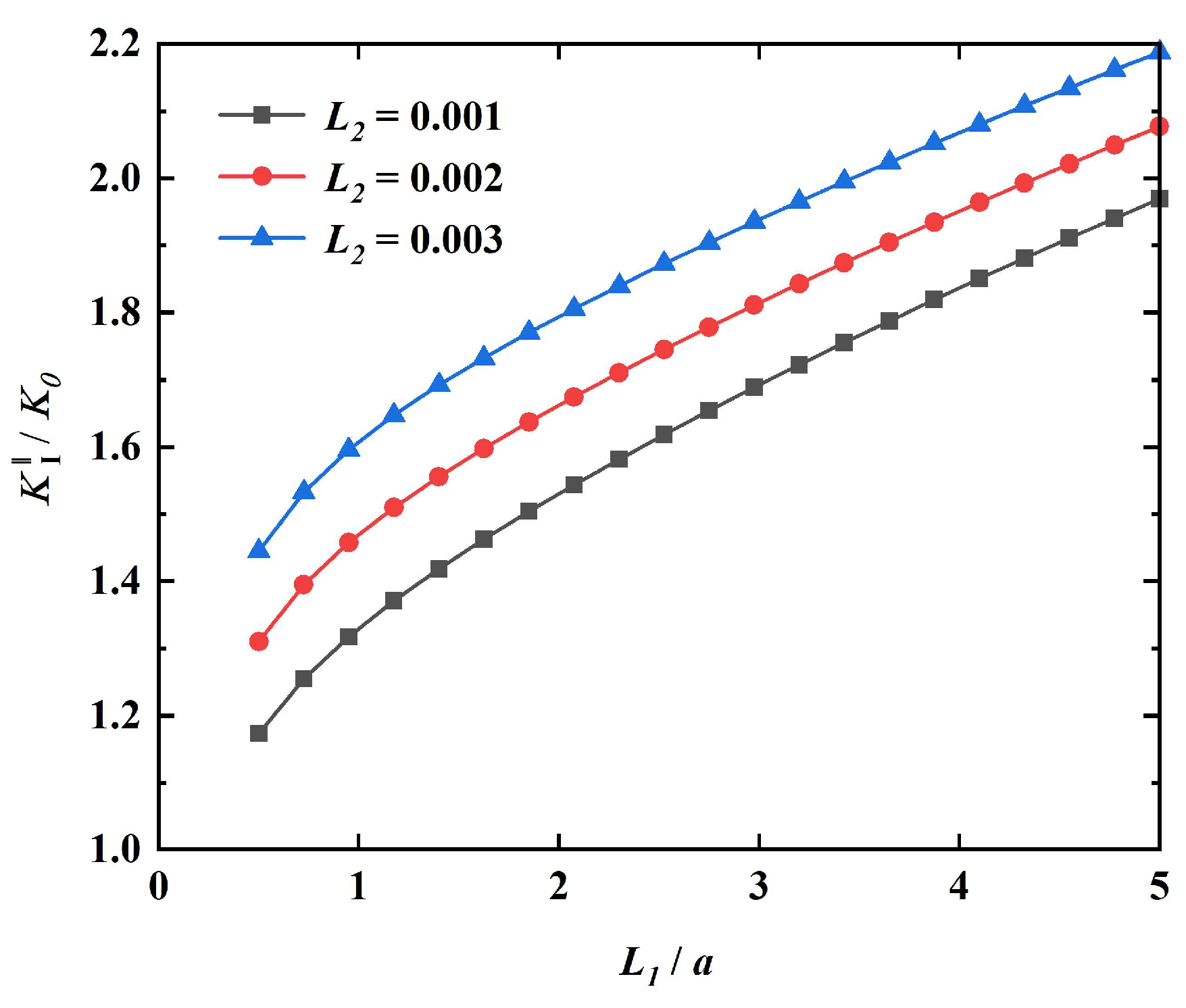
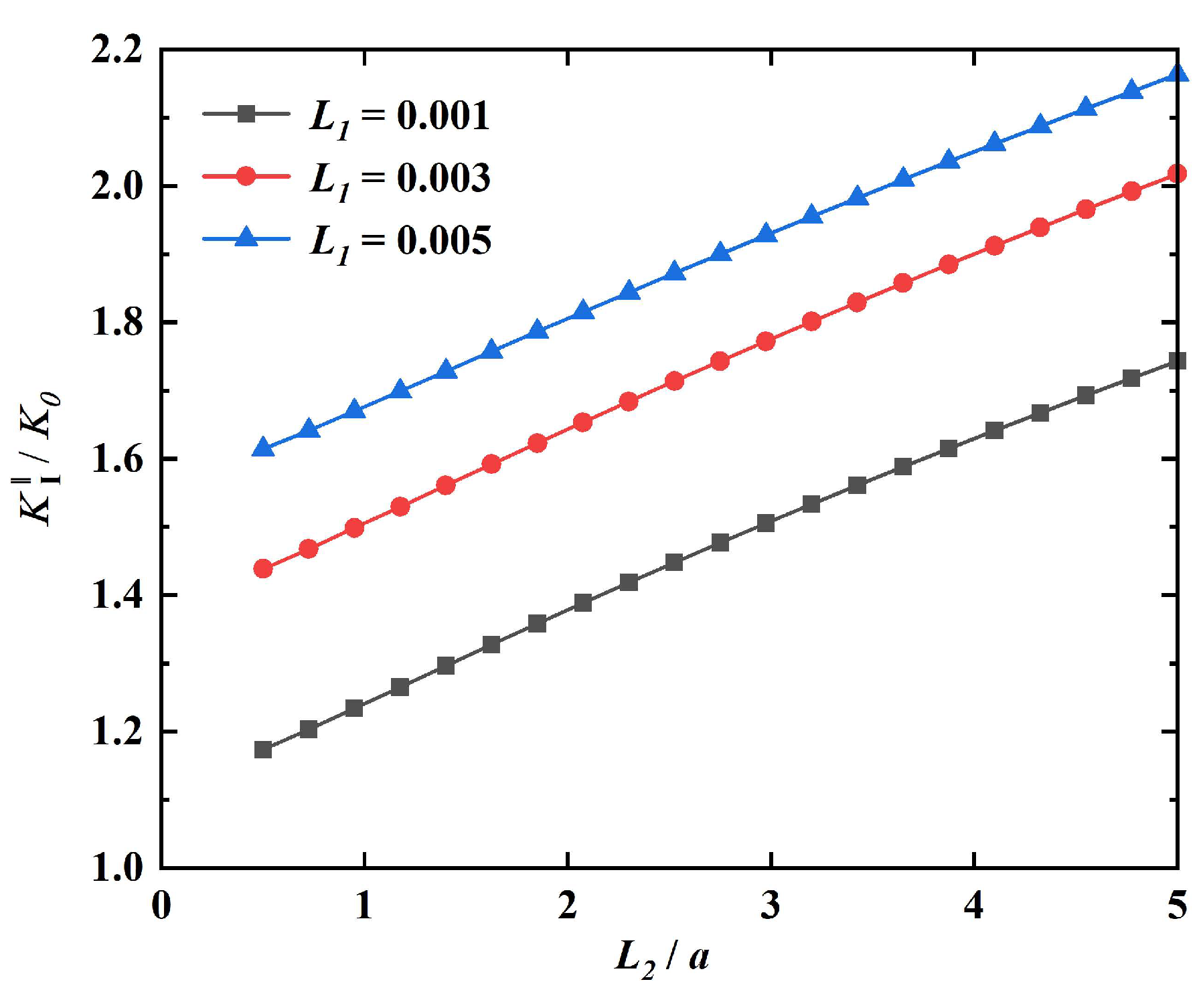
5. Numerical Results and Discussions

In order to illustrate the effect of geometric parameters on the stress intensity factor in this section, the following three figures are given for illustration. Taking $K_0=q\sqrt{\pi a}$, the effect on the dimensionless stress intensity factor as the geometry of the defect varies, as illustrated by Figure 2, Figure 3 and Figure 4.

The dimensions of the defect in Figure 2 are chosen as follows: $a=0.002m, L_2=0.003m$. The trend of the dimensionless stress intensity factor $K_{{\rm I}}^{\parallel }/K_0$ with geometric parameters $L_1/a$ is given in the cases of $b=0.001m,b=0.002m$, and $b=0.004m$, respectively. As can be seen from Figure 1, the stress intensity factor of the crack tip on the right side of the defective configuration increases with the increase in the crack length at the edge of the elliptical hole. The larger the length of the crack at the right side of the elliptical hole, the greater the value of the stress intensity factor at the crack tip, and the easier the crack propagation is when the sizes of the major and minor axes of the elliptical hole remain unchanged. When the major axis of the elliptical hole remains unchanged, and the greater the minor axis b of the elliptical hole is, the greater the change rate of the stress intensity factor relative to the crack length is.

The dimensions of the defect taken in Figure 2 are chosen as follows: $a=0.002m, b=0.001m$. The trend of the dimensionless stress intensity factor of $K_{{\rm I}}^{\parallel }/K_0$ with the geometric parameter $L_1/a$ is given in the cases of $L_2=0.001m,L_2=0.003m$, and $L_2=0.005m$, respectively. From Figure 3, it can be seen that the stress intensity factor at the tip of the crack on the right side of the defective configuration increases with the increase in the crack length at the elliptical hole edge. When the major axis and minor axis of the elliptical hole remain unchanged, the larger the crack on the left side of the elliptical hole edge, the larger the stress intensity factor of the crack tip on the right side of the elliptical hole, that is to say, the crack expands more easily.

The dimensions of the defect taken in Figure 4 are chosen as follows: $a=0.002m, b=0.001m$, and the trend of the dimensionless stress intensity factor of $K_{{\rm I}}^{\parallel }/K_0$ with the geometric parameter $L_2/a$ is given at $L_1=0.001m,L_1=0.003m$, and $L_1=0.005m$, respectively. As can be seen from Figure 2, the stress intensity factor at the crack tip on the right side of the defect configuration increases with the increase in the crack length at the edge of the elliptical hole on the left side of the defect.

6. Conclusions

In this paper, by means of a complex function method and conformal mapping technique, we solve the elastic problem of the Mode-I plane problem with two asymmetrical edge cracks emanating from an elliptical hole in two-dimensional decagonal quasicrystals. The analytical solution of the stress intensity factor at the crack tip is also obtained. Some simple and classical analytical results can be obtained from complex defects such as elliptical holes with double-asymmetrical long cracks. These results provide accurate analytical results for the application of the elliptical hole with two asymmetrical edge cracks, and have certain reference value for the study of two-dimensional quasicrystals fracture.