Novel Functional Materials of Hydrogen Storage B₂₀N₂₄: A First-Principles Calculation

Abstract

In this paper, a N-rich B–N polymorph named as B₂₀N₂₄ is proposed through first-principles calculations. The stability of the B₂₀N₂₄ polymorph at ambient conditions is confirmed using the phonon dispersion spectra and the Born stability criteria. Electronic properties calculations show that B₂₀N₂₄ exhibits a semiconducting feature, with a 0.87 eV direct band gap derived from HSE06 functions, which is much lower than many other B–N polymorphs. Specifically, owing to its cage-like framework, B₂₀N₂₄ may be used in hydrogen storage at a capacity of ~6.8 wt.%. The B₂₀N₂₄ polymorph enriches the B–N system theoretically, and this polymorph is promising for use in electronic devices and hydrogen storage.

1. Introduction

Boron nitride (BN) compounds have attracted much interest because of their intriguing behaviors. As for the experimental aspect, given that novel BN polymorphs with unique properties are synthesized, the potential applications of BN polymorphs in electronic devices and industries have increased. For example, the successfully synthesized nano-twinned cBN enhances the physical properties of cBN [1], such as a hardness value exceeding 100 GPa and an oxidization temperature achieving 1294 °C. Additionally, novel BN polymorphs with various morphological features, such as BN cluster [2], BN nanotube [3], BN nanosheets and nano-meshes [4,5], have been synthesized successfully, thereby enriching the applications of BN materials. Moreover, the ultralight three-dimensional (3D) BN foam [6], which has high permittivity and thermal stability, is a new ultralight material that can be used in water cleaning.

Some BN polymorphs synthesized in experiments have a B/N ratio of about 1.0, and this phenomenon is predominantly caused by defects in materials [7,8,9]. Theoretical studies have shown that many BN clusters with different sizes, such as B₁₂N₁₂ and B₃₆N₃₆ fullerene-like cluster, can be constructed [10,11,12]. Previous studies showed that the stoichiometric BN compound with purely B–N bonds in crystal structures is the generally stable framework and that nonstoichiometric frameworks may lead to energetic, unfavorable B–B and N–N dimers. However, nonstoichiometric BN structures have also been constructed in previous studies. Simone et al. [13] reported the first-principles calculations of the role of stoichiometry in the structure and energy of BN clusters. Results showed that B₃₂N₃₆ and B₆₀N₆₄ are more stable than their stoichiometric counterparts in a N-rich environment, even when dimers exist in the framework. Simultaneously, B–B and N–N bonds are unavoidable in these B-rich or N-rich BN polymorphs, and the reality is unclear as to the stability of N-rich B–N compounds which are constructed with purely B–N bonds.

Recently, many novel BN allotropes have been proposed [14,15], given the electronegative difference between the two elements. Wang et al. [14] reported a novel phase of boron nitride m-BN, in which, when utilizing the GGA (generalized gradient approximation) and LDA (local density approximation) functionals, the lattice constant of c-BN with the GGA functional is 0.166% higher than that of the experimental value, while the results of the LDA functional are 1.409% smaller than that of the experimental value. The results indicated that the m-BN is mechanically stable and dynamically stable, which makes for an indirect and wide band-gap semiconductor material, and the Fermi level and the band gap are not sensitive to the effect of pressure. In addition, m-BN is a potential superhard material with a hardness of 56.1 GPa. Most of the polymorphs composited with B and N have a stoichiometric B:N ratio of 1:1 [16,17,18,19,20,21,22,23,24]. For example, the tetragonal bct-BN [25], orthorhombic phase Z-BN [16], and P-BN [20], have been predicted, and both of them are constructed with 4- and 8-atom rings per unit cell. In terms of electronic properties, all BN allotropes mentioned above are semiconductors. Recently, several 3D metallic BN allotropes have been predicted by Dai et al. [18], Zhang et al. [21], etc. These metallic BN allotropes, which are different from conventional BN ceramics, can lead to new applications in electronic devices. In considering several N-rich B–N polymorphs, [26,27,28]. Li et al. [26] discovered that C222₁-B₃N₅ was a metastable material that can be recovered under ambient conditions, making it a promising high-energy-density material with an energy density of 3.44 kJ/g. Additionally, stress–strain calculations estimated a Vicker’s hardness of approximately 44 GPa. Structure searching also revealed a new sodalite-like clathrate BN structure that was metastable under ambient conditions. He et al. [27] reported that t-B₃N₄, with structural units composed of sp³ c-BN blocks and sp² N–N bonds, is metastable at ambient pressure but becomes energetically more stable than layered B₃N₄, h-BN, or N₂ under pressure. The electronic structure analysis showed that t-B₃N₄ was planar conductive with conduction interrupted by insulated B atomic layers along the c-axis. This unique 2D metallicity in 3D t-B₃N₄ has potential applications in electronic devices. The calculated Vickers hardness of t-B₃N₄ exceeded 40 GPa, indicating its superhard nature. Moreover, due to the strong N–N bonds along the c-axis, the axial ultra-incompressibility of t-B₃N₄ was even greater than that of c-BN and diamond. This type of boron nitride exhibited the combined electrical and mechanical properties of 2D metallicity in a 3D framework, in addition to superhardness and ultra-incompressibility. These findings open a new view of B–N functional materials.

In recent years, N-rich B–N polymorphs, such as superhard phases (C222₁-B₃N₅, B₂N₃) and metallic t-B₃N₄, have been predicted as novel functional materials, behaving as potential high-energy-density materials, due to the high energy of N–N dimers in their framework. In this work, B₂₀N₂₄ is constructed with fully B–N bonds, indicating that it is not a potential high-energy-density material. Moreover, hydrogen as a renewable energy has drawn people’s attention for many years, but one limited problem in its widespread application is the storage medium. In terms of advantages in gravimetric density, light element compounds, such as carbon materials, including C₆₀ fullerene and carbon nanotube, are good candidates for hydrogen storage. In recent years, extensive studies showed that porous BN polymorphs and BN cages exhibit promising applications in hydrogen storage [29,30]. For example, studies showed that BN nanotubes can store hydrogen at as much as 2.6 wt.% [29], and the B₃₆N₃₆ cage can reach to 4 wt.% [30]. Considering the cage-like structural features and low density of B₂₀N₂₄, it might be a candidate for hydrogen storage.

As previous studies have shown, structural prediction of a system can be executed via various methods, such as structural search programs, simulated annealing [10,11], basin hopping [14,15], metadynamics [16,17], evolutionary metadynamics [18,19], and so on. Additionally, given the structural similarities among different systems, more and more novel structures are predicted by changing the atoms of the revealed structures which have been synthesized or proposed in some other system or study. Carbon and BN are isoelectronic in structure, with many phases of the two systems sharing the same configurations. Some examples include: diamond and cubic BN, hexagonal diamond and wurtzite BN, carbon nanotube and BN nanotube, graphene and BN nanoribbons, and so on. Moreover, the Cco-C8 structure of carbon allotrope has been predicted to be a candidate for cold-compressed graphite. Crystals sharing the same framework within different systems not only exist in carbon and BN compounds, but also can be found in some other classes. Several crystal structures, such as rock-salt-type BN, have been proposed as a high-pressure phase of a BN compound, one which shares the framework of rock-salt crystal [31,32]. Therefore, z-BN with the same framework as Cco-C8 is proposed as a novel phase for a BN compound. It is therefore viable to change a carbon structure into B and N atoms alternatively during the BN structure-prediction process.

In this paper, considering the structural similarities between carbon and BN allotropes, the structure-searching processes are carried out in two steps. Firstly, carbon structure research processing is conducted. Secondly, we selected some carbon structures with cage-like configurations, replacing C atoms with B and N atoms alternatively, in order to avoid the B–B and N–N dimers in the framework. As a result, a three-dimensional cage-like B₂₀N₂₄ polymorph as a candidate for hydrogen storage is predicted.

2. Calculation Methods

We implemented the structural searching of carbon allotropes at ambient conditions through the CALYPSO code [33]. This method can predict novel structures, and facilitates the composition of known chemical compounds. The underlying structural relaxation was performed using the density functional theory within the local density approximation (LDA) as implemented in the Vienna Ab Initio Simulation Package (VASP) [34]. Subsequent structural optimizations and properties calculations were performed using ultrasoft pseudopotentials with a plane wave cutoff energy of 280 eV in the Cambridge Serial Total Energy Package (CASTEP) [35]. The electron–electron exchange interaction was described using the exchange-correlation function of Ceperley and Alder [36], as parametrized by Perdew and Zunger (CA-PZ) [37] in the LDA. To obtain a more accurate determination of electronic properties, band structure calculations were conducted using the hybrid Heyd–Scuseria–Ernzerhof function (HSE06) [38]. The k-point spacing of 2π × 0.04 Å was generated by the k-point grid within the Monkhorst–Pack scheme [39]. The elastic properties are predicted with CASTEP code. In this process, a unit cell was adopted. The elastic constants C_ij were derived based on the strain–stress relationship (Hooke’s law), which is within the range of elastic deformation; a finite strain was applied to the optimized structure, and the applied strain and the resulting stress were obtained [30]. The maximum applied strain amplitude was 0.3%, and the number of steps for each strain was set to 9 for this calculation. To verify the accuracy of our calculations, we calculated the lattice parameters and bond length for diamond and cubic BN. The results show that the lattice parameters of diamond and cubic BN are a = 3.528 Å and a = 3.580 Å, and the bond lengths of the C–C and B–N bonds are 1.528 Å and 1.550 Å, respectively, which are close to the results derived from experiments (3.567 Å and 1.545 Å for diamond, 3.615 Å and 1.565 Å for cubic BN). Therefore, we supposed that the calculations in this paper are feasible.

3. Results and Discussion

After structure-searching progresses, several carbon allotropes, such as diamond, graphite and CCo-C₈ [40] were obtained. These results confirmed the feasibility of our structural search methodology. Firstly, carbon allotropes with 8~30 atoms in per unit cell were systematically explored based on the first-principles calculations. Secondly, according to the geometries of carbon structures, we have selected some of the special configurations. During this process, these structures with odd rings are thrown away to avoid forming high energy B–B/N–N bonds in the atom’s process of subsequent change. Therefore, some cage-like carbon structures composed of even-membered rings are retained. Finally, carbon atoms are replaced with B and N atoms alternatively to avoid B–B/N–N bonds in the search for stable nonstoichiometric B–N polymorphs. Notably, according to the low energy and structure features, six cubic carbon allotropes, which had 7, 28, 44, 52, and 60 atoms in per unit cell, respectively, are selected among thousands of obtained novel carbon structures. The structural and geometric properties of these selected allotropes are investigated. The results show a mechanical and dynamical stable structure among these obtained structures, which is named as B₂₀N₂₄.

Figure 1 shows the optimized novel crystal structure and structural features of B₂₀N₂₄. At ambient pressure, three nonequivalent atoms assemble in a cubic lattice (space group I-43m) with a = b = c = 7.01 Å lattice parameter (Figure 1a). The Wyckoff atom positions of two nonequivalent B atoms, B1 and B2, are occupied 2d (0, 1/2, 1/4), 8c (0.3, 0.7, 0.3), and one N1 atom is occupied 24g (0.126, 0.625, 0.874), respectively. Figure 1a shows the primitive cell of the B₂₀N₂₄ polymorph. B1-N1-B2 atoms composed the hexagonal rings which can be viewed as puckered hBN layers, and these layers are connected to form a three-dimensional (3D) periodicity structure via sp³-hybrid B2 atoms. As shown in Figure 1b, the unit cell of the B₂₀N₂₄ polymorph can be viewed as a cage-like structure, one which the hBN-liked layers connected with B–N single bonds to form a cage with an open boundary. The opened cage-like structure connects with the gap’s overlapping and forms a 3D cage-like network with different cage-size in it (Figure 1c). The B1 atom at the 8c site is a trigonal coordinate with a trigonal N atom added to form B–N bond with length of d₁ = 1.43 Å, which is close to that of the sp²-hybrid B–N bonds in hBN. The B2 atom at the 12d site is a tetragonal coordinate with a trigonal N atom with a B–N distance of d₁ = 1.52 Å; when the two combine cages together and construct the 3D N-rich BN allotropes, it is comparable to the sp³-hybrid B–N bonds in cBN structure.

In order to clarify the energetic stability of the B₂₀N₂₄ polymorph, we calculated the formation energy via alpha-B and alpha-N₂ as precursors; the results of the convex hull of B–N compounds are plotted in Figure 2. As shown in Figure 2, the formation energies of some other B–N polymorphs are determined per-atom for comparison. As previous studies show, the layer-like h-B₃N₅ and h-B₂N₃ structures are stable at ambient pressure, and the bulked C₂₂₂₁-B₃N₅ [26] and t-B₂N₃ [28] are metastable, which can derive from the stable phase under high pressure conditions. Additionally, the bulked t-B₃N₄ [27] is at a metastable phase at ambient pressure. One can see that the formation energy of B₂₀N₂₄ is beyond the line at the N-rich part, so we have supposed that the B₂₀N₂₄ polymorph is at a metastable phase at ambient pressure.

The mechanical stability of B₂₀N₂₄ is validated by elastic constants calculations. The calculated elastic constants are C₁₁ = 427.0 GPa, C₄₄ = 240.4 GPa, and C₁₂ = 184.2 GPa, respectively. The structure of B₂₀N₂₄ possesses cubic lattice and the known Boron stability criteria for cubic lattice [41], i.e., C₁₁ > 0, C₄₄ > 0, C₁₁ > |C₁₂|, (C₁₁ + 2C₁₂) > 0. Obviously, these elastic constants satisfy the Boron stability criteria, thereby confirming that B₂₀N₂₄ is mechanically stable. Phonon dispersion curves were used to confirm the dynamic stability of B₂₀N₂₄, which is characterized by a lack of imaginary frequencies across the whole spectrum; the results are plotted in Figure 3. No imaginary frequency is observed across the whole Brillion Zone, indicating that B₂₀N₂₄ is dynamically stable. Therefore, we suppose that the B₂₀N₂₄ polymorph is at a metastable phase at ambient conditions.

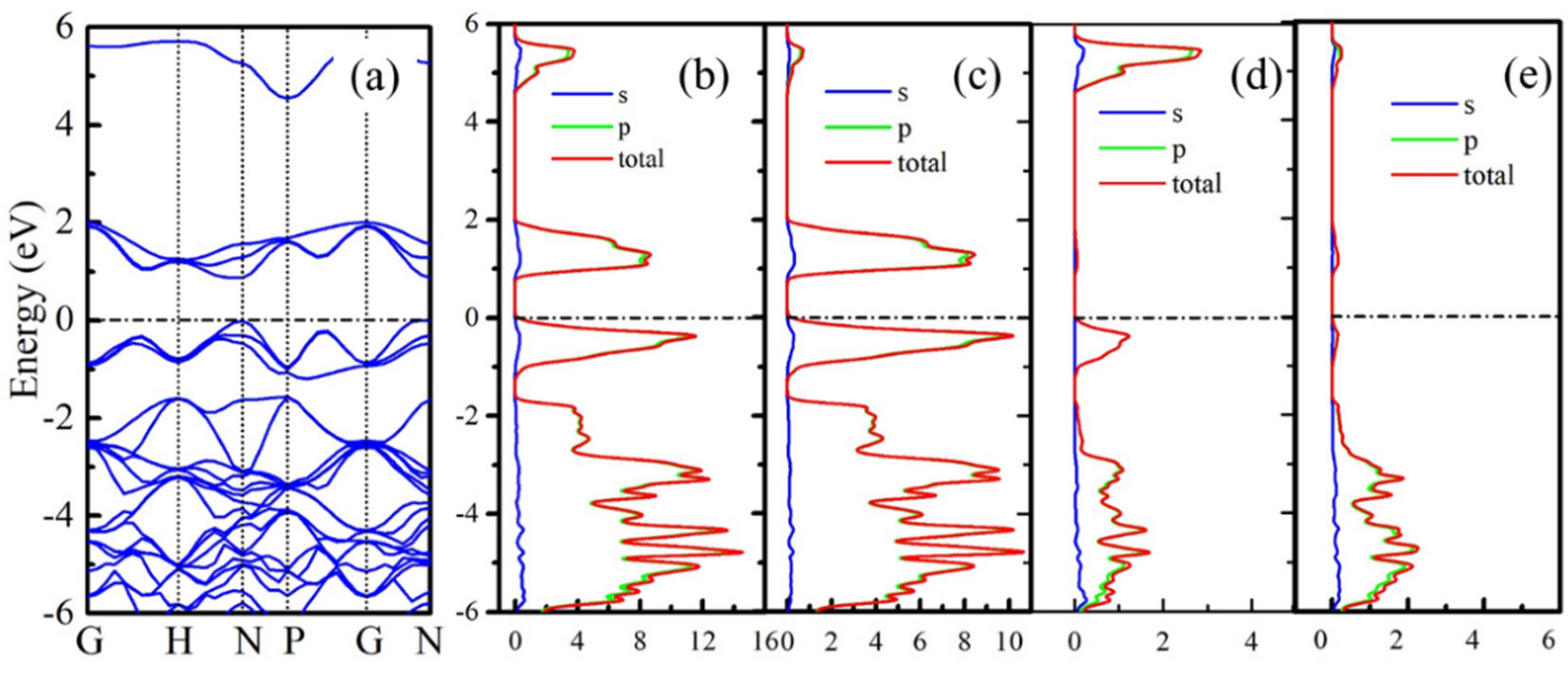
The electronic properties of B₂₀N₂₄ are studied by calculating the band structures and corresponding partial density of state (PDOS); the results are plotted in Figure 4. As shown in Figure 4a, the B₂₀N₂₄ structure exhibits a 0.87 eV direct band gap. In order to study the origination of valance band minima (VBM) and conductive band maximum (CBM), we further calculated the PDOS of three nonequivalent atoms PDOS in the framework, and the results are shown in Figure 4b–e. In Figure 4b, the electronic states at the Fermi level originate from the 2p orbits, and Figure 4c–e shows that the CBM and most of the VBM of B₂₀N₂₄ are contributed from the 2p state of N1 atoms. The contributions of B1 and B2 atoms to the CBM and VBM can be neglected.

In the following section, the endohedral H₂ molecule storage in B₂₀N₂₄ has been studied systematically. For a single H₂ molecule, we set it as occupying the center of the B₂₀N₂₄ cage and ignore other simultaneous sites. In other conditions, ones with more than one H₂ molecule, H₂ molecules are laid into the B₂₀N₂₄ cage randomly and kept isolated from each other, keeping the distance between two H₂ molecules larger than 0.74 Å (the H–H bond length in a H₂ molecule). The calculated formation energies with different n values are plotted in Figure 5. The formation energy of the nH₂@B₂₀N₂₄ complex is defined as: E_f = E_(BN+nH2) − E_BN − nE_H2, where E_(BN+nH2) is the total energy of nH₂@B₂₀N₂₄ complex, E_BN and E_H2 are the total energy of B₂₀N₂₄ and H₂ molecules, respectively, and n stands for the number of H₂ molecules set in the B₂₀N₂₄ polymorph. Figure 6 shows the atomic configurations of the nH₂@B₂₀N₂₄ complex. At n = 1, the H₂ molecule is set at the center of the framework (Figure 6a). Figure 6b shows the H₂@B₂₀N₂₄ complex after full geometrical optimization; the formation energy is −0.28 eV/atom. The H₂ molecule is isolated in the B₂₀N₂₄ cage, B-H and N-H bonds are not presented in this complex, and the H₂ molecule has a stretched H-H bond length of 0.777 Å. The volume of the complex (348.8 ų) is larger than that of B₂₀N₂₄ (347.5 ų), which means that the H₂ molecule brings out a structural deformation. As we know, a negative formation energy means an exothermic reaction and energetic-favorable status, indicating that the nH₂@B₂₀N₂₄ complex is stable relative to decomposition into a B–N compound and H₂ molecules. Therefore, we supposed that it was possible to form H₂@B₂₀N₂₄ complex at ambient conditions with a suitable precursor and method. As H₂ molecules increase, the distance between H₂ molecules becomes shorter and shorter, resulting in repulsive interactions between H₂ molecules; the attractive interactions between H₂ molecules and B/N atoms increase correspondingly. This induced a change in the bonding conditions of the complex after the full relaxation of the complex.

During the geometric optimization process, the H₂ molecules in the B₂₀N₂₄ cage move away from their initial position where we have set them initially, leading to some of the H₂ molecules remaining molecular and some others not. Giving the dangling bonds in the configuration, some H₂ molecules dissociate to bind with N/B atoms and form N-H/B-H bonds (Figure 6c). Interestingly, during this process, H atoms bind with N atoms more than with B atoms; this might be caused by fact that the N atom has higher electronegativity difference than does the B atom. The sp³ rehybridization of the formation of N-H/B-H bonds minimizes the total energy of the complex, and as the number of H₂ molecules increases, the number of dissociated H₂ molecules is decreased. Thus, the formation energy decreases from n = 1 to n = 10, and has a minimum value at n = 10, illustrating that the 10H₂@B₂₀N₂₄ complex is the most stable state of the nH₂@B₂₀N₂₄ complex. After that, as the H₂ molecule increases, at n = 11–16, the total energy of complex increases and tends to become positive. We supposed that this is because, with the increase of the number of hydrogen molecules in this BN structure, the framework of nH₂@B₂₀N₂₄ complex acquires more and more deformation. In this, B–N bonds are expanded, thereby inducing the high energy of B–N chemical bonds; also, the repulsion between H atoms is increased as the distance of H atoms grows closer, in order to attain the equilibrium state for the complex. Therefore, the energy levels of the nH₂@B₂₀N₂₄ complexes are raised. For nH₂@B₂₀N₂₄ complexes with n = 17, 18, and 19, the formation energies are positive, indicating that the storage is an endoergic reaction. When n = 20, several B–N bonds, such as the bond between the B–N pair (marked with red circles in Figure 6d), are stretched to ~1.75 Å, showing that B–N bonds are destroyed, while the H₂ molecules remain in the cage. However, the number of n increases to 21, and the framework of the nH₂@B₂₀N₂₄ complex is broken, resulting in a number of escaped H₂ molecules. Therefore, the maximum H₂ molecule storage capacity of H₂@B₂₀N₂₄ is 19, which corresponds to a gravimetric proportion of 6.8 wt.%.

As we have mentioned above, owing to the high chemical stability of the B–N compounds, this type is a good candidate for hydrogen storage. And, owing to the cage-like configuration of B₂₀N₂₄ structure, its storage ability is excellent. As we know, B–N materials are synthesized compounds. These materials are widely used in industries; most of the B–N compounds are semiconductors with wide band gap, and thus, they are also used in electronics. In recent years, more and more B–N materials have been predicted with the help of computational materials science. The studies of the novel structure of this class not only widen the crystal structure information relevant to it, but can also reveal more possible physical properties within the theoretical space. For one thing, in terms of structural configurations, the results in this work provide a useful method for structural prediction, not only in B–N compounds, but also in many other classes. For another, we provide a new way to design functional material. For example, the cage-like structure can be a candidate in hydrogen storage, and a fully sp³-hybridzed carbon or BN structure may be a good candidate among superhard materials.

Notably, we should make clear that the first-principles calculations are based on ambient conditions, in which the results are derived under 0 K and 0 GPa. Therefore, the hydrogen storage ability of B₂₀N₂₄ structure in this study is determined at 0 K. Considering the vibrations of atoms, the periodic boundary condition and some other conditions during the calculations at 0 K and 300 K, we supposed that the hydrogen storage capacity of B₂₀N₂₄ may not be as high as 6.8 wt.%. The hydrogen storage capacity of these B–N compounds at room temperature or at any other temperature, can be derived via molecular dynamics. Normally, it may be lower than the result at 0 K. Theoretically, determining the actual capacity of B₂₀N₂₄ at 300 K would require more calculations to reveal. In this work, the B₂₀N₂₄ structure is proposed as a novel compound of the B–N system, and can be viewed as a candidate for hydrogen storage, given its highly chemical inertness and cage-like structure.

4. Conclusions

In this paper, a global structural searching of carbon allotropes has been performed, and some novel allotropes with cage-like structures are selected as templates to construct their B–N counterparts by replacing atoms with B and N atoms alternatively. As a result, B₂₀N₂₄ is here proposed as a thermodynamically metastable nonstoichiometric N-rich B–N polymorph at ambient pressure. The mechanical and dynamic B₂₀N₂₄ has stabilities confirmed by the Born criteria and phonon spectra, respectively. B₂₀N₂₄ displays semiconducting features, with a 0.85 eV direct band gap. On the basis of its structural features, B₂₀N₂₄ can be seen as a candidate for hydrogen storage. Results show that 19 H₂ molecules, corresponding to 6.8 wt.%, can be stored in B₂₀N₂₄. B₂₀N₂₄ enriches the structures of B–N compounds, and its unique properties render it a promising functional material for electronic and hydrogen storage applications.