Two Conformational Polymorphs of a Bioactive Pyrazolo[3,4-d]pyrimidine
Abstract
1. Introduction
2. Materials and Methods
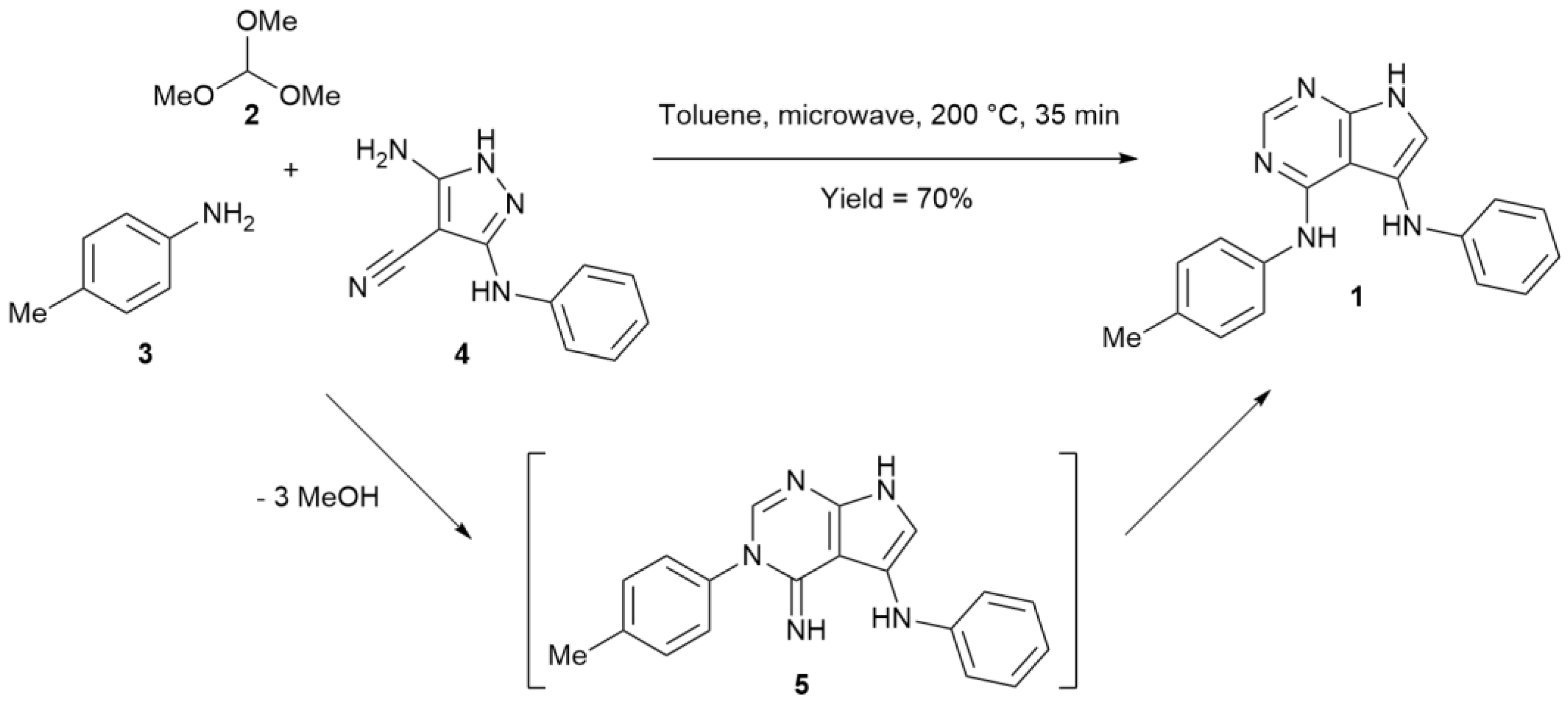
2.1. Synthesis and Crystallisation
2.2. Physiochemical Characterisation
2.3. X-ray Crystallography
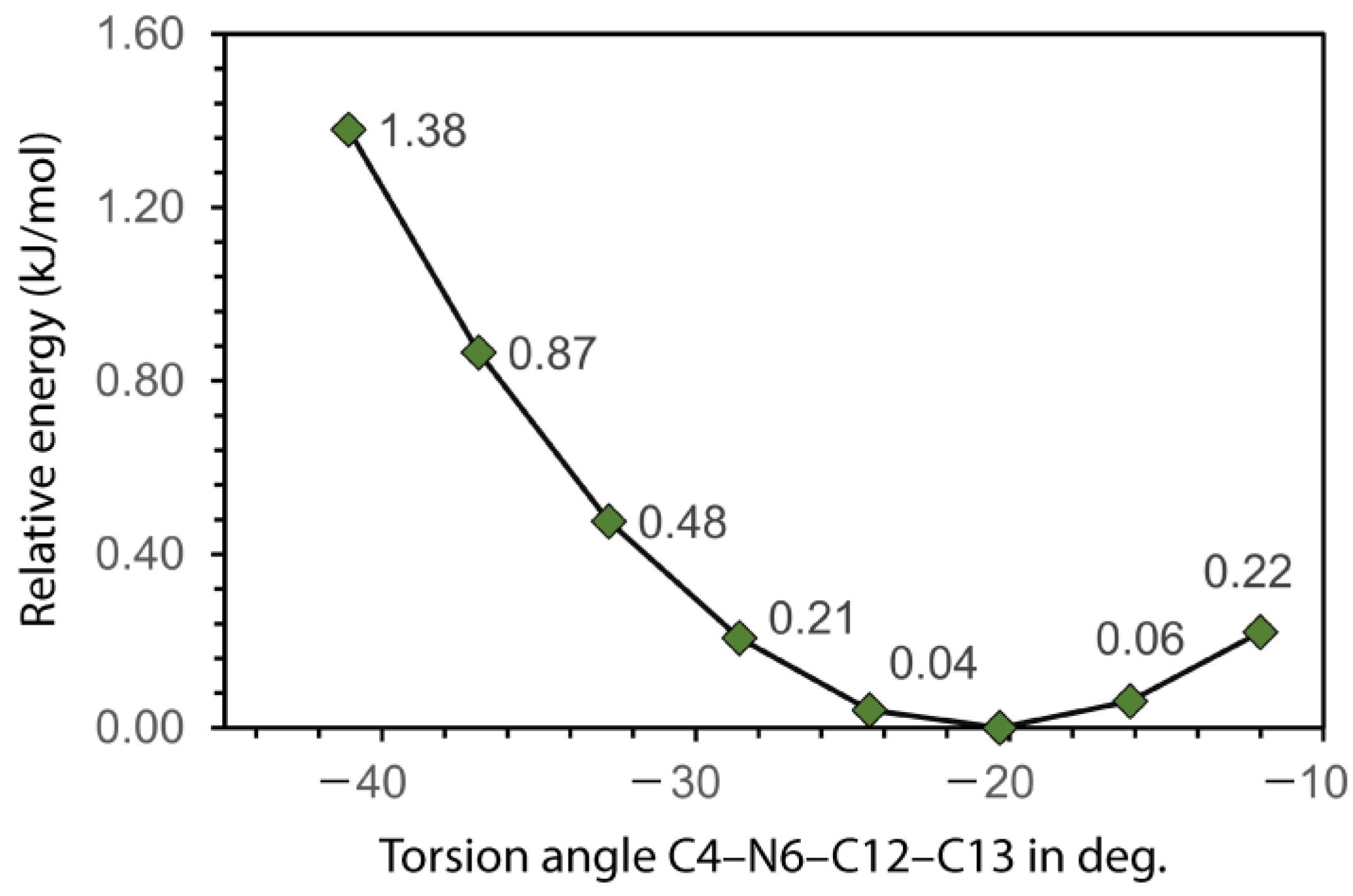
2.4. Computational Studies
3. Results and Discussion
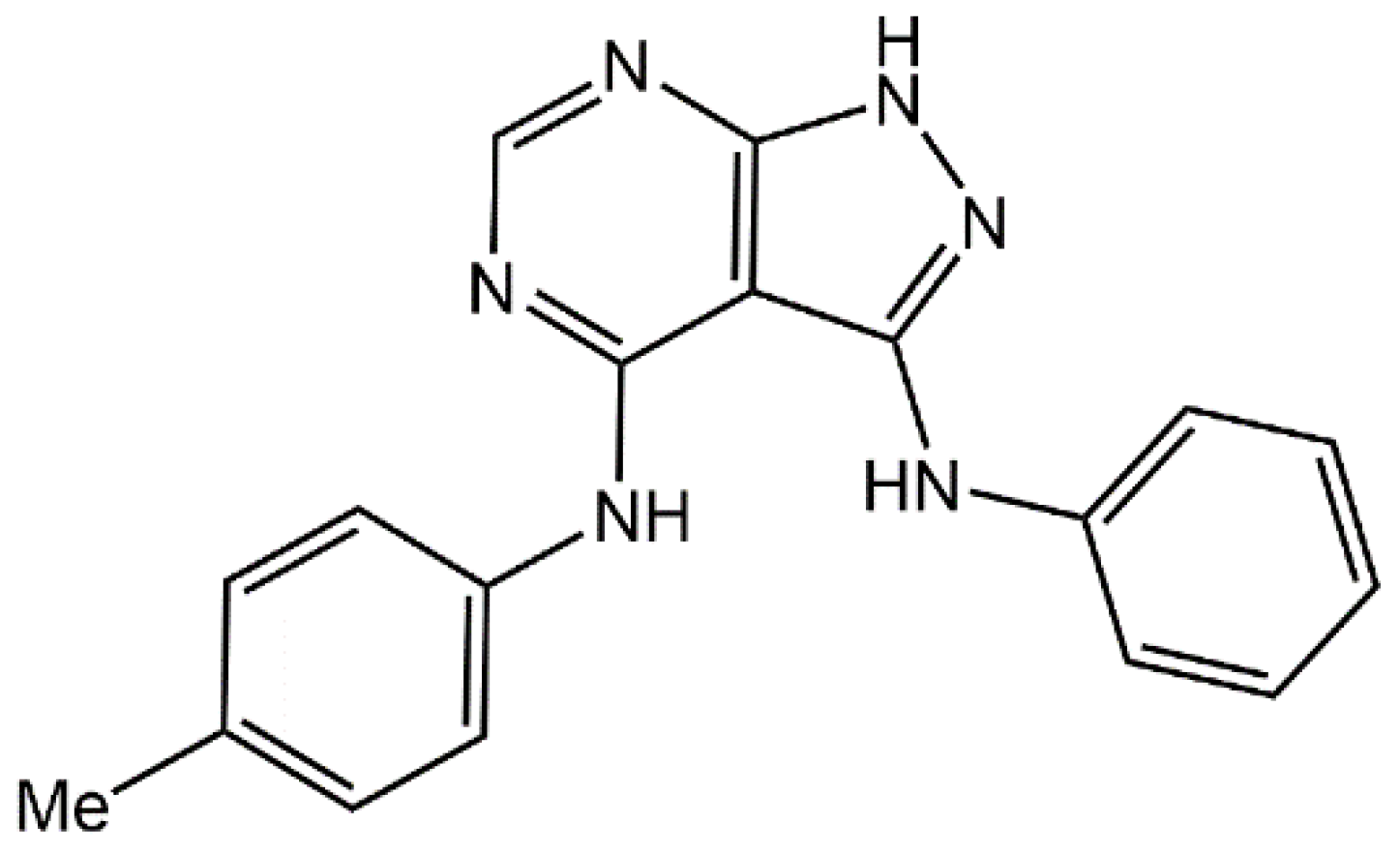
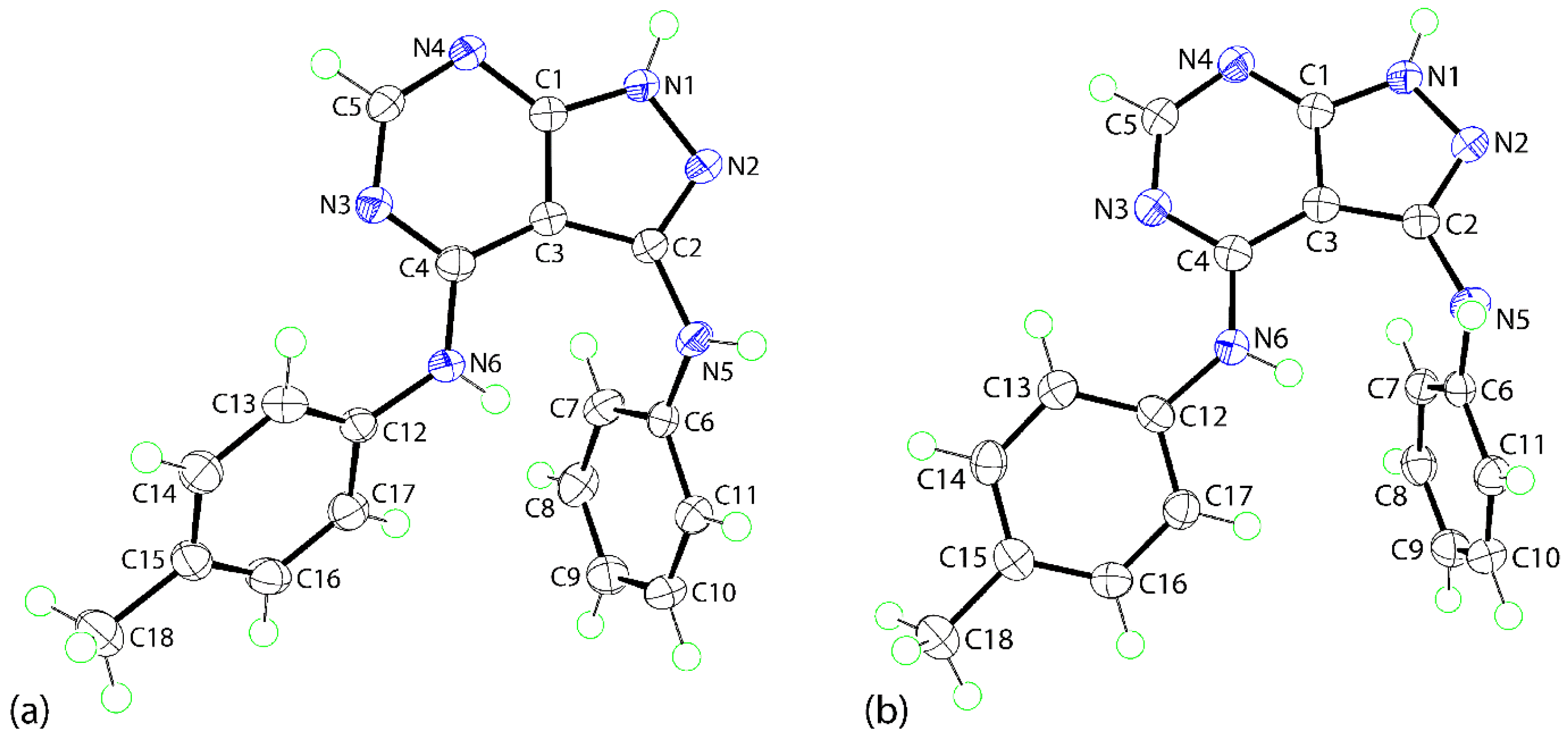
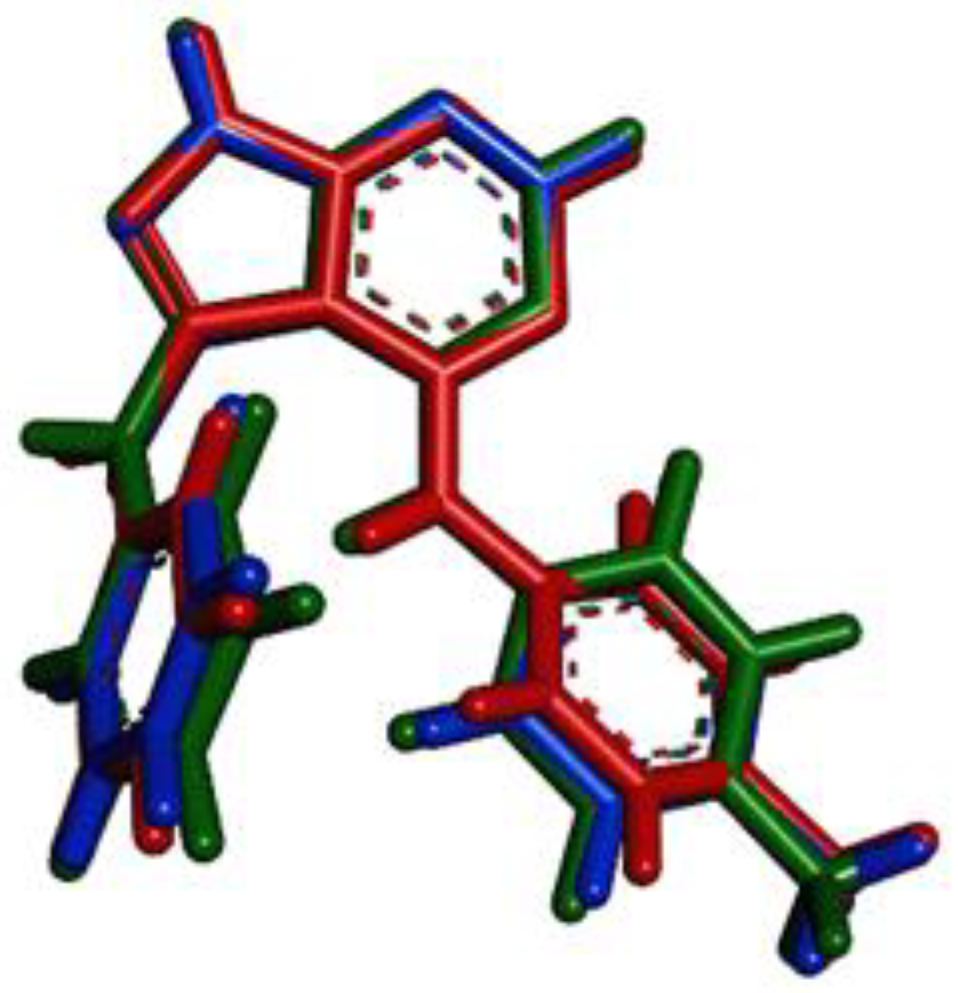
3.1. Molecular Structures
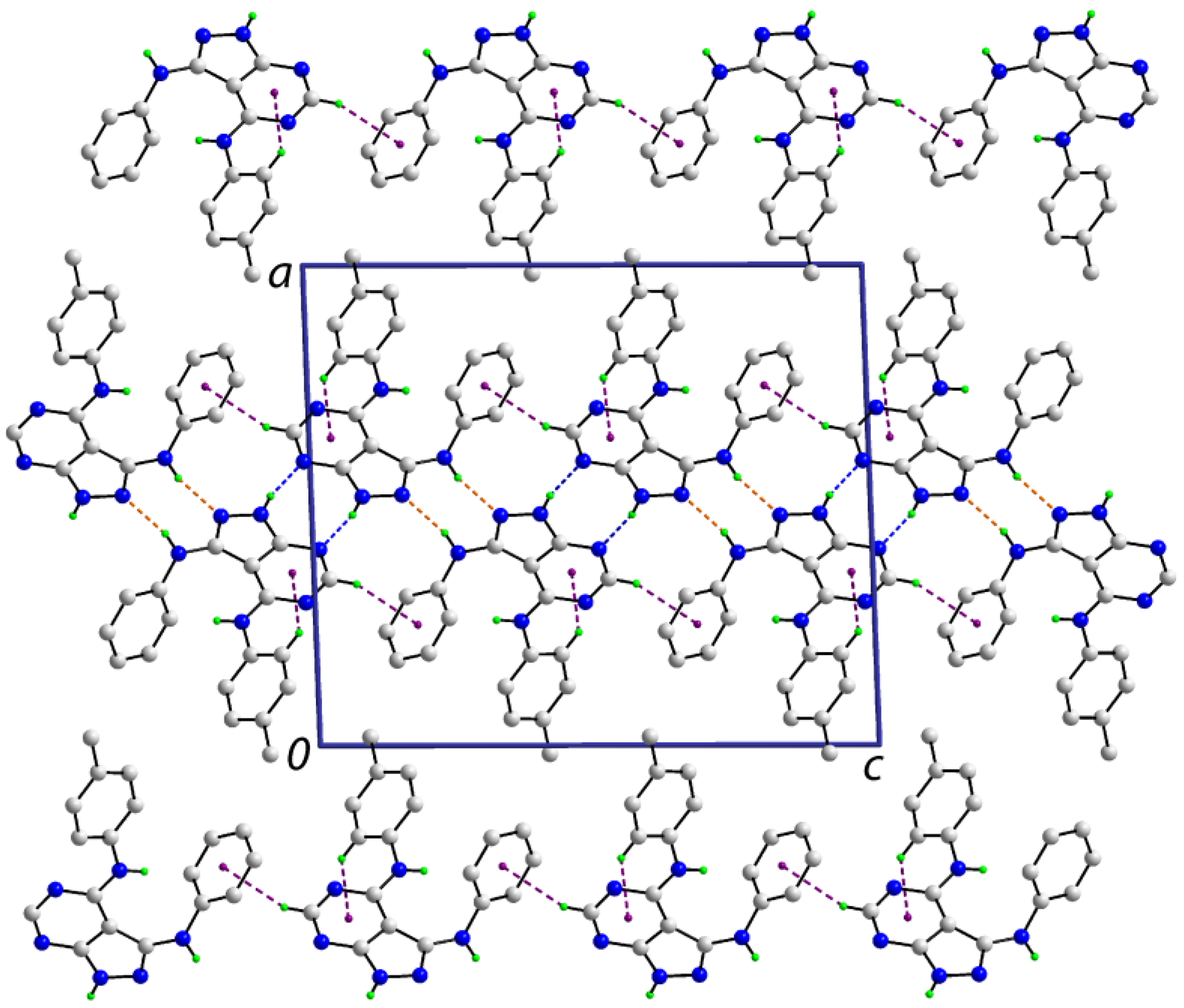
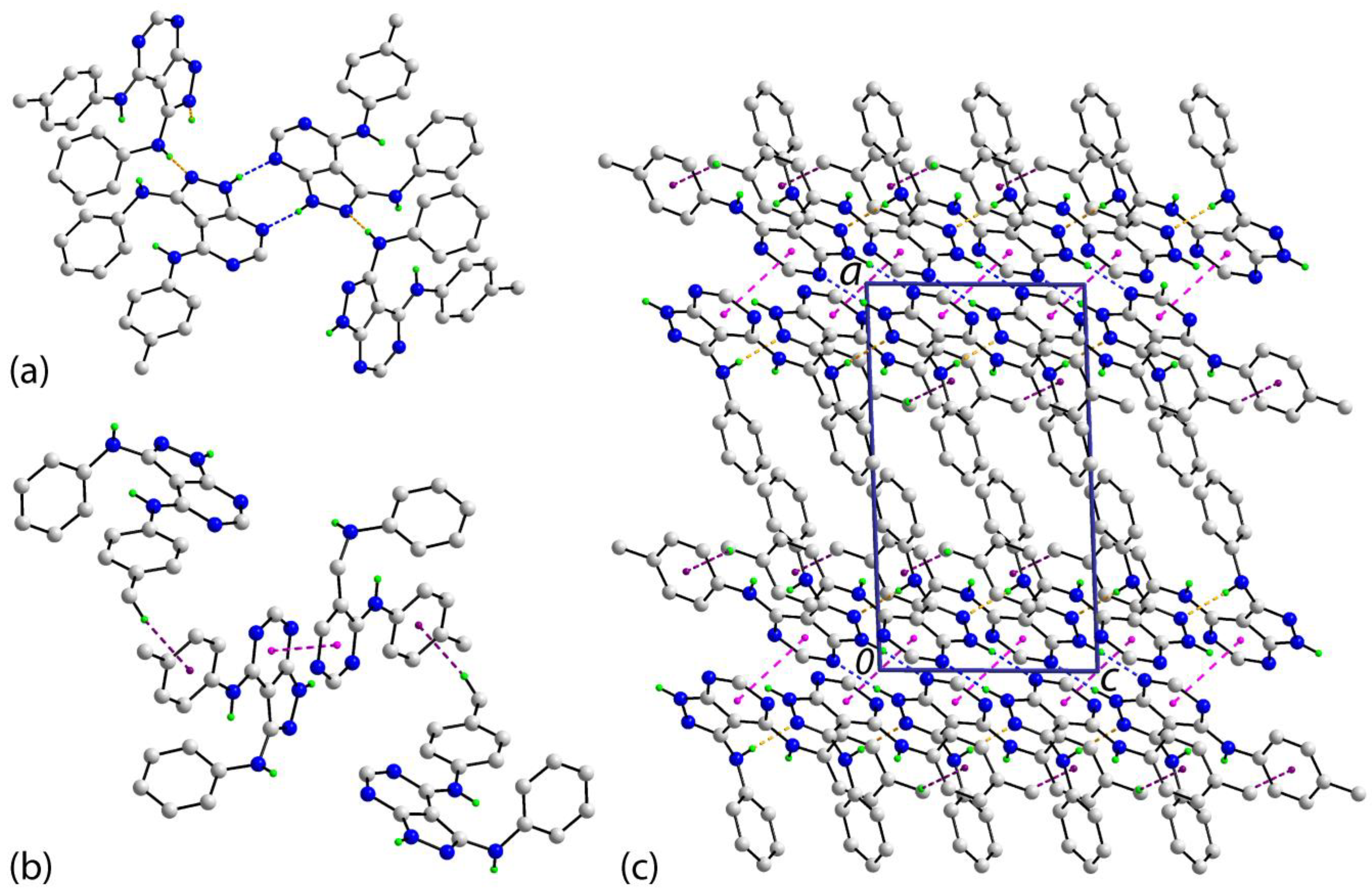
3.2. Molecular Packing
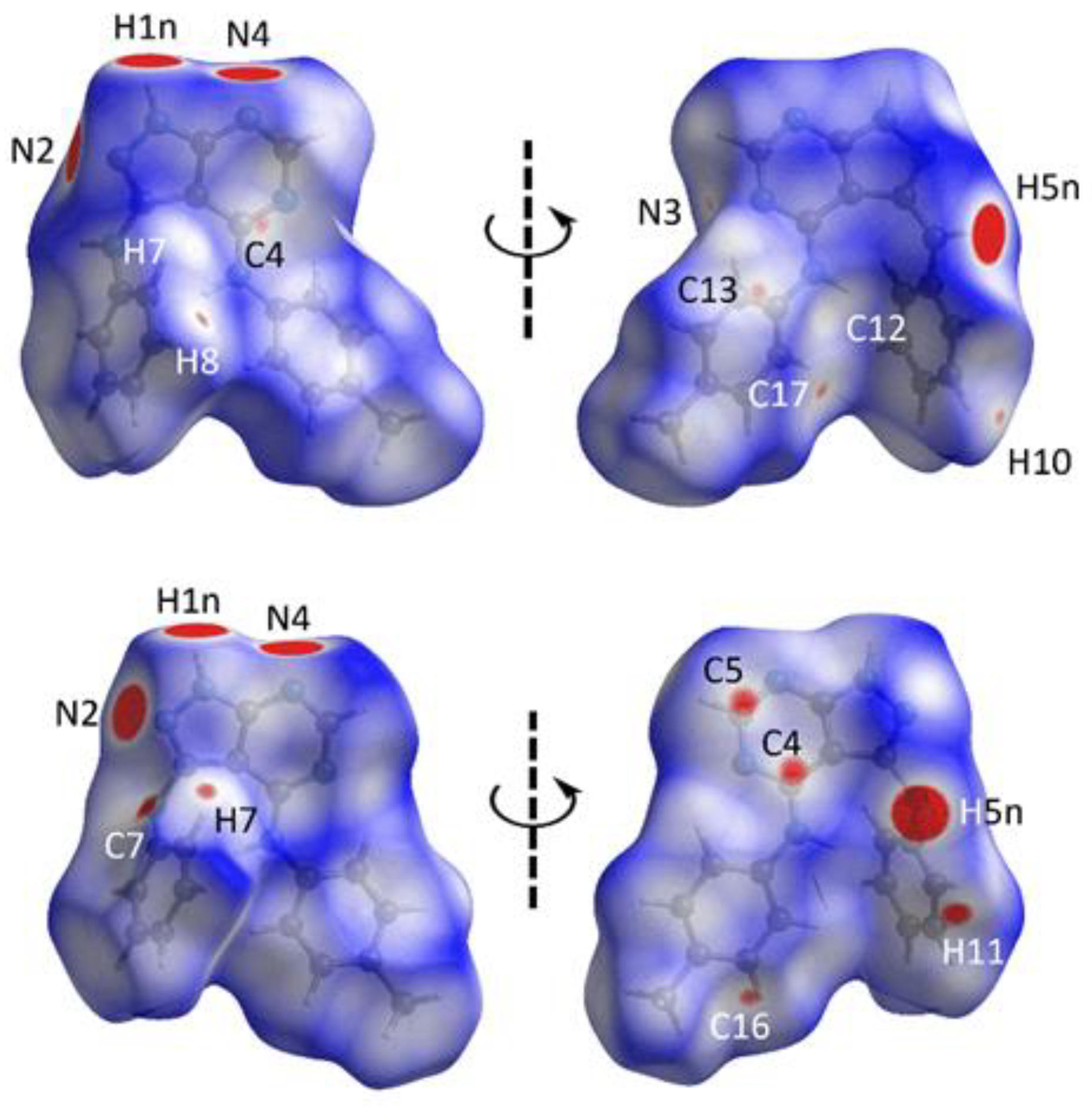
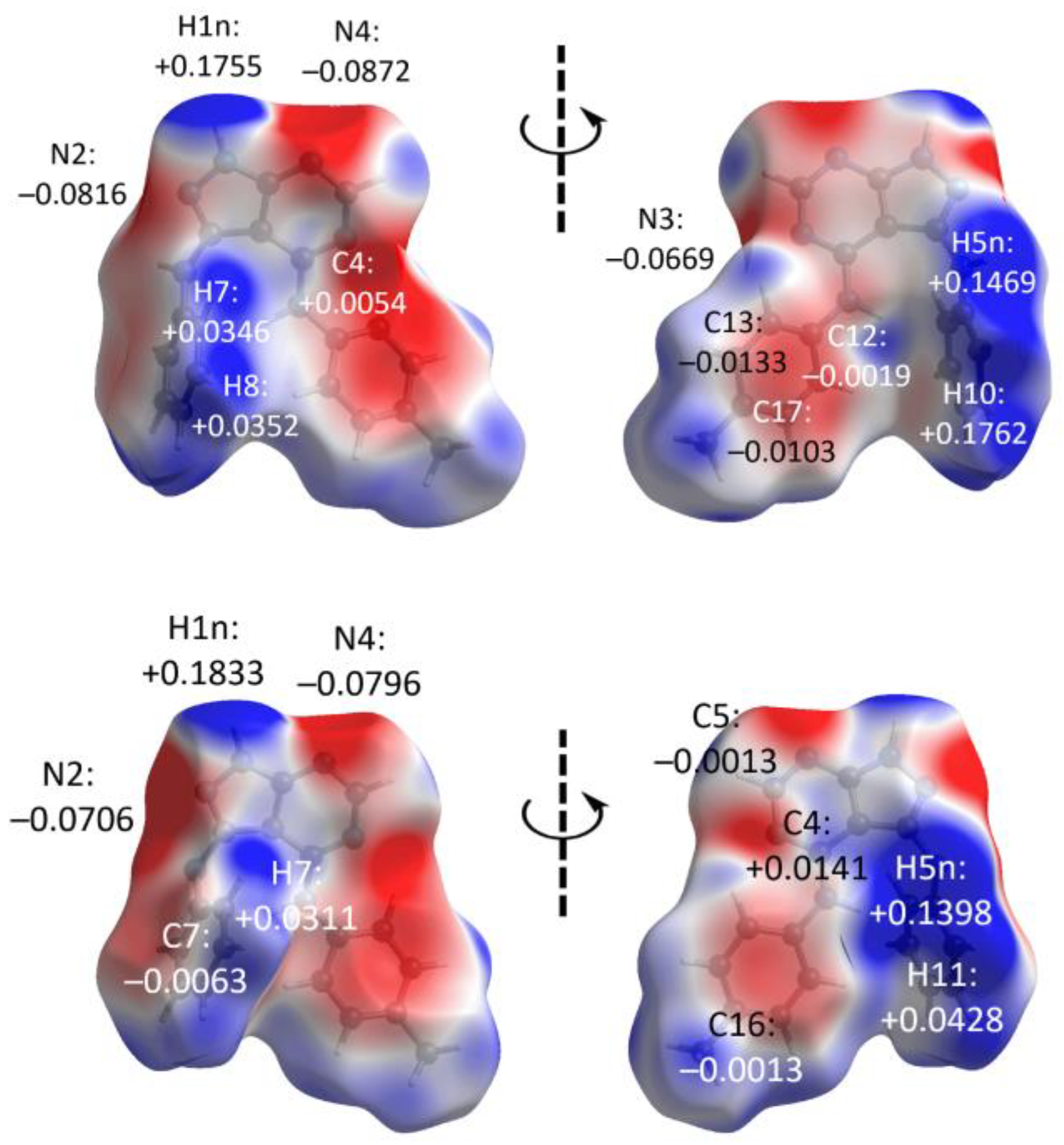
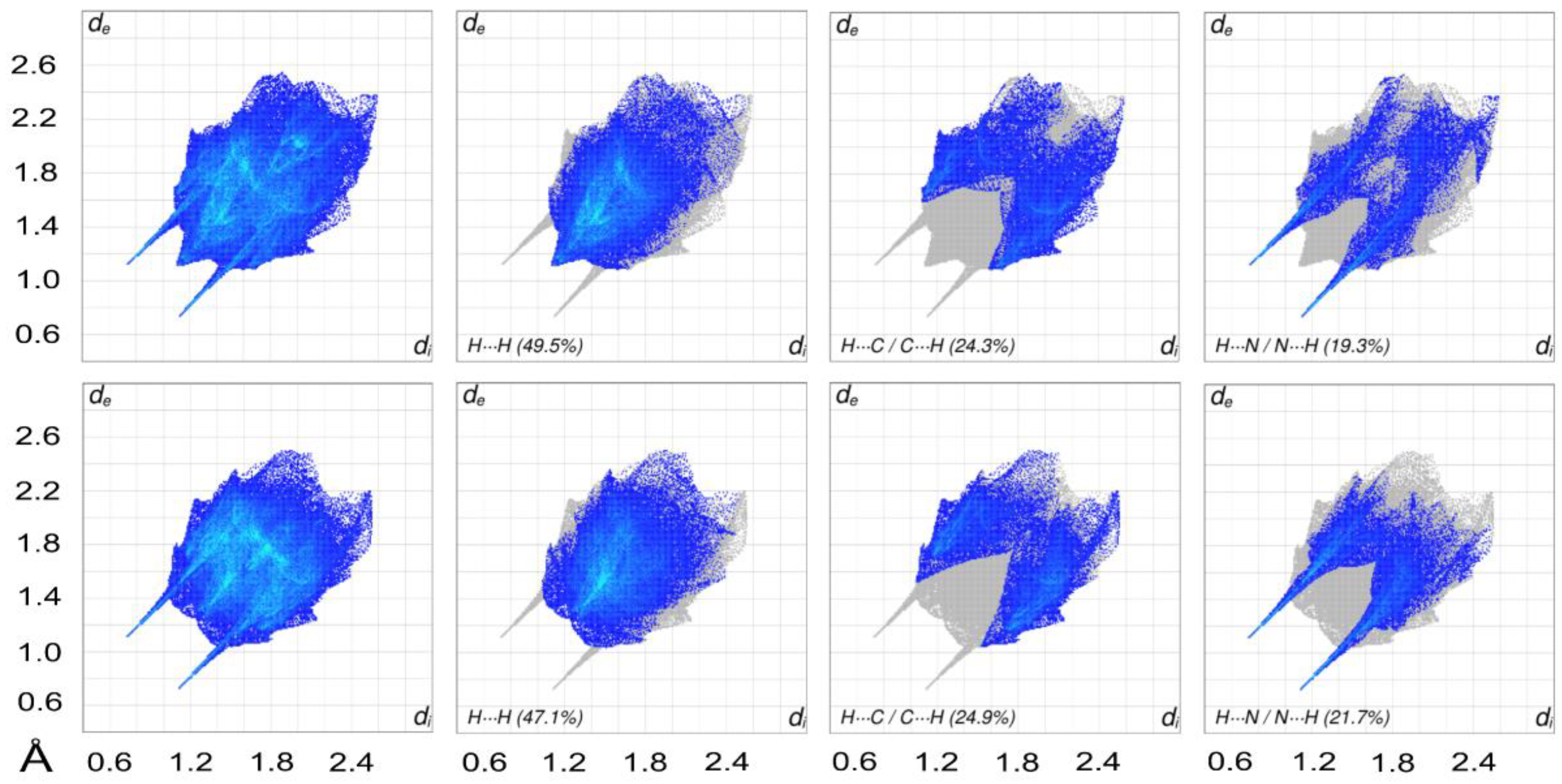
3.3. Hirshfeld Surface Analysis
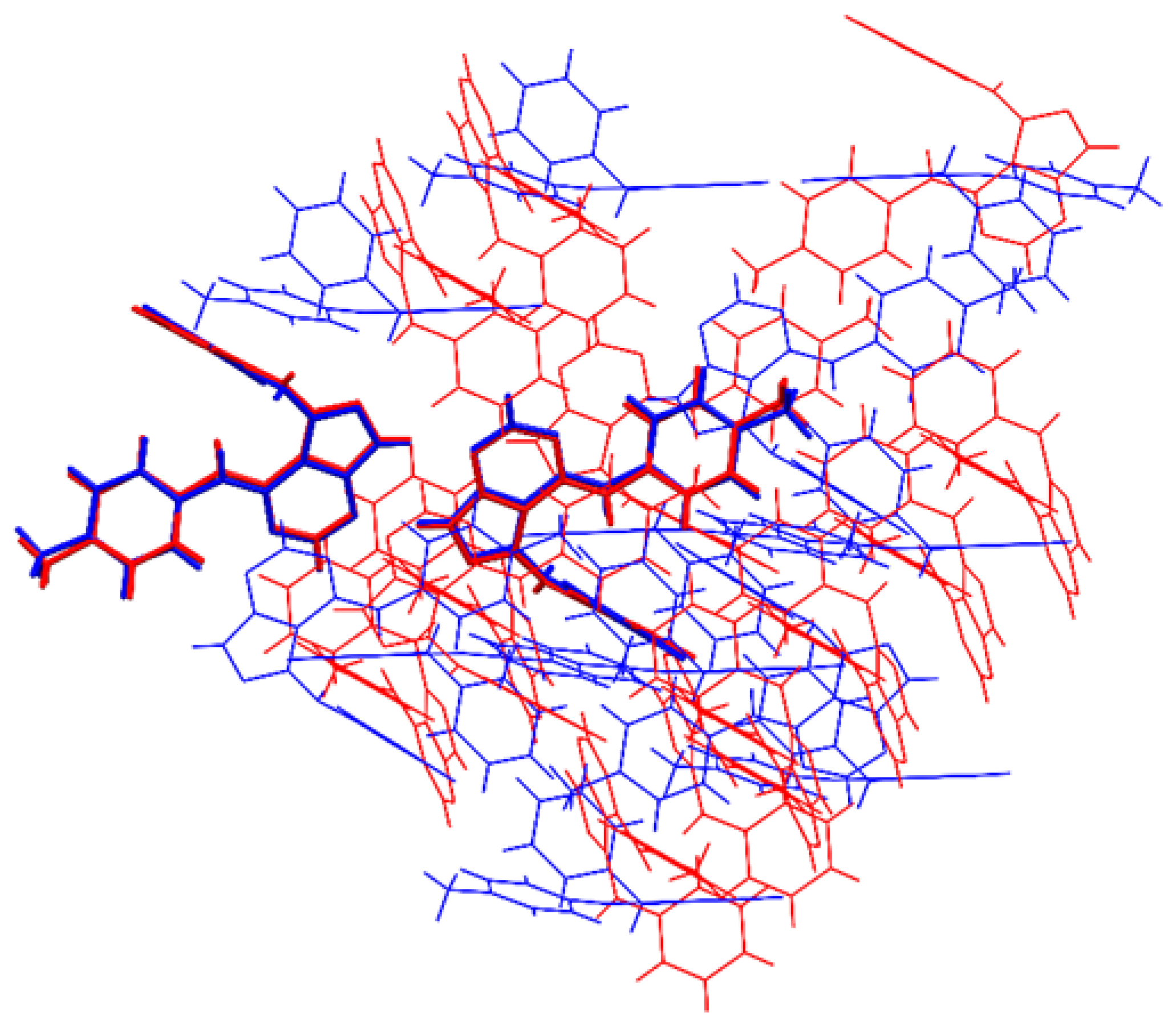
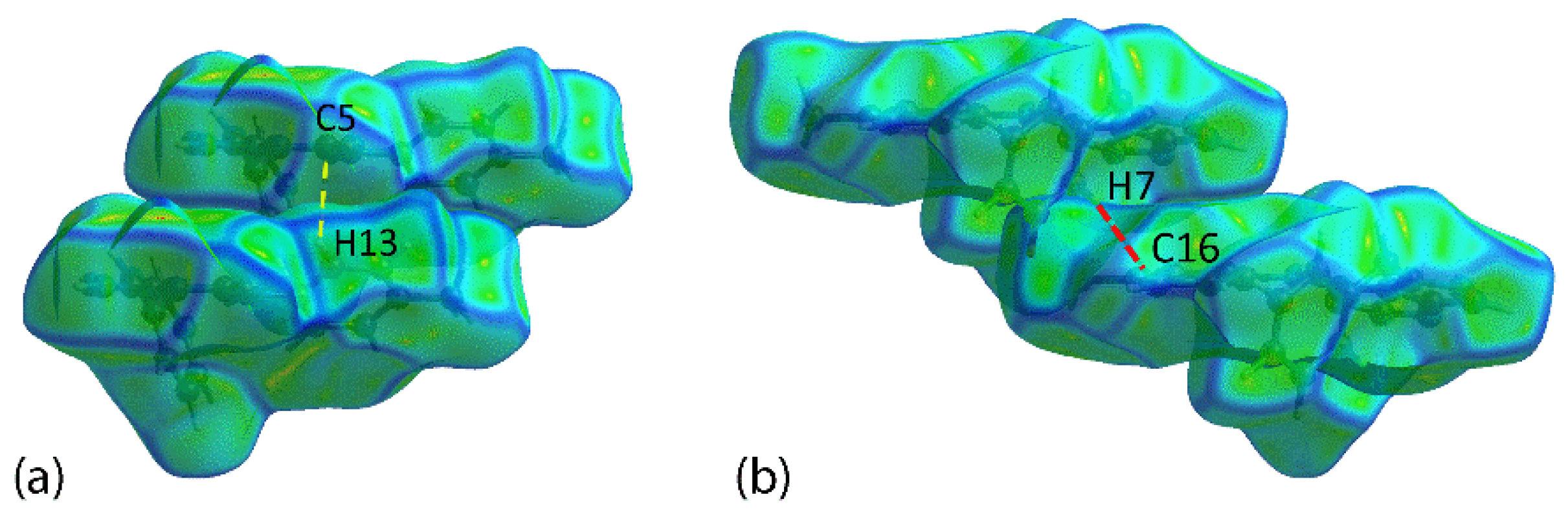
3.4. Interaction Energies
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brittain, H.G. Polymorphism in Pharmaceutical Solids, 2nd ed.; Informa Healthcare: New York, NY, USA, 2009. [Google Scholar]
- Cruz-Cabeza, A.J.; Reutzel-Edens, S.M.; Bernstein, J. Facts and fictions about polymorphism. Chem. Soc. Rev. 2015, 44, 8619–8635. [Google Scholar] [CrossRef]
- Bernstein, J. Polymorphism in Molecular Crystals, 2nd ed.; Oxford University Press: New York, NY, USA, 2020. [Google Scholar]
- Lee, A.Y.; Erdemir, D.; Myerson, A.S. Crystal Polymorphism in Chemical Process Development. Annu. Rev. Chem. Biomol. Eng. 2011, 2, 259–280. [Google Scholar] [CrossRef] [PubMed]
- Tandon, R.; Tandon, N.; Thapar, R.K. Patenting of polymorphs. Pharm. Pat. Anal. 2018, 7, 59–63. [Google Scholar] [CrossRef]
- Henck, J.O.; Griesser, U.J.; Burger, A. Polymorphie von Arzneistoffen: Eine wirtschaftliche Herausforderung? (Polymorphism of drug substances: An economic challenge?). Pharm. Ind. 1997, 59, 165–169. [Google Scholar]
- For the FDA Database on GRAS Compounds. Available online: https://www.fda.gov/food/food-ingredients-packaging/generally-recognized-safe-gras (accessed on 3 June 2023).
- Arora, K.K.; Zaworotko, M.J. Polymorphism in Pharmaceutical Solids; Brittain, H.G., Ed.; Informa Healthcare: London, UK, 2009; Volume 1, p. 281. [Google Scholar]
- Tiekink, E.R.T. Crystal Engineering. In Supramolecular Chemistry: From Molecules to Nanomaterials; Steed, J.W., Gale, P.A., Eds.; John Wiley & Sons Ltd.: Chichester, UK, 2012; pp. 2791–2828. [Google Scholar] [CrossRef]
- Aitipamula, S.; Chow, P.S.; Tan, R.B.H. Polymorphism in cocrystals: A review and assessment of its significance. CrystEngComm 2014, 16, 3451–3465. [Google Scholar] [CrossRef]
- Price, S.L. Computed crystal energy landscapes for understanding and predicting organic crystal structures and polymorphism. Acc. Chem. Res. 2009, 42, 117–126. [Google Scholar] [CrossRef]
- Aitipamula, S.; Chow, P.S.; Tan, R.B.H. Polymorphs and solvates of a cocrystal involving an analgesic drug, ethenzamide, and 3,5-dinitrobenzoic acid. Cryst. Growth Des. 2010, 10, 2229–2238. [Google Scholar] [CrossRef]
- McCrone, W.C. Physics and Chemistry of the Solid State; Fox, D., Labes, M.M., Weissberger, A., Eds.; Wiley Interscience: Hoboken, NJ, USA, 1965; Volume 2, p. 725. [Google Scholar]
- Caira, M.R. Crystalline polymorphism of organic compounds. Topics Curr. Chem. 1998, 198, 163–208. [Google Scholar] [CrossRef]
- Price, C.P.; Grzesiak, A.L.; Matzger, A.J. Crystalline polymorph selection and discovery with polymer heteronuclei. J. Am. Chem. Soc. 2005, 127, 5512–5517. [Google Scholar] [CrossRef]
- Braga, D.; Grepioni, F.; Maini, L.; Polito, M. Crystal polymorphism and multiple crystal forms. Struct. Bond. 2009, 132, 25–50. [Google Scholar] [CrossRef]
- Yu, L. Polymorphism in molecular solids: An extraordinary system of red, orange, and yellow crystals. Acc. Chem. Res. 2010, 43, 1257–1266. [Google Scholar] [CrossRef]
- Brittain, H.G. Polymorphism and solvatomorphism 2010. J. Pharm. Sci. 2012, 101, 464–484. [Google Scholar] [CrossRef] [PubMed]
- Callis, T.B.; Garrett, T.R.; Montgomery, A.P.; Danon, J.J.; Kassiou, M. Recent scaffold hopping applications in central nervous system drug discovery. J. Med. Chem. 2022, 65, 13483–13504. [Google Scholar] [CrossRef] [PubMed]
- Jayashree, B.S.; Nikhil, P.S.; Paul, S. Bioisosterism in drug discovery and development—An overview. Med. Chem. 2022, 18, 915–925. [Google Scholar] [CrossRef] [PubMed]
- Lamberth, C. Isosteric ring exchange as a useful scaffold hopping tool in agrochemistry. J. Agric. Food Chem. 2023. [Google Scholar] [CrossRef]
- Lim, F.P.L.; Dolzhenko, A.V. 1,3,5-Triazine-based analogues of purine: From isosteres to privileged scaffolds in medicinal chemistry. Eur. J. Med. Chem. 2014, 85, 371–390. [Google Scholar] [CrossRef]
- Baillache, D.J.; Unciti-Broceta, A. Recent developments in anticancer kinase inhibitors based on the pyrazolo[3,4-d]pyrimidine scaffold. RSC Med. Chem. 2020, 11, 1112–1135. [Google Scholar] [CrossRef]
- Rundles, R.W. The development of allopurinol. Arch. Intern. Med. 1985, 145, 1492–1503. [Google Scholar] [CrossRef]
- Ng, J.H.; Lim, F.P.L.; Tiekink, E.R.T.; Dolzhenko, A.V. 3,4-Diaminopyrazolo[3,4-d]pyrimidines: A new three-component microwave-assisted synthesis and anti-leukemic properties. Org. Biomol. Chem. 2023, 21, 3432–3446. [Google Scholar] [CrossRef]
- Rigaku Oxford Diffraction. CrysAlis PRO; Oxford Diffraction Ltd.: Oxfordshire, UK, 2017. [Google Scholar]
- Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. Sect. A Found. Crystallogr. 2008, 64, 112–122. [Google Scholar] [CrossRef]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. Sect. C Struct. Chem. 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Farrugia, L.J. WinGX and ORTEP for Windows: An update. J. Appl. Crystallogr. 2012, 45, 849–854. [Google Scholar] [CrossRef]
- Brandenburg, K. DIAMOND, Crystal Impact GbR.; Crystal Impact GbR.: Bonn, Germany, 2006. [Google Scholar]
- Spek, A.L. checkCIF validation ALERTS: What they mean and how to respond. Acta Crystallogr. Sect. E Crystallogr. Commun. 2020, 76, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 16, Revision, C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Chai, J.D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
- Dennington, R.; Keith, T.A.; Millam, J.M. GaussView, Version 6; Semichem Inc.: Shawnee Mission, KS, USA, 2016. [Google Scholar]
- Spackman, P.R.; Turner, M.J.; Mckinnon, J.J.; Wolff, S.K.; Grimwood, D.J.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer: A program for Hirshfeld surface analysis, visualization and quantitative analysis of molecular crystals. J. Appl. Crystallogr. 2021, 54, 1006–1011. [Google Scholar] [CrossRef]
- Tan, S.L.; Jotani, M.M.; Tiekink, E.R.T. Utilizing Hirshfeld surface calculations, non-covalent interaction (NCI) plots and the calculation of interaction energies in the analysis of molecular packing. Acta Crystallogr. Sect. E Crystallogr. Commun. 2019, 75, 308–318. [Google Scholar] [CrossRef]
- Spackman, M.A.; Jayatilaka, D. Hirshfeld surface analysis. CrystEngComm 2009, 11, 19–32. [Google Scholar] [CrossRef]
- Mackenzie, C.F.; Spackman, P.R.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer model energies and energy frameworks: Extension to metal coordination compounds, organic salts, solvates and open-shell systems. IUCrJ 2017, 4, 575–587. [Google Scholar] [CrossRef]
- Macrae, C.F.; Sovago, I.; Cottrell, S.J.; Galek, P.T.A.; McCabe, P.; Pidcock, E.; Platings, M.; Shields, G.P.; Stevens, J.S.; Towler, M.; et al. Mercury 4.0: From visualization to analysis, design and prediction. J. Appl. Crystallogr. 2020, 53, 226–235. [Google Scholar] [CrossRef] [PubMed]
- Motherwell, S.; Chisholm, J.A. COMPACK: A program for identifying crystal structure similarity using distances. J. Appl. Crystallogr. 2005, 38, 228–231. [Google Scholar] [CrossRef]
- Thomas, S.P.; Spackman, P.R.; Jayatilaka, D.; Spackman, M.A. Accurate lattice energies for molecular crystals from experimental crystal structures. J. Chem. Theory Comput. 2018, 14, 1614–1623. [Google Scholar] [CrossRef] [PubMed]
- Maschio, L.; Civalleri, B.; Ugliengo, P.; Gavezzotti, A. Intermolecular interaction energies in molecular crystals: Comparison and agreement of localized Møller–Plesset 2, dispersion-corrected Density Functional, and classical empirical two-body calculations. J. Phys. Chem. A 2011, 115, 11179–11186. [Google Scholar] [CrossRef]
- Zara, Z.; Iqbal, J.; Ayub, K.; Irfan, M.; Mahmood, A.; Khera, R.A.; Eliasson, B. A comparative study of DFT calculated and experimental UV/Visible spectra for thirty carboline and carbazole based compounds. J. Mol. Struct. 2017, 1149, 282–298. [Google Scholar] [CrossRef]
- Bayach, I.; Sarfaraz, S.; Sheikh, N.S.; Alamer, K.; Almutlaq, N.; Ayub, K. Hydrogen dissociation reaction on first-row transition metal doped nanobelts. Materials 2023, 16, 2792. [Google Scholar] [CrossRef]

| Polymorph | α | β |
|---|---|---|
| Formula | C18H16N6 | C18H16N6 |
| Molecular weight | 316.37 | 316.37 |
| Crystal size/mm3 | 0.03 × 0.03 × 0.08 | 0.08 × 0.13 × 0.15 |
| Colour | colorless | colorless |
| Crystal system | monoclinic | monoclinic |
| Space group | P21/c | P21/c |
| a/Å | 16.3112(4) | 14.4399(1) |
| b/Å | 5.0264(1) | 13.0065(1) |
| c/Å | 18.9678(3) | 8.1330(1) |
| β/° | 92.005(2) | 92.329(1) |
| V/Å3 | 1554.15(5) | 1526.22(2) |
| Z | 4 | 4 |
| Dc/g cm−3 | 1.352 | 1.377 |
| μ/mm−1 | 0.686 | 0.699 |
| Measured data | 19,228 | 18,706 |
| θ range/° | 4.7–67.1 | 3.1–67.1 |
| Unique data | 2757 | 2728 |
| Observed data (I ≥ 2.0σ(I)) | 2345 | 2510 |
| No. parameters | 227 | 227 |
| R, obs. data; all data | 0.035; 0.044 | 0.032; 0.034 |
| a; b in weighting scheme | 0.045; 0.601 | 0.038; 0.507 |
| Rw, obs. data; all data | 0.084; 0.090 | 0.078; 0.080 |
| Range of residual electron | −0.20–0.16 | −0.23–0.16 |
| density peaks/eÅ−3 |
| Parameter | α | β | Opt-1 |
|---|---|---|---|
| N1–N2 | 1.3769(15) | 1.3687(13) | 1.356 |
| C1–N1 | 1.3451(18) | 1.3457(15) | 1.345 |
| C2–N2 | 1.3174(19) | 1.3246(15) | 1.310 |
| C4–N3 | 1.3442(17) | 1.3429(15) | 1.329 |
| C5–N3 | 1.3441(18) | 1.3461(15) | 1.339 |
| C1–N4 | 1.3551(17) | 1.3565(15) | 1.339 |
| C5–N4 | 1.3281(18) | 1.3283(15) | 1.316 |
| C2–N5 | 1.3915(17) | 1.4097(15) | 1.388 |
| C4–N6 | 1.3554(17) | 1.3546(15) | 1.352 |
| C1–C3 | 1.3984(18) | 1.3930(16) | 1.395 |
| C2–C3 | 1.4309(18) | 1.4242(16) | 1.429 |
| C3–C4 | 1.4118(19) | 1.4188(16) | 1.416 |
| N2–C2–N5–C6 | −126.44(15) | −120.39(11) | −127.1 |
| C3–C2–N5–C6 | 60.4(2) | 61.44(16) | 57.9 |
| C2–N5–C6–C7 | 16.5(2) | 15.71(16) | 9.3 |
| C2–N5–C6–C11 | −163.22(13) | −166.32(10) | −168.5 |
| N3–C4–N6–C12 | −0.1(2) | 6.54(18) | 9.5 |
| C3–C4–N6–C12 | −178.83(13) | −172.70(11) | −170.8 |
| C4–N6–C12–C13 | −41.1(2) | −25.90(19) | −20.3 |
| C4–N6–C12–C17 | 144.09(14) | 155.39(12) | 160.7 |
| A | H | B | H···B | A···B | A–H···B | Symmetry Operation |
|---|---|---|---|---|---|---|
| α | ||||||
| N6 | H6n | Cg(C6–C11) | 2.879(10) | 3.7434(12) | 171.2(12) | x, y, z |
| N1 | H1n | N4 | 1.997(15) | 2.8722(17) | 167.1(14) | 1 − x, 1 − y, − z |
| N5 | H5n | N2 | 2.109(14) | 2.9673(17) | 166.5(13) | 1 − x, −½ + y, −½ − z |
| C5 | H5 | Cg(C6–C11) | 2.93 | 3.6934(15) | 138 | x, ½ − y, −½ + z |
| C13 | H13 | Cg(N3,N4,C1,C3–C5) | 2.80 | 3.4152(15) | 124 | x, −1 + y, z |
| β | ||||||
| N1 | H1n | N4 | 1.970(12) | 2.8584(14) | 171.1(13) | 2 − x, 1 − y, − z |
| N5 | H5n | N2 | 2.144(12) | 3.0137(13) | 168.1(12) | x, ½ − y, ½ + z |
| C18 | H18b | Cg(C12–C17) | 2.94 | 3.7507(14) | 141 | x, 3/2 − y, ½ + z |
| Cg(N3,N4,C1,C3–C5) | Cg(N3,N4,C1,C3–C5) | 3.5651(6) | 0 a | 2 − x, 1 − y, 1 − z |
| Contact | dnorm Distance (Å) | ΣvdW (Å) | Δ(ΣvdW − dnorm Distance) | Symmetry Operation |
|---|---|---|---|---|
| α | ||||
| N1–H1n···N4 | 1.88 | 2.64 | 0.758 | 1 − x, 1 − y, −z |
| N5–H5n···N2 | 1.98 | 2.64 | 0.661 | 1 − x, −½ + y, ½ − z |
| C8–H8···C17 | 2.71 | 2.79 | 0.083 | x, 1 + y, z |
| C10–H10···N3 | 2.58 | 2.64 | 0.058 | x, −½ − y, ½ + z |
| C4···C13 | 3.35 | 3.40 | 0.046 | x, 1 + y, z |
| C7–H7···C12 | 2.77 | 2.79 | 0.025 | x, 1 + y, z |
| C13–H13···C5 | 2.77 | 2.79 | 0.019 | x, −1 + y, z |
| β | ||||
| N1–H1n···N4 | 1.86 | 2.64 | 0.782 | 2 − x, 1 − y, −z |
| N5–H5n···N2 | 2.02 | 2.64 | 0.619 | x, ½ − y, ½ + z |
| C11–H11···C7 | 2.60 | 2.79 | 0.192 | x, ½ − y, ½ + z |
| C4···C5 | 3.27 | 3.40 | 0.126 | 2 − x, 1 − y, 1 − z |
| C7–H7···C16 | 2.69 | 2.79 | 0.098 | x, y, −1 + z |
| Contact | Eele | Epol | Edisp | Erep | Etot | Symmetry Operation |
|---|---|---|---|---|---|---|
| α | ||||||
| {N1–H1n···N4}2 | −107.0 | −17.5 | −15.9 | 70.6 | −69.9 | 1 − x, 1 − y, −z |
| C7–H7···C12 + C8–H8···C17 + C13–H13···C5 + C4 ···C13 | −13.3 | −2.4 | −68.3 | 28.7 | −55.3 | x, 1 + y, z |
| N5–H5n···N2 | −40.9 | −6.3 | −15.8 | 28.8 | −34.2 | 1 − x, −½ + y, ½ − z |
| C10–H10···N3 | −9.7 | −1.3 | −19.1 | 12.5 | −17.6 | x, −½ − y, ½ + z |
| β | ||||||
| {N1–H1n···N4}2 | −109.2 | −18.6 | −16.7 | 75.5 | −68.9 | 2 − x, 1 − y, −z |
| N5–H5n···N2 + C11–H11···C7 | −46.2 | −7.1 | −42.0 | 40.4 | −54.9 | x, ½ − y, ½ + z |
| C4 ···C5 | −4.1 | −1.3 | −48.1 | 18.8 | −34.6 | 2 − x, 1 − y, 1 − z |
| C7–H7···C16 | −7.5 | −1.0 | −37.2 | 15.1 | −30.7 | x, y, −1 + z |
| Polymorph | Eele | Epol | Edisp | Erep | Elattice |
|---|---|---|---|---|---|
| α | −92.5 | −14.8 | −97.9 | 80.5 | −124.6 |
| β | −94.1 | −15.4 | −117.3 | 91.2 | −135.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, S.L.; Tan, Y.S.; Ng, J.H.; Dolzhenko, A.V.; Tiekink, E.R.T. Two Conformational Polymorphs of a Bioactive Pyrazolo[3,4-d]pyrimidine. Crystals 2023, 13, 974. https://doi.org/10.3390/cryst13060974
Tan SL, Tan YS, Ng JH, Dolzhenko AV, Tiekink ERT. Two Conformational Polymorphs of a Bioactive Pyrazolo[3,4-d]pyrimidine. Crystals. 2023; 13(6):974. https://doi.org/10.3390/cryst13060974
Chicago/Turabian StyleTan, Sang Loon, Yee Seng Tan, Jia Hui Ng, Anton V. Dolzhenko, and Edward R. T. Tiekink. 2023. "Two Conformational Polymorphs of a Bioactive Pyrazolo[3,4-d]pyrimidine" Crystals 13, no. 6: 974. https://doi.org/10.3390/cryst13060974
APA StyleTan, S. L., Tan, Y. S., Ng, J. H., Dolzhenko, A. V., & Tiekink, E. R. T. (2023). Two Conformational Polymorphs of a Bioactive Pyrazolo[3,4-d]pyrimidine. Crystals, 13(6), 974. https://doi.org/10.3390/cryst13060974








