Abstract
Compared to X-rays, electrons have stronger interactions with matter. In electron diffraction, the low-order structure factors are sensitive to subtle changes in the arrangement of valence electrons around atoms when the scattering vector is smaller than the critical scattering vector. Therefore, electron diffraction is more advantageous for studying the distribution of atoms in the structure with atomic numbers smaller than that of sulfur. In this work, the crystal structure of Sr1.2Ca0.8Nb2O7 (SCNO-0.8) was analyzed using single-crystal X-ray diffraction (SC-XRD) and three-dimensional electron diffraction (3D-ED) techniques, respectively. Interestingly, the superstructure could only be identified by the 3D-ED technique, while no signal corresponding to the superstructure was detected from the SC-XRD data. The superstructure in SCNO-0.8 was disclosed to be caused by different tilting of NbO6 octahedra and the displacements of Sr/Ca atoms in the different atomic layers perpendicular to the a-axis. Therefore, the application of 3D-ED provides an effective method for studying superstructures caused by ordered arrangements of light atoms.
1. Introduction
Transmission electron microscopy (TEM) is a powerful tool for studying inorganic, organic, and biological materials. In TEM, the accelerated electron beam is focused on the specimen, and electrons interact with the material to produce diffraction. The structure of the material can be qualitatively analyzed by electron diffraction from different directions. Selected area electron diffraction (SAED) is one of the most commonly used electron diffraction modes and can reflect the structural characteristics of a micro-region, such as crystallinity, orientation, symmetry, and stacking faults. When collecting SAED data, it is necessary to align the zone axis of the crystal, which requires operators to possess high skills and patience. In addition, electron diffraction is dynamical. Electron multiple scattering usually causes the diffraction intensity to disperse from the stronger diffraction spots to the weaker diffraction spots, reducing the intensity difference between the diffraction spots in the diffraction pattern. As a result, the structural information contained is reduced. It can be seen that the relationships between diffraction intensities and the structure factor are very complicated. The diffraction intensity is not only related to atomic arrangements but is also affected by the sample thickness and the diffraction direction. Therefore, it is very difficult to analyze the material’s structure quantificationally by electron diffraction. The emergence of precession electron diffraction (PED) technology [] makes it possible to obtain the integral intensity of the diffraction vector from electron diffraction with a single zone axis. The principle of PED technology is to use the upper deflection coil to tilt the electron beam at a certain angle (the precession angle is typically 1~3 degrees) for conical rotation, while maintaining the same area of the sample being irradiated. Below the sample, the electron beams are simultaneously tilted in opposite directions so that the diffraction pattern remains stationary. Through the above operations, the electron beam is no longer incident along the direction of the zone axis, thus avoiding all the diffraction spots of the zone axis from becoming excited and interacted at the same time, which not only weakens the influence of multiple scattering, but also makes it easier to excite higher-order Laue zone diffraction spots. Compared to the diffraction spots obtained from conventional SAED, where the intensities are averaged, the experimental diffraction patterns obtained after precession exhibit significantly reduced dynamical scattering effects and are closer to the kinematical diffraction patterns. In most cases, the PED patterns also go to higher resolution than an SAED pattern collected from the same crystal. Therefore, the structural information obtained using PED is more accurate. Using the diffraction intensity of the kinematical approximation in PED, the structures of some materials have been quantificationally determined, such as heavy oxide perovskite-related structures [], minerals [], and zeolites [].
However, conventional PED only involves diffraction images collected along specific low-index zone axes. Such a collection method can only record finite diffraction vectors, whose completeness is low for complicated structure determination. Moreover, data often need to be collected for different crystals in order to achieve acceptable coverage, complicating the data-merging procedure. In 2007, Kolb [] first proposed the idea of three-dimensional electron diffraction (3D-ED):gradual rotation of the crystal with a fixed-angle step, collection of an electron diffraction pattern at each rotation angle, and reconstruction of a three-dimensional reciprocal space based on the geometry relationship. Compared to conventional in-zone ED patterns, the most obvious advantage of 3D-ED is that all reflections reachable in the tilt range of the TEM goniometer are sampled, thus maximizing data completeness []. Since the angular relationship between the diffraction patterns is known, it is possible to determine crystal parameters, extinction effect, diffraction intensities, and other information by analyzing the distribution of reconstructed reciprocal lattice spots in three-dimensional reciprocal space. The data collected using 3D-ED can be used to analyze crystal structures in a manner similar to single-crystal X-ray crystallography []. Compared to single-crystal X-ray diffraction (SC-XRD), 3D-ED has advantages for studying small-sized crystals [,] (<5 × 5 × 5 μm3) and polyphasic mixtures []. In recent years, with the rapid development of 3D-ED technology, researchers have developed a variety of data collection methods [], such as automated diffraction tomography (ADT) [], rotation electron diffraction (RED) [], precession-assisted electron diffraction tomography (PEDT) [], continuous rotation electron diffraction (cRED) [], electron diffraction tomography (EDT) [], fast electron diffraction tomography (fast-EDT) [], fast automated diffraction tomography (fast-ADT) [], low-dose electron diffraction tomography (LD-EDT) [], and microcrystal electron diffraction (MicroED) []. These collection methods are similar in concept, where a series of electron diffraction patterns are recorded from a crystal tilted around the goniometer axis. EDT refers to data collection by gradually tilting the crystal at a fixed angle and acquiring diffraction images at each tilting stage. However, the recorded diffraction intensity suffers from imprecise integration due to gaps between the positions of adjacent angles []. This missing wedge can be filled by the PED mode []. The combination of EDT with PED for data collection is referred to as PEDT. The 3D-ED data collected through PEDT allows for direct dynamic refinement of the analyzed structure, resulting in a more accurate structural model. 3D-ED technology has been widely used in the structural analysis of various materials, such as ITQ-62 [], SCM-14 [], ITQ-54 [], UTL-DBU [], and other molecular sieve structures, as well as in the analysis of the molecular structures of lysozyme, protease, catalase, and other proteins [,,,]. However, there are few reports on the use of 3D-ED to study the superstructures of materials.
The heavy atoms, which have more extranuclear electrons, have a stronger scattering ability when interacting with X-rays, and the light atoms do not. Therefore, it is difficult to determine the atomic positions of some light atoms, such as H, B, and O, when they coexist with heavy atoms. In electron diffraction, the diffraction generated by core electrons can be extended above the critical vector s (|s| = sinθ/λ), and the diffraction generated by the valence electrons is mostly confined below the critical vector s, typically in the range of 0.2~0.6 Å−1. Zhu [] conducted a quantitative comparison of the sensitivity of the atomic scattering factor to the valence charge distribution in X-ray and electron diffraction. The study found that the scattering factors of light atoms with atomic numbers lower than that of sulfur are more sensitive to valence charge density in electron diffraction than X-ray diffraction. Therefore, 3D-ED can be used to study the superstructure caused by the ordered arrangement of light atoms with atomic numbers lower than that of sulfur.
The Curie temperature of Sr2Nb2O7 (SNO) crystals is above 1300 °C, which gives it potential applications for high-temperature piezoelectric sensing [,,]. In 2002, Daniels [] discovered the incommensurate modulation structure of SNO at room temperature by SC-XRD. Subsequently, Lin [] synthesized doped SNO Sr2−xCaxNb2O7 (SCNO) and studied its second-harmonic generation (SHG) effect. Although the satellite diffraction peak, which was detected for SNO, was not observed in SCNO’s X-ray diffraction pattern. Due to the weak interaction between X-ray and O atoms in the NbO6 octahedrons, the superstructure introduced by NbO6 octahedrons with different tilting distributions may be ignored.
In this study, the structure of Sr1.2Ca0.8Nb2O7 (SCNO-0.8), synthesized using Lin’s reported method [], was investigated using 3D-ED. The results revealed that SCNO-0.8 has a two-fold superstructure along the a-axis direction. The NbO6 octahedron and Sr/Ca atoms have different degrees of tilting and displacements in different atomic layers perpendicular to the a-axis. By comparing the structure of SCNO-0.8 determined here with that analyzed by traditional SC-XRD, as well as the incommensurate structure of SNO reported in the literature, the relationship between the structure and nonlinear optical (NLO) properties of SCNO materials was further clarified. This work provides an effective method for studying the superstructures caused by the ordered arrangement of light atoms with atomic numbers lower than that of sulfur.
2. Materials and Methods
In this study, the single-crystal sample (Figure S1) was provided by Lin’s research group []. The ceramic sample of Sr1.2Ca0.8Nb2O7 (SCNO-0.8) was prepared using a solid-state synthesis method using the raw materials SrCO3 (99.50%, Sinopharm, Beijing, China), CaCO3 (99.50%, Sinopharm, Beijing, China), and Nb2O5 (99.90%, Alfa Aesar, Shanghai, China). These oxide powders were stoichiometrically weighed, mixed in ethanol by planetary ball milling for 4 h, and then dried. The resulting powder was placed in an alumina crucible and pre-calcined at 1200 °C for 2 h. After cooling, the powder was re-milled in ethanol for 4 h and pressed into pellets with a diameter of 10 mm and thickness of 1.5 mm using 6% polyvinyl alcohol (PVA, Hefei, China) as a binder. The pellets were sintered at 1330 °C for 2 h.
SC-XRD data were collected at room temperature using the Rigaku XtaLAB Synergy R single-crystal X-ray diffractometer (Mo Kα radiation, λ= 0.71073 Å, Tokyo, Japan). An FEI Tecnai G2 F20 S-TWIN transmission electron microscope (λ = 0.0251 Å, Hillsboro, OR, USA) was used to conduct 3D-ED experiments on the samples using PEDT. For the 3D-ED experiments, the sample tilt angle ranged from −64° to 47°, the tilt step was 1°, the precession angle was 1°, and the camera exposure time was 2 s. A Rigaku D/max-2550V powder X-ray diffractometer (Cu Kα radiation, λ = 0.15405 nm, Tokyo, Japan) was used to determine the phase of the powder.
Using the software CrysAlisPro [] (version: 1.171.39) and Pets2 [] (version: 2.2.20220915.1735) to reduce the SC-XRD data and 3D-ED data, respectively, the intensity distribution of all diffraction vectors in the three-dimensional reciprocal space can be obtained. Based on the intensity distribution of diffraction vectors in SC-XRD and 3D-ED obtained by reduction, the structure analysis of the corresponding data was carried out in Jana2006 [] (Version: 20/02/2023) using the SHELXT [] and Superflip [] algorithms, respectively. The least squares method was used to refine the structural parameters of the SC-XRD data and 3D-ED data based on kinematic diffraction theory and dynamical diffraction theory, respectively.
3. Results
3.1. Crystal Characterization of SCNO-0.8
Daniels [] reported that SNO has an incommensurate structure, and its modulated structure originated from the different tilting of NbO6 octahedra and the displacement of Sr1 atom. In order to further determine the fine structure of SCNO-0.8, SC-XRD and 3D-ED were applied. Figure 1a–c are reconstructed 0kl, h0l, and hk0 plane diffractions based on SC-XRD data, respectively. Based on SC-XRD, the cell parameters of SCNO-0.8 could be determined as a = 3.9379(3) Å, b = 26.7970(19) Å, c = 5.6484(6) Å, α = β = γ = 90°, with orthorhombic symmetry. The reflection conditions were h + k = 2n, h0l, h, l = 2n, 00l, l = 2n, suggesting the space group of Cmc21. The SHELXT [] algorithm was then used to analyze the structure. The coordinates and anisotropic temperature factors of all atoms in the structure were refined by using the least squares method based on the kinematical diffraction theory. Table S1 shows the crystallographic data and refinement parameters of SCNO-0.8 SC-XRD. Analysis of the data shows that the crystal structure of SCNO-0.8 determined by SC-XRD was consistent with that reported by Lin [], and a superstructure was not observed. 3D-ED data were then collected on single-crystal samples using PED tomography. The diffractions of the 0kl plane, h0l plane, and hk0 plane were reconstructed from the data, as shown in Figure 1d–f, respectively, which deduced a significantly different result from that obtained from the single crystal data. Along the a* direction, in addition to the main diffraction spots, which satisfied the reflection conditions of an orthorhombic unit cell with space group Cmc21 with strong intensity, there were also many satellite diffraction spots with weaker intensity on the h0l plane and hk0 plane (marked by red-dashed boxes), indicating the existence of a superstructure in the a-direction. The (00)C, (02)C, (002)C, and (004)C crystal planes (where the subscript C denotes an orthorhombic unit cell with space group Cmc21) marked by green arrow in Figure S2c can all be found with corresponding diffraction spots in Figure S2a. However, the (00)C crystal plane does not show a diffraction spot due to the extinction effect. Nonetheless, the presence of relatively weak diffraction spots (indicated by white dots) in Figure S2c suggests a doubling of certain interplanar spacings. For example, the (00)C and (00)C crystal planes can be indexed as (00)P and (00)P crystal planes (with subscript P indicating the superstructure unit cell). The (00)P crystal plane satisfies the reflection condition, thus there is no extinction in the diffraction pattern of the superstructure. The (00)P and (00)P crystal planes adjacent to them do not show diffraction spots due to the extinction effect, but nearby weak diffraction spots (marked by white arrow) that satisfy the reflection conditions can be indexed as (01)P, (0)P, (01)P, and (0)P crystal planes. Similarly, weak diffraction spots (indicated by white dots in Figure S2c) along the a-direction can also be observed in Figure S2d. Therefore, the reciprocal space of these superlattice reflections in Figure 1e,f can be indexed as ha* + kb* + lc* ± 1/2a*, where h, k, and l are integers. Hence, the cell parameters of SCNO-0.8 can be determined as a = 7.834(5) Å, b = 26.67(3) Å, c = 5.634(3) Å, and α = β = γ = 90° based on 3D-ED. The reflection conditions are 0kl, k = 2n, h0l, h + l = 2n, 00l, l = 2n, indicating the space group of Pmn21. The Superflip [] program was then used to solve the fine structure. The coordinates and isotropic temperature factors of all atoms in the structure were refined by using the least squares method based on the dynamical theory of diffraction, and the exact structure of SCNO-0.8 could then be obtained. The results show that SCNO-0.8 has a superstructure and the unit cell expands by 2 times in the a-direction. Table 1 shows the crystallographic data and dynamic refinement parameters, and Table S2 shows the structural parameters after dynamic refinement. Tables S3 and S4 show the bond length and bond angle data, respectively.
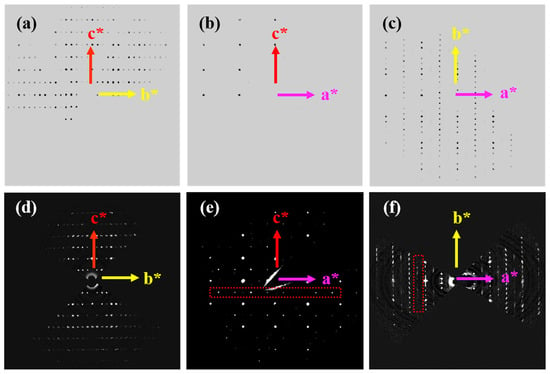
Figure 1.
(a–c) are the 0kl plane, h0l plane, and hk0 plane diffraction patterns, respectively, that were reconstructed from the SC-XRD data. (d–f) are the 0kl plane, h0l plane, and hk0 plane diffraction patterns, respectively, that were reconstructed from the 3D PEDT data.

Table 1.
Crystallographic data, details of the experiment, and dynamical refinement of PEDT.
3.2. Characterization of SCNO-0.8 Powder
Figure 2a shows powder X-ray diffraction data for SCNO-0.8. All diffraction peaks are consistent with the PDF#47-0492 card, and no diffraction peaks ascribed to any impurity phases were detected. Figure 2b shows the SAED collected by SCNO-0.8 powder along the [010] direction. It can be found that there were also several satellite diffractions with weaker intensities around the main diffraction point, indicating that the superstructure characteristics of SCNO-0.8 in the a-direction will not disappear due to the change in crystal size. Figure S3 shows the SAED data collected under the condition of maintaining the electron dose rate at less than 0.36 e− s−1 Å−2. Similarly, in addition to the strong main diffraction spots, it can also be found that there were many relatively weak diffraction spots (marked by the red arrows), indicating that the superstructure of SCNO-0.8 is not caused by electron irradiation produced by high electron doses in 3D-ED technology.
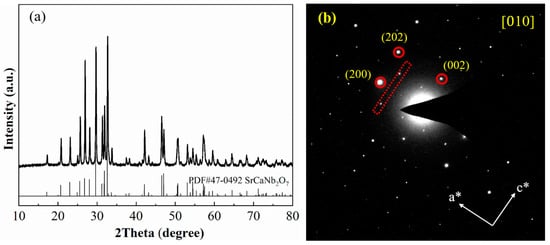
Figure 2.
(a) The powder X-ray diffraction pattern of SCNO-0.8samples (b) The SAED patterns collected along [010] zone axis of SCNO-0.8 powder sample.
Due to the strong interactions between electrons and matter, traditional SAED often exhibits significant dynamical effects. It can be understood that when the electron beam passes through the material, it undergoes multiple diffractions, resulting in the occurrence of multiple scattering dynamical effects. These effects disperse the diffraction intensity from the stronger diffraction spots to the weaker ones, resulting in an average intensity of the diffraction spots. As a result, the diffraction intensity obtained from conventional SAED is not accurate, which increases the difficulty in structural analysis []. The 3D-ED technique used in Section 2 of this article, compared to SAED captured along low-index zone axes, provides more comprehensive data and significantly reduces the effects of multiple scattering. Moreover, the data collection for 3D-ED only requires tilting the sample along a single axis, which reduces the difficulty for operators during data acquisition. Therefore, in this study, 3D-ED data is chosen for structure refinement instead of SAED data.
4. Discussion
The SCNO crystal structure belongs to the perovskite layer structure (PLS), with n = 4 of the general formula of AnBnO3n+2. The n also represents the number of constituent NbO6 octahedral layers that stack along the b-axis in SCNO [,,]. For Sr/Ca ions, there are six different crystallographic sites, which can be classified into two groups: one within the perovskite slab and coordinated by 12 oxygen atoms, and another near the boundary of the perovskite slab and coordinated by 10 oxide ions. For each position, it is occupied by mixed Sr/Ca with a ratio of 0.6/0.4.
Figure 3a,b represent the crystal structures determined by SC-XRD and 3D-ED, respectively, viewed along the a-axis direction. Through comparative analysis, it was found that in the structure determined by 3D-ED, there was a position shift of Sr/Ca atoms in different atomic layers perpendicular to the a-axis (as shown in the black-dashed circle in Figure 3b), while the NbO6 octahedron exhibits locally differential twists in the b–c plane. As shown in Figure S4a,b, the Nb-O-Nb angle changes correspondingly in both cases. In SCNO-0.8, as determined by SC-XRD, there is a mirror-symmetric plane inside the [Nb2O11]2− dimer (Figure 3c), and the connection mode along the a-axis of the [Nb2O11]2− dimer is O3-Nb1-O3-Nb1-O3, and all the Nb-O bond lengths in this direction are 1.994 Å. In contrast, in the superstructure of SCNO-0.8 as determined by 3D-ED, the [Nb2O11]2− dimer has a slightly twisted conformation (Figure 3d). Two Nb3O6 polyhedra have chiral symmetry, and their connection mode is O8-Nb3-O9-Nb3-O8. The length of the Nb-O bond changes (2.004 Å for O8-Nb3 and 1.993 Å for O9-Nb3), and the two Nb-O-Nb angles are also different (161.8° in SC-XRD > 157° in 3D-ED), indicating multiple directional twists of the NbO6 octahedron in the superstructure. Figure 3e,f represent the crystal structures determined by SC-XRD and 3D-ED, respectively, viewed along the c-axis direction. The Nb1O6 and Nb2O6 polyhedra drawn in Figure 3e correspond to those in Figure 3c, with no tilt occurring. In contrast, the polyhedra Nb3O6 and Nb6O6 drawn in Figure 3f can correspond to Figure 3d, both showing a tilt. This could be the origin of the superstructure. Based on the 3D-ED structural characterization in Section 3.1 of this paper, it can be confirmed that the superstructure, compared to the average structure obtained from SC-XRD, needs to be described with twice the lattice parameter a (as shown by the black solid box in Figure 3f). The displacement of Sr/Ca atoms in the SCNO-0.8 superstructure and different tilting of NbO6 octahedra are mainly due to the fact that when Ca2+ with a smaller ionic radius replaces Sr2+, the NbO6 octahedron rotates and twists to alleviate the internal stress and maintain structural stability [,,,].
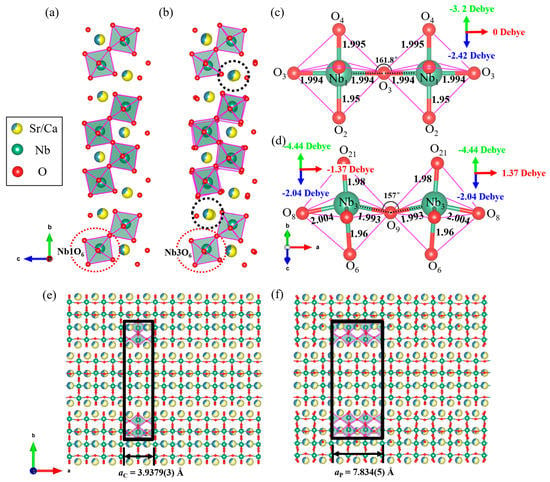
Figure 3.
(a) Structure of SCNO-0.8 view along the a-axis; (b) superstructure of SCNO-0.8 view along the a-axis; (c) [Nb2O11]2- dimer of SCNO-0.8 along [011] direction; (d) [Nb2O11]2− dimer of SCNO-0.8 superstructure along [011] direction. (The black-dashed box shows the offset Sr atom, and the red-dashed box shows the twisted [Nb2O11]2− dimer); (e) structure of SCNO-0.8 viewed along the c-axis; and (f) superstructure of SCNO-0.8 viewed along the c-axis (unit cell of SCNO-0.8 marked by the black solid box).
The SHG effect is closely related to polarization features, and the mutual superposition of polyhedral spontaneous polarization affects the macroscopic SHG performance of the crystal. The space group of the SCNO-0.8 superstructure is Pmn21, which belongs to the orthomorphic crystal system. There is a 21-pole axis in the c-direction, which leads to the non-coincidence of charge centers of atoms along the c-axis, forming a dipole moment and causing spontaneous polarization. On the contrary, the displacements of atoms along the a-axis and b-axis are neutralized by the presence of mirror and sliding planes, respectively. Therefore, the dipole moments of the polyhedron along the a-axis and b-axis do not contribute to the spontaneous polarization of the crystal. From the structural point of view, the dipole moment of SCNO-0.8 originates from the distortion of three polyhedral: NbO6, AO12, and AO10 (A = Sr/Ca). To better understand the synergistic effect of local dipole moments from different types of polyhedra, the local dipole moments (LDM) of each polyhedron were calculated using the bond valence sum approach [,]. Table 2 shows the dipole moment of the polyhedron along the polar axis c-axis of the SCNO-0.8 superstructure. It was found that the contribution of the overall net dipole moment mainly comes from the NbO6 octahedron. Tables S5 and S6 are the dipole moments of each polyhedron of SCNO-0.8, as determined by SC-XRD and 3D-ED, respectively. By comparison, the dipole moments of the NbO6 octahedron in the superstructure along the three directions a, b, and c have all changed, as shown in Figure 3c,d for the Nb1O6 and Nb3O6 octahedra. The dipole moments of two adjacent Nb1O6 octahedrons in the a-direction of the SCNO-0.8 structure, as determined by SC-XRD, are the same and equal to 0 Debye. However, in the superstructure, the dipole moment of a single Nb3O6 octahedron along the a-direction is greater than 0 (1.37 Debye), but the dipole moment is neutralized due to the presence of mirror planes in the a-direction and thus has no contribution to the net dipole moment. Similarly, the dipole moment in the b-direction also changes, but there is a slip plane in the b-direction, which also results in the neutralization of the dipole moment. In the c-direction of the polar axis, the local dipole moments in two structures also changed. There are six distinguishable crystallographic sites for Nb atoms in the superstructure, and their dipole moments along the c-direction are all different. Compared with the average structure of SCNO-0.8, as determined by SC-XRD, the octahedral dipole moments of Nb1O6 (2.13 Debye), Nb2O6 (1.81 Debye), and Nb3O6 (2.04 Debye) are all smaller than that of Nb1O6 in the average structure (2.42 Debye). The dipole moments of Nb4O6 (2.45 Debye) and Nb6O6 (4.19 Debye) in the superstructure are in between those of Nb1O6 and Nb2O6 (4.33 Debye) in the average structure. The octahedral dipole moment of Nb5O6 (5.01 Debye) is larger than that of the average structure. It can be seen that the variation of local NbO6 polyhedral dipole moments in the superstructure is more diverse than that of SCNO-0.8, as determined by SC-XRD, but the average contribution of the NbO6 octahedra to the unit cell net dipole moment in both structures are close to each other. Because the NbO6 octahedron has different degrees of tilting in all directions, SCNO-0.8 exhibits a superstructure, which causes a change in the dipole moment. At the same time, due to the displacement of atomic Sr/Ca, the dipole moment of the (Sr/Ca)Ox polyhedron also changes.

Table 2.
Magnitude (in Debye) of the polyhedral local dipole moments for superstructure SCNO-0.8 along the polar c-axis direction.
This study also calculated the polyhedral dipole moment of the parent material SNO with an incommensurately modulated structure (Table S7). Compared with Table 2, it can be seen that with the doping of Ca2+, the counteraction effect of the SrOx polyhedron at the A site on the net dipole moment is eliminated. Meanwhile, the NbO6 octahedron shows greater torsion, and its contribution to the net dipole moment increases to about two times. This is consistent with Lin’s [] report that the increase in net dipole moment enhances NLO properties and thus improves SHG performance.
5. Conclusions
In this paper, the structure of SCNO-0.8 was investigated using both SC-XRD and 3D-ED techniques. Unlike the average structure determined by SC-XRD, 3D-ED detects the superstructure of SCNO-0.8 along the a-direction. By analyzing crystal structure parameters and calculating polyhedral dipole moments based on bond valence theory, it was found that the superstructure of SCNO-0.8 originated from the different degrees of tilting of the NbO6 octahedron and the displacement of the Ca/Sr atoms. Compared to SNO, NbO6 octahedral distortion plays a major role in the increase in dipole moment and the enhancement of SHG properties. It can be seen that 3D-ED technology, as a powerful new tool, has advantages for studying superstructures caused by the ordered arrangement of light atoms. It has potential applications in analyzing the structure of compounds containing elements with an atomic mass lower than that of sulfur.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/cryst13060924/s1, Figure S1: SCNO-0.8 single crystal image; Figure S2: (a) and (b) are the h0l plane and hk0 plane diffraction pattern, respectively, that were reconstructed from the SC-XRD data respectively, that were reconstructed from the SC-XRD data. (c) and (d) are the h0l plane and hk0 plane diffraction pattern, respectively, that were reconstructed from the 3D PEDT data. (Each rectangle in the figure represents the unit cell of orthorhombic structure, and the white dots represent superstructure diffraction spots with relatively weak intensity); Figure S3: The SAED patterns collected along [01] the zone axis of the SCNO-0.8 powder sample; Figure S4: (a) NbO6 polyhedral of SCNO-0.8 average structure view along the a-axis, (b) NbO6 polyhedral of SCNO-0.8 superstructure view along the a-axis; Table S1: SC-XRD crystallographic data and structural refinement parameters; Table S2: Final dynamic refined superstructural parameters of SCNO-0.8; Table S3: Bond distances in the superstructure of SCNO-0.8; Table S4: Bond angles in the superstructure of SCNO-0.8; Table S5: magnitude (in Debye) of the polyhedral local dipole moments for SCNO-0.8 with average structure; Table S6: magnitude (in Debye) of the polyhedral local dipole moments for superstructure SCNO-0.8; Table S7: magnitude (in Debye) of the polyhedral local dipole moments for incommensurately modulated structure SNO.
Author Contributions
Conceptualization, K.M. and Z.Z.; methodology, K.M.; software, Z.Z.; validation, Z.Z., K.Z., and J.X.; formal analysis, Z.Z.; investigation, K.Z. and J.X.; resources, Z.Z. and J.X.; data curation, Z.Z.; writing—original draft preparation, K.M.; writing—review and editing, Z.Z. and J.X.; visualization, K.Z.; supervision, Z.Z.; project administration, Z.Z. and J.X.; funding acquisition, Z.Z. and J.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Shanghai Sailing Program, grant number 21YF1454400 and National Natural Science Foundation of China, grant number 22105218.
Data Availability Statement
The data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
Acknowledgments
Physicochemical measurements were performed at Shanghai Institute of Ceramics, Chinese Academy of Sciences.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Vincent, R.; Midgley, P.A. Double conical beam-rocking system for measurement of integrated electron diffraction intensities. Ultramicroscopy 1994, 53, 271–282. [Google Scholar] [CrossRef]
- Boulahya, K.; Ruiz-González, L.; Parras, M.; González-Calbet, J.M.; Nickolsky, M.S.; Nicolopoulos, S. Ab initio determination of heavy oxide perovskite related structures from precession electron diffraction data. Ultramicroscopy 2007, 107, 445–452. [Google Scholar] [CrossRef] [PubMed]
- Gemmi, M.; Nicolopoulos, S. Structure solution with three-dimensional sets of precessed electron diffraction intensities. Ultramicroscopy 2007, 107, 483–494. [Google Scholar] [CrossRef] [PubMed]
- Dorset, D.L.; Gilmore, C.J.; Jorda, J.L.; Nicolopoulos, S. Direct electron crystallographic determination of zeolite zonal structures. Ultramicroscopy 2007, 107, 462–473. [Google Scholar] [CrossRef] [PubMed]
- Kolb, U.; Gorelik, T.; Kubel, C.; Otten, M.T.; Hubert, D. Towards automated diffraction tomography: Part I--data acquisition. Ultramicroscopy 2007, 107, 507–513. [Google Scholar] [CrossRef]
- Gemmi, M.; Mugnaioli, E.; Gorelik, T.E.; Kolb, U.; Palatinus, L.; Boullay, P.; Hovmöller, S.; Abrahams, J.P. 3D Electron Diffraction: The Nanocrystallography Revolution. Acs Cent. Sci. 2019, 5, 1315–1329. [Google Scholar] [CrossRef]
- Burla, M.C.; Caliandro, R.; Carrozzini, B.; Cascarano, G.L.; Cuocci, C.; Giacovazzo, C.; Mallamo, M.; Mazzone, A.; Polidori, G. Crystal structure determination and refinement via SIR2014. J. Appl. Cryst. 2015, 48, 306–309. [Google Scholar] [CrossRef]
- Gruene, T.; Mugnaioli, E. 3D Electron Diffraction for Chemical Analysis: Instrumentation Developments and Innovative Applications. Chem. Rev. 2021, 121, 11823–11834. [Google Scholar] [CrossRef]
- Mugnaioli, E.; Lanza, A.E.; Bortolozzi, G.; Righi, L.; Merlini, M.; Cappello, V.; Marini, L.; Athanassiou, A.; Gemmi, M. Electron Diffraction on Flash-Frozen Cowlesite Reveals the Structure of the First Two-Dimensional Natural Zeolite. Acs Cent. Sci. 2020, 6, 1578–1586. [Google Scholar] [CrossRef]
- Bruhn, J.F.; Scapin, G.; Cheng, A.; Mercado, B.Q.; Waterman, D.G.; Ganesh, T.; Dallakyan, S.; Read, B.N.; Nieusma, T.; Lucier, K.W.; et al. Small Molecule Microcrystal Electron Diffraction for the Pharmaceutical Industry-Lessons Learned From Examining Over Fifty Samples. Front. Mol. Biosci. 2021, 8, 648603. [Google Scholar] [CrossRef]
- Samperisi, L.; Zou, X.; Huang, Z. Three-dimensional electron diffraction: A powerful structural characterization technique for crystal engineering. Crystengcomm 2022, 24, 2719–2728. [Google Scholar] [CrossRef]
- Zhang, D.; Oleynikov, P.; Hovmöller, S.; Zou, X. Collecting 3D electron diffraction data by the rotation method. Z Krist. 2010, 225, 94–102. [Google Scholar] [CrossRef]
- Boullay, P.; Palatinus, L.; Barrier, N. Precession Electron Diffraction Tomography for Solving Complex Modulated Structures: The Case of Bi5Nb3O15. Inorg. Chem. 2013, 52, 6127–6135. [Google Scholar] [CrossRef] [PubMed]
- Cichocka, M.O.; Angstrom, J.; Wang, B.; Zou, X.; Smeets, S. High-throughput continuous rotation electron diffraction data acquisition via software automation. J. Appl. Cryst. 2018, 51, 1652–1661. [Google Scholar] [CrossRef]
- Gemmi, M.; Oleynikov, P. Scanning Reciprocal Space for Solving Unknown Structures: Energy Filtered Diffraction Tomography and Rotation Diffraction Tomography Methods; Oldenbourg Wissenschaftsverlag: München, Germany, 2013; pp. 51–58. [Google Scholar] [CrossRef]
- Gemmi, M.; La Placa, M.G.I.; Galanis, A.S.; Rauch, E.F.; Nicolopoulos, S. Fast electron diffraction tomography. J. Appl. Cryst. 2015, 48, 718–727. [Google Scholar] [CrossRef]
- Plana-Ruiz, S.; Krysiak, Y.; Portillo, J.; Alig, E.; Estradé, S.; Peiró, F.; Kolb, U. Fast-ADT: A fast and automated electron diffraction tomography setup for structure determination and refinement. Ultramicroscopy 2020, 211, 112951. [Google Scholar] [CrossRef]
- Kodjikian, S.; Klein, H. Low-dose electron diffraction tomography (LD-EDT). Ultramicroscopy 2019, 200, 12–19. [Google Scholar] [CrossRef]
- Nannenga, B.L.; Shi, D.; Leslie, A.G.W.; Gonen, T. High-resolution structure determination by continuous-rotation data collection in MicroED. Nat. Methods 2014, 11, 927–930. [Google Scholar] [CrossRef]
- Bieseki, L.; Simancas, R.; Jorda, J.L.; Bereciartua, P.J.; Cantin, A.; Simancas, J.; Pergher, S.B.; Valencia, S.; Rey, F.; Corma, A. Synthesis and structure determination via ultra-fast electron diffraction of the new microporous zeolitic germanosilicate ITQ-62. Chem. Commun. (Camb) 2018, 54, 2122–2125. [Google Scholar] [CrossRef]
- Luo, Y.; Smeets, S.; Peng, F.; Etman, A.S.; Wang, Z.; Sun, J.; Yang, W. Synthesis and Structure Determination of Large-Pore Zeolite SCM-14. Chemistry 2017, 23, 16829–16834. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Yun, Y.; Zou, X.; Jorda, J.L.; Corma, A. ITQ-54: A multi-dimensional extra-large pore zeolite with 20 x 14 x 12-ring channels. Chem. Sci. 2015, 6, 480–485. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhang, C.; Jiang, J.; Yu, J.; Terasaki, O.; Mayoral, A. Structure Solution and Defect Analysis of an Extra-Large Pore Zeolite with UTL Topology by Electron Microscopy. J. Phys. Chem. Lett. 2020, 11, 3350–3356. [Google Scholar] [CrossRef] [PubMed]
- de la Cruz, M.J.; Hattne, J.; Shi, D.; Seidler, P.; Rodriguez, J.; Reyes, F.E.; Sawaya, M.R.; Cascio, D.; Weiss, S.C.; Kim, S.K.; et al. Atomic-resolution structures from fragmented protein crystals with the cryoEM method MicroED. Nat. Methods 2017, 14, 399–402. [Google Scholar] [CrossRef]
- Rodriguez, J.A.; Ivanova, M.I.; Sawaya, M.R.; Cascio, D.; Reyes, F.E.; Shi, D.; Sangwan, S.; Guenther, E.L.; Johnson, L.M.; Zhang, M.; et al. Structure of the toxic core of α-synuclein from invisible crystals. Nature 2015, 525, 486–490. [Google Scholar] [CrossRef]
- Nannenga, B.L.; Shi, D.; Hattne, J.; Reyes, F.E.; Gonen, T. Structure of catalase determined by MicroED. Elife 2014, 3, e03600. [Google Scholar] [CrossRef]
- Clabbers, M.T.B.; van Genderen, E.; Wan, W.; Wiegers, E.L.; Gruene, T.; Abrahams, J.P. Protein structure determination by electron diffraction using a single three-dimensional nanocrystal. Acta Crystallogr. Sect. D 2017, 73, 738–748. [Google Scholar] [CrossRef]
- Zheng, J.-C.; Zhu, Y.; Wu, L.; Davenport, J.W. On the sensitivity of electron and X-ray scattering factors to valence charge distributions. J. Appl. Cryst. 2005, 38, 648–656. [Google Scholar] [CrossRef]
- Ning, H.; Yan, H.; Reece, M.J. Piezoelectric Strontium Niobate and Calcium Niobate Ceramics With Super-High Curie Points. J. Am. Ceram. Soc. 2010, 93, 1409–1413. [Google Scholar] [CrossRef]
- Yan, H.; Ning, H.; Kan, Y.; Wang, P.; Reece, M.J. Piezoelectric Ceramics with Super-High Curie Points. J. Am. Ceram. Soc. 2009, 92, 2270–2275. [Google Scholar] [CrossRef]
- Chen, T.; Zhou, Z.; Liang, R.; Dong, X. Grain size effect on piezoelectric properties of Sr2Nb2O7 ceramics. J. Adv. Dielectr. 2018, 8, 1820003. [Google Scholar] [CrossRef]
- Daniels, P.; Tamazyan, R.; Kuntscher, C.; Dressel, M.; Lichtenberg, F.; van Smaalen, S. The Incommensurate Modulation of the Structure of Sr2Nb2O7. Acta Crystallogr. Sect. B Struct. Sci. 2002, 58, 970–976. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Wu, H.; Lin, Y.; Yuan, F.; Huang, Y.; Sun, S.; Teng, B.; Li, L.; Lin, Z. From Sr2Nb2O7 to CaxSr2–xNb2O7: An Effective Enhancement of Nonlinear Optical Activity by a Simple Way of Cation Substituting. Cryst. Growth Des. 2018, 18, 4140–4149. [Google Scholar] [CrossRef]
- Rothkirch, A.; Gatta, G.D.; Meyer, M.; Merkel, S.; Merlini, M.; Liermann, H.-P. Single-crystal diffraction at the Extreme Conditions beamline P02.2: Procedure for collecting and analyzing high-pressure single-crystal data. J. Synchrotron Radiat. 2013, 20, 711–720. [Google Scholar] [CrossRef] [PubMed]
- Palatinus, L.; Brazda, P.; Jelinek, M.; Hrda, J.; Steciuk, G.; Klementova, M. Specifics of the data processing of precession electron diffraction tomography data and their implementation in the program PETS2.0. Acta Crystallogr. Sect. B 2019, 75, 512–522. [Google Scholar] [CrossRef] [PubMed]
- Petříček, V.; Dušek, M.; Palatinus, L. Crystallographic Computing System JANA2006: General features. Z. Für Krist. Cryst. Mater. 2014, 229, 345–352. [Google Scholar] [CrossRef]
- Sheldrick, G. SHELXT-Integrated space-group and crystal-structure determination. Acta Crystallogr. Sect. A 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Palatinus, L.; Chapuis, G. SUPERFLIP—A computer program for the solution of crystal structures by charge flipping in arbitrary dimensions. J. Appl. Cryst. 2007, 40, 786–790. [Google Scholar] [CrossRef]
- Gemmi, M.; Lanza, A.E. 3D electron diffraction techniques. Acta Crystallogr. Sect. B 2019, 75, 495–504. [Google Scholar] [CrossRef]
- Zhou, Z.; Chen, T.; Dong, X.-L. Research Progress of Perovskite Layer Structured Piezoelectric Ceramics with Super High Curie Temperature. J. Inorg. Mater. 2018, 33, 251–258. [Google Scholar]
- Lichtenberg, F.; Herrnberger, A.; Wiedenmann, K. Synthesis, structural, magnetic and transport properties of layered perovskite-related titanates, niobates and tantalates of the type AnBnO3n+2, A′Ak−1BkO3k+1 and AmBm−1O3m. Prog. Solid State Chem. 2008, 36, 253–387. [Google Scholar] [CrossRef]
- Lichtenberg, F.R. Synthesis of perovskite-related layered AnBnO3n+2 = ABOXtype niobates and titanates and study of their structural, electric and magnetic properties. Prog. Solid State Chem. 2001, 29, 1–70. [Google Scholar] [CrossRef]
- Isupov, V.A. Crystal chemical aspects of the layered perovskite-like oxide ferroelectrics of the AnMnO3n+2 type. Ferroelectrics 1999, 220, 79–103. [Google Scholar] [CrossRef]
- Bellaiche, L.; Íñiguez, J. Universal collaborative couplings between oxygen-octahedral rotations and antiferroelectric distortions in perovskites. Phys. Rev. B 2013, 88, 014104. [Google Scholar] [CrossRef]
- Zhou, J.S.; Goodenough, J.B. Intrinsic structural distortion in orthorhombic perovskite oxides. Phys. Rev. B 2008, 77, 132104. [Google Scholar] [CrossRef]
- Goodenough, J.B.; Zhou, J.S. Orbital ordering in orthorhombic perovskites. J. Mater. Chem. 2007, 17, 2394–2405. [Google Scholar] [CrossRef]
- Brown, I.; Shannon, R. Empirical Bond-Strength--Bond-Length Curves for Oxides. Acta Crystallogr. Sect. A 1973, 29, 266. [Google Scholar] [CrossRef]
- Brown, I.D. Recent developments in the bond valence model of inorganic bonding. Phys. Chem. Miner. 1987, 15, 30–34. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).