Abstract
The processes of crystallization and melting, and the structure of ice formed under freezing in an alternating electromagnetic field with a frequency of 2.45 GHz have been studied using thermometry, differential scanning calorimetry, and X-ray diffraction. Using X-ray powder diffraction at 85 K, it was determined that the obtained samples consisted of several phases of hexagonal ice Ih, with a density 0.43 ÷ 2.58% higher than that of ordinary ice. The time necessary for this ice to crystallize was approximately 2.2 times shorter than that of ordinary ice not exposed to an alternating electromagnetic field. According to the data of differential scanning calorimetry, the melting of this ice was accompanied by an endothermic heat effect 9% greater than that of ordinary ice, and a melting point that was 1 °C lower. A similar effect is typical of the melting of metastable phases. We assume that the formation of ice Ih with increased density results from the action of an alternating electromagnetic field on the network of hydrogen bonds of liquid water which is a precursor for ice formation.
1. Introduction
The central problem in the food industry during the freezing and subsequent defrosting of foods is the degradation of their organoleptic qualities. This is mainly related to two factors that accompany the process of freezing of water and water systems in biological products: (i) the resulting crystalline ice has a larger specific volume than water and destroys the cellular structure of the product; (ii) during the storage of a frozen product, ice crystals grow due to the dehydration of adjacent tissues until they are completely dehydrated. Both of these factors have a highly negative effect on the organoleptic properties and physical and chemical characteristics of frozen foods: the cellular and intercellular structures of a product are destroyed, and the concentration of substances dissolved in water changes.
The problems of damage to the cellular structure and dehydration of foods by growing ice crystals are partially solved in practice by accelerating the process of freezing (the so-called shock freezing). Its use leads to a decrease in the size of crystals and somewhat increases the time of their growth to critical sizes during storage. Since this method is energy-consuming, a lot of studies suggest using alternative freezing methods. One of the proposed methods is the freezing of water under the action of an alternating electromagnetic field or a static electric field [1]. According to the experimental data, static electric fields reduce the temperature of water supercooling and increase the nucleation rate of ice crystals [2,3]. The theoretical calculations [4] show that a strong electrostatic field close to the electrical breakdown of water can result in the formation of new crystalline phases of ice and a significant change in the H2O phase diagram. However, both experimental and theoretical results on the effect of a static electric field on water crystallization are hardly suitable for practical application due to the use of small samples and very high electric fields.
A lot of experimental studies demonstrate that alternating electromagnetic fields with frequencies of several GHz cause a significant increase in the water crystallization rate, which is accompanied by a decrease in the crystallite size. It is assumed that this effect may result from thermal fluctuations under crystallization [5] or disturbance and partial destruction of hydrogen bonds in liquid water, which is a precursor of ice formation, caused by the action of microwave electromagnetic radiation [6]. Recent theoretical and experimental studies performed by X-ray tomography [7] have shown that the most likely reason for this effect is the action of microwave radiation on the network of liquid water hydrogen bonds. In this case, this should lead to a change in the structure of H2O molecule clusters in liquid water as well as a change in the structure, phase composition, and density of ice obtained under its freezing. As stated above, the density of ice formed after crystallization and the crystallite size are key characteristics for the preservation of biological objects. However, a change in the specific volume (density) of water after its freezing under the action of an EMF has not been studied before.
The present study is focused on determining the time of the crystallization of ice under the action of electromagnetic radiation with a frequency of 2.45 GHz; it is also an X-ray diffraction study of its structural state (amorphous or crystalline one, the type and parameters of the cell). Our investigation has shown for the first time that the freezing of water in a specially organized alternating electromagnetic field (EMF) not only significantly reduces the crystallization time but also allows the formation of ice with a specific volume significantly smaller than that of ordinary hexagonal ice Ih.
2. Materials and Methods
Figure 1 depicts the scheme of a laboratory setup that was employed for ice synthesis in an alternating EMF and for measurements of a change in the temperature of a sample over time during its cooling.

Figure 1.
The working chamber of the freezer for obtaining ice in an alternating electromagnetic field. 1—sample; 2—modules of an alternating EMF generation; 3—body of the working chamber; 4—cold air supply sleeve.
The freezer consisted of an air-cooled refrigerator and a heat-insulated working chamber. The air from the refrigerator evaporator circulated in a closed circuit through the working chamber along heat-insulated flexible sleeves (see Figure 1). The power of the freezer compressor was 2.5 kW. The temperature of the air supplied to the chamber was up to −30 °C. The heat-insulated working chamber was a cube with external dimensions of 1140 × 1140 × 1140 mm. Thus, the freezer enabled the simulation of conditions of a shock freezing chamber and provided a sufficient operating volume to perform experiments. The module of EM field generation was located in the working chamber of the freezer and consisted of three sources of electromagnetic radiation with a frequency of 2.45 GHz, uniformly spaced on a plane in a circle around the object to be frozen, and a control unit working on an Arduino processor. The processor controlled three solid-state relays (Shockley diodes) designed for a single-phase alternating voltage of up to 300 V and current up to 10 A. For control during the experiment, the current and voltage measurements were provided for each of the channels. The radiation sources were sequentially turned on using the program and generated EM radiation pulses with a duration of 0.5 s.
As an object of freezing, distilled water was used in two types of test tubes: hydrophobic plastic and hydrophilic glass. The volume of water in the plastic test tube was 1 mL, and that in the glass test tube was 8 mL.
To measure the temperature of the object during the experiment, a Micronor FOTEMP1-OEM-MNT fiber-optic thermometer was used since a fiber-optic sensor can operate in a medium with microwave radiation, and the device itself can record the dynamics of the temperature changes. The temperature readings were recorded every 10 s.
The melting of ice obtained in an EMF was studied by differential scanning calorimetry using a Perkin Elmer calorimeter. In contrast to the crystallization thermograms obtained under the action of EM radiation on a sample, the melting was investigated on a sample obtained after its synthesis in an alternating EMF and quenched to liquid nitrogen temperature.
Several ice samples frozen in electromagnetic fields were then immersed in liquid nitrogen, removed from the test tubes, and studied using X-ray powder diffraction at 85 K on a Siemens D500 diffractometer using Cu Kα1,2 radiation extracted by a secondary monochromator. The diffractometer was equipped with a specially designed nitrogen cryostat that allowed loading powdery samples from a bath with liquid nitrogen without their intermediate heating. The structure and the lattice parameters of the formed crystalline phases of ice were determined by full-profile Rietveld analysis of the X-ray diffraction patterns using the POWDERCELL2.4 program.The ice volume was also measured in two ways:
- -
- Visually in a graduated test tube;
- -
- Visually in a system with anti-freeze oil.
For the last measurements, we used AMG-10 anti-freeze oil that does not thicken down to T = −60 °C and is not miscible with water in the required temperature range of −30–25 °C.
3. Results
The kinetics of water crystallization were studied by measuring the temperature of water over time under its cooling. Figure 2 shows thermograms of the sample of water cooled in an alternating electromagnetic field and in its absence. The thermograms were obtained on samples with the same mass, i.e., m = 8 g, and had the close initial temperature of 22–24 °C.
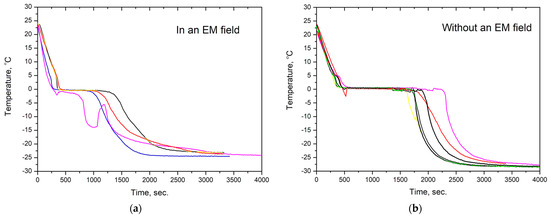
Figure 2.
(a) Temperature change over time for water cooled under the action of EM radiation with a frequency of 2.45 GHz and (b) without radiation. Differently colored curves stand for different but very similar water samples cooled in the same mode.
As can be seen from the figure, the temperature of ice crystallization onset was in the range of T= −3 – 0 °C both in the presence and absence of an electromagnetic field. In the thermogram of water cooling without an EMF, the average time of the isothermal part at T~0 °C corresponding to ice crystal nucleation and growth was 1280 (±159) seconds. When water was cooled under the action of electromagnetic radiation, the duration of the isothermal part was reduced 2.2 times to 576 (±93) seconds. Moreover, in some cases, instead of one pronounced isothermal part, the thermograms of water in an EMF had several such parts, followed by temperature rises and drops. It should be noted that the heating of ice and water under the action of microwave radiation should have increased the crystallization time and the temperature inside the sample after ice formation and also decreased the rate of liquid water cooling. However, no such effects were observed in all four thermograms, which may indicate a relatively weak intensity of electromagnetic radiation.
The melting of ice obtained in an EMF was studied by differential scanning calorimetry. In contrast to the crystallization thermograms obtained under the action of EM radiation on a sample, the melting was investigated on a sample obtained after its synthesis in an alternating EMF and quenched to liquid nitrogen temperature. An ice sample with a mass of 7.6 mg was loaded into the calorimeter cell at −170 °C and heated at a rate of 20 °C/min to 20 °C with subsequent cooling to −170 °C. In total, three such cycles of heating and cooling were completed. The resulting heating curves are shown in Figure 3.

Figure 3.
Endotherms of the melting of ice obtained under the action of EM radiation with a frequency of 2.45 GHz. The heating rate was 20 °C/min. The black line is the first heating of the sample, the red line is the second heating, and the blue line is the third heating. The sample was cooled down to −170 °C after each heating.
All three curves had only one heat absorption peak associated with ice melting. The amount of absorbed heat was 356 J/g for curve 1 and 338 and 332 J/g for curves 2 and 3. Considering the measurement error related to water evaporation from the DSC cell, the melting heats for curves 2 and 3 can be considered identical and coinciding with the melting enthalpy of ordinary ice [8]. However, the onset of the peak in curve 1 is shifted lower by approximately one degree on the temperature scale relative to the peaks in curves 2 and 3. This may indicate the beginning of heat absorption by the sample synthesized in an EMF at approximately −1 °C. Considering that the sample was loaded into the calorimeter cell in the form of individual particles, its poor heat contact with the ampoule bottom, on the contrary, should have increased the melting point. In addition, the heat effect in curve 1 was 356 J/g, which was 7% greater than the enthalpy of ice melting and beyond the instrumental error (±5%). Thus, one can assume that both a decrease in the time of the crystallization of ice under the action of a high-frequency EMF and a great heat effect during its melting may be related to the formation of ice with properties different from those of the ordinary one.
The structure and phase composition of ice formed in an alternating electric field were studied using X-ray diffraction at 85 K. It should be noted that all the investigated polycrystalline samples of ice frozen in plastic and glass test tubes were characterized by a strong texture, which could not be eliminated even by grinding in a mortar in liquid nitrogen. This greatly hampered the analysis of the X-ray diffraction patterns using full-profile Rietveld analysis; therefore, it was necessary to focus mainly on the angular position of the diffraction lines instead of their intensity. The grinding of the samples and the duration of their storage in liquid nitrogen did not affect the phase composition and parameters of the crystalline structure of the phases. Figure 4 illustrates a typical diffraction pattern of the sample of ice obtained in the glass test tube under the action of an alternating EMF in comparison with the calculated diffraction spectra of metastable ice Ic [9], ice Ih [10], as well as ices A and B, whose formation at normal pressure and under the action of an electric field was predicted earlier using theoretical calculations [4].
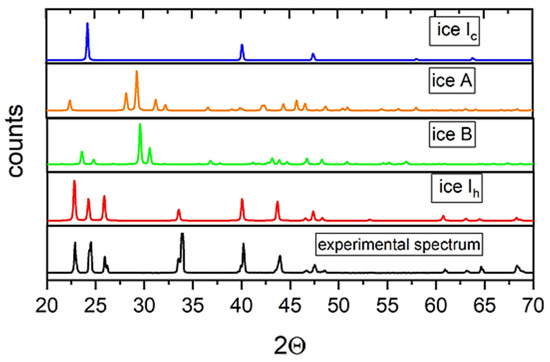
Figure 4.
Typical diffraction spectrum of ice synthesized under the action of EM radiation of 2.45 GHz (lower panel), calculated spectra of ices Ic, A, B, and Ih (upper panels).
As can be seen from the figure, the spectral lines of ice Ic partially coincide with the obtained diffraction spectrum. However, the calculated spectrum of cubic ice contains a peak at an angle of 2Θ = 58°, which was not observed in all the spectra of the obtained samples. In this case, it can be assumed that the obtained sample did not contain ice Ic in an amount sufficient for its registration by X-ray diffraction. This statement is also suitable for the so-called “stack” ice [11]: its diffraction spectrum should contain intense lines of ice Ic. The spectra of ices A and B contain a larger number of lines that were not observed in our spectra and, consequently, are also not suitable for describing the structure of the ice obtained. The calculated spectrum of ice Ih has the best agreement with the observed spectrum. However, the diffraction spectrum of this sample contains a significant number of split lines as compared with the spectrum of ordinary ice. The positions of these lines are shifted toward larger angles relative to ice obtained without the action of an EMF. We assumed that the obtained spectrum corresponded to hexagonal ice Ih with different unit cell volumes.
Figure 5 shows the calculation of the phase composition and molecular volume for this sample, which demonstrated that it contained a 41 vol.% of hexagonal ice with a molecular volume of 32 Å3 and a 59 vol.% of ice with a molecular volume of 31.75 Å3.

Figure 5.
Powder diffraction patterns of the ice samples measured at T = 85 K on a Siemens D500 X-ray diffractometer using Cu Kα radiation. The black curve is for the sample crystallized without a field (sample no. 1 from Table 1). The red curve is for the two-phase sample crystallized in an electromagnetic field (sample no. 4 from Table 1). A row of blue and red vertical bars under the diffraction patterns are the calculated positions of diffraction lines of the phases with a smaller and larger specific volume observed in sample no. 4.
Similar spectra were also observed for other ice samples crystallized in electromagnetic fields. The results of the measurement of the water molecule volume obtained for these samples in comparison with the data on ordinary ice measured in the present study and by the authors of [10] are listed in Table 1.

Table 1.
Parameters of the hexagonal phase cell in ice samples crystallized in electromagnetic fields and investigated using X-ray diffraction at 85 K with Cu Kα radiation. For comparison, the data [10] of the X-ray diffraction study of ice Ih (space group P63/mmc) crystallized in the absence of a field at 85 K, as well as our data at 100 K (sample no. 1), are provided.
The difference in the unit cell volumes was calculated relative to the volume of initial ice measured at 100 K since both spectra were registered on the same diffractometer. In turn, we considered the difference between the unit cell volume of ice obtained without an EMF and the literature data (0.32%) to be the maximum possible error of our X-ray diffraction measurements of the unit cell volume of hexagonal ice. In sample no. 2, approximately 30% of the ice crystalline phase with a volume 2.58% smaller than that of ice Ih was found. This value far exceeds the possible measurement error.
In all other samples shown in this table, the volume effect was significantly lower. As an example, the diffraction pattern for sample no. 4 is presented above. It contained 59% of the crystalline phase of ice with a volume 1.20% smaller than that of ice Ih and 41% of the crystalline phase of ice with a decrease in volume of 0.43%. The latter volume effect is the lowest of all the obtained values and is close to the maximum possible error of our X-ray diffraction measurements (0.32%).
We performed 327 measurements of the density of ice obtained by cooling water in an EMF in the graduated test tube, as well as in a system with anti-freeze oil. In two experiments carried out, the density of the sample at T = 248 K turned out to be equal to the density of liquid water of 1.01 g/cm3. In a much larger number of experiments, however, the density of ice was somewhat lower than that of water. It is worth noting that the greater the difference between the final density of ice and the density of initial water, the more often this value was obtained. For example, an ice density of 0.97 g/cm3 was obtained in 15 experiments; 0.96 g/cm3 was obtained in 36 experiments; and 0.95 g/cm3 was obtained in 178 experiments. Such a large variation in the obtained density values obtained by the volumetric method was caused by a significant error in the visual estimation of the volume of ice obtained in the presence and absence of an alternating EMF [12]. The difference in the volume effect obtained by different methods may be related to the peculiarities of X-ray powder diffraction measurements. Whereas in volumetric measurements the value of the entire ice volume was recorded, X-ray powder diffraction allowed determining the volume of crystalline phases only. Smaller ice crystals are known to be formed under the action of an alternating EMF. In this case, in the sample of ice obtained in this field, the fraction of the grain-boundary phase with an amorphous structure should increase, but its volume cannot be determined by X-ray diffraction.
However, another explanation for this difference is possible. It is known that with an increase in density (under the action of pressure), hexagonal ice has a lower thermal expansion coefficient [13,14,15]. In this case, with an increase in temperature, the denser ice obtained in an EMF should increase the volume by a smaller extent than the ordinary one. Correspondingly, at a temperature of 248 K, the difference between the volume of ordinary hexagonal ice and that of ice synthesized in an EMF can be much greater than the difference at a temperature of 85 K used for X-ray diffraction studies. Nevertheless, the X-ray powder diffraction method unambiguously indicates the formation of a denser phase of hexagonal ice under its crystallization in a high-frequency electromagnetic field.
4. Discussion
The use of low radiation power in our experiment did not result in the heating of water preventing its crystallization. It is known that, in this case, the penetration depth of EM waves with a frequency of 2.45 GHz in liquid water is small due to its high permittivity and, according to various data, is approximately 5–20 mm [16,17]. However, when ice crystals first arise, the penetration depth of radiation should significantly increase due to lower ice permittivity [18]. According to the literature data, during the crystallization of water, which is included in methylcellulose gel, the action of electromagnetic radiation with a frequency of 2.45 GHz reduces the average size of ice crystals by approximately 25% [6]. In this case, a smaller average size of crystallites correlates with a decrease in the time necessary for the crystallization of water to be present in the system. Considering that continuous EM radiation with a frequency of 2.45 GHz was also used in our study, as in [6], we assume that the decrease in the time of ice crystallization observed in our study should also be accompanied by the emergence of ice crystallites with reduced sizes.
A decrease in the crystallization time can be induced by both a decrease in heat generation and an increase in heat removal from the system [19]. According to our DSC data, the specific heat of melting and, correspondingly, crystallization, increased by approximately 9% for ice obtained under the action of microwave radiation. Thus, the total heat generation during water crystallization should have increased and, while preserving the same value of heat removal, the total crystallization time should have also increased. A change in heat removal from the system, while maintaining its geometry, is possible with an increase in the thermal conductivity of its constituent elements only. According to the data from [20], an increase in the density of ice with an increase in pressure does not change its thermal conductivity coefficient. Thus, we believe that the thermal conductivity coefficient of ice that is obtained under the action of radiation and contains a phase with increased density does not differ from that of ordinary ice. Moreover, we assume that the effect of microwave radiation does not change the physical properties of the test tube material. In this case, the only possibility for the heat removal of the system to increase is an increase in the thermal conductivity coefficient of liquid water. The use of three magnetrons switched on in series one after another can lead to the emergence of circulation in liquid water due to the interaction between radiation and the dipole moment of a water molecule. Furthermore, due to the low radiation power, the amplitude of water molecule oscillations is low, and, correspondingly, no heating of the sample occurs. The vortices arising under the action of radiation promote heat transfer from the inner part of the sample to the surface and, thus, lead to an increase in the rate of its cooling. The emergence of ice crystals additionally increases the rate of heat transfer since the thermal conductivity of ice is four times greater than that of liquid water. Thus, the decrease in the time of water crystallization under the action of electromagnetic radiation can be explained by an increase in the rate of heat transfer inside the sample. The emergence of smaller ice crystallites under the action of radiation can be explained by the appearance of additional nucleation centers.
In addition, it was assumed in [6] that the smaller size of ice crystallites formed in a high-frequency EMF is related to the disturbance of the network of hydrogen bonds in liquid water. Our X-ray diffraction data show that the effect of low-intensity EMF radiation with a frequency of 2.45 GHz, which is similar to that used in [6], leads to the formation of a denser phase of hexagonal ice Ih. According to the model published by Ponyatovsky and Sinitsyn [21], liquid water consists of clusters of H2O molecules whose structure corresponds to high- and low-density amorphous ices. The molar ratio between these clusters changes under the action of temperature and pressure, which results in the observed maximum density of liquid water at 277 K and normal pressure. We assume that the action of microwave radiation may also lead to an increase in the fraction of high-density molecular clusters in liquid water that is a precursor for ice formation. The oscillation period of an electromagnetic field and, correspondingly, water molecules at a frequency of 2.45 GHz, is approximately 1 ns. This value is much less than the 100–200 ns necessary for the formation of a critical ice nucleus [22]. This may be the reason for the suppression of the growth of ice crystals and may lead to a decrease in their size under the action of electromagnetic radiation. In turn, a possible increase in the fraction of high-density clusters in liquid water under the action of electromagnetic radiation is the reason for the formation of high-density hexagonal ice.
It is known that, in the absence of the transition of metastable phases to a state stable under given conditions, they should melt at a lower temperature [23]. We assume that the decrease in the melting temperature of the sample synthesized in EM radiation by one degree, detected using differential scanning calorimetry, is related to the presence of a significant fraction of denser hexagonal ice in a metastable state in the sample.
Water into and between cells is divided into three categories: bound water, immobilized water, and free water [24]. When frozen, ice crystals are formed from free water first [25]. The formation of large crystals leads to mechanical damage of the cells, their dehydration, and protein denaturation [26]. The data obtained in this study are primarily related to free water and the formation of ice crystals in it. As can be seen from our data, the effect of electromagnetic radiation with a frequency of 2.45 GHz on free water, which was organized in the manner indicated in the Materials and Methods section, significantly reduces the time of its crystallization, which in turn should lead to the formation of more desirable small ice crystals [6]. The discovered formation of a denser modification of hexagonal ice Ih under the action of EM radiation additionally reduces the size of crystallites and, thus, can significantly reduce the probability of damage to the cellular structure during freezing.
5. Conclusions
A comparative study of the characteristic times of crystallization, the heat effects of melting, and the phase composition of H2O with and without the action of electromagnetic radiation at a frequency of 2.45 GHz was carried out. The measurements of the time dependencies of the sample temperature showed that the action of a high-frequency electromagnetic field lead to a 2.2-fold decrease in the ice crystallization time as compared with control samples not subjected to electromagnetic radiation. According to the data obtained by DSC, the melting of ice crystallized under the action of electromagnetic radiation occurred at T = −1 °C, which might indicate the presence of a metastable phase in the sample. The studies performed using X-ray diffraction at 85 K demonstrated the presence of several phases of hexagonal ice which differed in the unit cell volumes. The unit cell volume of all the crystalline structures was 0.43 ÷ 2.58% smaller than that of hexagonal ice obtained by the traditional method without an alternating EMF. The data of the volumetric studies confirmed the compaction of most water samples (229 measurements out of 327) up to 0.95–0.97 g/cm3 after their crystallization in an alternating electromagnetic field. We assume that, under the action of electromagnetic radiation with a frequency of 2.45 GHz, disturbance or partial destruction of hydrogen bonds in liquid water occurs, leading to an increase in the fraction of clusters of H2O molecules with a short-range order corresponding to high-density amorphous ice. Under the continuing action of radiation, the cooling of such water leads to the emergence of a metastable phase of hexagonal ice Ih with increased density and reduces the time of its crystallization.
Author Contributions
I.V.K.: conceptualization, methodology, writing—review and editing; V.S.E.: writing—original draft preparation, methodology, investigation, formal analysis; G.G.F.: supervision, resources, funding acquisition; M.A.K.: investigation, visualization; A.R.O.: software, investigation, methodology. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
The work was carried out within the state task of Osipyan Institute of Solid State Physics RAS.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jha, P.K.; Xanthakis, E.; Jury, V.; Le-Bail, A. An Overview on Magnetic Field and Electric Field Interactions with Ice Crystallisation; Application in the Case of Frozen Food. Crystals 2017, 7, 299. [Google Scholar] [CrossRef]
- Wei, S.; Xiaobin, X.; Hong, Z.; Chuanxiang, X. Effects of dipole polarization of water molecules on ice formation under an electrostatic field. Cryobiology 2008, 56, 93–99. [Google Scholar] [CrossRef]
- Orlowska, M.; Havet, M.; Le-Bail, A. Controlled ice nucleation under high voltage DC electrostatic field conditions. Food Res. Inter. 2009, 42, 879–884. [Google Scholar] [CrossRef]
- Zhu, W.; Huang, Y.; Zhu, C.; Wu, H.-H.; Wang, L.; Bai, J.; Yang, J.; Francisco, J.S.; Zhao, J.; Yuan, L.-F.; et al. Room temperature electrofreezing of water yields a missing dense ice phase in the phase diagram. Nat. Commun. 2019, 10, 1925. [Google Scholar] [CrossRef]
- Xanthakis, E.; Le-Bail, A.; Ramaswamy, H. Development of an innovative microwave assisted food freezing process. Innov. Food Sci. Emerg. Technol. 2014, 26, 176–181. [Google Scholar] [CrossRef]
- Hanyu, Y.; Ichikawa, M.; Matsumoto, G. An improved cryofixation method: Cryoquenching of small tissue blocks during microwave irradiation. J. Micros 1992, 165, 255–271. [Google Scholar] [CrossRef]
- Sadot, M.; Curet, S.; Chevallier, S.; Le-Bail, A.; Rouaud, O.; Havet, M. Microwave assisted freezing part 2: Impact of microwave energy and duty cycle on ice crystal size distribution. Innov. Food Sci. Emerg. Technol. 2020, 62, 102359. [Google Scholar] [CrossRef]
- CRC Handbook of Chemistry and Physics, 2009−2010, 90th ed. J. Am. Chem. Soc. 2009, 131, 12862. [CrossRef]
- Shallcross, F.V.; Carpenter, G.B. X-Ray Diffraction Study of the Cubic Phase of Ice. J. Chem. Phys. 1957, 26, 782–784. [Google Scholar] [CrossRef]
- Röttger, K.; Endriss, A.; Ihringer, J.; Doyle, S.; Kuhs, W.F. Lattice constants and thermal expansion of H2O and D2O ice Ih between 10 and 265 K. Acta Cryst. B 1994, 50, 644–648. [Google Scholar] [CrossRef]
- Malkin, T.L.; Murray, B.J.; Salzmann, C.G.; Molinero, V.; Pickering, S.J.; Whale, T.F. Stacking disorder in ice I. Phys. Chem. Chem. Phys. 2015, 17, 60–76. [Google Scholar] [CrossRef] [PubMed]
- Pustogvar, A.; Kulyakhtin, A. Sea ice density measurements. Methods and uncertainties. Cold Reg. Sci. Technol. 2016, 131, 46–52. [Google Scholar] [CrossRef]
- Tchijov, V.; Keller, J.; Rodriguez-Romo, S.; Nagornov, O. Kinetics of Phase Transitions Induced by Shock-Wave Loading in Ice. J. Phys. Chem. B 1997, 101, 6215–6218. [Google Scholar] [CrossRef]
- Lupo, M.J.; Lewis, J.S. Mass-Radius Relationships in Icy Satellites. Icarus 1979, 40, 157–170. [Google Scholar] [CrossRef]
- Noya, E.G.; Menduina, C.; Aragones, J.L.; Vega, C. Equation of State, Thermal Expansion Coefficient, and Isothermal Compressibility for Ices Ih, II, III, V, and VI, as Obtained from Computer Simulation. J. Phys. Chem. C 2007, 111, 15877–15888. [Google Scholar] [CrossRef]
- Knyazev, V.Y.; Kossyi, I.A.; Malykh, N.I.; Yampolskii, E.S. Penetration of Microwave Radiation into Water: Effect of Induced Transparency. Tech. Phys. 2003, 48, 1489–1492. [Google Scholar] [CrossRef]
- Horikoshi, S.; Sumi, T.; Serpone, N. Unusual Effect of the Magnetic Field Component of the Microwave Radiation on Aqueous Electrolyte Solutions. J. Microw. Power Electromagn. Energy 2012, 46, 215–228. [Google Scholar] [CrossRef]
- Artemov, V.G.; Volkov, A.A. Water and Ice Dielectric Spectra Scaling at 0 °C. Ferroelectrics 2014, 466, 158–165. [Google Scholar] [CrossRef]
- Aleksandrov, V.D.; Golodenko, N.N.; Dremov, V.V.; Postnikov, V.A.; Sobol’, O.V.; Stasevich, M.V.; Shchebetovskaya, N.V. Using numerical simulation methods for the analysis of heating and cooling thermograms characterizing the melting and crystallization of water. Tech. Phys. Lett. 2009, 35, 415–417. [Google Scholar] [CrossRef]
- Andersson, O.; Suga, H. Thermal conductivity of the Ih and XI phases of ice. Phys. Rev. B Cond. Matter 1994, 50, 6583–6588. [Google Scholar] [CrossRef]
- Ponyatovsky, E.G.; Sinitsyn, V.V.; Pozdnyakova, T.A. The metastable T−P phase diagram and anomalous thermodynamic properties of supercooled water. J. Chem. Phys. 1998, 109, 2413–2422. [Google Scholar] [CrossRef]
- Matsumoto, M.; Saito, S.; Ohmine, I. Molecular dynamics simulation of the ice nucleation and growth process leading to water freezing. Nature 2002, 416, 409–413. [Google Scholar] [CrossRef] [PubMed]
- Brazhkin, V.; Lyapin, A. Metastable high-pressure phases of low-Z compounds: Creation of a new chemistry or a prompt for old principles? Nat. Mater. 2004, 3, 497–500. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.-Y.; Xie, J. Water dynamics and microbial communities of bigeye tuna (Thunnus obesus) during simulated cold chain logistics. J. Food Saf. 2020, 40, e12766. [Google Scholar] [CrossRef]
- Deng, Q.; Wang, Y.; Sun, L.; Li, J.; Fang, Z.; Gooneratne, R. Migration of Water in Litopenaeus Vannamei Muscle Following Freezing and Thawing. J. Food Sci. 2018, 83, 1810–1815. [Google Scholar] [CrossRef]
- Sun, Q.; Sun, F.; Xia, X.; Xu, H.; Kong, B. The comparison of ultrasound-assisted immersion freezing, air freezing and immersion freezing on the muscle quality and physicochemical properties of common carp (Cyprinus carpio) during freezing storage. Ultrason. Sonochem. 2019, 51, 281–291. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).