Abstract
Current thermal simulation methods are not suitable for small-size fast-activation thermal batteries, so this paper provides an improved simulation method to calculate thermal cell temperature changes using the COMSOL platform. A two-dimensional axisymmetric model of thermal batteries has been established, considering the actual heat release situation and the mobile heat source of thermal batteries. Based on it, the temperature change and electrolyte melting of thermal batteries under high-temperature conditions (50 °C) have been simulated, in which the temperature change law, thermal characteristics, and electrolyte melting characteristics have been analyzed in depth. The results show that the additional heating flakes and insulation design above and below the stack can effectively reduce heat loss. Most of the melting heat of the electrolyte flows in from the negative side. In addition, the thermal battery activation time has been calculated to be 91.2 ms at the moment when all the thermal battery electrolyte sheets begin to melt, and the absolute error was within 10% compared with the experimental results, indicating that the simulation model has high accuracy and can effectively broaden the simulation area of thermal batteries.
1. Introduction
Thermal batteries are a kind of primary battery mainly used for missile and rocket electronic instruments, which have short activation time, wide operating temperature range, and high output power characteristics [1,2]. When stored at room temperature, thermal battery electrolytes are a nonconductive solid, and the heating agent inside is ignited by an electric ignition or striker. When heated to the melting point, the electrolytes turn to a molten state and become ionic conductive. Thus, thermal batteries are activated [3,4,5]. However, in order to prevent unexpected thermal runaway or even explosion during battery operation, accurate and reliable thermal cell designs need to be further developed [6]. The melting points of thermal batteries with melting electrolytes generated by the pyrotechnic agent are mostly between 350 and 550 °C. The excess heat should not decompose the cathode and anode materials, so the choice of electrode materials for thermal batteries is a key factor that must be considered in the battery design. Among all, FeS2 is widely used as the cathode material in thermal batteries due to its high reliability, capacity, low cost, and material accessibility. However, it usually decomposes near the operating temperature of thermal batteries, resulting in a significant decrease in the operating voltage [7,8]. To suppress the decomposition, one novel choice is to directly modify the interface features of the FeS2 cathode material. For example, Liu et al. [9] modified the FeS2 cathode with Al2O3 nanoparticles. The high interface wettability expands the contact area, which increases the transport rate of lithium ions at the active-substance interface and suppresses the decomposition of FeS2. LiSi alloy is currently the most commonly used anode material, which becomes molten-state at 734 °C, though its structure deteriorates rapidly during abnormal discharge, resulting in leakage, short circuit, and even explosion of thermal batteries [7,10]. The ternary all-lithium electrolyte used in the isolation sheet has an ionic conductivity of 3.3 S/cm at 500 °C and a melting point of 430 °C [11]. The high ionic conductivity provides support for the high-power output of the battery, though the higher melting point also requires more pyrotechnic agents to provide energy, increasing the battery volume and cost. To block the flowing of electrolytes at high temperatures, MgO is always selected as the flow-blocking agent [12].
With the continuous development of thermal battery applications, the traditional thermal battery design relying on empirical “design-experimental verification-improvement” research methods can no longer meet the actual needs. Finite-element simulation technology is a modern design theory method widely used in electrochemical investigations. Commercial finite-element analysis software such as ANSYS, COMSOL, and PHOENICS [13] can simulate the internal temperature changes, electrolyte melting, voltage changes, and other data of thermal batteries, providing a more reliable theoretical basis for thermal battery design [14,15,16,17,18]. Computational models of molten salt battery performance focus on heat transfer and ignore electrochemical or mechanical phenomena. By predicting the spatial temperature distribution of each material, the maximum temperature reached by each material can be evaluated, and data such as the approximate time of the battery temperature rise time and lifetime can be obtained [8]. For the simulation calculation of thermal batteries, in the late 1970s, the Sandia National Laboratory (SNL) in the United States began thermal battery thermal simulation research using computer simulation methods. However, the computing power at that time was not enough, and the result was not ideal. Korean researchers such as Mun et al. [19] used COMSOL software to analyze the thermal characteristics of the activation and working stages of low-capacity thermal batteries. The simulation results of the large-capacity thermal battery were only 6% different from the experimental data. Dekel et al. [20] used the thermal battery simulator (TABS v3) developed by the Sandia National Laboratories to study thermal battery input parameters and obtained more realistic simulation results and model verification through understanding the relationship between uncertain input and probabilistic output. In order to study the thermal runaway and corrosion of thermal batteries, Jang Hyeon Cho et al. [21] studied the optimal discharge temperature of thermal batteries and studied the influence of thermal battery heating-sheet thickness on the temperature of positive and negative electrodes and electrolytes based on the COMSOL software, which contributed to the design of electrodes, electrolytes, heat sources, insulators, and other components. Haimovich et al. [22] developed a portable thermal batteries simulator and compared the calculation results of the simulator with multiple case studies. They found that the simulator had good accuracy and could support the analysis and development of most thermal battery structures and designs. Domestic researchers Wang et al. [16] carried out the development of some thermal battery simulation platforms and initially realized the automation of modeling, simulation, and postprocessing, which can obtain the thermal distribution, phase change characteristics, discharge voltage, and current density distribution of the activation and discharge process of the whole thermal battery. Chen et al. [15] used COMSOL software to study the phase transition and thermal characteristics in the activation process of thermal batteries. Based on the FLUENT software, Li et al. [5] carried out numerical calculations and experimental research on the performance of the thermal battery activation stage, considering the ignition heating-sheet time and using UDF and dynamic grid to achieve thermal battery thermal characterization. Compared to the experimental results, the error of the model was reduced from 10.6% to 1.6%, compared with the traditional model. In order to study the thermal runaway and corrosion of thermal batteries, Jang Hyeon Cho et al. [15] studied the optimal discharge temperature of thermal batteries and studied the influence of thermal battery heating sheet thickness on the temperature of positive and negative electrodes and electrolytes based on the COMSOL software, which contributed to the design of electrodes, electrolytes, heat sources, insulators, and other components. In addition, Wei et al. [11] conducted a thermal simulation of a small-size thermal battery based on ANSYS software. The calculation results with the experimentally-measured top core temperature and top insulation temperature were verified, which found that the maximum values and arrival times of the simulated and measured temperatures were (127.0 °C, 315 s) and (131.5 °C, 261 s), respectively. At the same time, the average temperature of the thermal battery was used as the standard for thermal battery activation, and the error was within 3.5%, compared with the experiment. Wang et al. [16] discussed a numerical simulation method based on the ANSYS thermal battery activation process, which realized the prediction of heat distribution and open-circuit voltage curve during activation and verified the open-circuit voltage simulation results through thermal battery activation experiments. The accuracy of the model was high. At present, the melting point of the thermal battery electrolytes is mostly used as the standard to determine thermal battery activation, for which the time scale is only on the microsecond level. This is a challenge for the models mentioned above to predict the activation time accurately. Based on it, the reported simulation methods are unable to accurately obtain the temperature and electrolyte phase transition characteristics during the activation of thermal batteries as a uniform heat source, which usually display large absolute errors. Furthermore, the cut-off time of thermal battery activations is usually determined by the temperature assumptions, in which thermal batteries are activated when the average and maximum temperature of each isolation piece reaches the electrolyte melting point. However, for thermal batteries with an activation time of microseconds, the predicted activation time error of this method is relatively large. To solve the limitations, this work will use the multiphysics simulation software COMSOL, combined with literature methods, to analyze the electrolyte average temperature change characteristics and thermal battery phase-transition characteristics. A simple user-defined heat-source function will be used to describe the thermal batteries more accurately. Simple custom functions will also be added to represent the method of moving the heat source, fully considering the various heat sources in the thermal battery activation process. The phase transition and thermal diffusion of the electrolyte will be simulated and calculated to study the temperature change and the electrolyte-phase change in the activation stage of the thermal battery at 50 °C. The temperature change characteristics, the electrolyte-phase change characteristics, and the activation time will be obtained. In addition, by analyzing the thermal battery electrolyte-melting characteristics during the activation-control process, the time when the cathode and anode are connected will be used as the cut-off time for the shortest activation time, which will overcome the uncertainty in predicting the activation time from the temperature results. The electrolyte melting state can also be used to analyze the load-carrying capacity of thermal batteries, which will show higher accuracy than the traditional open-circuit voltage-curve description method. This paper will provide a theoretical basis for the design of thermal batteries with better performance.
2. Methods
The flow chart of this work is shown in Figure 1. The simulation was performed using COMSOL Multiphysics 6.0 software, in which the solid heat transfer module solves the solid heat transfer problem in thermal battery simulation. The simulation of thermal batteries can be divided into four steps, including meshing, calculation and solution settings, and postprocess. The temperature system considered in this work is based on degrees Celsius.
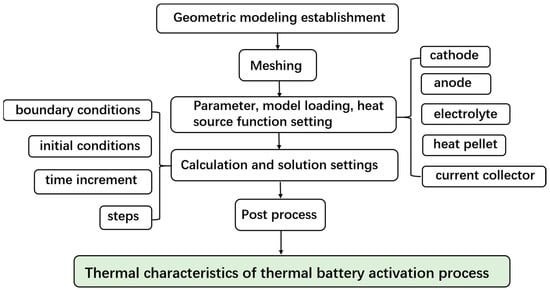
Figure 1.
The flow chart of this work.
During the geometric modeling establishment process, a thermal battery consists of a stack, a battery cover, and a battery case, of which the radius is about 10 mm. Every single cell is composed of a cathode, anode, heat pellet, electrolyte sheet, collector sheet, and felt ring. FeS2, LiSi, and LiF-LiBr-LiCl are chosen as the cathode, anode, and electrolyte, respectively. The current collector is Ni in this work. Eight single cells are stacked, bundled, and fixed to form a stack. The battery cover is composed of a cover plate, a terminal post, an asbestos pad, and a cover lead. The battery case consists of the insulation material and housing. The ignition head is located on the top of the stack and electricity is used for igniting, which has a much shorter time compared to the activation time, so the ignition time is ignored during the simulation. For the meshing of the simulation, the geometric model is discretized using a free triangular mesh provided by the COMSOL software, whose size is set to 353 mm2. There are 27,606 meshes with 5328 edge units and 157 vertex units. The smallest mesh quality is 0.082. The middle of the meshing is a stack composed of 14 battery single cells, the peripheral heating layer, and shell wraps the stack, while the grid is divided by a triangle, of which the density is increased in the area of the stack and the heating plate to make the calculation accuracy higher.
To build a thermal battery model, it is necessary to obtain basic parameters such as density, specific heat capacity, and thermal conductivity of each component. Parameters of electrolytes were directly taken from the supplier, and others were obtained from the literature [8,11,15]. All are standard parameters for the components. The main material parameters were summarized in Table 1 below.

Table 1.
Table of the main material parameters.
In the thermal battery activation stage, the heat from the pyrotechnic agent is transferred to the electrolyte phase change material region and transforms it into a liquid phase, connecting the cathode and anode, thus, it realizes the thermal battery conduction. In order to inhibit the fluidity of the molten electrolyte, magnesium oxide is added to the electrolyte layer and the cathode to reduce electrolyte leakage. The simulated electrolyte adopts LiF-LiBr-LiCl, which has a melting point of 430 °C and a melting heat of 266 J/g. The phase-change enthalpy of the electrolyte sheet and the cathode is set according to the phase-change material region [19].
The activation stage of thermal batteries includes physical and chemical processes such as heat source, heat release, heat conduction, heat convection, heat radiation, and phase change [15]. In this work, only the heat transfer process in the activation stage is considered while the heat of the chemical reaction and the Joule heat are ignored. The temperature change control equation of the thermal battery is as follows:
where represents the temperature change per unit volume, represents the incoming heat per unit volume; represent the density, heat capacity, and thermal conductivity of the material, respectively, represents temperature, and represents time. represents the heat of the thermal battery to ambient heat convection. represents the heat of melt required for melting molten salts in the electrolyte sheet and cathode sheet. The equation for and are as follows:
represents the temperature difference between the battery case and the ambient temperature and is the thermal conductivity.
represent the mass fraction, the heat of melt, and the liquid phase volume fraction of molten salts in phase change materials, respectively.
The initial temperature of the thermal battery was 50 °C and the test temperature was the ambient temperature. Additional heating plates and insulation mica gaskets in the upper and lower parts of the stack, as well as insulation layers on the sides to slow down the temperature loss of the thermal battery, were added to maintain a longer working time. The outer boundary of the thermal battery was set to thermal convection with a convection coefficient of 10 W m−1 k−1.
In order to obtain the temperature change of each component of the single cell, a temperature probe is set in the single cell area. In order to obtain the average temperature change of the electrolyte, domain probes are set up in each electrolyte region.
3. Results and Discussion
A multiphysics finite element analysis software that has the advantages of a simple interface, flexible definition of the model, and rich postprocessing functions have been used in this work. It is a finite element simulation software that can solve multiple physical field problems. The activation of thermal batteries is mainly a heat transfer process, so the thermal model established by the COMSOL software can be based on the transient heat-transfer physical fields. In order to simplify the calculation, the three-dimensional physical model is simplified to a two-dimensional axisymmetric model to simulate the heat-transfer process of thermal batteries, omitting the activation mechanism and other components that have little impact on heat transfer. The mesh has been meshed by a free triangle, and the established two-dimensional axisymmetric model and meshing are shown in Figure 2, which gives the specific thermal battery model and size.
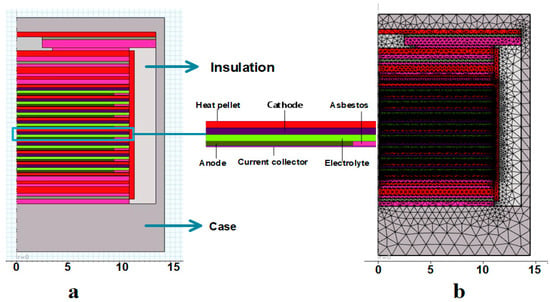
Figure 2.
(a) Thermal battery model and (b) the corresponding meshing diagram.
When a thermal battery works, it goes through two stages: the activation process and the discharge process. In order to obtain the temperature changes of the activation process and the phase transition of the electrolyte, this work mainly studies the thermal characteristics of the thermal battery activation stage. The time scale is within hundreds of milliseconds, and the transient solid heat-transfer model is established without considering the influence of current in the activation stage. The ignition method of the thermal battery is the first mechanical ignition, of which the time is directly measured by the experiment and recorded as t1. The heat-release melting electrolyte sheet time of the pyrochemical agent is recorded as t2, which is calculated by a simulation. Based on it, the predicted activation time is considered to be the value of t1 + t2. The stack is the main area in the thermal battery to generate heat and electricity [10]. Additional heating plates and asbestos pads are added above and below the stack to provide sufficient thermal energy for the thermal battery, maintaining the temperature of the stack and extending the working time of the battery.
According to the actual heat-release sequence and characteristics, the heat-source function is written. The top ignition strip of the thermal battery is ignited first, followed by the ignition strip on the top of the ignition stack, the side ignition strip, and each heating plate. Taking the ignition sheet as an example, a coordinate system for the ignition sheet has been established in Figure 3. The shaded area in the figure represents the reaction area. The calorific value of this area can be calculated based on the burning rate of the heating plate. The combustion direction is set according to the actual situation. The heat source function can be expressed as follows:
is the heat density of the ignition strip; is a piecewise function;
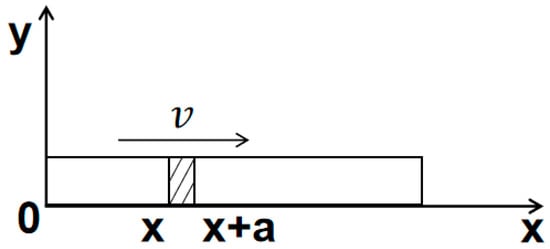
Figure 3.
Schematic diagram of heat release of the heat source of thermal battery.
The segmentation function is introduced to realize the continuous heat release of the heat source. The a is the heat source reaction area, set to 0.1 mm; v is the combustion speed. For different heat sources, the heat-source function needs to be written according to the actual model, in which the calorific value of the heat pellet is 1270 J/g and the burning rate is 9.8 cm/s. The heat release and the combustion rate of the pilot sheet are 1800 J/g and 1.5 m/s, respectively.
It is well known that the internal temperature data of thermal batteries by experimental measurements are difficult to obtain under the condition of maintaining the integrity of thermal batteries. Based on it, simulations about internal-temperature distribution and change have been performed by COMSOL. In order to obtain the temperature change of each component of the single cell, a temperature probe is set in the single-cell area. In addition, domain probes are set up in each electrolyte region to obtain the average temperature change of the electrolyte. According to the temperature cloud map at different moments of the simulation results (Figure 3), the temperature-change characteristics during the activation process of the thermal battery have been analyzed. The calculation results of the temperature probe show that the temperature rise of each component has been analyzed according to the temperature time change curve of the single cell. Additionally, the phase-transition characteristics of the thermal battery activation process have been analyzed and the activation time has been predicted according to the phase-transition situation.
To visually illustrate the internal temperature change of the thermal battery during activation, the temperature clouds of 60 ms, 140 ms, and 400 ms are selected, as shown in Figure 4. The upper and lower parts of the stack have a higher temperature due to the large number of heating plates, which can also better maintain the temperature of the thermal battery. At 60 ms, the heating plate is in an unburned state with the temperature of the burned area gradually rising. At 140 ms, the heating plates are all burned out and the heat is transferred inside the thermal cell; At 400 ms, the internal temperature of the stack tends to be stable. Then, the temperature is maintained at about 525 °C. In this situation, the thermal battery model is equipped with an asbestos insulation layer and the temperature of the stack drops slowly.
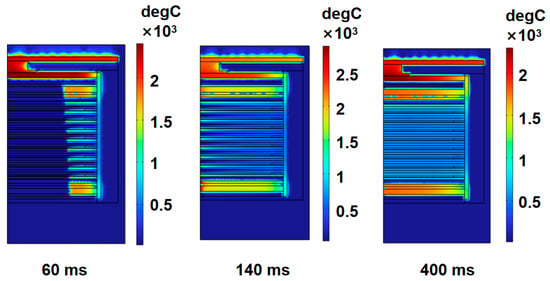
Figure 4.
Temperature cloud of thermal battery at different times.
As shown in Figure 5, the temperature change of the single cell (the fourth cell from top to bottom) is monitored during the activation process. The heat of the heating plate is transferred from the ignition strip to the components of the thermal battery within 400 ms. At 400 ms, the temperature tends to be consistent and is maintained at 525 °C, which is consistent with the temperature cloud result. The highest temperature of the heater pellets and the current collectors reach 1376 °C and 940 °C, respectively. The anode needs to withstand a thermal shock of 700 °C, but it does not reach the melting temperature of the LiSi alloy. The highest temperature of the cathode is 525 °C. The temperature curves of the cathode and the electrolyte sheet fluctuate slightly during the heating process, showing that a certain proportion of the electrolyte phase change material is added to the cathode, and a part of the heat is absorbed during the electrolyte melting process. Due to the working mechanism and fast-activation requirements of thermal batteries, the temperature of electrolytes rises faster than the as reported Li-ion battery electrolytes [23,24]. Based on it, the curves have a small fluctuation, which is in line with the actual situation.
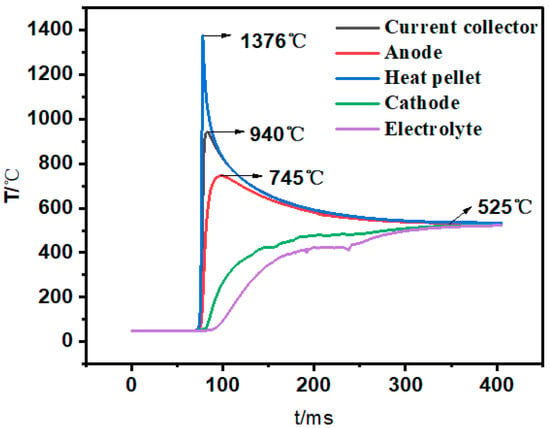
Figure 5.
Temperature-change diagram of thermal battery cells.
The average temperature rising curves of electrolytes are shown in Figure 6. Electrolyte 1 and electrolyte 8 represents the electrolyte in the single cell at the top and bottom of the stack, respectively, beside which additional heating plates are located. As a result, the temperature curves of electrolytes 1 and 8 have a faster temperature increase compared with other curves. The average temperature of all electrolytes exceeds the melting point of 430 °C at 142 ms.
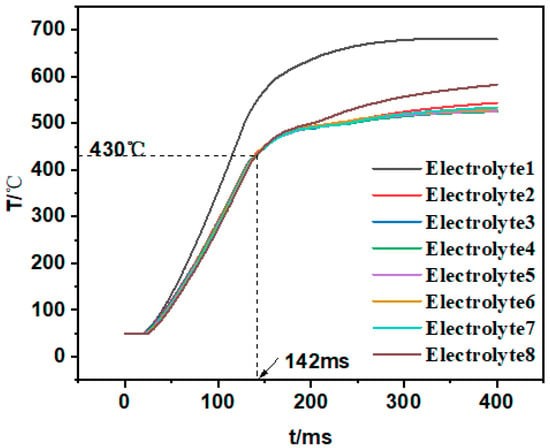
Figure 6.
Average temperature rising curves of the electrolytes.
In order to predict the activation time more accurately with the small-size thermal battery model, the phase-change domain is set in the electrolyte and cathode regions with the activation time predicted by the electrolyte melting situation. The phase change cloud of the thermal battery is shown in Figure 7, in which red regions indicate complete electrolyte melting while blue ones indicate unmelted. Due to the exothermic order of the heat pellet, the upper electrolyte sheet melts prior to the lower electrolyte sheet. The melting area spreads from the right to the left with all electrolytes beginning to melt at 90 ms until 270 ms. According to the analysis above, the temperature of the collector sheet and the anode in the single battery rises rapidly. The phase change cloud diagram of the thermal battery and the temperature map of the monomer can verify each other, indicating that the main heat flows into the electrolyte region from the anode. It can be seen from the literature [25,26] that the cathode material has a lower thermal diffusivity, and the heat is hard to enter the electrolyte from the cathode side, so the development of a higher thermal conductivity electrode material can reduce the activation time. It is believed that when all electrolytes begin to melt and connect the cathode and anode, the thermal battery is in an active state with an on-load capacity. Based on it, the electrolyte melting time at 50 °C t2 = 90 ms. Combined with the mechanical activation ignition time, the forecast for activation is 91.2 ms, which is consistent with the widely known experimental activation time of below 200 ms for thermal batteries.
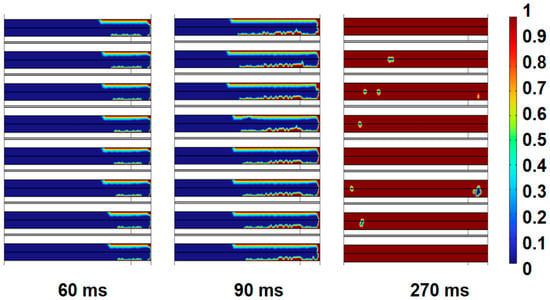
Figure 7.
Phase-change cloud diagram of thermal battery at different times.
To verify the reliability of the model, mechanical-activation experiments have been performed on thermal batteries. In the experiment, the (acoustic target) at the moment of hammer overload action was used as the zero point of the acquisition-activation time. The thermal battery has an operating voltage of 12 V. Five experiments have been conducted at high and low temperatures, and the test results are shown in Table 2.

Table 2.
Thermal battery activation-phase curve (time to reach the following voltages, unit ms).
Comparing the activation time predicted to the simulation with the activation time of the experimental test, the maximum relative error at high temperatures is only 3.8%, which is comparable with the reported results, indicating that the accuracy is high. It is believed that the analysis error is due to certain errors between the material property settings and calculation errors.
4. Conclusions
In this study, the “Solid Heat Transfer” module in the COMSOL multiphysics simulation software has been used to simulate heat generation and transfer during the activation process of thermal batteries. The custom function setting method of the mobile heat source and the activation time of thermal cells have been predicted according to the electrolyte melting characteristics. The temperature change characteristics and electrolyte phase transition characteristics of thermal batteries have been analyzed.
The heat pellet was set in the upper and lower parts of the thermal battery to maintain the internal temperature of the thermal battery. The thermal insulation shell could also reduce heat loss. The additional heat generated by the firework agent could slightly decompose the cathode material and have no effect on the anode material. Most of the melting electrolyte heat flowed in from the anode side with high thermal conductivity. The simulation model predicted that the activation time at 50 °C was 91.2 ms, with the relative error compared to experimental results being only 3.8%, which were comparable to the reported results using other methods. All these results can provide a theoretical basis for the design of thermal batteries with desirable performances.
Author Contributions
Methodology, K.L.; Validation, S.Z.; Formal analysis, S.Z.; Investigation, E.K.; Data curation, E.K., T.S. and J.L.; Writing—original draft preparation, K.L.; Writing—review & editing, T.Q.; Supervision, T.S. and J.L.; Project administration, Y.Z. and T.Q.; Funding acquisition, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 52022013 and No. 51974031), the Fund for Equipment Advance Research (80921020703), and State Key Laboratory of Explosion Science and Technology (No. QNKT23-17).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, C.; Zhang, X.; Cui, Y.X.; He, K.; Cao, Y.; Liu, X.J.; Zeng, C. A system-level thermal-electrochemical coupled model for evaluating the activation process of thermal batteries. Appl. Energy 2022, 328, 120177. [Google Scholar] [CrossRef]
- Choi, Y.; Ahn, T.Y.; Ha, S.H.; Lee, J.I.; Cho, J.H. Electrochemical properties of a lithium-impregnated metal foam anode (LIMFA FeCrAl) for molten salt thermal batteries. Sci. Rep. 2022, 12, 4474. [Google Scholar] [CrossRef] [PubMed]
- Yao, B.; Fu, L.C.; Liao, Z.; Zhu, J.J.; Yang, W.L.; Li, D.Y.; Zhou, L.P. Flexible NiS2 film as high specific capacity cathode for thermal battery. J. Alloys Compd. 2022, 900, 163448. [Google Scholar] [CrossRef]
- Cao, Y.; Dong, L.P.; Deng, Y.F.; Liu, H.Y.; Gao, C.Y.; Yang, X.W.; Wang, C.; Cui, Y.H. Working temperature maintenance of thermal batteries by using a slow heat supply component with layer structure and its positive effect on the improvement of electrochemical performance. Compos. Part B-Eng. 2021, 222, 109036. [Google Scholar] [CrossRef]
- Li, Q.; Shao, Y.Q.; Shao, X.D.; Liu, H.L.; Xie, G.N. Activation process modeling and performance analysis of thermal batteries considering ignition time interval of heat pellets. Energy 2021, 219, 119631. [Google Scholar] [CrossRef]
- Huang, X.R.; Liu, J.S.; Zeng, M.S.; Yang, X.W.; Liu, X.J. Effects of different MgO fiber structures on adhesive capacity and ionic migration of Li-Si/LiCl-KCl/FeS2 thermal batteries. Electrochim. Acta 2019, 324, 134918. [Google Scholar] [CrossRef]
- Guidotti, R.A.; Masset, P. Thermally activated (“thermal”) battery technology—Part I: An overview. J. Power Sources 2006, 161, 1443–1449. [Google Scholar] [CrossRef]
- Cho, J.-H.; Im, C.N.; Choi, C.H.; Ha, S.-H.; Yoon, H.-K.; Choi, Y.; Bae, J. Thermal stability characteristics of high-power, large-capacity, reserve thermal batteries with pure Li and Li(Si) anodes. Electrochim. Acta 2020, 353, 136612. [Google Scholar] [CrossRef]
- Liu, G.F.; Jiang, J.M.; Wang, X.F.; Tang, C.; Cui, Y.H.; Zhuang, Q.C. Al2O3 nanoparticles modified the FeS2 cathode to boost the interface wettability and electrochemical performance for thermal batteries. Mater. Lett. 2023, 330, 133290. [Google Scholar] [CrossRef]
- Guidotti, R.A.; Masset, P.J. Thermally activated (“thermal”) battery technology—Part IV. Anode materials. J. Power Sources 2008, 183, 388–398. [Google Scholar] [CrossRef]
- Lan, W.; Song, X.; Liu, X. Study on thermal simulation of thermal battery. Chin. J. Power Sources 2012, 36, 88–90. [Google Scholar]
- Zhang, P.; Liu, J.; Yang, Z.; Liu, X.; Yu, H. Using MgO fibers to immobilize molten electrolyte in thermal batteries. J. Solid State Electrochem. 2016, 20, 1355–1360. [Google Scholar] [CrossRef]
- Wu, Y.X.; Pei, C.X.; Zhang, H.B.; Liu, Y.; Jia, P.J. A Fast Finite Element Simulation Method of Phased Array Ultrasonic Testing and Its Application in Sleeve Fillet Weld Inspection. Appl. Sci. 2022, 12, 5384. [Google Scholar] [CrossRef]
- Wang, C.; Liu, B.; Lan, W.; Liu, X.; Cui, Y. Simulation investigation on activation of thermal battery based on ANSYS. Chin. J. Power Sources 2018, 42, 68. [Google Scholar]
- Chen, H.; Zhu, Y.; Li, W.; Bai, J. Thermal Characteristics of Thermal Batteries during Activation Based on Heat Transfer Simulation. Acta Armamentarii 2022, 43, 1194–1200. [Google Scholar]
- Wang, C.; Yang, Z.; Lan, W.; Liu, X.; Cui, Y. Numerical simulation method for open-circuit voltage of thermal battery in activation process. Chin. J. Power Sources 2018, 42, 697. [Google Scholar]
- Liu, M.; Liao, G. Research Development of Thermal Battery New Technology. Mod. Chem. Res. 2017, 03, 101. [Google Scholar]
- Trembacki, B.; Harris, S.R.; Piekos, E.S.; Roberts, S.A. Uncertainty Quantification Verification and Validation of a Thermal Simulation Tool for Molten Salt Batteries; Sandia National Lab.(SNL-NM): Albuquerque, NM, USA, 2016. [Google Scholar]
- Cho, J.; Park, B.; Kim, J.; Ha, S.-H.; Im, C. Electrochemical and thermal analysis of the thermal battery. In Proceedings of the 48th Power Sources Conference, Denver, CO, USA, 11–14 June 2018. [Google Scholar]
- Haimovich, N.; Dekel, D.R.; Brandon, S. A Simulator for System-Level Analysis of Heat Transfer and Phase-Change in Thermal Batteries: II. Multiple-Cell Simulations. J. Electrochem. Soc. 2014, 162, A350–A362. [Google Scholar] [CrossRef]
- Li, T.X.; Xu, J.; Wang, C.Y.; Wu, W.J.; Su, D.W.; Wang, G.X. The latest advances in the critical factors (positive electrode, electrolytes, separators) for sodium-sulfur battery. J. Alloys Compd. 2019, 792, 797–817. [Google Scholar] [CrossRef]
- Haimovich, N.; Dekel, D.R.; Brandon, S. A Simulator for System-Level Analysis of Heat Transfer and Phase Change in Thermal Batteries: I. Computational Approach and Single-Cell Calculations. J. Electrochem. Soc. 2009, 156, A442. [Google Scholar] [CrossRef]
- Wu, Z.H.; Huang, A.C.; Tang, Y.; Yang, Y.P.; Liu, Y.C.; Li, Z.P.; Zhou, H.L.; Huang, C.F.; Xing, Z.X.; Shu, C.M.; et al. Thermal Effect and Mechanism Analysis of Flame-Retardant Modified Polymer Electrolyte for Lithium-Ion Battery. Polymers 2021, 13, 1675. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.Z.; Xie, L.J.; Tang, Y.; Li, Y.; Jiang, J.C.; Huang, A.C. Thermal Safety Evaluation of Silane Polymer Compounds as Electrolyte Additives for Silicon-Based Anode Lithium-Ion Batteries. Processes 2022, 10, 1581. [Google Scholar] [CrossRef]
- Masset, P.J.; Guidotti, R.A. Thermal activated (“thermal”) battery technology: Part IIIb. Sulfur and oxide-based cathode materials. J. Power Sources 2008, 178, 456–466. [Google Scholar] [CrossRef]
- Freitas, G.C.S.; Peixoto, F.C.; Vianna, A.S. Modeling and simulation of the heat transfer in a thermal battery. In Proceedings of the ECCOMAS CFD 2006: Proceedings of the European Conference on Computational Fluid Dynamics, Egmond aan Zee, The Netherlands, 5–8 September 2006. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).