Denoising of the Poisson-Noise Statistics 2D Image Patterns in the Computer X-ray Diffraction Tomography
Abstract
1. Introduction
2. Results
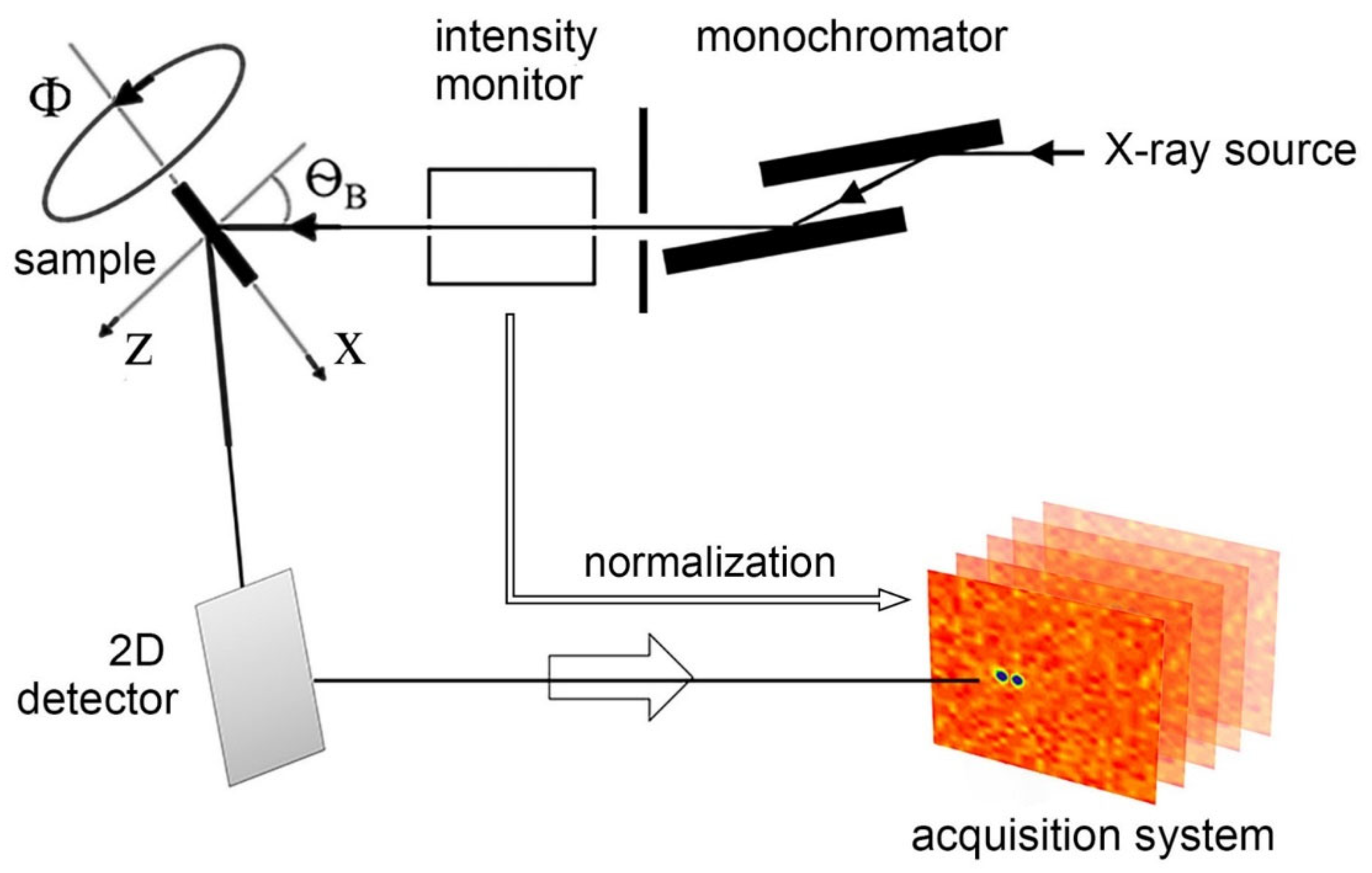
2.1. Simulating the 2D Poisson-Noise IPs Data Frames
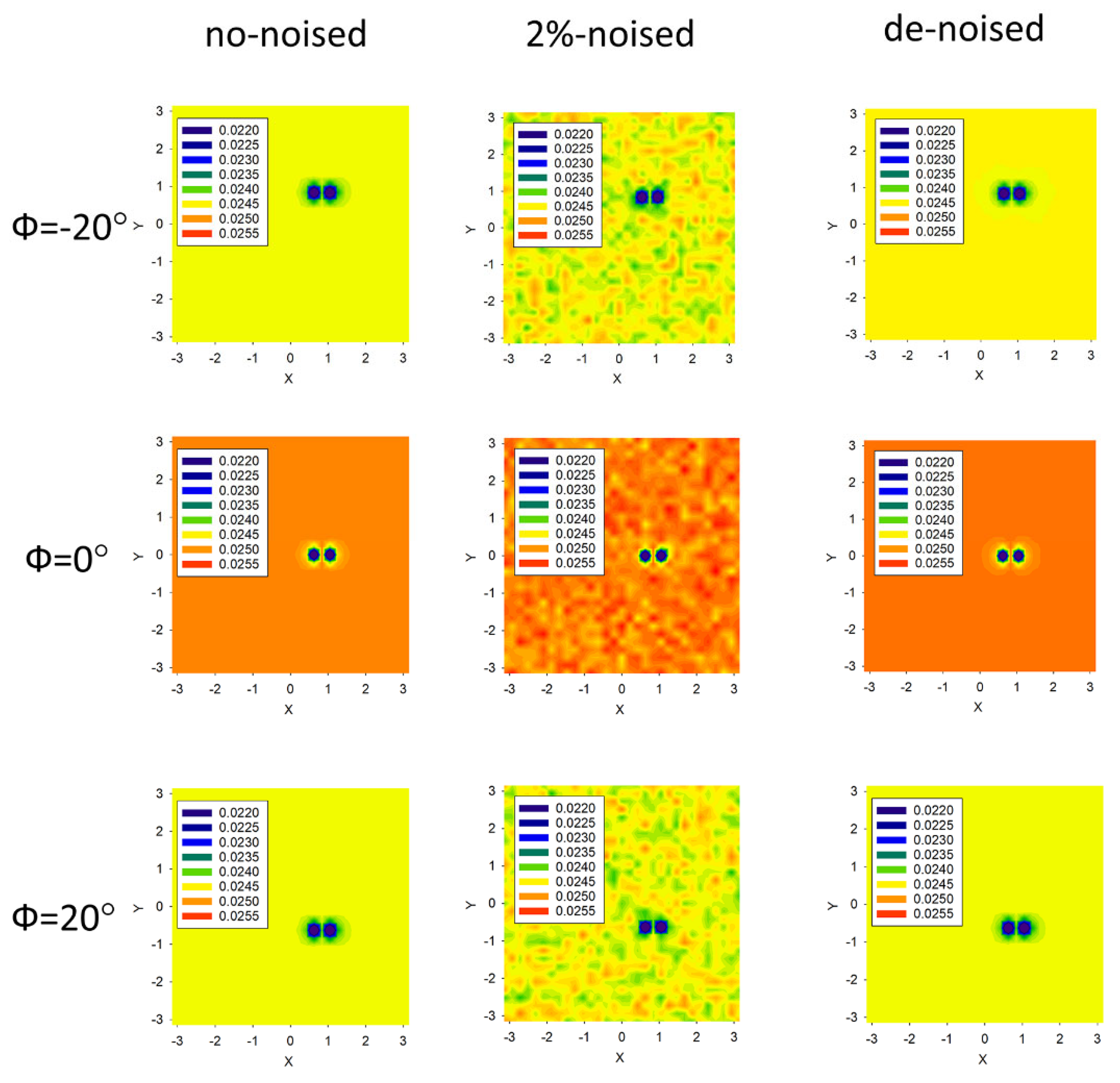
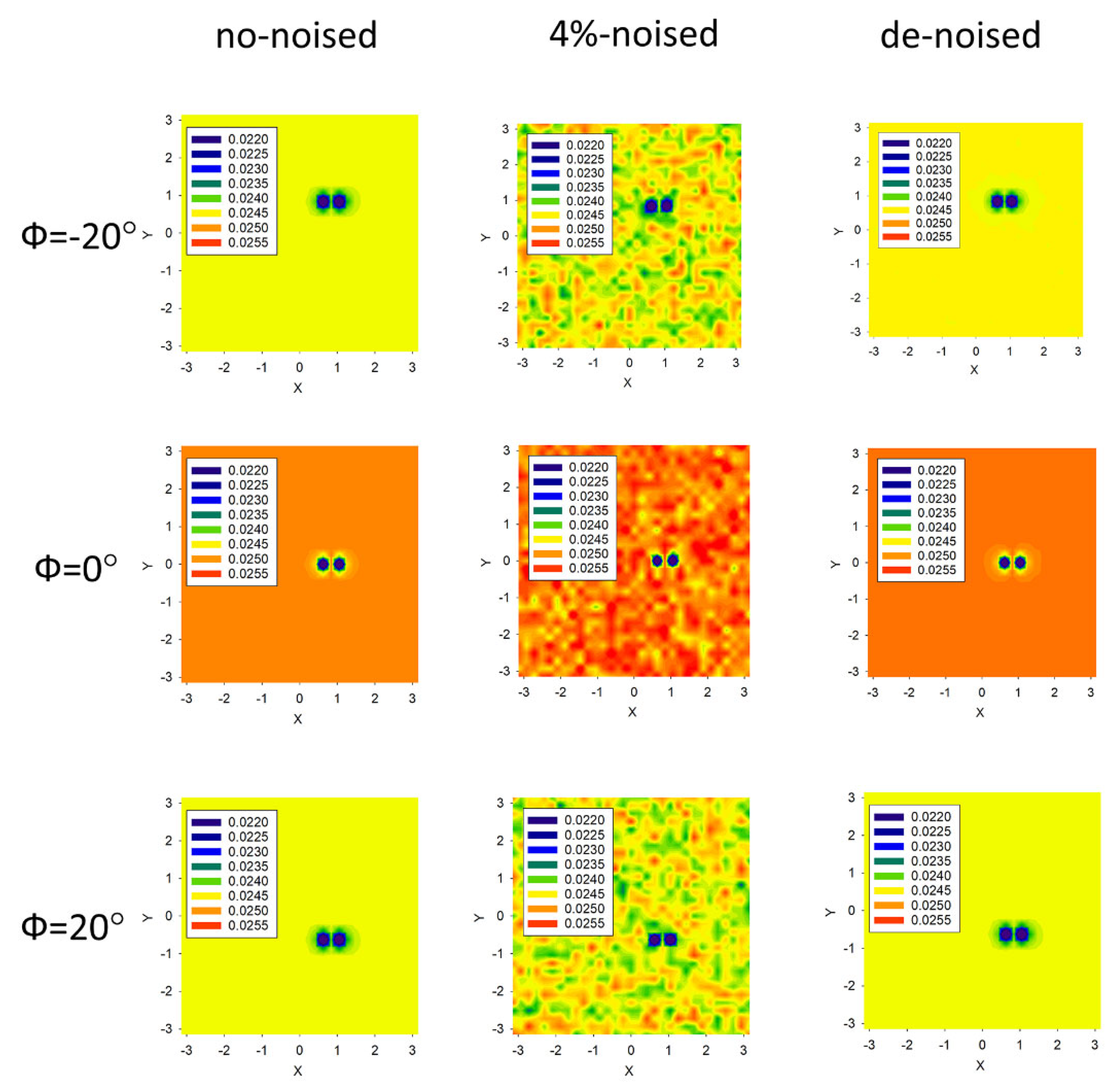
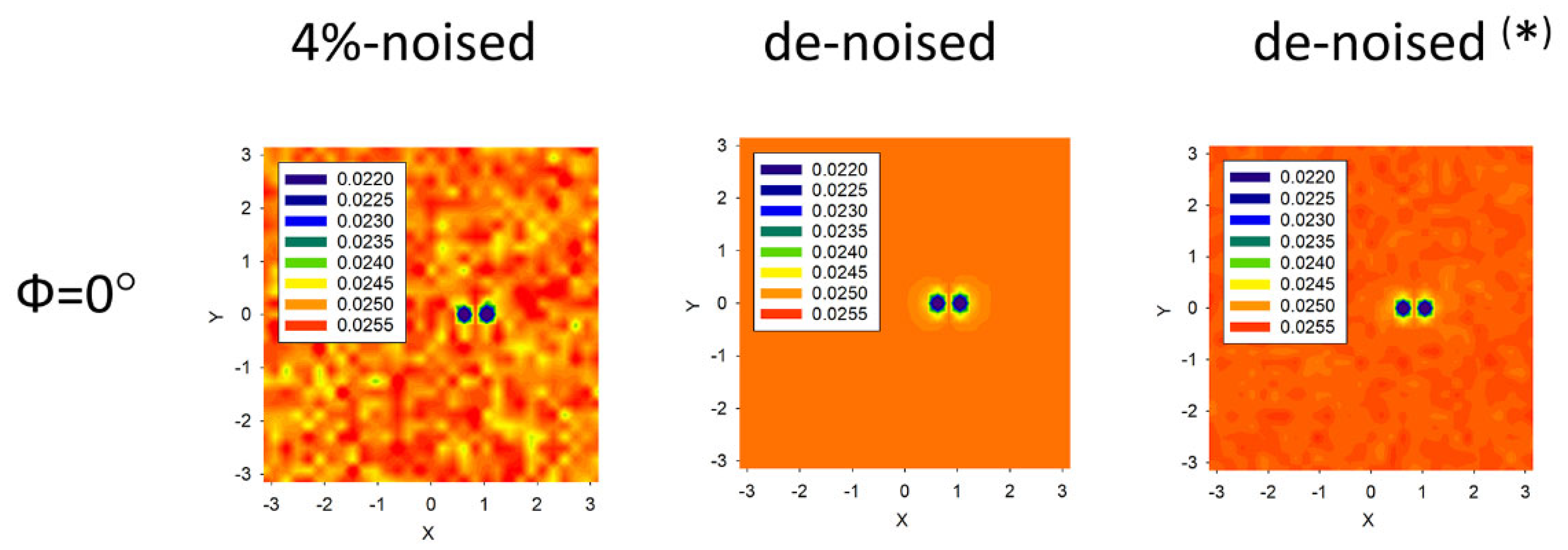
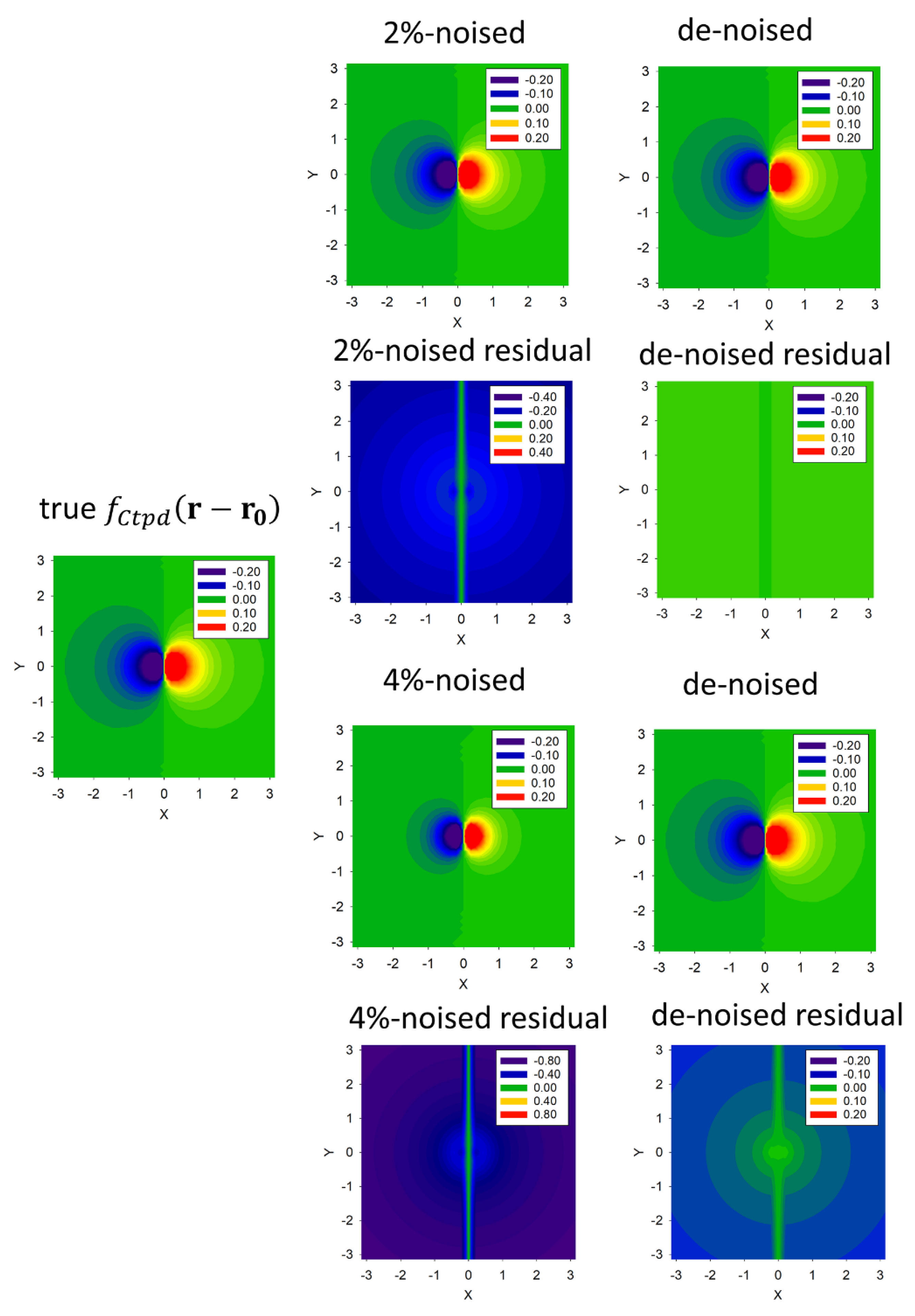
2.2. Statistical Denoising the 2D IPs Data Frames
3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- Do
- [ Assign the initial vector for 𝓟 ={ν, Z0, G}.
- Calculate the differential for the activated qNLM algorithm, 1 ≤ k ≤ K.
- the qNLM algorithm is applied until the criterion 10−10 for the SA switch number m = 0.
- Evaluate the figure of merit (FOM) Ɽk (see Equation (6)).
- Terminate the minimization procedure of the target function when it becomes less than 10−10 and/or the FOM value becomes less than 10−6 for k=K*, and the switch number m=0, respectively.]
- End Do.
References
- Bowen, D.K.; Tanner, B.K. High Resolution X-Ray Diffractometry and Topography; Taylor & Francis: New York, NY, USA, 1998. [Google Scholar]
- Chukhovskii, F.N. Dynamic Newton-gradient-direction-type algorithm for multilayer structure determination using grazing X-ray specular scattering: Numerical simulation and analysis. Acta Cryst. 2009, A65, 39–45. [Google Scholar] [CrossRef]
- Benediktovitch, A.; Feranchuk, I.; Ulyanenkov, A. Theoretical Concepts of X-Ray Nanoscale Analysis; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Ludwig, W.; Cloetens, P.; Härtwig, J.; Baruchel, J.; Hamelin, B.; Bastie, P. Three-dimensional imaging of crystal defects by ’topo-tomography. J. Appl. Cryst. 2001, 34, 602–607. [Google Scholar] [CrossRef]
- Danilewsky, A.N.; Wittge, J.; Croell, A.; Allen, D.; McNally, P.; Vagovič, P.; dos Santos Rolo, T.; Li, Z.; Baumbach, T.; Gorostegui-Colinas, E.; et al. Dislocation dynamics and slip band formation in silicon: In-situ study by X-ray diffraction imaging. J. Cryst. Growth 2011, 318, 1157–1163. [Google Scholar] [CrossRef]
- Hänschke, D.; Danilewsky, A.; Helfen, L.; Hamann, E.; Baumbach, T. Correlated three-dimensional imaging of dislocations: Insights into the onset of thermal slip in semiconductor wafers. Phys. Rev. Lett. 2017, 119, 215504. [Google Scholar] [CrossRef] [PubMed]
- Asadchikov, V.; Buzmakov, A.; Chukhovskii, F.; Dyachkova, I.; Zolotov, D.; Danilewsky, A.; Baumbach, T.; Bode, S.; Haaga, S.; Hänschke, D.; et al. X-ray topo-tomography studies of linear dislocations in silicon single crystals. J. Appl. Cryst. 2018, 51, 1616–1622. [Google Scholar] [CrossRef]
- Chukhovskii, F.N.; Konarev, P.V.; Volkov, V.V. X-Ray diffraction tomography recovery of the 3D displacement-field function of the Coulomb-type point defect in a crystal. Sci. Rep. 2019, 9, 14216. [Google Scholar] [CrossRef]
- Chukhovskii, F.N.; Konarev, P.V.; Volkov, V.V. Towards a solution of the inverse X-ray diffraction tomography challenge: Theory and iterative algorithm for recovering the 3D displacement field function of Coulomb-type point defects in a crystal. Acta Cryst. 2020, A76, 16–25. [Google Scholar] [CrossRef]
- Yang, W.; Hong, J.-Y.; Kim, J.-Y.; Paik, S.; Lee, S.H.; Park, J.-S.; Lee, G.; Kim, B.M.; Jung, Y.-J. A novel singular value decomposition-based denoising method in 4-dimensional computed tomography of the brain in stroke patients with statistical evaluation. Sensors 2020, 20, 3063. [Google Scholar] [CrossRef]
- Liu, N.; Schumacher, T. Improved denoising of structural vibration data employing bilateral filtering. Sensors 2020, 20, 1423. [Google Scholar] [CrossRef]
- Hendriksen, A.A.; Bührer, M.; Leone, L.; Merlini, M.; Vigano, N.; Pelt, D.M.; Marone, F.; di Michiel Batenburg, K.J.M. Deep denoising for multi-dimensional synchrotron X-ray tomography without high-quality reference data. Sci. Rep. 2021, 11, 11895. [Google Scholar] [CrossRef]
- Alvarez, J.L. Poisson-based detection limit and signal confidence intervals for few total counts. Health Phys. 2007, 93, 120–126. [Google Scholar] [CrossRef]
- Muller, J.V. Counting Statistics of a Poisson Process with Dead Time. B.I.P.M. Report 111, F92 Serves 1970. pp. 1–14. Available online: https://www.bipm.org/documents/20126/30822082/bipm%20publication-ID-1760/e8c6bac9-b6e0-27a7-2511-b27eb9ab6e07 (accessed on 15 December 2019).
- Bondarenko, V.I.; Konarev, P.V.; Chukhovskii, F.N. On the theory of reducing the level of statistical noise and filtering of 2D images of diffraction tomography. Cryst. Rep. 2020, 65, 821–826. [Google Scholar] [CrossRef]
- Hudgings, D.W.; Dragt, A.J. Signal averaging at modest cost. Am. J. Phys. 1972, 40, 1206–1211. [Google Scholar] [CrossRef]
- Hassan, U.; Anwar, M.S. Reducing noise by repetition: Introduction to signal averaging. Eur. J. Phys. 2010, 31, 453–465. [Google Scholar] [CrossRef]
- Kraftmakher, Y. Noise reduction by signal accumulation. Phys. Teach. 2006, 44, 528–530. [Google Scholar] [CrossRef]
- Blanchet, C.E.; Zozulya, A.V.; Kikhney, A.G.; Franke, D.; Konarev, P.V.; Shang, W.; Klaering, R.; Robrahn, B.; Hermes, C.; Cipriani, F.; et al. Instrumental setup for high-throughput small- and wide-angle solution scattering at the X33 beamline of EMBL Hamburg. J. Appl. Cryst. 2012, 45, 489–495. [Google Scholar] [CrossRef]
- Corzo, R.; Steel, E. Improving signal-to-noise ratio for the forensic analysis of glass using micro X-ray fluorescence spectrometry. X-Ray Spectrom. 2020, 49, 679–689. [Google Scholar] [CrossRef]
- An, S.; Reza, S.; Norlin, B.; Froejdh, C.; Thungstroem, G. Signal-to-noise ratio optimization in X-ray fluorescence spectrometry for chromium contamination analysis. Talanta 2021, 230, 122236. [Google Scholar] [CrossRef]
- Feng, P.; Luo, Y.; Zhao, R.; Huang, P.; Li, Y.; He, P.; Tang, B.; Zhao, X. Reduction of Compton background noise for X-ray fluorescence computed tomography with deep learning. Photonics 2022, 9, 108. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhao, L.; Ni, Z.; Xu, S.; Zhao, J.; Xiao, X.; Huang, J. Heterojunction structures for reduced noise in large-area and sensitive perovskite x-ray detectors. Sci. Adv. 2021, 7, eabg6716. [Google Scholar] [CrossRef] [PubMed]
- Devroye, L. The Computer generation of Poisson random variables. Computing 1981, 26, 197–207. [Google Scholar] [CrossRef]
- Chukhovskii, F.N.; Konarev, P.V.; Volkov, V.V. Statistical noise-filtering of the X-ray diffraction tomography data: Simulation and analysis. J. Mat. Sci. Appl. 2022, 6, 1–12. [Google Scholar] [CrossRef]
- Huynh-Thu, Q.; Ghanbari, M. Scope of validity of PSNR in image/video quality assessment. Electron. Lett. 2008, 44, 800. [Google Scholar] [CrossRef]
- Olbinado, M.P.; Just, X.; Gelet, J.-L.; Lhuissier, P.; Scheel, M.; Vagovic, P.; Sato, T.; Graceffa, R.; Schulz, J.; Mancuso, A.; et al. MHz frame rate hard X-ray phase-contrast imaging using synchrotron radiation. Opt. Express 2017, 25, 13857–13871. [Google Scholar] [CrossRef]
- Dudak, J. High-resolution X-ray imaging applications of hybrid-pixel photon counting detectors Timepix. Radiat. Meas. 2020, 137, 106409. [Google Scholar] [CrossRef]
- Jacobsen, C. Soft X-ray microscopy. Trends Cell Biol. 1999, 9, 44–47. [Google Scholar] [CrossRef]
| Noise Level, % | Number of 2D IPs Frames, N | Number of Noise-Averaged Frames per One IP, U | 𝓟(k)(end) | ||
|---|---|---|---|---|---|
| zero | 3 | 1 | (1.50;0.50;1.80) | 2.2 × 10−3 | 4.3 × 10−5 |
| zero | 101 | 1 | (1.50;0.50;1.80) | 1.7 × 10−3 | 2.9 × 10−5 |
| 2 | 3 | 1 | (1.59;0.49;1.66) | 0.5 | 0.11 |
| 2 | 101 | 1 | (1.48;0.50;1.79) | 0.2 | 0.03 |
| 2 | 3 | 100 | (1.51;0.50;1.81) | 0.1 | 0.01 |
| 2 (*) | 3 (*) | 100 (*) | (1.48;0.50;1.77) (*) | 0.4 (*) | 0.08 (*) |
| 4 | 3 | 1 | (2.04;0.51;2.18) | 1.1 | 0.23 |
| 4 | 101 | 1 | (1.59;0.50;1.86) | 0.4 | 0.09 |
| 4 | 3 | 100 | (1.54;0.50;1.83) | 0.3 | 0.04 |
| 4 (*) | 3 (*) | 100 (*) | (1.45;0.50;1.84) (*) | 0.7 (*) | 0.16 (*) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chukhovskii, F.N.; Konarev, P.V.; Volkov, V.V. Denoising of the Poisson-Noise Statistics 2D Image Patterns in the Computer X-ray Diffraction Tomography. Crystals 2023, 13, 561. https://doi.org/10.3390/cryst13040561
Chukhovskii FN, Konarev PV, Volkov VV. Denoising of the Poisson-Noise Statistics 2D Image Patterns in the Computer X-ray Diffraction Tomography. Crystals. 2023; 13(4):561. https://doi.org/10.3390/cryst13040561
Chicago/Turabian StyleChukhovskii, Felix N., Petr V. Konarev, and Vladimir V. Volkov. 2023. "Denoising of the Poisson-Noise Statistics 2D Image Patterns in the Computer X-ray Diffraction Tomography" Crystals 13, no. 4: 561. https://doi.org/10.3390/cryst13040561
APA StyleChukhovskii, F. N., Konarev, P. V., & Volkov, V. V. (2023). Denoising of the Poisson-Noise Statistics 2D Image Patterns in the Computer X-ray Diffraction Tomography. Crystals, 13(4), 561. https://doi.org/10.3390/cryst13040561






