Abstract
Nanostructured Cu–Ni alloys have become the focus of public attention due to their better corrosion resistance and high hardness in experimental measurements. First-principles calculation based on the density functional theory (DFT) has been confirmed as an effective tool and used to illustrate the mechanical properties of these alloys. In this paper, the DFT has been employed to calculate the mechanical properties of Cu–Ni alloys, including bulk modulus, shear modulus, Young’s modulus, anisotropic index, Poisson’s ratio, average velocity, and B/G. We find that the Ni-rich Cu–Ni alloys have relatively higher mechanical parameters, and the Cu-rich alloys have smaller mechanical parameters, which is consistent with previous experiments. This provides an idea for us to design alloys to improve alloy strength.
1. Introduction
Copper and copper-based alloys are commonly used in manufacturing, meaning they are indispensable metals in society. Cu is known to have excellent electrical conductivity, good ductility, and high thermal conductivity, which is an advantage when it is deformed in terms of the geometry structure of devices and microwires [1]. In order to improve the hardness of Cu to meet certain applications, researchers suggest reliable mechanisms that cause mechanical hardening: (1) solid solution strengthening, (2) precipitation hardening [2].
One of the most attractive Cu-based alloys are Cu–Ni binary compounds. Cu–Ni alloys are considered to possess good hardness and corrosion resistance [2,3,4]. Some Cu–Ni alloys have good electrocatalytic [5] and electrical [6] properties in conducting electricity. Other interesting characteristics of Cu–Ni alloys, such as thermal conductivity reduction in nanostructuration [4] and ferromagnetic features in Ni-rich Cu–Ni deposits [7], are revealed. The deposited films of nanostructured Cu-rich Cu–Ni have better corrosion protection than pure Cu, and films have a high hardness [2]. The mechanical properties are widely revealed in experiments for nanostructured Cu–Ni films; they find that Young’s modulus increases with the increasing Ni concentration, and Young’s modulus decreases with the decreasing Cu concentration [8,9,10].
Recently, the Cu–X alloys for Cu–Al, Cu–Sc, Cu–Zn, and Cu–Ce were discussed in formation energy by VASP, which shows that Cu–Ce displays high mechanical energy and strong bonds [11]. The charge density difference and Mulliken population of Mg–Gd–Cu alloys were calculated by first-principles calculations, where the Cu–Gd terminated interface is probably the most stable interface [12]. Cu–Zn4 alloy has a high Young’s modulus with lower elastic anisotropy, which is rationally recommended for improving the stiffness of Al–Cu–Zn alloys based on first-principles calculations [13]. It can be seen that the first-principles calculation is one of the most important tools to compute mechanical properties, aiming to improve stiffness. Cu–Ni-based alloys have high elasticity and high electrical conductivity [14,15,16], with the addition of Co improving the conductivity [14] and the addition of Sn enhancing the mechanical stability of alloys [15,16]. The high stiffness and corrosion protection found in experiments with Cu–Ni alloys has brought them wide attention. Those features of the mechanical properties of Cu–Ni alloys can also be obtained from calculations, but have been less reported previously.
Therefore, we consider first-principles calculations to discuss the mechanical properties of Cu–Ni alloys in nanostructuration, trying to support and promote the understanding of these alloys.
2. Computational Details
First-principles calculations based on density functional theory (DFT) are executed by the CASTEP code [17], where the GGA-PBE is chosen as the exchange-correlation energy functional and potential [18]. Total energy for cutoff is set to 440 eV to ensure the energy tolerances. K-point mesh for Monkhorst–Pack grid is set to 12 × 12 × 12; the actual spacing for mesh is 0.004 nm−1. In geometry optimization processing, the detailed convergence tolerance for atom is evinced by setting energy to 5.0 × 10−6 eV/atom, max. force to 0.01 eV/Å, max. stress to 0.02 GPa, and max. displacement to 5.0 × 10−5 nm, where the max. iteration is 100 to ensure the energy convergence. The Broyden–Fletcher–Goldfarb–Shanno (BFGS) method is applied to mathematical algorithm for convergence calculation [19].
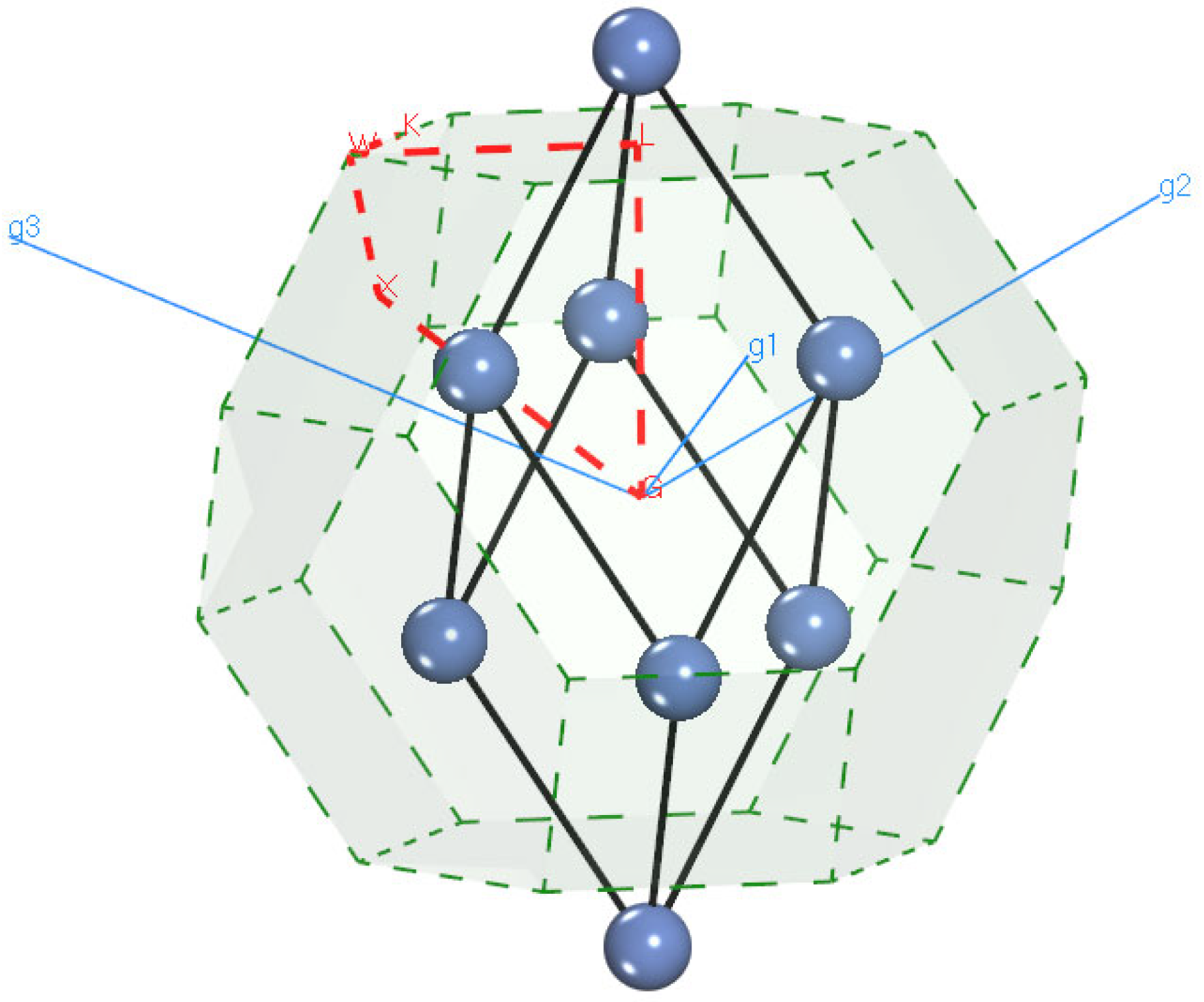
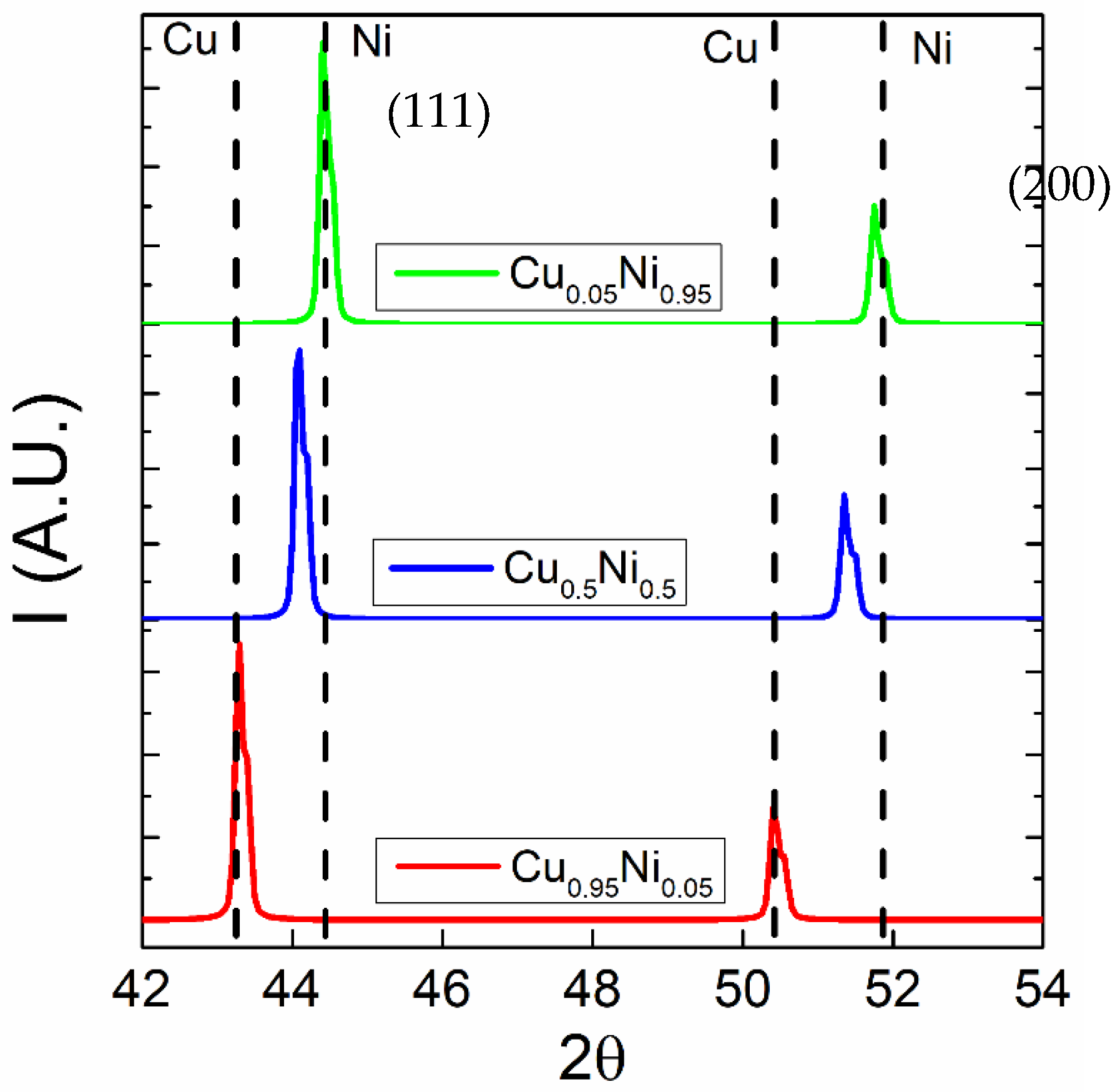
As shown in Figure 1, three Cu–Ni alloys are implanted in this paper, containing Cu0.5Ni0.5, Ni0.92Cu0.08, and Cu0.95Ni0.05 with same space group . Red points for k-point and green dash for Brillouin edge are marked, respectively. The vectors demonstrate the direction in reciprocal space by , , . The results of geometry optimization are listed in Table 1. It can be seen that the large Cu concentration has the larger lattice parameters, and the small atom percentage of Ni concentration has the smaller lattice parameters, which are consistent with experiments. Lattice parameters error is less than 2% compared with XRD data [2,9,10]. Figure 2 shows the simulated XRD patterns of Cu–Ni alloys based on pseudo-Voigt peak shape profile [20], where the peak broadening accounting for instrument broadening is described by Caglioti equation [21] by the U = 0.05, V = 0.002, and W = 0.002; the [UVW] is the direction of incident of the electron beam. It can be seen that the XRD patterns of Cu–Ni alloys are similar; the peak for (111) and (200) reflections shift towards larger angles as the Ni contents increase. The peak position and peak tendency for Cu–Ni alloys are in great agreement with experiments [2,9,10], conforming to the observed particle shapes and crystallite sizes. Hence, these structures are considered to further compute the mechanical properties with GGA-PBE functional.
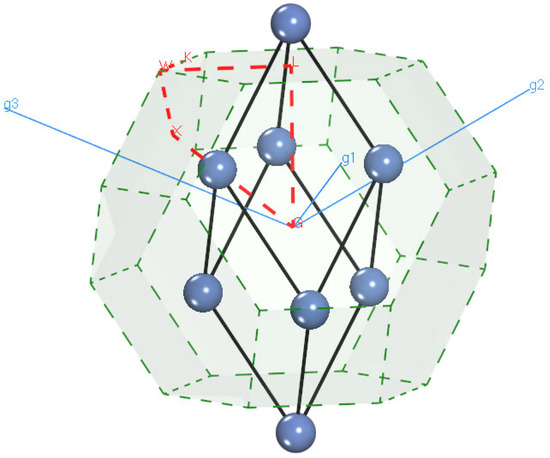
Figure 1.
Primitive cell of Cu–Ni; the blue atom corresponds to Cu and Ni; the contents of atom are Cu0.5Ni0.5, Ni0.92Cu0.08, and Cu0.95Ni0.05. Red line and point refer to integration path and k-point in Brillouin zone. , , are reciprocal vector.

Table 1.
Optimized lattice parameter for Cu–Ni alloys with experiments [2,9,10].
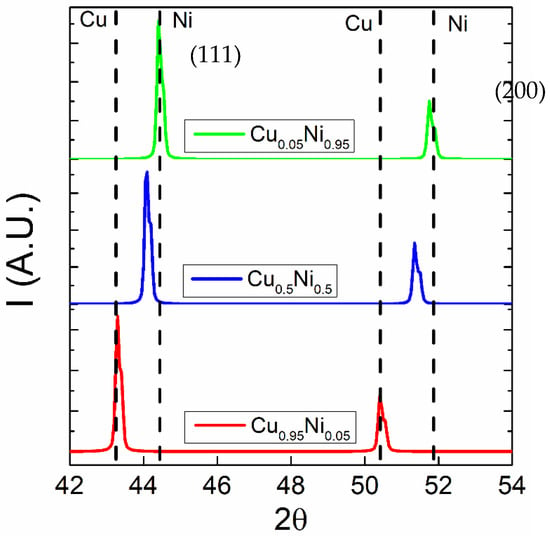
Figure 2.
Simulated XRD patterns of Cu–Ni alloy crystal in the 2θ = 42–54° range. The dashed lines indicate the position of the (111) and (200) fcc reflection for pure copper and pure nickel, the copper (Cu) is used for anode type, λ = 0.1540562 nm.
3. Mechanical Properties
The elastic constants are important to understand the physical properties and engineering applications [22,23,24]. Calculated elastic constant can be solved by energy density with tensors , which was first noted by Born and Huang [25]:
where the , are tensor notations in Voigt’s way. Then, the famous Hooke’s law can be listed:
The is elastic stress. When the elastic constants are obtained, the mechanical properties of the crystal can be solved by the elastic constant matrix. The Voigt, Reuss, and Hill [26,27,28] methods are popular approaches for mechanical properties including bulk modulus B, shear modulus G, average velocity vm, Young’s modulus E, ratio B/G, and Poisson’s ratio . In the cubic system, the equation can be simple:
Average value for Hill’s way is widely used to describe the mechanical properties, i.e.:
The average velocity for the crystal can be solved by [13]:
Other mechanical properties for Young’s modulus E, anisotropic index AU, and Poisson’s ratio v are expressed [13]:
The ratio of B/G has been an adopted criterion to judge the ductility and brittleness of solids; if B/G > 1.75, the solid behaves in a ductile manner, otherwise it behaves in a brittle manner [29]. Based on DFT, the energy density can be easily obtained. The calculated mechanical properties are shown in Table 2, solving from the Equations (3) to (13).

Table 2.
Calculated mechanical properties of Cu–Ni alloys, is elastic constant, B is bulk modulus, G is shear modulus, vm is average velocity, E is Young’s modulus, and is Poisson’s ratio.
Firstly, for different works, the Cu-rich Cu content in Cu–Ni alloys has a smaller Young’s modulus in their respective results, whatever the simulation or experimental measurements. Our calculated Young’s modulus is less small than that of these other experiments, which is caused by the slight difference in the approaching process. It is reasonable and meaningful to further discuss the mechanical properties in calculation for deep consideration.
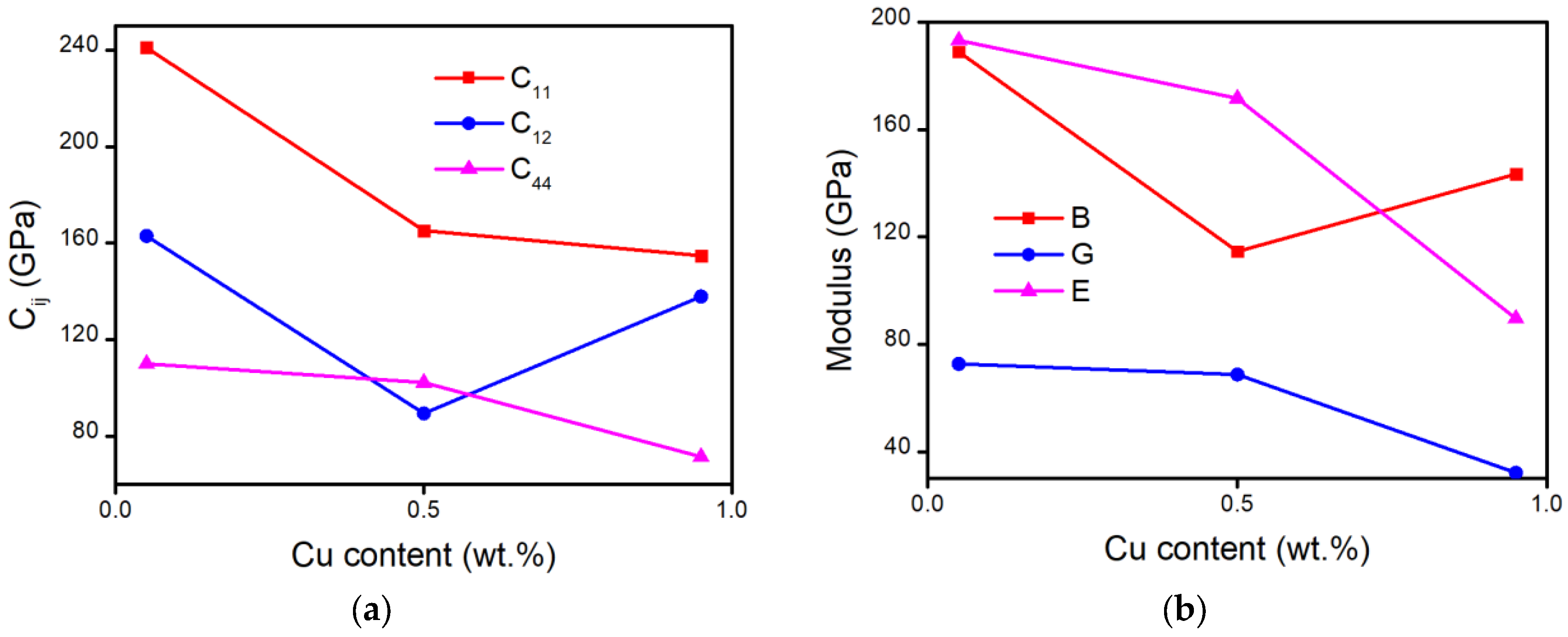
In Figure 3a, elastic constants refer to the deformation resistance of the crystal in anisotropy. In Voigt’s way, the subscript of C11 represents the deformation resistance in the x-axis for Cu–Ni alloys. The calculated elastic constant for C11 reduces with the increasing Cu content, indicating that the deformation resistance in the x-axis for Cu–Ni is becoming weak. Similarly, C44 represents the deformation resistance in the x,y-axis becoming weak, while C12 represents the deformation resistance in the y-axis to stress in the x-axis decreasing first, then increasing. The Cu content in the crystal has a great effect on deformation resistance in the x-axis. In Figure 3b, the popular moduli for materials are shown in different Cu content. Bulk modulus has a similar tendency as C12, showing the total deformation resistance of alloys. Shear modulus G and Young’s modulus E decrease in Cu-rich Cu content, predicting the fluctuation of hardness.
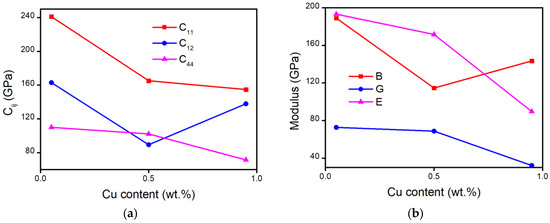
Figure 3.
Cu content-dependent mechanical properties: (a) elastic constants; (b) bulk modulus B, Shear modulus G, and Young’s modulus E.
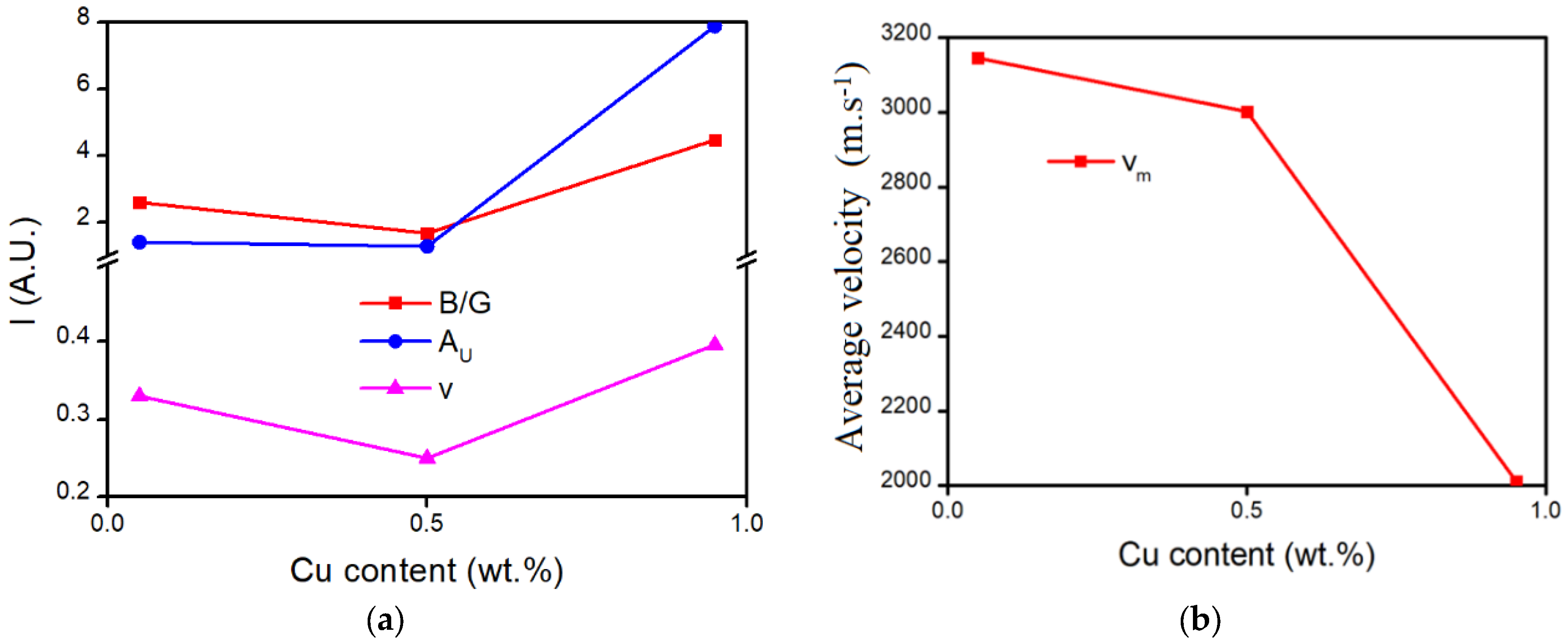
In Figure 4a, for the red curve, there is a typical transition from ductile to brittle. In Cu-rich Cu0.95Ni0.05 and Ni-rich Cu0.05Ni0.85 alloys, they are greatly ductile with the B/G > 1.75; meanwhile, the Cu-rich alloys have the higher ductility. On the other hand, the Cu0.5Ni0.5 alloys are brittle due to the B/G = 1.67. It shows that the right ratio for the binary compound of Cu–Ni systems is beneficial to improve the brittleness of pure metal. For the blue curve, the anisotropic index has the same tendency, where the Cu0.5Ni0.5 alloy with the smallest numerical index presented the lowest anisotropy. The low anisotropy with higher Young’s modulus shows that the Cu0.5Ni0.5 alloy has a great stiffness.
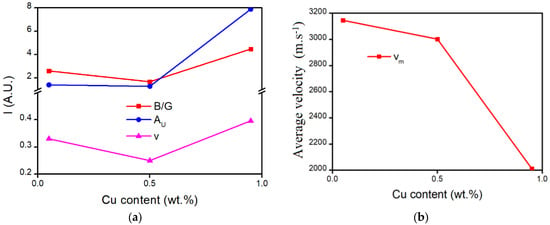
Figure 4.
Cu content-dependent brittleness and stiffness: (a) criterion for ductile and brittle B/G, anisotropic index AU, and Poisson’s ratio v; (b) average velocity vm.
For Poisson’s ratio in Figure 4a, we can obtain the same results as B/G. When the Poisson’s ratio v > 0.26, the alloys are ductile; otherwise, it behaves in a brittle way [13]. That is, the Cu0.5Ni0.5 alloy is brittle. In Figure 4b, the average velocity decreases with the increasing Cu content; the significant drop can be found in the Cu0.5Ni0.5 position. It shows that the Cu0.5Ni0.5 alloys have a good elastic strength by loading elastic wave velocity, almost comparable with pure copper.
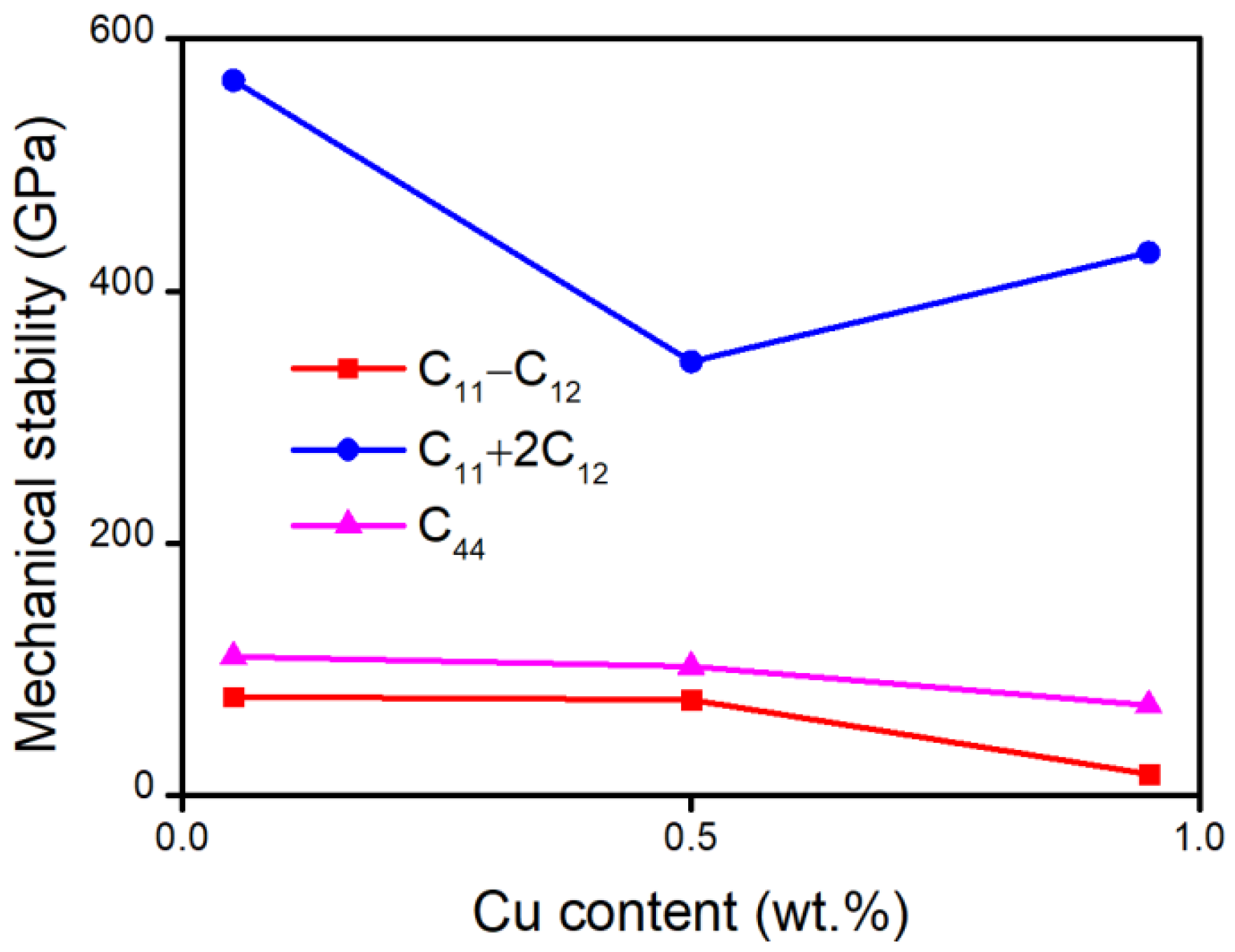
Elastic constant can be applied in a mechanical stability criterion, to reveal the mechanical stability of a crystal. For the cubic system, the criterion can be written simply [30]:
We put the elastic constants from Table 2 in the mechanical stability criterion, and the detailed results are shown in Figure 5; it can be seen that the alloys are mechanically stable.
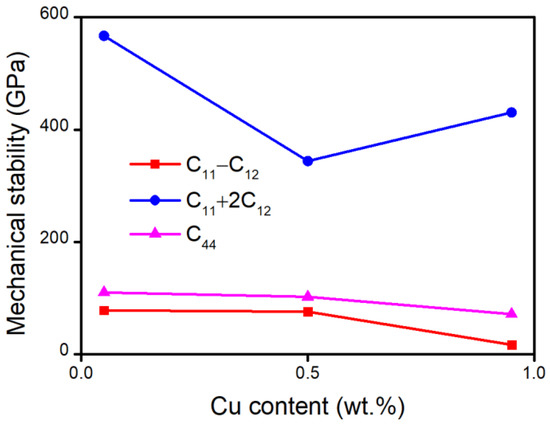
Figure 5.
Mechanical stability of Cu–Ni alloys.
4. Conclusions
First-principles calculations-based density functional theory is used in this paper; the lattice crystal and mechanical properties for Cu–Ni alloys are good, illustrated in the stiffness compared with the experiment for nanostructured Cu–Ni films. Firstly, we employ the pseudo-Voigt way to simulate the XRD results, showing the crystal is a reliable structure. Then, for the mechanical properties we computed, the main results are included as a list.
- Based on DFT, we calculated elastic constants, bulk modulus, shear modulus, Young’s modulus, anisotropic index AU, Poisson’s ratio v, average velocity, and B/G in this paper. It improves and supports the results for the experiment.
- Cu-rich and Ni-rich Cu–Ni alloys are ductile; the Ni-rich alloy has the highest uniaxial deformation resistance due to having the largest Young’s modulus.
- Cu0.5Ni0.5 as the most suitable binary compound is predicted to have great stiffness in the Cu–Ni system, due to the brittleness and low anisotropy.
Author Contributions
Conceptualization, C.J.; software, Z.L.; formal analysis, Y.W. and B.N.; resources, Q.L.; writing—original draft preparation, Y.W.; writing—review and editing, C.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data available on request from the authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Peterson, J.; Honnell, K.; Greeff, C.; Johnson, J.; Boettger, J.; Crockett, S. Global equation of state for copper. AIP Conf. Proc. 2012, 1426, 763. [Google Scholar]
- Varea, A.; Pellicer, E.; Pané, S.; Nelson, B.J.; Surinõach, S.; Baró, M.D.; Sort, J. Mechanical Properties and Corrosion Behaviour of Nanostructured Cu-rich CuNi Electrodeposited Films. Int. J. Electrochem. Sci. 2012, 7, 1288. [Google Scholar]
- Metikoš-Huković, M.; Babić, R.; Rončević, I.Š.; Grubač, Z. Corrosion resistance of copper–nickel alloy under fluid jet impingement. Desalination 2011, 276, 228. [Google Scholar] [CrossRef]
- Manzano, C.; Caballero-Calero, O.; Tranchant; Bertero, E.; Cervino-Solana, P.; Martin-Gonzales, M.; Philippe, L. Thermal conductivity reduction by nanostructuration in electrodeposited CuNi alloys. J. Mater. Chem. C 2021, 9, 3447. [Google Scholar] [CrossRef]
- Durivault, L.; Brylev, O.; Reyter, D.; Sarrazin, M.; Bélanger, D.; Roué, L. Cu–Ni materials prepared by mechanical milling: Their properties and electrocatalytic activity towards nitrate reduction in alkaline medium. J. Alloy. Compd. 2007, 432, 323. [Google Scholar] [CrossRef]
- Hur, S.; Kim, D.; Kang, B.; Yoon, S. The Structural and Electrical Properties of CuNi Thin-Film Resistors Grown on AlN Substrates for Π -Type Attenuator Application. J. Electrochem. Soc. 2005, 152, G472. [Google Scholar] [CrossRef]
- Chen, M.; Ma, E.; Hemker, K.J.; Sheng, H.; Wang, Y.; Cheng, X. Deformation twinning in nanocrystalline aluminum. Science 2003, 23, 1275. [Google Scholar] [CrossRef]
- Shen, T.; Koch, C.; Tsui, T.; Pharr, G. On the elastic moduli of nanocrystalline Fe, Cu, Ni, and Cu–Ni alloys prepared by mechanical milling/alloying. J. Mater. Res. 1995, 10, 2892. [Google Scholar] [CrossRef]
- Pellicer, E.; Varea, A.; Pané, S.; Nelson, B.J.; Menéndez, E.; Estrader, M.; Suriñach, S.; Baró, M.D.; Nogués, J.; Sort, J. Nanocrystalline Electroplated Cu–Ni: Metallic Thin Films with Enhanced Mechanical Properties and Tunable Magnetic Behavior. Adv. Funct. Mater. 2010, 20, 983. [Google Scholar] [CrossRef]
- Wang, C.; Bhuiyan, M.E.H.; Moreno, S.; Minary-Jolandan, M. Alloy with Controlled Composition from a Single Electrolyte Using Co-Electrodeposition. Appl. Mater. Interfaces 2020, 12, 18683. [Google Scholar] [CrossRef]
- Hui, J.; Zhang, X.; Yang, G.; Liu, T.; Liu, W. First-principles study of de-twinning in a FCC alloy. J. Solid State Chem. 2021, 293, 121765. [Google Scholar] [CrossRef]
- Hao, Y.; Chen, X.; Chen, B. The microstructure and property of lamellar interface in ternary Mg–Gd–Cu alloys: A combined experimental and first-principles study. J. Mater. Sci. 2021, 56, 9470. [Google Scholar] [CrossRef]
- Iwaoka, H.; Hircosawa, S. First-principles calculation of elastic properties of Cu-Zn intermetallic compounds for improving the stiffness of aluminum alloys. Comput. Mater. Sci. 2020, 174, 109479. [Google Scholar] [CrossRef]
- Wang, Z.; Li, J.; Fan, Z.; Zhang, Y.; Hui, S.; Peng, L.; Huang, G.; Xie, H.; Mi, X. Effects of Co Addition on the Microstructure and Properties of Elastic Cu-Ni-Si-Based Alloys for Electrical Connectors. Materials 2021, 14, 1996. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Hu, X.; Li, X.; Li, Z.; Zheng, Y.; Li, N.; Dong, C. Microstructure and electrical contact behavior of Al2O3-Cu/30W3SiC (0.5 Y2O3) composites. J. Mater. Res. Technol. 2022, 17, 1246. [Google Scholar] [CrossRef]
- Li, Z.; Cheng, Z.; Li, X.; Hu, Y.; Li, N.; Zheng, Y.; Shao, Y.; Liu, R.; Dong, C. Enthalpic interaction promotes the stability of high elastic Cu-Ni-Sn alloys. J. Alloy. Compd. 2022, 896, 163068. [Google Scholar] [CrossRef]
- Segall, M.; Lindan, P.; Probert, M.; Pickard, C.; Hasnip, P.; Clark, S.; Payne, M. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717. [Google Scholar] [CrossRef]
- Perdew, J.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Pfrommer, B.G.; Cote, M.; Louie, S.G.; Cohen, M.L. Relaxation of crystals with the quasi-Newton method. J. Comput. Phys. 1997, 131, 233. [Google Scholar] [CrossRef]
- Dasgupta, P. On Use of Pseudo-Voigt Profiles in Diffraction Line Broadening Analysis. Fizika A 2000, 9, 61. [Google Scholar]
- Caglioti, G.; Paoletti, A.; Ricci, F. Choice of Collimators for Crystal Spectrometers for Neutron Diffraction, Nuclear Instruments and Methods. Nucl. Instrum. 1958, 3, 223. [Google Scholar] [CrossRef]
- Katsura, T.; Tange, Y. A simple derivation of the Birch–Murnaghan equations of state (EOSs) and comparison with EOSs derived from other definitions of finite strain. Minerals 2019, 9, 745. [Google Scholar] [CrossRef]
- Kapahi, A.; Udaykumar, H. Dynamics of void collapse in shocked energetic materials: Physics of void–void interactions. Shock. Waves 2013, 23, 537. [Google Scholar] [CrossRef]
- Liu, W.; Liu, Q.; Zhong, M.; Gan, Y.; Liu, F.; Li, X.; Tang, B. Predicting impact sensitivity of energetic materials: Insights from energy transfer of carriers. Acta Mater. 2022, 236, 118137. [Google Scholar] [CrossRef]
- Born, M.; Huang, K. Dynamical Theory of Crystal Lattices. Oxford University Press: London, UK, 1954. [Google Scholar]
- Phacheerak, K.; Thanomngam, P. Pressure Dependence of Structural and Elastic Properties of Na2O: First-Principles Calculations. Intergrated Ferroelectr. 2022, 224, 256. [Google Scholar] [CrossRef]
- Yang, C.; Duan, Y.; Yu, J.; Peng, M.; Zheng, S.; Li, M. Elastic anisotropy and thermal properties of MBN (M = Al, Ga) systems using first-principles calculations. Vacuum 2023, 207, 111626. [Google Scholar] [CrossRef]
- Zhou, Y.; Lin, Y.; Wang, H.; Dong, Q.; Tan, J. First-principles study on the elastic anisotropy and thermal properties of Mg–Y compounds. J. Phys. Chem. Solids 2022, 171, 111034. [Google Scholar] [CrossRef]
- Wu, Y.; Ma, L.; Zhou, X.; Duan, Y.; Shen, L.; Peng, M. Insights to electronic structures, elastic properties, fracture toughness, and thermal properties of M23C6 carbides. Int. J. Refract. Met. Hard Mater. 2022, 109, 105985. [Google Scholar] [CrossRef]
- Gao, J.; Liu, Q.; Jiang, C.; Fan, D.; Zhang, M.; Liu, F.; Tang, B. Criteria of Mechanical Stability of Seven Crystal Systems and Its Application: Taking Silica as an Example. Chin. J. High Press. Phys. 2022, 36, 051101. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).