Next Article in Journal
Recent Developments of Carbon-Based Anode Materials for Flexible Lithium-Ion Batteries
Next Article in Special Issue
Structural Determination of the Hexacoordinated [Zn(L)2]2+ Complex Isomer Type Using Solution-State NMR, DFT Calculations and X-ray Crystallography
Previous Article in Journal
Influence of Nano-Sized SiC on the Laser Powder Bed Fusion of Molybdenum
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 12
Issue 9
10.3390/cryst12091277
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Perspective

NMR Crystallography as a Vital Tool in Assisting Crystal Structure Determination from Powder XRD Data

by
Kenneth D. M. Harris
School of Chemistry, Cardiff University, Park Place, Cardiff CF10 3AT, UK
Crystals 2022, 12(9), 1277; https://doi.org/10.3390/cryst12091277
Submission received: 3 August 2022 / Revised: 20 August 2022 / Accepted: 24 August 2022 / Published: 8 September 2022
(This article belongs to the Special Issue NMR Crystallography: Future Perspectives in Materials Characterization)
Browse Figures
Versions Notes

Abstract

:
Powder X-ray diffraction (XRD) and solid-state NMR spectroscopy are complementary techniques for investigating the structural properties of solids, and there are considerable opportunities and advantages to applying these techniques synergistically together in determining the structural properties of crystalline solids. This article provides an overview of the potential to exploit structural information derived from solid-state NMR data to assist and enhance the process of crystal structure determination from powder XRD data, focusing in particular on the structure determination of organic molecular materials.

1. Introduction

While single-crystal X-ray diffraction (XRD) is nowadays a very routine and powerful technique for determining the structural properties of crystalline materials [1], an intrinsic limitation of this technique is that a single-crystal specimen of appropriate size and quality must be available for the material of interest. Indeed, crystalline materials often cannot be prepared as single crystals of suitable size and quality, and are therefore unsuitable for single-crystal XRD studies, even using synchrotron-based micro-crystal XRD facilities. Nevertheless, such materials may be prepared instead as microcrystalline powders, allowing high-quality powder XRD data to be recorded and used for structure determination. However, as elaborated below, it is important to recognize that structure determination from powder XRD data is intrinsically more challenging than structure determination from single-crystal XRD data, and the quest to overcome these challenges has motivated the development of new and increasingly powerful techniques for achieving successful structure determination from powder XRD data [2,3,4,5,6,7,8,9,10,11,12], as discussed in Section 3.
In the case of single-crystal XRD data, experimental measurement of the intensities of diffraction maxima can generally be carried out straightforwardly and accurately, particularly as the measurement techniques allow each diffraction maximum to be individually resolved in three-dimensional reciprocal space. In contrast, as a consequence of the random orientational distribution of the crystallites in a typical polycrystalline powder sample, powder XRD data are recorded as a function of only one reciprocal-space variable (the diffraction angle 2θ), and the three-dimensional diffraction data that arise in a single-crystal XRD measurement are essentially “compressed” into one dimension in a powder XRD measurement (Figure 1a,b). As a consequence, there is usually considerable overlap of peaks in the powder XRD pattern (Figure 1c), which obscures information on the positions (2θ values) and intensities of individual diffraction peaks; unfortunately, attempts to carry out structure determination using unreliable information on peak positions and peak intensities extracted from the powder XRD data may ultimately lead to difficulties or failure. The peak overlap problem is generally less severe for materials with small unit cells and high symmetry (a situation often encountered for simple ionic materials), as the density of peaks in the powder XRD pattern is low. On the other hand, organic molecular solids typically have large unit cells and low symmetry, which gives rise to a high density of peaks in the powder XRD pattern, resulting in substantial peak overlap. In such cases, the structure determination process clearly becomes significantly more challenging.
In addition to the challenges discussed above, two further issues concerning the nature of the powder sample itself can make structure determination from powder XRD data problematic or even impossible. The first issue concerns the phase purity of the powder sample. If the powder sample contains one or more crystalline phases in addition to the crystalline phase of interest, it is likely that structure determination from powder XRD data will fail, unless the presence and identity of the additional crystalline phases can be established. Importantly, solid-state NMR and other experimental techniques can provide direct insights regarding the phase purity of a powder sample and the identity of additional crystalline phases present. From this information, it may be possible to establish which peaks in the powder XRD data arise from additional phases, allowing successful structure determination of the phase of interest to be carried out from the powder XRD data. The second issue concerns the distribution of crystallite orientations in the powder sample, for which the ideal situation is to have a completely random distribution of crystallite orientations. However, powder samples often exhibit “preferred orientation” (i.e., a non-random distribution of crystallite orientations), especially when the crystallites have a strongly anisotropic shape (e.g., long-needle or flat-plate morphologies). A consequence of preferred orientation is that the relative peak intensities in the experimental powder XRD pattern deviate from the intrinsic relative diffraction intensities characteristic of the crystal structure of the material, which has the potential to cause difficulties or failure in attempting to determine the crystal structure from the powder XRD data.
Although significant progress has been made in overcoming the challenges in this field, structure determination from powder XRD data is not yet a routine technique (at least compared to the relatively automated analysis of single-crystal XRD data), and independent structural insights obtained from other experimental and computational techniques can be highly beneficial in facilitating successful structure determination from powder XRD data. In this regard, solid-state NMR spectroscopy and powder XRD provide complementary information about the structural properties of solids, and there are therefore considerable opportunities to exploit these techniques together in the structural characterization of solids.
This article presents an overview of the vital ways in which solid-state NMR data can be exploited to enhance the process of structure determination from powder XRD data, with particular focus on structure determination of organic molecular materials. After a brief overview of the types of structural information that solid-state NMR data can provide within this context (Section 2) and an introduction to contemporary techniques and strategies for carrying out structure determination of organic materials from powder XRD data (Section 3), several examples are given to highlight the advantages of the synergistic use of solid-state NMR data and powder XRD data in this field (Section 4 and Section 5).
We emphasize that the discussion here is focused on structure determination of micro-crystalline materials for which the size of ordered crystalline domains is sufficiently large to give well-defined Bragg peaks in the powder XRD pattern. To elucidate the structural properties of nano-crystals and amorphous materials, on the other hand, alternative approaches for structure determination from X-ray scattering data may be exploited [13,14,15].

2. Overview of Opportunities to Utilize Solid-State NMR Data to Assist Structure Determination from Powder XRD Data

In general, experimental solid-state NMR data are influenced by the local structural properties in the vicinity of the nucleus for which the NMR data are measured, and can be interpreted directly in terms of specific structural features within the material of interest. In this context, solid-state NMR data can readily provide direct insights on a variety of structural properties that may augment the process of structure determination from powder XRD data, including: (i) assessing the phase purity of a polycrystalline sample, (ii) determining the number of crystallographically independent molecules in the asymmetric unit, (iii) establishing the existence of disorder in the crystal structure (for example, static positional disorder or dynamic disorder), (iv) providing insights on the conformational properties or the tautomeric form of the molecules present in the crystal structure, and (v) revealing the nature of specific intermolecular interactions that exist in the crystal structure, including quantitative determination of specific inter-nuclear distances. Several examples illustrating these issues are given in Section 4. The ability of solid-state NMR data to yield direct structural information on these aspects of a crystal structure can be a hugely valuable asset in assisting the process of structure determination from powder XRD data. As such, strategies for structure determination that combine the analysis of powder XRD data and solid-state NMR data represent an important area of activity within the field of research that is now popularly described as NMR Crystallography [16,17,18,19,20,21,22,23,24].
In addition to the opportunity to use solid-state NMR data to provide specific structural insights to enhance the process of structure determination from powder XRD data, solid-state NMR data can also serve a critical role in validation of the final refined crystal structure obtained in Rietveld refinement (the final stage of structure determination from powder XRD data; see Section 3). This opportunity relies on the fact that solid-state NMR data can now be calculated reliably for crystal structures via periodic DFT calculations using the GIPAW (Gauge Including Projector Augmented Wave) method [25,26,27,28,29]. In this context, the CASTEP code [30] is a popular and highly regarded program for applications in the calculation of solid-state NMR data for crystalline materials.
Following structure determination from powder XRD data, solid-state NMR data calculated using the DFT-GIPAW approach for the final refined crystal structure may be compared directly with experimental solid-state NMR data measured for the same material (Figure 2). Clearly, good agreement between calculated and experimental solid-state NMR data provides strong vindication for the correctness of the refined crystal structure, augmenting the validation that is provided by rigorous assessment [31] of the quality of fit between calculated and experimental powder XRD data in the Rietveld refinement process. Conversely, an unsatisfactory level of agreement between the calculated and experimental solid-state NMR data may suggest that certain aspects of the refined crystal structure are not correct. The strategy of comparing calculated and experimental solid-state NMR data in this way is becoming an increasingly popular approach for enhancing the scrutiny and validation of the final crystal structure obtained in structure determination from diffraction data [32,33,34,35,36,37,38] (not only in the case of structure determination from powder XRD data as highlighted in this article, but also to resolve structural uncertainties or ambiguities that may arise in structure determination from single-crystal XRD data). Examples illustrating this application of solid-state NMR data within the process of structure determination from powder XRD data are given in Section 5.

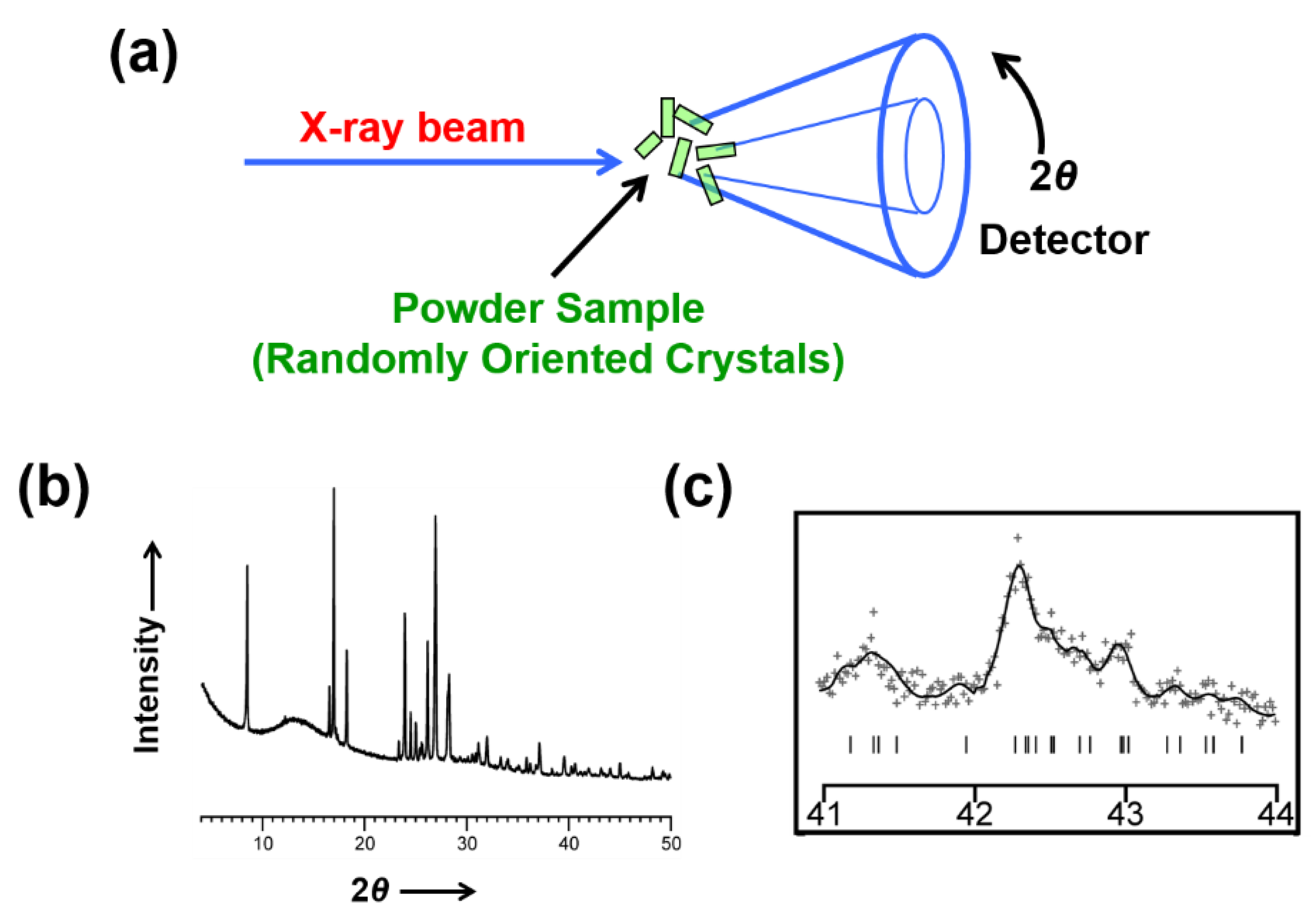
3. Overview of Structure Determination from Powder XRD Data

The main stages of structure determination from powder XRD data [2,3,4,5,6,7,8,9,10,11,12] are: (i) unit cell determination and space group assignment, (ii) structure solution, and (iii) structure refinement (Rietveld refinement). After determining the unit cell and space group in stage (i), the aim of the structure solution stage is to obtain an acceptable approximation to the correct crystal structure, using the unit cell and space group determined in stage (i), but starting from zero knowledge of the arrangement of atoms or molecules within the unit cell. If the crystal structure obtained in the structure solution stage is a sufficiently good approximation to the correct structure, a high-quality description of the structure can be obtained in the subsequent structure refinement stage. Structure refinement from powder XRD data is generally achieved fairly straightforwardly using the technique of Rietveld profile refinement [39]. In general, structure solution is the most challenging stage of structure determination from powder XRD data, particularly for the case of organic materials. However, in recent decades, significant progress has been made [2,3,4,5,6,7,8,9,10,11,12,40] in the development of techniques and strategies to overcome the challenges encountered in the structure solution stage.
The techniques for structure solution from powder XRD data fall into two broad categories: traditional approaches and direct-space approaches. The main features of these two different approaches for structure solution are now briefly described.
The traditional approach for structure solution follows a close analogy to the way in which structure solution is carried out from single-crystal XRD data. In this approach, the integrated intensities of individual peaks are extracted directly from the experimental powder XRD pattern to generate a set of integrated peak intensities, analogous to the data recorded in single-crystal XRD. The set of integrated peak intensities is then used in the types of structure solution calculation that have been developed for single-crystal XRD data. However, as a result of peak overlap in the powder XRD pattern (as discussed above), the integrated peak intensities extracted from the powder XRD pattern may be inaccurate and unreliable, leading to difficulties or even failure in attempting to solve the crystal structure using the integrated peak intensities. As noted above, the peak overlap problem can be particularly severe for materials (such as most organic molecular solids) with large unit cells and low symmetry, and consequently the traditional approach for structure solution may encounter particular challenges in these cases.
In the direct-space strategy [40], on the other hand, structure solution is tackled as a global optimization problem. In this approach, trial crystal structures are generated in direct space, and the quality of each trial structure is assessed by comparing the powder XRD pattern calculated for the trial structure and the experimental powder XRD pattern. In this regard, it is important to note that calculating the powder XRD pattern corresponding to any trial structure is an automatic calculation. For each trial structure, the quality of agreement between the calculated and experimental powder XRD patterns is quantified using a suitable figure-of-merit, such as the weighted powder profile R-factor Rwp (the R-factor normally used in Rietveld refinement). The use of Rwp is advantageous in this regard as it considers the entire digitized intensity profile in the experimental and calculated powder XRD patterns point-by-point, rather than considering the integrated intensities of individual peaks, and therefore the peak overlap in the powder XRD pattern is implicitly taken into consideration. It is important to note that Rwp uses the digitized experimental powder XRD data directly “as measured”, and the use of Rwp to assess the quality of trial structures generated in the context of direct-space structure solution circumvents the need to extract individual integrated peak intensities from the experimental powder XRD data.
The direct-space strategy tackles structure solution as a global optimization problem, and aims to find the trial structure that corresponds to optimal agreement (i.e., lowest Rwp) between calculated and experimental powder XRD data. This process is equivalent to exploring a hypersurface Rwp(Γ) to find the global minimum, where Γ represents the set of variables that define the trial structures. A critical feature underlying the success of the direct-space strategy for structure solution is that the molecular models used to create the trial structures incorporate a significant amount of reliable prior knowledge of molecular geometry (e.g., standard bond lengths, standard bond angles and known geometries of well-defined structural units such as aromatic rings). As a consequence, the structural variables in the set Γ comprise, for each molecule in the asymmetric unit, the position {x, y, z} and orientation {θ, φ, ψ} of the whole molecule relative to the unit cell axes, and a set of n torsion-angle variables {τ1, τ2, …, τn} to define the molecular conformation. With this definition, the number of structural variables in the set Γ is considerably lower than the number of structural variables that would arise if each atom in the asymmetric unit was allowed to move independently in the direct-space structure solution calculation (i.e., without incorporating any prior knowledge of the geometry of the molecule), facilitating a much more efficient direct-space search to locate the correct structure solution.
A wide range of global optimization algorithms are available, and may be applied to search for the trial structure that corresponds to the global minimum on the Rwp(Γ) hypersurface. In particular, Monte Carlo, Simulated Annealing and Genetic Algorithm techniques have been widely used in this field [2,3,4,5,6,7,8,9,10,11,12]. In almost all the examples of structure determination from powder XRD data discussed in this article, structure solution was carried out using the direct-space strategy implemented in the program EAGER [41,42,43,44,45,46,47,48,49,50,51,52], which carries out global optimization using a Genetic Algorithm that has been adapted and optimized for this field of application.
Structure determination of organic molecular solids from powder XRD data is now generally carried out using the direct-space strategy for structure solution (although several examples of successful structure determination of such materials using the traditional approach for structure solution have also been reported) followed by Rietveld refinement. In general, however, structure determination from powder XRD data is still far from routine, requiring careful assessment and user intervention at each stage of the structure determination process to ensure that the correct decisions are made at each stage. As discussed below, taking advantage of structural insights derived from solid-state NMR data at various stages of the structure determination process can help to facilitate a smooth and successful pathway through the structure determination process, as well as providing a critical and robust assessment of the correctness of the final crystal structure.

4. Examples of Using Solid-State NMR Data to Assist the Process of Structure Determination from Powder XRD Data

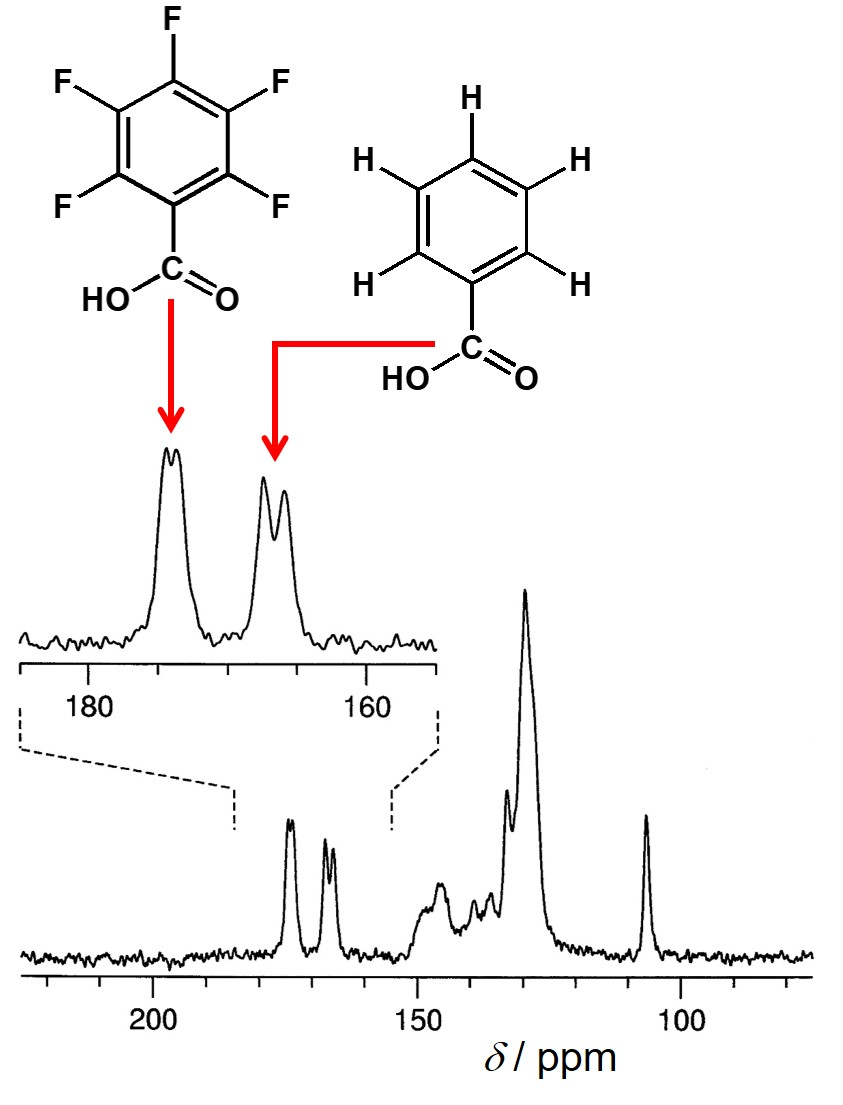
4.1. Determining the Number of Molecules in the Asymmetric Unit

An important issue prior to commencing a direct-space structure solution calculation from powder XRD data is to know the number (conventionally denoted Z’) of crystallographically independent molecules in the asymmetric unit, recalling that independent knowledge of Z’ can play an important role in assigning the correct space group symmetry for the crystal structure.
After the unit cell has been determined in the first stage of the structure determination process, the number of molecules in the unit cell (conventionally denoted Z) can usually be deduced straightforwardly from density considerations. However, for a given value of Z, different values of Z’ may still be possible, depending on the multiplicity of the space group. To illustrate this issue, we consider the example of a monoclinic system in the case in which analysis of peak intensities in the indexed powder XRD data gives no evidence for systematic absences, suggesting that the space group is P2, Pm or P2/m. If density considerations indicate that there are four molecules in the unit cell (Z = 4), the following scenarios could arise: (i) the space group is P2 or Pm (both of which have multiplicity = 2) with two molecules in the asymmetric unit (Z’ = 2), or (ii) the space group is P2/m (which has multiplicity = 4) with one molecule in the asymmetric unit (Z’ = 1). Fortunately, high-resolution solid-state NMR data can provide independent information on the value of Z’, which would allow one of the scenarios (i) or (ii) in this example to be assigned as correct.
In principle, the high-resolution solid-state 13C NMR spectrum of an organic material contains one peak for each crystallographically distinct 13C environment in the crystal structure (however, we note that, in practice, the actual number of observed peaks may be lower due to accidental overlap of peaks). Thus, after assigning each peak in the high-resolution solid-state 13C NMR spectrum to a specific 13C environment in the molecule, it is usually straightforward to deduce whether the asymmetric unit contains one, two or more molecules. In some cases, such analysis may lead to the conclusion that the asymmetric unit comprises only a fraction of the molecule, indicating that the molecule is located on a “special position” in the crystal structure, with a molecular symmetry element coinciding with a crystallographic symmetry element.
As an illustration of determining the number of molecules in the asymmetric unit from high-resolution solid-state 13C NMR data, we consider the example [53] of a 1:1 co-crystal containing benzoic acid (BA) and pentafluorobenzoic acid (PFBA). As shown in Figure 3, the solid-state 13C NMR spectrum contains two 13C NMR resonances for the carboxylic acid group of BA and two 13C NMR resonances for the carboxylic acid group of PFBA, indicating that the asymmetric unit contains two molecules of BA and two molecules of PFBA. From unit cell determination, the material was assigned as monoclinic, and density considerations suggested that there are eight molecules of BA and eight molecules of PFBA in the unit cell (i.e., eight formula units (BA) (PFBA) of the 1:1 co-crystal in the unit cell). Furthermore, analysis of systematic absences in the powder XRD data indicated that the crystal structure is C-centred and has a c-glide plane, indicating that the space group is either Cc or C2/c. In order to give the correct number of eight molecules of BA and eight molecules of PFBA in the unit cell, space group Cc (with multiplicity = 4) would correspond to two molecules of BA and two molecules of PFBA in the asymmetric unit, whereas space group C2/c (with multiplicity = 8) would correspond to one molecule of BA and one molecule of PFBA in the asymmetric unit. On this basis, it is clear that only space group Cc is consistent with the information derived from the solid-state 13C NMR data regarding the number of independent molecules in the asymmetric unit, and the structure determination from powder XRD was carried out successfully using this space group.
The next example illustrates a case in which high-resolution solid-state 13C NMR data provide evidence that the molecule in the crystal structure is located on a crystallographic symmetry element, focusing on the structure determination [54] of an early-generation dendrimeric material tetrakis [(3, 5-dimethoxybenzyloxy) methyl] methane (TDMM; Figure 4). In the high-resolution solid-state 13C NMR spectrum of this material (Figure 4a), the region of the spectrum (between 95 ppm and 101 ppm) corresponding to aromatic CH environments contains only six distinct peaks, which is half the number (12) of aromatic CH environments in a single molecule of TDMM. This observation suggests that the asymmetric unit comprises only half the molecule (Z’ = ½), with the central carbon atom of the molecule located on a crystallographic 2-fold rotation axis (Figure 4b). This information was crucial in setting up the correct structural model for direct-space structure solution, which proceeded successfully and led to the final refined crystal structure shown in Figure 4c.
Structure determination of a new polymorph (β phase) of the latent pigment DPP-Boc from powder XRD data [55] also utilized insights from high-resolution solid-state 13C NMR data. Following unit cell determination, the crystal system was assigned as triclinic and density considerations indicated that there is one molecule of DPP-Boc in the unit cell (Z = 1). However, solid-state 13C NMR data suggested that the asymmetric unit comprises half the DPP-Boc molecule (Z’ = ½). From this information, it is clear that the correct space group is P 1 ¯ , and direct-space structure solution was carried out successfully with the molecular inversion centre fixed at the crystallographic inversion centre.

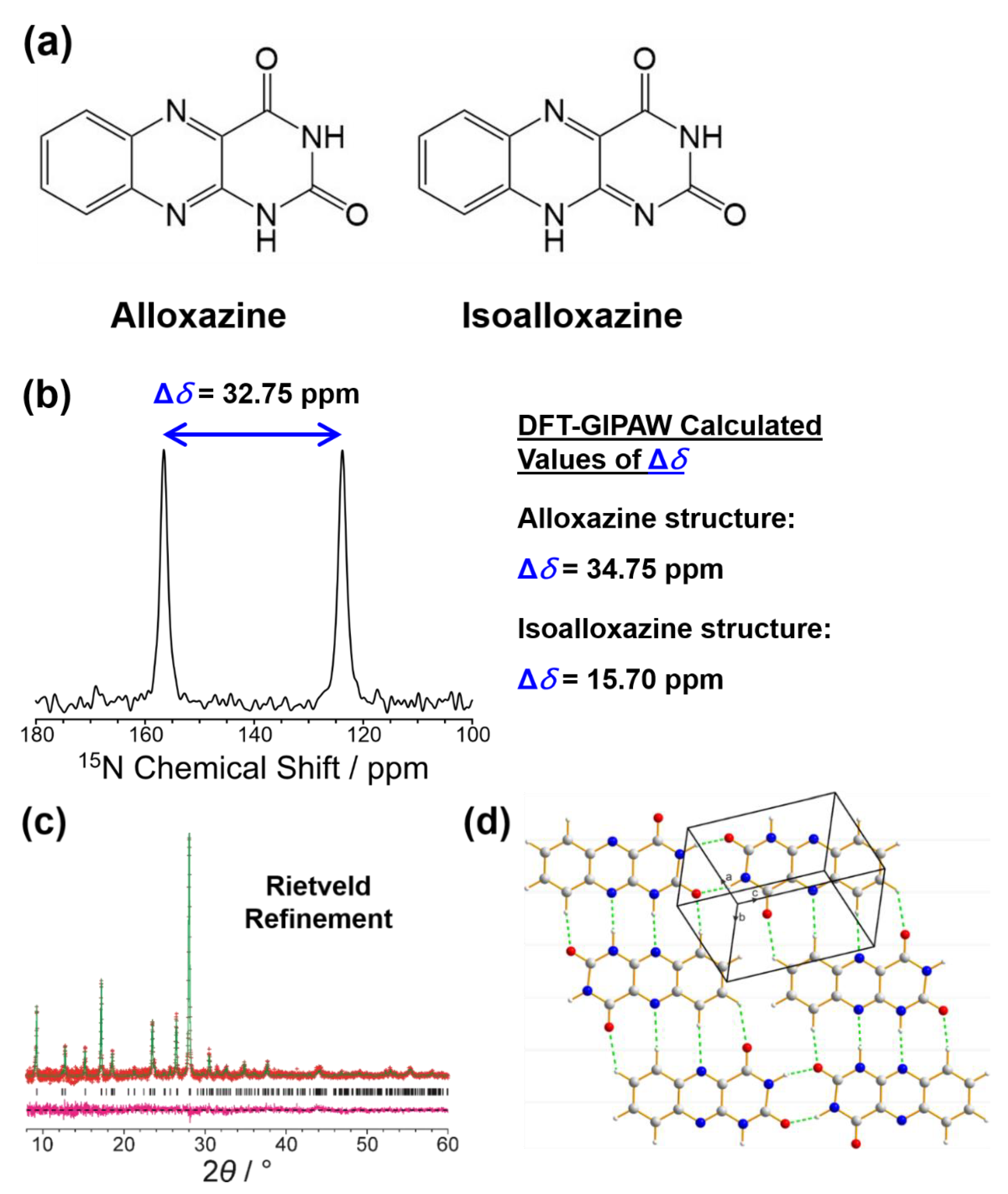
4.2. Determining the Geometric Features of the Molecule in the Crystal Structure, Focusing on Establishing the Correct Tautomeric Form

In general, the identity of the molecule(s) present in the crystal structure and the stoichiometry of the structure (e.g., in the case of solvate or co-crystal structures) may be established readily from a range of analytical techniques, including solid-state NMR, before commencing direct-space structure solution calculations from powder XRD data. However, an important issue in setting up an appropriate structural model for direct-space structure solution calculations is to have a reliable understanding of the geometry of the molecule in the crystal structure. In this context, we consider the case of molecules that can exist in different tautomeric forms.
An early example concerns structure determination of red fluorescein from powder XRD data [56], which exploited high-resolution solid-state 13C NMR to identify that the tautomeric form of the molecule present in the crystal structure is the quinoid tautomer, rather than the lactoid or zwitterionic tautomers. This structural knowledge allowed the correct tautomeric form to be used in direct-space structure solution calculations, leading to successful structure determination.
Another example involving assignment of the tautomeric form concerns the recent crystal structure determination of alloxazine [57], a tricyclic ring system found in many biologically important molecules, with structure determination carried out from powder XRD data. The alloxazine molecule can exist in two tautomeric forms (called alloxazine and isoalloxazine; Figure 5a), differing only in the position of one hydrogen atom in the molecule. For this reason, two virtually identical crystal structures—one containing the alloxazine tautomer and the other containing the isoalloxazine tautomer—were found to give a high-quality fit to the powder XRD data in Rietveld refinement. Indeed, the only significant difference between the crystal structures containing the alloxazine and isoalloxazine tautomers concerns the position of a hydrogen atom within an intermolecular N–H⋯N hydrogen bond (i.e., N–H⋯N versus N⋯H–N) linking neighbouring molecules, and it is therefore not surprising that the powder XRD patterns of the crystal structures containing the two tautomers are virtually indistinguishable. To establish the tautomeric form that actually exists in the material, high-resolution solid-state 15N NMR data were recorded (Figure 5b), with isotropic peaks at 123.81 and 156.56 ppm (chemical shift difference, 32.75 ppm). Although there are four distinct 15N environments in the crystal structure, the conditions of the solid-state 15N NMR measurement (involving 1H→15N cross-polarization with contact time τcp = 2 ms) gave signals only for the two 15N environments directly bonded to 1H (i.e., 15N–1H bonds). DFT-GIPAW calculations of the isotropic 15N chemical shifts for the two N–H environments in the crystal structures containing the alloxazine and isoalloxazine tautomers gave 15N resonances at 126.68 and 161.43 ppm (chemical shift difference, 34.75 ppm) for the alloxazine crystal structure and at 149.94 and 165.64 ppm (chemical shift difference, 15.70 ppm) for the isoalloxazine crystal structure. Clearly, the experimental values of isotropic 15N chemical shifts are in significantly better agreement with the calculated values for the crystal structure containing alloxazine, and the difference between the two 15N chemical shifts in the experimental spectrum (32.75 ppm) is significantly closer to the calculated difference for the crystal structure containing alloxazine (34.75 ppm) than the crystal structure containing isoalloxazine (15.70 ppm). These observations strongly support the conclusion that the material contains the alloxazine tautomer rather than the isoalloxazine tautomer. The high quality of fit in the Rietveld refinement and the final refined crystal structure containing the alloxazine tautomer are shown in Figure 5c,d.

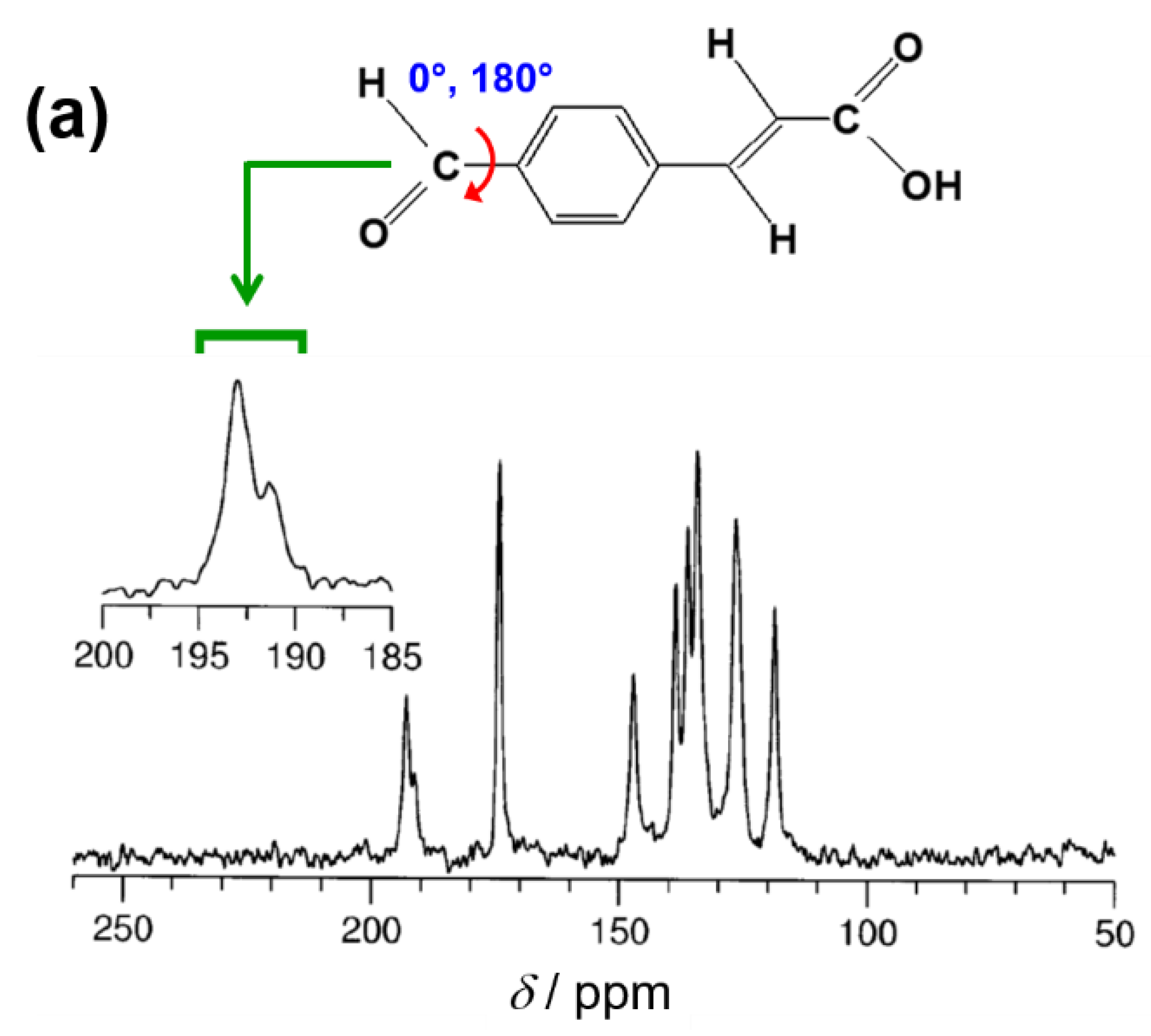
4.3. Detecting Disorder in a Crystal Structure from Solid-State NMR Data

Detailed insights regarding disorder in crystalline materials (either static positional disorder or dynamic disorder) can be obtained from solid-state NMR data, which may be particularly useful in assisting the structure determination of disordered materials from powder XRD data. For crystal structures containing significant disorder, it would generally be essential to incorporate a suitable description of the disorder within the definition of the structural model used in direct-space structure solution calculations, and clearly solid-state NMR data may provide vital information to allow an appropriate structural model to be established. However, if the disorder concerns only a localized part of the structure, it may be possible to achieve successful direct-space structure solution using an ordered structural model, and also to obtain a Rietveld refinement of reasonable quality using this ordered model, which may then be improved by incorporating an appropriate description of the disorder within the structural model. To illustrate this situation, we consider the structure determination of the β polymorph of p-formyl-trans-cinnamic acid (p-FCA) from powder XRD data [58] (Figure 6). For this material, direct-space structure solution from powder XRD data was achieved successfully on the basis of an ordered structural model, which then gave a good quality of fit in Rietveld refinement (Figure 6b; Rwp = 3.27%). However, inspection of the high-resolution solid-state 13C NMR spectrum of this material (Figure 6a) revealed that there are two peaks for the 13C site in the formyl group [59], while all other 13C sites in the molecule give only a single peak, suggesting that the formyl group may be disordered between two different local environments in the crystal structure, and with the remainder of the structure ordered. Integration of the two peaks for the formyl group in the solid-state 13C NMR spectrum suggests that the relative populations of the two local environments are 69% and 31%. Subsequent Rietveld refinement was carried out using a structural model in which the disorder is represented by two orientations of the formyl group, each with refined fractional occupancies; in each orientation (Figure 6a), the formyl group is co-planar with the aromatic ring, but the two orientations differ by 180° rotation about the C–C bond that links the formyl group and the aromatic ring. Rietveld refinement of the disordered model (Figure 6c) gave an improved quality of fit (Rwp = 2.87%), with refined fractional occupancies of 59% and 41% for the two orientations of the formyl group, in close agreement with the relative populations determined from the high-resolution solid-state 13C NMR data. In this example, if the existence of disorder in the crystal structure had not been revealed from inspection of the solid-state 13C NMR data, it is probable that the Rietveld refinement for the ordered model (Figure 6b) would have been considered as an acceptable quality of fit to the experimental powder XRD data, and the existence of disorder in the crystal structure may not have been apparent by considering the powder XRD data alone.

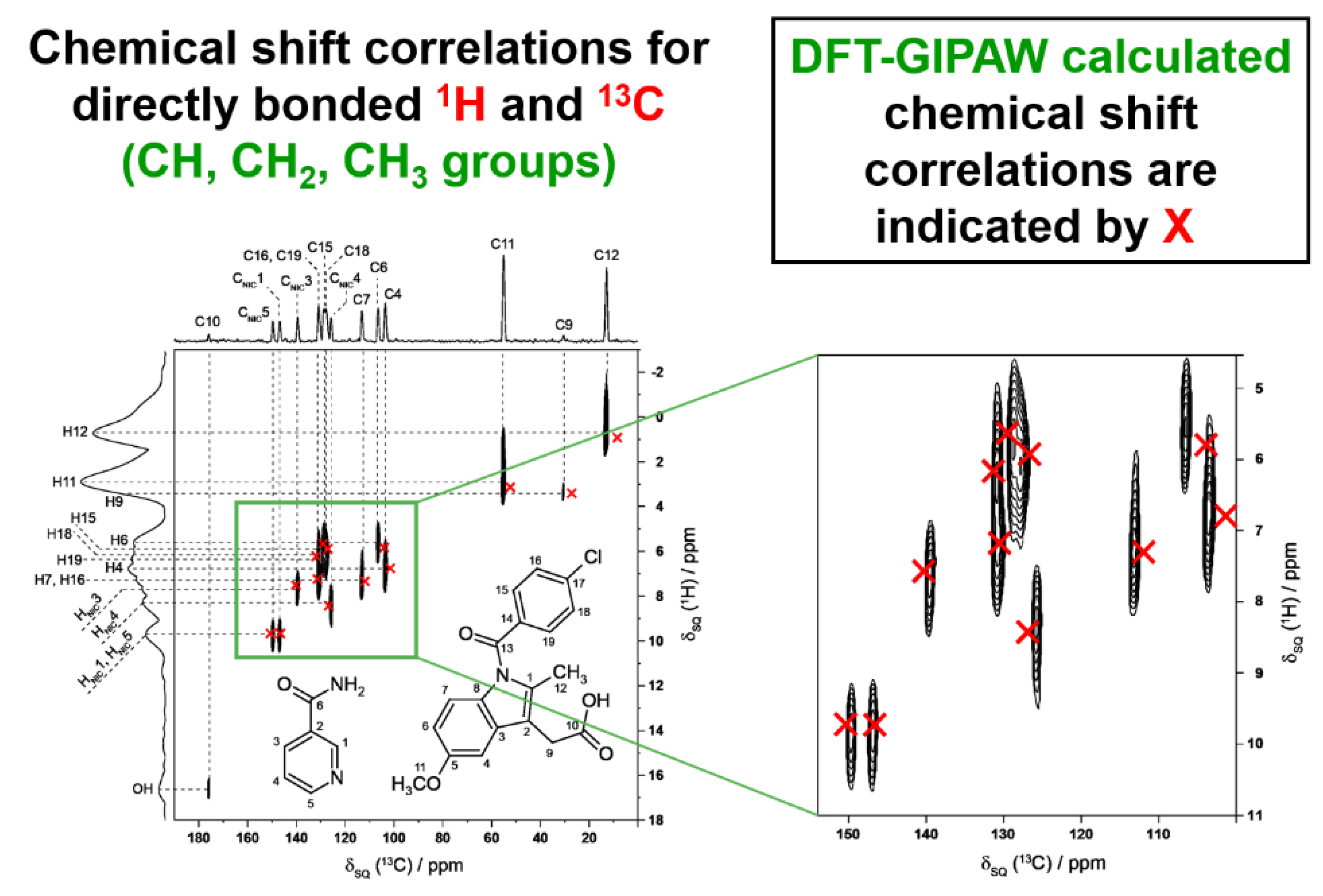
4.4. Enhancing Structure Solution Calculations Using Insights on Specific Internuclear Interactions

It is important to note that specific structural features deduced from solid-state NMR data may be utilized actively within the process of structure solution from powder XRD data, illustrated by the structure determination [60] of polymorph I of 3′,5′-bis-O-decanoyl-2′-deoxyguanosine [Figure 7; abbreviated as dG(C10)2], which represents one of the most challenging crystal structures of an organic material (a 90-atom molecule) to be determined from powder XRD data.
This work exploited the fact that measurements of internuclear coupling from solid-state NMR data yield information on specific intermolecular interactions, focusing on measurement of indirect (electron-coupled) dipole–dipole interactions (i.e., J-coupling) through hydrogen bonds [61,62] to allow the functional groups engaged in hydrogen-bonding interactions within the crystal structure to be identified directly from solid-state NMR data. Clearly, such knowledge may allow trial structures containing the correct hydrogen-bonding motif to be favoured in the structure solution process, and may serve as a basis to reject trial structures that contain incorrect hydrogen-bonding motifs.
In the structure determination of polymorph I of dG(C10)2 from powder XRD data [60], results from earlier solid-state NMR studies [63,64] of 15N⋯15N J-coupling in N–H⋯N hydrogen bonds within this material provided direct insights concerning the intermolecular hydrogen-bonding between guanine moieties, including a 2hJN7N10 coupling of 5.9 Hz, which suggests that the crystal structure contains a relatively strong N–H⋯N hydrogen bond involving N7 and N10 (Figure 7a). This information provided a robust criterion for acceptance or rejection of trial structures in assessing the results of direct-space structure solution from powder XRD data. As shown in Figure 7b, the N10–H⋯N7 hydrogen bonding predicted from the solid-state 15N NMR data is present in the final refined crystal structure.
Furthermore, comparison between the isotropic 1H, 13C and 15N chemical shifts and J-couplings calculated using DFT-GIPAW methodology for the final refined crystal structure of polymorph I of dG(C10)2 and the experimentally determined values of isotropic 1H and 13C chemical shifts [65] and 15N chemical shifts and J-couplings [64] provide additional scrutiny and validation of the crystal structure following the final Rietveld refinement [60]. As an illustration (Figure 7c), very good agreement is observed between calculated and experimental values of isotropic chemical shifts (with RMS deviations of 0.57 ppm for 1H NMR, 3.02 ppm for 13C NMR, and 2.01 ppm for 15N NMR).

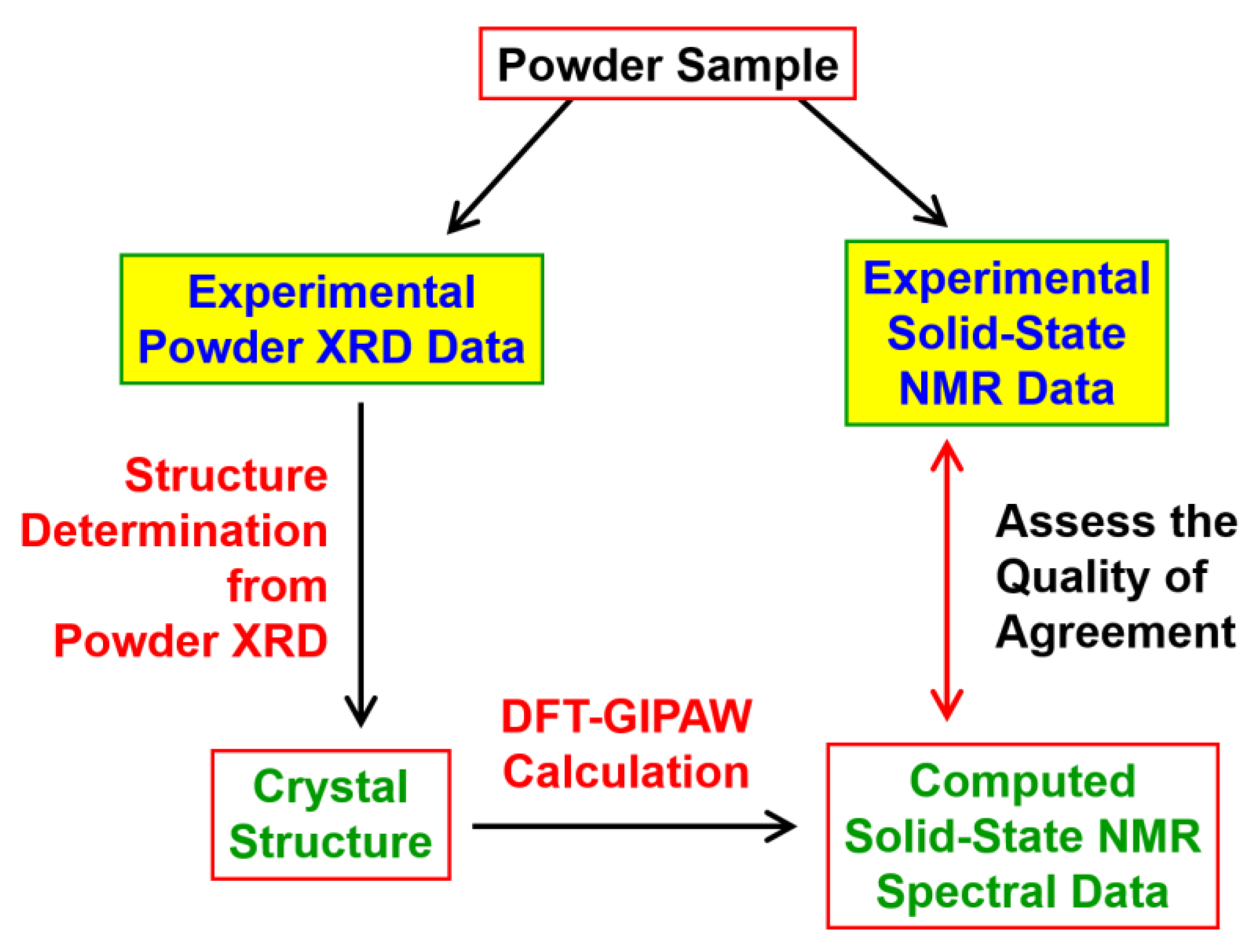
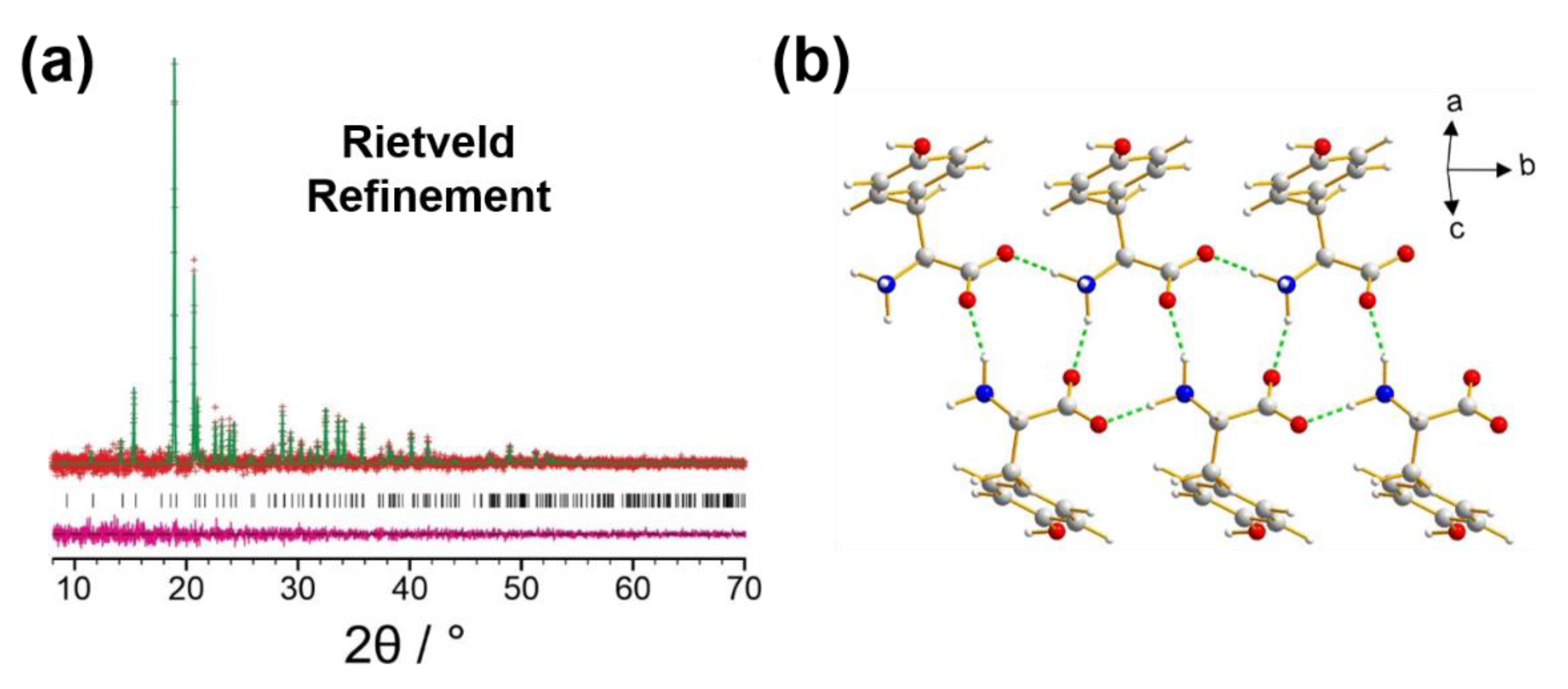
5. Examples of Using Solid-State NMR Data in Validation of the Final Crystal Structure Determined from Powder XRD Data

In structure determination of organic materials from powder XRD data, a strategy [33] that is now commonly applied in the process of validation of the final refined crystal structure is based on quantitative assessment of the compatibility between the crystal structure and solid-state NMR data recorded for the material of interest (see Figure 2). After Rietveld refinement, DFT-GIPAW calculations are used to calculate solid-state NMR data for the final refined crystal structure, followed by rigorous scrutiny of the level of agreement between experimental solid-state NMR data recorded for the material and the corresponding solid-state NMR data calculated for the final refined crystal structure. It is important to emphasize that this approach ensures that the quality of the final refined crystal structure is assessed both against the experimental powder XRD data (i.e., in the Rietveld refinement) and against the experimental solid-state NMR data, representing a robust validation of the correctness of the structure.
As an example of this approach [33], we consider the structure determination from powder XRD data of a 1:1 co-crystal containing indomethacin and nicotinamide, which is of relevance in pharmaceutical research [66]. Following successful structure solution using the direct-space strategy and subsequent Rietveld refinement, the isotropic 1H and 13C NMR chemical shifts were calculated for the final refined crystal structure using the DFT-GIPAW approach and were then compared (Figure 8) to the isotropic 1H NMR and 13C NMR chemical shifts measured experimentally for this material [67]. Clearly, the calculated chemical shifts are in excellent agreement with the experimentally measured chemical shifts, representing a robust validation of the structure determined from the powder XRD data. The only significant discrepancies between experimental (δexpt) and calculated (δcalc) values of the 1H and 13C chemical shifts arise for the 1H chemical shift for the OH group of indomethacin (δexpt = 16.3 ppm, δcalc = 18.5 ppm) and the 1H chemical shifts for the two 1H environments in the NH2 group of nicotinamide (δexpt = 9.0 ppm, δcalc = 10.5 ppm; δexpt = 7.3 ppm, δcalc = 8.8 ppm). However, it is notable that the difference between the 1H chemical shifts for the two 1H environments in the NH2 group in the experimental data (Δδ = 1.7 ppm) is exactly reproduced in the calculated data. For all three of these 1H environments, the experimental 1H chemical shift is lower than the calculated 1H chemical shift, which is related to the known temperature dependence of chemical shifts for 1H environments involved in hydrogen bonding [68,69,70] and the fact that the DFT-GIPAW calculation of solid-state NMR data considers a static hydrogen-bonded structure, whereas the actual material probed experimentally at ambient temperature is inevitably affected by the lattice dynamics in the crystal structure [71,72,73]. Thus, the crystal structure used in the DFT-GIPAW calculations (which is subjected to DFT geometry optimization before calculation of the solid-state NMR data) represents a static structure with stronger hydrogen bonding and hence higher 1H chemical shifts than the more dynamic situation that exists in the experimental system.
In addition to the good agreement between the experimental and calculated values of isotropic 1H and 13C chemical shifts, an even more robust validation is provided [33] by assessing two-dimensional correlations between 1H and 13C chemical shifts for directly bonded CH, CH2 and CH3 moieties (Figure 9). Again, excellent agreement is observed between the chemical shift correlations calculated for the final refined crystal structure and the chemical shift correlations measured from experimental solid-state NMR data for the co-crystal material. For the aromatic CH resonances, the calculated data are in particularly good agreement with the experimental two-dimensional 1H–13C correlation spectrum.
As another illustration of the utility of solid-state NMR data in the validation of the final refined crystal structure from powder XRD data, we consider the recent report [74] of the structure of a new polymorph (β polymorph) of l-tyrosine, prepared by crystallization from the gas phase following vacuum sublimation. In this case, structure solution was carried out both from powder XRD data and from three-dimensional electron diffraction (3D-ED) data, followed by Rietveld refinement from the powder XRD data (Figure 10a). The final refined crystal structure (Figure 10b) was validated both by DFT geometry optimization (which confirmed that the structure is a local minimum on the energy landscape) and consideration of high-resolution solid-state 13C NMR data (for which excellent agreement is observed between the isotropic 13C NMR chemical shifts in the experimental high-resolution solid-state 13C NMR spectrum and the corresponding values calculated for the crystal structure using DFT-GIPAW methodology; Figure 10c). Thus, in addition to giving excellent agreement with experimental powder XRD data in Rietveld refinement, the final refined crystal structure of the β polymorph of l-tyrosine is also in excellent agreement with experimental solid-state 13C NMR data.

6. Concluding Remarks

The research strategy described in this paper serves to highlight the significant advantages that can be gained by incorporating structural knowledge derived from solid-state NMR data in various stages of the process of structure determination from powder XRD data, including the use of solid-state NMR data to provide robust validation of the final refined structure obtained in Rietveld refinement. The opportunity to utilize solid-state NMR data in structure validation has benefitted significantly from progress in the development of DFT-GIPAW methodology for computing reliable solid-state NMR data for crystal structures, which allows direct and robust comparisons to be made between crystal structures and experimental solid-state NMR data.
Although the examples in this article have focused primarily on consideration of isotropic chemical shift measurements in solid-state NMR data for commonly studied nuclei such as 1H, 13C, and 15N NMR, the full range of NMR phenomena that may be studied for solid materials can be exploited within the NMR Crystallography field, including the study of anisotropic NMR interactions such as chemical shift anisotropy [75], electric-field gradient tensors derived from the study of quadrupolar nuclei [76,77] and direct dipole–dipole interactions [78,79,80]. Clearly, all of these types of solid-state NMR measurement may be exploited to enhance the process of structure determination from powder XRD data.
Furthermore, in addition to the opportunity to apply DFT-GIPAW calculations on “static” crystal structures following geometry optimization (as discussed above), there are also exciting prospects [81] to combine DFT-GIPAW methodology with ab initio molecular dynamics simulations [82], allowing the effects of the dynamic properties of the crystal structure to be taken into account in the calculation of solid-state NMR data.
Although structure determination from powder XRD data can proceed successfully and straightforwardly in many cases without requiring insights from other experimental and computational approaches, the opportunity to exploit insights from other techniques, in particular solid-state NMR data, within the structure determination process will always provide more confidence that the structure determination process is progressing along the correct pathway, and that the final refined crystal structure is reliable and correct. However, in pushing forward the boundaries of structure determination from powder XRD data to tackle structural problems of greater complexity, it is anticipated that the synergistic use of information from solid-state NMR data and other techniques will become an increasingly vital component of the protocol for structure determination from powder XRD data.

Funding

Preparation of this Perspective Article was not supported by external funding.

Acknowledgments

I am very grateful to members of my research group, collaborators and colleagues, mentioned as co-authors in the references, for their contributions to the research described in this article. Particular thanks are due to Colan Hughes for his contributions to our research in NMR Crystallography. Our research in this field has benefitted from discussions within the framework of the EPSRC Collaborative Computational Project in NMR Crystallography CCP-NC (awards EP/J010510/1 and EP/M022501/1) and from access to the U.K. High-Field Solid-State NMR Facility (this facility was funded by EPSRC and BBSRC (contract reference PR140003), as well as the University of Warwick, including part funding through Birmingham Science City Advanced Materials Projects 1 and 2 supported by Advantage West Midlands and the European Regional Development Fund).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Structure from Diffraction Methods; Bruce, D.W.; O’Hare, D.; Walton, R.I. (Eds.) John Wiley & Sons: Chichester, UK, 2014. [Google Scholar]
  2. Harris, K.D.M.; Tremayne, M. Crystal structure determination from powder diffraction data. Chem. Mater. 1996, 8, 2554–2570. [Google Scholar] [CrossRef]
  3. Harris, K.D.M.; Tremayne, M.; Kariuki, B.M. Contemporary advances in the use of powder X-ray diffraction for structure determination. Angew. Chem. Int. Ed. 2001, 40, 1626–1651. [Google Scholar] [CrossRef]
  4. Chernyshev, V.V. Structure determination from powder diffraction. Russ. Chem. Bull. 2001, 50, 2273–2292. [Google Scholar] [CrossRef]
  5. Harris, K.D.M.; Cheung, E.Y. How to determine structures when single crystals cannot be grown: Opportunities for structure determination of molecular materials using powder diffraction data. Chem. Soc. Rev. 2004, 33, 526–538. [Google Scholar] [CrossRef] [PubMed]
  6. Tremayne, M. The impact of powder diffraction on the structural characterization of organic crystalline materials. Phil. Trans. R. Soc. A 2004, 362, 2691–2707. [Google Scholar] [CrossRef]
  7. Černý, R.; Favré-Nicolin, V. Direct space methods of structure determination from powder diffraction: Principles, guidelines and perspectives. Z. Kristallogr. 2007, 222, 105–113. [Google Scholar] [CrossRef]
  8. Tsue, H.; Horiguchi, M.; Tamura, R.; Fujii, K.; Uekusa, H. Crystal structure solution of organic compounds from X-ray powder diffraction data. J. Synth. Org. Chem. Jpn. 2007, 65, 1203–1212. [Google Scholar] [CrossRef]
  9. David, W.I.F.; Shankland, K. Structure determination from powder diffraction data. Acta Crystallogr. Sect. A 2008, 64, 52–64. [Google Scholar] [CrossRef]
  10. Powder Diffraction: Theory and Practice; Dinnebier, R.E.; Billinge, S.J.L. (Eds.) RSC Publishing: Cambridge, UK, 2008. [Google Scholar]
  11. Harris, K.D.M. Powder diffraction crystallography of molecular solids. Top. Curr. Chem. 2012, 315, 133–178. [Google Scholar]
  12. Martí-Rujas, J. Structural elucidation of microcrystalline MOFs from powder X-ray diffraction. Dalton Trans. 2020, 49, 13897–13916. [Google Scholar] [CrossRef]
  13. Egami, T.; Billinge, S.J.L. Underneath the Bragg Peaks: Structural Analysis of Complex Materials; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
  14. Young, C.A.; Goodwin, A.L. Applications of pair distribution function methods to contemporary problems in materials chemistry. J. Mater. Chem. 2011, 21, 6464–6476. [Google Scholar] [CrossRef]
  15. Billinge, S.J.L. The rise of the X-ray atomic pair distribution function method: A series of fortunate events. Phil. Trans. R. Soc. A 2019, 377, 20180413. [Google Scholar] [CrossRef] [PubMed]
  16. Harris, R.K. NMR Crystallography: The use of chemical shifts. Solid State Sci. 2004, 6, 1025–1037. [Google Scholar] [CrossRef]
  17. Senker, J.; Seyfarth, L.; Voll, J. Determination of rotational symmetry elements in NMR Crystallography. Solid State Sci. 2004, 6, 1039–1052. [Google Scholar] [CrossRef]
  18. Taulelle, F. NMR Crystallography: Crystallochemical formula and space group selection. Solid State Sci. 2004, 6, 1053–1057. [Google Scholar] [CrossRef]
  19. Elena, B.; Pintacuda, G.; Mifsud, N.; Emsley, L. Molecular structure determination in powders by NMR Crystallography from proton spin diffusion. J. Am. Chem. Soc. 2006, 128, 9555–9560. [Google Scholar] [CrossRef]
  20. NMR Crystallography; Harris, R.K.; Wasylishen, R.E.; Duer, M.J. (Eds.) John Wiley & Sons: Chichester, UK, 2009. [Google Scholar]
  21. Martineau, C.; Senker, J.; Taulelle, F. NMR Crystallography. Ann. Rep. NMR Spectrosc. 2014, 82, 1–57. [Google Scholar]
  22. Ashbrook, S.E.; McKay, D. Combining solid-state NMR spectroscopy with first-principles calculations – a guide to NMR Crystallography. Chem. Commun. 2016, 52, 7186–7204. [Google Scholar] [CrossRef]
  23. Bryce, D.L. NMR Crystallography: Structure and properties of materials from solid-state nuclear magnetic resonance observables. IUCrJ 2017, 4, 350–359. [Google Scholar] [CrossRef]
  24. Hodgkinson, P. NMR Crystallography of molecular organics. Prog. Nucl. Magn. Reson. Spectrosc. 2020, 118–119, 10–53. [Google Scholar] [CrossRef]
  25. Pickard, C.J.; Mauri, F. All-electron magnetic response with pseudopotentials: NMR chemical shifts. Phys. Rev. B 2001, 63, 245101. [Google Scholar] [CrossRef]
  26. Harris, R.K.; Hodgkinson, P.; Pickard, C.J.; Yates, J.R.; Zorin, V. Chemical shift computations on a crystallographic basis: Some reflections and comments. Magn. Reson. Chem. 2007, 45, S174–S186. [Google Scholar] [CrossRef] [PubMed]
  27. Yates, J.R.; Pickard, C.J.; Mauri, F. Calculation of NMR chemical shifts for extended systems using ultrasoft pseudopotentials. Phys. Rev. B 2007, 76, 024401. [Google Scholar] [CrossRef]
  28. Charpentier, T. The PAW/GIPAW approach for computing NMR parameters: A new dimension added to NMR study of solids. Solid State Nucl. Magn. Reson. 2011, 40, 1–20. [Google Scholar] [CrossRef] [PubMed]
  29. Bonhomme, C.; Gervais, C.; Babonneau, F.; Coelho, C.; Pourpoint, F.; Azaïs, T.; Ashbrook, S.E.; Griffin, J.M.; Yates, J.R.; Mauri, F.; et al. First-principles calculation of NMR parameters using the gauge including projector augmented wave method: A chemist’s point of view. Chem. Rev. 2012, 112, 5733–5779. [Google Scholar] [CrossRef] [PubMed]
  30. Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Kristallogr. 2005, 220, 567–570. [Google Scholar] [CrossRef]
  31. Pan, Z.; Cheung, E.Y.; Harris, K.D.M.; Constable, E.C.; Housecroft, C.E. A case study in direct-space structure determination from powder X-ray diffraction data: Finding the hydrate structure of an organic molecule with significant conformational flexibility. Cryst. Growth Des. 2005, 5, 2084–2090. [Google Scholar] [CrossRef]
  32. Filip, X.; Borodi, G.; Filip, C. Testing the limits of sensitivity in a solid-state structural investigation by combined X-ray powder diffraction, solid-state NMR, and molecular modelling. Phys. Chem. Chem. Phys. 2011, 13, 17978–17986. [Google Scholar] [CrossRef]
  33. Dudenko, D.V.; Williams, P.A.; Hughes, C.E.; Antzutkin, O.N.; Velaga, S.P.; Brown, S.P.; Harris, K.D.M. Exploiting the synergy of powder X-ray diffraction and solid-state NMR spectroscopy in structure determination of organic molecular solids. J. Phys. Chem. C 2013, 117, 12258–12265. [Google Scholar] [CrossRef]
  34. Li, P.; Chu, Y.; Wang, L.; Wenslow, R.M.; Yu, K.; Zhang, H.; Deng, Z. Structure determination of the theophylline-nicotinamide cocrystal: A combined powder XRD, 1D solid-state NMR, and theoretical calculation study. CrystEngComm 2014, 16, 3141–3147. [Google Scholar] [CrossRef]
  35. Li, X.; Bond, A.D.; Johansson, K.E.; Van de Streek, J. Distinguishing tautomerism in the crystal structure of (Z)-N-(5-ethyl-2,3-dihydro-1,3,4-thiadiazol-2-ylidene)-4-methylbenzene sulfonamide using DFT-D calculations and 13C solid-state NMR. Acta Crystallogr. Sect. C 2014, 70, 784–789. [Google Scholar] [CrossRef] [PubMed]
  36. Reddy, G.N.M.; Cook, D.S.; Iuga, D.; Walton, R.I.; Marsh, A.; Brown, S.P. An NMR Crystallography study of the hemihydrate of 2′,3′-O-isopropylidineguanosine. Solid State Nucl. Magn. Reson. 2015, 65, 41–48. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  37. Sardo, M.; Santos, S.M.; Babaryk, A.A.; López, C.; Alkorta, I.; Elguero, J.; Claramunt, R.M.; Mafra, L. Diazole-based powdered cocrystal featuring a helical hydrogen-bonded network: Structure determination from PXRD, solid-state NMR and computer modeling. Solid State Nucl. Magn. Reson. 2015, 65, 49–63. [Google Scholar] [CrossRef]
  38. Watts, A.E.; Maruyoshi, K.; Hughes, C.E.; Brown, S.P.; Harris, K.D.M. Combining the advantages of powder X-ray diffraction and NMR Crystallography in structure determination of the pharmaceutical material cimetidine hydrochloride. Cryst. Growth Des. 2016, 16, 1798–1804. [Google Scholar] [CrossRef]
  39. Rietveld, H.M. A profile refinement method for nuclear and magnetic structures. J. Appl. Crystallogr. 1969, 2, 65–71. [Google Scholar] [CrossRef]
  40. Harris, K.D.M.; Tremayne, M.; Lightfoot, P.; Bruce, P.G. Crystal structure determination from powder diffraction data by Monte Carlo methods. J. Am. Chem. Soc. 1994, 116, 3543–3547. [Google Scholar] [CrossRef]
  41. Kariuki, B.M.; Serrano-González, H.; Johnston, R.L.; Harris, K.D.M. The application of a genetic algorithm for solving crystal structures from powder diffraction data. Chem. Phys. Lett. 1997, 280, 189–195. [Google Scholar] [CrossRef]
  42. Kariuki, B.M.; Psallidas, K.; Harris, K.D.M.; Johnston, R.L.; Lancaster, R.W.; Staniforth, S.E.; Cooper, S.M. Structure determination of a steroid directly from powder diffraction data. Chem. Commun. 1999, 1677–1678. [Google Scholar] [CrossRef]
  43. Tedesco, E.; Turner, G.W.; Harris, K.D.M.; Johnston, R.L.; Kariuki, B.M. Structure determination of an oligopeptide directly from powder diffraction data. Angew. Chem. Int. Ed. 2000, 39, 4488–4491. [Google Scholar] [CrossRef]
  44. Courvoisier, E.; Williams, P.A.; Lim, G.K.; Hughes, C.E.; Harris, K.D.M. The crystal structure of l-arginine. Chem. Commun. 2012, 48, 2761–2763. [Google Scholar] [CrossRef]
  45. Williams, P.A.; Hughes, C.E.; Lim, G.K.; Kariuki, B.M.; Harris, K.D.M. Discovery of a new system exhibiting abundant polymorphism: m-aminobenzoic acid. Cryst. Growth. Des. 2012, 12, 3104–3113. [Google Scholar] [CrossRef]
  46. Ma, X.; Lim, G.K.; Harris, K.D.M.; Apperley, D.C.; Horton, P.N.; Hursthouse, M.B.; James, S.L. Efficient, scalable and solvent-free mechanochemical synthesis of the OLED material Alq3 (q = 8-hydroxyquinolinate). Cryst. Growth. Des. 2012, 12, 5869–5872. [Google Scholar] [CrossRef]
  47. Martí-Rujas, J.; Meazza, L.; Lim, G.K.; Terraneo, G.; Pilati, T.; Harris, K.D.M.; Metrangolo, P.; Resnati, G. An adaptable and dynamically porous organic salt traps unique tetrahalide dianions. Angew. Chem. Int. Ed. 2013, 52, 13444–13448. [Google Scholar] [CrossRef] [PubMed]
  48. Williams, P.A.; Hughes, C.E.; Harris, K.D.M. l-Lysine: Exploiting powder X-ray diffraction to complete the set of crystal structures of the 20 directly-encoded proteinogenic amino acids. Angew. Chem. Int. Ed. 2015, 54, 3973–3977. [Google Scholar] [CrossRef]
  49. Al Rahal, O.; Hughes, C.E.; Williams, P.A.; Logsdail, A.J.; Diskin-Posner, Y.; Harris, K.D.M. Polymorphism of l-tryptophan. Angew. Chem. Int. Ed. 2019, 58, 18788–18792. [Google Scholar] [CrossRef]
  50. Brekalo, I.; Yuan, W.; Mottillo, C.; Lu, Y.; Zhang, Y.; Casaban, J.; Holman, K.T.; James, S.L.; Duarte, F.; Williams, P.A.; et al. Manometric real-time studies of the mechanochemical synthesis of zeolitic imidazolate frameworks. Chem. Sci. 2020, 11, 2141–2147. [Google Scholar] [CrossRef]
  51. Sun, T.; Hughes, C.E.; Guo, L.; Wei, L.; Harris, K.D.M.; Zhang, Y.; Ma, Y. Direct-space structure determination of covalent organic frameworks from 3D electron diffraction data. Angew. Chem. Int. Ed. 2020, 59, 22638–22644. [Google Scholar] [CrossRef]
  52. Al Rahal, O.; Williams, P.A.; Hughes, C.E.; Kariuki, B.M.; Harris, K.D.M. Structure determination of multicomponent crystalline phases of (S)-ibuprofen and l-proline from powder X-ray diffraction data, augmented by complementary experimental and computational techniques. Cryst. Growth Des. 2021, 21, 2498–2507. [Google Scholar] [CrossRef]
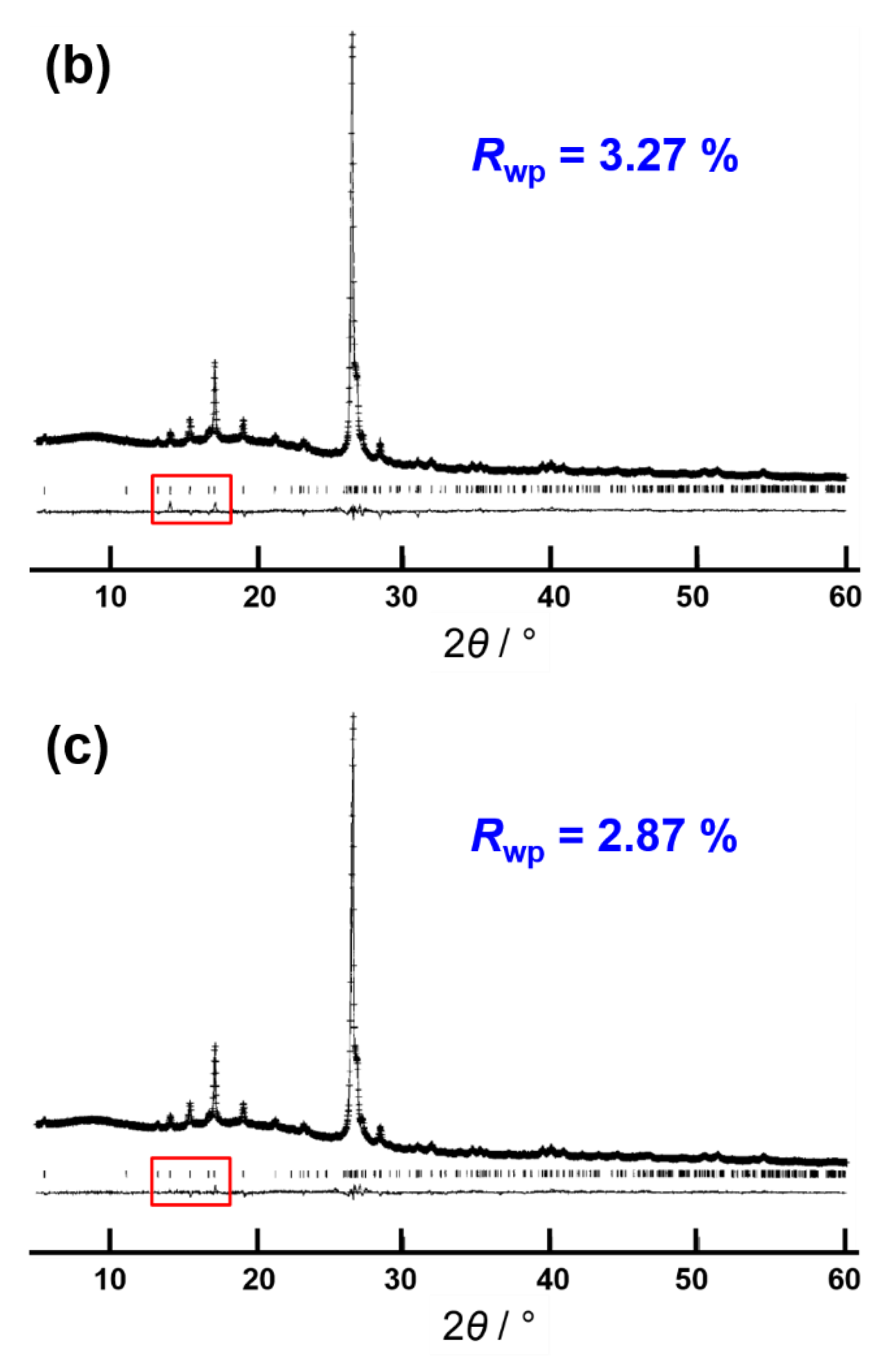
  53. Albesa-Jové, D.; Kariuki, B.M.; Kitchin, S.J.; Grice, L.; Cheung, E.Y.; Harris, K.D.M. Challenges in direct-space structure determination from powder diffraction data: A molecular material with four independent molecules in the asymmetric unit. ChemPhysChem 2004, 5, 414–418. [Google Scholar] [CrossRef]
  54. Pan, Z.; Xu, M.; Cheung, E.Y.; Harris, K.D.M.; Constable, E.C.; Housecroft, C.E. Understanding structural properties of a dendrimeric material directly from powder X-ray diffraction data. J. Phys. Chem. B 2006, 110, 11620–11623. [Google Scholar] [CrossRef]
  55. MacLean, E.J.; Tremayne, M.; Kariuki, B.M.; Harris, K.D.M.; Iqbal, A.F.M.; Hao, Z. Structural understanding of a polymorphic system by structure solution and refinement from powder X-ray diffraction data: The α and β phases of the latent pigment DPP-Boc. J. Chem. Soc. Perkin Trans. 2 2000, 1513–1519. [Google Scholar] [CrossRef]
  56. Tremayne, M.; Kariuki, B.M.; Harris, K.D.M. Structure determination of a complex organic solid from X-ray powder diffraction data by a generalized Monte Carlo method: The crystal structure of red fluorescein. Angew. Chem. Int. Ed. 1997, 36, 770–772. [Google Scholar] [CrossRef]
  57. Smalley, C.J.H.; Logsdail, A.J.; Hughes, C.E.; Iuga, D.; Young, M.T.; Harris, K.D.M. Solid-state structural properties of alloxazine determined from powder XRD data in conjunction with DFT-D calculations and solid-state NMR spectroscopy: Unraveling the tautomeric identity and pathways for tautomeric interconversion. Cryst. Growth Des. 2022, 22, 524–534. [Google Scholar] [CrossRef] [PubMed]
  58. Meejoo, S.; Kariuki, B.M.; Kitchin, S.J.; Cheung, E.Y.; Albesa-Jové, D.; Harris, K.D.M. Structural aspects of the β-polymorph of (E)-4-formylcinnamic acid: Structure determination directly from powder diffraction data and elucidation of structural disorder from solid-state NMR. Helv. Chim. Acta 2003, 86, 1467–1477. [Google Scholar] [CrossRef]
  59. Harris, K.D.M.; Thomas, J.M. Probing polymorphism and reactivity in the organic solid state using 13C NMR spectroscopy: Studies of p-formyl-trans-cinnamic acid. J. Solid State Chem. 1991, 94, 197–205. [Google Scholar] [CrossRef]
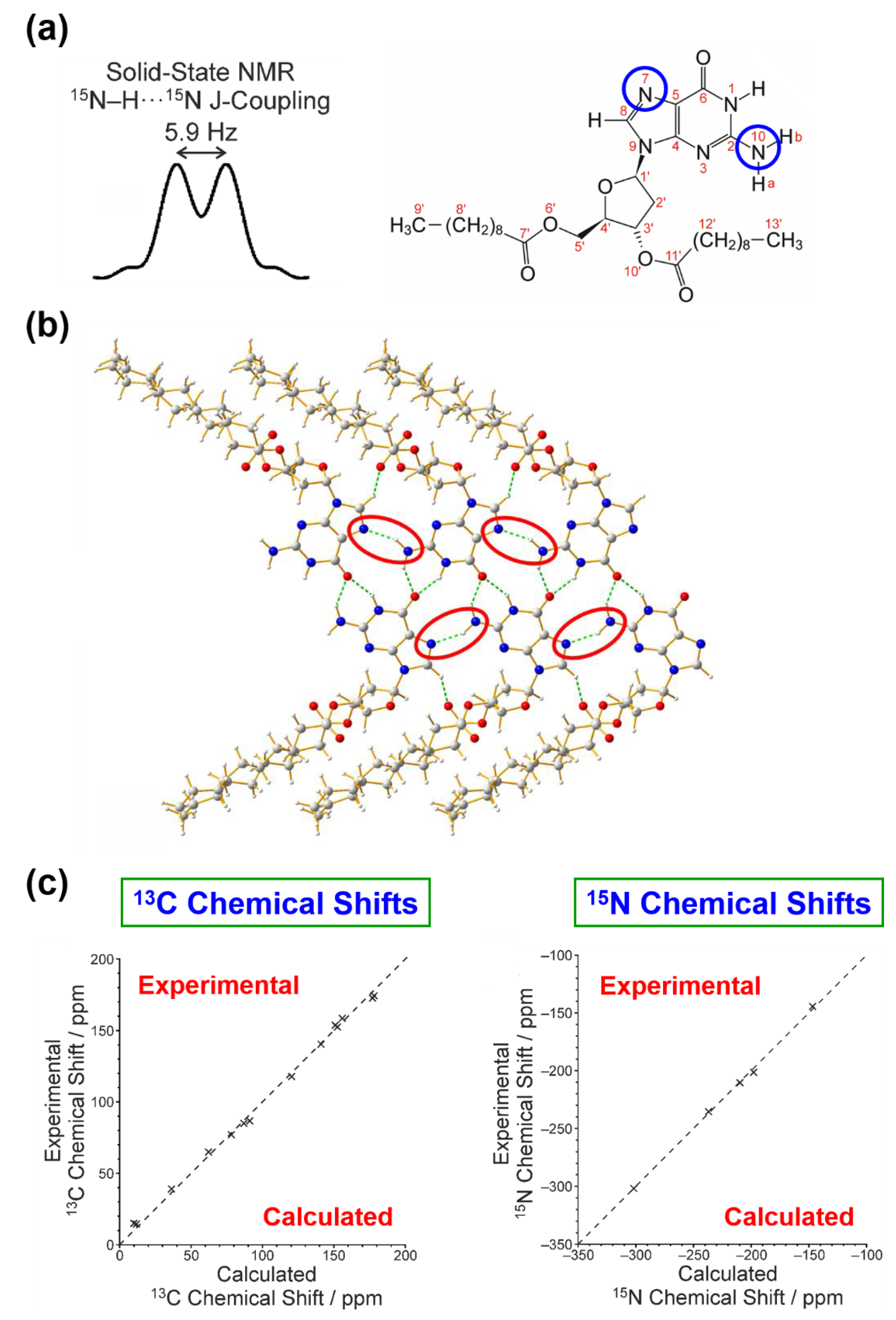
  60. Hughes, C.E.; Reddy, G.N.M.; Masiero, S.; Brown, S.P.; Williams, P.A.; Harris, K.D.M. Determination of a complex crystal structure in the absence of single crystals: Analysis of powder X-ray diffraction data, guided by solid-state NMR and periodic DFT calculations, reveals a new 2′-deoxyguanosine structural motif. Chem. Sci. 2017, 8, 3971–3979. [Google Scholar] [CrossRef]
  61. Dingley, A.J.; Grzesiek, S. Direct observation of hydrogen bonds in nucleic acid base pairs by internucleotide 2JNN couplings. J. Am. Chem. Soc. 1998, 120, 8293–8297. [Google Scholar] [CrossRef]
  62. Shenderovich, I.G.; Smirnov, S.N.; Denisov, G.S.; Gindin, V.A.; Golubev, N.S.; Dunger, A.; Reibke, R.; Kirpekar, S.; Malkina, O.L.; Limbach, H.-H. Nuclear magnetic resonance of hydrogen bonded clusters between F− and (HF)n: Experiment and theory. Ber. Bunsenges. Phys. Chem. 1998, 102, 422–428. [Google Scholar] [CrossRef]
  63. Pham, T.N.; Masiero, S.; Gottarelli, G.; Brown, S.P. Identification by 15N refocused INADEQUATE MAS NMR of intermolecular hydrogen bonding that directs the self-assembly of modified DNA bases. J. Am. Chem. Soc. 2005, 127, 16018–16019. [Google Scholar] [CrossRef]
  64. Pham, T.N.; Griffin, J.M.; Masiero, S.; Lena, S.; Gottarelli, G.; Hodgkinson, P.; Filipe, C.; Brown, S.P. Quantifying hydrogen-bonding strength: The measurement of 2hJNN couplings in self-assembled guanosines by solid-state 15N spin-echo MAS NMR. Phys. Chem. Chem. Phys. 2007, 9, 3416–3423. [Google Scholar] [CrossRef]
  65. Webber, A.L.; Masiero, S.; Pieraccini, S.; Burley, J.C.; Tatton, A.S.; Iuga, D.; Pham, T.N.; Spada, G.P.; Brown, S.P. Identifying guanosine self assembly at natural isotopic abundance by high-resolution 1H and 13C solid-state NMR spectroscopy. J. Am. Chem. Soc. 2011, 133, 19777–19795. [Google Scholar] [CrossRef] [PubMed]
  66. Alhalaweh, A.; Velaga, S.P. Formation of cocrystals from stoichiometric solutions of incongruently saturating systems by spray drying. Cryst. Growth Des. 2010, 10, 3302–3305. [Google Scholar] [CrossRef]
  67. Maruyoshi, K.; Iuga, D.; Antzutkin, O.N.; Alhalaweh, A.; Velaga, S.P.; Brown, S.P. Identifying the intermolecular hydrogen-bonding supramolecular synthons in an indomethacin-nicotinamide cocrystal by solid-state NMR. Chem. Commun. 2012, 48, 10844–10846. [Google Scholar] [CrossRef] [PubMed]
  68. Pickard, C.J.; Salager, E.; Pintacuda, G.; Elena, B.; Emsley, L. Resolving structures from powders by NMR Crystallography using combined proton spin diffusion and plane wave DFT calculations. J. Am. Chem. Soc. 2007, 129, 8932–8933. [Google Scholar]
  69. Webber, A.L.; Elena, B.; Griffin, J.M.; Yates, J.R.; Pham, T.N.; Mauri, F.; Pickard, C.J.; Gil, A.M.; Stein, R.; Lesage, A.; et al. Complete 1H resonance assignment of β-maltose from 1H–1H DQ-SQ CRAMPS and 1H (DQ-DUMBO)–13C SQ refocused INEPT 2D solid-state NMR spectra and first principles GIPAW calculations. Phys. Chem. Chem. Phys. 2010, 12, 6970–6983. [Google Scholar] [CrossRef]
  70. Brown, S.P.; Zhu, X.X.; Saalwachter, K.; Spiess, H.W. An investigation of the hydrogen-bonding structure in bilirubin by 1H double-quantum magic-angle spinning solid-state NMR spectroscopy. J. Am. Chem. Soc. 2001, 123, 4275–4285. [Google Scholar] [CrossRef]
  71. Mafra, L.; Santos, S.M.; Siegel, R.; Alves, I.; Paz, F.A.A.; Dudenko, D.; Spiess, H.W. Packing interactions in hydrated and anhydrous forms of the antibiotic ciprofloxacin: A solid-state NMR, X-ray diffraction, and computer simulation study. J. Am. Chem. Soc. 2012, 134, 71–74. [Google Scholar] [CrossRef]
  72. Dumez, J.N.; Pickard, C.J. Calculation of NMR chemical shifts in organic solids: Accounting for motional effects. J. Chem. Phys. 2009, 130, 104701. [Google Scholar] [CrossRef]
  73. de Gortari, I.; Portella, G.; Salvatella, X.; Bajaj, V.S.; van der Wel, P.C.A.; Yates, J.R.; Segall, M.D.; Pickard, C.J.; Payne, M.C.; Vendruscolo, M. Time averaging of NMR chemical shifts in the MLF peptide in the solid state. J. Am. Chem. Soc. 2010, 132, 5993–6000. [Google Scholar] [CrossRef]
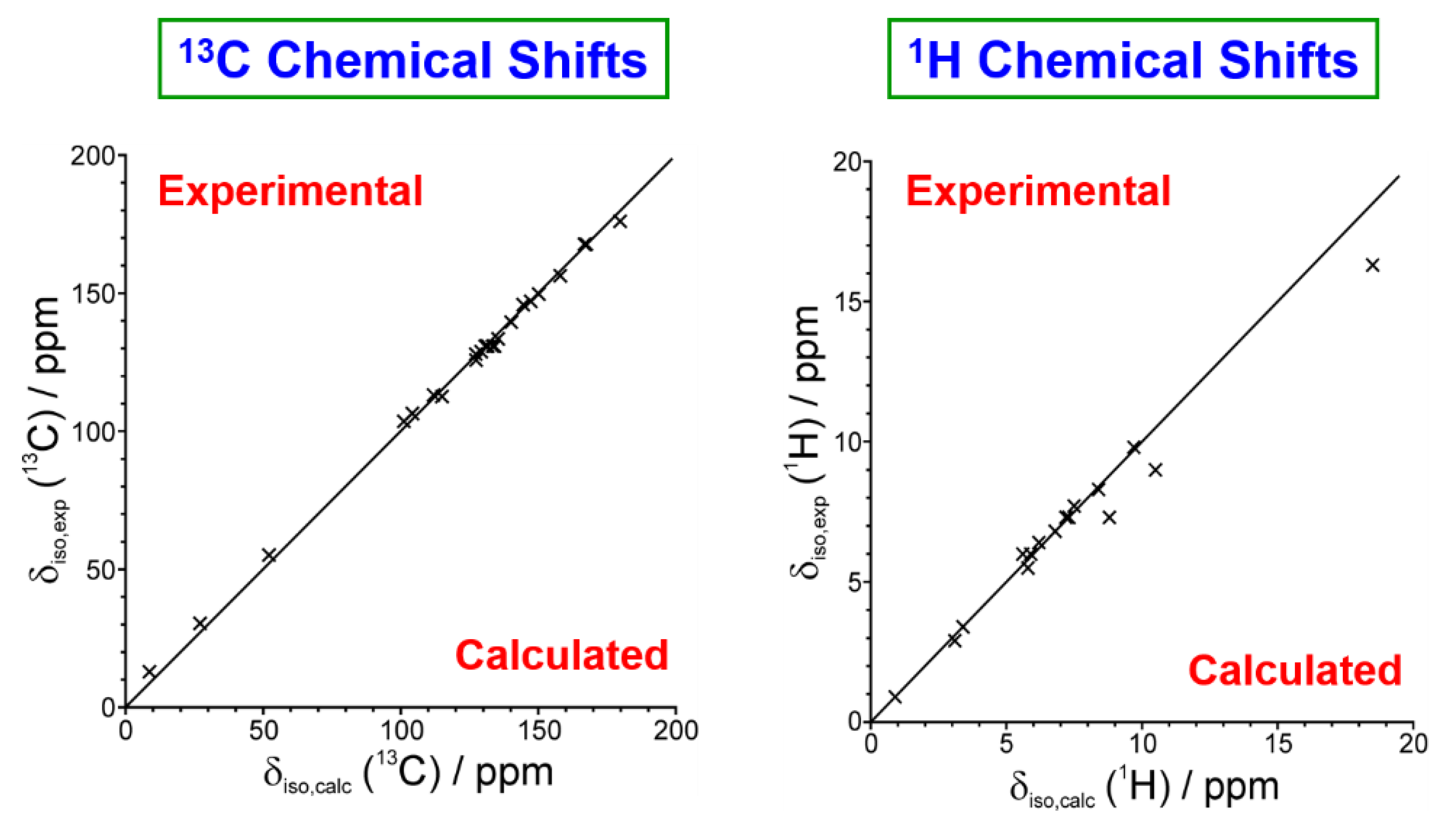
  74. Smalley, C.J.H.; Hoskyns, H.E.; Hughes, C.E.; Johnstone, D.N.; Willhammar, T.; Young, M.T.; Pickard, C.J.; Logsdail, A.J.; Midgley, P.A.; Harris, K.D.M. A structure determination protocol based on combined analysis of 3D-ED data, powder XRD data, solid-state NMR data and DFT-D calculations reveals the structure of a new polymorph of l-tyrosine. Chem. Sci. 2022, 13, 5277–5288. [Google Scholar] [CrossRef]
  75. Dawson, D.M.; Moran, R.F.; Sneddon, S.; Ashbrook, S.E. Is the 31P chemical shift anisotropy of aluminophosphates a useful parameter for NMR Crystallography? Magn. Reson. Chem. 2019, 57, 176–190. [Google Scholar] [CrossRef] [PubMed]
  76. Burgess, K.M.N.; Bryce, D.L. On the crystal structure of the vaterite polymorph of CaCO3: A calcium-43 solid-state NMR and computational assessment. Solid State Nucl. Magn. Reson. 2015, 65, 75–83. [Google Scholar] [CrossRef] [PubMed]
  77. Holmes, S.T.; Vojvodin, C.S.; Schurko, R.W. Dispersion-corrected DFT methods for applications in nuclear magnetic resonance crystallography. J. Phys. Chem. A 2020, 124, 10312–10323. [Google Scholar] [CrossRef] [PubMed]
  78. Chierotti, M.R.; Gobetto, R. NMR Crystallography: The use of dipolar interactions in polymorph and co-crystal investigation. CrystEngComm 2013, 15, 8599–8612. [Google Scholar] [CrossRef]
  79. Cerreia Vioglio, P.; Mollica, G.; Juramy, M.; Hughes, C.E.; Williams, P.A.; Ziarelli, F.; Viel, S.; Thureau, P.; Harris, K.D.M. Insights into the crystallization and structural evolution of glycine dihydrate by in-situ solid-state NMR spectroscopy. Angew. Chem. Int. Ed. 2018, 57, 6619–6623. [Google Scholar] [CrossRef]
  80. Thureau, P.; Sturniolo, S.; Zilka, M.; Ziarelli, F.; Viel, S.; Yates, J.R.; Mollica, G. Reducing the computational cost of NMR Crystallography of organic powders at natural isotopic abundance with the help of 13C-13C dipolar couplings. Magn. Reson. Chem. 2019, 57, 256–264. [Google Scholar] [CrossRef]
  81. Mazurek, A.H.; Szeleszczuk, Ł.; Pislak, D.M. A review on combination of ab initio molecular dynamics and NMR parameters calculations. Int. J. Mol. Sci. 2021, 22, 4378. [Google Scholar] [CrossRef]
  82. Iftimie, R.; Minary, P.; Tuckerman, M.E. Ab initio molecular dynamics: Concepts, recent developments, and future trends. Proc. Natl. Acad. Sci. USA 2005, 102, 6654–6659. [Google Scholar] [CrossRef] [Green Version]
Crystals 12 01277 g001 550
Figure 1. (a) Schematic representation of the experimental set-up for a powder XRD measurement. (b) Example of an experimental powder XRD pattern, in which the diffraction data are effectively compressed into one-dimension (i.e., scattered intensity as a function of the diffraction angle 2θ). (c) An expanded region of the powder XRD pattern illustrating significant peak overlap (“+” marks are experimental data points; the solid line is the best-fit powder XRD pattern to the experimental data; tick marks indicate the 2θ values corresponding to the positions of individual peaks).
Figure 1. (a) Schematic representation of the experimental set-up for a powder XRD measurement. (b) Example of an experimental powder XRD pattern, in which the diffraction data are effectively compressed into one-dimension (i.e., scattered intensity as a function of the diffraction angle 2θ). (c) An expanded region of the powder XRD pattern illustrating significant peak overlap (“+” marks are experimental data points; the solid line is the best-fit powder XRD pattern to the experimental data; tick marks indicate the 2θ values corresponding to the positions of individual peaks).
Crystals 12 01277 g001
Crystals 12 01277 g002 550
Figure 2. Schematic overview of the strategy to exploit solid-state NMR data in the validation of a crystal structure determined from powder XRD data.
Figure 2. Schematic overview of the strategy to exploit solid-state NMR data in the validation of a crystal structure determined from powder XRD data.
Crystals 12 01277 g002
Crystals 12 01277 g003 550
Figure 3. Experimental high-resolution solid-state 13C NMR data for the 1:1 co-crystal of benzoic acid and pentafluorobenzoic acid. The two peaks at ca. 167 ppm are due to the carboxylic acid group of benzoic acid. The two peaks at ca. 174 ppm are due to the carboxylic acid group of pentafluorobenzoic acid.
Figure 3. Experimental high-resolution solid-state 13C NMR data for the 1:1 co-crystal of benzoic acid and pentafluorobenzoic acid. The two peaks at ca. 167 ppm are due to the carboxylic acid group of benzoic acid. The two peaks at ca. 174 ppm are due to the carboxylic acid group of pentafluorobenzoic acid.
Crystals 12 01277 g003
Crystals 12 01277 g004 550
Figure 4. (a) Experimental high-resolution solid-state 13C NMR data recorded for TDMM. The region of the spectrum corresponding to the aromatic CH environments (between 95 ppm and 101 ppm, as indicated by the red circle) contains six distinct peaks, which is half the number (12) of aromatic CH environments in a single molecule, suggesting that the TDMM molecule is located on a 2-fold rotation axis in the crystal structure. (b) Illustration of the relationship between molecular symmetry and crystallographic symmetry in the crystal structure of TDMM, with the central carbon atom of the molecule located on a crystallographic 2-fold rotation axis; the six aromatic CH environments in the asymmetric unit are indicated by red circles. (c) The crystal structure of TDMM determined from powder XRD data (hydrogen atoms are omitted for clarity).
Figure 4. (a) Experimental high-resolution solid-state 13C NMR data recorded for TDMM. The region of the spectrum corresponding to the aromatic CH environments (between 95 ppm and 101 ppm, as indicated by the red circle) contains six distinct peaks, which is half the number (12) of aromatic CH environments in a single molecule, suggesting that the TDMM molecule is located on a 2-fold rotation axis in the crystal structure. (b) Illustration of the relationship between molecular symmetry and crystallographic symmetry in the crystal structure of TDMM, with the central carbon atom of the molecule located on a crystallographic 2-fold rotation axis; the six aromatic CH environments in the asymmetric unit are indicated by red circles. (c) The crystal structure of TDMM determined from powder XRD data (hydrogen atoms are omitted for clarity).
Crystals 12 01277 g004
Crystals 12 01277 g005 550
Figure 5. (a) The alloxazine and isoalloxazine tautomers, and (b) experimental high-resolution solid-state 15N NMR data, which provides strong evidence that the crystal structure of this material contains the alloxazine tautomer. (c) Final Rietveld refinement of the powder XRD data for the alloxazine tautomer, showing a very good quality of fit, and (d) the final refined crystal structure containing the alloxazine tautomer.
Figure 5. (a) The alloxazine and isoalloxazine tautomers, and (b) experimental high-resolution solid-state 15N NMR data, which provides strong evidence that the crystal structure of this material contains the alloxazine tautomer. (c) Final Rietveld refinement of the powder XRD data for the alloxazine tautomer, showing a very good quality of fit, and (d) the final refined crystal structure containing the alloxazine tautomer.
Crystals 12 01277 g005
Crystals 12 01277 g006a 550Crystals 12 01277 g006b 550
Figure 6. (a) Experimental high-resolution solid-state 13C NMR data recorded for the β polymorph of p-FCA, showing the presence of two peaks for the 13C environment of the formyl group, which is interpreted to arise from disorder between two orientations of the formyl group. (b) Rietveld refinement for the ordered structural model of the β polymorph of p-FCA (Rwp = 3.27%). (c) Rietveld refinement for the disordered structural model of the β polymorph of p-FCA (Rwp = 2.87%). Apart from the description of the order/disorder of the formyl group, all other aspects of the refinement calculations are the same in (b,c). The red boxes in (b,c) highlight the region of the powder XRD pattern corresponding to the greatest improvement in the quality-of-fit for the disordered model, assessed from the difference between the experimental and calculated powder XRD patterns.
Figure 6. (a) Experimental high-resolution solid-state 13C NMR data recorded for the β polymorph of p-FCA, showing the presence of two peaks for the 13C environment of the formyl group, which is interpreted to arise from disorder between two orientations of the formyl group. (b) Rietveld refinement for the ordered structural model of the β polymorph of p-FCA (Rwp = 3.27%). (c) Rietveld refinement for the disordered structural model of the β polymorph of p-FCA (Rwp = 2.87%). Apart from the description of the order/disorder of the formyl group, all other aspects of the refinement calculations are the same in (b,c). The red boxes in (b,c) highlight the region of the powder XRD pattern corresponding to the greatest improvement in the quality-of-fit for the disordered model, assessed from the difference between the experimental and calculated powder XRD patterns.
Crystals 12 01277 g006aCrystals 12 01277 g006b
Crystals 12 01277 g007 550
Figure 7. (a) Evidence from solid-state 15N NMR data recorded for polymorph I of dG(C10)2 for a 2hJN7N10 coupling of 5.9 Hz, which suggests that the crystal structure contains a relatively strong N–H⋯N hydrogen bond involving N7 and N10 (N7 and N10 are highlighted by blue circles). (b) The final refined crystal structure of polymorph I of dG(C10)2 with the N10–H⋯N7 hydrogen bonds highlighted by red ellipses. (c) Comparison of experimental and DFT-GIPAW calculated values of isotropic 13C NMR and 15N NMR chemical shifts for polymorph I of dG(C10)2.
Figure 7. (a) Evidence from solid-state 15N NMR data recorded for polymorph I of dG(C10)2 for a 2hJN7N10 coupling of 5.9 Hz, which suggests that the crystal structure contains a relatively strong N–H⋯N hydrogen bond involving N7 and N10 (N7 and N10 are highlighted by blue circles). (b) The final refined crystal structure of polymorph I of dG(C10)2 with the N10–H⋯N7 hydrogen bonds highlighted by red ellipses. (c) Comparison of experimental and DFT-GIPAW calculated values of isotropic 13C NMR and 15N NMR chemical shifts for polymorph I of dG(C10)2.
Crystals 12 01277 g007
Crystals 12 01277 g008 550
Figure 8. Comparison of experimental and DFT-GIPAW calculated values of isotropic 13C NMR and 1H NMR chemical shifts for the indomethacin-nicotinamide co-crystal.
Figure 8. Comparison of experimental and DFT-GIPAW calculated values of isotropic 13C NMR and 1H NMR chemical shifts for the indomethacin-nicotinamide co-crystal.
Crystals 12 01277 g008
Crystals 12 01277 g009 550
Figure 9. DFT–GIPAW calculated 1H and 13C chemical shift correlations (indicated by red crosses) for directly bonded CH, CH2 and CH3 moieties in the crystal structure of the indomethacin-nicotinamide co-crystal overlaid on the experimental 1H–13C correlation NMR spectrum. The green box highlights the region of the spectrum corresponding to the aromatic CH resonances.
Figure 9. DFT–GIPAW calculated 1H and 13C chemical shift correlations (indicated by red crosses) for directly bonded CH, CH2 and CH3 moieties in the crystal structure of the indomethacin-nicotinamide co-crystal overlaid on the experimental 1H–13C correlation NMR spectrum. The green box highlights the region of the spectrum corresponding to the aromatic CH resonances.
Crystals 12 01277 g009
Crystals 12 01277 g010a 550Crystals 12 01277 g010b 550
Figure 10. (a) Final Rietveld refinement of the powder XRD data for the β polymorph of l-tyrosine, showing a very good quality of fit, and (b) the hydrogen-bonding arrangement in the final refined crystal structure. (c) Experimental high-resolution solid-state 13C NMR spectrum for the β polymorph of l-tyrosine together with the values of isotropic 13C NMR chemical shifts calculated by DFT-GIPAW methodology for the crystal structure (indicated by the red lines above the spectrum). Spinning sidebands in the experimental spectrum are marked by asterisks.
Figure 10. (a) Final Rietveld refinement of the powder XRD data for the β polymorph of l-tyrosine, showing a very good quality of fit, and (b) the hydrogen-bonding arrangement in the final refined crystal structure. (c) Experimental high-resolution solid-state 13C NMR spectrum for the β polymorph of l-tyrosine together with the values of isotropic 13C NMR chemical shifts calculated by DFT-GIPAW methodology for the crystal structure (indicated by the red lines above the spectrum). Spinning sidebands in the experimental spectrum are marked by asterisks.
Crystals 12 01277 g010aCrystals 12 01277 g010b
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Harris, K.D.M. NMR Crystallography as a Vital Tool in Assisting Crystal Structure Determination from Powder XRD Data. Crystals 2022, 12, 1277. https://doi.org/10.3390/cryst12091277

AMA Style

Harris KDM. NMR Crystallography as a Vital Tool in Assisting Crystal Structure Determination from Powder XRD Data. Crystals. 2022; 12(9):1277. https://doi.org/10.3390/cryst12091277

Chicago/Turabian Style

Harris, Kenneth D. M. 2022. "NMR Crystallography as a Vital Tool in Assisting Crystal Structure Determination from Powder XRD Data" Crystals 12, no. 9: 1277. https://doi.org/10.3390/cryst12091277

APA Style

Harris, K. D. M. (2022). NMR Crystallography as a Vital Tool in Assisting Crystal Structure Determination from Powder XRD Data. Crystals, 12(9), 1277. https://doi.org/10.3390/cryst12091277

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop