Analysis of Smoluchowski’s Coagulation Equation with Injection
Abstract
:1. Introduction
2. Smoluchowski’s Coagulation Equation with Injection
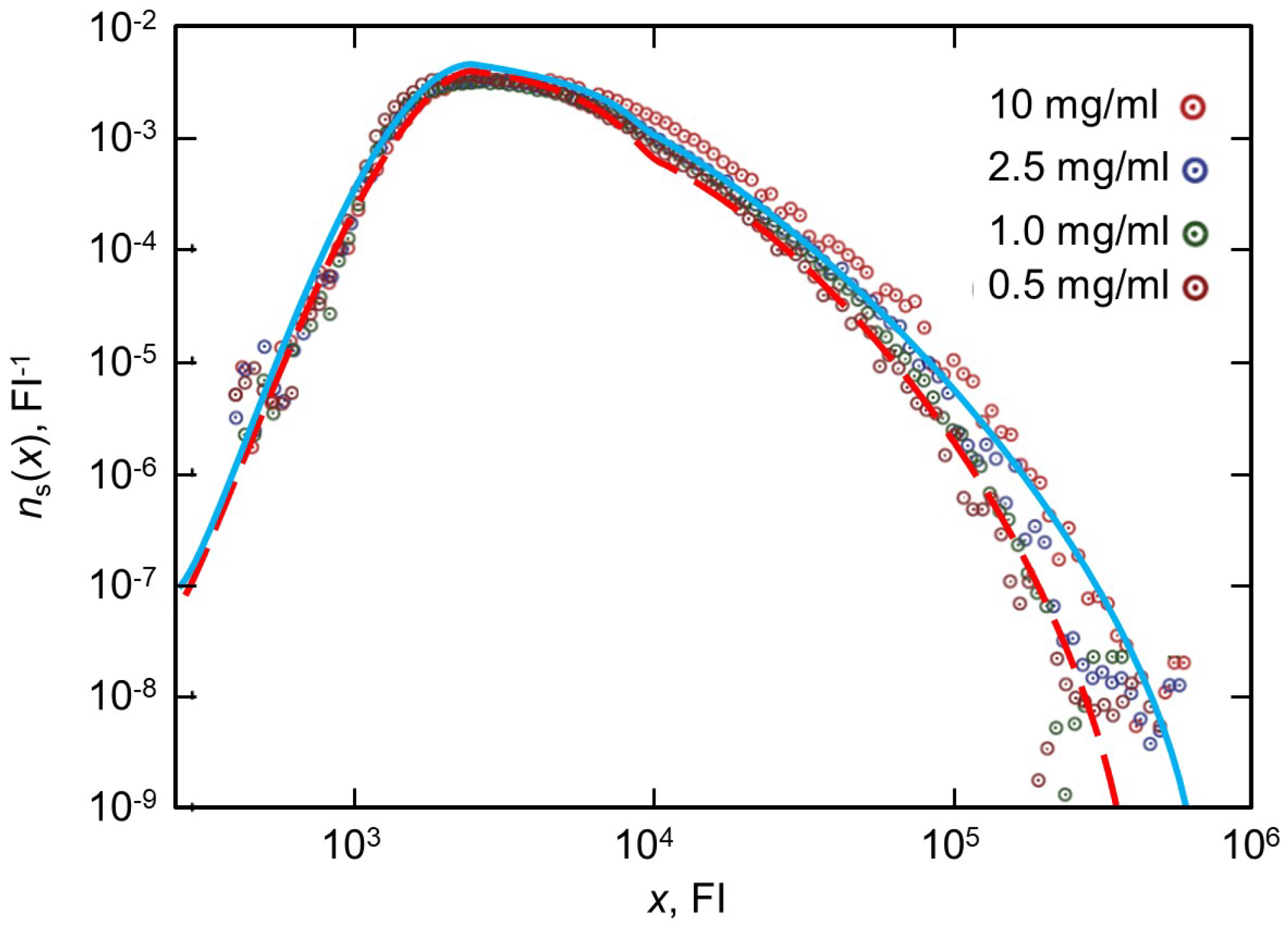
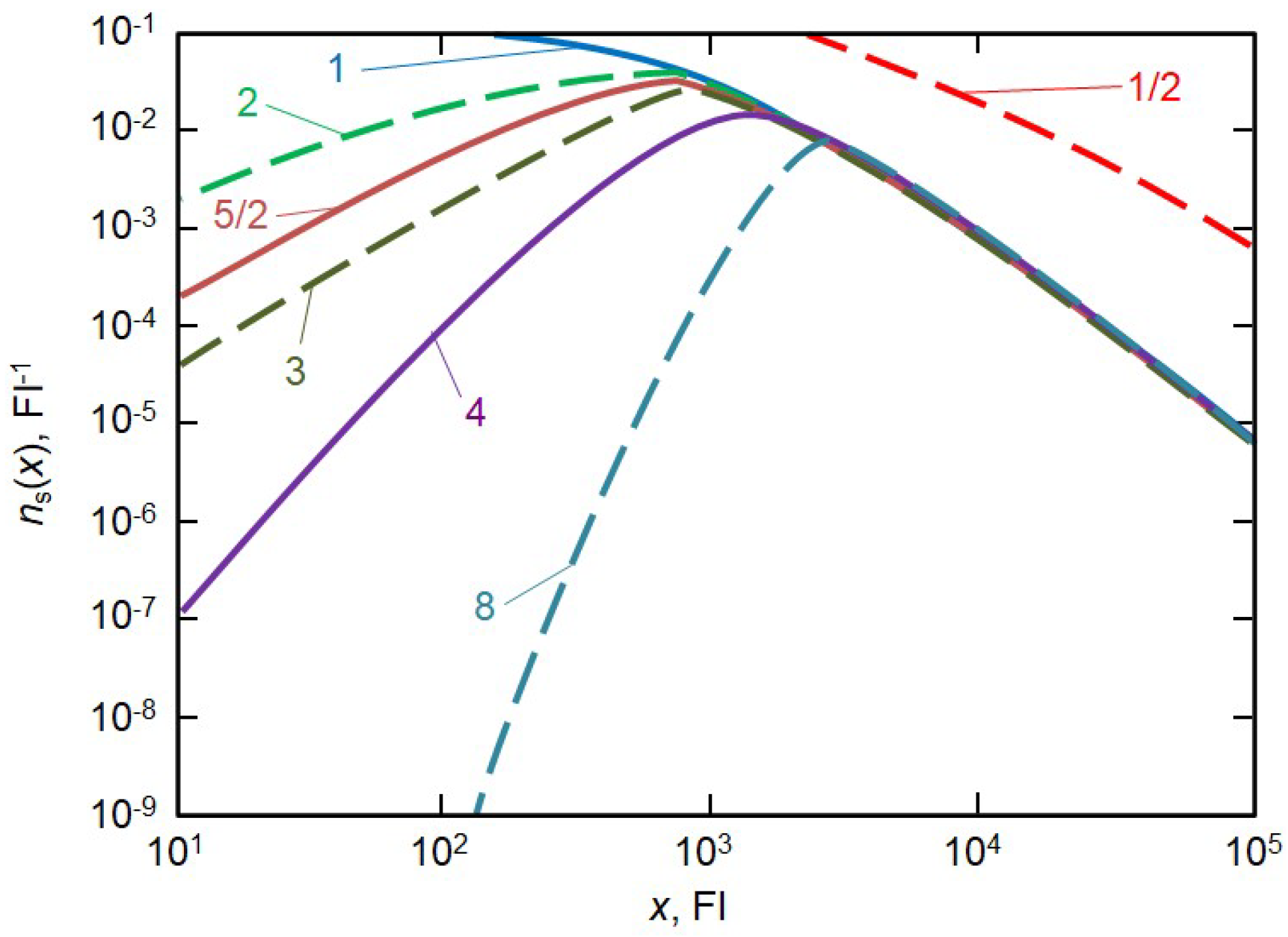
3. Exact Analytical Solutions for Steady-State Coagulation with Injection
3.1. Integer Values of the Parameter
3.2. Half-Integer Values of the Parameter
3.3. Source Term with Sub-Linear Prefactor and Exponential Decay
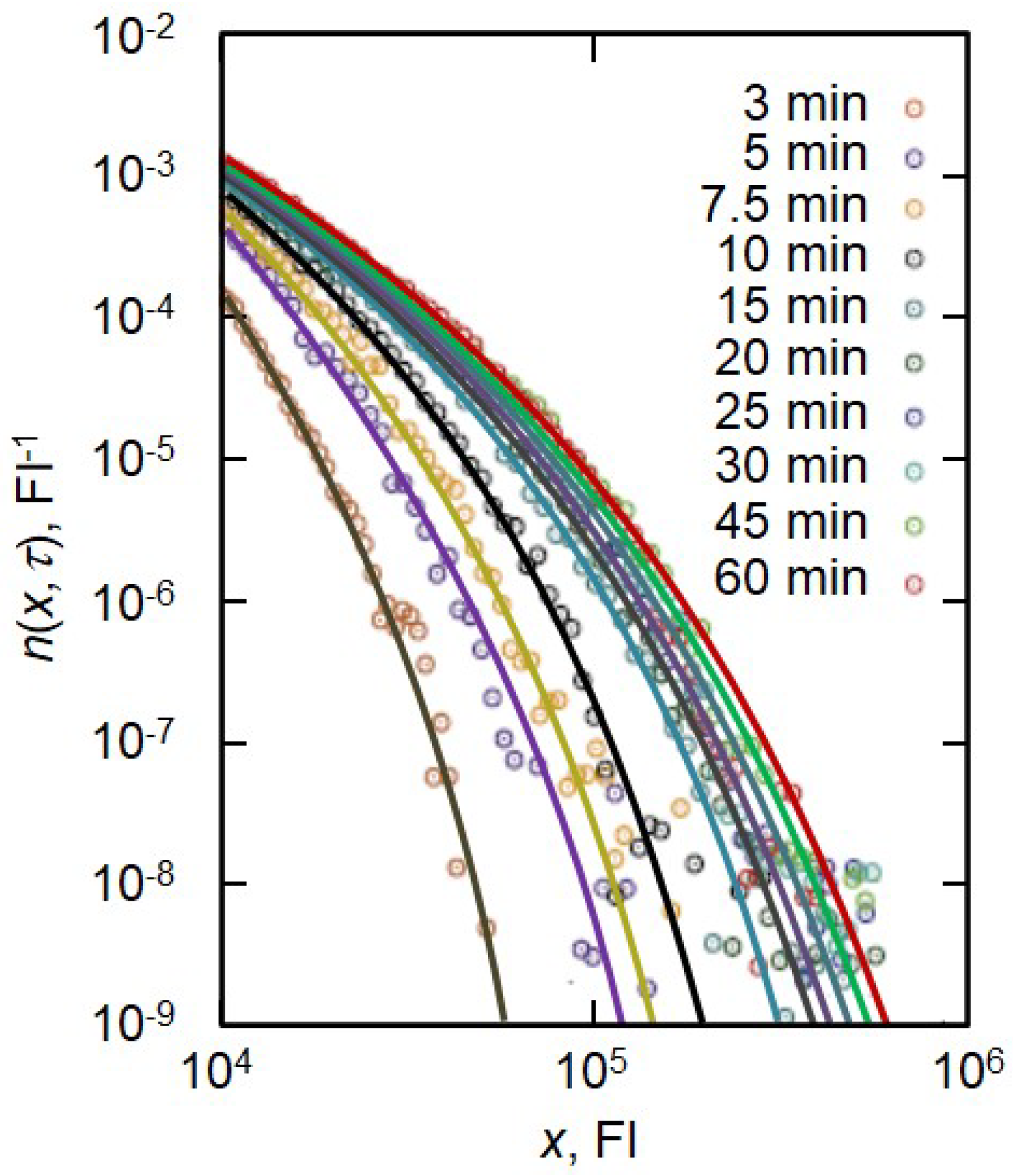
4. Unsteady-State Smoluchowski’s Coagulation Equation
4.1. Analytical Solution to the Coagulation Equation without Injection
4.2. Approximate Solution to the Unsteady Coagulation Equation with Injection
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Friedlander, S.K. Smoke, Dust, and Haze: Fundamentals of Aerosol Dynamics; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Williams, M.M.R.; Loyalka, S.K. Aerosol Science: Theory and Practice; Pergamon Press: Oxford, UK, 1991. [Google Scholar]
- Hayakawa, H. Irreversible kinetic coagulations in the presence of a source. J. Phys. A Math. Gen. 1987, 20, 801–805. [Google Scholar] [CrossRef]
- Takayasu, H. Steady-state distribution of generalized aggregation system with injection. Phys. Rev. Lett. 1989, 63, 2563–2565. [Google Scholar] [CrossRef] [PubMed]
- Cueille, S.; Sire, C. Droplet nucleation and Smoluchowski’s equation with growth and injection of particles. Phys. Rev. E 1998, 57, 881–900. [Google Scholar] [CrossRef]
- Alexandrov, D.V. Kinetics of particle coarsening with allowance for Ostwald ripening and coagulation. J. Phys. Condens. Matter 2016, 28, 035102. [Google Scholar] [CrossRef] [PubMed]
- Alexandrov, D.V.; Ivanov, A.A.; Alexandrova, I.V. Unsteady-state particle-size distributions at the coagulation stage of phase transformations. Eur. Phys. J. Spec. Top. 2019, 228, 161–167. [Google Scholar] [CrossRef]
- Castro, M.; Lythe, G.; Smit, J.; Molina-París, C. Fusion and fission events regulate endosome maturation and viral escape. Sci. Rep. 2021, 11, 7845. [Google Scholar] [CrossRef]
- Fedotov, S.; Alexandrov, D.; Starodumov, I.; Korabel, N. Stochastic model of virus-endosome fusion and endosomal escape of pH-responsive nanoparticles. Mathematics 2022, 10, 375. [Google Scholar] [CrossRef]
- Foret, L.; Dawson, J.E.; Villaseñor, R.; Collinet, C.; Deutsch, A.; Brusch, L.; Zerial, M.; Kalaidzidis, Y.; Jülicher, F. A general theoretical framework to infer endosomal network dynamics from quantitative image analysis. Curr. Biol. 2012, 22, 1381–1390. [Google Scholar] [CrossRef]
- Smoluchowski, M. Drei Vortrage uber Diffusion, Brownsche Bewegung und Koagulation von Kolloidteilchen. Z. Phys. 1916, 17, 557–585. [Google Scholar]
- Smoluchowski, M. Versuch einer mathematischen theorie der koagulationskinetik kolloider losungen. Z. Phys. Chem. 1917, 92, 129–168. [Google Scholar] [CrossRef]
- Simons, S. On steady-state solutions of the coagulation equation. J. Phys. A Math. Gen. 1996, 29, 1139–1140. [Google Scholar] [CrossRef]
- Alexandrov, D.V. The steady-state solutions of coagulation equations. Int. J. Heat Mass Trans. 2018, 121, 884–886. [Google Scholar] [CrossRef]
- Herlach, D.; Galenko, P.; Holland-Moritz, D. Metastable Solids from Undercooled Melts; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Barlow, D.A. Theory of the intermediate stage of crystal growth with applications to protein crystallization. J. Cryst. Growth 2009, 311, 2480–2483. [Google Scholar] [CrossRef]
- Barlow, D.A. Theory of the intermediate stage of crystal growth with applications to insulin crystallization. J. Cryst. Growth 2017, 470, 8–14. [Google Scholar] [CrossRef]
- Alexandrova, I.V.; Alexandrov, D.V.; Makoveeva, E.V. Ostwald ripening in the presence of simultaneous occurrence of various mass transfer mechanisms: An extension of the Lifshitz–Slyozov theory. Philos. Trans. R. Soc. A 2021, 379, 20200308. [Google Scholar] [CrossRef] [PubMed]
- Ramírez Zamora, R.M.; Espejel Ayala, F.; Solís López, M.; González Barceló, O.; Gómez, R.W.; Pérez Mazariego, J.L.; Navarro-González, R.; Schouwenaars, R. Optimisation and analysis of the synthesis of a cellular glass-ceramic produced from water purification sludge and clays. Appl. Clay Sci. 2016, 123, 232–238. [Google Scholar] [CrossRef]
- Buyevich, Y.A.; Natalukha, I. Unsteady processes of combined polymerization and crystallization in continuous apparatuses. Chem. Eng. Sci. 1994, 49, 3241–3247. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Ivanov, A.A.; Nizovtseva, I.G.; Lippmann, S.; Alexandrova, I.V.; Makoveeva, E.V. Evolution of a polydisperse ensemble of spherical particles in a metastable medium with allowance for heat and mass exchange with the environment. Crystals 2022, 12, 949. [Google Scholar] [CrossRef]
- Schumann, T.E.W. Theoretical aspects of the size distribution of fog particles. Q. J. R. Meteorol. Soc. 1940, 66, 195–208. [Google Scholar] [CrossRef]
- Wang, S.H.; Lee, C.W.; Tseng, F.G.; Liang, K.K.; Wei, P.K. Evolution of gold nanoparticle clusters in living cells studied by sectional dark-field optical microscopy and chromatic analysis. J. Biophotonics 2016, 9, 738–749. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Korabel, N.; Currell, F.; Fedotov, S. Dynamics of intracellular clusters of nanoparticles. Cancer Nanotechnol. 2022, 13, 15. [Google Scholar] [CrossRef]
- Alexandrova, I.V.; Alexandrov, D.V. A complete analytical solution of unsteady coagulation equations and transition between the intermediate and concluding stages of a phase transformation. Eur. Phys. J. Spec. Top. 2022, 231, 1115–1121. [Google Scholar] [CrossRef]
- Ditkin, V.A.; Prudnikov, A.P. Integral Transforms and Operational Calculus; Pergamon Press: Oxford, UK, 1965. [Google Scholar]
- von Doetsch, G. Anleitung zum Praktischen Gebrauch der Laplace-Transformation und der Z-Transformation; R. Oldenbourg: München, Germany, 1967. [Google Scholar]
- Alexandrov, D.V.; Galenko, P.K. The shape of dendritic tips. Philos. Trans. R. Soc. A 2020, 378, 20190243. [Google Scholar] [CrossRef]
- Hunt, J.R. Self-similar particle-size distributions during coagulation: Theory and experimental verification. J. Fluid Mech. 1982, 122, 169–185. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Ivanov, A.A.; Alexandrova, I.V. The influence of Brownian coagulation on the particle-size distribution function in supercooled melts and supersaturated solutions. J. Phys. A Math. Theor. 2019, 52, 015101. [Google Scholar] [CrossRef]
- Martin, S.; Kauffman, P. The evolution of under-ice melt ponds, or double diffusion at the freezing point. J. Fluid Mech. 1974, 64, 507–527. [Google Scholar] [CrossRef]
- Huppert, H.E. The fluid mechanics of solidification. J. Fluid Mech. 1990, 212, 209–240. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Aseev, D.L. One-dimensional solidification of an alloy with a mushy zone: Thermodiffusion and temperature-dependent diffusivity. J. Fluid Mech. 2005, 527, 57–66. [Google Scholar] [CrossRef]
- Peppin, S.S.L.; Huppert, H.E.; Worster, M.G. Steady-state solidification of aqueous ammonium chloride. J. Fluid Mech. 2008, 599, 465–476. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makoveeva, E.V.; Alexandrov, D.V.; Fedotov, S.P. Analysis of Smoluchowski’s Coagulation Equation with Injection. Crystals 2022, 12, 1159. https://doi.org/10.3390/cryst12081159
Makoveeva EV, Alexandrov DV, Fedotov SP. Analysis of Smoluchowski’s Coagulation Equation with Injection. Crystals. 2022; 12(8):1159. https://doi.org/10.3390/cryst12081159
Chicago/Turabian StyleMakoveeva, Eugenya V., Dmitri V. Alexandrov, and Sergei P. Fedotov. 2022. "Analysis of Smoluchowski’s Coagulation Equation with Injection" Crystals 12, no. 8: 1159. https://doi.org/10.3390/cryst12081159
APA StyleMakoveeva, E. V., Alexandrov, D. V., & Fedotov, S. P. (2022). Analysis of Smoluchowski’s Coagulation Equation with Injection. Crystals, 12(8), 1159. https://doi.org/10.3390/cryst12081159