A Comparison of Two Methods Modeling High-Temperature Fatigue Crack Initiation in Ferrite–Pearlite Steel
Abstract
1. Introduction
2. Materials and Methods
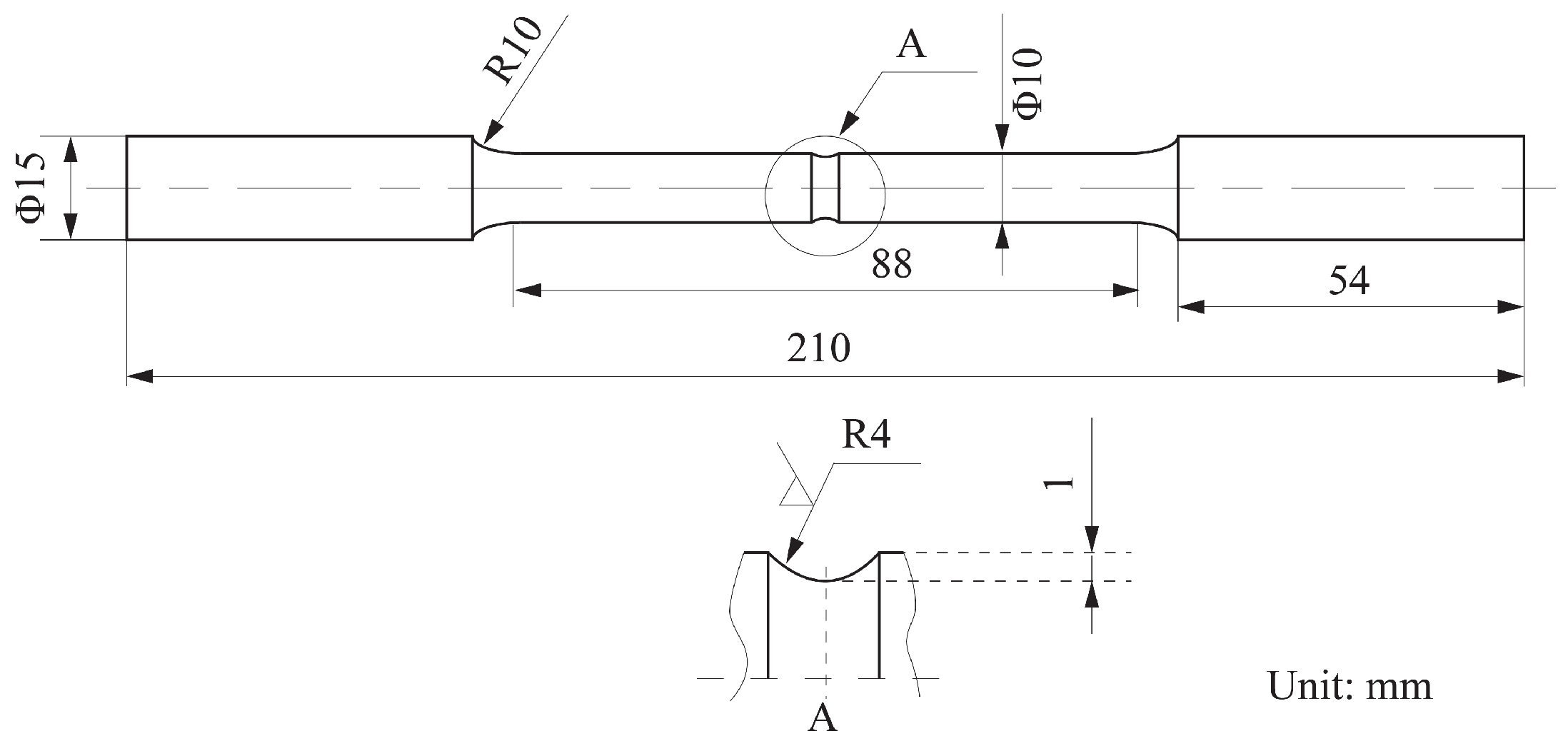
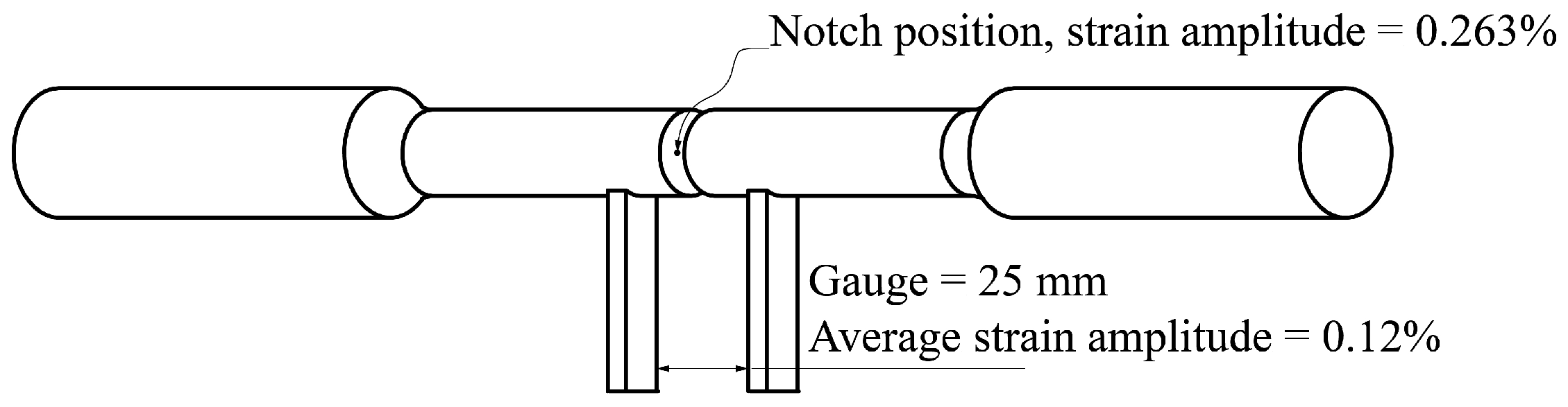
2.1. Material
2.2. Methods
3. Results
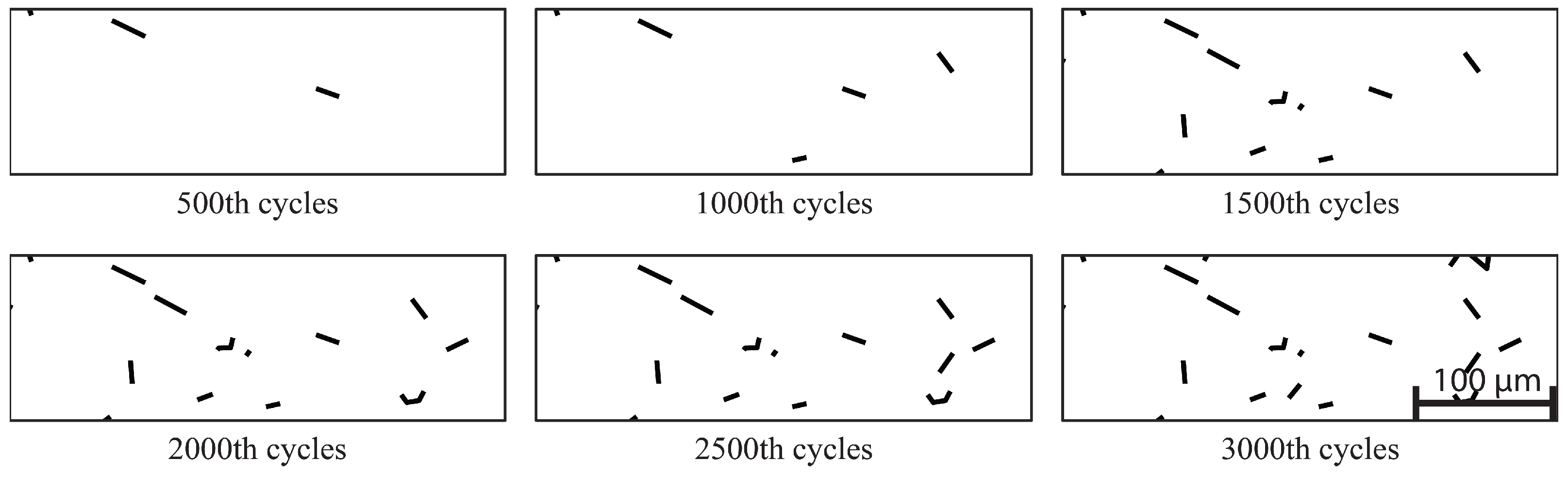
3.1. The First Approach for Crack Initiation Prediction
3.1.1. Generation of Geometric Model
3.1.2. Crack Initiation Model
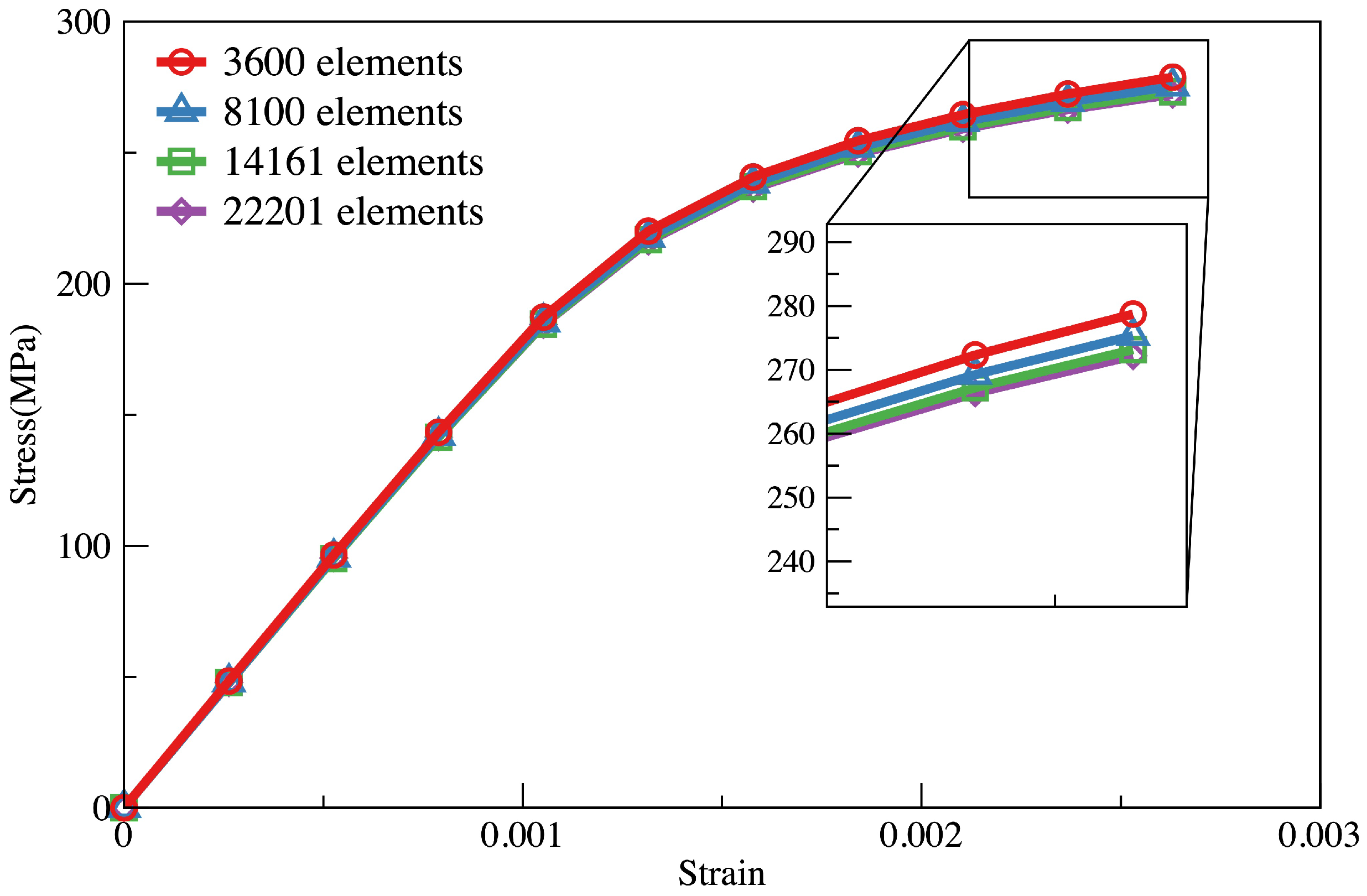
3.1.3. Computational Model Parameters’ Determination
3.1.4. Results of the First Approach
3.2. The Second Approach for Crack Initiation Prediction
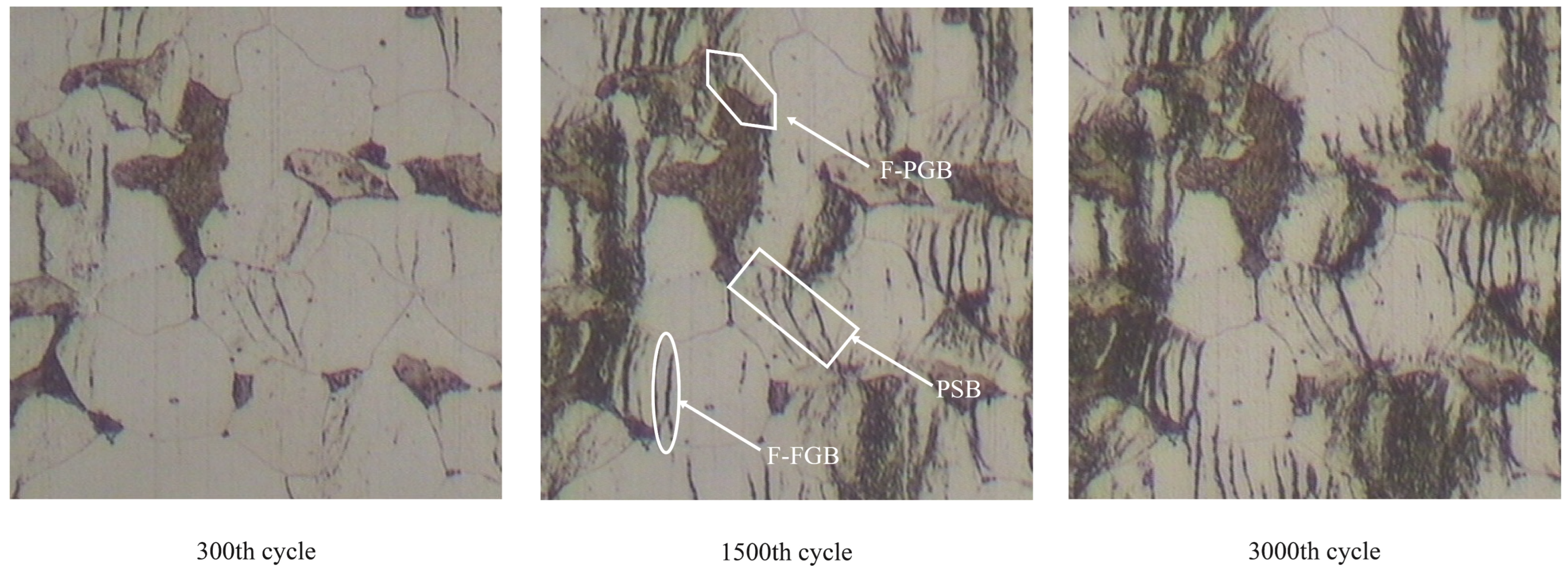
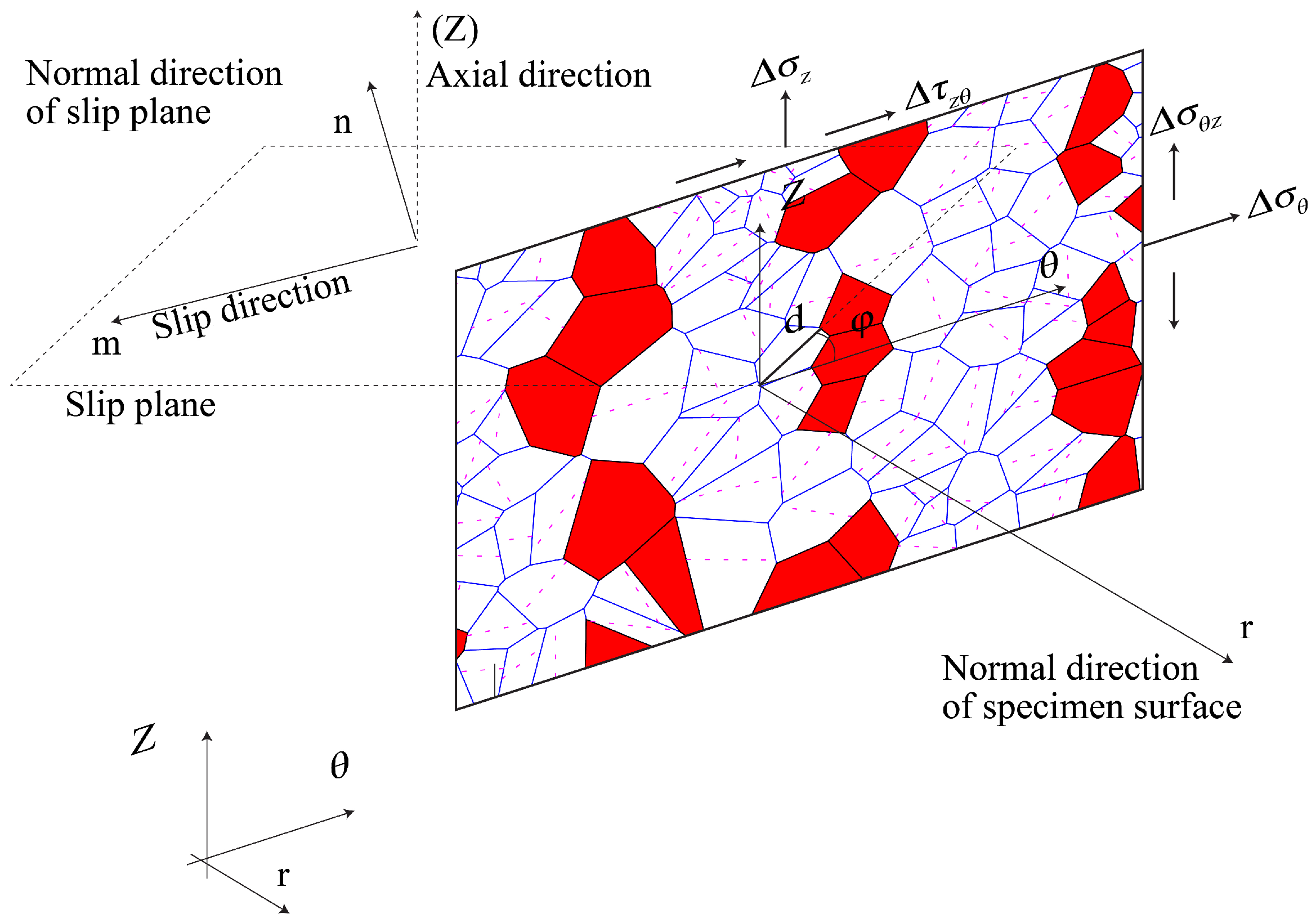
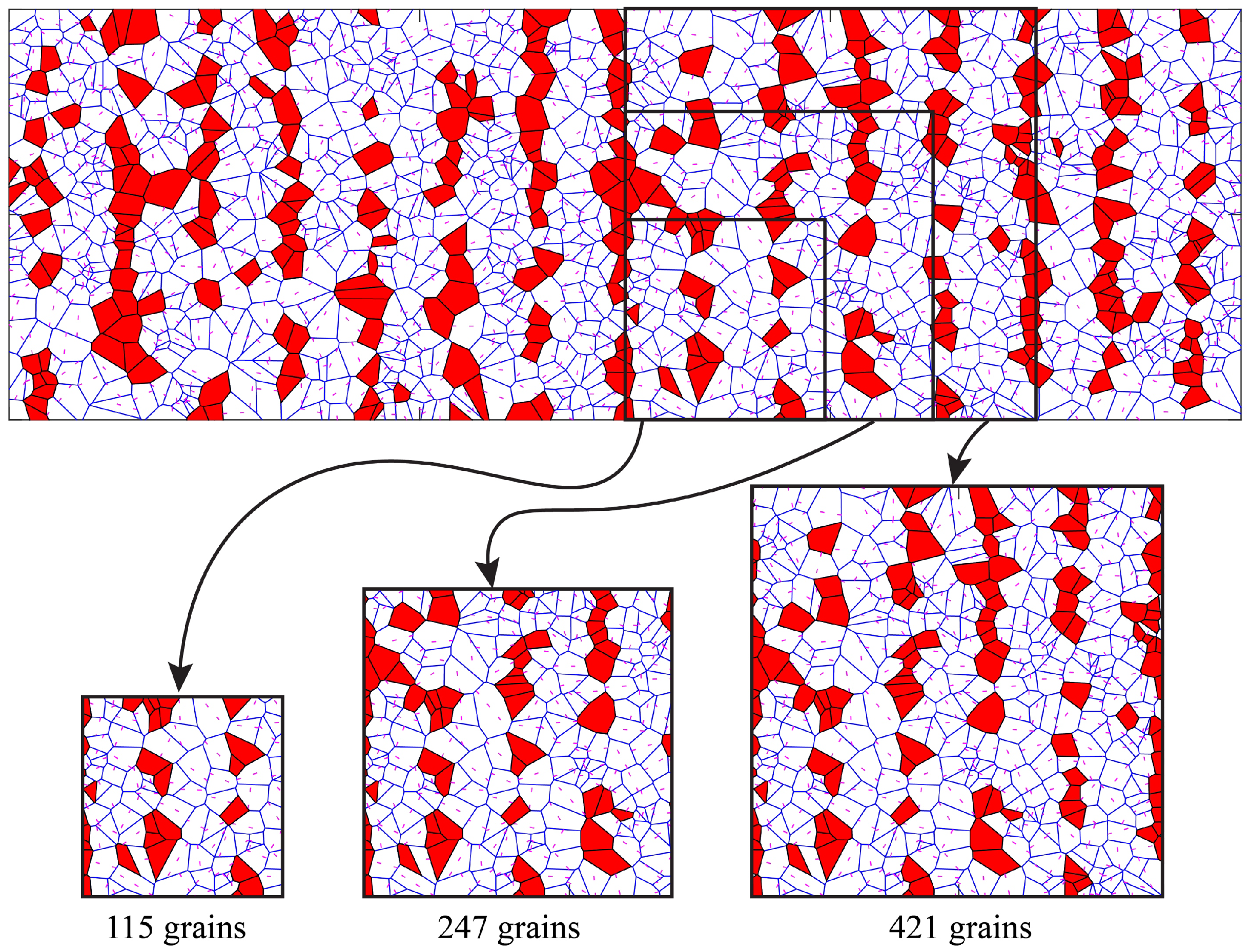
3.2.1. Generation of Microstructures
3.2.2. Constitutive Equations
3.2.3. Parameter Calibration
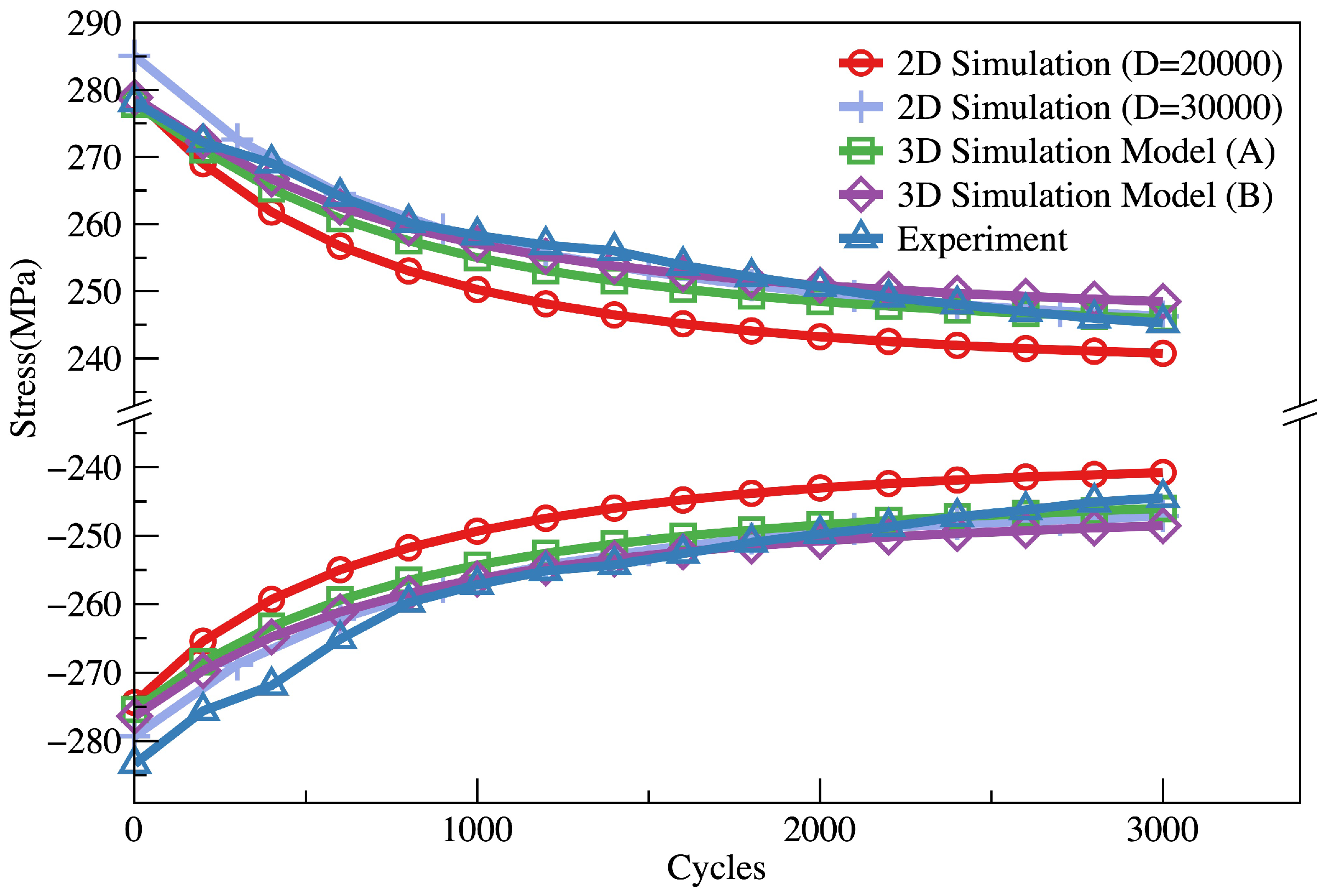
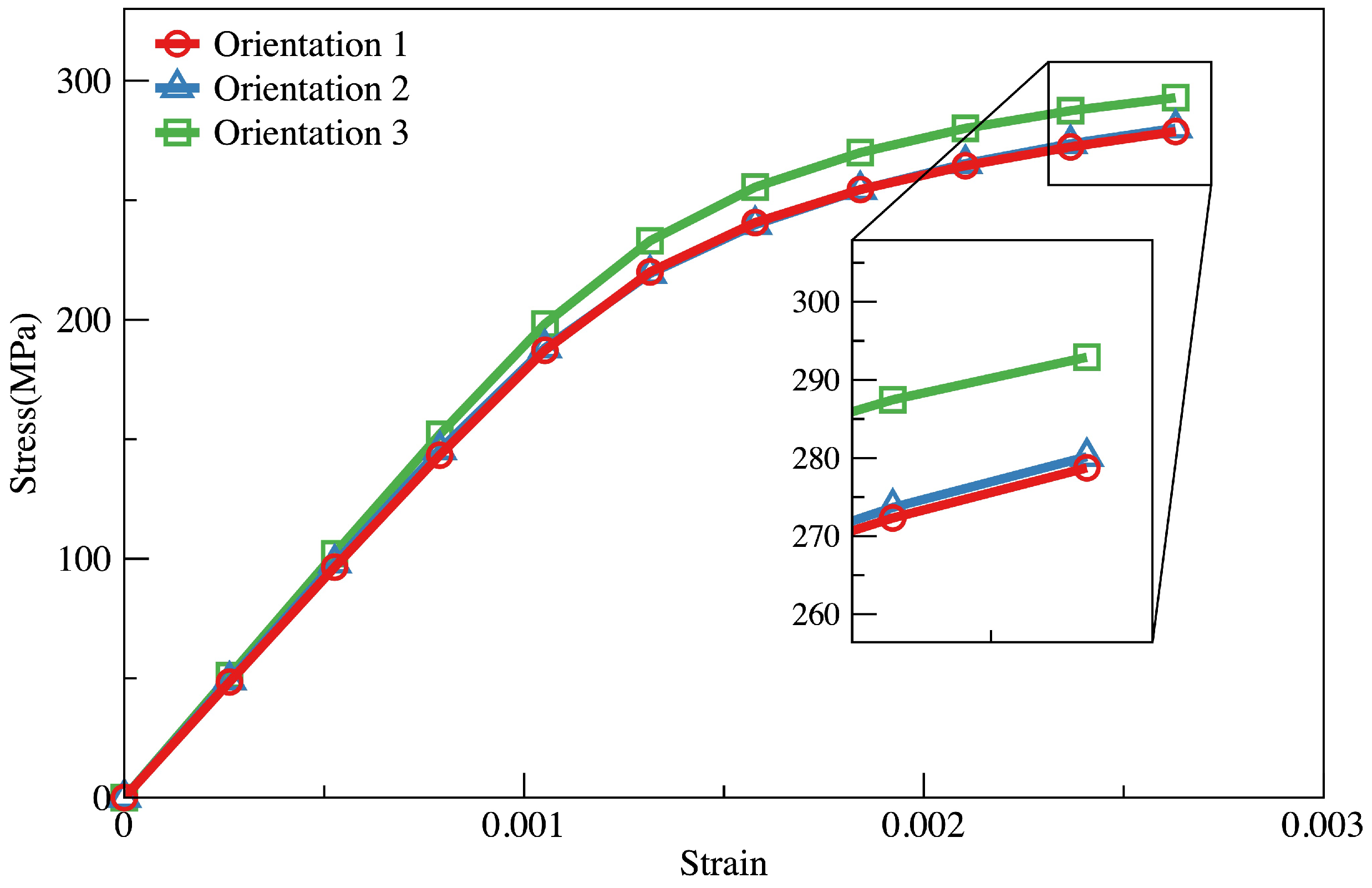
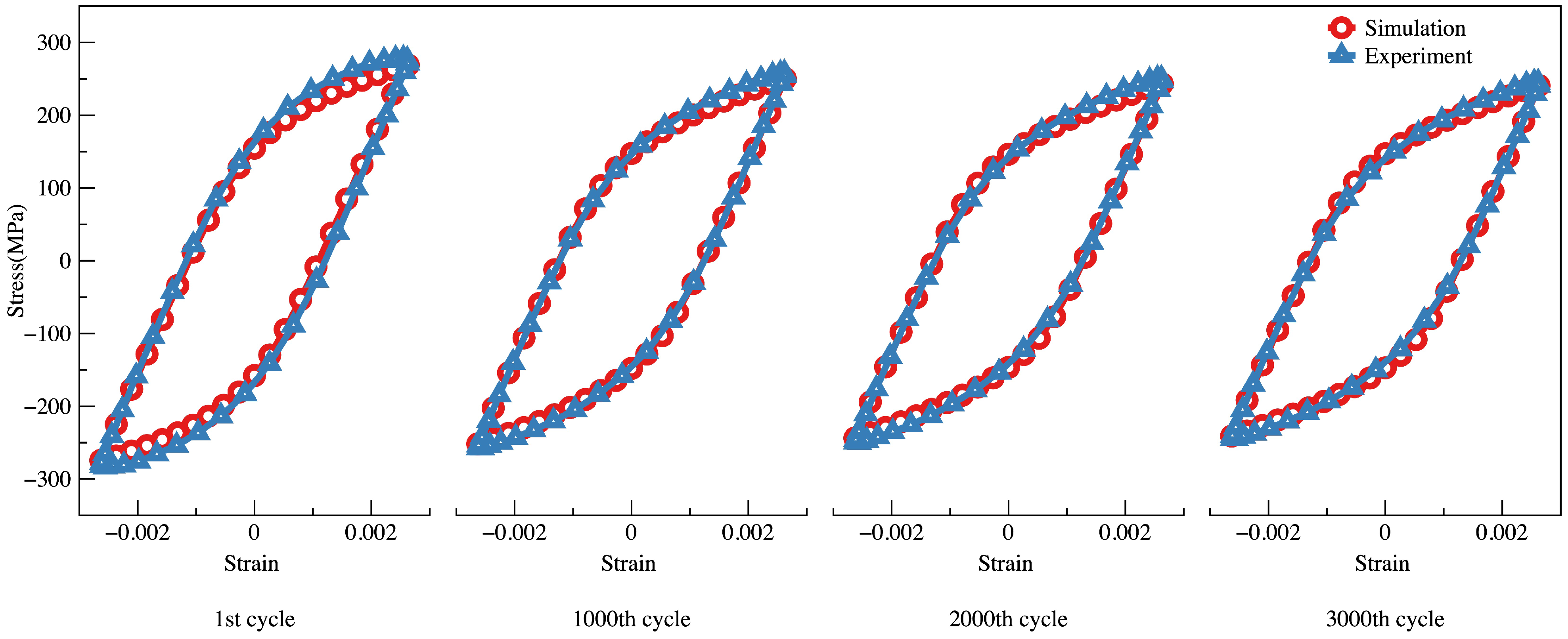
3.2.4. Simulation and Results
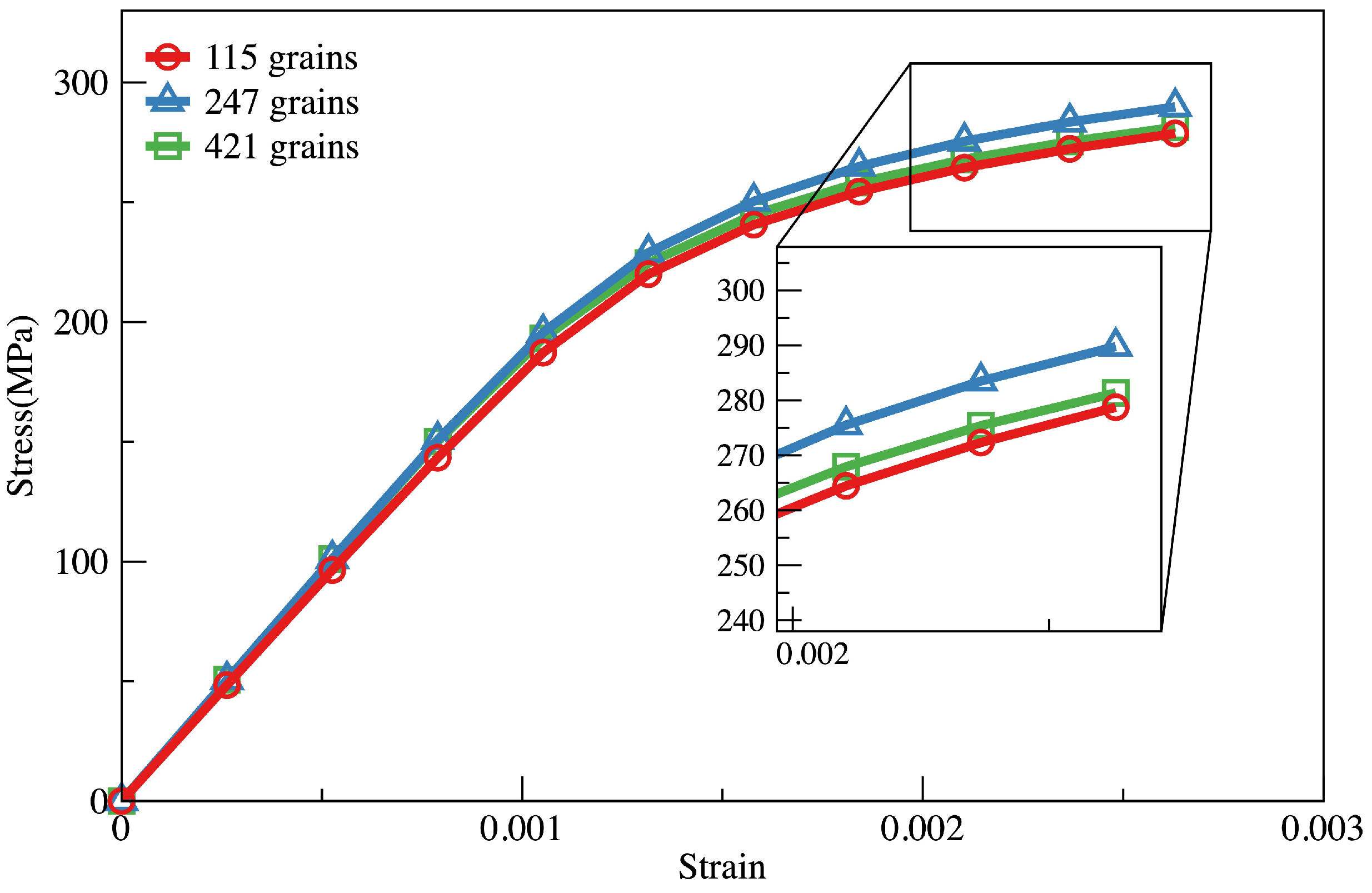
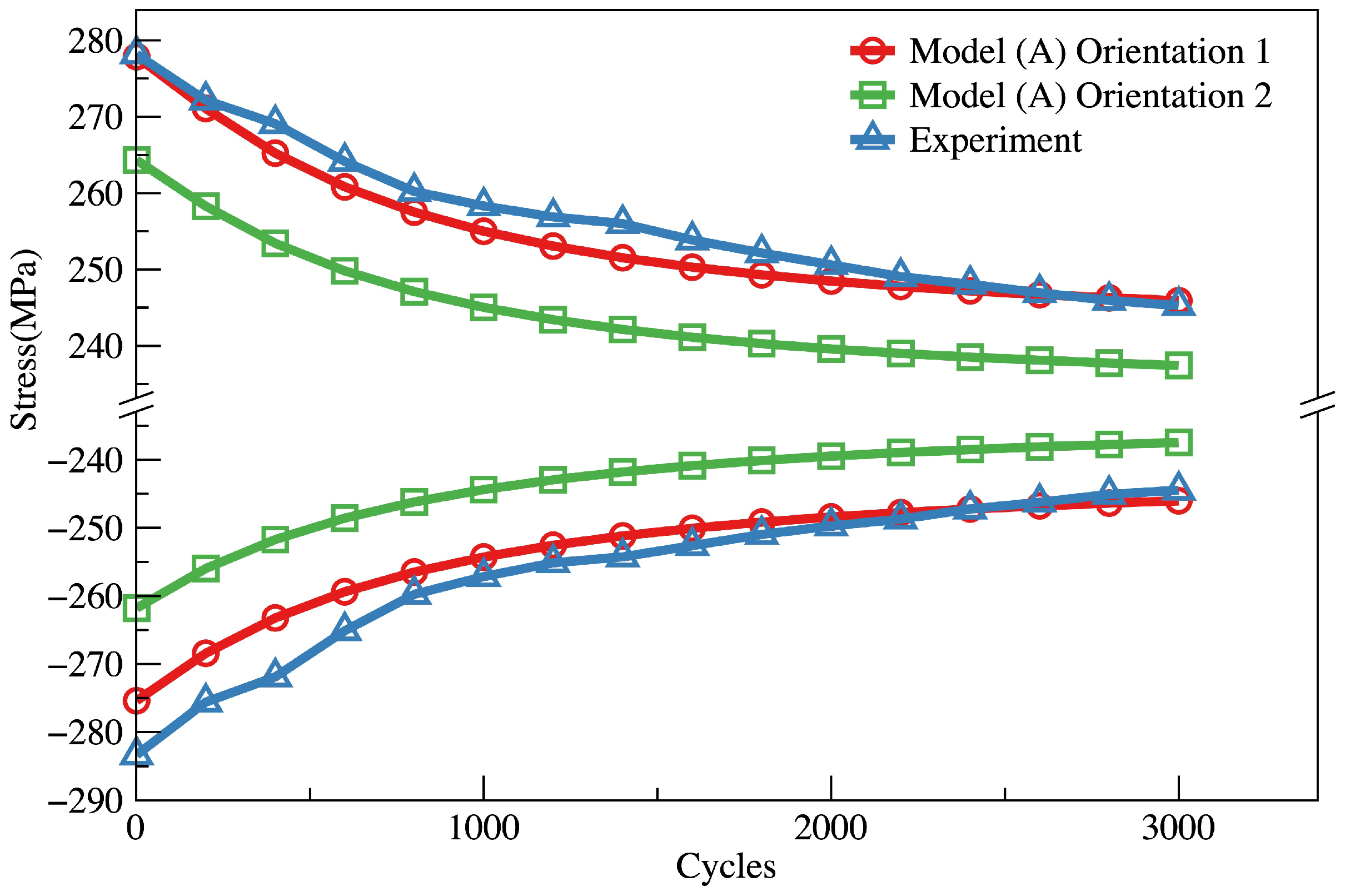
3.2.5. 3D Geometric Models
4. Discussion
- Both approaches are capable of predicting the fatigue crack initiation positions and initiation life in ferrite–pearlite steel; the crack density evolution is in good agreement with experiment results.
- The first approach determines whether a crack initiates by basal energy, which makes the simulation process much faster than the finite element method. However, stress and strain fields cannot be obtained from this approach.
- The second approach is based on CPFEM and more variables can be calculated, such as the stress and strain field, slip rate, resolved shear stress, etc., but a higher computational cost is required.
- Although the parameters are calibrated in 2D models, they can be applied to 3D models by recalibrating only one parameter.
- Both approaches are promising. For example, multiple slip systems can be introduced into the first approach, and more slip controlling parameters can be included in the second approach, such as temperature.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, L.; Wang, Z.; Zhao, J. Life prediction by ferrite–pearlite microstructural simulation of short fatigue cracks at high temperature. Int. J. Fatigue 2015, 80, 349–356. [Google Scholar] [CrossRef]
- Tokaji, K.; Ogawa, T.; Osako, S. The growth of microstructurally small fatigue cracks in a ferritic-pearlitic steel. In Fatigue & Fracture of Engineering Materials & Structures; Wiley Online Library: Hoboken, NJ, USA, 1988; Volume 11, pp. 331–342. [Google Scholar]
- Berisha, B.; Raemy, C.; Becker, C.; Gorji, M.; Hora, P. Multiscale modeling of failure initiation in a ferritic–pearlitic steel. Acta Mater. 2015, 100, 191–201. [Google Scholar] [CrossRef]
- Hoshide, T. Life prediction based on biaxial fatigue crack growth simulated in different microstructures modeled by using Voronoi-polygons. Procedia Eng. 2010, 2, 111–120. [Google Scholar] [CrossRef][Green Version]
- Hoshide, T.; Takahashi, Y. Simulation of directional distribution of slip-band crack under biaxial low cycle fatigue. JSME Int. J. Ser. A Solid Mech. Mater. Eng. 2004, 47, 397–402. [Google Scholar] [CrossRef][Green Version]
- Taylor, G.I.; Elam, C. The plastic extension and fracture of aluminium crystals. Proc. R. Soc. Lond. Ser. A Contain. 1925, 108, 28–51. [Google Scholar]
- Taylor, G.I. The mechanism of plastic deformation of crystals. Part I.—Theoretical. Proc. R. Soc. Lond. Ser. A Contain. 1934, 145, 362–387. [Google Scholar]
- Taylor, G.I.; Elam, C.F. Bakerian lecture: The distortion of an aluminium crystal during a tensile test. Proc. R. Soc. Lond. Ser. A Contain. 1923, 102, 643–667. [Google Scholar]
- Hill, R. Generalized constitutive relations for incremental deformation of metal crystals by multislip. J. Mech. Phys. Solids 1966, 14, 95–102. [Google Scholar] [CrossRef]
- Hill, R.; Rice, J. Constitutive analysis of elastic-plastic crystals at arbitrary strain. J. Mech. Phys. Solids 1972, 20, 401–413. [Google Scholar] [CrossRef]
- Huang, Y. A User-Material Subroutine Incroporating Single Crystal Plasticity in the ABAQUS Finite Element Program; Harvard Univ.: Cambridge, UK, 1991. [Google Scholar]
- Li, H.; Kang, G.; Yu, C. Modeling uniaxial ratchetting of magnesium alloys by a new crystal plasticity considering dislocation slipping, twinning and detwinning mechanisms. Int. J. Mech. Sci. 2020, 179, 105660. [Google Scholar] [CrossRef]
- Yue, Z. Surface roughness evolution under constant amplitude fatigue loading using crystal plasticity. Eng. Fract. Mech. 2005, 72, 749–757. [Google Scholar] [CrossRef]
- Asaro, R.J. Micromechanics of crystals and polycrystals. Adv. Appl. Mech. 1983, 23, 1–115. [Google Scholar]
- Sweeney, C.; Vorster, W.; Leen, S.; Sakurada, E.; McHugh, P.; Dunne, F. The role of elastic anisotropy, length scale and crystallographic slip in fatigue crack nucleation. J. Mech. Phys. Solids 2013, 61, 1224–1240. [Google Scholar] [CrossRef]
- Dunne, F.; Rugg, D.; Walker, A. Lengthscale-dependent, elastically anisotropic, physically-based hcp crystal plasticity: Application to cold-dwell fatigue in Ti alloys. Int. J. Plast. 2007, 23, 1061–1083. [Google Scholar] [CrossRef]
- Zhang, K.S.; Ju, J.W.; Li, Z.; Bai, Y.L.; Brocks, W. Micromechanics based fatigue life prediction of a polycrystalline metal applying crystal plasticity. Mech. Mater. 2015, 85, 16–37. [Google Scholar] [CrossRef]
- Ashton, P.; Harte, A.; Leen, S. A strain-gradient, crystal plasticity model for microstructure-sensitive fretting crack initiation in ferritic-pearlitic steel for flexible marine risers. Int. J. Fatigue 2018, 111, 81–92. [Google Scholar] [CrossRef]
- Franciosi, P.; Le, L.; Monnet, G.; Kahloun, C.; Chavanne, M.H. Investigation of slip system activity in iron at room temperature by SEM and AFM in-situ tensile and compression tests of iron single crystals. Int. J. Plast. 2015, 65, 226–249. [Google Scholar] [CrossRef]
- Du, C.; Maresca, F.; Geers, M.; Hoefnagels, J. Ferrite slip system activation investigated by uniaxial micro-tensile tests and simulations. Acta Mater. 2018, 146, 314–327. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, L.; Baxevanakis, K.; Zhao, L.; Bullough, C. Modelling short crack propagation in a single crystal nickel-based superalloy using crystal plasticity and XFEM. Int. J. Fatigue 2020, 136, 105594. [Google Scholar] [CrossRef]
- McDowell, D.; Dunne, F. Microstructure-sensitive computational modeling of fatigue crack formation. Int. J. Fatigue 2010, 32, 1521–1542. [Google Scholar] [CrossRef]
- Gu, T.; Stopka, K.S.; Xu, C.; McDowell, D.L. Prediction of maximum fatigue indicator parameters for duplex Ti–6Al–4V using extreme value theory. Acta Mater. 2020, 188, 504–516. [Google Scholar] [CrossRef]
- Dunne, F.; Wilkinson, A.; Allen, R. Experimental and computational studies of low cycle fatigue crack nucleation in a polycrystal. Int. J. Plast. 2007, 23, 273–295. [Google Scholar] [CrossRef]
- Hallberg, H.; Ås, S.K.; Skallerud, B. Crystal plasticity modeling of microstructure influence on fatigue crack initiation in extruded Al6082-T6 with surface irregularities. Int. J. Fatigue 2018, 111, 16–32. [Google Scholar] [CrossRef]
- Lin, B.; Zhao, L.; Tong, J.; Christ, H.J. Crystal plasticity modeling of cyclic deformation for a polycrystalline nickel-based superalloy at high temperature. Mater. Sci. Eng. A 2010, 527, 3581–3587. [Google Scholar] [CrossRef]
- Sajjad, H.M.; Hanke, S.; Güler, S.; Fischer, A.; Hartmaier, A. Modelling cyclic behaviour of martensitic steel with J2 plasticity and crystal plasticity. Materials 2019, 12, 1767. [Google Scholar] [CrossRef]
- Voronoi, G. Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Deuxième mémoire. Recherches sur les parallélloèdres primitifs. J. Angew. Math. 1908, 1908, 198–287. [Google Scholar] [CrossRef]
- Hoshide, T.; Kusuura, K. Life prediction by simulation of crack growth in notched components with different microstructures and under multiaxial fatigue. In Fatigue & Fracture of Engineering Materials & Structures; Wiley Online Library: Hoboken, NJ, USA, 1998; Volume 21, pp. 201–213. [Google Scholar]
- Stopka, K.S.; Gu, T.; McDowell, D.L. Effects of algorithmic simulation parameters on the prediction of extreme value fatigue indicator parameters in duplex Ti-6Al-4V. Int. J. Fatigue 2020, 141, 105865. [Google Scholar] [CrossRef]
- Quey, R.; Renversade, L. Optimal polyhedral description of 3D polycrystals: Method and application to statistical and synchrotron X-ray diffraction data. Comput. Methods Appl. Mech. Eng. 2018, 330, 308–333. [Google Scholar] [CrossRef]
- Kang, G.; Bruhns, O.T. New cyclic crystal viscoplasticity model based on combined nonlinear kinematic hardening for single crystals. Mater. Res. Innov. 2011, 15, s11–s14. [Google Scholar] [CrossRef]
- Hutchinson, J. Creep and plasticity of hexagonal polycrystals as related to single crystal slip. Metall. Trans. A 1977, 8, 1465–1469. [Google Scholar] [CrossRef]
- Bassani, J.L.; Wu, T.Y. Latent hardening in single crystals. II. Analytical characterization and predictions. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1991, 435, 21–41. [Google Scholar]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.D.; Bieler, T.R.; Raabe, D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Bandyopadhyay, R.; Prithivirajan, V.; Sangid, M.D. Uncertainty Quantification in the Mechanical Response of Crystal Plasticity Simulations. JOM 2019, 71, 2612–2624. [Google Scholar] [CrossRef]
- Luo, J.; Kang, G.; Shi, M. Simulation to the cyclic deformation of polycrystalline aluminum alloy using crystal plasticity finite element method. Int. J. Comput. Mater. Sci. Eng. 2013, 2, 1350019. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]










| C | Si | Mn | Cr | S | P |
|---|---|---|---|---|---|
| Name of Parameters | Units | Room Temperature | High Temperature |
|---|---|---|---|
| Temperature | °C | 20 | 500 |
| Yield strength | MPa | ||
| Tensile strength | MPa | ||
| Elongation | % | 32 | 45 |
| Elastic modulus | MPa | ||
| Poisson’s ratio | |||
| Fracture energy density | KJ/m | 2 | 2 |
| Shear modulus | GPa | 94 | 81 |
| Parameters | Units | Values |
|---|---|---|
| Temperature | °C | 500 |
| Strain rate | s | |
| Strain ratio | ||
| Strain amplitude |
| Parameters | Units | Values |
|---|---|---|
| G | GPa | 81 |
| 0.3 | ||
| MPa | 81 | |
| KJ/m | 2 | |
| Initial basal energy of PSB | 0.3∼0.5 | |
| Initial basal energy of F-FGB | 0.4∼0.6 | |
| Initial basal energy of F-PGB | 0.45∼0.65 |
| Parameters | Values | Units |
|---|---|---|
| , , | GPa | |
| , , | GPa | |
| A | MPa | |
| q | ||
| Q | MPa | |
| S | MPa | |
| K | MPa | |
| B | ||
| D | 20,000 | |
| MPa | ||
| MPa | ||
| N | (2D) 110(3D) | MPa |
| Experiment | 1 | 200 | 400 | 600 | 800 | 1000 | 1200 | 1400 | 1600 | 1800 | 2000 | 2200 | 2400 | 2600 | 2800 | 3000 |
| Simulation | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Z.; Wang, L.; Wang, Z.; He, Y. A Comparison of Two Methods Modeling High-Temperature Fatigue Crack Initiation in Ferrite–Pearlite Steel. Crystals 2022, 12, 718. https://doi.org/10.3390/cryst12050718
Fang Z, Wang L, Wang Z, He Y. A Comparison of Two Methods Modeling High-Temperature Fatigue Crack Initiation in Ferrite–Pearlite Steel. Crystals. 2022; 12(5):718. https://doi.org/10.3390/cryst12050718
Chicago/Turabian StyleFang, Zheng, Lu Wang, Zheng Wang, and Ying He. 2022. "A Comparison of Two Methods Modeling High-Temperature Fatigue Crack Initiation in Ferrite–Pearlite Steel" Crystals 12, no. 5: 718. https://doi.org/10.3390/cryst12050718
APA StyleFang, Z., Wang, L., Wang, Z., & He, Y. (2022). A Comparison of Two Methods Modeling High-Temperature Fatigue Crack Initiation in Ferrite–Pearlite Steel. Crystals, 12(5), 718. https://doi.org/10.3390/cryst12050718






