Abstract
Al–Mg–Zn alloys reinforced by T–Mg32(Al,Zn)49 phase had higher structure stability and strength than Al–Zn–Mg–(Cu) alloys reinforced by MgZn2 phase, but the reasons for these two kind of alloys was not well-known. To reveal the discrepancy between T phase and MgZn2 phase, the lattice parameters, cohesive energy, and electronic structure as well as the elastic properties were investigated based on density functional theory. Four types of T phase unit cell were employed according to symmetry of space group. The calculated lattice constants well-agreed with experimental data. Compared to MgZn2 phase, T phases obtained lower cohesive energy owing to their partial covalent bond, which may result in a higher structure stability. The elastic modulus E of T phase depended on the occupation of Al atom, and the effect of the occupation of Al atom on the structure and properties of T phase was also discussed.
1. Introduction
Al–Zn–Mg–(Cu) aluminum alloys strengthened by MgZn2 phase are widely used in aerospace and automotive contexts due to their high specific strength. However, typical Al–Zn–Mg–(Cu) aluminum alloys, such as 7075, 7050, and 7055 alloys, have poor corrosion resistance [1], as there is an electrode potential difference between MgZn2 phase and aluminum matrix. Furthermore, MgZn2 phase tended to coarsen at high temperature, resulting in a low thermal stability [2], limiting their application in high-temperature parts.
Recently, investigation of Al–Mg–Zn alloys reinforced by T–Mg32(Al,Zn)49 phase has attracted the attention of researchers at home and abroad [3,4,5]. The research by Zhang [6,7] showed that Al–Mg–Zn alloy obtained a higher strength and toughness than the commercial 7000 series aluminum alloy owing to the strength of T phase. Takata [8] proposed that Al5Mg3.5Zn(at%) alloy has a higher heat resistance than 7055 alloy. Although the microstructure properties of aluminum alloys strengthened by T phase and MgZn2 phase have been reported [9,10,11], there are few reports on the discrepancy between T phase and MgZn2 phase to reveal the reasons for the high strength and structure stability of Al–Mg–Zn alloys.
The electronic structure of MgZn2 phase was studied based on first-principles calculations. The electronic structure of MgZn2 phase was analyzed in terms of band structure, density of states and electron density [12]. A systematic investigation of coherent interfaces of MgZn2 phase was studied using the first-principles method [13]. The electronic structure and pseudogap of T phase were also investigated on the basis of the quasicrystal model; however, the mechanical properties and electronic structure of T phase were not well known.
In this paper, 1/1 approximant structural [14] of Mg32(Al,Zn)49 phase was employed, which was cubic with space group Im3 containing 162 atomic sites. The electronic structures of Mg32(Al,Zn)49 phase and MgZn2 phase were compared by ab initio methods, and the differences elastic properties of Mg32(Al,Zn)49 phase and MgZn2 phase were revealed at the atomic scale, providing the theoretical basis for the development of new high-performance aluminum alloys.
2. Computational Method
The first-principles calculation was carried out based on density functional theory (DFT) [15] using the software VASP [16]. The interaction between electrons and ions was described using the projection-augmented wave (PAW) method [17]. The electron configuration was described by 3S23P1, 3S2 and 3d104s2 valence states for Al, Mg and Zn, respectively. The Perdew–Burke–Ernzer (PBE) [18] method of generalized gradient approximation (GGA) [19] was used to describe the exchange-correlation energy functional between electrons. The cut-off energy of the plane wave function of electrons was set at 400 eV, and Monkhorst–Pack k-point grids for the Brillouin-zone integration were applied with linear Kmesh-resolved value of less than 0.03 2πÅ−1 along each periodic direction in reciprocal space, to optimize the geometry and calculate elastic constants. Furthermore, the density of states (DOS) was calculated on the condition of less than 0.015 2πÅ−1 along each periodic direction in reciprocal space.
Crystal structures of MgZn2 and T phases were shown in Figure 1. MgZn2 phase belonged to the hexagonal structure with the space group P63/mmc, and T-phase model in this calculation had eight sites (A–H) [20], among which Al atoms occupied one position in A and Mg occupied D, E, G, and H positions without any chemical disorder. The Al and Zn atoms usually occupied the B, C, and F atomic sites with chemical disorder. This atomic structure involved a large amount of chemical disorder on sites B, C, and F. Such chemical disorder was eliminated to carry out efficient calculations.
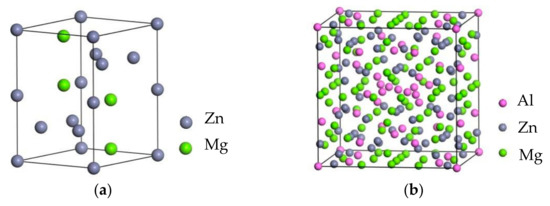
Figure 1.
Crystal structure: (a) MgZn2; (b) T-(Al,Zn)98Mg64.
According to the symmetry of Im3 space group (cubic crystal), four configurations of Al: Zn: Mg = 13: 36: 32 and Al: Zn: Mg = 25: 24: 32 were constructed, as Al and Zn atoms occupied site B, C, and F sites respectively [14]. The space group of the calculation model and the space occupying situation were shown in the Table 1.

Table 1.
The model structure of T phases.
3. Results and Discussion
3.1. Crystal Structure and Stability
In order to ensure the accuracy of the study, the geometric structure of the crystal structure was firstly optimized, and the lattice constants after optimization were listed in Table 2 in comparison with the results of other authors using the same calculation method. It showed that the optimized lattice constants were well-consistent with the experimental values and calculated values.
The cohesive energy () was a measure of the force to bind atoms together in the solid state, so it showed the structural stability of the alloys. It can be calculated by Formula (1) [21].
where was the total energy of the unit cell and , were the total energies of the isolated A and B atoms in the free state.
The equilibrium formation enthalpy () of a compound can refer to the energy consumed for a crystal decomposed into pure crystal elements at equilibrium status. If the equilibrium formation enthalpy of crystal mesophase was lower, the ability of alloying elements composed of this phase was stronger [22].
where , were the energy per atom of pure elements at equilibrium status. and referred to the number of A and B atoms in unit cell, respectively.
Considering the precipitation of MgZn2 phase and T phase from Al solid solution, the fcc-based formation enthalpy () of these phases can be calculated as follow [23]:
where , were the per atom energies of A and B in the fcc state. The fcc-based formation enthalpy eliminated the promotion energy, promoting a constituent from its equilibrium structure to the fcc structure [23].
As shown in Table 2, compared with the calculation of the equilibrium formation enthalpies, the fcc-based formation enthalpies of each phase were lower as the elimination of the promotion energy, but still had the similar change trend. T phase obtained higher formation enthalpy than that of MgZn2 phase, but had lower cohesive energy, indicating that the T phase was more difficult to form, and gained higher melting point and thermal stability. As for T phase, the formation enthalpy gradually increased with increase in Al atoms and decrease in Zn, implying that T phase was difficult to form. However, there was a decreasing tend for the cohesive energy, resulting in higher thermal stability.

Table 2.
Lattice parameters, cohesive energy , and formation enthalpy of the phases T-phase, MgZn2.
Table 2.
Lattice parameters, cohesive energy , and formation enthalpy of the phases T-phase, MgZn2.
| Phase | Sum | Source | Lattice Parameter/Å | (kJ·mol−1) | (kJ·mol−1) | (kJ·mol−1) | ||
|---|---|---|---|---|---|---|---|---|
| a | b | c | ||||||
| MgZn2 | Mg4Zn8 | This work | 5.187 | - | 8.561 | −132.617 | −13.186 | −14.849 |
| Ref [24] | 5.208 | - | 8.506 | −132.628 | −13.346 | - | ||
| Exp [25] | 5.221 | - | 8.567 | - | - | - | ||
| T | Al26Zn72Mg64-C | This work | 14.17 | - | - | −172.040 | −9.728 | 11.158 |
| Al26Zn72Mg64-B | 14.23 | - | - | −169.8 | −7.488 | −8.918 | ||
| Al50Zn48Mg64-F | 14.32 | - | - | −206.406 | −6.952 | −8.013 | ||
| Al50Zn48Mg64-BC | 14.37 | - | - | −204.836 | −5.319 | −6.444 | ||
| Al6Zn11Mg11 | Exp [8] | 14.20 | - | - | - | - | - | |
On the other hand, the occupation of Al and Zn significantly effected the formation enthalpy and the cohesive energy. As for T–Al26Zn72Mg64 phase, both the formation enthalpy and the cohesive energy of the occupation site C by Al atom were lower than that of site B, thus Al atom was inclined to occupy site C. Similarly, Al atom in T–Al50Zn48Mg64 phase occupied site F with higher probability, and B, C were not simultaneously occupied. The calculated result was consistent with the experimental data, where the atom occupation probability was summarized as B (83.4% Zn, 16.6%A1), C (51%Zn, 49% A1), F (48% Zn, 52%A1) [20].
3.2. Elastic Properties
The elastic constant described the stiffness of the crystal in response to the applied strain [26]. When the strain was very small, the energy of the system had a quadratic linear relationship with the strain (Hooke’s law). Based on the energy–strain relationship, a certain elastic constant or a combination of the elastic constants of crystal can be obtained by applying strain in different orientations and sizes to the system, and finally the elastic constant matrix of crystal can be obtained. The specific calculation results of phase elastic constants in this work were shown in Table 3.

Table 3.
Calculated elastic constants of phases MgZn2 and T phase, /GPa.
Based on the calculated quadratic elastic coefficient matrix, the elastic properties of polycrystalline systems can be obtained using Voigt–Reuss–Hill approximation [29]. According to Born–Huang’s lattice dynamical theory, the mechanical stability criterion can be expressed as:
Hexagonal system:
Cubic system:
MgZn2 phase is a hexagonal P63/mmc system with six independent constants (, , , , and ), in which . The Voigt and Reuss boundary values of hexagonal crystal system (MgZn2) were calculated by the following formula [30].
where the B indicates bulk modulus, G is shear modulus, and the subscripts v and r indicate the Voigt and Reuss values, respectively.
T phase is Im3 structure and belongs to the cubic crystal. There are only three independent elastic constants ( and ). The bulk modulus and shear modulus of the cubic crystal system can be calculated by the equations [31].
The Voigt–Reuss–Hill approximations, averaging Voigt and Reuss, were considered as the best estimation of the theoretical polycrystalline elastic modulus. The polycrystalline Young’s modulus and Poisson’s ratio can be calculated from the values of elastic modulus as follows [32]:
The elastic properties parameters of the MgZn2 and T phase calculated in this work were shown in Table 4.

Table 4.
Bulk modulus B (GPa), Shear modulus G (GPa), Young’s modulus E (GPa), Poisson’s ratio ν and B/G of MgZn2 and T phase.
Poisson’s ratio (ν) was the elastic constant of the transverse deformation of the material, reflecting the lateral shrinkage capacity of the material. In the range of 0 to 0.5, the smaller Poisson’s ratio, the harder the material, the smaller the toughness. The ratio of bulk modulus to shear modulus (G/B) can predict the brittleness and toughness of polycrystalline materials. It usually took the value of 0.57 as the critical point of the brittleness and toughness. Metal materials were usually less than 0.57 with good toughness, and the value G/B of the material decreased with the increase of toughness. Table 4 showed that both T phase and MgZn2 phase had good toughness as illustrated by the parameters of G/B and ν.
As for T phase, Al26Zn72Mg64-C phase obtained the highest value of E among the different occupation of Al, Zn atoms, and the value of Young’s modulus E of Al26Zn72Mg64-C was higher than that of MgZn2 phase, indicating that Al26Zn72Mg64-C phase gained higher stiffness. It should be noted that the Young’s modulus E of Al50Zn48Mg64-F phase was slightly higher than that of MgZn2 phase, while T phase with the other atoms occupation gained lower Young’s modulus E than MgZn2 phase. It was implied that the properties of aluminum alloy reinforced by T phase depended on the type of T phase structure.
3.3. Electronic Structures
To illustrate the differences between T phase and MgZn2 phase for structural stability and elastic properties, the total and partial DOS of the T phase and MgZn2 phase were calculated in the present work, respectively, and presented in Figure 2. The common feature of T phase and MgZn2 phase was that there were sharp peaks on the DOS of −8 to −7 eV, which was a typical feature of transition metal caused by the Zn 3d state, indicating that the 3d state was relatively localized, the corresponding band was relatively narrow.
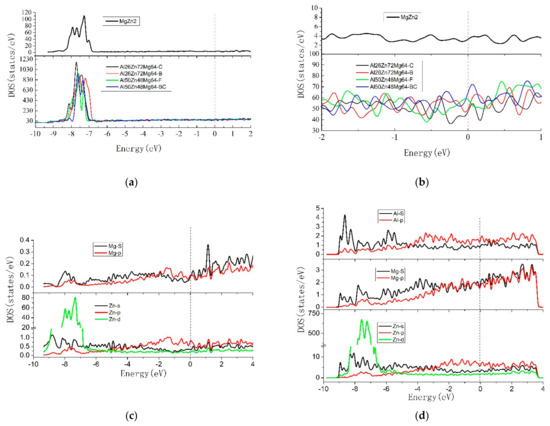
Figure 2.
The DOS diagrams: (a) TDOS from −10 to 2 ev of MgZn2 and T-phases; (b) TDOS from −4 to 2 ev of MgZn2 and T-phases; (c) PDOS of MgZn2; (d) PDOS of Al26Zn72Mg64-C.
A larger version of the red dotted line (−2 ev to 1 ev) in Figure 2a was shown in Figure 2b. The Fermi level was set at zero energy and marked by the vertical dotted line in Figure 2b. The inconspicuous gap of DOS located at Fermi energy level, showed that both MgZn2 phase and T phase mainly presented metallic features, which was mainly controlled by Mg3s, 2p and Al3s, 3p states.
Electron localization function (ELF) can effectively analyze the degree of electron localization and was used to describe the probability of electron pairs in a multi-electron system to clarify the bonding nature [33]. Compared to DOS, ELF was a suitable tool at determining the nature of the chemical bonding. ELF around these atoms in real space lattice was plotted to reveal the feature of bonding. In Figure 3, ELF = 1 corresponding to the top of the scale with crimson indicates the complete localization, and the middle of the scale with green indicates ELF = 1/2, corresponding to an electron-gas-like type. The calculation results showed that ELF values of MgZn2 phase was about 0.46 and had the characteristics of electron-gas-like, inferring that the electronic localization was small in MgZn2 phase, and the interatomic electron mainly presented metal bond. The values of ELF were 0.840, 0.829, 0.857, and 0.844 for Al26Zn72Mg64–C, Al26Zn72Mg64-B, Al50Zn48Mg64–F, and Al50Zn48Mg64–BC phase, respectively. ELF values of T phases were larger than that of MgZn2 phase, revealing that T phase presented the characteristics of partial covalent bond. As showed in Figure 3, the Al–Zn, Mg–Mg bonding contributed to the high electron localization for Al26Zn72Mg64–C and Al26Zn72Mg64–B. As for Al50Zn48Mg64, the simultaneous substitution of B, C position by Al atom formed Mg-Zn, Mg-Mg electron localization, while the substitution of F position by Al atom led to the highest electron localization owing to the Al–Al and Mg–Mg bonding. Furthermore, the ELF values of T phase were well-agreed with the higher cohesive energy and phase stability as shown in Table 2.
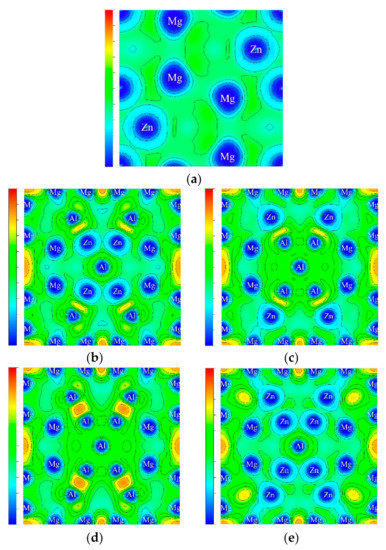
Figure 3.
ELF contours: (a) () plane of MgZn2; (b–e) (002) plane of (b) Al26Zn72Mg64–C; (c) Al26Zn72Mg64–B; (d) Al50Zn48Mg64–F; (e) Al50Zn48Mg64–BC.
Bader charge can be used to characterize the interatomic ionic bonding. Bader charge calculation results showed that the valence charge of Mg atom in MgZn2 phase was −1.43 e− and the valence charge of Zn atom was +0.67 and +0.80 e−. The average charge per atom was about 0.95 e−, thus there were also ionic bonds between atoms of MgZn2 phase. Similarly, the average charges per atom of T phase were 1.10e−, 0.92e−, 0.99e−, and 0.93e− for Al26Zn72Mg64–C, Al26Zn72Mg64–B, Al50Zn48Mg64–F, and Al50Zn48Mg64–BC phase, respectively. T phase where Al atom respectively occupied the site of C, F had higher Bader charge than MgZn2 phase, while the Bader charge of T phase was slightly lower than that of MgZn2 phase when Al atom occupied the site of B and B, C. To a certain extent, the charge transfer indicated the strength of ion interaction, and was positively correlated with Young’s E modulus, which was consistent with the mechanical analysis results previously calculated in Table 4.
4. Conclusions
First-principles calculations were applied to explore the cohesive energy, the formation enthalpy, the elastic properties, and the electronic structures of T phase and MgZn2 phase based on density functional theory. The calculated lattice constants well-agreed with experimental data, revealing the effectiveness of the proposed theoretical models. Al atom in T phase was inclined to occupy the site of C and F in crystal structure. Compared to MgZn2 phase, T phases obtained lower cohesive energy owing to their partial covalent bond, and revealed that the structural stability of T phase was higher than that of MgZn2 phase. T phase where Al atom occupied the site of C and F obtained higher elastic modulus, which well-agreed with the calculation of Bader charge per atom.
Author Contributions
B.N. and D.C. conceived and designed the research; Y.S., T.F., F.L. and H.Q. performed the first principles calculation; Y.S. and S.Z. wrote the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by R & D plan for key areas in Guangdong Province (2020B01 0186001), Special Innovation Projects of Universities in Guangdong Province (2018KTSCX240), Core technology research project of Foshan(1920001000412), R & D plan for key areas in Jiangxi Province (20201BBE51009), Basic and applied basic research fund project in Guangdong Province(2020b15120093), Science and technology project in Guangdong (2020B121202002) and Innovation driven project of science and technology plan in Jiangxi Yichun.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ma, Z.; Liu, J.; Liu, S.; Zhang, Y.; Deng, Y. Quench-induced contributions of high angle grain boundary and low angle grain boundary to exfoliation corrosion propagation in an AlZnMgCu alloy. J. Mater. Res. Technol. 2021, 15, 6866–6870. [Google Scholar] [CrossRef]
- Huo, W.; Hou, L.; Zhang, Y.; Zhang, J. Warm formability and post-forming microstructure/property of high-strength AA 7075-T6 Al alloy. Mater. Sci. Eng. A 2016, 675, 44–54. [Google Scholar] [CrossRef]
- Nakatsuka, S.; Ishihara, M.; Takata, N. Tensile Properties of a Heat-Resistant Aluminium Alloy Strengthened by T-Al6Mg11Zn11 Intermetallic Phase. MRS Adv. 2019, 4, 1485–1490. [Google Scholar] [CrossRef]
- Takata, N.; Ishihara, M.; Suzuki, A. Microstructure and strength of a novel heat-resistant aluminum alloy strengthened by T-Al6Mg11Zn11 phase at elevated temperatures. Mater. Sci. Eng. A 2018, 739, 62–70. [Google Scholar] [CrossRef]
- Takata, N.; Okano, T.; Suzuki, A. Microstructure of intermetallic-reinforced Al-Based alloy composites fabricated using eutectic reactions in Al–Mg–Zn ternary system. Intermetallics 2018, 95, 48–58. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, D.; Liu, H.; Zhuang, L.; Zhang, J. Precipitation hardening and intergranular corrosion behavior of novel Al–Mg–Zn(–Cu) alloys. J. Alloys Compd. 2020, 853, 157199. [Google Scholar] [CrossRef]
- Ding, Q.; Zhang, D.; Pan, Y.; Hou, S.; Zhang, J. Strengthening mechanism of age-hardenable Al–xMg–3Zn alloys. Mater. Sci. Technol. 2020, 35, 1071–1080. [Google Scholar] [CrossRef]
- Takata, N.; Takagi, R.; Li, R.; Ishii, H.; Suzuki, A.; Kobashi, M. Precipitation morphology and kinetics of T-Al6Mg11Zn11 intermetallic phase in Al–Mg–Zn ternary alloys. Intermetallics 2021, 139, 107364. [Google Scholar] [CrossRef]
- Takata, N.; Okano, T.; Aikawa, M. Morphology and mechanical properties of the T-Al6Mg11Zn11 phase in the eutectic microstructure of Al–Zn–Mg ternary alloys. Intermetallics 2020, 124, 106881. [Google Scholar] [CrossRef]
- Montagné, P.; Tillard, M. On the adaptability of 1/1 cubic approximant structure in the Mg–Al–Zn system with the particular example of Mg32Al12Zn37. J. Alloys Compd. Interdiscip. J. Mater. Sci. Solid-State Chem. Phys. 2016, 656, 159–165. [Google Scholar] [CrossRef]
- Shi, Z.; Zhang, W. A transmission electron microscopy investigation of crystallography of τ-Mg32(Al, Zn)49 precipitates in a Mg–Zn–Al alloy. Scr. Mater. 2011, 64, 201–204. [Google Scholar] [CrossRef]
- Andrae, D.; Paulus, B.; Wedig, U. A First-Principles Study of Electronic Structure of the Laves Phase MgZn2. Z. Anorg. Allg. Chem. 2014, 639, 1963–1967. [Google Scholar] [CrossRef]
- Li, X.; Ma, H.; Dai, Z. First-principles study of coherent interfaces of Laves-phase MgZn2 and stability of thin MgZn2 layers in Mg-Zn alloys. J. Alloys Compd. 2017, 696, 109–117. [Google Scholar] [CrossRef] [Green Version]
- Inukai, M.; Zijlstra, E.S.; Sato, H. Origin of the DOS pseudogap and Hume–Rothery stabilization mechanism in RT-type Al48Mg64Zn48 and Al84Li52Cu24 1/1-1/1-1/1 approximants. Philos. Mag. 2011, 91, 4247–4263. [Google Scholar] [CrossRef]
- Nityananda, R.; Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Resonance 2017, 22, 809–811. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1998, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Budimir, M.; Damjanovic, D.; Setter, N. Piezoelectric Response and Free Energy Instability in the Perovskite Crystals BaTiO3, PbTiO3 and Pb(Zr,Ti)O3. Phys. Rev. B 2006, 73, 4106. [Google Scholar] [CrossRef] [Green Version]
- Sun, W.; Lincoln, F.J.; Sugiyama, K. Structure refinement of (Al, Zn)49Mg32-type phases by single-crystal X-ray diffraction. Mater. Sci. Eng. A 2000, 294, 327–330. [Google Scholar]
- Wu, M.M.; Jiang, Y.; Wang, J.W. Structural, elastic and electronic properties of Mg(Cu1−xZnx)2 alloys calculated by first-principles. J. Alloys Compd. 2011, 509, 2885–2890. [Google Scholar] [CrossRef]
- Hui, Z.; Shang, S.; Saal, J.E. Enthalpies of formation of magnesium compounds from first-principles calculations. Intermetallics 2009, 17, 878–885. [Google Scholar]
- Wolverton, C.; Ozolins, V. First-principles aluminum database: Energetics of binary Al alloys and compounds. Phys. Rev. B Condens. Matter Mater. Phys. 2006, 73, 144104.1–144104.14. [Google Scholar] [CrossRef]
- Liao, F.; Fan, S.; Deng, Y. First-principle Calculations of Mechanical Properties of Al2Cu, Al2CuMg and MgZn2 Intermetallics in High Strength Aluminum Alloys. J. Aeronaut. Mater. 2016, 6, 74–78. [Google Scholar]
- Komura, Y.; Tokunaga, K. Structural studies of stacking variants in Mg-base Friauf–Laves phases. Acta Crystallogr. 1980, 36, 1548–1554. [Google Scholar] [CrossRef]
- Wei, Z.; Liu, L.; Li, B. Structural, elastic and electronic properties of intermetallics in the Pt–Sn system: A density functional investigation. Comput. Mater. Sci. 2009, 46, 921–931. [Google Scholar]
- Wu, M.; Li, W.; Tang, B. First-principles study of elastic and electronic properties of MgZn2 and ScZn2 phases in Mg–Sc–Zn alloy. J. Alloys Compd. 2010, 506, 412–417. [Google Scholar] [CrossRef]
- Seidenkranz, T.; Hegenbarth, E. Single-crystal elastic constants of MgZn2 in the temperature range from 4.2 to 300 K. Phys. Status Solidi 2010, 33, 205–210. [Google Scholar] [CrossRef]
- Hill, R. A self-consistent mechanics of composite materials. J. Mech. Phys. Solids 1965, 13, 213–222. [Google Scholar] [CrossRef]
- Li, Y.; Gao, Y.; Bing, X. Theoretical study on the stability, elasticity, hardness and electronic structures of W-C binary compounds. J. Alloys Compd. 2010, 502, 28–37. [Google Scholar] [CrossRef]
- Boucetta, S.; Zegrar, F. Density functional study of elastic, mechanical and thermodynamic properties of MgCu with a CsCl-type structure. J. Magnes. Alloys 2013, 1, 6. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Zhao, E.; Xiang, H. Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles. Phys. Rev. B 2007, 76, 296–300. [Google Scholar]
- Chen, K.; Kamran, S. Bonding Characteristics of TiC and TiN. Modeling Numer. Simul. Mater. Ence 2013, 3, 7–11. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).