Crystal Breakage Due to Combined Normal and Shear Loading

Abstract

Combined normal and shear stress on particles occurs in many devices for solid–liquid separation. Protein crystals are much more fragile compared to conventional crystals because of their high water content. Therefore, unwanted crystal breakage is to be expected in the processing of such materials. The influence of pressure and shearing has been investigated individually in the past. To analyze the influence of combined shear and normal stress on protein crystals, a modified shear cell for a ring shear tester is used. This device allows one to accurately vary the normal and shear stress on moist crystals in a saturated particle bed. Analyzing the protein crystals in a moist state is important because the mechanical properties change significantly after drying. The results show a big influence of the applied normal stress on crystal breakage while shearing. Higher normal loading leads to a much bigger comminution. The shear velocity, however, has a comparatively negligible influence.

1. Introduction

In recent years, alternative methods to purify and formulate proteins have been investigated. One example is preparative protein crystallization [1], which provides the opportunity to replace a costly chromatography step with selective protein crystallization. Crystalline proteins offer several advantages. By influencing the crystal shape and size, product characteristics like handling, shelf life, and drug release properties can be adjusted [2,3]. One well-known example is the use of crystalline insulin to achieve a depot effect and constant bioavailability [4]. Conventionally, protein crystallization on a larger scale uses the displacement method. Added anti-solvents (typically salts) reduce the target protein’s solubility and, thus, create the required supersaturation. Inherently, this method has some major disadvantages. First, the anti-solvent is typically added as a solution, which dilutes and, thus reduces the final crystal concentration in the suspension. Second, the final solution has high ion strength and, finally, high local supersaturation at the anti-solvent inlet leads to a broad crystal size distribution, lower reproducibility, and increased danger of amorphous precipitation [5]. Evaporative crystallization tackles these disadvantages, but is not suitable for proteins because of the required high temperatures. Groß and Kind [5] introduced low temperature water evaporation crystallization for proteins and demonstrated the applicability for the model system lysozyme from hen-egg white. Small scale filtration experiments of such crystallizate by Radel et al. [6,7] allowed to determine the process functions of this particle system. Using these process functions, the low temperature water evaporation crystallization method was adapted and implemented by Dobler et al. [8] for an integrated, quasi-continuous apparatus concept. Barros Groß and Kind [9] further investigated how seeding affects the crystal size distribution and demonstrated high reproducibility and control over crystal sizes and the width of the size distribution.

One major difference between protein and conventional crystals is the high water content in the protein crystal, which can account for up to 80% of the crystal mass. This makes such crystals soft and sensitive to mechanical stress [10]. Cornehl et al. [11] investigated crystal breakage of aggregated and needle-shaped lysozyme crystals under compressive stress. In process engineering, compressive stress occurs, for example, in press or cake filtration. Other apparatuses for filtration, such as the cross-flow filter (BoCross Dynamic, BOKELA GmbH, Karlsruhe, Germany) are characterized by high shear stress due to integrated agitators. In these cases, Cornehl et al. [12] also observed crystal comminution. In crystallization itself, comminution is partly a desirable effect. For example, collision of the crystals with each other as well as with internals, walls, and stirrers creates new crystallization nuclei that subsequently grow into larger crystals. For the use of crystallization as a formulation step for downstream processing of proteins [3,13], comminution after crystallization is usually not desired, since a change in particle size distribution (PSD) also changes the product properties.

Sediments can be compacted by both normal and shear stress. If both types of stress are combined, the achievable compaction is more pronounced, as used, for example, by Illies et al. [14] for the dewatering of filter cakes. Höfgen et al. [15] used an apparatus with high pressure dewatering rolls for filtration and dewatering. With this system, the shear and normal forces are individually adjustable and adaptable to the application at hand. Hammerich et al. [16] modified a shear cell for the Schulze ring shear tester to allow the measurement of fluid saturated particulate networks. This provides the opportunity to study the rheology and flow behavior of saturated sediments. The higher achievable compaction with combined shear and compression indicates bigger mechanical stress. Hence, a more pronounced comminution for protein crystals is to be expected in this case. The setup with the modified shear cell can, therefore, be used to observe comminution at a defined normal stress and shear velocity.

2. Theory

Particle breakage occurs when the material strength is exceeded. In addition to a one-time high mechanical load, fracture due to several lower load cycles is also conceivable. In this case, the loading history of the particle must be taken into account. For comminution processes such as grinding, the occurrence of particle or aggregate breakage is the basic requirement. In most solid–liquid separation applications, particle breakage is undesirable and usually leads to a deterioration of the process result. Basically, a distinction must be made between the stress in a particulate network and on the individual particle. In the following, the special focus is on compressive and shear stress.

In a particulate network under compressive stress, the imposed mechanical load is degradable by rearrangement processes, deformation, and fracture of the particles. For an axial, one-dimensional load, such as that applied by a piston, the effects mentioned above result in the highest load being applied in the immediate vicinity of the piston. The load decreases with increasing distance from the piston in the sediment. If the sediment is compressible, the highest compaction is to be expected in the vicinity of the piston [17]. In the upper particle layers, absorption of the input mechanical energy takes place due to elastic and plastic deformation and particle breakage, such that the mechanical energy transmitted via contact points decreases. Thus, the lowest stresses are present at the greatest distance from the piston center and at the bottom [18].

Shear stresses occur in process engineering, for example, on agitators, valves, and in pumps. Fluid-induced mechanical stress occurs in a suspension due to the existing flow. In addition to the fluid-induced stress, collisions between particles and particles with agitators or walls take place. These collisions lead to particle abrasion and, at high loads, to particle breakage. In crystallization, such abrasion is partly desirable, as it creates new crystallization nuclei for secondary nucleation.

Shear loading is also possible for saturated sediments. This applies to the transport of flowable sediments in equipment, such as the tubular centrifuge or decanter centrifuge, as well as to the targeted use of combined normal and shear loading for mechanical dewatering. When normal and shear forces are superimposed, significantly higher densities and, thus, lower residual moisture content can be achieved [14,15]. In such scenarios, the particles rub against each other and, in the case of mechanically labile particle systems, abrasion or fracture occurs.

Comminution

The PSD, particle shape, and sediment structure have a big influence on the energy absorption and stress distribution in the particle bed. Furthermore, the overall stress is affected by the normal and shear stress as well as the shear velocity. As stress increases, comminution occurs in addition to compaction. Comminution leads to new fracture surfaces and rearrangement processes. The smaller the particles, the higher the energies required to cause comminution.

Population balances can be used to model the comminution of different particle size classes. The probability of breakage, P, during impact loading is given for many materials by the exponential function

$$P=1-exp\left(-fxk\left(E_M-E_{M,\min }\right)\right)$$

(1)

with f as the material parameter, x as the particle diameter, k as the number of load cycles, $E_M$ as mass-related stress energy, and $E_{M,\min }$ as the threshold value of the mass-related stress energy [18]. The breakage fraction $\overline{P}$ is identical to the breakage probability for a single grain. In a collective, the breakage fraction can be described by normalization with the master curve

$$\frac{\overline{P}}{{\overline{P}}_{\infty }}=1-exp\left(-{\left(\frac{E_M}{E_{M,c}}\right)}^{\beta }\right).$$

(2)

The quantity ${\overline{P}}_{\infty }$ is the upper limit of $\overline{P}$ and $\beta$ is a curve parameter. $E_{M,c}$ is a characteristic value of $E_M$ for which different approaches, taking into account the particle size, exist [19].

A fracture force can be determined on a single grain via compression or indentation tests. Nanoindentation is a suitable method for small particles that are to be examined moist, as in the case of protein crystals. Depending on the particle shape, different loads are conceivable. For an elongated particle, for example, a three-point bending test is possible. To cause particle fracture in a particulate network, a higher force than the fracture force of the single particle is necessary. This is due to the absorption of mechanical stress by rearrangement and deformation processes. Particle breakage is divided into the following phases:

1.

cracking;

2.

crack initiation;

3.

crack propagation.

Cracking starts as soon as the material strength is exceeded. Therefore, cracks preferentially form at locations that are already under stress or where defects are present. Defects can be, for example, lattice defects in a crystal. When the energy is low, a dormant crack is formed in this way. If no further stress takes place, the crack does not propagate and no fracture occurs. Only at a sufficiently high energy does crack initiation and subsequent crack propagation occur. The energy required for crack propagation at the cracking front must be continuously replenished.

Therefore, two conditions apply to particle breakage. On the one hand, there is the force condition, i.e., overcoming the binding forces for the formation of a crack, and on the other hand, there is the energy condition. The latter states that energy consumed at the crack front must be continuously supplied [20].

3. Materials and Methods

3.1. Crystallization

Isometric lysozyme crystals are produced with displacement crystallization. Two stock solutions are prepared. Solution one is an 25 $\mathrm{mmol}$ ${\mathrm{L}}^{-1}$ acetic acid buffer at pH 4.5. Solution two has the same composition but also contains 80 $\mathrm{g}$ ${\mathrm{L}}^{-1}$ NaCl. After dissolving 100 $\mathrm{g}$ ${\mathrm{L}}^{-1}$ lysozyme (Granulated lysozyme, OVOBEST Eiprodukte GmbH & Co. KG, Neuenkirchen-Vörden, Germany) from hen egg-white in 125 $\mathrm{m}$$\mathrm{L}$ of stock solution one, 125 $\mathrm{m}$$\mathrm{L}$ of stock solution two is added at a rate of 1 $\mathrm{m}$$\mathrm{L}$ ${\min }^{-1}$ with a membrane pump. Afterwards, the crystals grow in the aging phase until the supersaturation is reduced to zero. During the whole crystallization process, which takes about 16 $\mathrm{h}$, the solution is stirred with a blade stirrer at 350 ${\min }^{-1}$.

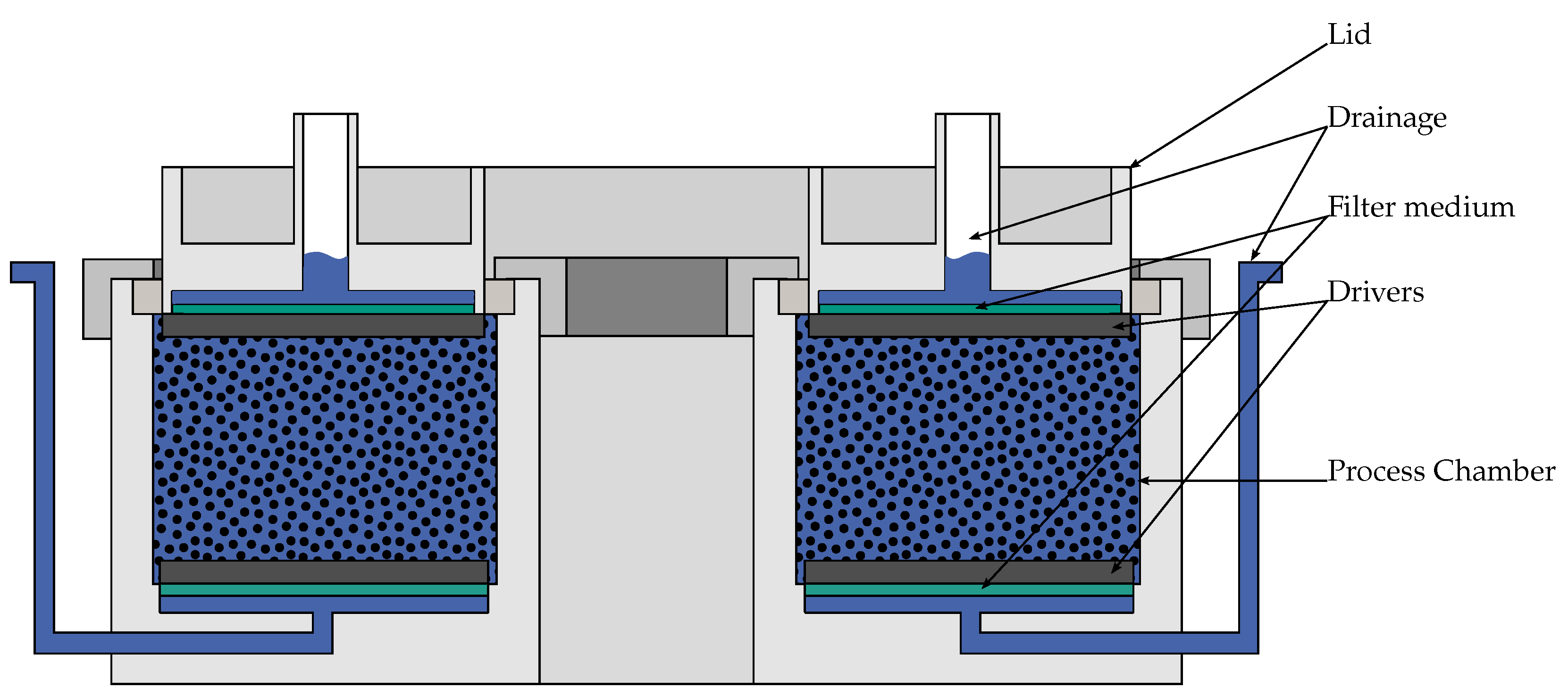
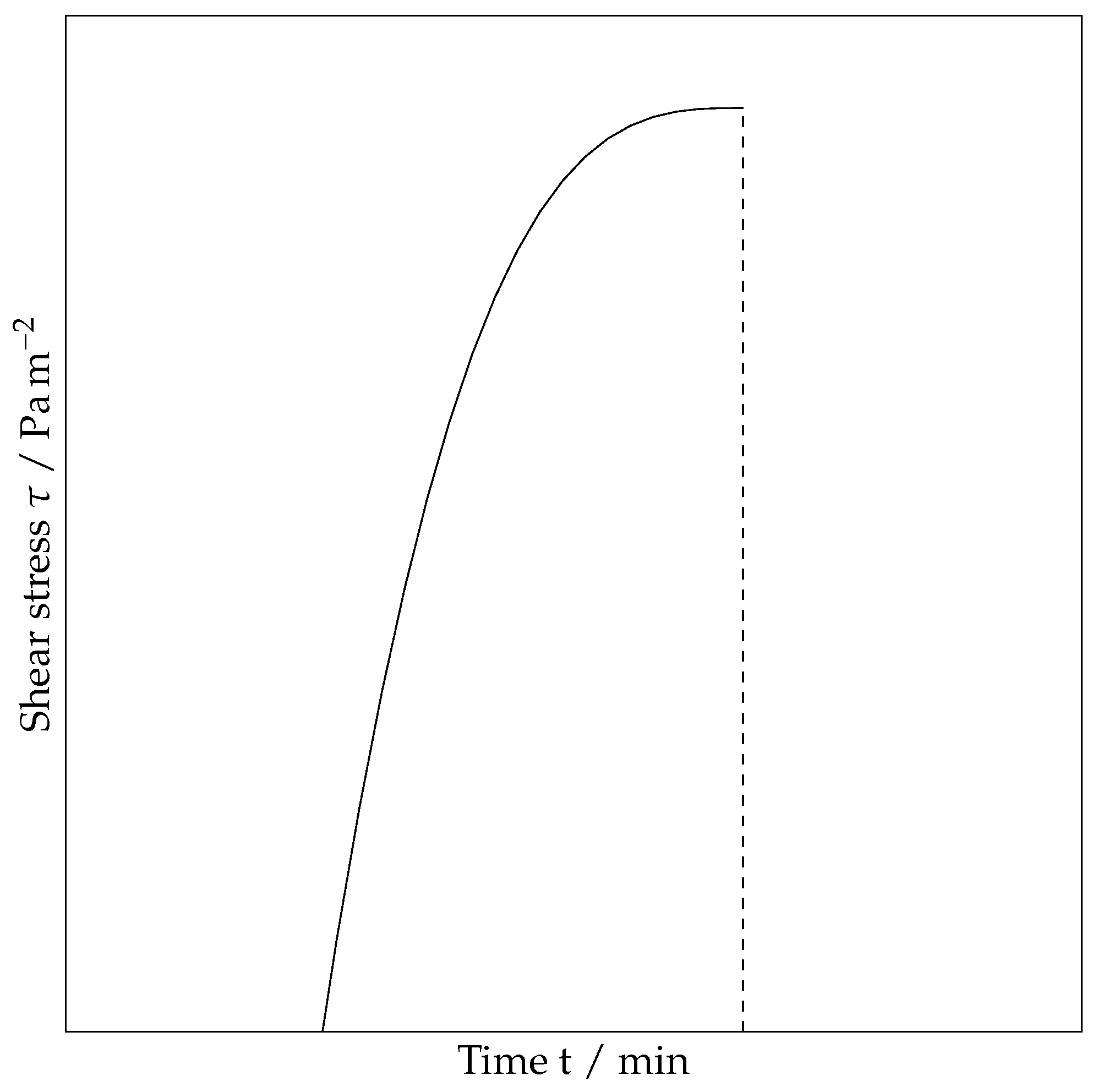
3.2. Modified Shear Cell and Ring Shear Tester

For the combined normal and shear loading, sediments of isometric lysozyme crystals are used as a model system for protein crystals. The mechanical properties of dried and moist crystals differ greatly. Therefore, for a realistic assessment of the material behavior, it is important to measure the crystals as close as possible to the actual process conditions. To load the crystals in a saturated sediment, the ring shear tester (RST-01.pc, Dr. Dietmar Schulze) is used. This device is common in the field of bulk mechanics to characterize the flow properties of dry powders. The bulk material is placed in a shear cell. The shear cell lid with attached drivers is placed on the bulk material and hooked onto a weight. The normal stress of the system is determined by the applied weight. For shearing, the shear cell rotates, but the shear cell lid is connected and fixed to bending beams via tie rods. The shear stress can, therefore, be measured at the bending beams.

Modifications to the shear cell are necessary for the measurement of moist sediments. A detailed explanation of the modified shear cell can be found in Hammerich et al. [16]. Therefore, the modifications are only roughly outlined in the following. When moist sediments are loaded, compaction results in the displacement of fluid, which must escape from the system. In contrast, when the sediment is stretched back, it must be ensured that no desaturation occurs.

The structural implementation of the ring-shaped modified shear cell is shown as a sectional view in Figure 1. The shear cell lid consists of two parts, which are sealed against each other by Teflon rings. To allow liquid to escape, but at the same time retain the particles, filter media with a support structure are installed on the top and bottom of the shear cell, shown in green in Figure 1. The drivers and the bottom plate of the shear cell are visualized in gray. On the bottom of the shear cell, below the filter medium, a drainage channel is located, which allows the displaced fluid to escape. The L-shaped profile ensures that the drainage channel is always filled with liquid. Thus, the sediment does not desaturate in the event of back expansion. For the same purpose, there is a riser tube for the displaced liquid on the shear cell lid.

Due to the additional Teflon seals and the slightly different design, the measured values for normal and shear stress cannot be determined directly. A correction for the friction contributions of the seals is required. For this purpose, Hammerich et al. [16] developed a variant of the shear cell with strain gauges for load measurement and determined correction functions for the normal and shear stress. These functions can be found in [16]. The correction functions depend on the seal set used and, therefore, must be recalibrated when replacing the seals.

An experiment with the ring shear tester and the modified shear cell is divided into the following phases:

1.

sample preparation;

2.

shear cell assembly;

3.

shear cell preparation;

4.

shear test.

Sample preparation consists of preparing isometric lysozyme crystals via displacement crystallization. To provide a sufficient amount of crystallizate, and to compensate for minor variations between the different batches, three individual crystallization batches have to be prepared and mixed. The crystals settle overnight. The following day, the supernatant can be decanted. This increases the concentration of crystallizate when the sediment is resuspended and the higher solids volume fraction prevents segregation due to zone sedimentation.

When assembling the shear cell, the filter medium (Trakedge $0.2$ $\mathsf{\mu }$$\mathrm{m}$, Sabeu GmbH & Co. KG, Northeim, Germany) the support structures, and the base plate have to be installed in the bottom part of the shear cell. The shear cell bottom is placed into a customized centrifuge insert for the beaker centrifuge (ZK 630, Berthold Hermle AG, Gosheim, Germany). This insert allows the sediment to be built up by centrifugation directly in the shear cell. Suspension is added to the beaker, so that the processing chamber of the shear cell bottom is slightly overfilled. The sample is centrifuged at a speed of 1500 ${\min }^{-1}$ for 10 $\min$. This corresponds to a maximum relative centrifugal acceleration of $C=500$. Due to the comparably low centrifugal acceleration, the normal loading of the particulate network is low and a change in PSD due to centrifugation can be avoided. After removal from the centrifuge, the sediment has been built up in the shear cell processing chamber. The supernatant is discarded carefully. The L-shaped drainage channels are filled with supernatant. To ensure a defined sediment level for the different tests, excess sediment is carefully removed using a scraper with a fixed length.

The same filter membrane, support structures, and drivers must also be mounted on the shear cell lid. The shear cell lid consists of two parts and, therefore, requires sealing with Teflon O-rings. The assembled lid is centered and placed on the shear cell with the sediment. By softly pressing on the lid, it is fixed in the correct orientation.

The shear cell preparation takes place next. The assembled shear cell is inserted into the ring shear tester device, the tie rods are installed, and the counterweight is attached to the lid. To finally position the shear cell lid in a defined way, a normal load of 40,180 Pa is applied. This causes the lid to slide into position and displace some fluid from the sediment. The riser tubes are then filled with supernatant. Afterwards, the normal load is removed, and the shear cell is now ready for the actual shear test.

The shear test consists of applying the defined normal stress and then shearing the specimen by rotating the bottom part of the shear cell. The adjustable parameters are the shear velocity, the normal stress, and the shear duration. For the characterization of powders, the default shear velocity is $1.5$ $\mathrm{m}$$\mathrm{m}$ ${\min }^{-1}$. The velocity is varied in the range of 0.48–4.5 $\mathrm{m}$$\mathrm{m}$ ${\min }^{-1}$ for the combined shear and normal loading of the moist protein crystals. In the experiments, the shearing time is varied in such a way that the shearing path remains constant. A schematic plot of the shear stress versus shear duration is shown in Figure 2. After removal of the sheared sediment from the shear cell, samples for measuring the PSD with laser scattering are taken and resuspended in supernatant. Additionaly, samples are cut out of the sediment with a polyimide tube for characterization with micro computed tomography (µCT). To assess the influence of centrifugation and the compaction at shear cell preparation on the PSD, samples of the initial solution and after centrifugation and compaction without shearing in the ring shear apparatus are also analyzed.

3.3. Micro Computed Tomography Analytic

The working principle and sample preparation as well as post processing are explained in detail in Dobler et al. [8]. Thus, the preparation of the samples is only briefly outlined in the following. The polyimide tubes holding the samples of the compressed and sheared sediment are deep-frozen with liquid nitrogen. Afterwards, the pore fluid is removed with lyophilization. The removal of pore fluid ensures better contrast between particles and the surrounding air. For the measurement in the µCT (Zeiss Xradia Versa 520, Carl Zeiss Microscopy GmbH, Oberkochen, Germany), the sample tube has to be glued onto a dress pin and mounted on a sample holder. At an energy of 50 $\mathrm{W}$, 2201 projections (X-ray images) are taken from the sample at different rotation angles. These projections are reconstructed to a 3D 16 grayscale image stack. The resulting voxel size is about 400 $\mathrm{n}$$\mathrm{m}$.

4. Results and Discussion

The shear stress applied in the shear cell has a gradient and, thus, varies in the sample. Directly at the shear cell lid, between the drivers protruding into the sample, the shear stress is zero. Below the drivers, the highest load occurs, which then decreases towards the bottom of the shear cell. This also results in differences with regard to the comminution that occurs. No comminution takes place directly between the drivers of the lid.

The resulting shear zones are also visible in µCT images of the loaded sediment. Figure 3 shows an image of the top of the sediment after shearing with a normal stress of 88,396 Pa. No comminution, but only compression, takes place in the uppermost layer of the sediment (green). This is the area between the approximately 2 $\mathrm{m}$$\mathrm{m}$ long drivers, which protrude into the sample. When disassembling the shear cell, a small amount of the sediment sticks to the shear cell lid. Thus, the height of the undamaged crystal layer is approximately 600 $\mathsf{\mu }$$\mathrm{m}$. The impression of these drivers in the sediment are also visible on the top of the µCT images in Figure 4. The particles in the area between the grooves of the top layer in Figure 4 experience no shear force. In Figure 3, the sharply delineated, red-colored layer directly below has the highest shear force. The resulting comminution of the crystals is so strong, that the crystal structure can no longer be visualized with the µCT. The particle sizes and the porosity is too low for the CT scan resolution. This is shown by the fact that practically no crystal edges can be seen.

Comminution at the bottom of the shear cell and at the very top between the drivers is much less pronounced than at the top, directly below the drivers, of the saturated sediment. This fact is also confirmed by µCT scans of a model sediment in the initial unloaded and sheared condition in a miniaturized shear cell. The visualization of these scans is shown in Figure 4. The particles colored in green are a model system with lower density, which therefore have a different gray value in the tomography. Thus, the initial and final position of these particles can be marked. The grooves seen on the top of the sediment are from the drivers. To better visualize the green particles, the other gray material in the front area is shown faded. In the initial state on the left side of Figure 4, the green tracer particles are present in a vertical stripe in the sediment. After a shear path of about 45 ${}^{\circ }$, the distribution of the tracer particles shown on the right is obtained. A large part of the tracer particles remains unsheared and stays together in a strip. In the upper region near the lid, however, there is a clear distribution of the tracer material along the shear path. In this area, the particles experience high shear stress, which, in the case of mechanically sensitive materials, also causes comminution. The distribution of the particles also explains why not all large particles are crushed. In the lower area of the sediment and at the top between the drivers, basically no comminution takes place.

Figure 5 shows the PSD of the unloaded suspension and of two layers of the sediment after shearing. The comminution of the sheared samples compared to the unloaded initial suspension can be seen. Furthermore, it can be seen from Figure 5, that the PSD of the top layer of the bulk has a higher fines content than the lower layer and the total sediment. The sheared total curve in Figure 5 is a laser diffraction measurement of a resuspendend sample of the sediment with complete sediment height. This curve, therefore, represents all layers in the sample. The comminution is particularly pronounced for the $x_{10}$ diameter, which is only between 10–15% of the unloaded suspension. The $x_{90}$ diameter decreases much less and is in the range between 75–85%. This can be explained by the aforementioned unequal shear stress in the sediment. Large particles remain intact at the bottom of the bulk and at the same time an increase in very small particles is observed. Thus, the PSD broadens.

Various variables influencing comminution are conceivable. In particular, the applied normal stress and the shear velocity probably have an effect on crystal breakage. These two influencing variables are, therefore, considered in more detail in this study. The covered shear path for all experiments remains a constant 15 $\mathrm{m}$$\mathrm{m}$ in order to exclude the influence of different shear paths. For the evaluation of the changes of the PSD, the comparison between the respective unloaded suspension and a resuspended sample of the total sediment after loading is used. The PSD is obtained with laser diffraction.

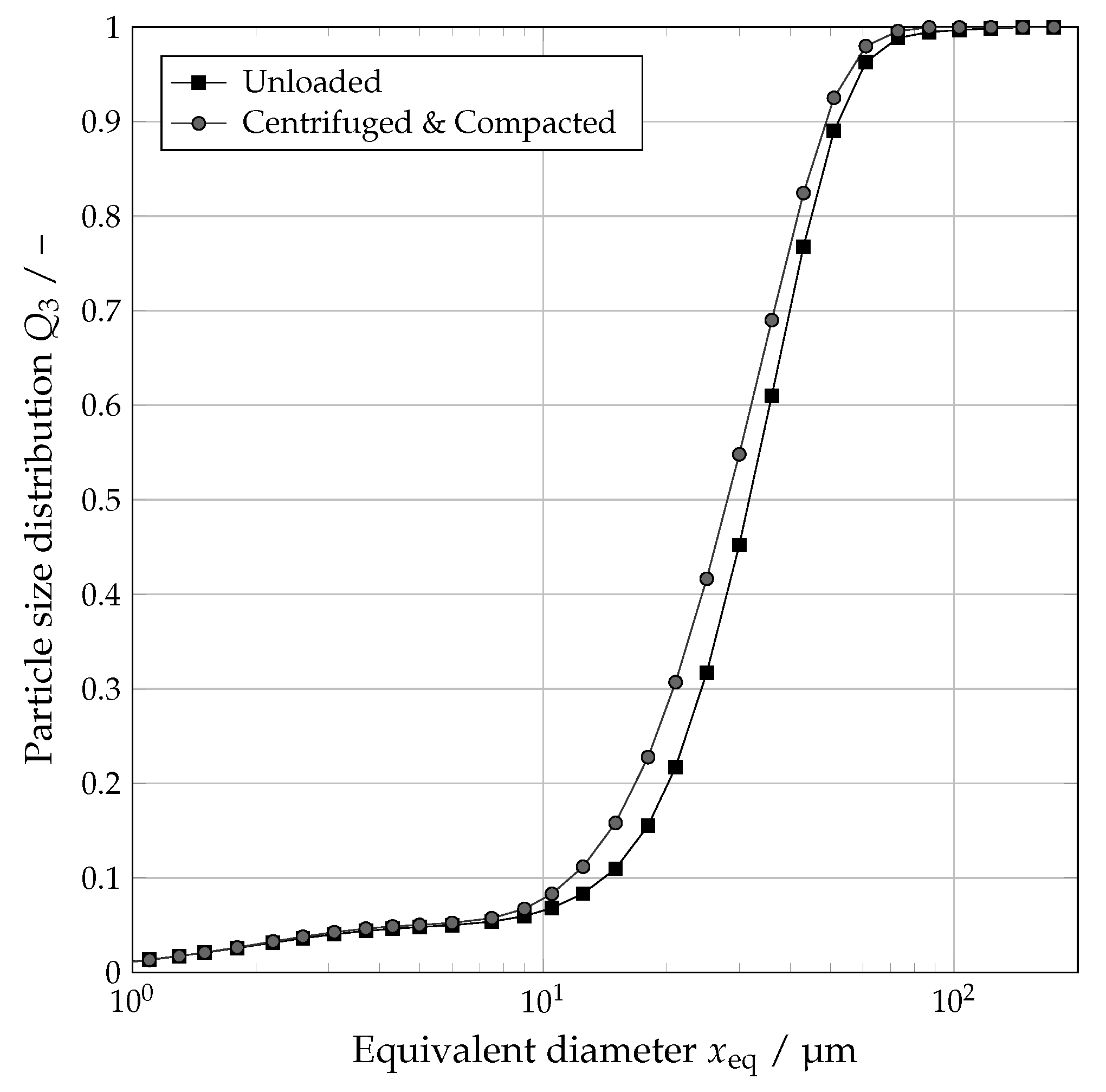
4.1. Influence of Centrifugation and Compaction

It is conceivable that centrifugation and compaction for sample preparation in the ring shear tester also causes particle size reduction. To assess this influence, the PSDs of unloaded and centrifuged and compacted samples are shown in Figure 6. Compacted in this context means an applied normal load of the sediment in the ring shear tester with ${\sigma }_{\mathrm{n}}$ = 40,180 Pa, without shear loading and after centrifugation.

The resulting PSDs can be seen in Figure 6. The crystals in Figure 6 are centrifuged at a speed of 1500 ${\min }^{-1}$ and subsequently compacted in the ring shear tester. Afterwards, the sediment has been resuspended in supernatant for the determination of the PSD with laser diffraction. They show a slight shift towards smaller particle sizes. However, the whole PSD is shifted and no increase in fines is observed. The shift is so weakly pronounced that comminution is negligible compared to the sheared samples. This slight change in PSD can also be explained by minor temperature variation during measurement and is not necessarily due to centrifugation. Hence, the preparation of the shear cell and the subsequent sampling, does not affect the PSD significantly. In summary, therefore, neither the load in the centrifuge nor the additional normal load in the shear cell causes significant particle size reduction or crystal breakage.

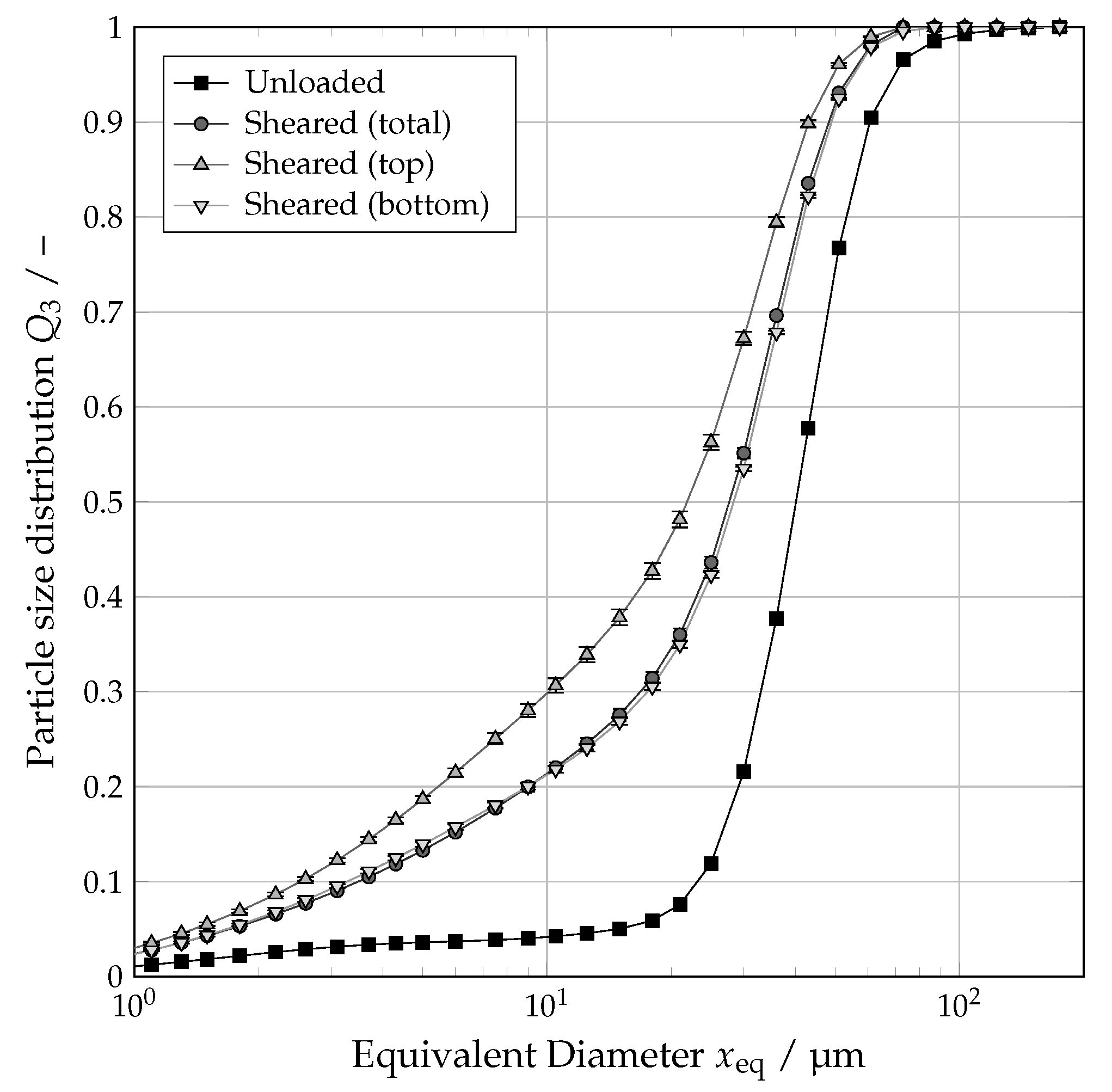
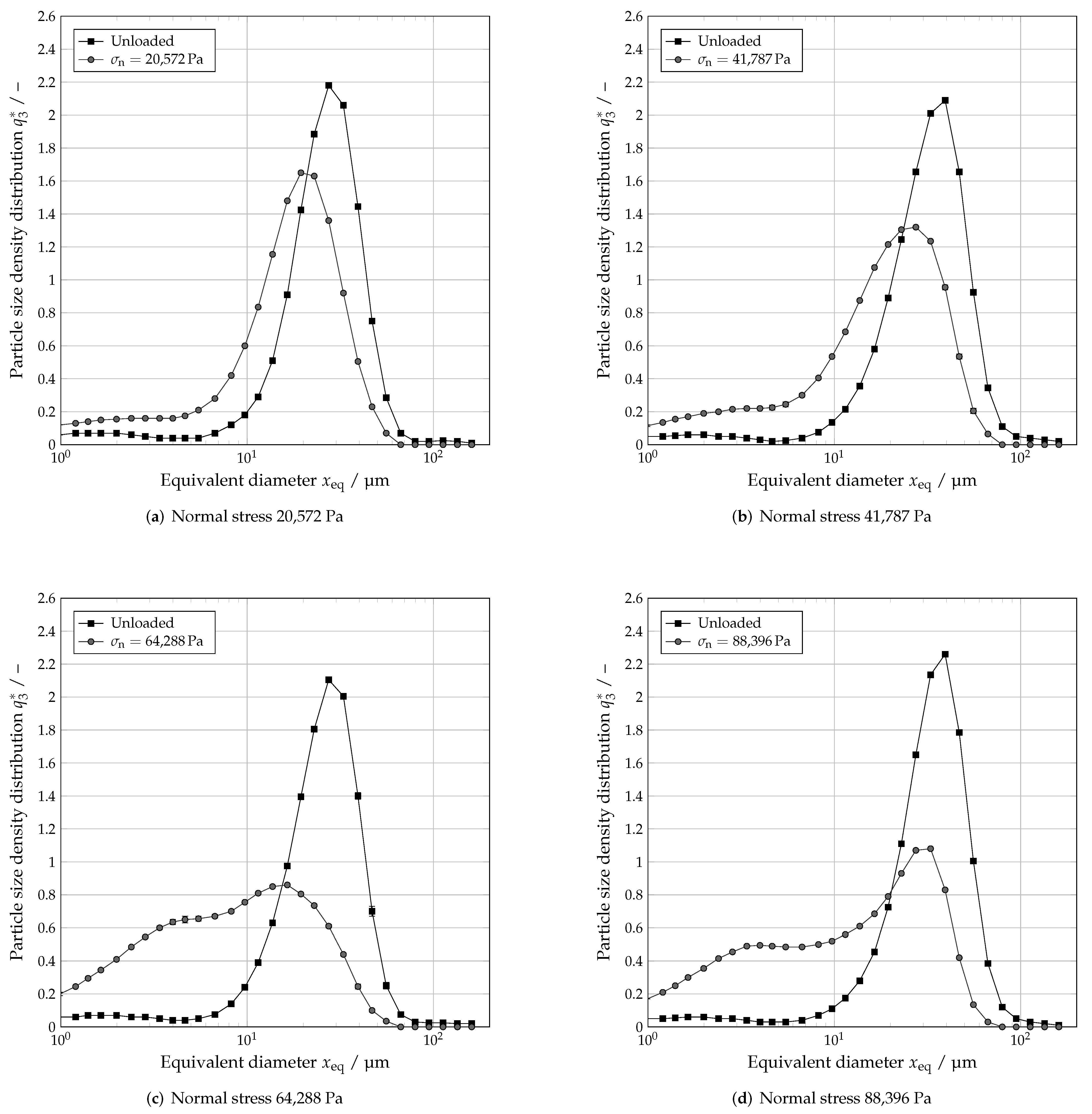
4.2. Influence of Normal Stress

Shear tests at a constant shear velocity of $1.5$ $\mathrm{m}$$\mathrm{m}$ ${\min }^{-1}$ and varying normal stresses are used to evaluate the influence of the applied normal stress on comminution. The transformed particle size density distribution $q_3^{*}$ for varying normal stress is shown to visualize the comminution. Since this is a biological system that has natural fluctuations during crystallization, the initial distribution is also displayed for each normal stress.

The resulting PSDs are shown in Figure 7. Already at a low normal load of 20,572 Pa a size reduction, as well as a shift of the particle sizes, can be observed and the distribution width increases by about 40%. The $x_{90}$ and $x_{50}$ diameters decrease significantly at this low load to 78 and 68% compared to the unloaded particle sizes. The most significant decrease is observed for the $x_{10}$ diameter. This diameter is reduced to 30% after loading.

At a higher normal stress of 41,787 Pa, the same effects occur more strongly. The distribution width increases by 62% compared to the unloaded specimen. The characteristic diameters $x_{90}$ and $x_{50}$ are now only 74 and 58% of the initial sizes, respectively. The $x_{10}$ diameter also decreases significantly to 19%. The density distribution shows an increase in fines and a reduction of large particles. Compared to the normal stress of 20,572 Pa, the comminution at 41,787 Pa is more pronounced and the PSD is significantly wider. In the density distribution, this fact is shown by the reduction and broadening of the peak.

A further increase of the normal stress to 64,288 Pa leads to an obvious change in the particle size density distribution. The peak, still clearly visible in the unloaded sample, has almost completely disappeared. A strong increase of very small particles and an intense broadening of the distribution can be observed. The amount of larger particles decreases somewhat, but is still present in the shear-loaded sample. The distribution width is 147% higher compared to the unloaded sample. The $x_{90}$ diameter decreases to 63%. The median diameter also decreases significantly and is 32% of the initial diameter. This is a much greater decrease compared to the lower normal loadings. The $x_{10}$ diameter amounts to 15% of the initial unloaded diameter.

An increase of the normal stress beyond this to 88,396 Pa does not cause any further significant comminution of the particles. The distribution width is broadened with an increase of 136%. This is similar to the previous normal stress. The $x_{90}$ diameter is 68% of the initial diameter. The median and $x_{10}$ diameters are reduced to 38 and 12%, respectively. These values are also similar to the previous normal stress level. There is a clear increase in small particles.

The comparison of the different normal stresses shows a clear influence of the applied stress on the occurring comminution. Low normal stresses result in less comminution. However, even small normal stresses cause a widening of the PSD and a significant decrease of the $x_{10}$ diameter. With an increase of the normal stress, the comminution intensifies and the distribution width increases significantly. The median diameter is strongly reduced. Since the shear load in the sediment has a gradient, large particles are always retained, which is reflected in a less pronounced reduction of the $x_{90}$ diameter. Above a normal stress of 64,288 Pa, an increase in normal stress does not result in additional comminution. The decrease in characteristic diameter, increase in distribution width, and comminution are similar. This indicates an upper limit above which the normal stress loses its influence. The comminution is probably not only due to particle breakage but also to abrasion. Abrasion is caused by the friction of the crystals against each other, which, for example, abrades the corners of the crystals.

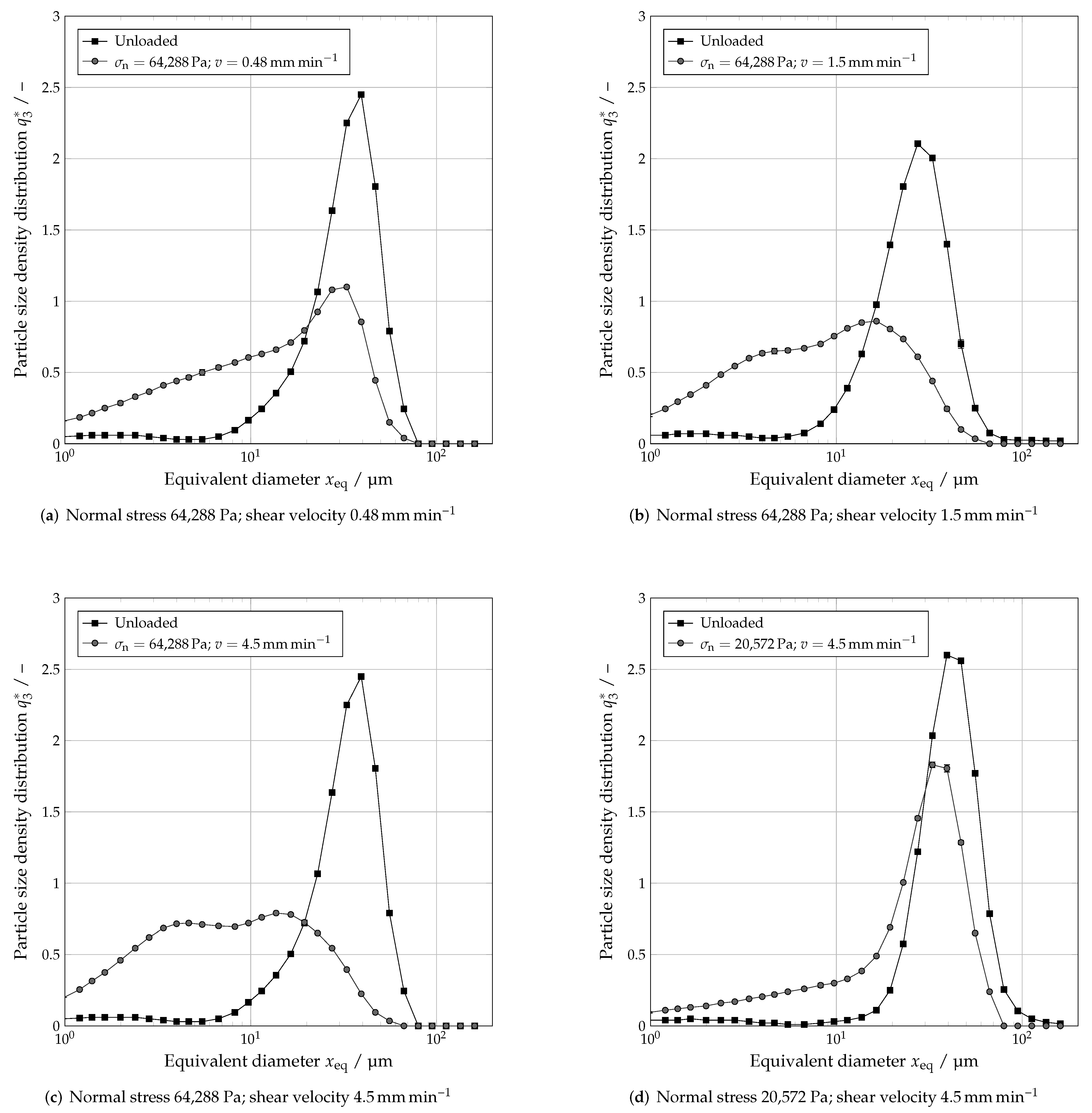
4.3. Influence of Shear Velocity

In addition to the normal stress, an influence of the shear velocity on the comminution is also conceivable. In order to investigate this influence, sediments of isometric lysozyme crystals are loaded with the three shear velocities 0.48, 1.5 and 4.5$\mathrm{m}$$\mathrm{m}$ ${\min }^{-1}$ at a constant normal stress of 64,288 Pa and a constant shear path. The particle size density distributions of the unloaded and sheared specimens with different shear velocities are shown in Figure 8.

Even at the lowest shear velocity in Figure 8, top left, there is a strong comminution of the particle collective. The distribution width increases by 138% and the $x_{90}$ and median diameters decrease to 75 and 41%, respectively. The $x_{10}$ diameter reduces significantly to 15% compared to the unloaded suspension. Increasing the shear velocity to $1.5$ $\mathrm{m}$$\mathrm{m}$ ${\min }^{-1}$ shows higher comminution for the $x_{90}$ and $x_{50}$ diameters and an increase in the distribution width. The respective values are analogous to Figure 7 at the corresponding normal load of 64,288 Pa. A further increase of the shear velocity to $4.5$ $\mathrm{m}$$\mathrm{m}$ ${\mathrm{s}}^{-1}$ leads to a very similar particle size density distribution of the sheared crystals compared to the previous shear velocity. The reduction of the characteristic median and $x_{90}$ diameter is more pronounced by a few percentage points.

The lower right plot in Figure 8 shows the particle size density distribution of a sediment after shearing at a speed of $4.5$ $\mathrm{m}$$\mathrm{m}$ ${\min }^{-1}$ and a normal stress of ${\sigma }_n$ = 20,572 Pa. Here, it can be seen that the normal stress has a stronger influence on the comminution than the shear velocity. At a high shear velocity and low normal stress, the comminution is less. The $x_{90}$ diameter is still 80% of the initial particle size. The median diameter decreases to 69% and the $x_{10}$ diameter reduces significantly to 15%. The reduction in the median and $x_{90}$ diameters thus corresponds almost exactly to the values at a normal load of 20,572 Pa and a shear velocity of $1.5$ $\mathrm{m}$$\mathrm{m}$ ${\min }^{-1}$ from Figure 7. However, the reduction in $x_{10}$ diameter is more pronounced at the higher shear velocity.

5. Conclusions

In summary, it can be stated that crystal breakage always occurs in the case of combined normal and shear loading of lysozyme crystals. This is also true for normal stresses, for which no reduction in particle sizes can be detected without shear loading. In the case of combined stress, an increase in normal stress until a value of 64,288 Pa leads to significantly higher comminution. The shear velocity, on the other hand, has a much smaller effect on comminution and is a negligible influence compared to the normal stress. The high increase in fines can be explained by crystal abrasion in addition to crystal breakage. A higher normal stress increases the friction in the sediment, which is why crystal corners and edges rub off. This contributes to the strong increase in fines.

Superposition of compressive and shear stress occurs in many technical apparatuses and must, therefore, be minimized in order to avoid undesirable comminution of protein crystals. Examples of an apparatus with superimposed stress include pumps, tubular centrifuges, decanter centrifuges, and cross-flow filters. With high crystal concentrations, such as those that occur during water evaporation crystallization, the risk of particle abrasion or particle collision is increased.