Characterization of Tungstates of the Type Hf1−xLnxW2O8−x/2 (Ln = Eu, Tm, Lu) Synthesized Using the Hydrothermal Method
Abstract
:1. Introduction
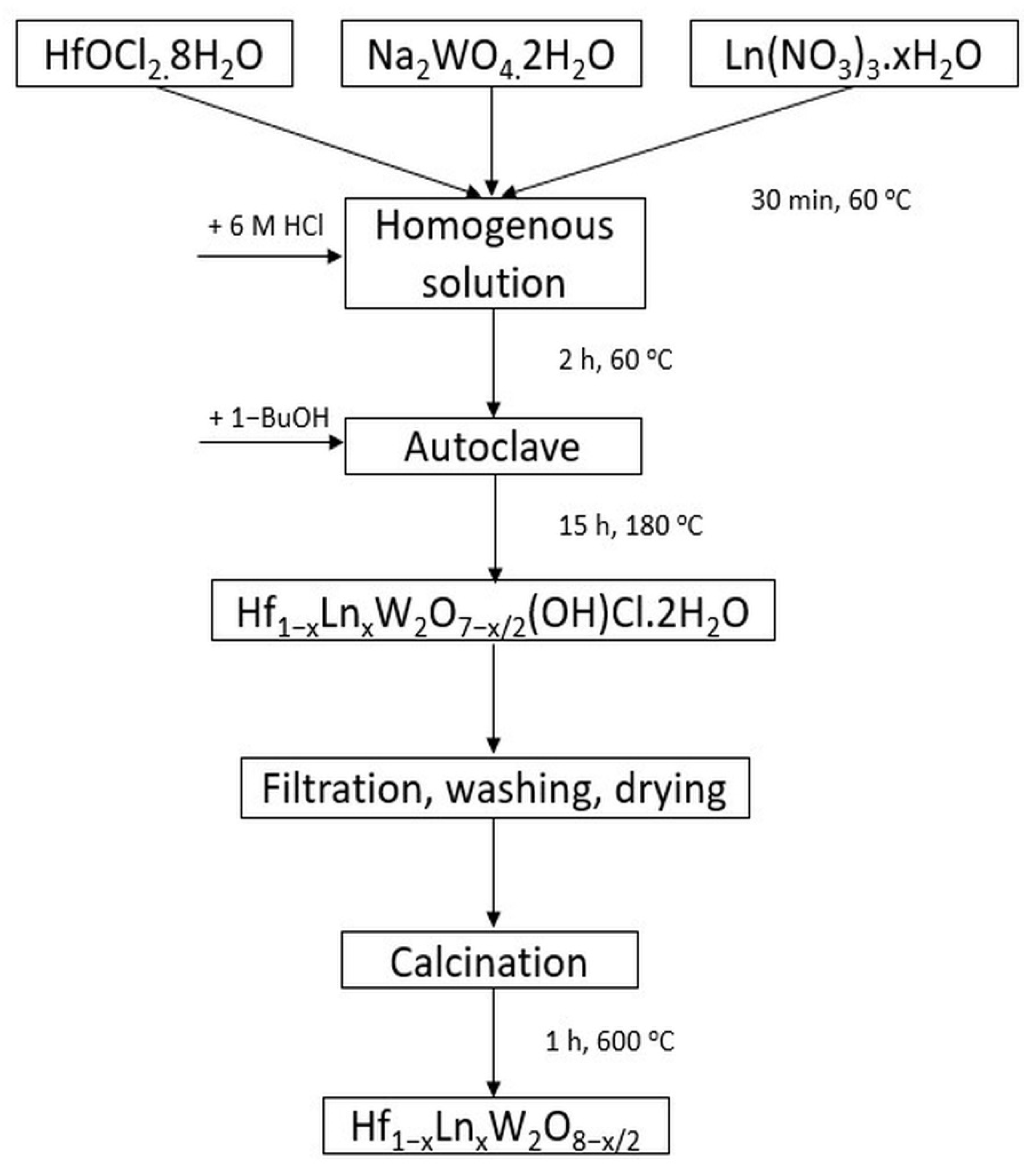
2. Materials and Methods
3. Results
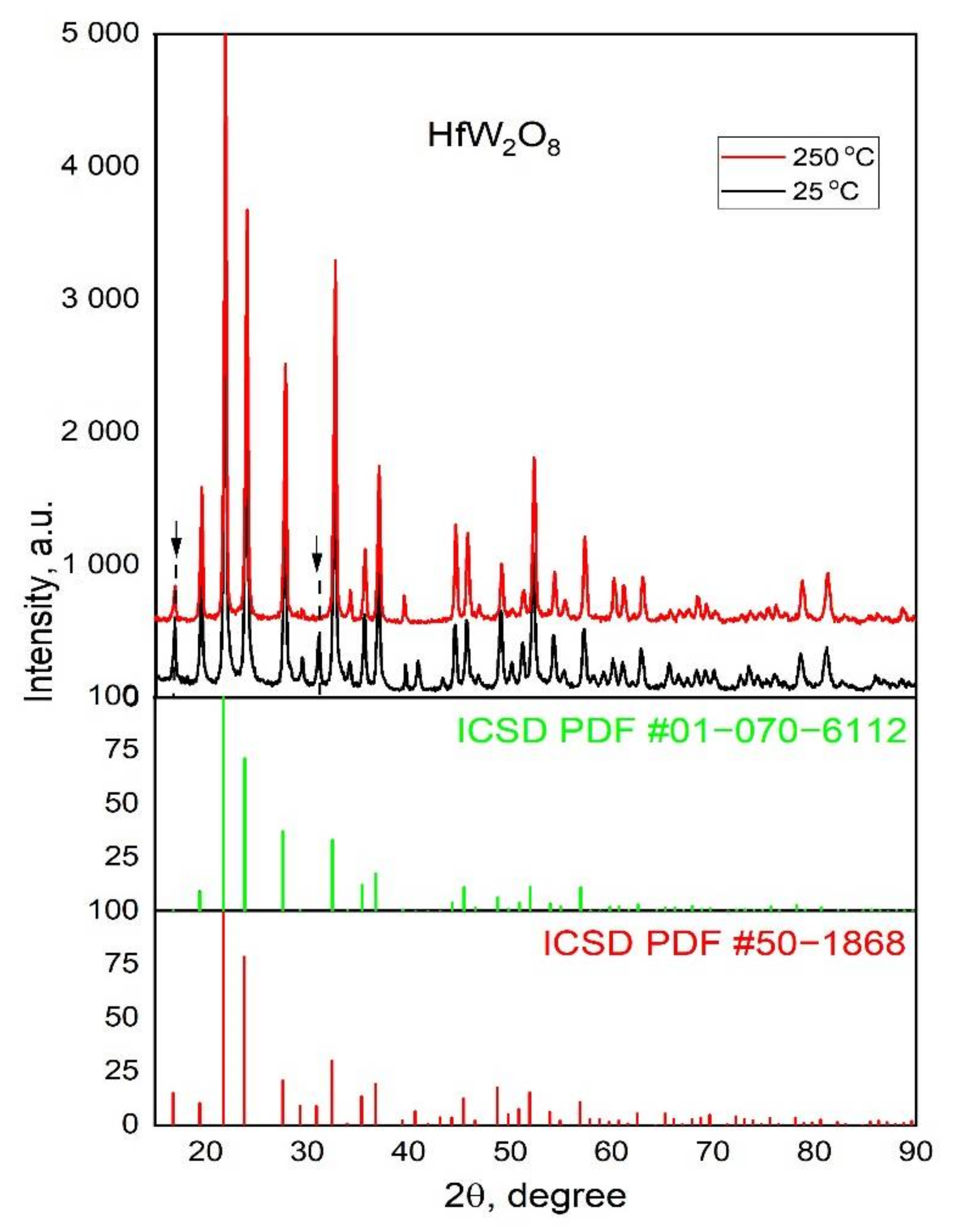
3.1. XRD of α-HfW2O8 and β-HfW2O8
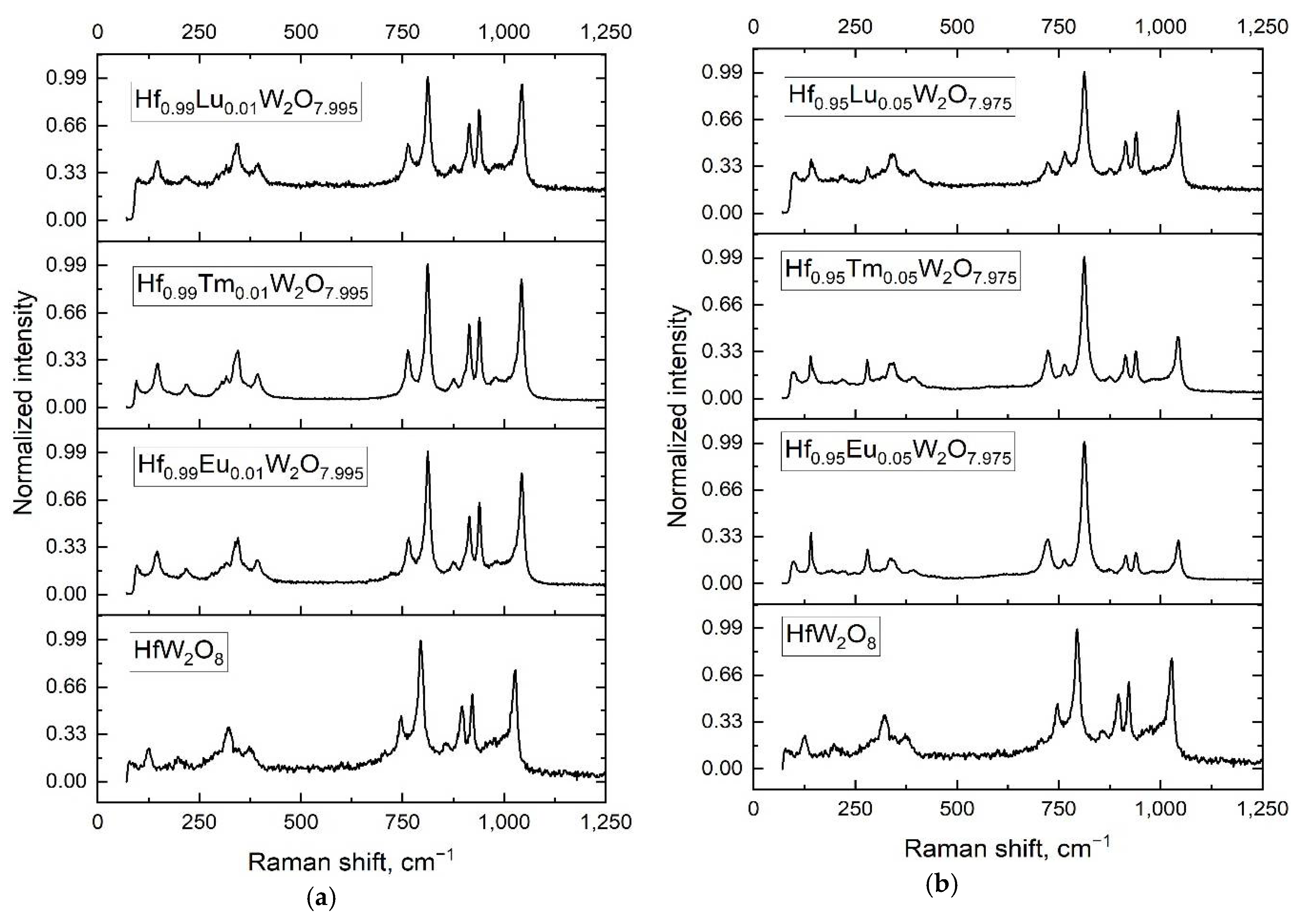
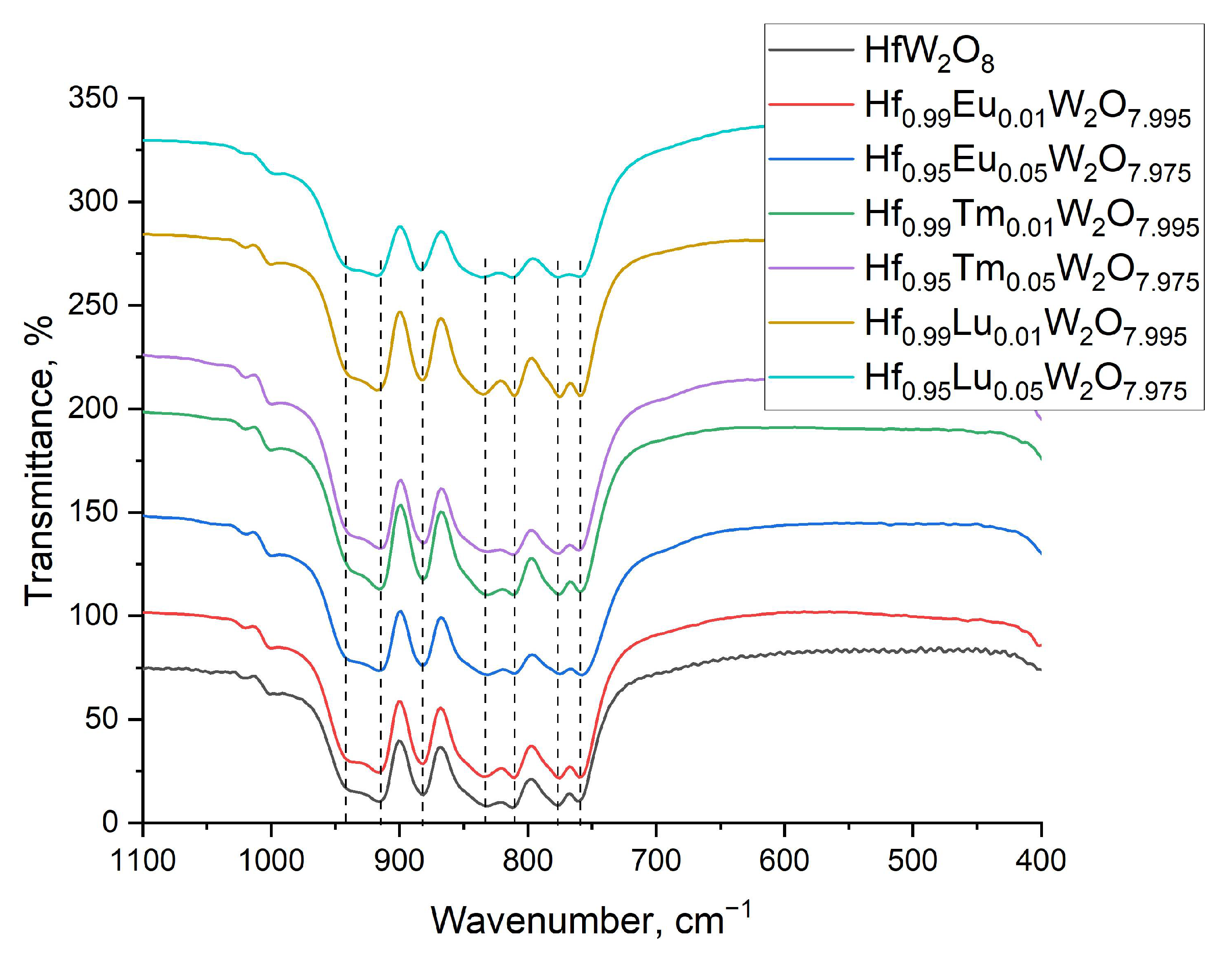
3.2. Characterization of the Solid Solutions Hf1−xLnxW2O8−x/2 by XRD; Raman and IR Spectroscopy—Homogeneity of the Samples; Influence of Ln3+
3.3. The Morphology of the Samples by Electron Microscopy, SEM, and TEM
3.4. Phase Transition; Reversibility; and the Coefficients of Thermal Expansion in the Pure HfW2O8 and in the Solid Solutions Hf1−xLnxW2O8−x/2 (x = 0.01 and 0.05)
3.4.1. The Phase Transition α-HfW2O8 to β-HfW2O8 and its Reversibility
3.4.2. Unit Cell Parameters and Coefficients of Thermal Expansion (CTE)
3.4.3. Order-to-Disorder Phase Transition for Hf1−xLnxW2O8−x/2 (x = 0.01; 0.05) and the Role of Ln3+
3.5. UV–Vis Absorption of the Solid Solutions and the Energy of the Band Gaps
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Takenaka, K. Negative thermal expansion materials: Technological key for control of thermal expansion. Sci. Technol. Adv. Mater. 2012, 13, 013001. [Google Scholar] [CrossRef] [PubMed]
- Lind, C. Two decades of negative thermal expansion research: Where do we stand? Materials 2012, 5, 1125–1154. [Google Scholar] [CrossRef] [PubMed]
- Sanson, A.; Chen, J. Towards the control of thermal expansion: From 1996 to today. Front. Chem. 2019, 7, 284. [Google Scholar] [CrossRef] [PubMed]
- Evans, D.L.; Fischer, G.R.; Geiger, J.E.; Martin, F.W. Thermal expansions and chemical modifications of cordierite. J. Am. Ceram. Soc. 1980, 63, 629–634. [Google Scholar] [CrossRef]
- Phillips, A.E.; Goodwin, A.L.; Halder, G.J.; Southon, P.D.; Kepert, C.J. Nanoporosity and exceptional negative thermal expansion in single-network cadmium cyanide. Angew. Chem. 2008, 120, 1418–1421. [Google Scholar] [CrossRef]
- Azuma, M.; Chen, W.-T.; Seki, H.; Czapski, M.; Smirnova, O.; Oka, K.; Mizumaki, M.; Watanuki, T.; Ishimatsu, N.; Kawamura, N.; et al. Colossal negative thermal expansion in BiNiO3 induced by intermetallic charge transfer. Nat. Commun. 2011, 2, 347. [Google Scholar] [CrossRef] [Green Version]
- Shi, N.; Song, Y.; Xing, X.; Chen, J. Negative thermal expansion in framework structure materials. Coord. Chem. Rev. 2021, 449, 214204. [Google Scholar] [CrossRef]
- Evans, J.S.; Mary, T.A.; Vogt, T.; Subramanian, M.A.; Sleight, A.W. Negative thermal expansion in ZrW2O8 and HfW2O8. Chem. Mater. 1996, 8, 2809–2823. [Google Scholar] [CrossRef]
- Evans, J.S.O.; David, W.I.F.; Sleight, A.W. Structural investigation of the negative thermal expansion material ZrW2O8. Acta Cryst. 1999, B55, 333–340. [Google Scholar] [CrossRef]
- Mary, T.A.; Evans, J.S.O.; Vogt, T.; Sleight, A.W. Negative thermal expansion from 0.3 to 1050 Kelvin in ZrW2O8. Science 1996, 272, 90–92. [Google Scholar] [CrossRef] [Green Version]
- Gallington, L.C.; Chapman, K.W.; Morelock, C.R.; Chupas, P.J.; Wilkinson, A.P. Dramatic softening of the negative thermal expansion material HfW2O8 upon heating through its WO4 orientational order-disorder phase transition. J. Appl. Phys. 2014, 115, 053512. [Google Scholar] [CrossRef]
- Yamamura, Y.; Nakajima, N.; Tsuji, T. Calorimetric and X-ray diffraction studies of a-to-b structural phase transitions in HfW2O8 and ZrW2O8. Phys. Rev. B 2001, 64, 184109. [Google Scholar] [CrossRef]
- Yamamura, Y.; Nakajima, N.; Tsuji, T.; Koyano, M.; Iwasa, Y.; Saito, K.; Sorai, M. Heat capacity and Gruneisen function of negative thermal expansion compound HfW2O8. Solid State Commun. 2002, 121, 213–217. [Google Scholar] [CrossRef]
- Encheva, E.D.; Nedyalkov, M.K.; Tsvetkov, M.P.; Milanova, M.M. The influence of the modification of zirconium tungstate with Eu(III) on the α→β phase transition temperature and optical band gap. Bulg. Chem. Comm. Spec. Issue F 2018, 50, 143–149. [Google Scholar]
- De Meyer, C.; Bouree, F.; Evans, J.S.O.; de Buysser, K.; Bruneel, E.; van Driessche, I.; Hoste, S. Structure and phase transition of Sn-substituted Zr1−xSnxW2O8. J. Mater. Chem. 2004, 14, 2988–2994. [Google Scholar] [CrossRef]
- De Buysser, K.; van Driessche, I.; Putte, B.V.; Vanhee, P.; Schaubroeck, J.; Hoste, S. Study of negative thermal expansion and shift in phase transition temperature in Ti4+- and Sn4+-substituted ZrW2O8 materials. Inorg. Chem. 2008, 47, 736–741. [Google Scholar] [CrossRef] [Green Version]
- Yamamura, Y.; Masago, K.; Kato, M.; Tsuji, T. Comprehensive interpretation of a substitution effect on an order-disorder phase transition in A1−xMxW2O8−y (A = Zr, Hf; M = trivalent cations) and other ZrW2O8-based solid solutions. J. Phys. Chem. B 2007, 111, 10118–10122. [Google Scholar] [CrossRef] [PubMed]
- Yamamura, Y.; Nakajima, N.; Tsuji, T.; Kojima, A.; Kuroiwa, Y.; Sawada, A.; Aoyagi, S.; Kasatani, H. Drastic lowering of the order-disorder phase transition temperatures in Zr1−xMxW2O8−y (M = Sc, Y, In) solid solutions. Phys. Rev. B 2004, 70, 104107. [Google Scholar] [CrossRef]
- Nakajima, N.; Yamamura, Y.; Tsuji, T. Synthesis and physical properties of negative thermal expansion materials Zr1−xMxW2O8−y (M = Sc, In, Y) substituted for Zr(IV) sites by M(III) ions. Solid State Commun. 2003, 128, 193–196. [Google Scholar] [CrossRef]
- Li, H.-H.; Han, J.-S.; Ma, H.; Huang, L.; Zhao, X.-H. Zr1−xLnxW2O8−x/2 (Ln = Eu, Er, Yb): Solid solutions of negative thermal expansion-synthesis, characterization and limited solid solubility. J. Solid State Chem. 2007, 180, 852–857. [Google Scholar] [CrossRef]
- Rodriguez-Carvajal, J. Recent developments of the program fullprof. In Newsletter in Commission on Powder Diffraction; IUCr: Chester, UK, 2001; Volume 26, pp. 12–19. [Google Scholar]
- Kameswari, U.; Sleight, A.W.; Evans, J.S. Rapid synthesis of ZrW2O8 and related phases, and structure refinement of ZrWMoO8. Int. J. Inorg. Mater. 2000, 2, 333–337. [Google Scholar] [CrossRef]
- Thummavichai, K.; Wang, N.; Xu, F.; Rance, G.; Xia, Y.; Zhu, Y. In situ investigations of the phase change behavior of tungsten oxide nanostructures. R. Soc. Open Sci. 2018, 5, 171932. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yamamura, Y.; Nakajima, N.; Tsuji, T.; Koyano, M.; Iwasa, Y.; Katayama, S.; Saito, K.; Sorai, M. Low-temperature heat capacities and Raman spectra of negative thermal expansion compounds ZrW2O8 and HfW2O8. Phys. Rev. B 2002, 66, 014301. [Google Scholar] [CrossRef]
- Jorgensen, J.D.; Hu, Z.; Shor, S.; Sleight, A.W.; Evans, J.S.O. Pressure-induced cubic-to-orthorhombic phase transformation in the negative thermal expansion material HfW2O8. J. Appl. Phys. 2001, 89, 3184–3188. [Google Scholar] [CrossRef]
- Chen, B.; Muthu, D.V.S.; Liu, Z.X.; Sleight, A.W.; Kruger, M.B. High-pressure Raman and infrared study of HfW2O8. Phys. Rev. B 2001, 64, 214111. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst. 1976, A32, 751–767. [Google Scholar] [CrossRef]
- Ross-Medgaarden, E.I.; Wachs, E.I. Structural determination of bulk and surface tungsten oxides with UV-vis diffuse reflectance spectroscopy and Raman spectroscopy. J. Phys. Chem. C 2007, 111, 15089–15099. [Google Scholar] [CrossRef]
- Tauc, J.; Grigorovici, R.; Vancu, A. Optical properties and electronic structure of amorphous germanium. Phys. Status Solidi B 1966, 15, 627–637. [Google Scholar] [CrossRef]
- Ouyang, L.; Xu, Y.-N.; Ching, W.Y. Electronic structure of cubic and orthorhombic phases of ZrW2O8. Phys. Rev. B 2002, 65, 113110. [Google Scholar] [CrossRef]
- Church, J.S.; Cant, N.W.; Trimm, D.L. Stabilisation of aluminas by rare earth and alkaline earth ions. Appl. Catal. 1993, 101, 105. [Google Scholar] [CrossRef]
- Muthu, D.V.S.; Chen, B.; Sleight, A.W.; Wrobel, J.M.; Kruger, M.B. ZrW2O8 and HfW2O8: Band gap shifts under pressure. Solid State Commun. 2002, 122, 25–28. [Google Scholar] [CrossRef]



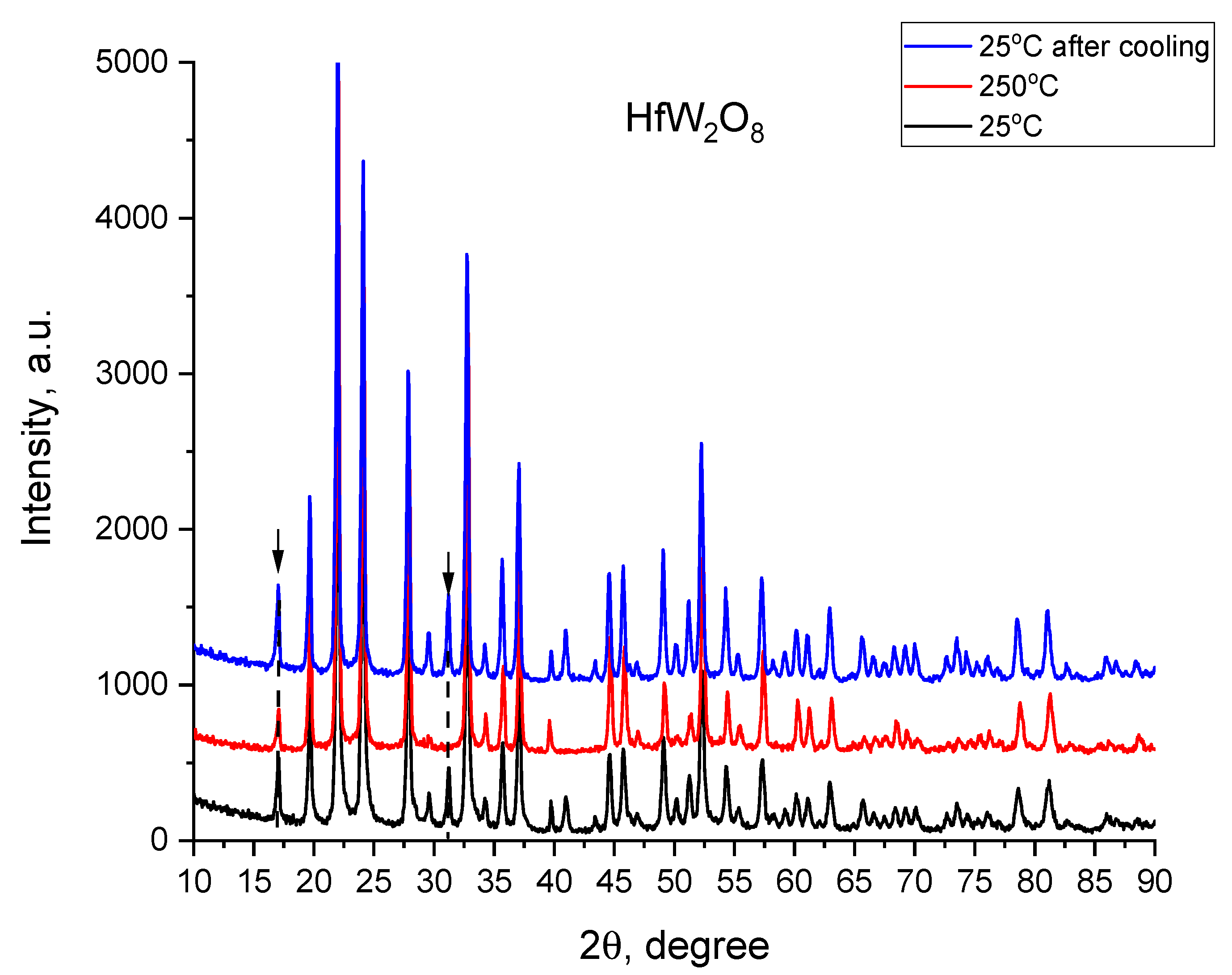

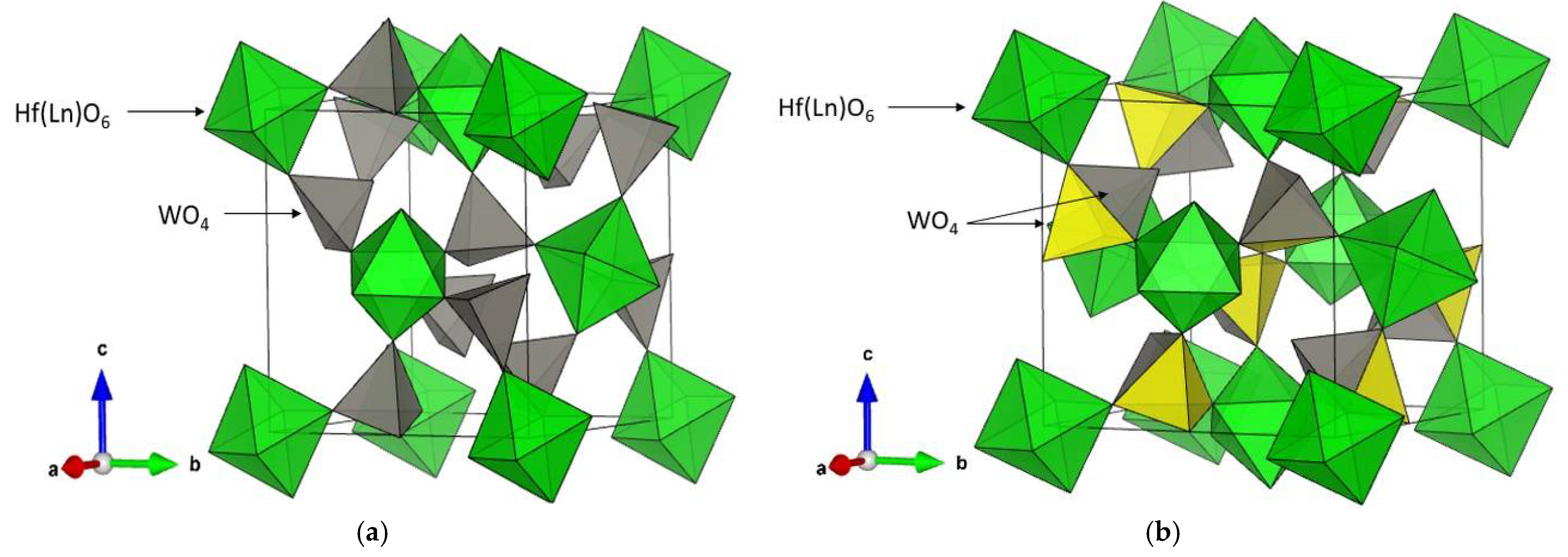
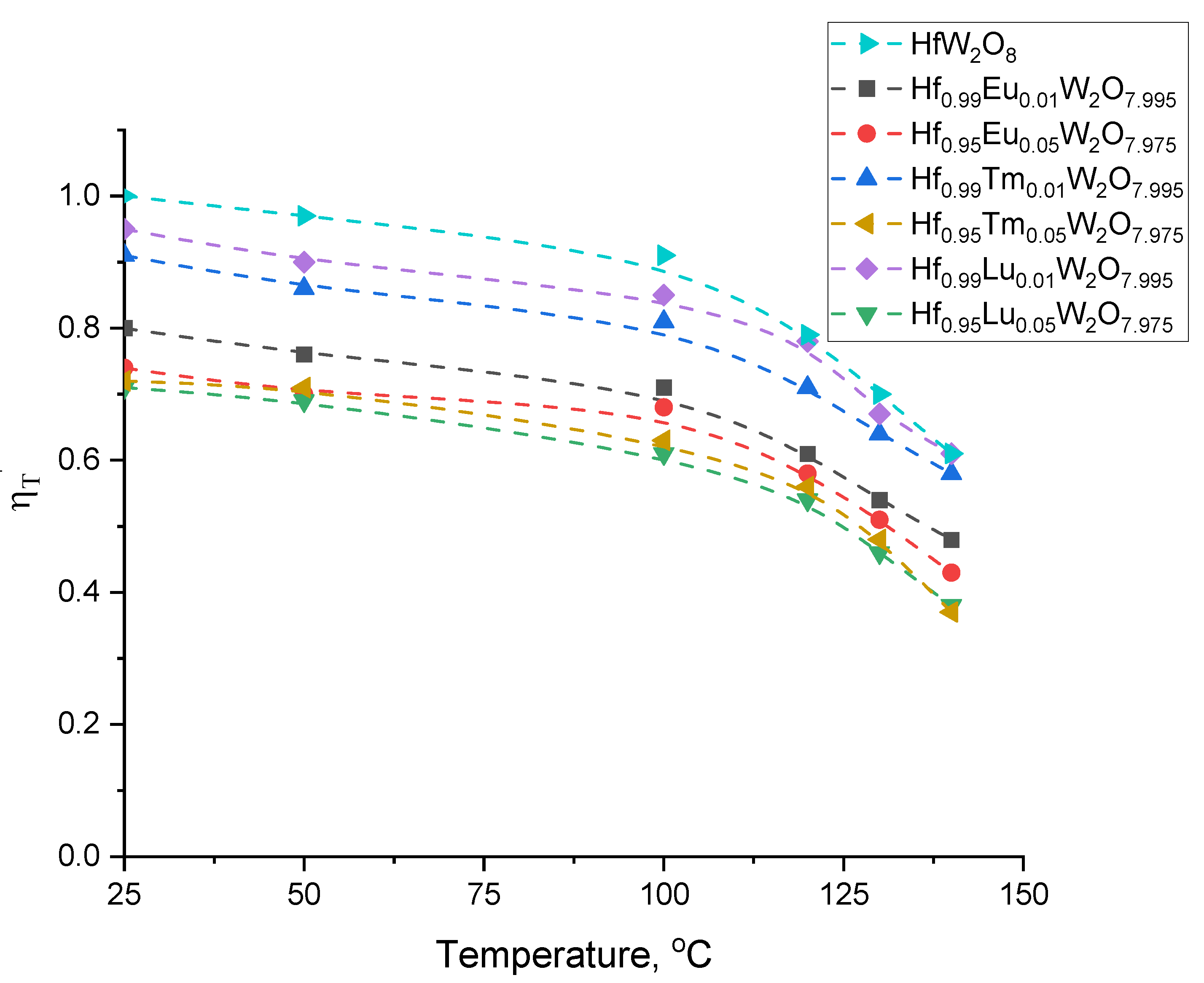
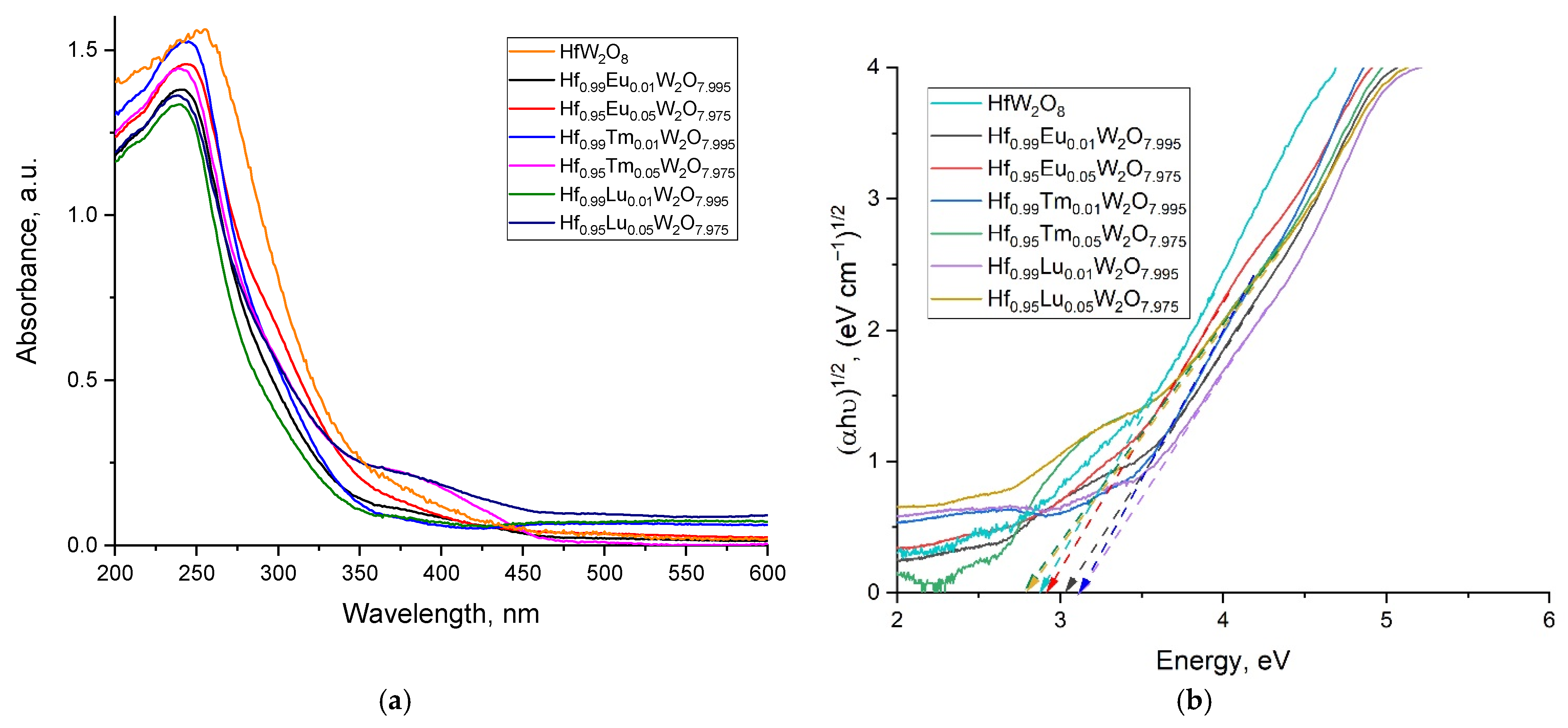
| T °C | HfW2O8 | Hf1−xEuxW2O8−x/2 | Hf1−xTmxW2O8−x/2 | Hf1−xLuxW2O8−x/2 | ||||
|---|---|---|---|---|---|---|---|---|
| x = 0.01 | x = 0.05 | x = 0.01 | x = 0.05 | x = 0.01 | x = 0.05 | |||
| Unit cell parameters, Å | 25 | 9.1244(2) | 9.1246(3) | 9.1245(1) | 9.1245(1) | 9.1245(1) | 9.1244(1) | 9.1243(1) |
| 100 | 9.1174(1) | 9.1179(1) | 9.1177(1) | 9.1171(1) | 9.1170(1) | 9.1173(1) | 9.1172(1) | |
| 200 | 9.1055(1) | 9.1058(2) | 9.1057(1) | 9.1050(3) | 9.1049(1) | 9.1049(1) | 9.1048(1) | |
| 250 | 9.1050(1) | 9.1051(1) | 9.1053(2) | 9.1044(1) | 9.1046(1) | 9.1044(1) | 9.1045(2) | |
| CTE, ×10−6 K−1 | 25–100 | −10.22 | −9.79 | −9.94 | −10.81 | −10.96 | −10.38 | −10.36 |
| 200–250 | −1.10 | −1.54 | −0.87 | −1.32 | −0.66 | −1.10 | −0.66 | |
| 25–250 | −9.45 | −9.49 | −9.35 | −9.79 | −9.69 | −9.74 | −9.64 | |
| № | Sample | Band Gap Eg, eV |
|---|---|---|
| 1 | α-HfW2O8 | 2.87 |
| 2 | α-ZrW2O8 | 2.84 [31] |
| 3 | Hf0.99Eu0.01W2O7,995 | 3.02 |
| 4 | Hf0.95Eu0.05W2O7.975 | 2.92 |
| 5 | Hf0.99Tm0.01W2O7.995 | 3.10 |
| 6 | Hf0.95Tm0.05W2O7.975 | 2.78 |
| 7 | Hf0.99Lu0.01W2O7.995 | 3.12 |
| 8 | Hf0.95Lu0.05W2O7.975 | 2.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsvetkov, M.; Nedyalkov, M.; Valcheva, E.; Milanova, M. Characterization of Tungstates of the Type Hf1−xLnxW2O8−x/2 (Ln = Eu, Tm, Lu) Synthesized Using the Hydrothermal Method. Crystals 2022, 12, 327. https://doi.org/10.3390/cryst12030327
Tsvetkov M, Nedyalkov M, Valcheva E, Milanova M. Characterization of Tungstates of the Type Hf1−xLnxW2O8−x/2 (Ln = Eu, Tm, Lu) Synthesized Using the Hydrothermal Method. Crystals. 2022; 12(3):327. https://doi.org/10.3390/cryst12030327
Chicago/Turabian StyleTsvetkov, Martin, Martin Nedyalkov, Evgenia Valcheva, and Maria Milanova. 2022. "Characterization of Tungstates of the Type Hf1−xLnxW2O8−x/2 (Ln = Eu, Tm, Lu) Synthesized Using the Hydrothermal Method" Crystals 12, no. 3: 327. https://doi.org/10.3390/cryst12030327
APA StyleTsvetkov, M., Nedyalkov, M., Valcheva, E., & Milanova, M. (2022). Characterization of Tungstates of the Type Hf1−xLnxW2O8−x/2 (Ln = Eu, Tm, Lu) Synthesized Using the Hydrothermal Method. Crystals, 12(3), 327. https://doi.org/10.3390/cryst12030327








