Comparison of Dynamical and Empirical Simulation Methods of Secondary Dendrite Arm Coarsening

Abstract

The physical and mechanical properties of an entirely (wrought alloys) or partly (cast alloys) dendritically solidified alloy strongly depend on the secondary dendrite arm spacing (SDAS). The casting practice and the simulation of solidification need a usable but simple method to calculate the SDAS during and at the end of solidification as a function of the cooling rate. Based on many solidification experiments, a simple equation to calculate the SDAS (empirical method) is known to use the local solidification time, which can be obtained from the measured cooling curves (equiaxed solidification), or can be calculated from the temperature gradient and front velocity (directional solidification). This equation is not usable for calculating the SDAS during solidification. Kirkwood developed a semi-empirical method based on the liquid phase’s diffusion, which contains only one geometric factor that seems constant for different alloys. This equation contains some physical parameters that depend on the temperature, so the equation cannot be integral in closed form. In the present work, first, we show the effect of the curvature of the solid/liquid interface on the equilibrium concentrations and then the different processes of SDA coarsening. In our earlier paper, we demonstrated that using the empirical method, the final SDAS can be calculated with acceptable correctness in the case of four unidirectional solidification experiments of Al-7wt%Si alloy. The present work shows that numerically integrated Kirkwood’s equations used the known cooling curve; the SDAS can be calculated at the end and during solidification in good agreement with these experimental results. Compared to the two calculation methods, we stated that the correctness of the methods is similar. Still, the results of the solidification simulation (the microsegregation) will be more correct using the dynamical method. It is also shown that with the dynamical method, the SDAS can be calculated from any type of cooling curve, and using the dynamical method, it is proved that some different SDASs could belong to the same local solidification time.

1. Introduction

Casting usually is the first step in the production of alloys. During this technological step, from the melt, solid material forms with various microstructures. Most alloys consist of a dendritic microstructure entirely (wrought alloys) or partly (cast alloys) after solidification. In the case of wrought alloys, the homogenization time of microsegregation depends on the secondary dendrite arm spacing; it increases with the increase in the secondary dendrite arm spacing by the square law [1], while the physical properties (electric and heat conduction), chemical properties (corrosion) [2], mechanical properties (hardness, yield strength, final tensile strength, and elongation) [3,4], and performance of cast materials directly depend on the parameters of the dendritic microstructure, such as primary (PDAS) and secondary (SDAS) dendrite arm spacing. The part of the dendritic structure with the most volume consists of secondary dendrite arms, and the properties mentioned before mainly depend on the SDAS. Because of these facts, there is considerable interest in determining the effect of solidification parameters on SDAS changes during solidification. The final SDAS depends on the cooling rate; an increased cooling rate produces a smaller SDAS, or a longer local solidification time results in a bigger SDAS. There are four different models to explain the change in SDAS.

The first model was proposed by Kattamis et al. [5], which assumed that the arms’ radius is constant except for one thin arm and the thin arm becomes thinner due to the curvature effect. The second model proposed by Chernov et al. [6] assumed that there is an arm whose root is smaller than the other parts, and the arm is separate from the root. The third model, which Kahlweit [7] proposes, assumes the same arm distribution as the first model but considers that the small arm melts back toward the root. The fourth model proposed by Glicksman [8] supposes the coalescence of two adjacent arms. These models predict a relationship between final SDAS (λ₂) and local solidification time (t₀) (in agreement with the results of the experiments):

$${\lambda }_2=K·t_0^n$$

(1)

where K is constant for one alloy but depends on the initial concentration, and n changes between 0.25 and 0.45 [9,10,11,12,13,14,15].

Some different analytical and numerical models exist in the literature to calculate the SDAS during and at the end of solidification as a function of the solidification time. Kirkwood [16] proposed a diffusion model for isotherm coarsening:

$${\lambda }_2^3\left(t\right)=\frac{128D_{L }\sigma T}{L{m}_L\left(1-k\right)C_L} t$$

(2)

where t is the time, D_L is the diffusion coefficient in the melt, σ is the solid/liquid interfacial tension, T is the temperature, L is the latent heat of melting, m_L is the slope of the liquidus line, C_L is the equilibrium concentration of the melt on the solid/liquid surface k the partition coefficient, and t is the time.

This model can also successfully predict the arm spacing during and at the end of solidification using constant parameters if the temperature range of solidification is not too high; the parameters are not changed extremely.

In the present paper, we compare these two models with experimental results published earlier [16] to show the capability of these models.

2. Theory of Coarsening

The driving force of the coarsening of the secondary dendrite arms (similar to the coarsening of a solid particle in a solid matrix, like precipitation) is a decrease in the surface energy of the system, which acts on the curved surface through the Gibbs–Thomson effect. The equilibrium concentration in the liquid phase on the solid phase’s surface depends on the curvature of the solid phase. As a consequence of this, diffusion in the liquid phase from high to low solute regions will result in the coarsening of the SDA, as will be seen below in detail.

2.1. Effect of the Radius of the Solid Phase on the Equilibrium Concentrations

The liquidus and the solidus curves of the equilibrium phase diagram (Figure 1, approximated by straight lines), TL (R = ∞) and TS (R = ∞) show the temperature as a function of the concentration if the interface is planar (the radius, R = ∞). Suppose the solid phase has a convex surface, where R+ < ∞ means the solidus and the liquidus lines are shifted to the lower temperature (green arrow), while the solid phase has a concave surface (e.g., at the dendrite root), where R− < ∞ means, the lines are shifted to a higher temperature (red arrow) in connection with the Gibbs–Thompson theory.

2.2. Process of the Coarsening

Figure 2a shows the cross-section of two solid-phase cylinders (later solid particles) in the liquid phase. The surface of the particles is convex, and the radius of them is different, R+ > r+. The equilibrium concentrations of the liquid and solid phases (C_L(R+), C_L(r+), and C_S(R+), C_S(r+)) on the surface of the solid particles are shown in Figure 3 at a given T temperature, C_L(R+), > C_L(r+), and C_S(R+) > C_S(r+)). Figure 2b shows the concentration distribution between the two solid particles in the liquid phase, C_L(R+) > C(r+), and then the alloying element diffuses from the big particle to the small one (blue arrow in Figure 3a), decreasing the concentration near the big particle and increasing it near the small particle. Because the equilibrium concentration must remain, some solid phase (dx(R+)) solidifies on the surface of the big particle, increasing the liquid phase concentration with dC = C_L(R+) − C_S(R+), while some solid phase (dx(r+)) remelts from the small particle and decreases the liquid phase concentration with dC = C_L(r+) − C_S(r+). Then, the big particle grows (light blue part), and the small one remelts (yellow part). During this process, the R+ increases and the r+ decreases, so the concentration difference increases, and the diffusion velocity also increases. Finally, the small particle will completely remelt. During the process, the red arrows show the movement of the interface.

Figure 4 shows the case when the surface of the big particle is convex while the surface of the small opposite of the big particle is concave. In this case, the C_L(r−) > C_L(R+) (see Figure 5), so the alloying element diffuses from the small particle to the big one (blue arrow in Figure 4a). As a result, the small particle grows (light blue part), and the big one remelts. If the time is long enough, the big one can remelt completely. During the process, the red arrows show the movement of the interface again. The process is similar if the negative radius is equal to or bigger than the positive one, but the concentration is different, and so the velocity of the diffusion is smaller.

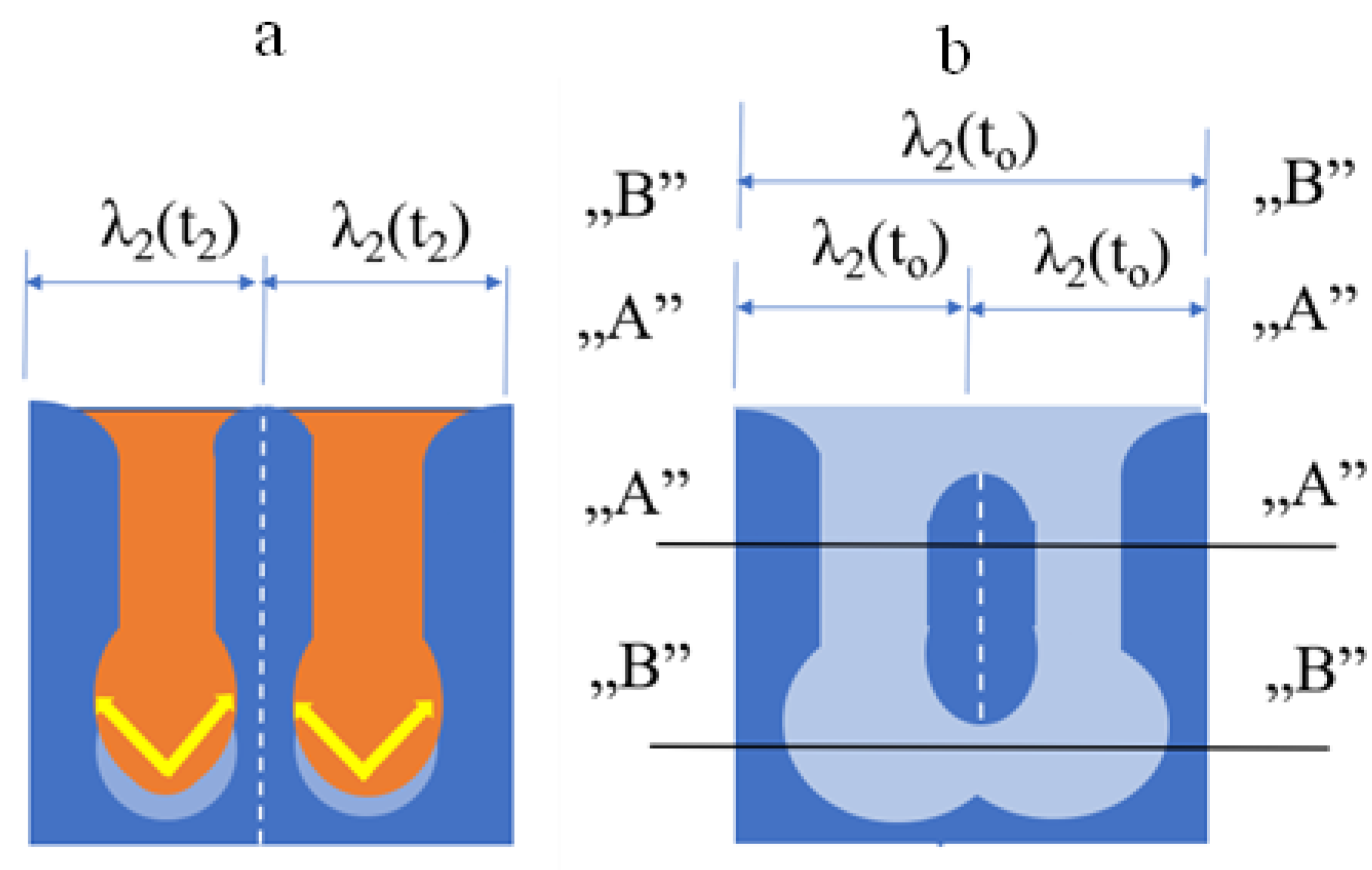
2.3. Models of the Coarsening of Secondary Dendrite Arms

The literature proposes four physical models for coarsening the secondary dendrite arm (SDA). These are shown in Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10. In the figures, blue, light blue, and red colors illustrate the solid phase at time t₁, the solid phase that solidified from time t₁ to t₂ and from time t₂ to the end of solidification (local solidification time, t₀), and the melt, respectively. The yellow arrows show the direction of the diffusion of the alloying element. In Figure 6, at time t₁, between the two halves of the big secondary dendrite arms (SDA) with a radius R is another small one with radius r, where R > r. The secondary dendrite arm spacing (SDAS) is the distance between the center of the two arms (dotted lines). It must be noted that it is measurable only between the edges of the SDA in practice.

In Figure 7, the radial remelting model is shown [5]. The liquid phase concentration at the surface of the big SDA is higher than at the small one (convex type), and then the diffusion between the arms carries the alloying element from the big SDA to the small one. As a result, the big SDA grows, and the small one begins to remelt (time t₂, Figure 7a). Finally, the small SDA totally remelts, and the SDAS will be two times more locally (time t₀, Figure 7b).

In the case of the axial model [7], there is a concentration difference between the big SDA and the tip of the small SDA (convex type). Consequently, the alloying element diffuses from the surface of the big SDA to the tip of the small one, then the small one remelts in the axial direction (Figure 8a), producing two times more SDAS (Figure 8b). In Figure 9, this process can be seen in the unidirectional solidification of pure succinonitrile where A and B are two big secondary dendrite arms in time t₁ and t₂ [8].

We note that some parts of the small SDA can also remain in the case of radial and axial remelting (Figure 10). In that case, two different SDASs are measurable: in the “A”–“A” section, the measured SDAS is double the original, while in the “B”–“B” section, it remains the same as the original. Figure 11 shows the result of this process in the case of the unidirectionally solidified Al-7%Si alloy.

The surface is concave near the root of the SDAs, where they connect to the primary arm (Figure 12) [6]. The concentration of the liquid phase at the root (C_L(r−) is higher than the concentration at the surface of the big and small SDAs ((C_L(R+) and (C_L(r+) (Figure 5)), and then the diffusion carries the alloying element from the root to the big and small SDAs. As a result, the root of the big and small SDAs begins to remelt (Figure 12a), and the part of the primary arm grows (concave type). Finally, the root of the small SDA remelts, and the remaining part will be closed between the two big arms (Figure 12b). In this case (similarly to Figure 11), two different SDASs are measurable: in the “A”–“A” section, it is double, and in the “B”–“B” section, it is the same as the original.

Two adjacent small SDASs can connect by simple growing (Figure 13). If the crystallography direction of the two SDAs is the same (between the SDA would be some difference), and any impurities between the two arms such as oxide do not remain, they can coalesce and form a big SDA with double SDAS. Figure 14 shows this process in the case of unidirectionally solidified succinonitrile [17].

We note that these four different processes of “coarsening” can overlap each other in the final SDAS.

3. Experiments

3.1. Alloy

Hydro Aluminium Rolled Products GmbH provided grain-refined and non-grain-refined Al-7wt%Si alloy for the CETSOL project. The alloy was made from high-purity 99.99wt% Al and 99.99wt%Si material using a vacuum metallurgy process. An addition of 0.5wt% master alloy AlTi5B was used for grain refinement.

3.2. Solidification Experiments

The experiments were performed in a vertical Bridgman-type tube furnace having four heating zones. Around the furnace is a 2-pole magnetic inductor that can produce a rotating magnetic field (RMF). The sample diameter was 8 mm, and the length was 100 mm. The temperature distribution was measured at 13 points by K-type thermocouples. The details of the furnace, the inductor, and the construction of the sample holder are presented in [10].

Four solidification experiments were carried out with different parameters (

Table 1. Parameters of GB experiments.

Sample	Alloy	Initial G K/mm	Stage I		Stage II
			v1 mm/s	z1 mm	v2 mm/s	z2 mm	RMF
GB1	Al + 7wt%Si +GR	4	0.02	50	0.2	60	No
GB2	Al + 7wt%Si	4	0.02	50	0.2	60	0.5 mT
GB5	Al + 7wt%Si +GR	4	0.02	50	0.02	60	No
GB6	Al + 7wt%Si	4	0.02	50	0.02	60	0.5 mT

). The sample moving velocity (v1) in Stage I was 0.02 mm/s. The z1 length of Stage I was 50 mm, so the steady-state solidification conditions were obtained in Stage I. In Stage II, the moving velocity of the GB1 and GB2 samples was 0.2 mm/s, and it was 0.02 mm/s for the GB5 and GB6 experiments. The z2 length was 60 mm. Before the solidification phase started, a thermal homogenization for 1800 s for all four samples was applied. The GB2 and GB6 samples were stirred with RMF of 0.5 mT in Stage II.

3.3. Measuring Method of Secondary Dendrite Arm Spacing (SDAS)

The longitudinal section of the samples was divided into 35 parts along the sample axis. The thicknesses of each part were 2.85 mm and 8 mm along and perpendicular to the sample axis. A total of 200 SDAS values were measured in all parts. A line was laid across the secondary arms (perpendicular to them, longitudinal with the primary dendrite arms), and the number of crossings was counted manually.

A detailed analysis of the microstructure of samples was described in [19], where the results of four space experiments (performed in the framework of the CETSOL VI project) were compared with the results of four Ground Base (GB) experiments.

3.4. Cooling Curves

The temperature (cooling curve) was measured by 13 thermocouples (Figure 15, TC1–TC13). During the analysis, it was supposed that the undercooling of the primary dendrite tips and eutectic could be neglected. This means that the solidification starts at the liquidus temperature (TL) and is completed when the eutectic temperature (TE) is reached. The details of the analysis were presented in two earlier papers [18,19].

4. Simulation of the Secondary Dendrite Arm Spacing (SDAS)

4.1. Empirical Simulation Method

In [19], we showed that the final secondary dendrite arm spacing could be calculated by the well-known empirical equation using the temperature gradient and the solid/liquid front velocity in the case of unidirectional solidification:

$${\lambda }_2\left(t_0\left(x_s\right)\right)=K{[t_0\left(x_s\right)]}^{\frac{1}{3}}=K{\left(\frac{\mathsf{\Delta }T\left(x_s\right)}{\dot{T}\left(x_s\right)}\right)}^{\frac{1}{3}}=K{\left(\frac{\mathsf{\Delta }T\left(x_s\right)}{G\left(x_s\right)v\left(x_s\right)}\right)}^{\frac{1}{3}}$$

(3)

where ΔT(x_s) is the temperature range of solidification, t₀ is the local solidification time at x_s is the position in the sample, and K is a constant for the alloy.

The temperature range of solidification depends on the actual concentration of the sample. v and G changed along with the sample, and they were different at the S/L and E/L fronts at a given x_s. Consequently, we used the values of v_av(x_s) and G_av(x_s):

$$v_{av}\left(x_s\right)=\frac{v_{SL}\left(x_s\right)+v_{EL}\left(x_s\right)}{2}$$

(4)

$$G_{av}\left(x_s\right)=\frac{G_{SL}\left(x_s\right)+G_{EL}\left(x_s\right)}{2}$$

(5)

where v_SL(x_s), v_EL(x_s), and G_SL(x_s), G_SL(x_s) are the front velocities and the temperature gradients at the S/L and E/L fronts, respectively. So:

$${\lambda }_2\left(x_s\right)=K{\left(\frac{\mathsf{\Delta }T\left(x_s\right)}{G_{av}\left(x_s\right)v_{av}\left(x_s\right)}\right)}^{\frac{1}{3}}$$

(6)

The advantage of this method is that with our method, described in [18], it is possible to calculate the G and v parameters at an arbitrary point of the sample, not only where the temperature as a function of time (cooling curve) was measured. In Figure 19 the measured and the calculated SDAS are compared, and the agreement is quite good. The disadvantage of this method is that:

(i)

The change of the SDAS during solidification cannot be calculated, so this method is not good enough for the simulation of microsegregation;

(ii)

This simulation method is usable for only directional solidification when the temperature gradient and the solid/liquid front velocity can be determined.

In the case of equiaxed solidification, when the temperature gradient and the front velocity cannot be calculated, the simple form of this equation is usable:

$${\lambda }_2\left(t_0\right)=K{[t_0]}^{\frac{1}{3}}$$

(7)

The problem with this equation is that it cannot take into account the form of the cooling curve; with the same local solidification time but a different form of the cooling curve, we will obtain the same SDAS.

4.2. Dynamical Simulation Method

A semi-empirical model was developed to describe the secondary arm spacing in alloys after dendritic solidification based on the research of Kattamis et al. [5] and Kirkwood [16]. This model is based on the different coarsening processes shown earlier. The initial SDAs have different thicknesses and curvature radii; there is diffuse mass transport between the arms in the mushy zone, leading to the disappearance of small arms and the growth of bigger ones. Kirkwood gave a function to describe the isotherm coarsening of the SDAS:

$${\lambda }_2^3\left(t\right)=\frac{128 D_L\left(T\left(t\right)\right)\sigma \left(T\left(t\right)\right)T}{L m_L\left(T\left(t\right)\right)(1-k\left(T\left(t\right)\right)C_L\left(T\left(t\right)\right)}t$$

(8)

where D_L is the diffusion coefficient in the melt, σ is the solid/liquid interfacial energy, T is the liquidus temperature, L is the latent heat of melting, m_L is the slope of the liquidus line, C_L is the equilibrium concentration of the melt on the solid/liquid surface, and k is the partition coefficient.

As Equation (6) cannot be integral in closed form, after some simplification, the authors describe the SDAS in the final microstructure as a result of coarsening:

$${\lambda }_2^3\left(t_0\right)=\frac{128 D_L \sigma T\ln \left(C_E/C_0\right)}{L m_L\left(1-k\right)\left(C_E-C_0\right)} t_0$$

(9)

where C₀ and C_E are the concentration of the alloy and the eutectic, respectively.

To describe the SDAS as a function of time, in [20], the author proposed a numerical solution to Equation (6) that can follow the change of the SDAS during solidification:

$$\begin{gathered} {\lambda }_2^3\left(t\right)={\lambda }_2^3\left(t=0\right)+G\underset{t=0}{\overset{t}{\int }}\frac{ D_L\left(T\left(t\right) \right) \sigma \left(T\left(t\right)\right)T}{L m_L\left(T\left(t\right)\right)(1-k\left(T\left(t\right)\right)C_L\left(T\left(t\right)\right)}dt \\ \approx {\lambda }_2^3\left(t=0\right)+G {\displaystyle \sum }_{t=0 }^t\frac{ D_L\left(T\left(t\right)\right) \sigma \left(T\left(t\right)\right) T}{L m_L\left(T\left(t\right)\right)(1-k\left(T\left(t\right)\right) C_L\left(T\left(t\right)\right)}\Delta t \end{gathered}$$

(10)

where G is a geometric factor.

Using Equation (6), the SDAS vs. time was successfully first calculated in the case of a unidirectional solidified Al-Cu alloy [21], and then Cu-10Sn [22], Mg-Al [23], and Mg-Al-Zn [24], to simulate microsegregation. Battle and Pehlke [25] compared the experimental results of microsegregation in Al-Cu alloys with models that included empirical (Equation (7)) and dynamical coarsening equations (Equation (10)). They noted that it was still not possible to conclude which approach gave more accurate results. As they used only the final SDAS calculated by Equation (10) during the simulation, and the final SDAS calculated by Equations (7) and (10) were practically the same, it was not a surprise that the simulation result was also the same.

5. Results and Discussion

5.1. Material Constants

All of the material constants originate from the literature (

Table 2. Material constants used in the simulations.

Partition Coefficient	k	0.13	wt%/wt%
Liquidus slope	mL	−6.587	K/wt%
Geometric factor	G	33	-
Interfacial energy	σ	9.3 × 10−2	J/m2
Latent heat	L	3.97 × 105	J/kg
Si liquid diffusion	D0	1.3 × 10−7	m2/s
	Q	30,000	J/mol
Density	ρ	2.475 × 103	kg/m3
Alloy concentration	C0	7.0	wt%

). As the liquidus and solidus slopes of the Al-Si alloy are nearly constant (see Figure 16), the liquidus slope (m_L) and the partition ratio (k) were constant during the simulation. Of course, if they change with the temperature, it is possible to consider them during the simulation.

5.2. Simulation Method

The SDAS as a function of time can be calculated using the cooling curve, T(t), by the dynamical method. Before the simulation, we must test the effect of the number of time steps on the accuracy of the calculated results. Figure 17 shows the final SDAS as a function of the number of time steps. The number of time steps changed from 10 to 400; if it is higher than 40, the difference in the final SDAS is negligible. So, in all our simulations, the number of time steps was equal to or higher than 40. The λ₂(t = 0) was negligible because its effect is minimal on the final SDAS [20].

5.3. Capability of the Dynamical Method

The capability of the dynamical method is illustrated in Figure 18. It shows the change of the SDAS during solidification as a function of time in the case of the GB1 sample. The SDAS(t) curves start at the time when the solid/liquid front meets the position of the given thermocouple. The yellow squares indicate the final value of the SDAS. Figure 18b shows the SDAS(T) functions in the case of three positions in the sample where the cooling rate was significantly different.

5.4. Comparison of the Results of Two Simulation Methods and the Measured SDAS

In Figure 19, the results of the empirical (Calc 1) and the dynamical (Calc 2) simulation method are compared with the measured one. Because only the final SDAS was measured in the GB samples, we can compare it with the results of the two simulation methods.

Our empirical method shown in [18,19] can calculate the average temperature gradient (Gav) and average solid/liquid front velocity (vav) and then the local solidification time (t₀) in any sample position. Taking into account the macrosegregation (by the change of solidification temperature range, ΔT), the final SDAS can also be calculated there if the K constant in Equation (4) is known. This method is not usable when only the cooling curve is measured at nondirectional solidification. In that case, the local solidification time can be determined from the cooling curve. In addition, it is impossible to consider the macrosegregation (concentration change) (Equation (5)) and the form of the cooling curve, which can change the final SDAS, as we show in Section 6. The SDAS was calculated at 40 positions of the samples, and they were practically the same as the measured one (Figure 20). The K = 5.2 constant was determined using the measured SDAS.

As we show in Figure 18 and Figure 19, the change of the SDAS during and naturally at the end of solidification can be calculated with the dynamical simulation. Using the cooling curves of the fully remelted part of the GB samples (GB1, GB2, and GB6: from TC3 to TC13; GB5: from TC2 to TC13), the SDAS was calculated by Equation (8). For the calculation, only one empirical parameter was used (geometric parameter G = 33), which seems to be constant for the aluminum alloys [20,23,24]. This simulation method can consider the temperature function of all physical constants and the form of the cooling curve. In the simulation of the solidification of the solid solution type of alloys, using this method, consider the change of the SDAS, which affects the microsegregation [20,23,24]. The calculated final SDAS is about the same as the measured and calculated one.

Similarly, to the empirical simulation, it is possible to determine the K constant of Equation (5) from the simulated data. Figure 20 shows Log(SDAS) vs. Log(t₀). The exponent is 0.33, which is the attribute of the dynamical simulation. The constant of the straight line (R² = 0.9977) is 0.6794, and then K = 10^0.6794 = 4.779, similar to the constant determined by the simulation method (Section 5.2)).

5.5. Effect of Form of Cooling Curves

All the models and measured relationships between the SDAS and local solidification time give a function independent of the form of the cooling curve for a given alloy. This means that if the local solidification is the same, the SDAS is also the same. Using Equation (8), the effect of the form of cooling curves on the SDAS is shown. In Figure 21, the local solidification time is 104 s for all types of cooling curves (Figure 21a). The details of the cooling curves are shown in

Table 3. Temperature—time paths.

Sample	T1 start °C	T Stop, °C	Cool. rate K/s	Hold s	T2 Start °C	T2 Stop °C	Cool. Rate K/s	SDAS µm	Fs %
1	614	574	0.384	-	-	-		16.2
2	614	604	10	100	604	RT	10	23.4	16
3	614	594	10	100	594	RT	10	21.8	31
4	614	584	10	100	584	RT	10	20.4	42
5	614	575	10	100	575	RT	10	19.3	51
SDASmax/SDASmin = 23.4/16.2 = 1.44

. Samples 2–5 were cooled down fast to a temperature between the TL and TE, held at this temperature for 100 s, and again cooled down fast under the TE. Similar cooling curves exist for the isothermal coarsening experiments and semi-solid or rheocasting. The developed SDAS is compared with the SDAS of Sample 1, which was cooled down continuously (similar to the BG samples). Samples 2–5 contain different fractions of solid phase at a given temperature (see Table 3). After complete solidification, these samples will contain two fragments; one of them will be coarse, developed during isotherm holding, and the other finer, developed during fast cooling from the isotherm. As can be seen (Figure 21b), the coarsening kinetics (SDAS vs. time) are different; the smallest SDAS was developed in the case of Sample 1 (16.2 µm) and the biggest in the case of Sample 2, which was held above the TE (23.4 µm). The difference increases with the decrease in the isotherm (Figure 21c). The maximum rate is 1.44.

In Figure 22, the local solidification time is 400 s in the case of the four different cooling curves (

Table 4. Temperature—time paths.

Sample	T1 Start °C	T Stop, °C	Cool. Rate K/s	Hold s	T2 Start °C	T2 Stop °C	Cool. Rate K/s	SDAS µm	Fs %
6	614	RT	0.1	-	-	-		34.6	-
7	614	594	1	180	594	RT	1	33	31
8	614	575	1	360	-	-	-	29.3	51
9	614	594	0.052	-	594	RT	10	36.7	31
SDASmax/SDASmin = 36.7/29.3 = 1.25

.). Sample 6 is cooled down at 1.0 K/s continuously under the TE. Sample 7 is cooled down at 1.0 K/s to 594 °C, held at this temperature for 180 s, and after, it is cooled at 0.1 K/s under the TE. The solid fraction at 594 C is 31%, similar to Sample 3, but because Sample 7 cooled down continuously under the TE after isothermal coarsening, the microstructure is coarser uniformly. Sample 8 is similar to Sample 5, but the cooling rate is 1.0 K/s, and the holding time is 360 s. Sample 9 is cooled to 594 C at 0.052 K/s and immediately under the TE at 10 K/s. The solid fraction, in this case, is also 31% when the cooling rate changes. The microstructure is uniform and coarse as in Sample 6.

The simulation of SDAS coarsening proves that different SDASs appertain to the same local solidification time.

6. Summary and Conclusions

It is well known that the secondary dendrite arm spacing changes during solidification. The driving force of the coarsening of the secondary dendrite arm is a decrease in the surface energy of the system, which acts on the curved surface through the Gibbs–Thomson effect. The equilibrium concentration in the liquid phase on the solid phase’s surface depends on the curvature of the solid phase. Consequently, diffusion in the liquid phase from high to low solute regions will result in the coarsening of the SDA. Four different processes result in the coarsening of the SDA: axial, radial, remelting of the root, and coalescence of the SDA, as shown in detail.

Usually, an empirical equation is used to calculate the final SDAS: ${\lambda }_2\left(t_0\right)=K{[t_0]}^{\frac{1}{3}}$. The local solidification time can be determined directly from the cooling curve or the average solid/liquid interface velocity and temperature gradient, considering the solidification temperature interval, ΔT. Kirkwood [16] gave a function to describe the isotherm coarsening of the SDA, which was extended for the changing temperature (continuous cooling) to develop the dynamical method [20].

The results of the two simulation methods were compared with the results of four unidirectional solidification experiments performed earlier with Al-7% Si alloy [19].

Based on the comparison of the results of simulations and the experiments, it can be stated as follows:

(i)

The two simulation methods describe well enough the measured final SDAS (at t₀). With the empirical method, it is possible to calculate the final SDAS in an arbitrary position of the sample, while because the dynamical simulation must know the cooling curve, with the dynamical method, it is possible to calculate the final SDAS, and the cooling curves were determined.

(ii)

As with the empirical method, it is possible to calculate only the final SDAS; with the dynamical method, the SDAS can be calculated during solidification too. So, using the dynamical method, the results of the solidification simulation (the microsegregation) will be more correct.

(iii)

The dynamical simulation proved that the final SDAS depends on the form of the cooling curve, which could change during solidification. The dynamical method can consider the form of the cooling curve, and then it can be usable for any type of solidification.

(iv)

In contrast with the current fact that one SDAS belongs to one local solidification time, it was shown that it is not valid; the difference between the SDAS can be either ~50%.