Red-Green-Blue Mini-LEDs Lighting Design with High Uniformity under Thin Form Factor

Abstract

We present a design of a non-imaging system based on a ray-tracing methodology. This system is mainly made of polycarbonate, while part of its surface is coated with metal. The Zemax^® optical simulation tool was used to calculate the optimal parameters of this system, such as heights, widths, and angles. This design aims to improve the light distribution uniformity of blended red-green-blue mini light-emitting diodes. Our simulation results show that this design can achieve 93% light distribution uniformity in a 36 mm × 36 mm area, and the height of this design is less than 5 mm.

1. Introduction

With the shrinkage in semiconductor size, light-emitting diode (LED) light sources have become smaller and smaller. Mini-LEDs have been a concept in recent years. By reducing the size of traditional LEDs to 100–200 μm, mini-LEDs have been commercialized for backlight sources in consumer electronics applications. Local dimming can significantly improve the contrast ratio at relatively low energy consumption [1]. However, the illuminance distribution on the target plane from an LED light source decreases rapidly as the angle of incidence increases, and the light intensity distribution of LEDs approximates the Lambert cosine distribution. Therefore, LED luminaries are generally required to redistribute the spatial distribution of the LED’s light energy through appropriate primary or secondary optics to the light pattern. To achieve high-quality LED illumination, we must address the uniformity of light.

Our purpose is to uniformly disperse the mini Red-Green-Blue LED light source on a 37.4 mm × 37.4 mm plane at a distance of only 5 mm with Red-Green-Blue LEDs. The above-mentioned task is a rather difficult job. It is impossible to design a lens to achieve uniform lighting at a short distance and a large angle, even with multiple light sources. At the beginning of developing the light guide plate, we referred to King-Lien Lee and Kun-Yu He [2] and used microstructures of different shapes on the base plate to change the direction of light. We chose the first design with the best uniformity among the three structures. As a result, the uniformity achieved with this structure remained at 50~60%. Next, we referred to the light guide plate designed by Chung-Feng Jeffrey Kuo and Te-Li Su [3]. The inclined plate design that they use evenly destroys the waveguide. However, the structure will be fragile if the edge part is too thin. Therefore, note that the slope of the inclined plate cannot be too steep.

On the other hand, the space in which the traditional lens stands is too large. Therefore, we use Fresnel [4,5,6], freeform [7,8,9], and microlens [10,11] to adjust the light distribution. This design reduces the amount of material required compared to a conventional lens by dividing the lens into a set of concentric annular sections. These circles are formed with an identical pitch or height and are manufactured into a triangular form along the tangent of their convex. Therefore, the Fresnel lens is more compact, cost-effective, and lightweight than a conventional convex lens. In addition, it allows for the construction of large aperture and short focal length lenses. However, Yi-Cheng Chen et al. [4] mentioned that a messy distribution of illuminance due to refraction by surface discontinuities, particularly along the groove facets, usually occurs. Therefore, we decided not to use this design.

A free-form lens has become a trend in LED optics design due to its advantages in design freedom, compact size, and accurate light control. During the last few years, most of the research on the freeform lens has been conducted [7,8,9], and methods have been developed. The methods include the simultaneous multiple surface (SMS) method, the tailored freeform surface method, partial differential equations, the discontinuous freeform lens method, and the continuous freeform lens method. However, the working distance (the distance from the light source to the detector) is more than ten times longer than in previous works. Furthermore, they also use the Red-Green-Blue LED array as a lighting source [8]. When modeling multiple light sources, we cannot place all lighting sources on the center axis of the illumination system. The angle of incidence also increases when the lighting sources are away from the center axis, resulting in poor uniformity. In addition, we have to face the challenge of the three-color mixing issue. Most approaches elongate the light propagation distance to achieve a light-mixing effect. However, our design can only rely on the mirrored cone to evenly break up the three-color light.

In this paper, we place a reflective mirrored cone 0.5 mm above the mini-LED. It disperses the high-intensity light into the polycarbonate, where the waveguide will occur. Naturally, different shapes of the light guide plate would cause other light output conditions. Here, we also know how important the role of the mirrored cone and waveguide is. With these two critical optical components, we can achieve light mixing and maximization of the divergence angle at a very short distance. Shrinking traditional lenses to the micrometer level reduces space and improves optical quality. More importantly, this design is suitable for a short working distance situation. The research of W. Sun [10] showed that even at such a short distance, there are designs to improve uniformity. In the next section, we will discuss designing microlenses to deal with light uniformity.

2. Design Principles

For designing uniform lighting based on solid-state devices and light-emitting diodes (LEDs), the ray-tracing method is the most popular. In our first-order calculation, we utilized the ray-tracing method to predict the outcome of the energy distribution. The ray-tracing method is based on Snell’s law described by Equation (1):

$$n_{air}{\sin \theta }_{air} = n_{lens}{\sin \theta }_{lens}$$

(1)

where n_air and n_lens are the refractive indices of air and lens, respectively. θ_air and θ_lens are the angles between the surface normal line and incident ray in air and inside the lens, respectively. We assumed that the LEDs are separated from the optical lenses by air. Generally speaking, the area of an LED chip is smaller than that of the target plane. One may need to use a negative power lens, also known as a concave lens, to expand the lighting area, as shown in Figure 1a. When considering the refracted light described by Equation (1), the zero-degree light from an LED chip is not redirected at all because the slope in the middle of the surface of traditional concave lenses is flat, which means conventional concave lenses are unable to effectively diffuse the brightest light emitted by LEDs. Furthermore, an LED chip shows the highest brightness at zero degrees due to the Lambertian distribution of an LED lighting pattern. Therefore, the target plane has the brightest spot right on the top of a LED chip, as shown by the thickest line in Figure 1a. As we move away from the center axis of an LED chip, the brightness drops accordingly. To overcome this difficulty, we placed a mirrored cone above the light source to split the light within a short distance.

The second challenge for us is to expand the lighting angle from an LED. At first, we still intended to use a concave or Fresnel lens to achieve this goal, but the results were not satisfactory enough, which can be explained by Equation (1). The refractive index of air is equal to one, while that of a lens is approximately 1.5. The critical angle in the visible light spectrum is approximately 42° for the incidence from an ordinary lens to air. In other words, the energy of an LED will be limited to less than 84°. We adopted the design of light guide plates, which are widely used in edge-lighting screens. They can expand the lighting area widely and achieve high brightness uniformity simultaneously. This is conceptually similar to spreading the light uniformly over a long distance.

Finally, to further increase the distribution uniformity and reduce the total internal reflection (TIR), we added microlenses on the top of the light guide plates. The flat surface of a light guide plate can trap the light inside it. As a result of the small radius of the curvature of microlenses, light can be extracted from the light guide effectively. With an appropriate design, one can control the level of extracted light brightness.

Figure 1b shows the schematic diagram of our strategy. A mirrored cone is placed on the LEDs to redirect the brightest light into a light guide. The light guide is long enough to distribute the lighting to a larger target plane and improve the lighting uniformity. Microlenses are applied to extract light from the light guide to further improve its efficiency.

3. Results

The Zemax optical simulation tool was used to simulate the light distribution result. In our illumination design, we used 20,000 rays to simulate the lighting results. The calculated transmission process of the light beam is based on the Fresnel equations. The reflections and refractions under different polarizations are considered for all 20,000 rays at all surfaces. In ZEMAX^®, it is performed in the non-sequential mode as a standard illumination system design process [12]. We adjusted the parameters of our design on the basis of simulation results. We placed a square detector plane, whose width is 37.4 mm (half width W = 18.7 mm) and is located 5 mm away from the light source, to measure the uniformity of the lighting. Furthermore, there are 200 × 200 pixels on the detector plane, each of which will record the energy received from the light source. All the following discussions are based on the simulation results of the light energy that is received by the pixels on the detector plane. We also chose the combination of red, green, and blue light-emitting diodes (LEDs) as our light source of blended lighting systems; their wavelengths are 650 nm, 550 nm, and 450 nm, respectively, while their power is all 1 watt and all of them are Lambertian sources. Furthermore, their side lengths are all 0.28 mm × 0.35 mm, and the gap between them is 0.14 mm. The simulation layout is illustrated in Figure 2.

At first, we tried to design a concave lens system to redistribute the energy emitted by LEDs. However, we soon found that it is not easy to reach high light distribution uniformity with concave lenses under the condition that the height of our system cannot exceed 5 mm. Because our design is expected to be applied to blended lighting systems, power efficiency, uniformity, and color difference are all of concern. We define the uniformity U in Equation (2):

$$U = \frac{E_{ave}}{E_{rms}}$$

(2)

where $E_{ave}$ is the average energy received by all the pixels on the detector planes and $E_{rms}$ is the root mean square (RMS) of the energy received by each pixel of the detector plane. We assumed that the green LED would be placed in the center below our design while the red one is on the left side and the blue one is on the right side; as a result, the left-half detector plane will receive more red light whereas the right-half detector plane will receive more blue light. We define the color difference D in Equation (3):

$$D = \frac{E_{Lave}}{E_{Rave}}$$

(3)

where $E_{Lave}$ is the average energy received by all the pixels in the left-half detector plane, while $E_{Rave}$ is the average energy received by all the pixels in the right-half detector plane. Due to the structural symmetry and the fact that the refractive index of polycarbonate for red light and blue light is approximately 3% different, we can suppose that the color difference and the uniformity of red light will be reasonably close to those of blue light, and the color difference of green light will be close to zero. Thus, we will first discuss the simulation results of red light only, and then we will discuss the simulation results of all light colors at the end. Last but not least, we define the power efficiency P by Equation (4):

$$P = \frac{E_{received}}{E_{emitted}}$$

(4)

where $E_{received}$ is the total energy received by all the pixels on the detector plane and $E_{emitted}$ is the total energy emitted by the light source.

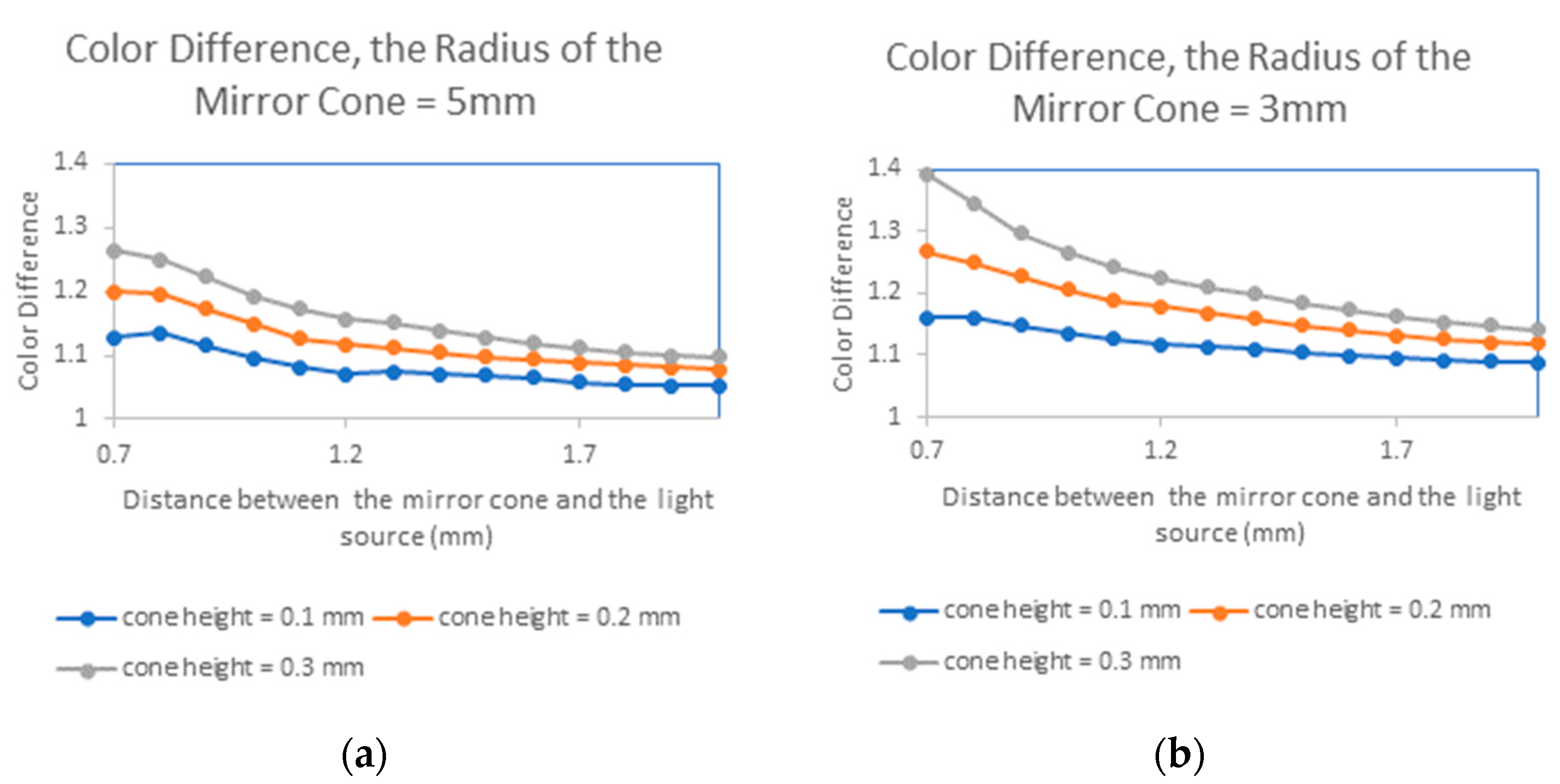
In our design process, we first decided to place a mirrored cone above the light source; in this step, the whole system contained only a hovering mirror cone, a plane-back mirror, and a light source. The next issue is to select the height and radius of that mirror cone and adjust the distance between the mirrored cone and the light source. Since the blue and red LEDs of the light source are 0.42 mm apart while the detector plane is only 5 mm away from the light source, the color difference will be noticeable if the distance between the mirrored cone and the light source (d0) is too small or if the height of the mirrored cone (h0) is too tall. Moreover, if the radius of the mirrored cone (r) is too long, the center of the detector plane will receive little power. In contrast, if the radius of the mirrored cone is too small, most of the light emitted by LEDs will arrive directly at the detector plane without reflection, leading to a highly bright ring in the center of the detector plane. Figure 3 shows the variation in color difference for different heights and radii of the mirrored cone and the distances between the mirrored cone and the light source. The simulation results show that the color difference barely changes if the distance between the mirrored cone and the light source is more than 1.7 mm. If the height of the mirrored cone is shorter or the radius of the mirrored cone is longer, the color difference will be lower. We chose the mirrored cone whose radius is 5 mm and height is 0.1 mm, with the distance between it and the light source equal to 1.9 mm. We did not choose a mirrored cone with a longer radius because a large mirror cone will cause the center of the detector plane to receive little power, which will significantly reduce uniformity.

To ensure our design is easily fabricated, we introduced a large polycarbonate cuboid block with a hollow cylinder space at the bottom of it, and the mirrored cone was placed on the ceiling of that space. Taking total internal reflection (TIR) into account, we added some microlens arrays on the polycarbonate cuboid block. At first, we uniformly placed the same tiny convex lenses on the polycarbonate block. Then, we adjusted the radius of curvature of these microlenses on the lighting results. If a specific area of the detector plane received more light energy than others, we would increase the radius of curvature of the microlenses. All the parameters of the microlens array will be mentioned below. The power efficiency will be less than 1% without the microlens array. In this step, our design reached 93% uniformity, while the color difference is equal to 1.03; however, the power efficiency is only 42.7%, which is not high enough. Finally, we refer to the design of edge-lighting light guide plates and slightly tilt the back mirror of our design. Figure 4 shows the relationship between the tilted angle of the back mirror and the power efficiency. We found that as long as the oblique angle of the back mirror is more than 0.1°, the power efficiency rises significantly compared to the original plane back mirror. However, the power efficiency becomes saturated if we continue to increase the tilted angle.

Figure 5 and Figure 6 show the structure of our final design, and all units are millimeters (mm). Figure 5 is the side view of our final design, and the surfaces, represented by red lines, are coated with perfect conductors (metal) that will reflect all the incident light by 100%. Figure 6 shows the bottom view and top view of our final design. A hollow cylinder is placed in the middle of our design and a mirrored cone is placed on the ceiling of that space. In addition, we adopted the design of edge-lighting light guide plates and coated the side and bottom of our system with metal to redirect the light and make the energy spread more widely. Lastly, the microlens arrays on the top of our system can be classified into two groups. The microlens array in zone 1 is composed of convex lenses with clear aperture = 0.1 mm, a radius of curvature = 0.14 mm, thickness = 0.05 mm, and a gap between neighbors = 0.05 mm. The microlens array in zone 3 is composed of convex lenses with a clear aperture = 0.25 mm, a radius of curvature = 0.35 mm, thickness = 0.15 mm, and a gap between neighbors = 0.25 mm. In zone 2, no microlens is placed on the surface of that region.

Figure 7 shows the simulation results of our final design. Figure 7a–c show the simulation results if we only consider red, green, or blue LEDs, respectively. According to our simulation result, our design can reach 93% light distribution uniformity with 70% energy efficiency for the three colors of LEDs from the light source. The color difference is 1.056 and 0.946 for red and blue LEDs.

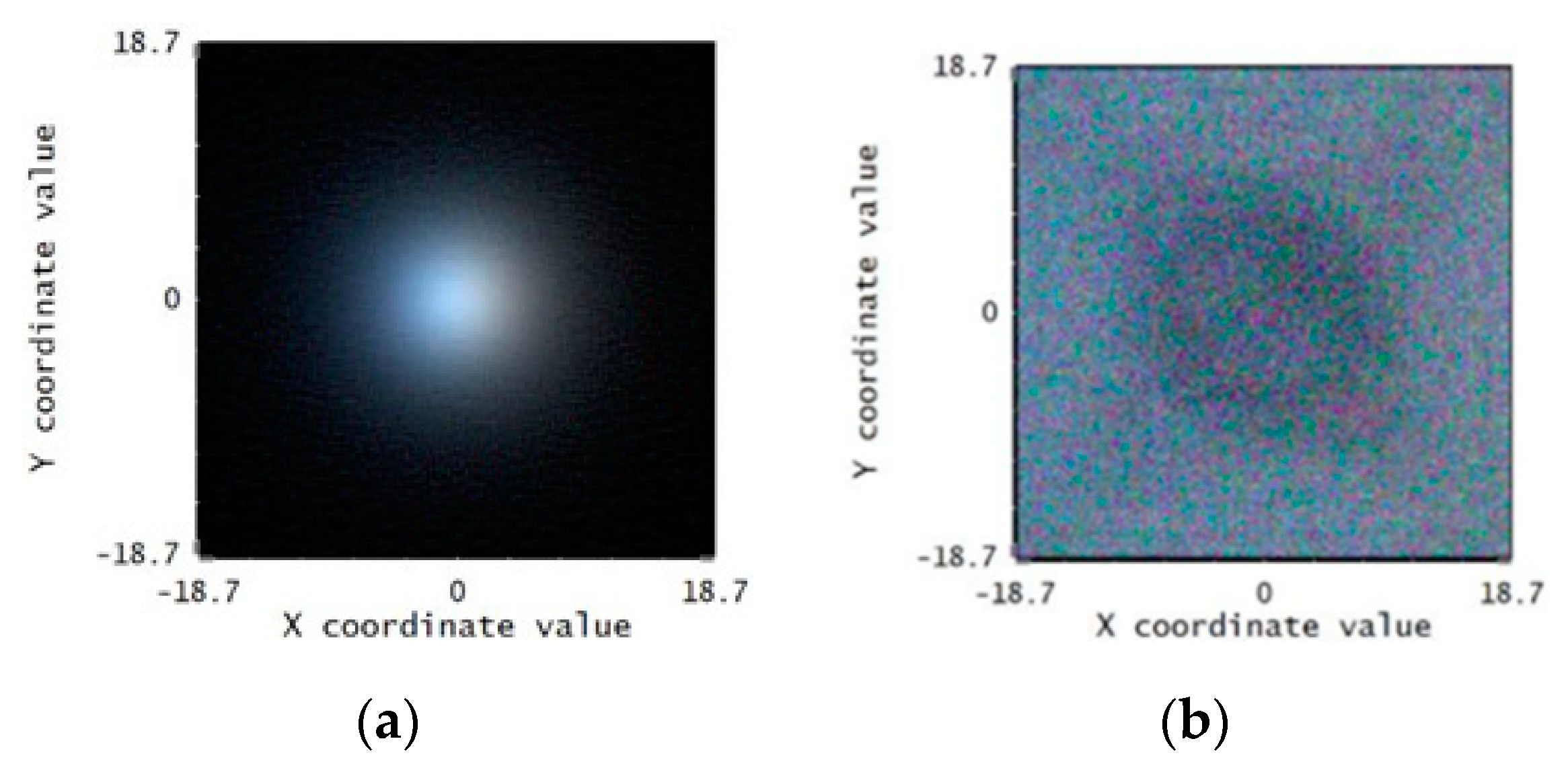
Figure 8a shows the simulation result if the system contains only three colors of LED light sources.

Table 1. The comparison of lighting uniformity between bare LEDs and our design.

	Bare LEDs	Our Design
Uniformity	35%	93%
Power efficiency	94%	70%

shows the uniformity and power efficiency of bare LEDs and our design. In this case, the uniformity is only 35% and most of the light energy is concentrated in the center of the detector plane. Figure 8b is the simulation result of three colors of LED light sources covered by our system. Our design can potentially be applied to mini-LED displays in the future.

4. Conclusions

We have successfully introduced a novel design that can significantly increase the uniformity of blended lighting nonimaging systems within a 5 mm thickness. By using a mirrored cone, tilted light plate, and microlenses, we can redistribute the light with a uniformity of over 90%.

Table 2. The comparison chart for different methodologies.

Methodology	Fresnel Lens [4]	Fresnel Lens [5]	Freeform Lens [7]	Freeform Lens [9]	Microlens [10]	This Work
Target plane	1.0 × 0.8 m2	12 × 12 cm2	5 × 3 m2	r = 0.45 m	113.26 mm2	36 × 36 mm2
Working distance	1 m	100 mm	6 m	1 m	52 mm	5 mm
Ratio	1.067	1.2	0.833	0.9	0.2	7.2
Efficiency	71%	N.A.	92%	89.20%	82%	70%
Component Sizes	N.A.	N.A.	25 × 25 mm2	r = 4.75 mm	20.9 × 15.7 mm2	37.4 × 37.4 mm2
Thickness	N.A.	3.05 mm	20 mm	4 mm	N.A.	2.2 mm
Angle (degree)	56.16	61.93	45.24	48.46	11.31	149
Lighting Source	1	1	1	1	3	3

lists different methodologies to redistribute light. The ratio is defined as the length of the target plane over the thickness of the lighting system. A higher ratio means that light can be redistributed over a shorter distance, indicating that the light can be expanded at a larger angle. Compared with other methods, our proposed lighting system can redistribute light from LEDs in a more compact form factor, making this design suitable for portable gadgets.