Ingredients for Generalized Models of κ-Phase Organic Charge-Transfer Salts: A Review
Abstract
:1. Introduction
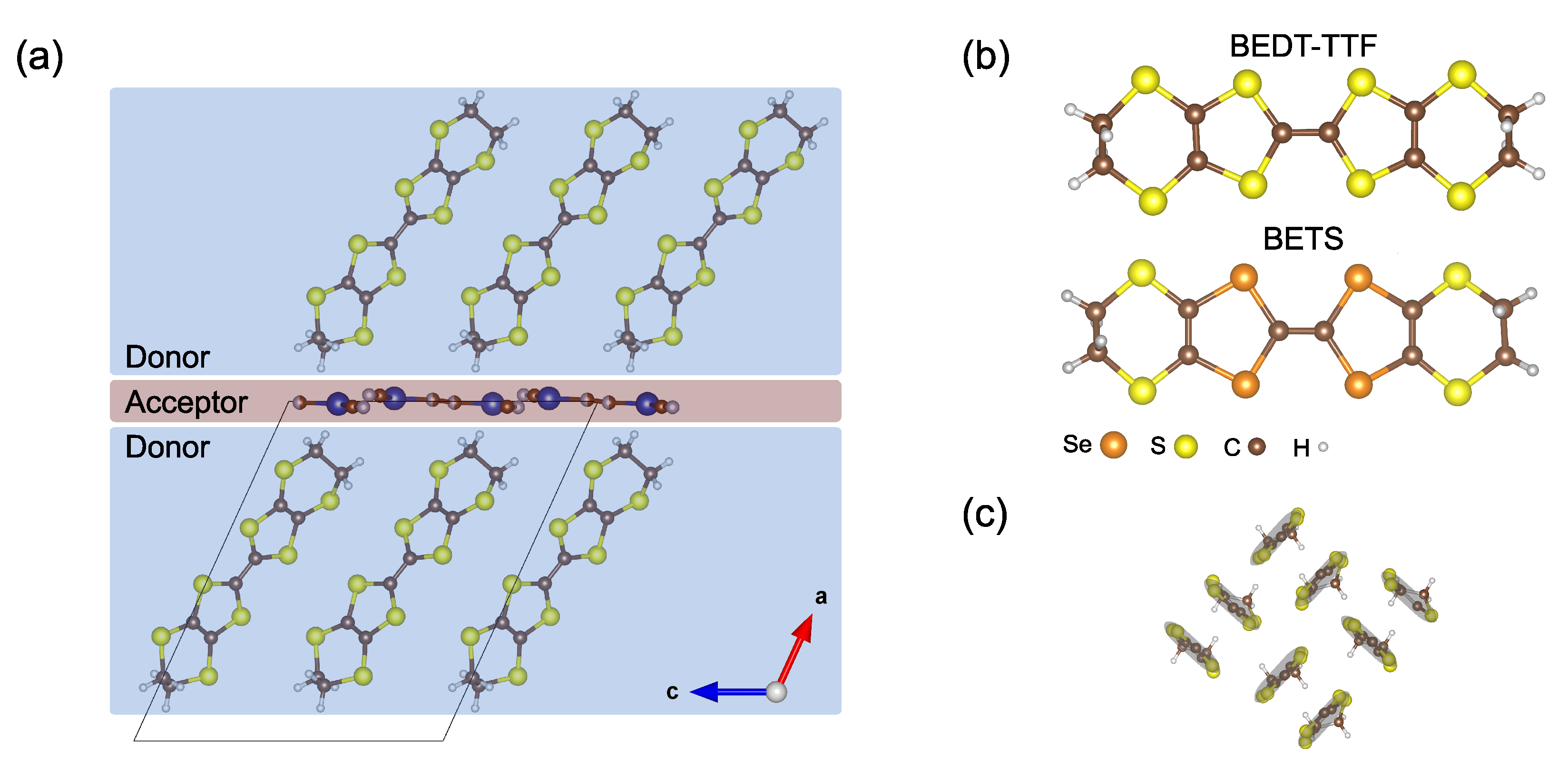
1.1. Crystal and Electronic Structure
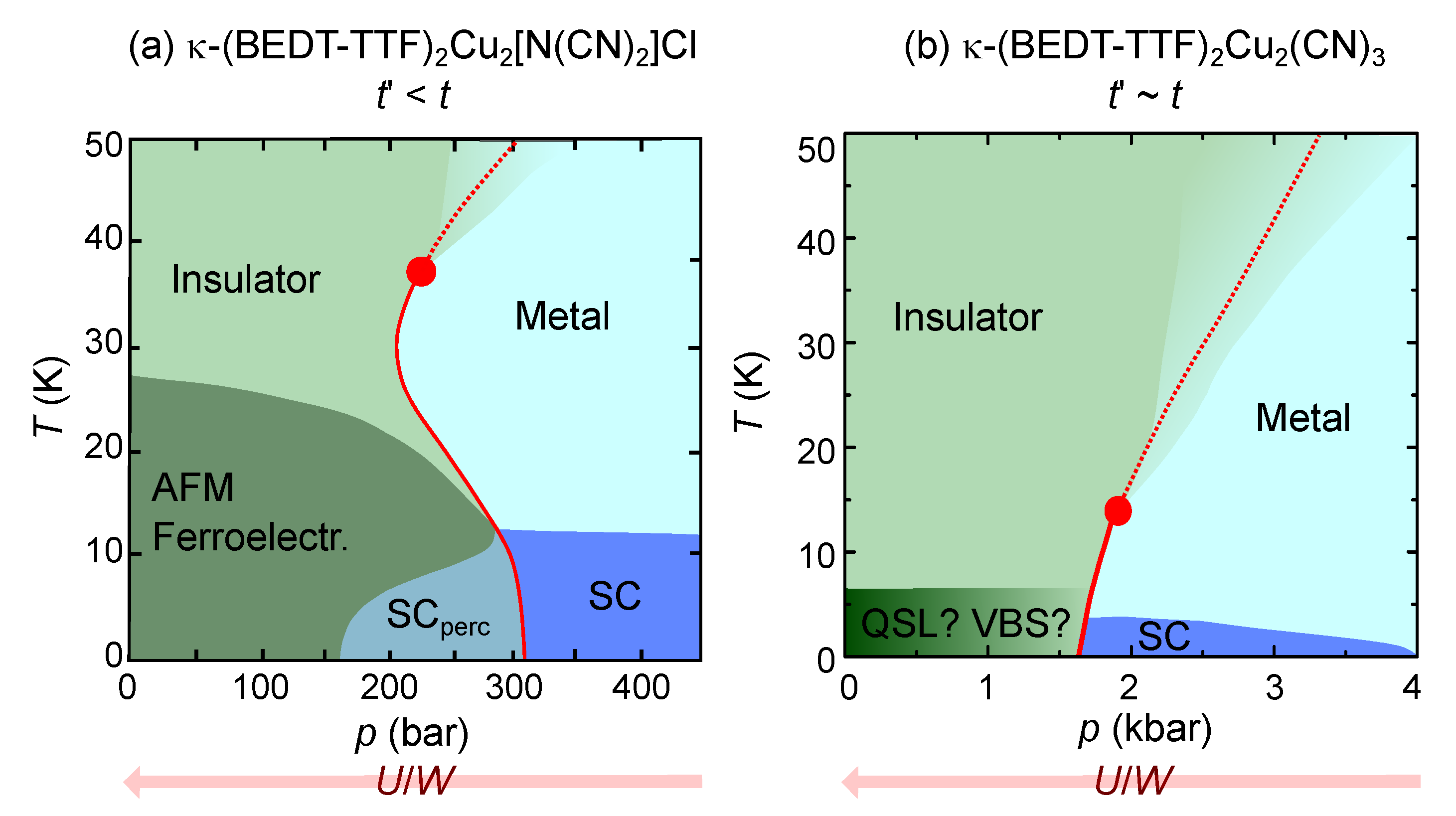
1.2. Phase Diagram
1.3. Outline of This Review
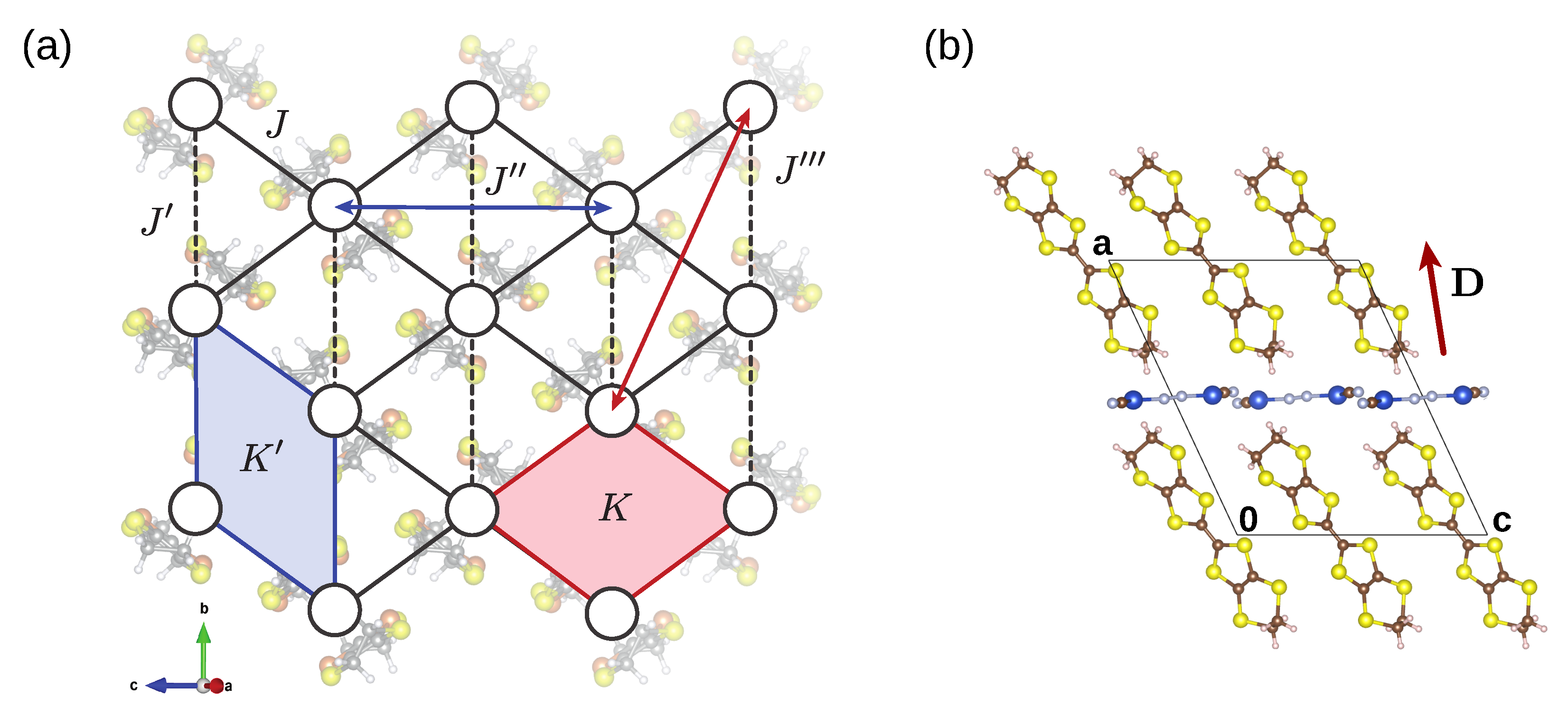
2. Magnetic Exchange beyond Heisenberg
2.1. Magnetic Bilinear Anisotropic Interactions
2.2. Four-Spin Ring Exchange
3. New Physics in the Extended Molecule-Based Model
3.1. Ferroelectricity in the Mott Insulating Ground State
3.2. Superconductivity in Extended Molecule-Based Models
4. Coupling of Correlated Electrons to the Crystal Lattice
4.1. Critical Elasticity around the Mott Critical Endpoint
4.2. Phonon Anomalies Probed by Inelastic Neutron Scattering
5. Role of Disorder
5.1. Experimental Study of Phenomena Close to the Mott Transition under Controlled Disorder
5.2. Disorder in the Magnetic Phase: Scenario of a Valence Bond Solid Host with Orphan Spins
6. Conclusions and Outlook
- As discussed in the review, ab-initio extracted magnetic models for triangular -phase charge-transfer salts indicate the importance of four-spin interaction terms with spin-orbit coupling effects, as well as, in the presence of a magnetic field, possible products of an odd number of spin operators, such as the scalar spin chirality. What (quantum) phases are to be expected arising from these interactions that are relevant for these materials?
- How do intra-dimer charge and spin degrees of freedom conspire in the ground-state properties of frustrated Mott insulating -phase charge-transfer salts? In particular, what impact do the intra-dimer charge degrees of freedom have in promoting (impeding) the formation of long-range spin order? Can these effects be theoretically described with models containing both, spin and charge degrees of freedom?
- What is the role of magnetoelastic coupling in the formation of novel states of matter, such as putative spin-liquid states in -(BEDT-TTF)? Can we develop accurate models to capture these effects?
- Can we quantitatively describe the impact of disorder on the properties of these charge-transfer salts close to the Mott metal–insulator transition experimentally and theoretically? To this end, how can we accurately quantify the level of disorder in real materials and determine the nature of the disorder and their spatial distribution? Which models and methods allow to theoretically describe the interaction between disorder and bulk properties properly?
- What novel phases may be realized under non-equilibrium conditions [176]?
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kanoda, K. Recent progress in NMR studies on organic conductors. Hyperfine Interact 1997, 104, 235–249. [Google Scholar] [CrossRef]
- Toyota, N.; Lang, M.; Müller, J. Low-Dimensional Molecular Metals; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Limelette, P.; Wzietek, P.; Florens, S.; Georges, A.; Costi, T.A.; Pasquier, C.; Jérome, D.; Mézière, C.; Batail, P. Mott Transition and Transport Crossovers in the Organic Compound κ-(BEDT-TTF)2Cu[N(CN)2]Cl. Phys. Rev. Lett. 2003, 91, 016401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fournier, D.; Poirier, M.; Castonguay, M.; Truong, K.D. Mott Transition, Compressibility Divergence, and the P-T Phase Diagram of Layered Organic Superconductors: An Ultrasonic Investigation. Phys. Rev. Lett. 2003, 90, 127002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pustogow, A.; Rösslhuber, R.; Tan, Y.; Uykur, E.; Böhme, A.; Wenzel, M.; Saito, Y.; Löhle, A.; Hübner, R.; Kawamoto, A.; et al. Low-temperature dielectric anomaly arising from electronic phase separation at the Mott insulator-metal transition. npj Quantum Mater. 2021, 6, 9. [Google Scholar] [CrossRef]
- Kagawa, F.; Miyagawa, K.; Kanoda, K. Magnetic Mott criticality in a κ-type organic salt probed by NMR. Nat. Phys. 2009, 5, 880–884. [Google Scholar] [CrossRef]
- Furukawa, T.; Miyagawa, M.; Taniguchi, H.; Kato, R.; Kanoda, K. Quantum criticality of Mott transition in organic materials. Nat. Phys. 2015, 11, 221–224. [Google Scholar] [CrossRef] [Green Version]
- Isono, T.; Terashima, T.; Miyagawa, K.; Kanoda, K.; Uji, S. Quantum criticality in an organic spin-liquid insulator κ-(BEDT-TTF)2Cu2(CN)3. Nat. Commun. 2016, 7, 13494. [Google Scholar] [CrossRef] [Green Version]
- Gati, E.; Garst, M.; Manna, R.; Tutsch, U.; Wolf, B.; Bartosch, L.; Schubert, H.; Sasaki, T.; Schlueter, J.; Lang, M. Breakdown of Hooke’s law of elasticity at the Mott critical endpoint in an organic conductor. Sci. Adv. 2016, 2, e160146. [Google Scholar] [CrossRef] [Green Version]
- Shimizu, Y.; Miyagawa, K.; Kanoda, K.; Maesato, M.; Saito, G. Spin Liquid State in an Organic Mott Insulator with a Triangular Lattice. Phys. Rev. Lett. 2003, 91, 107001. [Google Scholar] [CrossRef] [Green Version]
- Powell, B.J.; McKenzie, R.H. Quantum frustration in organic Mott insulators: From spin liquids to unconventional superconductors. Rep. Prog. Phys. 2011, 74, 056501. [Google Scholar] [CrossRef]
- Riedl, K.; Valentí, R.; Winter, S.M. Critical spin liquid versus valence-bond glass in a triangular-lattice organic antiferromagnet. Nat. Commun. 2019, 10, 2561. [Google Scholar] [CrossRef] [Green Version]
- Pustogow, A. Thirty-Year Anniversary of κ-(BEDT-TTF)2Cu2(CN)3: Reconciling the Spin Gap in a Spin-Liquid Candidate. Solids 2022, 3, 93–110. [Google Scholar] [CrossRef]
- Wosnitza, J. Superconductivity of organic charge-transfer salts. J. Low Temp. Phys. 2019, 197, 250–271. [Google Scholar] [CrossRef]
- Guterding, D.; Altmeyer, M.; Jeschke, H.O.; Valentí, R. Near-degeneracy of extended s + dx2−y2 and dxy order parameters in quasi-two-dimensional organic superconductors. Phys. Rev. B 2016, 94, 024515. [Google Scholar] [CrossRef] [Green Version]
- Lunkenheimer, P.; Müller, J.; Krohns, S.; Schrettle, F.; Loidl, A.; Hartmann, B.; Rommel, R.; de Souza, M.; Hotta, C.; Schlueter, J.; et al. Multiferroicity in an organic charge-transfer salt that is suggestive of electric-dipole-driven magnetism. Nat. Mater. 2012, 11, 755–758. [Google Scholar] [CrossRef]
- Komatsu, T.; Matsukawa, N.; Inoue, T.; Saito, G. Realization of Superconductivity at Ambient Pressure by Band-Filling Control in κ-(BEDT-TTF)2Cu2(CN)3. J. Phys. Soc. Jpn. 1996, 65, 1340–1354. [Google Scholar] [CrossRef]
- Kandpal, H.C.; Opahle, I.; Zhang, Y.Z.; Jeschke, H.O.; Valentí, R. Revision of Model Parameters for κ-Type Charge Transfer Salts: An Ab Initio Study. Phys. Rev. Lett. 2009, 103, 067004. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hotta, C. Theories on Frustrated Electrons in Two-Dimensional Organic Solids. Crystals 2012, 2, 1155. [Google Scholar] [CrossRef] [Green Version]
- Pustogow, A.; Bories, M.; Löhle, A.; Rösslhuber, R.; Zhukova, E.; Gorshunov, B.; Tomić, S.; Schlueter, J.A.; Hübner, R.; Hiramatsu, T.; et al. Quantum spin liquids unveil the genuine Mott state. Nat. Mater. 2018, 17, 773. [Google Scholar] [CrossRef]
- Lefebvre, S.; Wzietek, P.; Brown, S.; Bourbonnais, C.; Jérome, D.; Mézière, C.; Fourmigué, M.; Batail, P. Mott Transition, Antiferromagnetism, and Unconventional Superconductivity in Layered Organic Superconductors. Phys. Rev. Lett. 2000, 85, 5420–5423. [Google Scholar] [CrossRef]
- Kagawa, F.; Itou, T.; Miyagawa, K.; Kanoda, K. Transport criticality of the first-order Mott transition in the quasi-two-dimensional organic conductor κ-(BEDT-TTF)2Cu[N(CN)2]Cl. Phys. Rev. B 2004, 69, 064511. [Google Scholar] [CrossRef] [Green Version]
- Kurosaki, Y.; Shimizu, Y.; Miyagawa, K.; Kanoda, K.; Saito, G. Mott Transition from a Spin Liquid to a Fermi Liquid in the Spin-Frustrated Organic Conductor κ-(ET)2Cu2(CN)3. Phys. Rev. Lett. 2005, 95, 177001. [Google Scholar] [CrossRef] [Green Version]
- Zverev, V.N.; Kartsovnik, M.V.; Biberacher, W.; Khasanov, S.S.; Shibaeva, R.P.; Ouahab, L.; Toupet, L.; Kushch, N.D.; Yagubskii, E.B.; Canadell, E. Temperature-pressure phase diagram and electronic properties of the organic metal κ-(BETS)2Mn[N(CN)2]3. Phys. Rev. B 2010, 82, 155123. [Google Scholar] [CrossRef] [Green Version]
- Zverev, V.N.; Biberacher, W.; Oberbauer, S.; Sheikin, I.; Alemany, P.; Canadell, E.; Kartsovnik, M.V. Fermi surface properties of the bifunctional organic metal κ-(BETS)2Mn[N(CN)2]3 near the metal-insulator transition. Phys. Rev. B 2019, 99, 125136. [Google Scholar] [CrossRef] [Green Version]
- Vyaselev, O.M.; Kartsovnik, M.V.; Biberacher, W.; Zorina, L.V.; Kushch, N.D.; Yagubskii, E.B. Magnetic transformations in the organic conductor κ-(BETS)2Mn[N(CN)2]3 at the metal-insulator transition. Phys. Rev. B 2011, 83, 094425. [Google Scholar] [CrossRef] [Green Version]
- Castellani, C.; Castro, C.D.; Feinberg, D.; Ranninger, J. New Model Hamiltonian for the Metal-Insulator Transition. Phys. Rev. Lett. 1979, 43, 1957–1960. [Google Scholar] [CrossRef]
- Kotliar, G.; Lange, E.; Rozenberg, M.J. Landau Theory of the Finite Temperature Mott Transition. Phys. Rev. Lett. 2000, 84, 5180–5183. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Georges, A.; Kotliar, G.; Krauth, W.; Rozenberg, M.J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 1996, 68, 13–125. [Google Scholar] [CrossRef] [Green Version]
- Vučičević, J.; Terletska, H.; Tanasković, D.; Dobrosavljević, V. Finite-temperature crossover and the quantum Widom line near the Mott transition. Phys. Rev. B 2013, 88, 075143. [Google Scholar] [CrossRef] [Green Version]
- Terletska, H.; Vučičević, J.; Tanasković, D.; Dobrosavljević, V. Quantum Critical Transport near the Mott Transition. Phys. Rev. Lett. 2011, 107, 026401. [Google Scholar] [CrossRef] [PubMed]
- Ferber, J.; Foyevtsova, K.; Jeschke, H.O.; Valentí, R. Unveiling the microscopic nature of correlated organic conductors: The case of κ-(ET)2Cu[N(CN)2]BrxCl1−x. Phys. Rev. B 2014, 89, 205106. [Google Scholar] [CrossRef]
- Leiner, J.C.; Jeschke, H.O.; Valentí, R.; Zhang, S.; Savici, A.T.; Lin, J.Y.Y.; Stone, M.B.; Lumsden, M.D.; Hong, J.; Delaire, O.; et al. Frustrated Magnetism in Mott Insulating (V1−xCrx)2O3. Phys. Rev. X 2019, 9, 011035. [Google Scholar] [CrossRef] [Green Version]
- Miksch, B.; Pustogow, A.; Javaheri Rahim, M.; Bardin, A.A.; Kanoda, K.; Schlueter, J.A.; Hübner, R.; Scheffler, M.; Dressel, M. Gapped magnetic ground state in quantum spin liquid candidate κ-(BEDT-TTF)2Cu2(CN)3. Science 2021, 372, 276. [Google Scholar] [CrossRef]
- Miyagawa, K.; Kawamoto, A.; Nakazawa, Y.; Kanoda, K. Antiferromagnetic Ordering and Spin Structure in the Organic Conductor, κ-(BEDT-TTF)2Cu[N(CN)2]Cl. Phys. Rev. Lett. 1995, 75, 1174–1177. [Google Scholar] [CrossRef]
- Pustogow, A.; Le, T.; Wang, H.H.; Luo, Y.; Gati, E.; Schubert, H.; Lang, M.; Brown, S.E. Impurity moments conceal low-energy relaxation of quantum spin liquids. Phys. Rev. B 2020, 101, 140401. [Google Scholar] [CrossRef] [Green Version]
- Matsuura, M.; Sasaki, T.; Naka, M.; Müller, J.; Stockert, O.; Piovano, A.; Yoneyama, N.; Lang, M. Phonon renormalization effects accompanying the 6 K anomaly in the Quantum Spin Liquid Candidate κ-(BEDT-TTF)2Cu2(CN)3. arXiv 2022, arXiv:2208.05096. [Google Scholar]
- Pustogow, A.; Kawasugi, Y.; Sakurakoji, H.; Tajima, N. Chasing the spin gap through the phase diagram of a frustrated Mott insulator. arXiv 2022, arXiv:2209.07639. [Google Scholar]
- Koretsune, T.; Hotta, C. Evaluating model parameters of the κ- and β′-type Mott insulating organic solids. Phys. Rev. B 2014, 89, 045102. [Google Scholar] [CrossRef]
- Nakamura, K.; Yoshimoto, Y.; Kosugi, T.; Arita, R.; Imada, M. Ab initio Derivation of Low-Energy Model for κ-ET Type Organic Conductors. J. Phys. Soc. Jpn. 2009, 78, 083710. [Google Scholar] [CrossRef] [Green Version]
- Nakamura, K.; Yoshimoto, Y.; Imada, M. Ab initio two-dimensional multiband low-energy models of EtMe3Sb[Pd(dmit)2]2 and κ-(BEDT-TTF)2Cu(NCS)2 with comparisons to single-band models. Phys. Rev. B 2012, 86, 205117. [Google Scholar] [CrossRef] [Green Version]
- Jeschke, H.O.; de Souza, M.; Valentí, R.; Manna, R.S.; Lang, M.; Schlueter, J.A. Temperature dependence of structural and electronic properties of the spin-liquid candidate κ-(BEDT-TTF)2Cu2(CN)3. Phys. Rev. B 2012, 85, 035125. [Google Scholar] [CrossRef] [Green Version]
- Tocchio, L.F.; Feldner, H.; Becca, F.; Valentí, R.; Gros, C. Spin-liquid versus spiral-order phases in the anisotropic triangular lattice. Phys. Rev. B 2013, 87, 035143. [Google Scholar] [CrossRef]
- Starykh, O.A. Unusual ordered phases of highly frustrated magnets: A review. Rep. Prog. Phys. 2015, 78, 052502. [Google Scholar] [CrossRef]
- Szasz, A.; Motruk, J.; Zaletel, M.P.; Moore, J.E. Chiral spin liquid phase of the triangular lattice Hubbard model: A density matrix renormalization group study. Phys. Rev. X 2020, 10, 021042. [Google Scholar] [CrossRef]
- Yamashita, S.; Nakazawa, Y.; Oguni, M.; Oshima, Y.; Nojiri, H.; Shimizu, Y.; Miyagawa, K.; Kanoda, K. Thermodynamic properties of a spin-1/2 spin-liquid state in a κ-type organic salt. Nat. Phys. 2008, 4, 459. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.S.; Lee, P.A. U(1) Gauge Theory of the Hubbard Model: Spin Liquid States and Possible Application to κ-(BEDT-TTF)2Cu2(CN)3. Phys. Rev. Lett. 2005, 95, 036403. [Google Scholar] [CrossRef] [Green Version]
- Manna, R.S.; Wolf, B.; de Souza, M.; Lang, M. High-resolution thermal expansion measurements under helium-gas pressure. Rev. Sci. Instrum. 2012, 83, 085111. [Google Scholar] [CrossRef] [Green Version]
- Hartmann, S.; Gati, E.; Yoshida, Y.; Saito, G.; Lang, M. Thermal Expansion Studies on the Spin-Liquid-Candidate System κ-(BEDT-TTF)2Ag2(CN)3. Phys. Status Solidi 2019, 256, 1800640. [Google Scholar] [CrossRef]
- Shimizu, Y.; Miyagawa, K.; Kanoda, K.; Maesato, M.; Saito, G. Emergence of inhomogeneous moments from spin liquid in the triangular-lattice Mott insulator κ-(ET)2Cu2(CN)3. Phys. Rev. B 2006, 73, 140407. [Google Scholar] [CrossRef] [Green Version]
- Riedl, K.; Gati, E.; Zielke, D.; Hartmann, S.; Vyaselev, O.M.; Kushch, N.D.; Jeschke, H.O.; Lang, M.; Valentí, R.; Kartsovnik, M.V.; et al. Spin Vortex Crystal Order in Organic Triangular Lattice Compound. Phys. Rev. Lett. 2021, 127, 147204. [Google Scholar] [CrossRef]
- Lang, M.; Müller, J. Quasi-Twodimensional Organic Superconductors. In Superconductivity Review; Citeseer: University Park, PA, USA; OPA: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Wosnitza, J. Quasi-Two-Dimensional Organic Superconductors. J. Low Temp. Phys. 2007, 146, 641–667. [Google Scholar] [CrossRef]
- McKenzie, R.H. Similarities Between Organic and Cuprate Superconductors. Science 1997, 278, 820–821. [Google Scholar] [CrossRef]
- Schmalian, J. Pairing due to Spin Fluctuations in Layered Organic Superconductors. Phys. Rev. Lett. 1998, 81, 4232–4235. [Google Scholar] [CrossRef] [Green Version]
- Kino, H.; Kontani, H. Phase Diagram of Superconductivity on the Anisotropic Triangular Lattice Hubbard Model: An Effective Model of κ-(BEDT-TTF) Salts. J. Phys. Soc. Jpn. 1998, 67, 3691–3694. [Google Scholar] [CrossRef] [Green Version]
- Kyung, B.; Tremblay, A.M. Mott transition, antiferromagnetism, and d-wave superconductivity in two-dimensional organic conductors. Phys. Rev. Lett. 2006, 97, 046402. [Google Scholar] [CrossRef] [Green Version]
- Hébert, C.D.; Sémon, P.; Tremblay, A.M.S. Superconducting dome in doped quasi-two-dimensional organic Mott insulators: A paradigm for strongly correlated superconductivity. Phys. Rev. B 2015, 92, 195112. [Google Scholar] [CrossRef] [Green Version]
- Watanabe, T.; Yokoyama, H.; Tanaka, Y.; Inoue, J.I. Superconductivity and a Mott Transition in a Hubbard Model on an Anisotropic Triangular Lattice. J. Phys. Soc. Jpn. 2006, 75, 074707. [Google Scholar] [CrossRef] [Green Version]
- Guterding, D.; Diehl, S.; Altmeyer, M.; Methfessel, T.; Tutsch, U.; Schubert, H.; Lang, M.; Müller, J.; Huth, M.; Jeschke, H.O.; et al. Evidence for Eight-Node Mixed-Symmetry Superconductivity in a Correlated Organic Metal. Phys. Rev. Lett. 2016, 116, 237001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zantout, K.; Altmeyer, M.; Backes, S.; Valentí, R. Superconductivity in correlated BEDT-TTF molecular conductors: Critical temperatures and gap symmetries. Phys. Rev. B 2018, 97, 014530. [Google Scholar] [CrossRef] [Green Version]
- Chao, K.; Spałek, J.; Oleś, A. Canonical perturbation expansion of the Hubbard model. Phys. Rev. B 1978, 18, 3453. [Google Scholar] [CrossRef]
- Gros, C.; Joynt, R.; Rice, T.M. Antiferromagnetic correlations in almost-localized Fermi liquids. Phys. Rev. B 1987, 36, 381. [Google Scholar] [CrossRef] [PubMed]
- Winter, S.M.; Riedl, K.; Valentí, R. Importance of spin-orbit coupling in layered organic salts. Phys. Rev. B 2017, 95, 060404. [Google Scholar] [CrossRef]
- Balents, L. Spin liquids in frustrated magnets. Nature 2010, 464, 199–208. [Google Scholar] [CrossRef] [PubMed]
- Bernevig, B.A. Topological insulators and topological superconductors. In Topological Insulators and Topological Superconductors; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Riedl, K. First Principles Studies of Frustrated Spin Systems: From Low-Energy Models to Experiments. Ph.D. Thesis, Goethe-Universität Frankfurt am Main, Frankfurt am Main, Germany, 2019. [Google Scholar]
- Shekhtman, L.; Entin-Wohlman, O.; Aharony, A. Moriya’s anisotropic superexchange interaction, frustration, and Dzyaloshinsky’s weak ferromagnetism. Phys. Rev. Lett. 1992, 69, 836–839. [Google Scholar] [CrossRef] [PubMed]
- Pratt, F.L.; Baker, P.J.; Blundell, S.J.; Lancaster, T.; Ohira-Kawamura, S.; Baines, C.; Shimizu, Y.; Kanoda, K.; Watanabe, I.; Saito, G. Magnetic and non-magnetic phases of a quantum spin liquid. Nature 2011, 471, 612. [Google Scholar] [CrossRef] [PubMed]
- Motrunich, O.I. Variational study of triangular lattice spin-1/2 model with ring exchanges and spin liquid state in κ-(ET)2Cu2 (CN)3. Phys. Rev. B 2005, 72, 045105. [Google Scholar] [CrossRef] [Green Version]
- Block, M.S.; Sheng, D.N.; Motrunich, O.I.; Fisher, M.P.A. Spin Bose-Metal and Valence Bond Solid Phases in a Spin-1/2 Model with Ring Exchanges on a Four-Leg Triangular Ladder. Phys. Rev. Lett. 2011, 106, 157202. [Google Scholar] [CrossRef] [Green Version]
- Holt, M.; Powell, B.J.; Merino, J. Spin-liquid phase due to competing classical orders in the semiclassical theory of the Heisenberg model with ring exchange on an anisotropic triangular lattice. Phys. Rev. B 2014, 89, 174415. [Google Scholar] [CrossRef] [Green Version]
- Cookmeyer, T.; Motruk, J.; Moore, J.E. Four-spin terms and the origin of the chiral spin liquid in Mott insulators on the triangular lattice. Phys. Rev. Lett. 2021, 127, 087201. [Google Scholar] [CrossRef]
- Vyaselev, O.M.; Kato, R.; Yamamoto, H.M.; Kobayashi, M.; Zorina, L.V.; Simonov, S.V.; Kushch, N.D.; Yagubskii, E.B. Properties of Mn2+ and π-Electron Spin Systems Probed by 1H and 13C NMR in the Organic Conductor κ-(BETS)2Mn [N (CN)2]3. Crystals 2012, 2, 224–235. [Google Scholar] [CrossRef] [Green Version]
- Vyaselev, O.M.; Biberacher, W.; Kushch, N.D.; Kartsovnik, M.V. Interplay between the d- and π-electron systems in magnetic torque of the layered organic conductor κ-(BETS)2Mn[N(CN)2]3. Phys. Rev. B 2017, 96, 205154. [Google Scholar] [CrossRef] [Green Version]
- Mori, T.; Katsuhara, M. Estimation of πd-Interactions in Organic Conductors Including Magnetic Anions. J. Phys. Soc. Jpn. 2002, 71, 826–844. [Google Scholar] [CrossRef]
- Konoike, T.; Uji, S.; Terashima, T.; Nishimura, M.; Yasuzuka, S.; Enomoto, K.; Fujiwara, H.; Zhang, B.; Kobayashi, H. Magnetic-field-induced superconductivity in the antiferromagnetic organic superconductor κ-(BETS)2FeBr4. Phys. Rev. B 2004, 70, 094514. [Google Scholar] [CrossRef]
- Kartsovnik, M.V.; Kunz, M.; Schaidhammer, L.; Kollmannsberger, F.; Biberacher, W.; Kushch, N.D.; Miyazaki, A.; Fujiwara, H. Interplay between conducting and magnetic systems in the antiferromagnetic organic superconductor κ-(BETS)2FeBr4. J. Supercond. Nov. Magn. 2016, 29, 3075–3080. [Google Scholar] [CrossRef] [Green Version]
- Jaccarino, V.; Peter, M. Ultra-high-field superconductivity. Phys. Rev. Lett. 1962, 9, 290. [Google Scholar] [CrossRef]
- Vyaselev, O.M.; Kartsovnik, M.V.; Kushch, N.D.; Yagubskii, E.B. Staggered spin order of localized π-electrons in the insulating state of the organic conductor κ-(BETS)2Mn[N(CN)2]3. JETP Lett. 2012, 95, 565–569. [Google Scholar] [CrossRef]
- Hotta, C. Quantum electric dipoles in spin-liquid dimer Mott insulator κ-ET2Cu2(CN)3. Phys. Rev. B 2010, 82, 241104. [Google Scholar] [CrossRef] [Green Version]
- Kaneko, R.; Tocchio, L.F.; Valentí, R.; Becca, F. Charge orders in organic charge-transfer salts. New J. Phys. 2017, 19, 103033. [Google Scholar] [CrossRef] [Green Version]
- Seo, H.; Hotta, C.; Fukuyama, H. Toward Systematic Understanding of Diversity of Electronic Properties in Low-Dimensional Molecular Solids. Chem. Rev. 2004, 104, 5005–5036. [Google Scholar] [CrossRef]
- Lunkenheimer, P.; Loidl, A. Dielectric spectroscopy on organic charge-transfer salts. J. Phys. Condens. Matter 2015, 27, 373001. [Google Scholar] [CrossRef] [Green Version]
- Abdel-Jawad, M.; Terasaki, I.; Sasaki, T.; Yoneyama, N.; Kobayashi, N.; Uesu, Y.; Hotta, C. Anomalous dielectric response in the dimer Mott insulator κ-(BEDT-TTF)2Cu2(CN)3. Phys. Rev. B 2010, 82, 125119. [Google Scholar] [CrossRef] [Green Version]
- Gati, E.; Fischer, J.K.H.; Lunkenheimer, P.; Zielke, D.; Köhler, S.; Kolb, F.; von Nidda, H.A.K.; Winter, S.M.; Schubert, H.; Schlueter, J.A.; et al. Evidence for Electronically Driven Ferroelectricity in a Strongly Correlated Dimerized BEDT-TTF Molecular Conductor. Phys. Rev. Lett. 2018, 120, 247601. [Google Scholar] [CrossRef]
- Manna, R.S.; de Souza, M.; Brühl, A.; Schlueter, J.A.; Lang, M. Lattice Effects and Entropy Release at the Low-Temperature Phase Transition in the Spin-Liquid Candidate κ-(BEDT-TTF)2Cu2(CN)3. Phys. Rev. Lett. 2010, 104, 016403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lang, M.; Lunkenheimer, P.; Müller, J.; Loidl, A.; Hartmann, B.; Hoang, N.H.; Gati, E.; Schubert, H.; Schlueter, J.A. Multiferroicity in the Mott Insulating Charge-Transfer Salt κ-(BEDT-TTF)2Cu[N(CN)2]Cl. IEEE Trans. Magn. 2014, 50, 2700107. [Google Scholar] [CrossRef] [Green Version]
- Itoh, K.; Itoh, H.; Naka, M.; Saito, S.; Hosako, I.; Yoneyama, N.; Ishihara, S.; Sasaki, T.; Iwai, S. Collective Excitation of an Electric Dipole on a Molecular Dimer in an Organic Dimer-Mott Insulator. Phys. Rev. Lett. 2013, 110, 106401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gomi, H.; Imai, T.; Takahashi, A.; Aihara, M. Purely electronic terahertz polarization in dimer Mott insulators. Phys. Rev. B 2010, 82, 035101. [Google Scholar] [CrossRef] [Green Version]
- Gomi, H.; Ikenaga, M.; Hiragi, Y.; Segawa, D.; Takahashi, A.; Inagaki, T.J.; Aihara, M. Ferroelectric states induced by dimer lattice disorder in dimer Mott insulators. Phys. Rev. B 2013, 87, 195126. [Google Scholar] [CrossRef]
- van den Brink, J.; Khomskii, D.I. Multiferroicity due to charge ordering. J. Phys. Condens. Matter 2008, 20, 434217. [Google Scholar] [CrossRef]
- Nad, F.; Monceau, P. Dielectric Response of the Charge Ordered State in Quasi-One-Dimensional Organic Conductors. J. Phys. Soc. Jpn. 2006, 75, 051005. [Google Scholar] [CrossRef]
- Lunkenheimer, P.; Hartmann, B.; Lang, M.; Müller, J.; Schweitzer, D.; Krohns, S.; Loidl, A. Ferroelectric properties of charge-ordered α-(BEDT-TTF)2I3. Phys. Rev. B 2015, 91, 245132. [Google Scholar] [CrossRef] [Green Version]
- Takano, Y.; Hiraki, K.; Yamamoto, H.; Nakamura, T.; Takahashi, T. Charge disproportionation in the organic conductor, α-(BEDT-TTF)2I3. J. Phys. Chem. Solids 2001, 62, 393–395. [Google Scholar] [CrossRef]
- Tomić, S.; Dressel, M. Ferroelectricity in molecular solids: A review of electrodynamic properties. Rep. Prog. Phys. 2015, 78, 096501. [Google Scholar] [CrossRef] [PubMed]
- Sedlmeier, K.; Elsässer, S.; Neubauer, D.; Beyer, R.; Wu, D.; Ivek, T.; Tomić, S.; Schlueter, J.A.; Dressel, M. Absence of charge order in the dimerized κ-phase BEDT-TTF salts. Phys. Rev. B 2012, 86, 245103. [Google Scholar] [CrossRef] [Green Version]
- Tomić, S.; Pinterić, M.; Ivek, T.; Sedlmeier, K.; Beyer, R.; Wu, D.; Schlueter, J.A.; Schweitzer, D.; Dressel, M. Magnetic ordering and charge dynamics in κ-(BEDT-TTF)2Cu[N(CN)2]Cl. J. Phys. Condens. Matter 2013, 25, 436004. [Google Scholar] [CrossRef] [Green Version]
- Pinterić, M.; Čulo, M.; Milat, O.; Basletić, M.; Korin-Hamzić, B.; Tafra, E.; Hamzić, A.; Ivek, T.; Peterseim, T.; Miyagawa, K.; et al. Anisotropic charge dynamics in the quantum spin-liquid candidate κ-(BEDT-TTF)2Cu2(CN)3. Phys. Rev. B 2014, 90, 195139. [Google Scholar] [CrossRef] [Green Version]
- Pinterić, M.; Lazić, P.; Pustogow, A.; Ivek, T.; Kuveždić, M.; Milat, O.; Gumhalter, B.; Basletić, M.; Čulo, M.; Korin-Hamzić, B.; et al. Anion effects on electronic structure and electrodynamic properties of the Mott insulator κ-(BEDT-TTF)2Ag2(CN)3. Phys. Rev. B 2016, 94, 161105. [Google Scholar] [CrossRef] [Green Version]
- Dressel, M.; Lazić, P.; Pustogow, A.; Zhukova, E.; Gorshunov, B.; Schlueter, J.A.; Milat, O.; Gumhalter, B.; Tomić, S. Lattice vibrations of the charge-transfer salt κ-(BEDT-TTF)2Cu2(CN)3: Comprehensive explanation of the electrodynamic response in a spin-liquid compound. Phys. Rev. B 2016, 93, 081201. [Google Scholar] [CrossRef] [Green Version]
- Lazić, P.; Pinterić, M.; Rivas Góngora, D.; Pustogow, A.; Treptow, K.; Ivek, T.; Milat, O.; Gumhalter, B.; Došlić, N.; Dressel, M.; et al. Importance of van der Waals interactions and cation-anion coupling in an organic quantum spin liquid. Phys. Rev. B 2018, 97, 245134. [Google Scholar] [CrossRef] [Green Version]
- Rösslhuber, R.; Pustogow, A.; Uykur, E.; Böhme, A.; Löhle, A.; Hübner, R.; Schlueter, J.A.; Tan, Y.; Dobrosavljević, V.; Dressel, M. Phase coexistence at the first-order Mott transition revealed by pressure-dependent dielectric spectroscopy of κ-(BEDT-TTF)2-Cu2(CN)3. Phys. Rev. B 2021, 103, 125111. [Google Scholar] [CrossRef]
- Drichko, N.; Beyer, R.; Rose, E.; Dressel, M.; Schlueter, J.A.; Turunova, S.A.; Zhilyaeva, E.I.; Lyubovskaya, R.N. Metallic state and charge-order metal-insulator transition in the quasi-two-dimensional conductor κ-(BEDT-TTF)2Hg(SCN)2Cl. Phys. Rev. B 2014, 89, 075133. [Google Scholar] [CrossRef]
- Lines, M.E.; Glass, A.M. Principles and Applications of Ferroelectrics and Related Materials; Related Materials; Clarendon Press: Oxford, UK, 1977. [Google Scholar]
- Hassan, N.; Cunningham, S.; Mourigal, M.; Zhilyaeva, E.I.; Torunova, S.A.; Lyubovskaya, R.N.; Schlueter, J.A.; Drichko, N. Evidence for a quantum dipole liquid state in an organic quasi–two-dimensional material. Science 2018, 360, 1101. [Google Scholar] [CrossRef] [Green Version]
- Hassan, N.M.; Thirunavukkuarasu, K.; Lu, Z.; Smirnov, D.; Zhilyaeva, E.I.; Torunova, S.; Lyubovskaya, R.N.; Drichko, N. Melting of charge order in the low-temperature state of an electronic ferroelectric-like system. npj Quantum Mater. 2020, 5, 15. [Google Scholar] [CrossRef]
- Kuroki, K.; Kimura, T.; Arita, R.; Tanaka, Y.; Matsuda, Y. dx2−y2− versus dxy− like pairings in organic superconductors κ-(BEDT-TTF)2X. Phys. Rev. B 2002, 65, 100516. [Google Scholar] [CrossRef] [Green Version]
- Watanabe, H.; Seo, H.; Yunoki, S. Phase Competition and Superconductivity in κ-(BEDT-TTF)2X: Importance of Intermolecular Coulomb Interactions. J. Phys. Soc. Jpn. 2017, 86, 033703. [Google Scholar] [CrossRef]
- Sekine, A.; Nasu, J.; Ishihara, S. Polar charge fluctuation and superconductivity in organic conductors. Phys. Rev. B 2013, 87, 085133. [Google Scholar] [CrossRef] [Green Version]
- Gomes, N.; De Silva, W.W.; Dutta, T.; Clay, R.T.; Mazumdar, S. Coulomb-enhanced superconducting pair correlations and paired-electron liquid in the frustrated quarter-filled band. Phys. Rev. B 2016, 93, 165110. [Google Scholar] [CrossRef] [Green Version]
- Majumdar, P.; Krishnamurthy, H.R. Lattice Contraction Driven Insulator-Metal Transition in the d = ∞ Local Approximation. Phys. Rev. Lett. 1994, 73, 1525–1528. [Google Scholar] [CrossRef] [PubMed]
- Hassan, S.R.; Georges, A.; Krishnamurthy, H.R. Sound Velocity Anomaly at the Mott Transition: Application to Organic Conductors and V2O3. Phys. Rev. Lett. 2005, 94, 036402. [Google Scholar] [CrossRef] [Green Version]
- Kuo, H.H.; Chu, J.H.; Palmstrom, J.C.; Kivelson, S.A.; Fisher, I.R. Ubiquitous signatures of nematic quantum criticality in optimally doped Fe-based superconductors. Science 2016, 352, 958. [Google Scholar] [CrossRef] [Green Version]
- Fernandes, R.; Chubukov, A.; Schmalian, J. What drives nematic order in iron-based superconductors? Nat. Phys. 2014, 10, 97. [Google Scholar] [CrossRef] [Green Version]
- Achkar, A.J.; Zwiebler, M.; McMahon, C.; He, F.; Sutarto, R.; Djianto, I.; Hao, Z.; Gingras, M.J.P.; Hücker, M.; Gu, G.D.; et al. Nematicity in stripe-ordered cuprates probed via resonant X-ray scattering. Science 2016, 351, 576. [Google Scholar] [CrossRef] [Green Version]
- Cano, A.; Civelli, M.; Eremin, I.; Paul, I. Interplay of magnetic and structural transitions in iron-based pnictide superconductors. Phys. Rev. B 2010, 82, 020408. [Google Scholar] [CrossRef]
- Böhmer, A.E.; Meingast, C. Electronic nematic susceptibility of iron-based superconductors. C. R. Phys. 2016, 17, 90–112. [Google Scholar] [CrossRef]
- Gati, E.; Xiang, L.; Bud’ko, S.L.; Canfield, P.C. Hydrostatic and Uniaxial Pressure Tuning of Iron-Based Superconductors: Insights into Superconductivity, Magnetism, Nematicity, and Collapsed Tetragonal Transitions. Ann. Phys. 2020, 532, 2000248. [Google Scholar] [CrossRef]
- Manna, R.S.; de Souza, M.; Kato, R.; Lang, M. Lattice effects in the quasi-two-dimensional valence-bond-solid Mott insulator EtMe3P[Pd(dmit)2]2. Phys. Rev. B 2014, 89, 045113. [Google Scholar] [CrossRef] [Green Version]
- Manna, R.S.; Hartmann, S.; Gati, E.; Schlueter, J.A.; De Souza, M.; Lang, M. Low-Temperature Lattice Effects in the Spin-Liquid Candidate κ-(BEDT-TTF)2Cu2(CN)3. Crystals 2018, 8, 87. [Google Scholar] [CrossRef] [Green Version]
- Sushkov, A.B.; Jenkins, G.S.; Han, T.H.; Lee, Y.S.; Drew, H.D. Infrared phonons as a probe of spin-liquid states in herbertsmithite ZnCu3(OH)6Cl2. J. Phys. Condens. Matter 2017, 29, 095802. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Pustogow, A.; Bories, M.; Puphal, P.; Krellner, C.; Dressel, M.; Valentí, R. Lattice dynamics in the spin-12 frustrated kagome compound herbertsmithite. Phys. Rev. B 2020, 101, 161115. [Google Scholar] [CrossRef] [Green Version]
- Kaib, D.A.S.; Biswas, S.; Riedl, K.; Winter, S.M.; Valentí, R. Magnetoelastic coupling and effects of uniaxial strain in α-RuCl3 from first principles. Phys. Rev. B 2021, 103, L140402. [Google Scholar] [CrossRef]
- Ferrari, F.; Valentí, R.; Becca, F. Variational wave functions for the spin-Peierls transition in the Su-Schrieffer-Heeger model with quantum phonons. Phys. Rev. B 2020, 102, 125149. [Google Scholar] [CrossRef]
- Ferrari, F.; Valentí, R.; Becca, F. Effects of spin-phonon coupling in frustrated Heisenberg models. Phys. Rev. B 2021, 104, 035126. [Google Scholar] [CrossRef]
- Metavitsiadis, A.; Brenig, W. Phonon renormalization in the Kitaev quantum spin liquid. Phys. Rev. B 2020, 101, 035103. [Google Scholar] [CrossRef]
- Ye, M.; Fernandes, R.M.; Perkins, N.B. Phonon dynamics in the Kitaev spin liquid. Phys. Rev. Res. 2020, 2, 033180. [Google Scholar] [CrossRef]
- Matsuura, M.; Sasaki, T.; Iguchi, S.; Gati, E.; Müller, J.; Stockert, O.; Piovano, A.; Böhm, M.; Park, J.T.; Biswas, S.; et al. Lattice Dynamics Coupled to Charge and Spin Degrees of Freedom in the Molecular Dimer-Mott Insulator κ-(BEDT-TTF)2Cu[N(CN)2]Cl. Phys. Rev. Lett. 2019, 123, 027601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Müller, J.; Lang, M.; Steglich, F.; Schlueter, J.A.; Kini, A.M.; Sasaki, T. Evidence for structural and electronic instabilities at intermediate temperatures in κ-(BEDT-TTF)2X for X = Cu[N(CN)2]Cl, Cu[N(CN)2]Br and Cu(NCS)2: Implications for the phase diagram of these quasi-two-dimensional organic superconductors. Phys. Rev. B 2002, 65, 144521. [Google Scholar] [CrossRef] [Green Version]
- Zacharias, M.; Bartosch, L.; Garst, M. Mott Metal-Insulator Transition on Compressible Lattices. Phys. Rev. Lett. 2012, 109, 176401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zacharias, M.; Rosch, A.; Garst, M. Critical elasticity at zero and finite temperature. Eur. Phys. J. Spec. Top. 2015, 224, 1021–1040. [Google Scholar] [CrossRef] [Green Version]
- Pintschovius, L.; Rietschel, H.; Sasaki, T.; Mori, H.; Tanaka, S.; Toyota, N.; Lang, M.; Steglich, F. Observation of superconductivity-induced phonon frequency changes in the organic superconductor kappa-(BEDT-TTF)2 Cu(NCS)2. Europhys. Lett. EPL 1997, 37, 627–632. [Google Scholar] [CrossRef]
- Sasaki, T.; Ito, I.; Yoneyama, N.; Kobayashi, N.; Hanasaki, N.; Tajima, H.; Ito, T.; Iwasa, Y. Electronic correlation in the infrared optical properties of the quasi-two-dimensional κ-type BEDT-TTF dimer system. Phys. Rev. B 2004, 69, 064508. [Google Scholar] [CrossRef] [Green Version]
- Yamada, Y.; Takatera, H.L.; Huber, D. Critical Dynamical Phenomena in Pseudospin-Phonon Coupled Systems. J. Phys. Soc. Jpn. 1974, 36, 641–648. [Google Scholar] [CrossRef]
- Wosnitza, J. Fermi Surfaces of Organic Superconductors. Int. J. Mod. Phys. 1993, 7, 2707–2741. [Google Scholar] [CrossRef]
- Müller, J.; Hartmann, B.; Rommel, R.; Brandenburg, J.; Winter, S.M.; Schlueter, J.A. Origin of the glass-like dynamics in molecular metals κ-(BEDT-TTF)2X: Implications from fluctuation spectroscopy and ab initio calculations. New J. Phys. 2015, 17, 083057. [Google Scholar] [CrossRef]
- Kang, L.; Akagi, K.; Hayashi, K.; Sasaki, T. First-principles investigation of local structure deformation induced by X-ray irradiation in κ-(BEDT-TTF)2Cu[N(CN)2]Br. Phys. Rev. B 2017, 95, 214106. [Google Scholar] [CrossRef]
- Sasaki, T. Mott-Anderson Transition in Molecular Conductors: Influence of Randomness on Strongly Correlated Electrons in the κ-(BEDT-TTF)2X System. Crystals 2012, 2, 374–392. [Google Scholar] [CrossRef]
- Gati, E.; Tutsch, U.; Naji, A.; Garst, M.; Köhler, S.; Schubert, H.; Sasaki, T.; Lang, M. Effects of Disorder on the Pressure-Induced Mott Transition in κ-(BEDT-TTF)2Cu[N(CN)2]Cl. Crystals 2018, 8, 38. [Google Scholar] [CrossRef] [Green Version]
- Hartmann, B.; Müller, J.; Sasaki, T. Mott metal-insulator transition induced by utilizing a glasslike structural ordering in low-dimensional molecular conductors. Phys. Rev. B 2014, 90, 195150. [Google Scholar] [CrossRef] [Green Version]
- Gati, E.; Winter, S.M.; Schlueter, J.A.; Schubert, H.; Müller, J.; Lang, M. Insights from experiment and ab initio calculations into the glasslike transition in the molecular conductor κ-(BEDT-TTF)2Hg(SCN)2Cl. Phys. Rev. B 2018, 97, 075115. [Google Scholar] [CrossRef] [Green Version]
- Su, X.; Zuo, F.; Schlueter, J.A.; Kelly, M.E.; Williams, J.M. Structural disorder and its effect on the superconducting transition temperature in the organic superconductor κ-(BEDT-TTF)2Cu[N(CN)2]Br. Phys. Rev. B 1998, 57, R14056–R14059. [Google Scholar] [CrossRef]
- Yoneyama, N.; Sasaki, T.; Nishizaki, T.; Kobayashi, N. Disorder Effect on the Vortex Pinning by the Cooling-Process Control in the Organic Superconductor κ-(BEDT-TTF)2Cu[N(CN)2]Br. J. Phys. Soc. Jpn. 2004, 73, 184–189. [Google Scholar] [CrossRef] [Green Version]
- Hartmann, B.; Zielke, D.; Polzin, J.; Sasaki, T.; Müller, J. Critical Slowing Down of the Charge Carrier Dynamics at the Mott Metal-Insulator Transition. Phys. Rev. Lett. 2015, 114, 216403. [Google Scholar] [CrossRef] [Green Version]
- Guterding, D.; Valentí, R.; Jeschke, H.O. Influence of molecular conformations on the electronic structure of organic charge transfer salts. Phys. Rev. B 2015, 92, 081109. [Google Scholar] [CrossRef] [Green Version]
- Sasaki, T.; Sano, K.; Sugawara, H.; Yoneyama, N.; Kobayashi, N. Influence of randomness on the Mott transition in κ-(BEDT-TTF)2X. Phys. Status Solidi 2012, 249, 947–952. [Google Scholar] [CrossRef]
- Analytis, J.G.; Ardavan, A.; Blundell, S.J.; Owen, R.L.; Garman, E.F.; Jeynes, C.; Powell, B.J. Effect of Irradiation-Induced Disorder on the Conductivity and Critical Temperature of the Organic Superconductor κ-(BEDT-TTF)2Cu(SCN)2. Phys. Rev. Lett. 2006, 96, 177002. [Google Scholar] [CrossRef] [Green Version]
- Sano, K.; Sasaki, T.; Yoneyama, N.; Kobayashi, N. Electron Localization near the Mott Transition in the Organic Superconductor κ-(BEDT-TTF)2Cu[N(CN)2]Br. Phys. Rev. Lett. 2010, 104, 217003. [Google Scholar] [CrossRef] [Green Version]
- Yoneyama, N.; Furukawa, K.; Nakamura, T.; Sasaki, T.; Kobayashi, N. Magnetic Properties of X-ray Irradiated Organic Mott Insulator κ-(BEDT-TTF)2Cu[N(CN)2]Cl. J. Phys. Soc. Jpn. 2010, 79, 063706. [Google Scholar] [CrossRef]
- Sasaki, T.; Oizumi, H.; Honda, Y.; Yoneyama, N.; Kobayashi, N. Suppression of Superconductivity by Nonmagnetic Disorder in Organic Superconductor κ-(BEDT-TTF)2Cu(NCS)2. J. Phys. Soc. Jpn. 2011, 80, 104703. [Google Scholar] [CrossRef] [Green Version]
- Antal, A.; Fehér, T.; Yoneyama, N.; Forró, L.; Sasaki, T.; Jánossy, A. Spin and Charge Transport in the X-ray Irradiated Quasi-2D Layered Compound: κ-(BEDT-TTF)2Cu[N(CN)2]Cl. Crystals 2012, 2, 579–589. [Google Scholar] [CrossRef] [Green Version]
- Sasaki, S.; Iguchi, S.; Yoneyama, N.; Sasaki, T. X-ray Irradiation Effect on the Dielectric Charge Response in the Dimer–Mott Insulator κ-(BEDT-TTF)2Cu2(CN)3. J. Phys. Soc. Jpn. 2015, 84, 074709. [Google Scholar] [CrossRef]
- Furukawa, T.; Miyagawa, K.; Itou, T.; Ito, M.; Taniguchi, H.; Saito, M.; Iguchi, S.; Sasaki, T.; Kanoda, K. Quantum Spin Liquid Emerging from Antiferromagnetic Order by Introducing Disorder. Phys. Rev. Lett. 2015, 115, 077001. [Google Scholar] [CrossRef] [Green Version]
- Urai, M.; Furukawa, T.; Seki, Y.; Miyagawa, K.; Sasaki, T.; Taniguchi, H.; Kanoda, K. Disorder unveils Mott quantum criticality behind a first-order transition in the quasi-two-dimensional organic conductor κ-(ET)2Cu[N(CN)2]Cl. Phys. Rev. B 2019, 99, 245139. [Google Scholar] [CrossRef]
- Yamamoto, R.; Furukawa, T.; Miyagawa, K.; Sasaki, T.; Kanoda, K.; Itou, T. Electronic Griffiths Phase in Disordered Mott-Transition Systems. Phys. Rev. Lett. 2020, 124, 046404. [Google Scholar] [CrossRef]
- Belitz, D.; Kirkpatrick, T.R. The Anderson-Mott transition. Rev. Mod. Phys. 1994, 66, 261–380. [Google Scholar] [CrossRef]
- Dobrosavljević, V.; Kotliar, G. Mean Field Theory of the Mott-Anderson Transition. Phys. Rev. Lett. 1997, 78, 3943–3946. [Google Scholar] [CrossRef] [Green Version]
- Shinaoka, H.; Imada, M. Soft Hubbard Gaps in Disordered Itinerant Models with Short-Range Interaction. Phys. Rev. Lett. 2009, 102, 016404. [Google Scholar] [CrossRef] [Green Version]
- Chiesa, S.; Chakraborty, P.B.; Pickett, W.E.; Scalettar, R.T. Disorder-Induced Stabilization of the Pseudogap in Strongly Correlated Systems. Phys. Rev. Lett. 2008, 101, 086401. [Google Scholar] [CrossRef] [Green Version]
- Heidarian, D.; Trivedi, N. Inhomogeneous Metallic Phase in a Disordered Mott Insulator in Two Dimensions. Phys. Rev. Lett. 2004, 93, 126401. [Google Scholar] [CrossRef] [Green Version]
- Pezzoli, M.E.; Becca, F. Ground-state properties of the disordered Hubbard model in two dimensions. Phys. Rev. B 2010, 81, 075106. [Google Scholar] [CrossRef] [Green Version]
- Tanasković, D.; Dobrosavljević, V.; Abrahams, E.; Kotliar, G. Disorder Screening in Strongly Correlated Systems. Phys. Rev. Lett. 2003, 91, 066603. [Google Scholar] [CrossRef] [Green Version]
- Aguiar, M.C.O.; Dobrosavljević, V.; Abrahams, E.; Kotliar, G. Critical Behavior at the Mott-Anderson Transition: A Typical-Medium Theory Perspective. Phys. Rev. Lett. 2009, 102, 156402. [Google Scholar] [CrossRef] [Green Version]
- Aguiar, M.C.O.; Dobrosavljević, V. Universal Quantum Criticality at the Mott-Anderson Transition. Phys. Rev. Lett. 2013, 110, 066401. [Google Scholar] [CrossRef] [Green Version]
- Bragança, H.; Aguiar, M.C.O.; Vučičević, J.; Tanasković, D.; Dobrosavljević, V. Anderson localization effects near the Mott metal-insulator transition. Phys. Rev. B 2015, 92, 125143. [Google Scholar] [CrossRef] [Green Version]
- Byczuk, K.; Hofstetter, W.; Vollhardt, D. Mott-Hubbard Transition versus Anderson Localization in Correlated Electron Systems with Disorder. Phys. Rev. Lett. 2005, 94, 056404. [Google Scholar] [CrossRef]
- Lee, H.; Jeschke, H.O.; Valentí, R. Competition between disorder and Coulomb interaction in a two-dimensional plaquette Hubbard model. Phys. Rev. B 2016, 93, 224203. [Google Scholar] [CrossRef] [Green Version]
- Anderson, P.W. Absence of Diffusion in Certain Random Lattices. Phys. Rev. 1958, 109, 1492–1505. [Google Scholar] [CrossRef] [Green Version]
- Lee, P.A.; Ramakrishnan, T.V. Disordered electronic systems. Rev. Mod. Phys. 1985, 57, 287–337. [Google Scholar] [CrossRef]
- Radonjić, M.c.v.M.; Tanasković, D.; Dobrosavljević, V.; Haule, K. Influence of disorder on incoherent transport near the Mott transition. Phys. Rev. B 2010, 81, 075118. [Google Scholar] [CrossRef] [Green Version]
- Diehl, S.; Methfessel, T.; Tutsch, U.; Müller, J.; Lang, M.; Huth, M.; Jourdan, M.; Elmers, H.J. Disorder-induced gap in the normal density of states of the organic superconductor κ-(BEDT-TTF)2Cu[N(CN)2]Br. J. Phys. Condens. Matter 2015, 27, 265601. [Google Scholar] [CrossRef]
- Westerberg, E.; Furusaki, A.; Sigrist, M.; Lee, P.A. Random Quantum Spin Chains: A Real-Space Renormalization Group Study. Phys. Rev. Lett. 1995, 75, 4302–4305. [Google Scholar] [CrossRef] [Green Version]
- Westerberg, E.; Furusaki, A.; Sigrist, M.; Lee, P.A. Low-energy fixed points of random quantum spin chains. Phys. Rev. B 1997, 55, 12578–12593. [Google Scholar] [CrossRef] [Green Version]
- Yamashita, M.; Nakata, N.; Kasahara, Y.; Sasaki, T.; Yoneyama, N.; Kobayashi, N.; Fujimoto, S.; Shibauchi, T.; Matsuda, Y. Thermal-transport measurements in a quantum spin-liquid state of the frustrated triangular magnet κ-(BEDT-TTF)2Cu2(CN)3. Nat. Phys. 2009, 5, 44. [Google Scholar] [CrossRef] [Green Version]
- Buzzi, M.; Nicoletti, D.; Fava, S.; Jotzu, G.; Miyagawa, K.; Kanoda, K.; Henderson, A.; Siegrist, T.; Schlueter, J.; Nam, M.S.; et al. Phase Diagram for Light-Induced Superconductivity in κ-(ET) 2- X. Phys. Rev. Lett. 2021, 127, 197002. [Google Scholar] [CrossRef]
- Khomskii, D.I. Spin chirality and nontrivial charge dynamics in frustrated Mott insulators: Spontaneous currents and charge redistribution. J. Phys. Condens. Matter 2010, 22, 164209. [Google Scholar] [CrossRef]
- Mi, X.; Hou, D.; Wang, X.; Liu, C.; Xiong, Z.; Li, H.; Wang, A.; Chai, Y.; Qi, Y.; Li, W.; et al. Observation of Ferroelectricity in the Kitaev Paramagnetic State of α-RuCl3. arXiv 2022, arXiv:2205.09530. [Google Scholar]
- Vojta, M. Lattice symmetry breaking in cuprate superconductors: Stripes, nematics, and superconductivity. Adv. Phys. 2009, 58, 699–820. [Google Scholar] [CrossRef]
- Mackenzie, A.P.; Thomas Scaffidi, C.W.H.; Maeno, Y. Even odder after twenty-three years: The superconducting order parameter puzzle of Sr2RuO4. npj Quantum Mater. 2017, 40, 40. [Google Scholar] [CrossRef] [Green Version]
- Wosnitza, J.; Zvyagin, S.A.; Zherlitsyn, S. Frustrated magnets in high magnetic fields—Selected examples. Rep. Prog. Phys. 2016, 79, 074504. [Google Scholar] [CrossRef] [Green Version]
- Spaldin, N.A.; Ramesh, R. Advances in magnetoelectric multiferroics. Nat. Mater. 2019, 18, 203–212. [Google Scholar] [CrossRef]
- Sunko, V.; McGuinness, P.H.; Chang, C.S.; Zhakina, E.; Khim, S.; Dreyer, C.E.; Konczykowski, M.; Borrmann, H.; Moll, P.J.W.; König, M.; et al. Controlled Introduction of Defects to Delafossite Metals by Electron Irradiation. Phys. Rev. X 2020, 10, 021018. [Google Scholar] [CrossRef] [Green Version]
- Cho, K.; Kończykowski, M.; Teknowijoyo, S.; Tanatar, M.A.; Prozorov, R. Using electron irradiation to probe iron-based superconductors. Supercond. Sci. Technol. 2018, 31, 064002. [Google Scholar] [CrossRef] [Green Version]
- Leroux, M.; Mishra, V.; Ruff, J.P.C.; Claus, H.; Smylie, M.P.; Opagiste, C.; Rodière, P.; Kayani, A.; Gu, G.D.; Tranquada, J.M.; et al. Disorder raises the critical temperature of a cuprate superconductor. Proc. Natl. Acad. Sci. USA 2019, 116, 10691–10697. [Google Scholar] [CrossRef]



| Material | ||||
|---|---|---|---|---|
| -Cl | 482; 165; [64] | 62; 21 [67] | 0.34 | 0.13 |
| -AgCN | 250; 158; * [64] | 20; 13 [67] | 0.63 | 0.08 |
| -CuCN | 228; 268; * [64] | 18; 18 [12] | 1.18 | 0.08 |
| -BCN | 131; 366; [64] | 05; 15 [67] | 2.79 | 0.04 |
| -Mn | 260; 531; * [51] | 16; 39 [51] | 2.04 | 0.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riedl, K.; Gati, E.; Valentí, R. Ingredients for Generalized Models of κ-Phase Organic Charge-Transfer Salts: A Review. Crystals 2022, 12, 1689. https://doi.org/10.3390/cryst12121689
Riedl K, Gati E, Valentí R. Ingredients for Generalized Models of κ-Phase Organic Charge-Transfer Salts: A Review. Crystals. 2022; 12(12):1689. https://doi.org/10.3390/cryst12121689
Chicago/Turabian StyleRiedl, Kira, Elena Gati, and Roser Valentí. 2022. "Ingredients for Generalized Models of κ-Phase Organic Charge-Transfer Salts: A Review" Crystals 12, no. 12: 1689. https://doi.org/10.3390/cryst12121689
APA StyleRiedl, K., Gati, E., & Valentí, R. (2022). Ingredients for Generalized Models of κ-Phase Organic Charge-Transfer Salts: A Review. Crystals, 12(12), 1689. https://doi.org/10.3390/cryst12121689






