Abstract
The primary purpose of this study is to analyze non-autonomous femtosecond waves with various geometrical configurations correlated to the generalized derivative nonlinear Shrödinger equation (NLSE) with variable coefficients. Numerous academic publications, especially in nonlinear optics, material science, semiconductor, chemical engineering, and many other fields, have looked into this model since it is closer to real-world situations and has more complex wave structures than models with constant coefficients. It can serve as a reflection for the slowly altering inhomogeneities, non-uniformities, and forces acting on boundaries. New complex wave solutions in two different categories are proposed: implicit and elliptic (or periodic or hyperbolic) forms are obtained for this model via the unified method. Indeed, the innovative wave solutions that were achieved and reported here are helpful for investigating optical communication applications as well as the transmission characteristics of light pulses.
1. Introduction
Studies on optical wave solutions through optical fiber media that demonstrate quintic nonlinearity and self-steepening influence have become vigorous, continuous and are motivated by their important applications, owing to their ability of propagating long distances without wane and due to their various geometrical structures, to high-capacity fiber telecommunications, and to all optical switches [1,2,3,4,5]. In many aspects of mathematics and science, including nonlinear optics, hydrodynamics, quantum physics, nonlinear acoustics, and many others, the nonlinear Schrödinger equation (NLSE) and its relatives have an essential role in this aspect [6,7,8,9,10,11,12]. The NLSE is the most essential equation in chemistry since it addresses the quantum-mechanical interaction of particles [13]. Therefore, it is important to find precise solutions for a wide variety of compounds and geometries when developing new substances such as medications or catalysts.
The NLSE’s dispersion and nonlinear coefficients, which depict the frequency curvature versus wave number dispersion and the carrier frequency change with signal amplitude, play a crucial role in finding its analytical solutions [14]. The NLSE promotes soliton solutions that can be used in electronic circuits, ultrafast soliton switches, soliton lasers, and optoelectronic devices [15,16,17]. Regarding nonlinear optics, non-Kerr and Kerr nonlinearity have received much attention [18]. The research field of ultrafast events in nonlinear optical fibers has been analyzed by higher-order NLSE, along with order three dispersion, self-steepness, self-frequency shift, and other phenomena [19,20,21].
Many different approaches have been proposed in the effort to tackle the enormous variety of distinct forms of NLSE. For the NLSE with arbitrary dual-power law parameters, Kudryashov and Biswas [22] employed the method of transformation of dependent and independent variables to establish solitary wave solutions. The higher dimension NLSE that occurred in the regions of irregular dispersion was analyzed via the extended Riccati equation mapping scheme in [23]. Additionally, the authors found approximations to some of the obtained solutions, among them the bright and dark optical solitons, using the q-homotopy algorithm coupled with the Laplace transform. In nonlinear optical fibers, bright and dark optical solitons of the (2 + 1)-dimensional perturbed NLSE were researched and addressed by Wazwaz [24]. In the recent past, unstable NLSE was solved using the modified extended mapping technique [25]. In [26], the (G’/G)-expansion strategy was implemented to acquire the specific wave solutions of the equation. A simple equation strategy for forming the results of unstable NLS equations was elaborated by Lu et al. in [27].
This paper demonstrates new types of wave solutions for the generalized derivative NLSE with varying coefficients (Vc-GDNLSE) [28] via an efficient technique, namely the unified method [29,30]. In this case, when the nonlinearity parameter and dispersion coefficient are treated as variable functions in optical communication, the NLSE model with variable coefficients simulates significant phenomena [31]. The Vc-GDNLSE has the following structure [28].
where , , and are arbitrary functions in z and is a complex-valued function that symbolizes the electric field. Equation (1) is commonly utilized when its coefficients are constants, in other words, it has the construction stated underneath
where , , and denote sequentially the group velocity dispersion, the cubic nonlinearity, and the quintic parameters. Additionally, the two parameters and are progressively taken into account as the group velocity and the self-steepening effect. This model, which takes higher-order effects into account, is important in determining how femtosecond waves behave in optical fibers. Equation (2) becomes the Kaup–Newell equation, which characterizes how the polarized nonlinear Alfvén waves spread in plasmas when [32]. While it represents the Chen–Lee–Liu equation, which describes how cubic and quadratic nonlinearities interact to predict short-pulse spread in a frequency-doubling crystal when [33].
The layout of the article is divided into the following three sections: the construction of the unified technique is covered in Section 2. The application of the aforesaid approach to solve our problem is described in Section 3, and the discussion of the dynamic properties of the produced solutions is explored through different figures. Finally, the conclusions are covered in Section 4.
2. An Overview of the Applied Method
In this section, we provide the following nonlinear differential equation with variable coefficients (Vc-NDE) to illustrate the unified method’s algorithm. Suppose we have a Vc-NDE provided by
where is a polynomial function in its arguments given by Equation (1).
We implement the wave transformation into (3). Thus, (3) takes the new form
where is an arbitrary function, and [34,35].
For Equation (4), the unified method divides its outcomes into two groups: polynomial and rational structures, respectively given by [29,30]
and
where , , and are free functions in z and verifies the next auxiliary equation
where are functions in z. For in Equation (7), the obtained solutions are classified into implicit or elementary ones and for , we obtain periodic or elliptic solutions (more discussions are found in [29,30]). Herein, we restrict our discussion to the polynomial-type solutions for Equation (2). In contrast, the other solutions of this equation will be studied in a future work in relation to the conformable derivative.
3. Complex Wave Solutions for Equation (1) via the Unified Method
This section contains several complex wave solutions with various geometrical patterns for the model specified by Equation (1). First, we insert the new transformation and into Equation (1) which yields two different ODE:
and
wherein . Multiplying Equation (9) by and integrating it with respect to , we obtain the relation
where the integration constant equals zero. Again, utilizing Equation (10) into Equation (8) reveals a new ODE in the form
Multiplying Equation (11) by and integrating both sides with respect to in the presence of changing variable , we obtain
where , , and and the integration constant is considered to be zero.
We assume that Equation (5) is a general solution of Equation (12). After using the balancing principle in [29,30], we get subject to .
Category I. and or
Geometrical 1 (. Solution with solitary wave form.
Clearly, from the relation , we get and the solution is formulated as
where verifies Equation (7) as
Substituting Equations (13) and (14) into Equation (12) and setting all coefficients of identical zero, a system of algebraic equations is constructed that can be solved as follows:
where . Thus, Equation (1) has the general solution:
where , , , and .
The absolute, the real part, the complex part of the solution given by (16) are depicted in Figure 1.
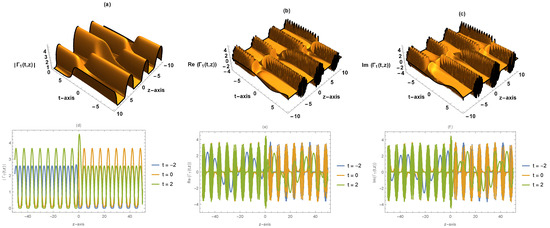
Figure 1.
(a,d) Absolute value of . (b,e) Real part of . (c,f) Imaginary part of . The complex solitary wave solution given by (16) in 3D and 2D plots for , , , , , , .
Geometrical pattern 2 (. Solution with exponential function form.
Substituting Equations (17) and (18) into Equation (12) and setting all coefficients of identical zero, a system of algebraic equations is constructed and gives the next solutions:
where . Consequently, we get the general solution for Equation (1) as
where , , and . The absolute, the real part, the complex part of the solution given by (20) are depicted in Figure 2.
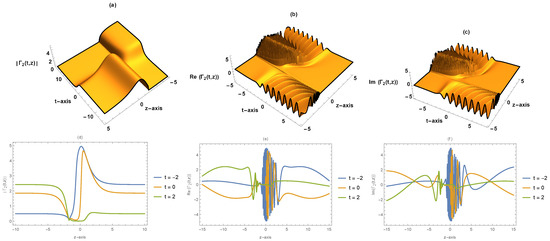
Figure 2.
(a,d) Absolute value of . (b,e) Real part of . (c,f) Imaginary part of . The complex bright-dark solitary wave solution given by (20) in 3D and 2D plots for , , , , , , .
Category II. and
Here, we find solutions in elliptic function form. To this end, we suppose that
where verifies Equation (7) as
Substituting Equations (21) and (22) into Equation (12) and setting all coefficients of identical zero, a system of algebraic equations is constructed that can be solved as follows:
where and . After that, the general solution of Equation (1) is given by
where , , and satisfies Equation (22).
It is worth noting that Equation (22) gives different possible solutions of the Jacobi elliptic function type that are related to the choices of .
For a special case when are constants, Equation (22) gives a variety of Jacobi elliptic function solutions (JEFS) stated in Table 1 and Table 2, according to suitable choices of the free parameters existing in the obtained solutions [36]:

Table 1.
JEFS with different types .

Table 2.
JEFS for and .
The absolute, the real part, the complex part of the solution given by (24) are depicted in Figure 3.
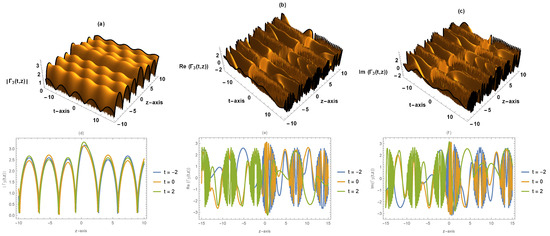
Figure 3.
(a,d) Absolute value of . (b,e) Real part of . (c,f) Imaginary part of . The complex elliptic wave solution given by (24) in 3D and 2D plots for , , , , , , , , , , .
4. Conclusions
The fundamental purpose of this research is to use the unified method to acquire new non-autonomous implicit and explicit complex wave solutions for the Vc-GDNLSE in the context of optical fibers, particularly in the realm of optical networks. Solitons, exponential rational solutions, and elliptic (or periodic or hyperbolic) wave solutions are among the geometrical structures used to generate the outcomes of the polynomial type. 3D and 2D figures are presented to analyze the dynamical behavior for the obtained solutions by choosing suitable values for the free parameters and arbitrary functions included in these solutions. Our main strategy can minimize the number of computational predictions and is simple to use for a range of physical problems in the areas of optics and applied sciences. The results show that the suggested technique is successful, straightforward, and efficient.
Author Contributions
Data curation, K.A.; Formal analysis, M.A. and K.A.; Methodology, M.S.O. and M.A.; Project administration, F.A. and K.A.; Resources, F.A.; Software, M.A.; Writing—original draft, M.A. and M.S.O.; Writing review and editing, M.A. and M.S.O. All authors have read and agreed to the published version of the manuscript.
Funding
The manuscript is funded by the Deanship of Scientific Research, Islamic University of Madinah (project number: 442/2020).
Data Availability Statement
All data and materials are available for everyone.
Acknowledgments
This research work is supported by Deanship of Scientific Research, Islamic University of Madinah (project number: 442/2020). Many thanks to our colleagues in Deanship of Scientific Research, Islamic University of Madinah for their cooperation and complete support to achieve this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Malomed, B.A. Soliton Management in Periodic Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Pal, R.; Goyal, A.; Loomba, S.; Raju, T.S.; Kumar, C.N. Compression of optical similaritons induced by cubic-quintic nonlinear media in a graded-index waveguide. J. Nonlinear Opt. Phys. Mater. 2016, 25, 1650033. [Google Scholar] [CrossRef]
- Yang, Y.; Yan, Z.; Mihalache, D. Controlling temporal solitary waves in the generalized inhomogeneous coupled nonlinear Schrödinger equations with varying source terms. J. Math. Phys. 2015, 56, 053508. [Google Scholar] [CrossRef]
- Xu, H.; Hou, X.; Chen, L.; Mei, Y.; Zhang, B. Optical Properties of InGaN/GaN QW with the Same Well-Plus-Barrier Thickness. Crystals 2022, 12, 114. [Google Scholar] [CrossRef]
- Alotaibi, H. Explore Optical Solitary Wave Solutions of the kp Equation by Recent Approaches. Crystals 2022, 12, 159. [Google Scholar] [CrossRef]
- Fermann, M.E.; Kruglov, V.I.; Thomsen, B.C.; Dudley, J.M.; Harvey, J.D. Self-similar propagation and amplification of parabolic pulses in optical fibers. Phys. Rev. Lett. 2000, 84, 6010. [Google Scholar] [CrossRef] [PubMed]
- Chabchoub, A.; Grimshaw, R.H. The hydrodynamic nonlinear Schrödinger equation: Space and time. Fluids 2016, 1, 23. [Google Scholar] [CrossRef]
- Richardson, C.D.; Schlagheck, P.; Martin, J.; Vandewalle, N.; Bastin, T. Nonlinear Schrödinger wave equation with linear quantum behavior. Phys. Rev. A 2014, 89, 032118. [Google Scholar] [CrossRef]
- Tamang, J.; Saha, A. Dynamical properties of nonlinear ion-acoustic waves based on the nonlinear Schrödinger equation in a multi-pair nonextensive plasma. Z. Fur Naturforschung A 2020, 75, 687–697. [Google Scholar] [CrossRef]
- Hosseini, K.; Osman, M.S.; Mirzazadeh, M.; Rabiei, F. Investigation of different wave structures to the generalized third-order nonlinear Scrödinger equation. Optik 2020, 206, 164259. [Google Scholar] [CrossRef]
- Choudhuri, A.; Porsezian, K. Higher-order nonlinear Schrödinger equation with derivative non-Kerr nonlinear terms: A model for sub-10-fs-pulse propagation. Phys. Rev. A 2013, 88, 033808. [Google Scholar] [CrossRef]
- Akbar, M.A.; Wazwaz, A.M.; Mahmud, F.; Baleanu, D.; Roy, R.; Barman, H.K.; Mahmoud, W.; Al Sharif, M.A.; Osman, M.S. Dynamical behavior of solitons of the perturbed nonlinear Schrödinger equation and microtubules through the generalized Kudryashov scheme. Results Phys. 2022, 43, 106079. [Google Scholar] [CrossRef]
- Scherbela, M.; Reisenhofer, R.; Gerard, L.; Marquet, P.; Grohs, P. Solving the electronic Schrödinger equation for multiple nuclear geometries with weight-sharing deep neural networks. Nat. Comput. Sci. 2022, 2, 331–341. [Google Scholar] [CrossRef]
- Chen, X. On the rigorous derivation of the 3D cubic nonlinear Schrödinger equation with a quadratic trap. Arch. Ration. Mech. Anal. 2013, 210, 365–408. [Google Scholar] [CrossRef]
- Monterola, C.; Saloma, C. Solving the nonlinear Schrodinger equation with an unsupervised neural network. Opt. Express 2001, 9, 72–84. [Google Scholar] [CrossRef] [PubMed]
- Stajanca, P.; Bugar, I. Nonlinear ultrafast switching based on soliton self-trapping in dual-core photonic crystal fibre. Laser Phys. Lett. 2016, 13, 116201. [Google Scholar] [CrossRef]
- Begleris, I.; Horak, P. Frequency-banded nonlinear Schrödinger equation with inclusion of Raman nonlinearity. Opt. Express 2018, 26, 21527–21536. [Google Scholar] [CrossRef]
- Marhic, M.E.; Andrekson, P.A.; Petropoulos, P.; Radic, S.; Peucheret, C.; Jazayerifar, M. Fiber optical parametric amplifiers in optical communication systems. Laser Photonics Rev. 2015, 9, 50–74. [Google Scholar] [CrossRef]
- Wright, L.G.; Ziegler, Z.M.; Lushnikov, P.M.; Zhu, Z.; Eftekhar, M.A.; Christodoulides, D.N.; Wise, F.W. Multimode nonlinear fiber optics: Massively parallel numerical solver, tutorial, and outlook. IEEE J. Sel. Top. Quantum Electron. 2017, 24, 1–16. [Google Scholar] [CrossRef]
- Az-Zo’bi, E.; Al-Maaitah, A.F.; Tashtoush, M.A.; Osman, M.S. New generalised cubic-quintic-septic NLSE and its optical solitons. Pramana 2022, 96, 184. [Google Scholar] [CrossRef]
- Osman, M.S.; Tariq, K.U.; Bekir, A.; Elmoasry, A.; Elazab, N.S.; Younis, M.; Abdel-Aty, M. Investigation of soliton solutions with different wave structures to the (2+ 1)-dimensional Heisenberg ferromagnetic spin chain equation. Commun. Theor. Phys. 2020, 72, 035002. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Biswas, A. Optical solitons of nonlinear Schrödinger’s equation with arbitrary dual-power law parameters. Optik 2022, 252, 168497. [Google Scholar] [CrossRef]
- Akinyemi, L.; Senol, M.; Osman, M.S. Analytical and approximate solutions of nonlinear Schrödinger equation with higher dimension in the anomalous dispersion regime. J. Ocean. Eng. Sci. 2022, 7, 143–154. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Bright and dark optical solitons of the (2+1)-dimensional perturbed nonlinear Schrödinger equation in nonlinear optical fibers. Optik 2022, 251, 168334. [Google Scholar] [CrossRef]
- Arshad, M.; Seadawy, A.R.; Lu, D.; Jun, W. Optical soliton solutions of unstable nonlinear Schröodinger dynamical equation and stability analysis with applications. Optik 2018, 157, 597–605. [Google Scholar] [CrossRef]
- Arbabi, S.; Najafi, M. Exact solitary wave solutions of the complex nonlinear Schrödinger equations. Optik 2016, 127, 4682–4688. [Google Scholar] [CrossRef]
- Lu, D.; Seadawy, A.; Arshad, M. Applications of extended simple equation method on unstable nonlinear Schrödinger equations. Optik 2017, 140, 136–144. [Google Scholar] [CrossRef]
- Mecelti, A.; Triki, H.; Azzouzi, F.; Wei, X.; Biswas, A.; Yildirim, Y.; Alshehri, H.M.; Zhou, Q. New chirped gray and kink self-similar waves in presence of quintic nonlinearity and self-steepening effect. Phys. Lett. A 2022, 437, 128104. [Google Scholar] [CrossRef]
- Adel, M.; Aldwoah, K.; Alahmadi, F.; Osman, M.S. The asymptotic behavior for a binary alloy in energy and material science: The unified method and its applications. J. Ocean. Eng. Sci. 2022, in press. [Google Scholar] [CrossRef]
- Osman, M.S.; Ghanbari, B.; Machado, J.A.T. New complex waves in nonlinear optics based on the complex Ginzburg-Landau equation with Kerr law nonlinearity. Eur. Phys. J. Plus 2019, 134, 20. [Google Scholar] [CrossRef]
- Zhang, J.L.; Li, B.A.; Wang, M.L. The exact solutions and the relevant constraint conditions for two nonlinear Schrödinger equations with variable coefficients. Chaos Solitons Fractals 2009, 39, 858–865. [Google Scholar] [CrossRef]
- Kaup, D.J.; Newell, A.C. An exact solution for a derivative nonlinear Schrödinger equation. J. Math. Phys. 1978, 19, 798–801. [Google Scholar] [CrossRef]
- Tarla, S.; Ali, K.K.; Yilmazer, R.; Osman, M.S. New optical solitons based on the perturbed Chen-Lee-Liu model through Jacobi elliptic function method. Opt. Quantum Electron. 2022, 54, 131. [Google Scholar] [CrossRef]
- Osman, M.S.; Machado, J.A.T.; Baleanu, D. On nonautonomous complex wave solutions described by the coupled Schrödinger-Boussinesq equation with variable-coefficients. Opt. Quantum Electron. 2018, 50, 73. [Google Scholar] [CrossRef]
- Abdel-Gawad, H.I.; Tantawy, M. Mixed-type soliton propagations in two-layer-liquid (or in an elastic) medium with dispersive waveguides. J. Mol. Liq. 2017, 241, 870–874. [Google Scholar] [CrossRef]
- Zhang, L.H. Travelling wave solutions for the generalized Zakharov-Kuznetsov equation with higher-order nonlinear terms. Appl. Math. Comput. 2009, 208, 144–155. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).