Dynamic Behavior of a Novel High-Strength and Ductile Near-α Titanium Ti-Al-Mo-Zr-Fe-B Alloy
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussions
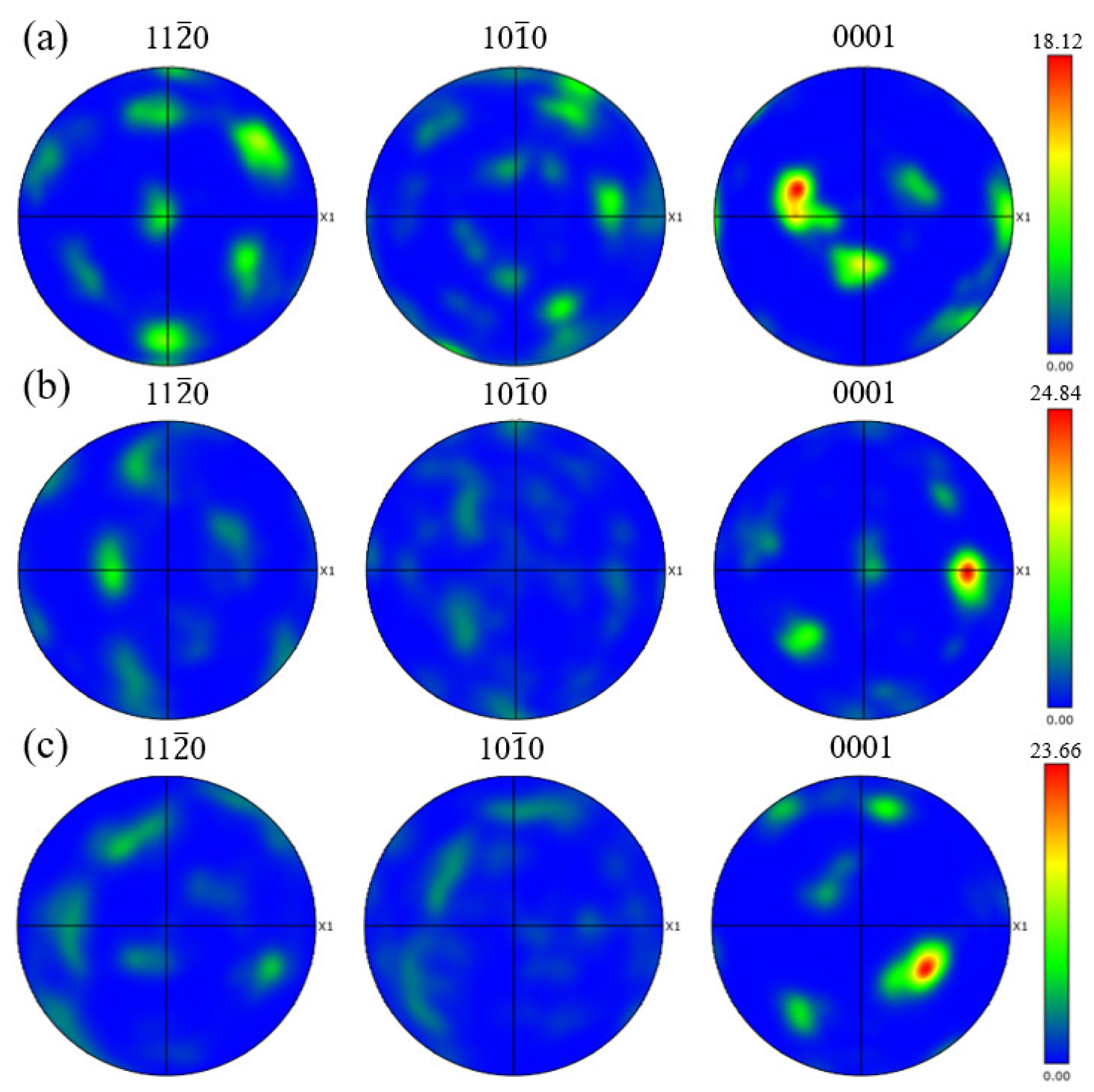
3.1. Initial Microstructure
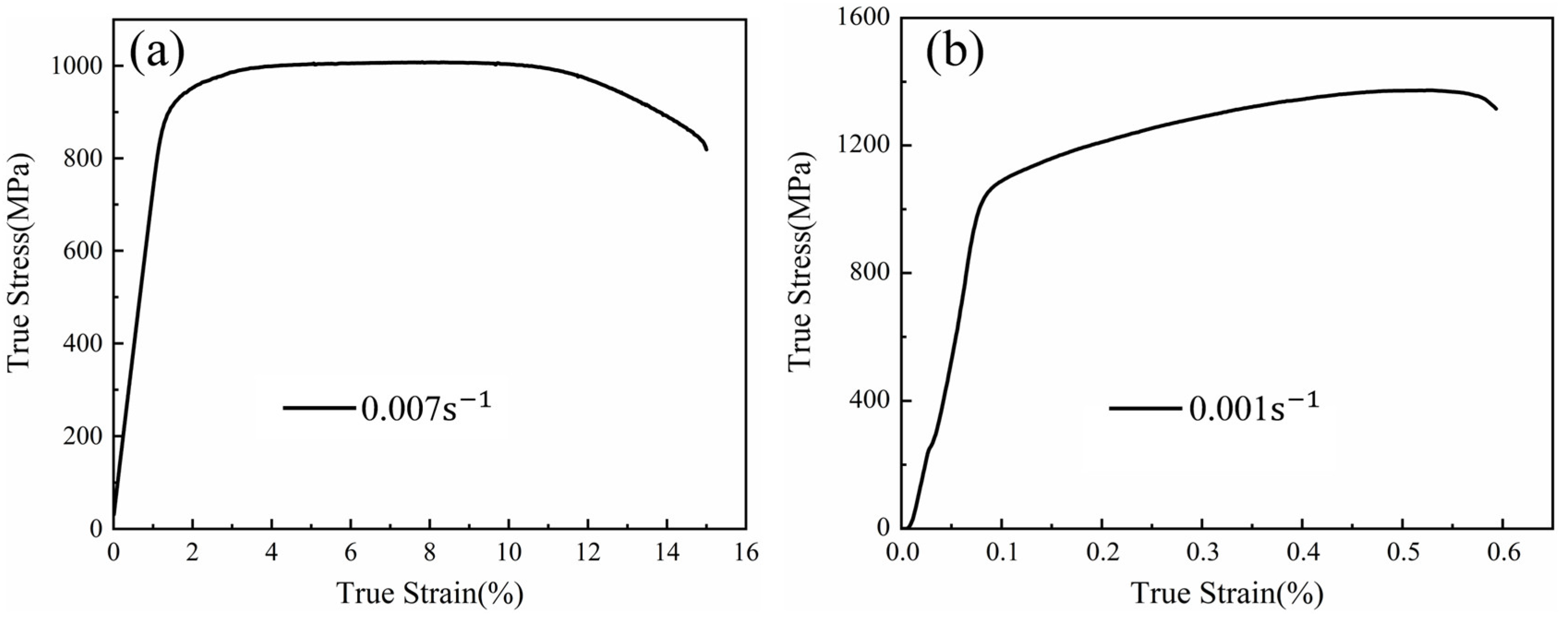
3.2. Quasi-Static Tensile and Compression Experiment
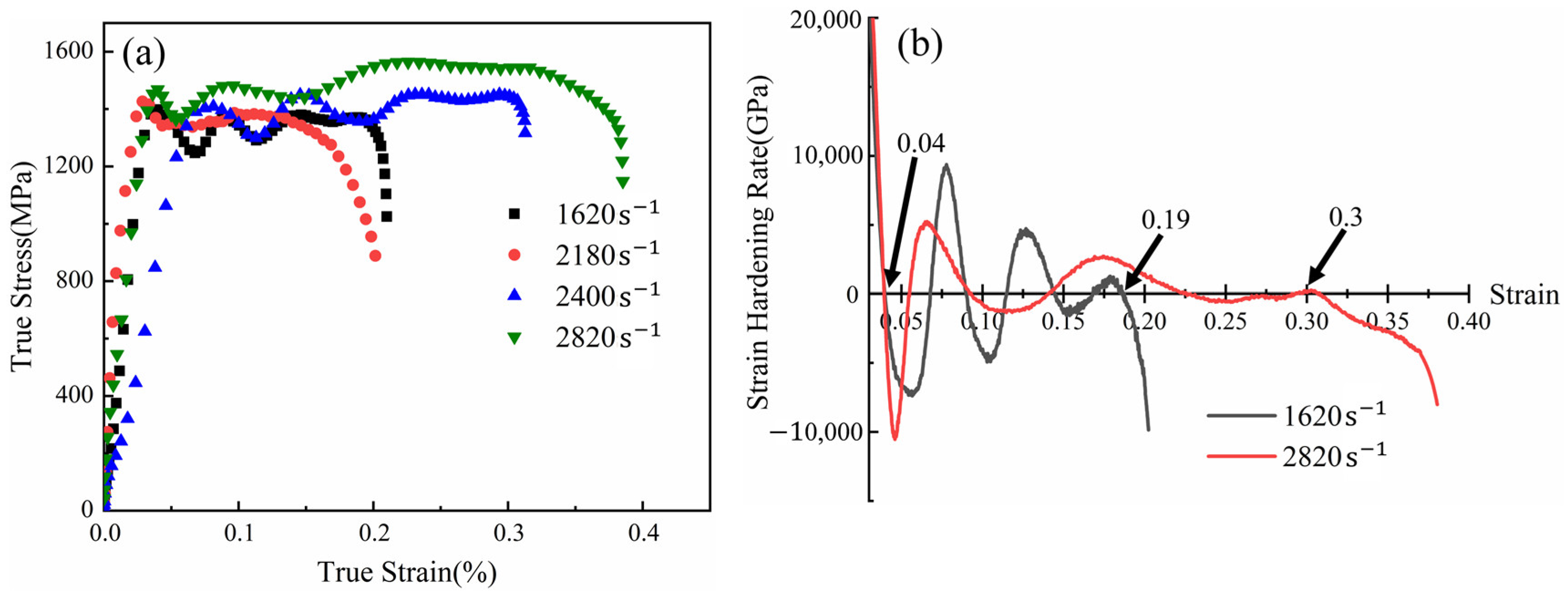
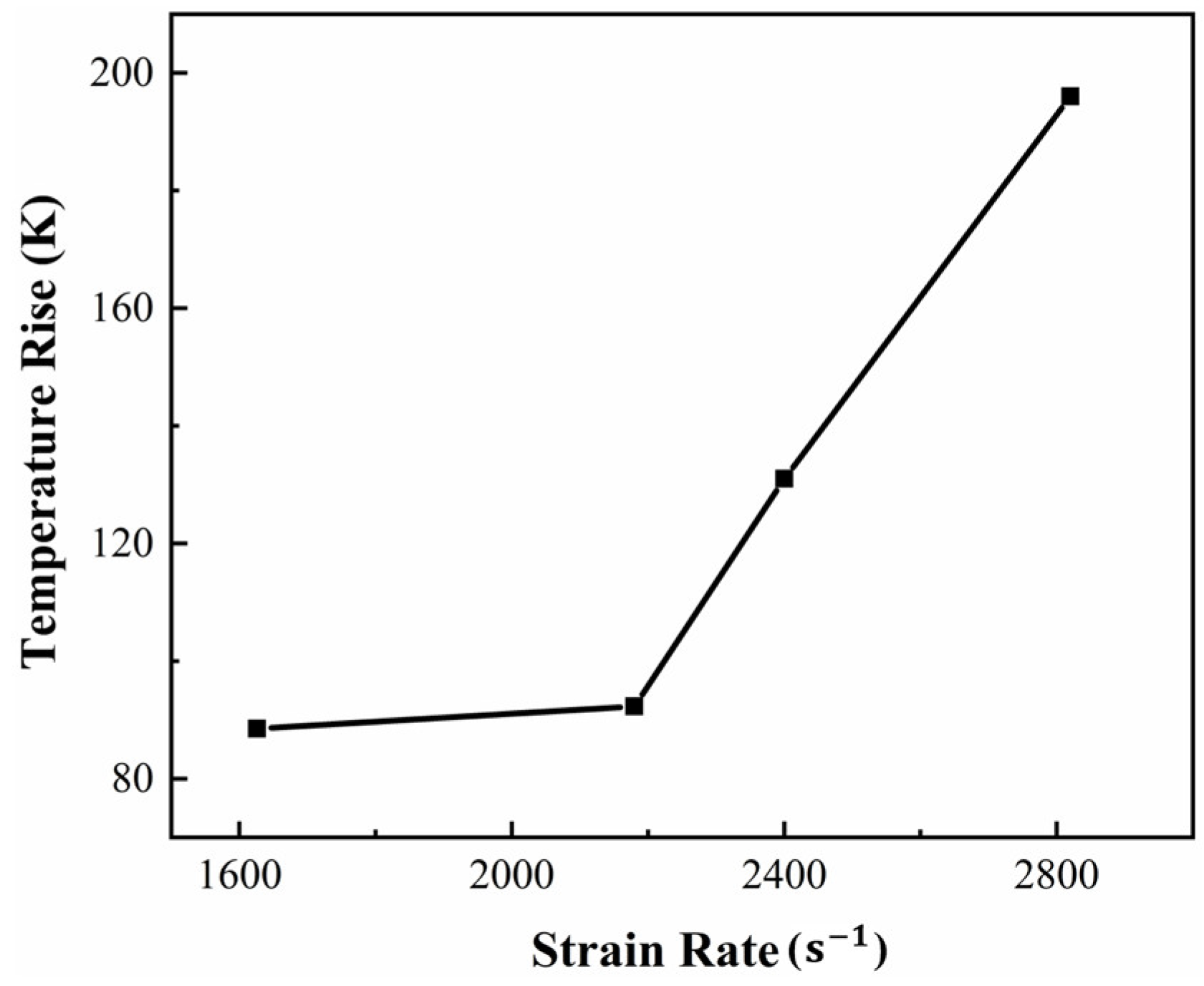
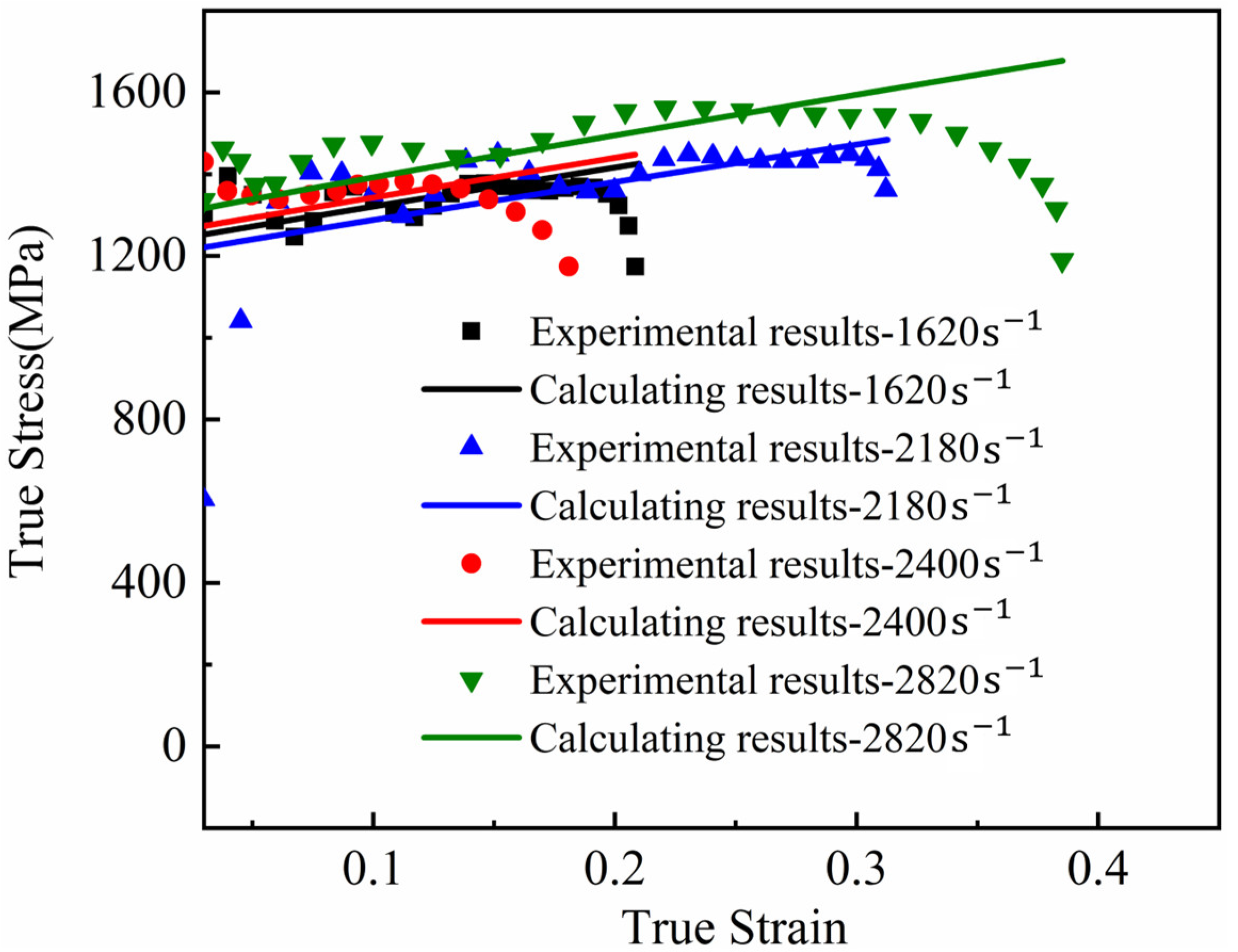
3.3. Dynamic Compression Experiment
4. The Johnson–Cook Constitutive Equation
5. Conclusions
- (1)
- A novel near-α titanium Ti-6Al-1Mo-2Zr-0.55Fe-0.1B alloy was developed, which possesses simultaneous high strength (>1000 MPa) and ductility (>15%).
- (2)
- The strength of the alloy under dynamic loading enhanced significantly compared with the quasi-static compression and increased with the increase in the strain rate. An abundance of deformation twins released the dislocation pile-up and coordinated the plastic deformation of the alloy during the dynamic loading.
- (3)
- The Johnson–Cook constitutive equation was modified by the adiabatic temperature rise term, and a nonlinear fit was performed to construct a dynamic constitutive relationship at room temperature, which could describe the rheological behavior of the alloy under high strain rate conditions at room temperature.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zang, M.C.; Niu, H.Z.; Liu, S.; Yu, J.S.; Zhang, H.R.; Zhang, D.L. Achieving high tensile strength-ductility synergy of a fully-lamellar structured near alpha titanium alloy at extra-low temperatures. J. Alloy. Compd. 2022, 923, 166363. [Google Scholar] [CrossRef]
- Mahender, T.; Anantha Padmanaban, M.R.; Balasundar, I.; Balasundarc, I.; Raghuc, T. On the optimization of temperature and cooling rate to maximize strength and ductility of near α titanium alloy IMI 834. Mater. Sci. Eng. A 2021, 827, 142052. [Google Scholar] [CrossRef]
- Ballat-Durand, D.; Bouvier, S.; Risbet, M.; Pantleonb, W.F. Through analysis of the microstructure changes during linear friction welding of the near-α titanium alloy Ti-6Al-2Sn-4Zr-2Mo (Ti6242) towards microstructure optimization. Mater. Charact. 2019, 151, 38–52. [Google Scholar] [CrossRef]
- Cheng, M.; Yu, B.; Guo, R.; Shi, X.H.; Xu, L.; Qiao, J.W.; Yang, R. Electron beam welding of a novel near α high temperature titanium alloy powder compact: Effect of post-welding heat treatment on tensile properties. J. Mater. Res. Technol. 2021, 10, 153–163. [Google Scholar] [CrossRef]
- Chuvil’Deev, V.N.; Kopylov, V.I.; Nokhrin, A.V.; Tryaev, P.V.; Tabachkovad, Y.N.; Chegurov, M.K.; Kozlova, N.A.; Mikhaylov, A.S.; Ershova, A.V.; Grayznov, M.Y.; et al. Effect of severe plastic deformation realized by rotary swaging on the mechanical properties and corrosion resistance of near-α-titanium alloy Ti-2.5Al-2.6Zr. J. Alloy. Compd. 2019, 785, 1233–1244. [Google Scholar] [CrossRef]
- Meng, K.; Guo, K.; Yu, Q.; Miao, D.; Yao, C.; Wang, Q.F.; Wang, T.S. Effect of annealing temperature on the microstructure and corrosion behavior of Ti-6Al-3Nb-2Zr-1Mo alloy in hydrochloric acid solution. Corros. Sci. 2021, 183, 109320. [Google Scholar] [CrossRef]
- Su, B.; Wang, B.; Luo, L.S.; Wang, L.; Su, Y.Q.; Wang, F.X.; Xu, Y.J.; Han, B.S.; Huang, H.G.; Guo, J.J.; et al. The corrosion behavior of Ti-6Al-3Nb-2Zr-1Mo alloy: Effects of HCl concentration and temperature. J. Mater. Sci. Technol. 2021, 74, 143–154. [Google Scholar] [CrossRef]
- Ren, J.Q.; Wang, Q.; Zhang, B.B.; Wang, Y.; Liu, W.F.; Lu, X.F.; Li, S.Z.; Chen, R.J. Charpy impact anisotropy and the associated mechanisms in a hot-rolled Ti-6Al-3Nb-2Zr-1Mo alloy plate. Mater. Sci. Eng. A 2022, 831, 142187. [Google Scholar] [CrossRef]
- Wang, Q.; Ren, J.Q.; Wu, Y.K.; Jiang, P.; Li, J.Q.; Sun, Z.J.; Liu, X.T. Comparative study of crack growth behaviors of fully-lamellar and bi-lamellar Ti-6Al-3Nb-2Zr-1Mo alloy. J. Alloy. Compd. 2019, 789, 249–255. [Google Scholar] [CrossRef]
- Ren, J.Q.; Wang, Q.; Zhang, B.B.; DanYang, D.; Lu, X.F.; Zhang, X.B.; Zhang, X.D.; Hu, J.Y. Influence of microstructure on fatigue crack growth behavior of Ti-6Al-3Nb-2Zr-1Mo alloy: Bimodal vs. Lamellar Struct. Intermet. 2021, 130, 107058. [Google Scholar] [CrossRef]
- Guo, Y.H.; Liu, G.; Huang, Y. A complemented multiaxial creep constitutive model for materials with different properties in tension and compression. Eur. J. Mech.—A/Solids 2022, 93, 104510. [Google Scholar] [CrossRef]
- Xiong, J.H.; Li, S.K.; Gao, F.Y.; Zhang, J.X. Microstructure and mechanical properties of Ti6321 alloy welded joint by GTAW. Mater. Sci. Eng. A 2015, 640, 419–423. [Google Scholar] [CrossRef]
- Gao, F.Y.; Gao, Q.; Jiang, P.; Liu, Z.Y.; Liao, Z.Q. Microstructure and mechanical properties of Ti6321 alloy welded joint by EBW. Int. J. Lightweight Mater. Manuf. 2018, 1, 265–269. [Google Scholar] [CrossRef]
- Arab, A.; Chen, P.W.; Guo, Y.S. Effects of microstructure on the dynamic properties of TA15 titanium alloy. Mech. Mater. 2019, 137, 103121. [Google Scholar] [CrossRef]
- Chiou, S.T.; Cheng, W.C.; Lee, W.S. The analysis of the microstructure changes of a Fe–Mn–Al alloy under dynamic impact tests. Mater. Sci. Eng. A 2004, 386, 460–467. [Google Scholar] [CrossRef]
- Zhou, T.F.; Wu, J.J.; Che, J.G.; Wang, Y.; Wang, X.B. Dynamic shear characteristics of titanium alloy Ti-6Al-4V at large strain rates by the split Hopkinson pressure bar test. Int. J. Impact Eng. 2017, 109, 167–177. [Google Scholar] [CrossRef]
- Jiang, X.J.; Chen, G.Y.; Men, X.L.; Dong, X.L.; Han, R.H.; Zhang, X.Y.; Liu, R.P. Ultrafine duplex microstructure and excellent mechanical properties of TC4 alloy via a novel thermo-mechanical treatment. J. Alloy. Compd. 2018, 767, 617–621. [Google Scholar] [CrossRef]
- Aguilar, C.; Aguirre, T.; Martínez, C.; Martíneza, C.; De Barbieri, F.; SanMartína, F.; Salinas, V.; Alfonso, I. Improving the mechanical strength of ternary beta titanium alloy (Ti-Ta-Sn) foams, using a bimodal microstructure. Mater. Des. 2020, 195, 108945. [Google Scholar] [CrossRef]
- Chong, Y.; Bhattacharjee, T.; Park, M.H.; Shibata, A.; Tsuji, N. Factors determining room temperature mechanical properties of bimodal microstructures in Ti-6Al-4V alloy. Mater. Sci. Eng. A 2018, 730, 217–222. [Google Scholar] [CrossRef]
- Lv, Y.F.; Fu, H.; Zhang, Y.H.; An, F.B.; Jiang, B. Effects of forging and heat treatment process on microstructure and mechanical properties of Ti80 titanium alloy bars. Hot Work. Technol. 2021, 9, 81–83. [Google Scholar]
- Xu, X.F.; Tayyeb, A.; Wang, L.; Cheng, H.W.; Zhou, Z.; Ning, Z.X.; Liu, X.P.; Liu, A.J.; Zhang, B.B.; Cheng, X.W. Research on dynamic compression properties and deformation mechanism of Ti6321 titanium alloy. J. Mater. Res. Technol. 2020, 9, 11509–11516. [Google Scholar] [CrossRef]
- Dai, J.C.; Min, X.H.; Wang, L. Dynamic response and adiabatic shear behavior of β-type Ti–Mo alloys with different deformation modes. Mater. Sci. Eng. A 2022, 857, 144108. [Google Scholar] [CrossRef]
- Pu, B.; Li, W.B.; Zhang, Q.; Zheng, Y.; Wang, X.M. Research on the dynamic compressive deformation behavior of 3D-Printed Ti6Al4V. Metals 2021, 11, 1327. [Google Scholar] [CrossRef]
- Zhang, T.; Wei, D.X.; Lu, E.; Wang, W.; Wang, K.S.; Li, X.Q.; Zhang, L.Q.; Kato, H.; Lu, W.J.; Wang, L.Q. Microstructure evolution and deformation mechanism of α+β dual-phase Ti-xNb-yTa-2Zr alloys with high performance. J. Mater. Sci. Technol. 2022, 131, 68–81. [Google Scholar] [CrossRef]
- Chai, Y.F.; Shan, L.; Jiang, B.; Yang, H.B.; He, C.; Hao, W.X.; He, J.J.; Yang, Q.S.; Yuan, M.; Pan, F.S. Ameliorating mechanical properties and reducing anisotropy of as-extruded Mg-1.0Sn-0.5Ca alloy via Al addition. Prog. Nat. Science. Mater. Int. 2021, 31, 722–730. [Google Scholar] [CrossRef]
- Qin, D.Y.; Lu, Y.F.; Guo, D.Z.; Zheng, L.; Liu, Q.; Zhou, L. Tensile deformation and fracture of Ti–5Al–5V–5Mo–3Cr–1.5Zr–0.5Fe alloy at room temperature. Mater. Sci. Eng. A 2013, 587, 100–109. [Google Scholar] [CrossRef]
- Guo, Z.; Miodownik, A.P.; Saunders, N.; Schillé, J.P. Influence of stacking-fault energy on high temperature creep of alpha titanium alloys. Scr. Mater. 2006, 54, 2175–2178. [Google Scholar] [CrossRef]
- Xu, F.; Zhang, X.Y.; Ni, H.T.; Cheng, Y.M.; Zhu, Y.T.; Liu, Q. Effect of twinning on microstructure and texture evolutions of pure Ti during dynamic plastic deformation. Mater. Sci. Eng. A 2013, 564, 22–33. [Google Scholar] [CrossRef]
- Liu, Q.; Fang, L.M.; Xiong, Z.W.; Yang, J.; Tan, Y.; Liu, Y.; Zhang, Y.J.; Tan, Q.; Hao, C.C.; Cao, L.H.; et al. The response of dislocations, low angle grain boundaries and high angle grain boundaries at high strain rates. Mater. Sci. Eng. A 2021, 822, 141704. [Google Scholar] [CrossRef]
- Sung-Il, B.; Ratnesh, K.G.; Sharvan, K.; David, N.S. Temperature increases and thermoplastic microstructural evolution in adiabatic shear bands in a high-strength and high-toughness 10 wt.% Ni steel. Acta Mater. 2021, 205, 116568. [Google Scholar] [CrossRef]
- Xu, Y.B.; Yang, H.J.; Meyers, M.A. Dynamic recrystallization in the shear bands of Fe–Cr–Ni monocrystal: Electron backscatter diffraction characterization. Scr. Mater. 2008, 58, 691–694. [Google Scholar] [CrossRef]
- Yang, D.K.; Cizek, P.; Hodgson, P.D.; Wen, C.E. Microstructure evolution and nanograin formation during shear localization in cold-rolled titanium. Acta Mater. 2010, 58, 4536–4548. [Google Scholar] [CrossRef]


| Elements | Al | Mo | Zr | Fe | B | Ti |
|---|---|---|---|---|---|---|
| wt.% | 5.8 | 1.07 | 1.85 | 0.57 | 0.044 | Bal. |
| Tensile | Compression | |||||
|---|---|---|---|---|---|---|
| Alloy Composition | YS/MPa | TS/MPa | Strain (%) | YS/MPa | UCS/MPa | Strain (%) |
| Ti-6Al-1Mo-2Zr-0.55Fe-0.1B | 927 | 1005 | 15.1 | 1018 | 1370 | 60 |
| Ti-6Al-2Zr-1Mo-3Nb [20,21] | 842 | 932 | 22 | 881 | 1046 | 50 |
| Alloy Composition | Ti-6Al-1Mo-2Zr-0.55Fe-0.1B | Ti-6Al-2Zr-1Mo-3Nb [21] | |||||
|---|---|---|---|---|---|---|---|
| Strain rate | |||||||
| UCS /MPa | 1398 | 1438 | 1454 | 1567 | 1348 | 1418 | 1478 |
| Strain | 0.21 | 0.21 | 0.31 | 0.39 | 0.13 | 0.22 | 0.30 |
| 229 | 240 | 335 | 515 | 158 | 299 | 422 | |
| State | Avg·GS (μm) | HAGB (%) | LAGB (%) | The Fraction of Grain in Different States (%) | ||
|---|---|---|---|---|---|---|
| Recrystallized | Substructured | Deformed | ||||
| Initial | 6.43 | 45.58 | 54.42 | 44.4 | 51.9 | 3.7 |
| 1620 s−1 | 5.51 | 68.84 | 31.16 | 6.6 | 67.6 | 25.8 |
| 2820 s−1 | 5.3 | 82.37 | 17.63 | 5.2 | 21.7 | 73.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, C.; Wang, C.; He, M.; Dong, Y.; Alexandrov, I.V.; Chang, H. Dynamic Behavior of a Novel High-Strength and Ductile Near-α Titanium Ti-Al-Mo-Zr-Fe-B Alloy. Crystals 2022, 12, 1584. https://doi.org/10.3390/cryst12111584
Yan C, Wang C, He M, Dong Y, Alexandrov IV, Chang H. Dynamic Behavior of a Novel High-Strength and Ductile Near-α Titanium Ti-Al-Mo-Zr-Fe-B Alloy. Crystals. 2022; 12(11):1584. https://doi.org/10.3390/cryst12111584
Chicago/Turabian StyleYan, Chi, Chu Wang, Miaoxia He, Yuecheng Dong, I. V. Alexandrov, and Hui Chang. 2022. "Dynamic Behavior of a Novel High-Strength and Ductile Near-α Titanium Ti-Al-Mo-Zr-Fe-B Alloy" Crystals 12, no. 11: 1584. https://doi.org/10.3390/cryst12111584
APA StyleYan, C., Wang, C., He, M., Dong, Y., Alexandrov, I. V., & Chang, H. (2022). Dynamic Behavior of a Novel High-Strength and Ductile Near-α Titanium Ti-Al-Mo-Zr-Fe-B Alloy. Crystals, 12(11), 1584. https://doi.org/10.3390/cryst12111584










