Abstract
First-principles calculations of the stability, electronic, and magnetic properties of full-Heusler compound V2FeSi and Fe2VSi in regular () and inverse () structures have been performed using density functional theory within an SCAN meta-GGA functional. It is found that the crystal lattice is energetically more favorable for V2FeSi, while Fe2VSi forms the structure. In both cases, the electronic structure of the energetically stable modifications corresponds to half-metallic ferrimagnets. Magnetic properties of energetically favorable structures obey the Slater–Pauling rule. All considered properties of the studied structures are explained within the crystal orbital Hamilton population analysis.
1. Introduction
Heusler alloys are intermetallic compounds with a wide range of compositions attracting much attention due to their potential applications as thermoelectric, spintronic, and magnetostrictive materials. The structural, electronic, thermodynamic, and magnetic properties of many Heusler compounds have previously been studied experimentally [1,2,3,4,5,6,7,8,9,10,11] and theoretically [12,13,14,15,16,17,18,19,20,21,22]. Some of the Heusler alloys are half-metals with 100% spin polarization and high structural stability that is critically important for spintronic applications [12].
Spintronics and magnetoelectronics compose one of the most rapidly expanding fields in nanoscience [23,24,25]. Half-metallic magnetic compounds play a crucial role in this development. These materials present usual metallic behavior for the one-spin direction, while an energy gap in the band structure is present in the other spin direction similarly to semiconductors. The interest in these compounds is not least due to the fact that the properties of complete Heusler alloys strongly depend on their structure and composition.
Thirty years ago, Nishino et al. [4] investigated the Heusler connection of Fe3Si with a cubic structure D03 and (Mx)3Si, (M = Ti, V, Cr, Mn, Co, and Ni) using electrical resistance and reported that the ferromagnetic transition occurs in the range 0 0.2 for M = V. When studying the thermodynamic properties of the Heusler compound (Vx)3Si with a D03 structure, (0 0.2), it was suggested that the atomic disorder of the V position by Fe atoms leads to the appearance of magnetic frustration [6]. An experimental study of the magnetic properties of Heusler alloys based on Fe2VSi showed that Fe2VSi exhibits ferromagnetism with a slight substitution of V by magnetic transition metals [7]. Photoemission spectroscopy was used to study the electronic structures of compounds of Heusler type VxSi in the concentration range of .
As the vanadium concentration increases, the crystal structure of VxSi changes from D03 to in the concentration range [26]. Photoemission spectroscopy studies show that Fe2VSi alloy has a pseudogap near the Fermi level at [8].
An early theoretical modeling of the electronic properties of Fe2CrxSi (x = 0, 0.5, 1.0) employing the FP-LAPW method with the PBEsol functional showed that alloys Fe2VSi do not exhibit half-metallicity [21]. LMTO-ASA band structure calculations were performed for paramagnetic (PM), ferromagnetic (FM), and antiferromagnetic (AFM) orderings of VSi alloys [22]. It was found that AFM ordering is the most stable configuration. As for the magnetic moments, they slightly increase on Fe atoms from FM to AFM. The result for ()2()Si indicates the possibility of the existence of Fe atoms with large magnetic moments due to atomic disorder between the Fe and V atoms [22]. The AFM nature of the ordering in Fe2VSi was confirmed by experimental studies, where a negative value of the Weiss temperature was obtained [6].
Here, we perform a comparative study of the properties of V2FeSi and Fe2VSi Heusler alloys for both and structures to identify the origins responsible for the formation of various crystal structures. In addition, this study aims to examine the properties of Heusler alloys from the perspective of the local environment and to analyze their impact on the magnetic and electronic properties. It should be noted that to the best of our knowledge, there are no available experimental data on the properties of V2FeSi alloys, and one theoretical research paper mentioned this compound among other full Heusler alloys [18].
2. Materials and Methods
The electronic structure calculations were performed within the density functional method implemented in the VASP software package [27,28,29]. Core electrons were approximated using projector augmented wave (PAW) pseudopotentials [30], and valence electrons were represented with a set of plane wave basis with a cutoff energy of 700 eV. The exchange–correlation functional was treated using SCAN (meta-GGA) [31]. The valence configurations have been chosen as Mn (3d64s1), Fe (3d64s2), V (), and Si (). The Brillouin zone was sampled using a Monkhorst–Pack [32] k-point mesh of 10 × 10 × 10. These parameters ensured good convergence in total energy. The convergence tolerance for the calculations was chosen as the difference in total energy within eV/atom.
The formation enthalpy was calculated by the formula:
where H is the enthalpy of each component (X = V, Fe; Y = Fe, V; Z = Si), and N is the number of formula units (f.u.) in a unit cell. A negative indicates that a structure is stable relative to the decomposition into constituent elements.
The non-empirical strongly constrained and appropriately normed (SCAN) meta-generalized gradient approximation (meta-GGA) within the density functional theory predicts accurate geometries and energies of diversely bonded molecules and materials (including covalent, metallic, ionic, hydrogen, and van der Waals bonds) [31,33]. The computational cost of hybrid functionals can be 10 or 100 times greater than for semi-local functionals in standard plane-wave codes, especially for metallic systems. Another problem with hybrids is that a universal exact-exchange mixing parameter is not determined by any exact condition.
To analyze the nature of chemical bonding in the considered structures, a crystal orbital Hamilton population analysis (COHP) was used [34,35,36]. According to this formalism, the formation of anti-bonding orbitals occurs when the COHP value taken with the opposite sign becomes negative. We also use the integrated crystal orbital Hamilton population (ICOHP) to measure the strength of the chemical bonding and explain the differences in the stability of crystal structures and the values of atomic magnetic moments.
Atomic structures were visualized in the VESTA package [37]. We use the VASPKIT code to postprocess the calculated data from VASP [38].
3. Results
Atoms in the structures of Heusler alloys YZ (X, Y are transition metals, Z is a chemical element of the main group) are located in four different sites A, B, C and D with coordinates (0, 0, 0), (0.25, 0.25, 0.25), (0.5, 0.5, 0.5), and (0.75, 0.75, 0.75), respectively. The D-site usually contains an s- or p-element, while A-, B-, and C-sites usually contain d-elements.
In the case of the structure (Figure 1a), all X atoms are equivalent and occupy the A- and C-sites. The Y and Z atoms occupy the B- and D-sites, respectively. The first coordination sphere of X atoms includes four Y and four Z atoms, while the second one consists of six X atoms. Y atoms have eight X atoms as nearest neighboring positions, and the next-nearest neighbors are six Z atoms. In turn, Z atoms are surrounded by eight X atoms in the first coordination sphere and six Y atoms in the second coordination sphere.
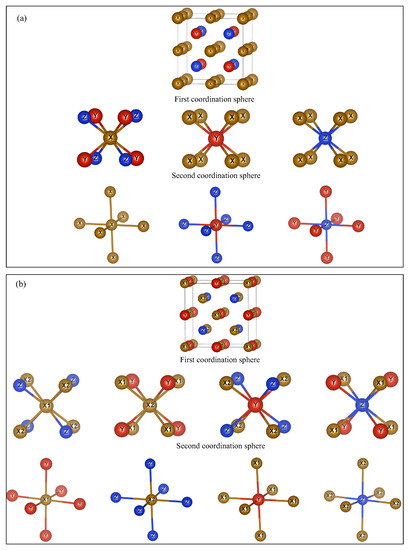
Figure 1.
Crystal structure and nearest and next-nearest local environment of Heusler compounds in (a) and (b) structures.
In the structure, there is a permutation of X atoms in the C-site and Y atoms in the B-site. In this case, the structure is characterized by two symmetrically non-equivalent X atoms, which are designated as X1 and X2, respectively. These atoms differ in their local environment. In the first coordination sphere, X1 atoms are surrounded by metal and non-metal atoms (four X2 and four Z atoms), while X2 atoms are surrounded only by metal atoms (four X1 and four Y atoms). This difference in the local environment determines the difference in the physical properties of X1 and X2 atoms. Y atoms have four Z and four X2 atoms in the first coordination sphere and six X1 atoms in the second coordination sphere. Z atoms have four X1 and four Y atoms as nearest neighbors, and six X2 atoms as next-nearest neighbors.
3.1. Structure Stability
The results of the formation enthalpy calculations are given in Table 1. The calculated formation enthalpies of all compounds are negative, which indicates their stability with respect to decomposition into the isochemical mixture 2M1 + M2 + Si (M1 = V, Fe; M2 = Fe, V) and the possibility of their formation in the experiment. In the case of V2FeSi, the energetically more favorable phase is , while for Fe2VSi, the energetically more favorable phase is . The result obtained is consistent with the available experimental data, where it is reported that Fe2VSi is realized in the structure [6]. It should be noted that there are no such experimental data for V2FeSi.

Table 1.
Calculated formation enthalpies and energy differences between and structures of V2FeSi and Fe2VSi.
The equilibrium lattice parameters and magnetic moments of V2FeSi and Fe2VSi for both and structures are given in Table 2. The lattice constants Fe2VSi- calculated using the SCAN functional are about 2% smaller than the previous theoretical (GGA) and experimental results [6,21]. This is because the simulation was carried out at zero temperature, while the experimentally measured value was obtained at room temperature. Accounting for thermal expansion within SCAN calculations should give a more accurate agreement with the experimental data. It should be noted that in GGA-based calculations [21], the volume of the structure was not relaxed and fixed to the experimental one from ref [6].

Table 2.
Calculated lattice parameters (Å) and magnetic moments () of V2FeSi and Fe2VSi in regular and inverse structures in comparison with available theoretical and experimental data.
3.2. Electronic Structure: Density of States
In Figure 2, the total electron densities of states (TDOS) of V2FeSi and Fe2VSi compounds in and structures are shown. V2FeSi and Fe2VSi, in their energetically favorable structures (Figure 2a) and (Figure 2d), respectively, reveal electronic properties close to half-metallic. There are pseudogaps in TDOS for α-states V2FeSi- and β-states for Fe2VSi-. All the metastable structures are metallic.
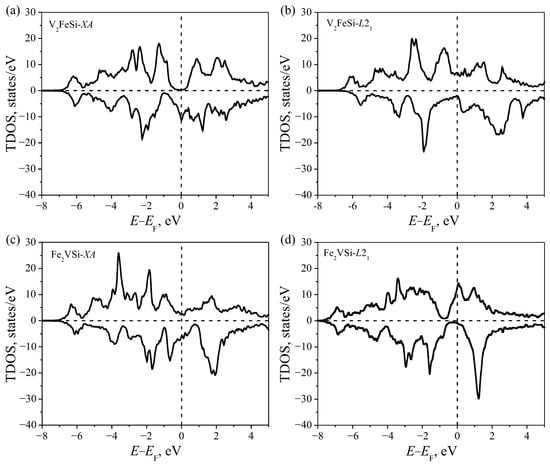
Figure 2.
Calculated total density of states for V2FeSi in (a) and (b) structures, and for Fe2VSi in (c) and (d) structures.
The projected densities of states (PDOS) for the investigated structures are presented in Figure 3 and Figure 4. In all cases considered, the contribution of the Si-p states is much smaller than the contributions of the d-states of transition metals and becomes significant at energies below −3 eV (here and below, the energy levels are counted from the Fermi level).
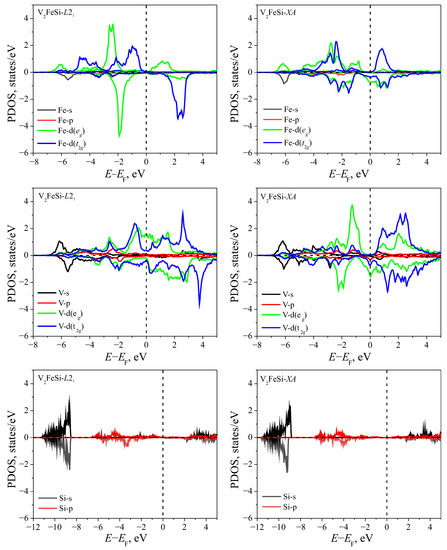
Figure 3.
The partial density of states for V2FeSi of both and structures. Zero on the energy axis corresponds to the Fermi level.
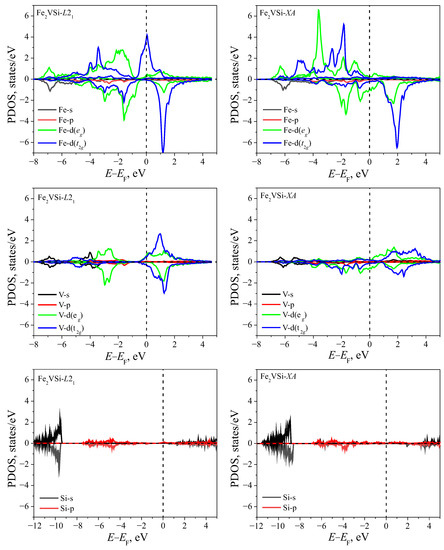
Figure 4.
The partial density of states for Fe2VSi of both and structures. Zero on the energy axis corresponds to the Fermi level.
For the metastable V2FeSi- (Figure 3), there is an energy gap near the Fermi level for the d-states of Fe atoms. In this case, the electronic structure typical for metals is formed due to the and states on V atoms. In the case of the V2FeSi- structure, the bandgap occurs for the spin-majority states. The metallic properties of β-states are due to the electrons of vanadium atoms.
For the compound Fe2VSi (Figure 4), in the case of an energetically favorable lattice, the metallic properties of α-states are provided by the electrons of Fe atoms. The -states of V atoms create a pseudogap with a relatively poor density of states. The metallic properties of the Fe2VSi- metastable structure are created by the states on Fe atoms and electrons on V atoms.
The location of Fe and V atoms in the structure plays a substantial role in the appearance of half-metallic properties in the considered Heusler alloys. From the obtained results, it can be seen that the bonds that arise between the neighboring metal atoms are responsible for the appearance of a half-metallic pseudogap. Since the nearest metal–metal neighbors are located along the (111) direction in the structure, the formation of bonds is mainly associated with the overlapping of the orbitals of Fe and V atoms. It should also be noted that a half-metallic pseudogap appears only when the B-site is occupied by a V atom with a relatively small magnetic moment. If the B-site is occupied by an Fe atom with a relatively large magnetic moment, then the energy gap disappears and the alloy becomes metal.
The absence of conduction electrons near the Fermi level, or the formation of a bandgap, for a particular spin projection indicates that these electrons are localized and participate in the formation of covalent bonds. In contrast, the presence of an electron density near indicates the metallic nature of the bond in this compound. The covalent bond is more vital than the metallic one, which should result in stabilizing the respective structures compared to structures with a metallic bond. This effect can be quantified using the COHP analysis, which has also been carried out and presented in the following.
3.3. Electronic Structure: Chemical Bonding
The results of the COHP analysis for interactions between atoms of the first and second coordination spheres are shown in Figure 5 and Figure 6. For Fe2VSi, the interatomic bonds from −1 eV to the Fermi level are antibonding except for the Si–V interaction. −COHP for β-states near the Fermi level are close to zero (Figure 5a,b), which corresponds to the non-bonding nature of the bond. The stability of the system is ensured by the electronic bonds of the nearest neighbors Si–Fe and V–Fe, which formed electronic states with energies below −3 eV and −2.5 eV (here and below, all energies are considered relative to the Fermi level) (Figure 5a). In addition, the interactions between atoms in the second Si–V coordination sphere at energies below −4 eV make a significant contribution (Figure 5b). This nature of interatomic bonds, in which α-states (except Si–V in the second coordination sphere) are anti-bonding and β-states are non-bonding, explains the metallic behavior of the α-electrons and reduced DOS for the β-electrons.
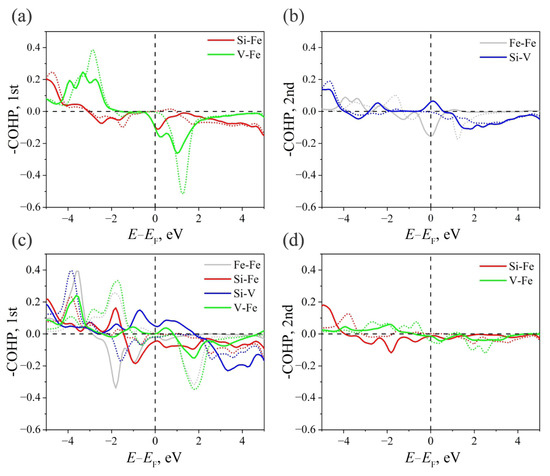
Figure 5.
−COHP for (a) the first and (b) the second coordination spheres of atoms in the Fe2VSi Heusler alloy of structure . −COHP for (c) the first and (d) second coordination spheres of atoms in the Fe2VSi Heusler alloy of the structure.
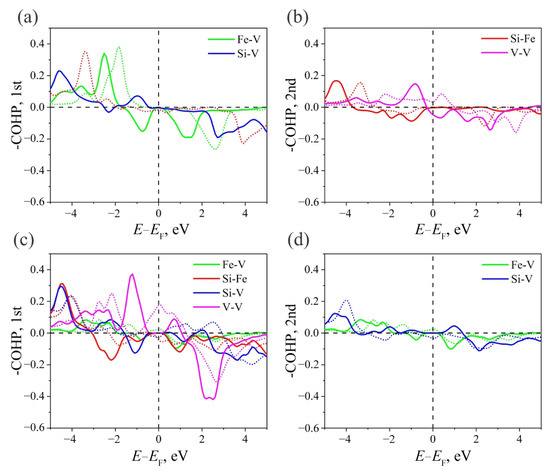
Figure 6.
−COHP for (a) the first and (b) the second coordination spheres of atoms in the V2FeSi Heusler alloy of the structure. −COHP for (c) the first and (d) second coordination spheres of atoms in the V2FeSi Heusler alloy of the structure.
In the Fe2VSi- system near , all interactions between atoms in the first coordination sphere are anti-bonding or nearly non-bonding (Figure 5c,d). The exception is Si–V (α-states), which has a bonding character. The interaction between atoms in the second coordination sphere near the Fermi level is close to non-bonding, except for the interaction of V–Fe (β-states), which are anti-bonding. At lower energies, the V–Fe bond for both spin projections has a weak bonding character. The Si–Fe (α-states) bond is anti-bonding down to energies of −4 eV, while the Si–Fe (β-states) bond is non-bonding down to −3 eV. This character of chemical bonds, which is mainly non-bonding and anti-bonding for both spin projections near , explains the metallic properties of the Fe2VSi- structure.
A similar analysis can be carried out in the case of V2FeSi compounds (Figure 6a,b). V2FeSi- is characterized by a non-bonding character of chemical bonding between the atoms of the first coordination sphere with a weak anti-bonding interaction of the β-states of the Si–V bond near . In the second coordination sphere, near the Fermi level, the Si–Fe bond has a non-bonding character for both spin projections. The presence of anti-bonding interactions for both spin projections provides the metallic character of V2FeSi-. As in the cases considered above, the stability of the structure is ensured by the interaction between deep-lying states.
V2FeSi- is characterized by a non-bonding character of chemical bonding near the Fermi level for all α-states for both considered coordination spheres (Figure 6c,d). In the first coordination sphere, V–V (β-states) bonds have a pronounced bonding character, while Si–V (β-states) and Si–Fe (β-states) are anti-bonding. In the second coordination sphere, Fe–V (β-states) and Si–V (β-states) bonds have a bonding and anti-bonding character, correspondingly. The presence of anti-bonding α-states does not make the system conductive for these states, since α-PDOS(V) near the Fermi level is zero, which explains the presence of a bandgap for α-states (Figure 3). The presence of anti-bonding states and non-zero PDOS for β-states for d-electrons near provides the metallic properties of the system for electrons of a given spin direction.
The integrated −COHP values to (−ICOHPs) are presented in Table 3. Here, we have considered the values for the first three coordinate spheres of each atom. The maximum contribution of the third coordination sphere to the total value of −COHP (∑) is 2.6 % (V2FeSi-). For this reason, the contribution of the interaction of atoms in this coordination sphere is not considered in detail. Since the distances between atoms and their environment in the fourth coordination sphere are 4.8–5 Å, we neglect the contribution of these interactions.

Table 3.
Calculated −ICOHP values for all types of atomic pairs in the first and second coordination spheres. The average values of all interatomic interactions are given for the third coordination sphere. R stands for interatomic distances. The data are given for different spin projections—α and β states. The total corresponds to the sum of α and β values of −ICOHP, while ∑ means the sum of average −ICOHP values for all three coordination spheres.
The value ∑ for the Fe2VSi- structure is greater than the corresponding value for Fe2VSi-. This fact means that the chemical bonds in Fe2VSi- are more substantial than in Fe2VSi-, which explains the lower values of the ground-state energy and the formation enthalpy of Fe2VSi- (Table 1). For V2FeSi, the ratio of ∑ of the and structures is opposite; i.e., chemical bonds in V2FeSi- are weaker than in V2FeSi-. The relations obtained between the values of ∑ explain why the and structures are more favorable for the Fe2VSi and V2FeSi, respectively.
The total −ICOHP for the interaction of atoms of the first coordination sphere is approximately two times greater than the corresponding value for the second coordination sphere. The most considerable dependence on the spin direction is observed for pairs of Fe–Fe atoms. For these pairs of atoms, the −ICOHP values of α-states are 2 (, second shell) and 3 (, first shell) times smaller than the corresponding values for β-states. In all considered Fe2VSi and V2FeSi lattices, the d electrons of the Fe and V atoms are strongly coupled to the p electrons of Si. In both Fe2VSi modifications, the Fe1–Fe2 () and Fe–Fe () bonds are almost two times weaker than the analogous V1–V2 () and V–V () bonds in the V2FeSi system. −ICOHP for V–Fe bonds between nearest neighbors is approximately the same for all considered structures. The Fe–V interaction between the atoms in the second coordination sphere is more vital in the V2FeSi- compared to the same value in Fe2VSi-. It should be noted that in the Fe2VSi system, the average values of −ICOHP in the structure are more significant than the corresponding values in the structure for all three coordination spheres considered. In the case of V2FeSi, the structure is stabilized due to the contribution of the interaction of atoms in the second coordination sphere.
3.4. Magnetic Properties
The value of the magnetic moments of individual transition metal atoms depends on the local environment. It could be assumed that the magnetic moment of the d-element atom will decrease with an increase in the concentration of Z atoms in its nearest neighboring positions. For example, it was stated in ref [26,40] that in ordered Fex alloys, an increase in the concentration of Si in the first coordination sphere of Fe leads to a decrease in the magnetic moment. However, this statement is not entirely true, since the main effect on the change in the magnetic moment of the atom is still exerted by the next-nearest neighbors located in the second coordination sphere [41]. The presence of d-elements at the nearest neighboring positions leads to the formation of strong σ-bonds between the d-electrons of these atoms. In this case, the delocalization of d-electrons and a decrease in the magnetic moment are observed [41,42].
The results of magnetic moment calculations for all structures considered are summarized in Table 2. To determine the preferred magnetic configuration for each structure, in addition to initial ferromagnetic configuration, we have performed the calculations with initial antiferromagnetic configurations. As reported in ref [43], we have considered one initial antiferromagnetic configuration for structures and three possible antiferromagnetic configurations for structures (Figure 7). Regardless of the choice of the initial magnetic configuration, the relaxation of Fe2VSi-, Fe2VSi-, and V2FeSi- lead to ferrimagnetic ordering, while the relaxation of V2FeSi- lead to ferromagnetic ordering.
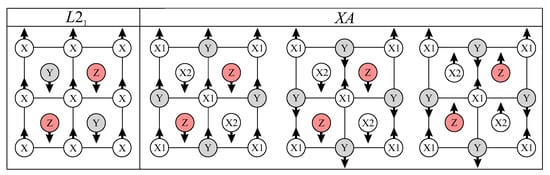
Figure 7.
The types of initial antiferromagnetic configurations for and structures.
According to available experimental data, Fe2VSi is an antiferromagnet, while our calculations showed that it should be a ferrimagnet. Such inconsistency between experiments and calculations may be due to the fact that antiferromagnetism in Fe2VSi is found to strongly depend on the degree of atomic disorder, as was stated by Nishihara et al. [39]. Such a theory–experiment discrepancy is also reported for Mn2FeSi [43,44] and Mn3Si [45].
In the case of V2FeSi, the values of the total magnetic moments of the structure (2.0 /f.u.) obtained using the SCAN functional completely obey the Slater–Pauling (S-P) rule up to the orientation of the magnetic moments. According to this rule, the total magnetic moment in Heusler alloys can be found by the formula , where is the total number of valence electrons per unit cell, and – the magnetic moment per formula unit. The structure (4.02 /f.u.) does not satisfy this rule due to the ferromagnetic bonding of the V and Fe atoms. For Fe2VSi, the value of the total magnetic moment of the structure (0.92 ) is close to the S-P rule prediction of 1.0 /f.u. For the type, the value of the total magnetic moment, equal to 2.48 , is significantly different from the S-P rule obtained value (Table 2). In all the cases considered, the magnitudes of atomic magnetic moments of transition-metal atoms are smaller for stable structures of the corresponding stoichiometry except for V atoms at the A sites of the V2FeSi compound.
An analysis of the −ICOHP values also makes it possible to explain the dependence of the magnetic moment on the transition-metal atoms in the considered compounds. The results obtained correspond to the fact that the weaker the interaction of atoms in the environment, the greater the magnitude of the magnetic moment on them.
In the case of Fe atoms, their magnetic moment corresponds to α states. For this reason, we consider the −ICOHP values for α-states. The −ICOHP(α) values averaged over the first and second coordination spheres of Fe atoms in Fe2VSi compounds are the 0.402 eV/bond for the structure and the 0.334 eV/bond (Fe1) and 0.248 eV/bond (Fe2) for the structure. For V2FeSi, the corresponding −ICOHP values are 0.292 () and 0.465 (). As the values of −ICOHP decrease, the value of the magnetic moment on the Fe atoms increases (Table 2).
A similar analysis in the case of V atoms gives the same dependence of the magnitude of the magnetic moment on the atom on the value of −ICOHP (taking into account the direction of the spin). The −ICOHP values averaged over the first and second coordination spheres of V atoms in V2FeSi compounds are 0.485 eV/bond for the structure and 0.394 eV/bond (V1), and 0.477 eV/bond (V2) for the structure. For Fe2VSi, the corresponding –ICOHP values are 0.536 () and 0.502 ().
Thus, there is a direct correlation between the value of −ICOHP on a transition metal atom and the value of its magnetic moment. The smaller −ICOHP, the larger the value of μ. It should be noted that in the case of V2FeSi-, in contrast to Fe2VSi-, the interaction of α states is more vital. For this reason, the bandgap appears in it for α states, although the total magnetic moment is directed upwards.
4. Conclusions
We have employed the DFT method with SCAN to investigate the electronic and magnetic properties of Fe2VSi and V2FeSi alloys. It is concluded that Fe2VSi is stable in regular structure, while V2FeSi is stable in inverse structure. Both alloys are ferrimagnets and reveal electronic properties close to half-metallic with pseudogaps in β-states for Fe2VSi- and -states for V2FeSi-. In addition, structural stability, electronic and magnetic properties of considered Heusler alloys have been explained in terms of chemical bonding within the COHP formalism.
Author Contributions
Conceptualization, T.I. and V.K.; methodology, T.I.; validation, T.I. and N.S.; formal analysis, N.M. and A.A.; investigation, N.M. and A.A.; writing—original draft preparation, A.A., N.M., N.S., and T.I.; writing—review and editing, F.A. and V.K.; visualization, N.M.; supervision, T.I. and V.K.; funding acquisition, T.I. All authors have read and agreed to the published version of the manuscript.
Funding
This work was performed under the grant project AP08855879 “First-principles design of effective magnetostriction materials for practical applications” for 2020–2022 by the Ministry of Education and Science of the Republic of Kazakhstan. One of the authors (VVK) acknowledges the Russian Science Foundation (grant No. 21-42-00035).
Data Availability Statement
Not applicable.
Acknowledgments
The calculations were performed at the supercomputer cluster provided by the Materials Modeling and Development Laboratory at NUST “MISIS”. The authors are grateful to the Supercomputer Center, Novosibirsk State University, for access to the resources of the cluster.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bakkar, S.A. New Inverse-Heusler Materials with Potential Spintronics Applications; Southern Illinois University at Carbondale: Carbondale, IL, USA, 2017. [Google Scholar]
- Granovskii, A.; Soboleva, E.; Fadeev, E.; Dubenko, I.; Aryal, A.; Samassekou, H.; Pandey, S.; Stadler, S.; Mazumdar, D.; Ali, N.; et al. Martensitic Phase Transition in Magnetic Thin Films Based on Inverse Mn2FeSi Heusler Alloys. J. Exp. Theor. Phys. 2020, 130, 117–122. [Google Scholar] [CrossRef]
- Miki, H.; Ohoyama, K.; Funahashi, S.; Tomiyoshi, S.; Yamaguchi, Y. Crystallographic and magnetic structure of the itinerant-electron antiferromagnets Mn3−xTxSi (T = Cr, Fe). Phys. B Condens. Matter 1995, 213, 360–362. [Google Scholar] [CrossRef]
- Nishino, Y.; Inoue, S.Y.; Asano, S.; Kawamiya, N. Anomalous temperature dependence of the electrical resistivity in binary and pseudobinary alloys based on Fe3Si. Phys. Rev. B 1993, 48, 13607. [Google Scholar] [CrossRef] [PubMed]
- Endo, K.; Tokiyama, M.; Matsuda, H.; Ooiwa, K.; Goto, T.; Arai, J. Anomalous Transport and Magnetic Properties in Fe2+xV1−xSi in Relation to the Origin of GMR. J. Phys. Soc. Jpn. 2004, 73, 1944–1952. [Google Scholar] [CrossRef]
- Ito, M.; Kai, K.; Furuta, T.; Manaka, H.; Terada, N.; Hiroi, M.; Kondo, A.; Kindo, K. Thermodynamic properties of Heusler Fe2VSi. AIP Adv. 2018, 8, 055703. [Google Scholar] [CrossRef]
- Nagano, T.; Uwanuyu, S.; Kawakami, M. Magnetic properties of the Fe2MnSi- and Fe2VSi-based Heusler alloys. J. Magn. Magn. Mater. 1995, 140, 123–124. [Google Scholar] [CrossRef]
- Cui, Y.; Kimura, A.; Miyamoto, K.; Sakamoto, K.; Xie, T.; Qiao, S.; Nakatake, M.; Shimada, K.; Taniguchi, M.; Fujimori, S.I.; et al. Electronic structures of Fe3−xVxSi probed by photoemission spectroscopy. Phys. Status Solidi (A) 2006, 203, 2765–2768. [Google Scholar] [CrossRef]
- Nishino, Y.; Kato, M.; Asano, S.; Soda, K.; Hayasaki, M.; Mizutani, U. Semiconductorlike behavior of electrical resistivity in Heusler-type Fe2VAl compound. Phys. Rev. Lett. 1997, 79, 1909. [Google Scholar] [CrossRef]
- Ullakko, K.; Huang, J.K.; Kantner, C.; O’Handley, R.C.; Kokorin, V.V. Large magnetic-field-induced strains in Ni2MnGa single crystals. Appl. Phys. Lett. 1996, 69, 1966–1968. [Google Scholar] [CrossRef]
- Ullakko, K.; Huang, J.; Kokorin, V.; O’Handley, R. Magnetically controlled shape memory effect in Ni2MnGa intermetallics. Scr. Mater. 1997, 36, 1133–1138. [Google Scholar] [CrossRef]
- Rasul, M.N.; Javed, A.; Khan, M.A.; Hussain, A. Structural stability, mechanical, electronic and magnetic behaviour of quaternary ScNiCrX (X = Al, Ga) Heusler alloys under pressure. Mater. Chem. Phys. 2019, 222, 321–332. [Google Scholar] [CrossRef]
- Abada, A.; Amara, K.; Hiadsi, S.; Amrani, B. First principles study of a new half-metallic ferrimagnets Mn2-based full Heusler compounds: Mn2ZrSi and Mn2ZrGe. J. Magn. Magn. Mater. 2015, 388, 59–67. [Google Scholar] [CrossRef]
- Ze-Jin, Y.; Qing-He, G.; Heng-Na, X.; Ju-Xiang, S.; Xian-Wei, W.; Zhi-Jun, X. Pressure-induced magnetic moment abnormal increase in Mn2FeAl and non-continuing decrease in Fe2MnAl via first principles. Sci. Rep. 2017, 7, 16522. [Google Scholar] [CrossRef]
- Qi, S.; Zhang, C.H.; Chen, B.; Shen, J.; Chen, N. First-principles study on the ferrimagnetic half-metallic Mn2FeAs alloy. J. Solid State Chem. 2015, 225, 8–12. [Google Scholar] [CrossRef]
- Khandy, S.A.; Chai, J.D. Novel half-metallic L21 structured full-Heusler compound for promising spintronic applications: A DFT-based computer simulation. J. Magn. Magn. Mater. 2019, 487, 165289. [Google Scholar] [CrossRef]
- Abuova, F.; Inerbaev, T.; Abuova, A.; Merali, N.; Soltanbek, N.; Kaptagay, G.; Seredina, M.; Khovaylo, V. Structural, Electronic and Magnetic Properties of Mn2Co1−xVxZ (Z = Ga, Al) Heusler Alloys: An Insight from DFT Study. Magnetochemistry 2021, 7, 159. [Google Scholar] [CrossRef]
- Skaftouros, S.; Özdoğan, K.; Şaşıoğlu, E.; Galanakis, I. Generalized Slater-Pauling rule for the inverse Heusler compounds. Phys. Rev. B 2013, 87, 024420. [Google Scholar] [CrossRef]
- Lue, C.S.; Ross, J.H., Jr.; Chang, C.; Yang, H. Field-dependent specific heat in Fe2VAl and the question of possible 3d Heavy Fermion behavior. Phys. Rev. B 1999, 60, R13941. [Google Scholar] [CrossRef]
- Endo, K.; Matsuda, H.; Ooiwa, K.; Itoh, K. Antiferromagnetism in a Heusler alloy Fe2VSi. J. Phys. Soc. Jpn. 1995, 64, 2329–2332. [Google Scholar] [CrossRef]
- Joshi, P.K.; Kumar, K.; Arora, G.; Mali, D.; Jangid, P.K.; Ahuja, B.L. First-principles investigations of electronic and magnetic properties of Fe2V1−xCrxSi Heusler alloys. J. Phys. Conf. Ser. 2021, 1849, 012030. [Google Scholar] [CrossRef]
- Fujii, S.; Ishida, S.; Asano, S. Antiferromagnetism and atomic disorder in Fe2VSi. J. Phys. Soc. Jpn. 2004, 73, 459–463. [Google Scholar] [CrossRef]
- Hirohata, A.; Yamada, K.; Nakatani, Y.; Prejbeanu, I.L.; Dieny, B.; Pirro, P.; Hillebrands, B. Review on spintronics: Principles and device applications. J. Magn. Magn. Mater. 2020, 509, 166711. [Google Scholar] [CrossRef]
- Elphick, K.; Frost, W.; Samiepour, M.; Kubota, T.; Takanashi, K.; Sukegawa, H.; Mitani, S.; Hirohata, A. Heusler alloys for spintronic devices: Review on recent development and future perspectives. Sci. Technol. Adv. Mater. 2021, 22, 235–271. [Google Scholar] [CrossRef]
- Kim, S.K.; Beach, G.S.D.; Lee, K.J.; Ono, T.; Rasing, T.; Yang, H. Ferrimagnetic spintronics. Nat. Mater. 2022, 21, 24–34. [Google Scholar] [CrossRef] [PubMed]
- Niculescu, V.; Burch, T.; Budnick, J. A local environment description of hyperfine fields and atomic moments in Fe3−xTxSi alloys. J. Magn. Magn. Mater. 1983, 39, 223–267. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Sun, J.; Remsing, R.C.; Zhang, Y.; Sun, Z.; Ruzsinszky, A.; Peng, H.; Yang, Z.; Paul, A.; Waghmare, U.; Wu, X.; et al. Accurate first-principles structures and energies of diversely bonded systems from an efficient density functional. Nat. Chem. 2016, 8, 831–836. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Zhang, Y.; Kitchaev, D.A.; Yang, J.; Chen, T.; Dacek, S.T.; Sarmiento-Perez, R.A.; Marques, M.A.L.; Peng, H.; Ceder, G.; Perdew, J.P.; et al. Efficient first-principles prediction of solid stability: Towards chemical accuracy. Npj Comput. Mater. 2018, 4, 9. [Google Scholar] [CrossRef]
- Deringer, V.L.; Tchougréeff, A.L.; Dronskowski, R. Crystal orbital Hamilton population (COHP) analysis as projected from plane-wave basis sets. J. Phys. Chem. A 2011, 115, 5461–5466. [Google Scholar] [CrossRef] [PubMed]
- Dronskowski, R.; Bloechl, P.E. Crystal orbital Hamilton populations (COHP): Energy-resolved visualization of chemical bonding in solids based on density-functional calculations. J. Phys. Chem. 1993, 97, 8617–8624. [Google Scholar] [CrossRef]
- Maintz, S.; Deringer, V.L.; Tchougréeff, A.L.; Dronskowski, R. LOBSTER: A tool to extract chemical bonding from plane-wave based DFT. J. Comput. Chem. 2016, 37, 1030–1035. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA: A Three-Dimens. Vis. Syst. Electron. Struct. Anal. J. Appl. Crystallogr. 2008, 41, 653–658. [Google Scholar] [CrossRef]
- Wang, V.; Xu, N.; Liu, J.C.; Tang, G.; Geng, W.T. VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
- Nishihara, H.; Ono, K.; Neumann, K.U.; Ziebeck, K.; Kanomata, T. Complex magnetism in Fe2VSi. Phys. B Condens. Matter 2003, 329, 1107–1108. [Google Scholar] [CrossRef]
- Bertotti, G.; Ferchmin, A.; Fiorillo, E.; Fukamichi, K.; Kobe, K.; Roth, S. Magnetic alloys for technical applications. Soft magnetic alloys, Invar and Elinvar alloys. Landolt Bornstein New Ser. 1994, 3, 33–142. [Google Scholar]
- Zamkova, N.; Zhandun, V.; Ovchinnikov, S.; Sandalov, I. Effect of local environment on moment formation in iron silicides. J. Alloys Compd. 2017, 695, 1213–1222. [Google Scholar] [CrossRef]
- Draganyuk, O.N.; Zhandun, V.S.; Zamkova, N.G. Effect of the local environment on the magnetic properties of Mn3Si: Hybrid ab initio and model study. Phys. Status Solidi (B) 2019, 256, 1900228. [Google Scholar] [CrossRef]
- Draganyuk, O.N.; Zhandun, V.S.; Zamkova, N.G. Half-metallicity in Fe2MnSi and Mn2FeSi heusler compounds: A comparative ab initio study. Mater. Chem. Phys. 2021, 271, 124897. [Google Scholar] [CrossRef]
- Aryal, A.; Bakkar, S.; Samassekou, H.; Pandey, S.; Dubenko, I.; Stadler, S.; Ali, N.; Mazumdar, D. Mn2FeSi: An antiferromagnetic inverse-Heusler alloy. J. Alloys Compd. 2020, 823, 153770. [Google Scholar] [CrossRef]
- Faleev, S.V.; Ferrante, Y.; Jeong, J.; Samant, M.G.; Jones, B.; Parkin, S.S. Origin of the tetragonal ground state of Heusler compounds. Phys. Rev. Appl. 2017, 7, 034022. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).