Abstract
Diffuse interface descriptions offer many advantages for the modeling of microstructure evolution. However, the numerical representation of moving diffuse interfaces on discrete numerical grids involves spurious grid friction, which limits the overall performance of the model in many respects. Interestingly, this intricate and detrimental effect can be overcome in finite difference (FD) and fast Fourier transformation (FFT)-based implementations by employing the so-called sharp phase-field method (SPFM). The key idea is to restore the discretization-induced broken translational invariance (TI) in the discrete phase-field equation by using analytic properties of the equilibrium interface profile. We prove that this method can indeed eliminate spurious grid friction in the three-dimensional space. Focusing on homogeneous driving forces, we quantitatively evaluate the impact of spurious grid friction on the overall operational performance of different phase-field models. We show that the SPFM provides superior degrees of interface isotropy with respect to energy and kinetics. The latter property enables the frictionless motion of arbitrarily oriented diffuse interfaces on a fixed 3D grid.
1. Introduction
Diffuse interface descriptions, such as phase-field models, provide an elegant way of modeling microstructure evolution involving phase or domain boundary motions. In these models, the diffuse interfaces serve as “smeared out” volumetric surrogates for surface-type defects. The surface-type defects are carriers of physical access energy and their motion is driven by the Gibbs–Thompson effect of reducing the total amount of surface energy as well as other volumetric driving forces. As compared to sharp interface descriptions, the difficult problem of explicit surface tracking is avoided, which allows for any topological evolution of the phase or domain structures, such as interface instabilities, shape bifurcations, nonlinear pattern selection, particle nucleation, or dissolution. Phase-field methods are extensively used in the simulation of complex microstructure evolution problems, such as solidification [1,2,3,4,5], solid-state transformations [6,7,8,9,10], crack propagation [11,12,13,14], ferro-electric domain evolution [15], grain growth [16,17,18], as well as many other [19,20,21,22,23].
Quite often, the width of the diffuse interface appears to be the smallest physical length-scale in the system. Clearly, in order to increase the numerical efficiency in all these cases, one is interested in choosing the smallest possible numerical width resolution, while still keeping the benefits from the diffuse interface description. So far, spurious grid friction (or grid pinning in the phase-field equation) has been the major limiting factor in this regard.
For an understanding of what spurious grid friction is, consider an interface between two phases at different bulk-free energy density levels. The level difference, also called the driving force, induces an interface motion lowering the total free energy of the system by lowering the volume of the high-energy phase. After a transient period of time, a homogeneous and time-independent driving force should always result in a stationary state with a constant transformation velocity. The resulting stationary interface velocity is proportional to the driving force and is exactly prescribed by energy conservation principles.
Figure 1 illustrates the influence of spurious grid friction on the stationary interface motion. An animated version of this figure is provided in the Supplementary Materials. We compare the resulting interface motion for different dimensionless profile resolutions , i.e., the ratio between the phase-field profile width and the numerical grid spacing. In Figure 1a, the phase-field values at different grid points (full symbols) and the least square fit of the profile function Equation (3) around the interface region are plotted. On the right, in Figure 1b, the total interface energy and the fitting value for the phase-field profile width are plotted both as a function of the dimensionless position of the interface center , which takes an integer value whenever a grid point is located in the middle of the interface. For the conventional continuum field (CF) type phase-field models, the interface propagates with a clearly smaller average velocity than expected. This indicates a spurious, friction-like loss of energy during the interface motion. Further, we obtain oscillations in the interface energy and velocity as the interface center passes one grid point after the other. With the decreasing profile resolution, we obtain increasingly larger drops in the average values as well as increasing oscillation amplitudes. For the CF model, this culminates in fully destroyed interface kinetics at the profile resolution and below, which is commonly referred to as grid pinning, see yellow curves in Figure 1. Grid friction and pinning during stationary interface motion in phase-field modeling has been studied earlier [24,25]. Please note, that the coupling of the phase-field to a local bulk energy density difference is prototypical for many advanced phase-field models. In the modeling of microstructure evolution, such inhomogeneous driving forces are calculated from local temperatures [26,27,28], local concentrations [29,30,31,32,33], local strains [34,35,36] or combinations of these [37,38,39,40].
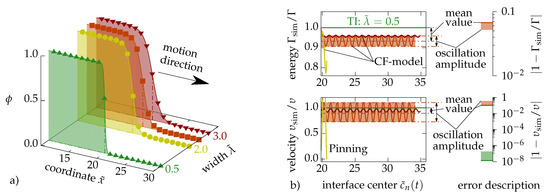
Figure 1.
Illustration of the influence of spurious grid friction on the motion of a constantly driven, planar interface. (a) Comparison of conventional continuum field (CF) models for different phase-field profile resolutions with the translational invariant (TI) model for (green curves) (b) The energy density and the interface velocity, as measured during the simulation, are plotted as functions of the advancing interface center . The dimensionless driving force is . The CF model is subject to pinning for the case of . The logarithmic scale bar on the right shows how much smaller the relative velocity error for the TI model is in comparison to those from the CF model. An animated version of this figure is provided in the Supplementary Materials.
Recently, Finel et al. found a strikingly novel and surprisingly simple way to deal with spurious grid friction in one dimension [41]. The method is conceptually related to previous suggestions to improve the numerical performance of phase-field solvers based on the phase-field profile function [42,43,44,45,46,47,48]. Similar formulations involving the section-wise defined sinus, such as phase-field profiles, have been independently proposed by J. Eiken [49]. The key is to restore the translational invariance (TI) in the discretized phase-field equation by using analytical properties of the phase-field profile function, see Figure 1, the green curve. The TI model, as shown by the green curves in Figure 1, is neither subject to grid friction nor grid pinning even though the phase-field width has been chosen as small as . We should note that choosing means that over of the hyperbolic tangent interface profile is resolved by just one grid point, see Equation (3).
The aim of this work is to prove that spurious grid friction can be eliminated by the sharp phase-field method in one dimension as well as in three dimensions. We define the test configurations, which allow the comprehensive, quantitative evaluation of the intricate influence of grid friction effects on the operational performance of different phase-field models within a unified finite difference (FD) framework. The starting point is the stationary interface motion in one dimension driven by a constant chemical potential density difference. Depending on the modeling details, spurious grid friction and pinning can seriously limit the total parameter range of the reasonable spatial resolution. In the three-dimensional case, the interface orientation relative to the orientation of the computational grid appears as an additional degree of freedom. Keeping the uniform, cubic computational grid fixed, we investigate the influence of varying interface orientations on the stationary motion, see Figure 2. The realization of this configuration requires imposing special boundary conditions for the phase-field, which meets the boundary plains under angles that are different from or . Within this article, we newly propose suitable boundary conditions for this purpose. Deviations of the resulting interface velocity from the theoretic expectations reveal the effect of spurious grid friction. We show that the SPFM can also provide frictionless motion of planar interfaces for arbitrary interface orientations, even in the case of the very low numerical resolution of the diffuse interface profile. Finally, we discuss possible grid friction effects on the 3D shape evolution of a single particle within a matrix phase at constant particle phase volume.
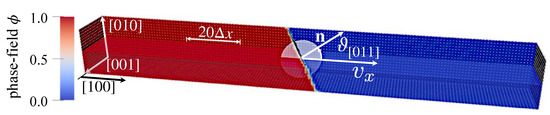
Figure 2.
The stationary interface motion simulation with interface orientations, which differ from the principal axes of the computational grid.
The article is structured as follows: The theoretic aspects of grid friction and how the sharp phase-field method deals with it are presented in Section 2.1. This is followed by the description of the newly proposed contact angle boundary conditions for the phase-field in Section 2.2. In Section 2.3, we discuss a new method for the accurate local measure of the interface center and profile width by nonlinear profile interpolation. The presentation and discussion of the results can be found in Section 3. It starts with the one-dimensional study of the effect of grid friction and grid pinning on the operational limits of different phase-field models, in Section 3.1. In Section 3.2, we discuss the case of stationary interface motion with nontrivial interface orientations in the three-dimensional space with the aim of quantitatively evaluating the residual kinetic grid anisotropy of different phase-field models. Section 3.3 is devoted to the quantitative evaluation of the residual energetic grid anisotropy of different phase-field models, by considering the particle shape evolution toward quasi-equilibrium conditions at constant phase volumes. Finally, based on the present results, in Section 3.4, we discuss the potential computational gains of using the SPFM, also going beyond the finite difference (FD) method.
2. Methods
2.1. The Sharp Phase Field Method (SPFM)
We begin by going through the necessary discretization methods in order to implement the SPFM computationally. The discretized simulation domain in three dimensions consists of a uniform, Cartesian grid of cubic shape, as is usual for simulations based on the finite difference (FD) method, where one is restricted to operating on equispaced, orthogonal grids. We describe orientations and directions relative to the simple cubic computational grid using a Miller index notation system, where the three primitive translation vectors, i.e., , conveniently correspond to the system’s orthonormal Cartesian basis vectors. The SPFM is based on a discrete Helmholtz free energy functional , with a grid spacing along the principle axes. The discrete Helmholtz free energy density associated with the grid point is given by
where the discrete directional phase-field derivatives, , are approximated by forward differencing and denotes a numerical grid vector connecting two neighboring grid points along the direction number k. Besides the central grid point , the formulation involves grid points on the first three neighboring shells , with , as summarized in Table 1. For a given neighboring shell with neighboring nodes, the coefficients are correct for the multiplicity of the shell. Each of the three different summations, i.e., , and , over all the directions constituting a certain neighboring shell results in an independent approximation of the continuous phase-field square gradient contribution to the free energy density. The relative weightings of the three different realizations are chosen to obtain the best possible energetic isotropy [41,50]. All the equilibrium potentials are minimal at and . These states correspond to the two distinct phases of the system. denotes the width of the diffuse interface, is the interface energy density, and is an interface energy calibration parameter. A positive bulk free energy density difference favors the growth of phase at the expense of phase . The interpolation function has to satisfy and . Further, a vanishing slope at is demanded, to keep the local minima of the total potential energy density at and .

Table 1.
The three different neighboring shells and all related grid directions within the simple cubic numerical grid. Exemplary determination of the grid coupling parameter set for the formulation, which restores translational invariance (TI) in the directions of the numerical lattice.
The Allen–Cahn equation prescribes the time evolution of the phase-field to be proportional to the functional derivative of F with respect to the phase-field, i.e., . We write [51,52]
where M is a kinetic coefficient comparable to a diffusion coefficient with dimension . The functional derivative is defined as where the second directional derivative, , is approximated by backward differencing, i.e., , and abbreviates the partial phase-field derivative . The continuum phase-field Equation (2) promotes solutions of the form
where is the unit normal interface vector and denotes the central interface position, moving with the velocity . During the stationary motion of a planar interface, a constant amount of energy per unit time interval dissipates via the progressing phase transformation. Thus, total energy conservation dictates the phase transformation rate as well as the interface velocity to be exactly determined by the driving force via . We should note that the phase-field parameter , the controlling width of the hyperbolic tangent interface profile, is not uniquely defined in the literature. Here, the is defined in such a way that the fraction of of the total transition from to happens within the distance of [18,50].
In equilibrium, i.e., , the phase-field Equation (2) reduces the discrete force equilibrium condition [50]:
where we approximate the Laplacian of by combining forward and backward differencing to the second-order central difference formula, as is usual within the FD method. Note that solutions obtained from conventional phase-field implementations do not strictly satisfy the discrete force equilibrium condition. Not even the ideal solution Equation (3) strictly satisfies Equation (4), if the conventional quartic double well potential is imposed. Generally, these violations of the discrete force equilibrium condition become increasingly severe for small profile resolution numbers.
In Figure 3, we evaluate the degree of satisfaction of the discrete force equilibrium condition with respect to the ideal profile function (3) for different phase-field models. Therefore, a phase-field is initialized according to the ideal profile function (3) such that the interface is located in the middle of the computational domain. The total grid friction force acting on the ideal interface is given by the system integral over (4). While the continuum force integral clearly vanishes, the discrete force integral typically oscillates, when the ideal profile is moved on the computational grid. In Figure 3, we plot the oscillation amplitude A of the discrete interface force as a function of the interface orientation for different models. The conventional continuum field (CF) model (dash-dotted curves), as obtained using the quartic double well potential , provides quite large equilibrium force oscillations. For (yellow curves), the force oscillations clearly reach order unity, which indicates that the model cannot be operated at such a small profile resolution. The situation changes for substantially larger profile resolution numbers, as shown exemplarily by the red curves in Figure 3 for the resolution .
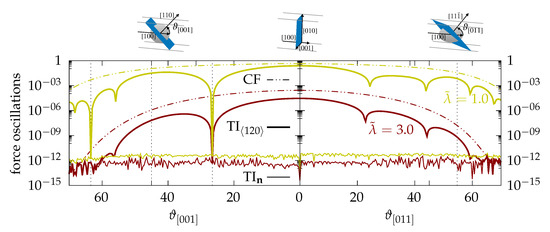
Figure 3.
Logarithmic plot of the oscillation amplitude A of the total grid friction forces, i.e., the system integral over Equation (4), using the ideal profile function (3) as a function of the interface orientation angles and . Two different profile resolutions are compared: (yellow curves) and (red curves). The dash-dotted curves indicate the continuum field (CF) model, where no translational invariance (TI) is restored. The thick solid curves indicate the TI model, which uses global grid coupling parameters (5) to restore TI for interfaces oriented normal to the -directions. The TI model (thin curves) restores TI locally in the direction of the local interface normal . The system size is .
Interestingly, for a given interface orientation , we can find a modified equilibrium potential, which strictly satisfies the discrete equilibrium condition Equation (4), thus providing zero grid friction forces for arbitrarily small profile resolution numbers. Therefore, this modified potential restores the translational invariance (TI) in the phase-field equation and it is derived as follows. The discrete forces equilibrium condition holds if all directional components are simultaneously satisfied. One individual component can be satisfied at any real-time during the propagation of the interface, based on the following additional property, , of the ideal phase-field profile function. Therefore, we introduced the grid coupling parameters as
Inserting this addition property into the force equilibrium condition, we obtain the th component of the derivative of the modified equilibrium potential [50]. Further, integration leads to the th component of the modified equilibrium potential
which further satisfies to allow for easy calculation of the total interface energy (1) using an arbitrary phase-field by [53,54]. In the continuum limit , Equation (6) converges to the conventional CF potential, , as shown in Figure 4.
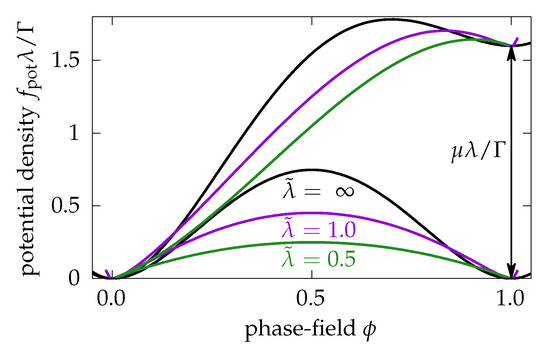
Figure 4.
Joint potential energy density, , as a function of the phase-field with the vanishing (approximately parabolic curves) and non-vanishing (approximately sigmoid shaped curves) driving force, for different values of the dimensionless interface width . The equilibrium potential is given by Equation (6), and .
This new potential strictly eliminates grid friction forces only for those ideal profiles having interface orientations that properly relate to the unit normal vector used to construct the set of grid coupling parameters defined by Equation (5). In the last two columns of Table 1, we construct a set of exemplary grid coupling parameters based on the unit vector pointing in the direction of the computational grid. For the usage of the grid coupling parameters within the sum over the equilibrium potentials Equation (6), the order or the signs are not important. The final potential value is only determined by the absolute values of the grid coupling parameters, as given in the last column in Table 1. Note that all unit vectors pointing in one of the crystallographically equivalent grid directions, as obtained by all possible permutations and negations of the components, provide the identical final potential value. In this regard, the construction has the advantage that it provides the maximum possible number of 24 different equivalent lattice directions since . The resulting sharp phase-field model, which is constructed from this set of grid coupling parameters, is denoted as the TImodel. The thick solid curves in Figure 3 show that the TImodel provides vanishing force oscillations for those interface orientations that match any of the equivalent numerical lattice directions. However, the grid friction force evaluation in Figure 3 also reveals quite narrow interface orientation windows in which the force oscillation amplitudes are found to be substantially below the level of the CF model. This highlights the sensitivity of the method with respect to interface orientations.
In [50], we propose a sharp phase-field model, as denoted by the TI model, which uses locally adaptive grid coupling parameters. These grid coupling parameters are calculated based on the locally measured interface orientation. Concerning the grid friction force evaluation shown in Figure 3, this model (thin curves) provides very small grid friction force oscillations regardless of the interface orientation and the profile resolution. This already indicates that the TI model eliminates spurious grid friction for arbitrarily oriented planar interfaces in 3D. For a sufficiently accurate determination of the locally adaptive grid coupling parameters based on the local interface orientation , the reader is referred to [50].
Within this article, we compare the behavior of different phase-field models with respect to grid friction effects. All these models have been implemented within a unified finite difference (FD) framework. An overview of the considered models is given in Table 2. The models basically differ in their choices for the equilibrium potentials and for the interpolation function .

Table 2.
Overview of the considered models constructed within the unified finite difference (FD) framework.
The continuum field (CF) models are obtained in the limit . In this limit the equilibrium potentials (6) converge to the classical quartic double-well potential , and no translational invariance (TI) is restored. Imposing this potential, we obtain finite difference implementations for phase-field models that correspond to conventional Allen–Cahn type models using a hyperbolic tangent profile. The best possible comparability to the present sharp phase-field models is reached by employing the same interface energy calibrated 27 grid point approximation of the Laplace operator in the phase-field Equation (6). Different CF models result from three different choices for the interpolation function: (i) the natural interpolation function , (i) the most frequently used interpolation function , which provides infinite phase stability, and (iii) the broken rational interpolation function .
TI is obtained when the new equilibrium potential, given by Equation (6) is imposed in conjunction with the natural interpolation function . When the grid coupling parameters in equilibrium potentials are set to the fixed set , then TI is restored for all directions of the computational grid, with parallel to one of the directions. These models are denoted as TI. A combination of the new equilibrium potentials with other interpolation functions turns out to not be useful because the non-equilibrium phase-field profile alternation destroys the carefully restored TI again. In the case of the TI model, the grid coupling parameters are calculated based on the locally determined interface normal vector [50]. Then, TI is restored locally in the local interface normal direction .
All models have been separately calibrated using the procedure discussed in [50]. The result of these calibration procedures is a set of profile resolution-dependent calibration parameters and for each model. However, not all of these calibration parameter functions turn out to be practically different. For instance, the energy calibration parameter function turns out to be equal for all different sharp phase-field models. The different calibration parameter functions are illustrated in Figure 5 and the association with the different models is explained in the last column of Table 2.
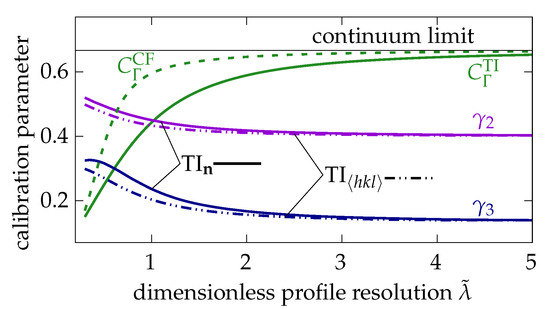
Figure 5.
Different interface energy calibration parameters (solid and dashed green curves) and ponderation coefficients (solid and dash-dotted violet curves), (solid and dash-dotted blue curves) as functions of the profile resolution . .
2.2. Contact Angle Boundary Conditions
The simulation of interface propagation in directions other than the directions of the computational grid requires special boundary conditions for the phase-field. In these simulations, the interface has to meet the boundaries under a definite contact angle. Here, a boundary condition for the phase-field, enforcing a given interface orientation angle with respect to the boundary plane, is newly proposed and implemented. Physically the condition can be understood as a wetting angle of droplets on a surface [55,56]. We use the addition property of the ideal phase-field profile Equation (3) to impose the profile shift, , on the boundary. This shift relates to the angle and enforces the phase-field to meet the boundary plane with proper orientation.
The case when a phase front with the interface normal meets a boundary plane with direction under an angle is shown in Figure 6. The interface is visualized by the gray plane, which relates to the contour of the phase-field. The grid points associated with the computational domain are indicated as colored spheres, with the color denoting the respective phase-field value. Grid points associated with the boundary are indicated as gray spheres. The boundary value at is calculated as
with . The idea behind Equation (7) is to calculate the boundary value at from the neighboring phase-field value at using the addition property of ideal profile function Equation (3), and imposing a profile-shift by the length along the interface’s normal direction. Experience from the simulations with different phase-field models has shown that the accuracy of the proposed contact angle boundary conditions depends on how well the respective phase-field model reproduces the ideal hyperbolic tangent profile.
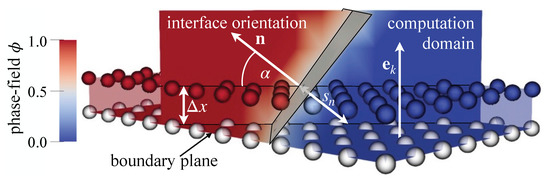
Figure 6.
Schematic illustration of the boundary conditions for the phase-field, which enforces the wetting or contact angle between the interface normal and the direction normal to the boundary plane.
2.3. Measure of the Interface Position and Width
A practical way to accurately determine the actual central interface position , as well as the current profile width for the given phase-field simulation results, is to fit the ideal profile function (3) to the data using least squares. This could be done, for instance, using the Marquardt–Levenberg algorithm [50]. However, for practical reasons, it is not always possible to determine these quantities in such an elaborate way. In these cases, one would rather desire to have an easy and efficient method that, for instance, just interpolates the central interface position , i.e., the contour, based on the known positions and phase-field values at the neighboring grid points. Note that a simple linear interpolation turns out to be not useful in the present case. The linear interpolation results are not sufficiently accurate if the phase-field profile width is small compared to the grid spacing.
Here, we propose a new nonlinear interpolation technique to calculate the contour position based on the analytic phase-field profile (3). The contour position denotes the interpolated position between two neighboring grid points at the positions and , separated by the lattice vector , where the phase-field takes the value , with the contour-level . The two neighboring grid points are located on opposite sides of the contour position along the direction k, such that the following condition is satisfied. Based on the two different phase-field values and two different contour positions can be calculated as
where is a unit vector parallel to the direction k and denotes the directional phase-field width, as determined by the phase-field parameter and the a priori unknown projection of the unit normal interface orientation vector onto the th direction. Assuming the two contour positions to be equal , we obtain an estimation for the directional phase-field width
3. Results and Discussion
3.1. Frictionless Interface Motion in 1D
First, we consider the constantly driven motion of a planar interface in one dimension. After a certain time that depends on the model and profile width, the system reaches a stationary state of motion where the interface velocity is exactly known from energy conservation principles and is given as We perform a simulation study with highly comparable individual simulation runs, with a constant time resolution of . In all the individual simulation runs the interface center has passed at least a minimum number of four grid points (corresponds to time steps) even after the system has reached a stationary state. To reduce the overall computational demands, the whole system is incrementally shifted back by one grid point, whenever the fraction of the energetically favored phase reaches of the system [57,58]. Then, it is sufficient to resolve the total system by just 50 grid points, which is ten times the maximally employed profile resolution. We should note that, especially in the cases of the higher spatial resolution numbers , some models require very long transient times to relax from the initial ideal profile to the stationary state.
In Figure 7, we compare average relative interface velocities as well as the stationary oscillation amplitudes as a function of the constant driving force for a number of different models. As illustrated in Figure 1b, the oscillation amplitudes are indicated by the transparently colored areas connected to the solid lines. The colored areas start from the oscillation amplitude value and end at the mean value. When the colored area is found above the mean value, we encounter the desirable situation that the measured value oscillates around the theoretic expectation. In contrast, colored areas below the mean value denote the undesirable case when the theoretic expectation is located somewhere outside the oscillation interval.
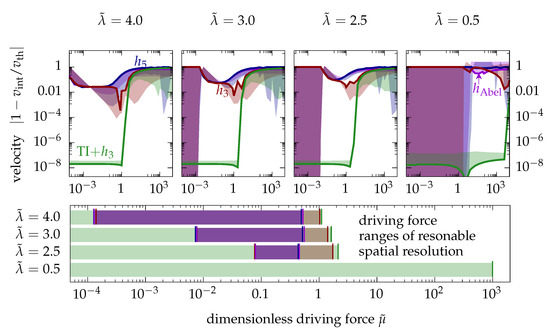
Figure 7.
Logarithmic errors of the stationary interface velocity as a function of the dimensionless driving force for different profile resolutions: . The behavior of different models is compared: (i) continuum field (CF) model with (violet), (ii) CF model with (blue), (iii) CF model with (red) and (iv) the sharp phase-field model with Translational invariance (TI) (green). Solid lines denote the mean relative errors and the oscillations are indicated as transparently colored areas (see Figure 1). The bottom plot compares the parameter windows of reasonable spatial resolution evaluated for the different models. Here, a model is reasonably resolved if the mean velocity error is lower than 10%.
Figure 7 shows that all continuum field (CF) models are subject to grid pinning for the profile resolution and dimensionless driving forces below . Due to the absence of any interface motion in these cases, the mean relative velocity error takes the value 1 and the measured oscillation amplitude vanishes, resulting in the large colored areas below the solid lines on the left side in the logarithmic plots. For increasing profile resolutions, the onset of pinning is shifted towards smaller dimensionless driving forces, as also clearly visible in Figure 7. At a profile resolution of , we find a limited parameter window of driving forces in which the mean relative error is minimal and nearly constant at a value of about . This significant residual error at the comparably large profile resolutions indicates the relevance of spurious grid friction in conventional phase-field modeling. In contrast, the sharp phase-field model provides very small relative velocity errors and oscillations amplitudes on the order of the time discretization error for all resolutions . This indicates that spurious grid friction and grid pinning is truly eliminated in the one-dimensional sharp phase field model.
We further discuss the application of large dimensionless driving forces or small interface energy densities. Limitations with respect to large dimensionless driving forces exist in any phase-field model and denote a relevant restriction of the general applicability of these models. In all kinds of diffuse interface descriptions, the interface energy area density is somehow distributed over the localized volume covered by the diffuse interface. Then, the morphological changes due to the interface energy, i.e., the so-called capillary forces, are modeled by a volume density equivalent, which is inversely proportional to the width of the diffuse interface. The wider the diffuse interface is chosen, the smaller the volume density equivalent of the interface energy is. Therefore, large dimensionless driving forces are the natural consequence of coarse-graining or upscaling of simulations. An important example is the simulation of dendritic solidification, which involves small capillary lengths and large diffusion lengths, resulting in small dendritic tip radii as well as medium secondary- and large primary dendrite arm spacings [58,59,60]. A less complex example is the study of the development of interface instabilities, such as the diffusional Mullins–Sekerka-[61] or the elastic Asaro–Tiller–Grinfeld instability [62,63,64,65]. Both require the interface energy to be comparably small.
Naturally, the choice of the interpolation function is gaining more importance at large dimensionless driving forces. First, we consider the case of imposing the natural interpolation function: [41,64,66]. In this case the ideal phase-field profile Equation (3) remains an analytic solution of the phase-field Equation (2) even at finite driving forces. Then the maximal possible driving force is given by the condition of phase stability. Phase stability demands the driving force to be small enough to guarantee meta-stability of the high energy phase: The two local minima of the potential energy density at have to be separated by a (local) maximum in between. For the CF model, phase stability requires the dimensionless driving force to be below , with and . The TI model provides a profile resolution-dependent phase stability limit, which nicely reflects the behavior of the model [50].
Changing the interpolation function can provide phase stability for larger driving forces. One example is the interpolation function , which has been first proposed by Abel et al. [28]. The advantage of this interpolation function is that a thermodynamically consistent extension to the case of multiple phases is comparably easy [67,68,69]. With regard to the condition of phase stability, we obtain a maximally possible driving force for this interpolation function of An even more common choice for the interpolation function is (see e.g., [22,31,70,71,72]). The CF model even provides phase stability for infinitely large driving forces, which is of course a highly desirable property. However, using interpolation functions other than the natural one leads to altered non-equilibrium phase-field profiles.
The profile alternation grows with increasing driving force. Stronger alternations in turn also lead to stronger grid friction effects. For large dimensionless driving forces, the two CF models and are both limited by grid friction, while the two models are limited by the condition of phase stability. Neither the use of nor that of is useful in the sharp phase-field model, as the altered non-equilibrium profile destroys any restored TI.
In the lower part of Figure 7, the parameter ranges of reasonable spatial resolution are evaluated for each of the different models. A model is set to be reasonably spatially resolved when the relative velocity error during constantly driven interface motion is found to be less than . The CF models cannot reasonably operate at profile resolutions below 2; however, the sharp phase-field model can. For very small profile resolutions, the sharp phase-field model provides surprisingly high limits of phase stability [50].
3.2. Frictionless Interface Motion in 3D
A phase-field model can be anisotropic with respect to interface kinetics as well as interface energetics. Here, we investigate both effects separately. The residual kinetic anisotropy is studied by considering the constantly driven stationary motion of planar interfaces with varying interface orientations . In a stationary system state, the interface normal velocity is exactly determined by energy conservation principles Within the fixed Cartesian grid comprised of equispaced grid points, differently oriented interfaces meet the cubic domain boundaries under specific angles. This requires the employment of the special boundary conditions for the phase-field, as discussed in Section 2.2. The different interface orientations result from continuous rotations around the two different axes and , as sketched on top of the plot in Figure 8. The respective rotation angles between the interface normal direction and the direction, i.e., the direction, are denoted by and , respectively. To evaluate the degree of isotropy of the interface kinetics, we perform a simulation study consisting of many highly comparable individual simulations with an equal component of the interface velocity for all individual simulations. Therefore, the imposed driving forces are chosen to decrease with increasing orientation angles, i.e., with , and a time discretization of . Running each individual simulation for at least time steps ensures that the interface center has passed at least five grid points along the direction.
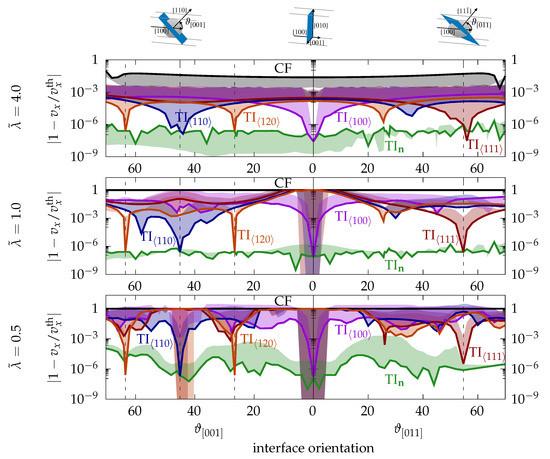
Figure 8.
The relative error in the component of the stationary velocity as functions of the interface orientation angles and . The results from the continuum field (CF) model, various TI models and the TI model are compared for three different profile resolutions , and . The imposed driving force decreases with increasing orientation angles, i.e., with and in any case . The time discretization is .
In Figure 8, we compare the orientation-dependent error (mean value as well as oscillation amplitude) in the interface velocity for different phase-field models. The relative mean errors are depicted by the solid lines and the relative oscillation amplitudes are visualized as colored areas, as has been previously illustrated on the right-hand side of Figure 1b.
The black curves show the results from the continuum field (CF) model. Only for the profile resolution , the CF model is not subject to pinning. Note that the vanishing force oscillations at the profile resolutions and have been omitted in Figure 8 for the CF model. Even for a profile resolution as large as the CF model is still characterized by a significant kinetic anisotropy of about 3%, which is on the scale of the mean relative error in the interface velocity.
All of the sharp phase-field models are more accurate in this regard, in some configurations even by more than an order of magnitude. For a profile resolution of , none of these models is subject to a kinetic anisotropy larger than . However, similar to the onset of grid pinning this situation quickly changes when the profile resolution is decreased. The TI models denote sharp phase-field models with a restored translational invariance (TI) in the directions, as also discussed in Section 2.1. As expected, for interface orientations close to the directions of restored TI, we obtain extremely small errors in the interface velocity. However, already slightly misoriented interfaces propagate at velocities that are clearly below the expectation. The resulting errors in the interface velocity indicate the existence of finite grid friction effects during the stationary interface motion in these directions. Even spurious grid pinning is observed at the profile resolutions and for interface orientations in the vicinity of the direction or less pronounced in the direction for most of the TI models, as clearly visible in Figure 8.
The green curves in Figure 8 show the behavior of the TI model, where the TI has been locally restored in the local direction of interface motion. This provides very accurate interface velocities for all orientations, even if the phase-field width is chosen to be as small as . The resulting velocity error is basically given by the residual error in the time discretization. This observation indicates that this model indeed provides frictionless motion of planar interfaces with arbitrary orientations in the three-dimensional space.
It should be noted that the TI models differ from the original 3D sharp phase-field model purposed by Finel in some respects [41]. We use a finite difference (FD) implementation that operates on a simple cubic computational grid, whereas the 3D sharp phase-field model is formulated on a fcc grid using a spectral FFT-based solver. Both aspects are expected to significantly influence the modeling behavior with regard to the present investigation on the residual anisotropy profile of the interface kinetics.
3.3. Interface Energy-Driven Shape Relaxation
To quantify the residual grid anisotropy of the interfacial energy, we consider the shape evolution of a single particle towards the quasi-equilibrium state under constant particle volume [35,53,73,74]. The 3D simulations of size begin with an initially cubic particle, as shown in the inset of Figure 9a. During the simulation, a homogeneous and time-dependent driving force is imposed, such that the integral volume of the particle neither shrinks nor grows [51,52,75]. The shape evolution of the particle is driven by the minimization of the total interface energy. Figure 9a shows the relaxation of the particles’ total interface energy as a function of the simulation time during the shape evolution. It rapidly approaches a distinct shape that reflects the effective interface energy anisotropy. In the case of a fully isotropic model, the resulting equilibrium shape will be an ideal sphere. Thus, the residual interface energy anisotropy is defined as the deviation of the resulting equilibrium shape from the shape of an ideal sphere.
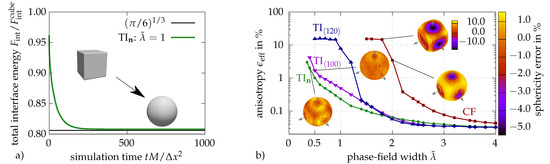
Figure 9.
Investigation of the residual energetic anisotropy by interface energy relaxation of an initially cubic particle at constant particle volume. (a) Total interface energy as a function of the simulation time. (b) Anisotropy of the final quasi-equilibrium phase-fields as a function of the phase-field width for different phase-field models. Insets: Phase-field contours together with their sphericity errors plotted as color-value. For , the extended error range is plotted aside from the inset.
The residual interface energy anisotropy of a certain phase-field model operating at a certain profile resolution is evaluated from the finally relaxed phase-field at the end of the respective simulation. The anisotropy is evaluated from nonlinearly interpolated contour points. The nonlinear interpolation of contour positions based on a given phase-field is described in Section 2.3. For each contour position, we calculate its distance from the particle’s barycenter and divide this by the mean radius . This ratio is called the local sphericity error and is provided as the color value in the contour plots of the quasi-equilibrium shapes shown in Figure 9b. Finally, the overall residual anisotropy of this particular simulation is given by , where and denote the smallest and largest distance between the contour positions and the particle’s barycenter, respectively.
Figure 9b shows the evaluation of the residual interface energy anisotropy as a function of the profile resolution for different phase-field models. For the largest profile resolution all models show very small residual anisotropies with sphericity errors below . Already at profile resolutions of and below the continuum field (CF) model provides the highest sphericity errors of the quasi-equilibrium particle shape due to the onset of pinning. The partially pinned particle contours for the cases and are exemplarily shown as insets in Figure 9b). For profile resolutions below , larger anisotropies due to spurious grid pinning are also observed using the TI models, especially in the generic cases, when the faces of the initial cube are not accidentally aligned with the directions of restored TI. The residual interface energy anisotropies obtained for the TI model are generally very low but, of course, gradually increase with decreasing profile resolution, leading to maximal sphericity errors of for or for .
3.4. Potential Computational Gains
Next, we discuss the potential computational gains by using the sharp phase-field method (SPFM) in a broader context. In this work, we prove that the SPFM can indeed eliminate spurious grid friction and grid pinning in three-dimensional simulations. So far, these detrimental effects have been the major resolution limiting factors in the phase-field equation. Then, the consequence of their elimination is that we obtain higher accuracy at substantially coarser numerical resolution!
The SPFM allows operating at dimensionless profile resolutions of , where it still provides a reasonably good degree of energetic isotropy, i.e., the residual interface energy anisotropy is below , as shown in Figure 9. Such a low profile resolution offers a tremendous savings potential in terms of the number of degrees of freedom required in a phase field simulation. Fully utilizing this potential can lead to much faster computation. At the same spatial resolution, the SPFM involves more calculations on the node level, especially in the case of locally adaptive translational invariance (TI). However, such kind of higher workloads on the node level can be efficiently distributed on parallel computing processors.
The SPFM involves strong coupling between the numerical solution method and the imposed modeling potentials. This is primarily reflected by the grid coupling parameters (5), which are needed for the local evaluation of the phase-field potential. Here, we report on the quantitative testing of this method using the finite difference (FD) method. Besides this, the method has already been successfully tested with a fast Fourier transformation (FFT)-based solvers, as the original SPFM by A. Finel et al. was realized using a spectral solver Finel et al. [41]. Therefore, we know that the results and conclusions presented here are valid for both methods. The transferability of the method as well as the results to other numerical methods, such as the finite element (FE) of the finite volume (FV) method, are subject to ongoing research. Based on our experience with 3D simulations of isotropic solidification using locally adaptive TI Fleck and Schleifer [50], we expect the method to also work on non-regular grids, with changing distances and orientations between neighboring nodes, if the grid coupling parameters are correctly determined.
4. Conclusions
The intricate effects of spurious grid friction, grid pinning, and grid anisotropy limit the performance of conventional phase-field models in many ways. To a large extent, these limitations can be overcome by the sharp phase field method (SPFM) [41,50]. We quantitatively evaluated the operational limits of different phase-field models with and without the SPFM within a unified finite difference framework. An overview of all the different models, considered in this work, is given in Table 2. The operational limits of the models are defined as the borders in the parameter space separating reasonable from erroneous model behavior. The parameter space of interest is spanned by the dimensionless driving force and the dimensionless profile resolution . The key results and findings of this work can be summarized as follows:
- Spurious grid friction is studied by means of simulations of stationary interface motion in one dimension, as shown in Figure 7. In the limit of small driving forces, all CF models are limited by grid pinning, while the sharp phase-field model is entirely free of this effect. With respect to the important case of large dimensionless driving forces, all models involving the natural interpolation function are limited by the condition of phase stability. The other models are limited by spurious grid friction due to increasingly stronger alternations of the phase-field profile.
- The residual kinetic anisotropy of the models is evaluated by systematic variations of the interface orientation within the 3D simulation of the constantly driven interface motion. When imposing a one-grid-point interface resolution (as small as a high degree of kinetic isotropy) can only be obtained by employing models, which locally restore translational invariance (TI) in the local direction of interface motion. The global restoration of TI in fixed directions provides substantial kinetic anisotropies already at dimensionless profile resolutions of , as shown in Figure 8.
- The residual anisotropy of the interfacial energy is evaluated by means of a shape relaxation simulation of one initially cubic particle in a system under the constraint of a constant particle volume. Figure 9 shows the evaluation of the sphericity of the quasi-equilibrium particle shapes as a function of the phase-field profile resolution for different phase-field models. In any case, the different sharp phase-field models provide substantially lower energetic anisotropies as compared to the conventional CF model. However, for profile resolutions below , grid pinning is observed in unlucky cases using models with a global restoration of TI in fixed lattice directions. The TI model reliably provides very small residual interface energy anisotropies.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/cryst12101496/s1, Supplementary_material_S1_Pinning_animation.mpg: This movie is an animated version of Figure 1. It illustrates the influence of spurious grid friction and grid pinning on the motion of a planar interface in one dimension. We compare the behavior of the conventional phase-field formulation for different phase-field widths with the behavior of the sharp phase-field model (green curves). Supplementary_material_S2_Steady_state_interface_motion.mpg: This movie is an animated visualization of the evolution of the phase-field during the simulation of stationary motion of a planar interface with propagates under an angle of with respect to the computational grid using the TI model with . Supplementary_material_S3_ContactAngleBC.mpg: This movie illustrates the function of the newly proposed boundary conditions. They enforce a finite contact angle between the interface normal and the boundary plane. In this movie, we show a simulation of the shape-evolution of an initially cubic particle toward its spherical equilibrium shape under conserved phase volume. The particle is in contact with the bottom boundary, where a contact angle of 80° with respect to the boundary plane is enforced.
Author Contributions
Conceptualization, M.F. model and code development, M.F., F.S. and P.Z.; investigation, M.F., F.S. and P.Z.; validation, M.F., F.S. and P.Z.; writing—original draft preparation, M.F.; writing—review and editing, M.F., F.S. and P.Z.; supervision, M.F.; funding acquisition, M.F. All authors have read and agreed to the published version of the manuscript.
Funding
The work is funded by the Deutsche Forschungsgemeinschaft (DFG)–431968427.
Data Availability Statement
The research data sets generated during the current study are available from the corresponding author upon reasonable request.
Acknowledgments
We thank A. Finel from ONERA, Châtillon, France for fruit-full discussions on this issue.
Conflicts of Interest
The authors have no conflict of interest to declare.
Abbreviations
The following abbreviations are used in this manuscript:
| SPFM | sharp phase-field method |
| CF | continuum field |
| TI | translational invariance |
| FD | finite difference |
| FFT | fast Fourier transformation |
References
- Debierre, J.M.; Guérin, R.; Kassner, K. Crystal growth in a channel: Pulsating fingers, merry-go-round patterns, and seesaw dynamics. Phys. Rev. E 2013, 88, 042407. [Google Scholar] [CrossRef] [PubMed]
- Bollada, P.C.; Goodyer, C.E.; Jimack, P.K.; Mullis, A.M.; Yang, F.W. Three dimensional thermal-solute phase field simulation of binary alloy solidification. J. Comp. Phys. 2015, 287, 130–150. [Google Scholar] [CrossRef]
- Kurz, W.; Rappaz, M.; Trivedi, R. Progress in modelling solidification microstructures in metals and alloys. Part II: Dendrites from 2001 to 2018. Int. Mater. Rev. 2021, 66, 30–76. [Google Scholar] [CrossRef]
- Tourret, D.; Liu, H.; LLorca, J. Phase-field modeling of microstructure evolution: Recent applications, perspectives and challenges. Prog. Mater. Sci. 2021, 123, 100810. [Google Scholar] [CrossRef]
- Wang, K.; Boussinot, G.; Brener, E.A.; Spatschek, R. Quantitative nondiagonal phase field modeling of eutectic and eutectoid transformations. Phys. Rev. B 2021, 103, 184111. [Google Scholar] [CrossRef]
- Asta, M.; Beckermann, C.; Karma, A.; Kurz, W.; Napolitano, R.; Plapp, M.; Purdy, G.; Rappaz, M.; Trivedi, R. Solidification microstructures and solid-state parallels: Recent developments, future directions. Acta Mater. 2009, 57, 941–971. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J. Phase field modeling of defects and deformation. Acta Mater. 2010, 58, 1212. [Google Scholar] [CrossRef]
- Jokisaari, A.; Naghavi, S.; Wolverton, C.; Voorhees, P.W.; Heinonen, O. Predicting the morphologies of γ’ precipitates in cobalt-based superalloys. Acta Mater. 2017, 141, 273–284. [Google Scholar] [CrossRef]
- Mianroodi, J.; Shanthraj, P.; Kontis, P.; Cormier, J.; Gault, G.; Svendsen, B.; Raabe, D. Atomistic phase field chemomechanical modeling of dislocation-solute-precipitate interaction in Ni-Al-Co. Acta Mater. 2019, 175, 250–261. [Google Scholar] [CrossRef]
- Mianroodi, J.R.; Shanthraj, P.; Svendsen, B.; Raabe, D. Phase-Field Modeling of Chemoelastic Binodal/Spinodal Relations and Solute Segregation to Defects in Binary Alloys. Materials 2021, 14, 1787. [Google Scholar] [CrossRef]
- Pons, A.J.; Karma, A. Helical crack-front instability in mixed-mode fracture. Nature 2010, 464, 85. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.H.; Bouchbinder, E.; Karma, A. Instability in dynamic fracture and the failure of the classical theory of cracks. Nat. Phys. 2017, 13, 1186–1190. [Google Scholar] [CrossRef]
- Lubomirsky, Y.; Chen, C.H.; Karma, A.; Bouchbinder, E. Universality and Stability Phase Diagram of Two-Dimensional Brittle Fracture. Phys. Rev. Lett. 2018, 121, 134301. [Google Scholar] [CrossRef] [PubMed]
- Mesgarnejad, A.; Karma, A. Vulnerable window of yield strength for swelling-driven fracture of phase-transforming battery materials. npj Comp. Mater. 2020, 6, 58. [Google Scholar] [CrossRef]
- Yadav, A.; Nguyen, K.; Hong, Z.; García-Fernández, P.; Aguado-Puente, P.; Nelson, C.; Das, S.; Prasad, B.; Kwon, D.; Cheema, S.; et al. Spatially resolved steady-state negative capacitance. Nature 2019, 565, 468–471. [Google Scholar] [CrossRef]
- Moelans, N.; Blanpain, B.; Wollants, P. Quantitative Phase-Field Approach for Simulating Grain Growth in Anisotropic Systems with Arbitrary Inclination and Misorientation Dependence. Phys. Rev. Lett. 2008, 101, 025502. [Google Scholar] [CrossRef]
- Darvishi Kamachali, R.; Abbondandolo, A.; Siburg, K.; Steinbach, I. Geometrical grounds of mean field solutions for normal grain growth. Acta Mater. 2015, 90, 252–258. [Google Scholar] [CrossRef]
- Dimokrati, A.; Le Bouar, Y.; Benyoucef, M.; Finel, A. S-PFM model for ideal grain growth. Acta Mater. 2020, 201, 147–157. [Google Scholar] [CrossRef]
- Ni, Y.; Yu, S.; Jiang, H.; He, L. The shape of telephone cord blisters. Nat. Commun. 2017, 8, 14138. [Google Scholar] [CrossRef]
- Tonks, M.; Aagesen, L. The Phase Field Method: Mesoscale Simulation Aiding Material Discovery. Annu. Rev. Mater. Res. 2019, 49, 79–102. [Google Scholar] [CrossRef]
- Aagesen, L.; Schwen, D.; Tonks, M.; Zhang, Y. Phase-field modeling of fission gas bubble growth on grain boundaries and triple junctions in UO2 nuclear fuel. Comp. Mater. Sci. 2019, 161, 35–45. [Google Scholar] [CrossRef]
- Kim, K.; Sherman, Q.; Aagesen, L.; Voorhees, P. Phase-field model of oxidation: Kinetics. Phys. Rev. E 2020, 101, 022802. [Google Scholar] [CrossRef] [PubMed]
- Gránásy, L.; Rátkai, L.; Tóth, G.I.; Gilbert, P.U.P.A.; Zlotnikov, I.; Pusztai, T. Phase-Field Modeling of Biomineralization in Mollusks and Corals: Microstructure vs Formation Mechanism. JACS Au 2021, 1, 1014–1033. [Google Scholar] [CrossRef] [PubMed]
- Karma, A.; Rappel, W.J. Quantitative phase-field modeling of dendritic growth in two and three dimensions. Phys. Rev. E 1998, 57, 4323–4349. [Google Scholar] [CrossRef]
- Bösch, A.; Müller-Krumbhaar, H.; Shochet, O. Phase-field models for moving boundary problems: Controlling metastability and anisotropy. Z. Phys. B 1995, 97, 367–377. [Google Scholar] [CrossRef]
- Wang, S.L.; Sekerka, R.; Wheeler, A.; Murray, B.; Coriell, S.; Braun, R.; McFadden, G. Thermodynamically-consistent phase-field models for solidification. Physica D 1993, 69, 189–200. [Google Scholar] [CrossRef]
- Kobayashi, R. Modeling and numerical simulations of dendritic crystal growth. Physica D 1993, 63, 410–423. [Google Scholar] [CrossRef]
- Abel, T.; Brener, E.; Müller-Krumbhaar, H. Three-dimensional growth morphologies in diffusion-controlled channel growth. Phys. Rev. E 1997, 55, 7789–7792. [Google Scholar] [CrossRef]
- Echebarria, B.; Folch, R.; Karma, A.; Plapp, M. Quantitative phase-field model of alloy solidification. Phys. Rev. E 2004, 70, 061604. [Google Scholar] [CrossRef]
- Eiken, J.; Böttger, B.; Steinbach, I. Multiphase-field approach for multicomponent alloys with extrapolation scheme for numerical application. Phys. Rev. E 2006, 73, 066122. [Google Scholar] [CrossRef]
- Aagesen, L.; Gao, Y.; Schwen, D.; Ahmed, K. Grand-potential-based phase-field model for multiple phases, grains, and chemical components. Phys. Rev. E 2018, 98, 023309. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Boussinot, G.; Hüter, C.; Brener, E.; Spatschek, R. Modeling of dendritic growth using a quantitative nondiagonal phase field model. Phys. Rev. Mater. 2020, 4, 033802. [Google Scholar] [CrossRef]
- Zimbrod, P.; Schilp, J. Modelling of microstructures during in-situ alloying in additive manufacturing for efficient material qualification processes. In Proceedings of the Simulation in Produktion und Logistik 2021: 19. ASIM-Fachtagung Simulation in Produktion und Logistik, Erlangen, Germany, 15–17 September 2021. [Google Scholar]
- Fleck, M.; Pilipenko, D.; Spatschek, R.; Brener, E.A. Brittle fracture in viscoelastic materials as a pattern-formation process. Phys. Rev. E 2011, 83, 046213. [Google Scholar] [CrossRef] [PubMed]
- Bhadak, B.; Sankarasubramanian, R.; Choudhury, A. Phase-Field Modeling of Equilibrium Precipitate Shapes under the Influence of Coherency Stresses. Metall. Mater. Trans. A 2018, 49, 5705–5726. [Google Scholar] [CrossRef]
- Mesgarnejad, A.; Pan, C.; Erb, R.M.; Shefelbine, S.J.; Karma, A. Crack path selection in orientationally ordered composites. Phys. Rev. E 2020, 102, 013004. [Google Scholar] [CrossRef]
- Steinbach, I. Phase-field models in materials science. Modell. Sim. Mater. Sci. Eng. 2009, 17, 073001. [Google Scholar] [CrossRef]
- Steinbach, I. Phase-Field Model for Microstructure Evolution at the Mesoscopic Scale. Annu. Rev. Mater. Res. 2013, 43, 89. [Google Scholar] [CrossRef]
- Cottura, M.; Le Bouar, Y.; Appolaire, B.; Finel, A. Role of elastic inhomogeneity in the development of cuboidal microstructures in Ni-based superalloys. Acta Mater. 2015, 94, 15–25. [Google Scholar] [CrossRef]
- Song, Y.; Tourret, D.; Mota, F.; Pereda, J.; Billia, B.; Bergeon, N.; Trivedi, R.; Karma, A. Thermal-field effects on interface dynamics and microstructure selection during alloy directional solidification. Acta Mater. 2018, 150, 139–152. [Google Scholar] [CrossRef]
- Finel, A.; Le Bouar, Y.; Dabas, B.; Appolaire, B.; Yamada, Y.; Mohri, T. Sharp Phase Field Method. Phys. Rev. Lett. 2018, 121, 025501. [Google Scholar] [CrossRef]
- Glasner, K. Nonlinear Preconditioning for Diffuse Interfaces. J. Comp. Phys. 2001, 174, 695–711. [Google Scholar] [CrossRef]
- Weiser, M. Pointwise nonlinear scaling for reaction–diffusion equations. Appl. Num. Math. 2009, 59, 1858–1869. [Google Scholar] [CrossRef][Green Version]
- Debierre, J.M.; Guérin, R.; Kassner, K. Phase-field study of crystal growth in three-dimensional capillaries: Effects of crystalline anisotropy. Phys. Rev. E 2016, 94, 013001. [Google Scholar] [CrossRef] [PubMed]
- Gong, T.Z.; Chen, Y.; Cao, Y.F.; Kang, X.H.; Li, D.Z. Fast simulations of a large number of crystals growth in centimeter-scale during alloy solidification via nonlinearly preconditioned quantitative phase-field formula. Comp. Mater. Sci. 2018, 147, 338–352. [Google Scholar] [CrossRef]
- Shen, J.; Xu, J.; Yang, J. A New Class of Efficient and Robust Energy Stable Schemes for Gradient Flows. SIAM Rev. 2019, 61, 474–506. [Google Scholar] [CrossRef]
- Ji, K.; Molavi Tabrizi, A.; Karma, A. Isotropic finite-difference approximations for phase-field simulations of polycrystalline alloy solidification. J. Comput. Phys. 2022, 457, 111069. [Google Scholar] [CrossRef]
- Sakane, S.; Takaki, T.; Aoki, T. Parallel-GPU-accelerated adaptive mesh refinement for three-dimensional phase-field simulation of dendritic growth during solidification of binary alloy. Mater. Theory 2022, 6, 3. [Google Scholar] [CrossRef]
- Eiken, J. Numerical solution of the phase-field equation with minimized discretization error. IOP Conf. Ser. Mater. Sci. Eng. 2012, 33, 012105. [Google Scholar] [CrossRef]
- Fleck, M.; Schleifer, F. Sharp phase-field modeling of isotropic solidification with a super efficient spatial resolution. Eng. Comput. 2022, accepted. [Google Scholar] [CrossRef]
- Fleck, M.; Federmann, H.; Pogorelov, E. Phase-field modeling of Li-insertion kinetics in single LiFePO4-nano-particles for rechargeable Li-ion battery application. Comp. Mater. Sci. 2018, 153, 288–296. [Google Scholar] [CrossRef]
- Fleck, M.; Mushongera, L.; Pilipenko, D.; Ankit, K.; Emmerich, H. On phase-field modeling with a highly anisotropic interfacial energy. Eur. Phys. J. Plus 2011, 126, 95. [Google Scholar] [CrossRef]
- Schleifer, F.; Holzinger, M.; Lin, Y.Y.; Glatzel, U.; Fleck, M. Phase-field modeling of a γ/γ″ microstructure in nickel-base superalloys with high γ″ volume fraction. Intermetallics 2020, 120, 106745. [Google Scholar] [CrossRef]
- Schleifer, F.; Fleck, M.; Holzinger, M.; Lin, Y.Y.; Glatzel, U. Phase-Field Modeling of γ′ and γ″ Precipitate Size Evolution during Heat Treatment of Ni-Base Superalloys, Superalloys 2020; Springer International Publishing: Cham, Germany, 2020; Chapter 49; pp. 500–508. [Google Scholar]
- Ben Said, M.; Selzer, M.; Nestler, B.; Braun, D.; Greiner, C.; Garcke, H. A Phase-Field Approach for Wetting Phenomena of Multiphase Droplets on Solid Surfaces. Langmuir 2014, 30, 4033–4039. [Google Scholar] [CrossRef] [PubMed]
- Diewald, F.; Lautenschlaeger, M.; Stephan, S.; Langenbach, K.; Kuhn, C.; Seckler, S.; Bungartz, H.J.; Hasse, H.; Müller, R. Molecular dynamics and phase field simulations of droplets on surfaces with wettability gradient. Comp. Meth. Appl. Mech. Eng. 2020, 361, 112773. [Google Scholar] [CrossRef]
- Fleck, M.; Brener, E.A.; Spatschek, R.; Eidel, B. Elastic and plastic effects on solid-state transformations: A phase field study. Int. J. Mater. Res. 2010, 4, 462. [Google Scholar] [CrossRef]
- Fleck, M.; Querfurth, F.; Glatzel, U. Phase field modeling of solidification in multi-component alloys with a case study on the Inconel 718 alloy. J. Mater. Res. 2017, 32, 4605–4615. [Google Scholar] [CrossRef]
- Tourret, D.; Karma, A. Three-dimensional dendritic needle network model for alloy solidification. Acta Mater. 2016, 120, 240–254. [Google Scholar] [CrossRef]
- Tourret, D.; Sturz, L.; Viardin, A.; Založnik, M. Comparing mesoscopic models for dendritic growth. IOP Conf. Ser. Mater. Sci. Eng. 2020, 861, 012002. [Google Scholar] [CrossRef]
- Mullins, W.; Sekerka, R. Stability of a Planar Interface During Solidification of a Dilute Binary Alloy. J. Appl. Phys. 1964, 35, 444–451. [Google Scholar] [CrossRef]
- Asaro, R.; Tiller, W. Interface morphology development during stress corrosion cracking: Part I. Via surface diffusion. Metall. Mater. Trans. A 1972, 3, 1789–1796. [Google Scholar] [CrossRef]
- Grinfeld, M. The stress driven instability in elastic crystals: Mathematical models and physical manifestations. J. Nonlin. Sci. 1993, 3, 35–83. [Google Scholar] [CrossRef]
- Kassner, K.; Misbah, C.; Müller, J.; Kappey, J.; Kohlert, P. Phase-field modeling of stress-induced instabilities. Phys. Rev. E 2001, 63, 036117. [Google Scholar] [CrossRef]
- Spatschek, R.; Fleck, M. Influence of stress on interface kinetics. Phil. Mag. Lett. 2007, 87, 909. [Google Scholar] [CrossRef]
- Pilipenko, D.; Fleck, M.; Emmerich, H. On numerical aspects of phase-field fracture modelling. Eur. Phys. J. Plus 2011, 126, 100. [Google Scholar] [CrossRef]
- Moelans, N. A quantitative and thermodynamically consistent phase-field interpolation function for multi-phase systems. Acta Mater. 2011, 59, 1077–1086. [Google Scholar] [CrossRef]
- Moelans, N.; Blanpain, B.; Wollants, P. Quantitative analysis of grain boundary properties in a generalized phase field model for grain growth in anisotropic systems. Phys. Rev. B 2008, 78, 024113. [Google Scholar] [CrossRef]
- Bollada, P.C.; Jimack, P.K.; Mullis, A.M. Towards a Physically Consistent Phase-Field Model for Alloy Solidification. Metals 2022, 12, 272. [Google Scholar] [CrossRef]
- Plapp, M. Unified derivation of phase-field models for alloy solidification from a grand-potential functional. Phys. Rev. E 2011, 84, 031601. [Google Scholar] [CrossRef]
- Ohno, M.; Takaki, T.; Shibuta, Y. Variational formulation of a quantitative phase-field model for nonisothermal solidification in a multicomponent alloy. Phys. Rev. E 2017, 96, 033311. [Google Scholar] [CrossRef]
- Greenwood, M.; Shampur, K.N.; Ofori-Opoku, N.; Pinomaa, T.; Wang, L.; Gurevich, S.; Provatas, N. Quantitative 3D phase field modelling of solidification using next-generation adaptive mesh refinement. Comp. Mater. Sci. 2018, 142, 153. [Google Scholar] [CrossRef]
- Holzinger, M.; Schleifer, F.; Glatzel, U.; Fleck, M. Phase-field modeling of γ′-precipitate shapes in nickel-base superalloys and their classification by moment invariants. Eur. Phys. J. B 2019, 92, 208. [Google Scholar] [CrossRef]
- Lin, Y.Y.; Schleifer, F.; Holzinger, M.; Ta, N.; Skrotzki, B.; Darvishi Kamachali, R.; Glatzel, U.; Fleck, M. Quantitative shape-classification of misfitting precipitates during cubic to tetragonal transformations: Phase-field simulations and Experiments. Materials 2021, 14, 1373. [Google Scholar] [CrossRef] [PubMed]
- Nestler, B.; Wendler, F.; Selzer, M.; Stinner, B.; Garcke, H. Phase-field model for multiphase systems with preserved volume fractions. Phys. Rev. E 2008, 78, 011604. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).