A Novel Photo Elasto-Thermodiffusion Waves with Electron-Holes in Semiconductor Materials with Hyperbolic Two Temperature
Abstract
1. Introduction
2. Basic Equations
3. The Solution of the Problem
4. Boundary Conditions
- (I)
- The isothermal boundary condition (thermally insulated system) subjected to thermal shock is taken at the free surface when as:
- (II)
- The hole charge carrier at the free surface condition, with Laplace transformation application, yields:
- (III)
- The plasma boundary condition at the free surface when the carrier density diffusion is transported and photo-generated during the recombination processes by applying Laplace transform. In this case, the plasma condition can be rewritten in the following form:
- (IV)
- The mechanical stress condition at the free surface when
- (V)
- The other mechanical conditions can be chosen when the traction component of the stress is free at when using the Fourier and Laplace transform as:
5. Inversion of the Fourier—Laplace Transforms
6. Numerical Results and Discussions
6.1. Results Validation
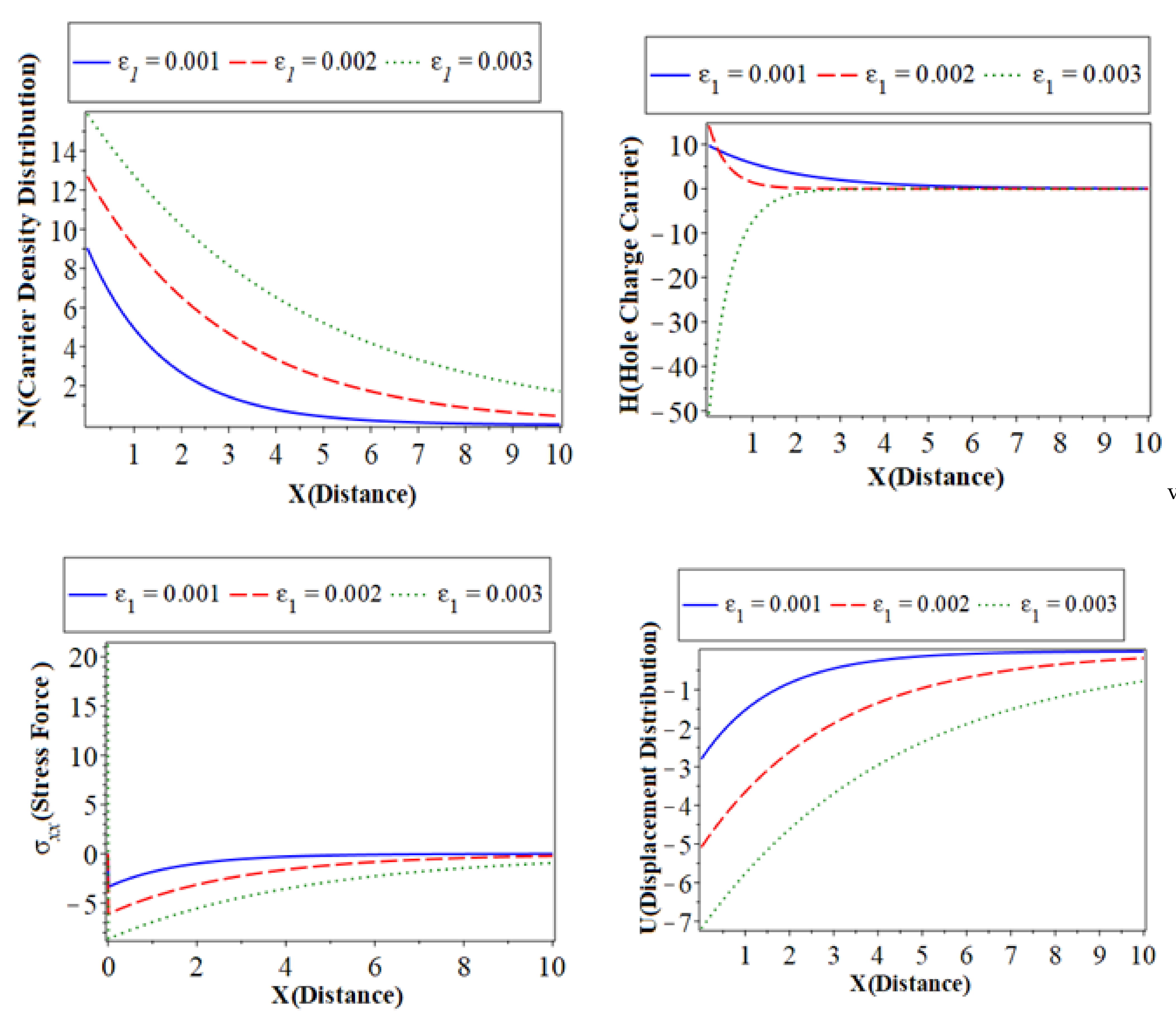
6.2. The Effect of Thermoelastic Coupling Parameters
 ) with a blue color curve represent the case when
the dashed lines (
) with a blue color curve represent the case when
the dashed lines ( ) with red color curve express the case at , and the dotted lines (
) with red color curve express the case at , and the dotted lines ( ) with a green color curve show the case at . The first subfigure represents the temperature () distribution against the horizontal distance [30]. The temperature distribution starts from the maximum positive value for all three cases. In the case of the distribution takes on the exponential behavior with a smooth decrease. On the other hand, when and the distribution of displacement decreases sharply in the first range; it takes on exponential propagation behavior until it reaches a minimum value near the zero line for the rough surface. The second subfigure displays the conduction heat () distribution with the distance , which takes on the same behavior as the first subfigure in the first category. The third subfigure displays the carrier density distribution against the distance in variation values of the thermoelastic parameter. However, a small change in thermoelastic coupling parameters has no significant effect on the carrier density, which has a similar quality behavior. The fourth subfigure describes the hole charge density with the distance. This subfigure shows that the amplitude values of the heat conduction distribution increase with the decrease in the values of the thermoelastic coupling parameters due to acceleration of thermal waves and photothermal excitation. The fifth subfigure displays the increases of stress force amplitude, due to the mechanical loads, tends to increase the value of thermoelastic coupling parameters. The sixth subfigure displays the displacement distributions against the distance x which show that the curves are carried out from the negative value approach to zero at all cases. On the other hand, all the physical quantities under study are affected by changes in the thermoelastic coupling parameter. This is because the absolute value of the main fields is very sensitive to the changes of the thermoelastic coupling parameter.
) with a green color curve show the case at . The first subfigure represents the temperature () distribution against the horizontal distance [30]. The temperature distribution starts from the maximum positive value for all three cases. In the case of the distribution takes on the exponential behavior with a smooth decrease. On the other hand, when and the distribution of displacement decreases sharply in the first range; it takes on exponential propagation behavior until it reaches a minimum value near the zero line for the rough surface. The second subfigure displays the conduction heat () distribution with the distance , which takes on the same behavior as the first subfigure in the first category. The third subfigure displays the carrier density distribution against the distance in variation values of the thermoelastic parameter. However, a small change in thermoelastic coupling parameters has no significant effect on the carrier density, which has a similar quality behavior. The fourth subfigure describes the hole charge density with the distance. This subfigure shows that the amplitude values of the heat conduction distribution increase with the decrease in the values of the thermoelastic coupling parameters due to acceleration of thermal waves and photothermal excitation. The fifth subfigure displays the increases of stress force amplitude, due to the mechanical loads, tends to increase the value of thermoelastic coupling parameters. The sixth subfigure displays the displacement distributions against the distance x which show that the curves are carried out from the negative value approach to zero at all cases. On the other hand, all the physical quantities under study are affected by changes in the thermoelastic coupling parameter. This is because the absolute value of the main fields is very sensitive to the changes of the thermoelastic coupling parameter.6.3. The Effect of the Phase-Lag of the Temperature Gradient
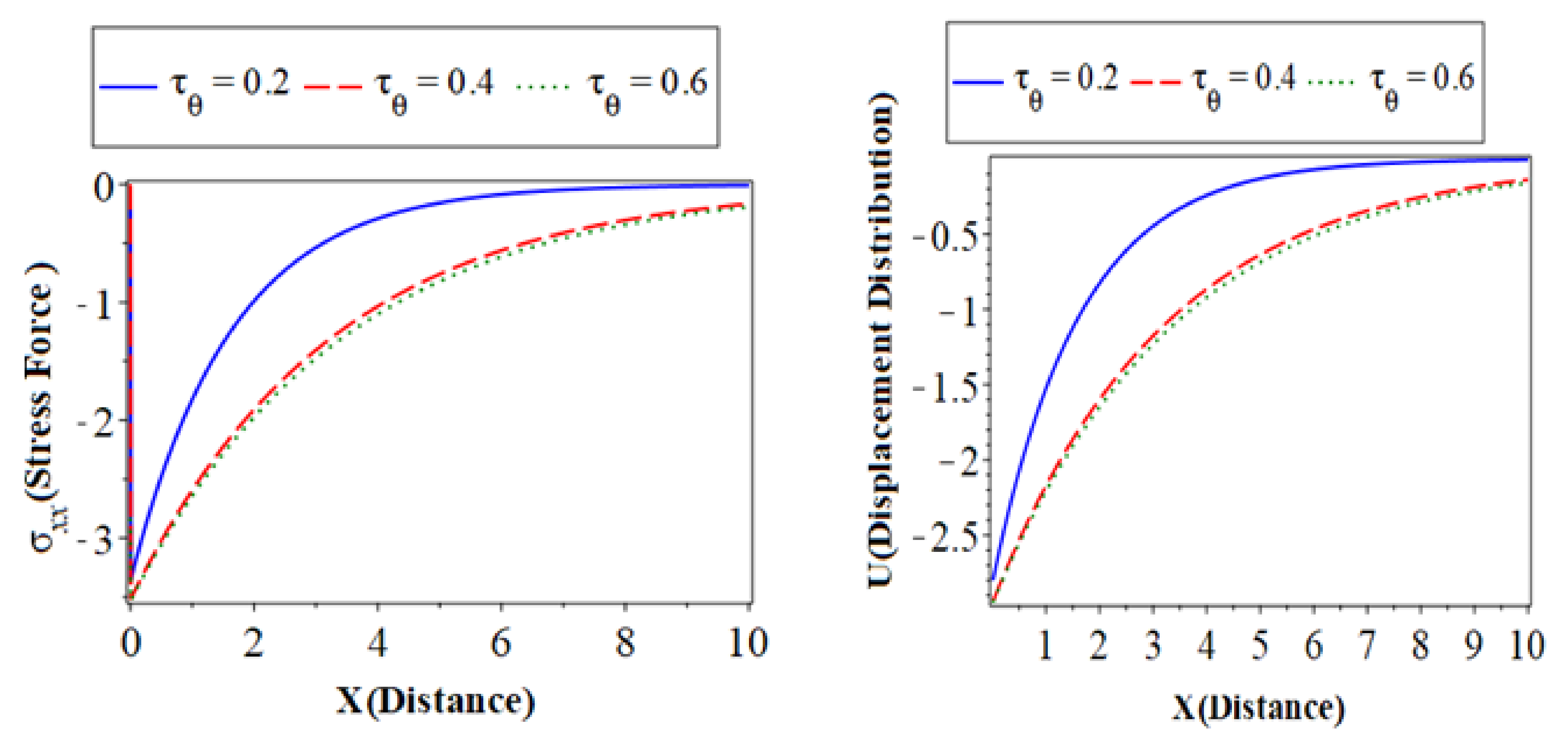
 ) with a blue color curve represent the case when ,the dashed lines (
) with a blue color curve represent the case when ,the dashed lines ( ) with red color curve express the case at and the dotted lines (
) with red color curve express the case at and the dotted lines ( ) with a green color curve show the case at .The first subfigure displays the temperature () distribution with the distance . It takes on the same behavior of the temperature distribution in the above subfigure for the thermoelastic coupling parameters and that has the same behavior of temperature distribution. The third describes the carrier density distribution against the distance in variation values of the phase-lags of the temperature gradients that have the same behavior of temperature distribution and heat conduction. The fourth subfigure displays the hole charge carrier to increase the value of thermoelastic coupling parameters. The fifth subfigure displays that the increase of amplitude, due to the mechanical loads, tends to increase the value of the phase-lag of the temperature gradients. The sixth subfigure represents the distribution against the horizontal distance the distribution takes on the exponential behavior with a smooth increase. When and the distribution of displacement increases sharply in the first range; it takes on exponential propagation behavior until it reaches a minimum value near the zero line. The values of the examined fields grow as the phase-lags of the temperature gradients‘ value decreases; this can be seen from the curves’ behavior.
) with a green color curve show the case at .The first subfigure displays the temperature () distribution with the distance . It takes on the same behavior of the temperature distribution in the above subfigure for the thermoelastic coupling parameters and that has the same behavior of temperature distribution. The third describes the carrier density distribution against the distance in variation values of the phase-lags of the temperature gradients that have the same behavior of temperature distribution and heat conduction. The fourth subfigure displays the hole charge carrier to increase the value of thermoelastic coupling parameters. The fifth subfigure displays that the increase of amplitude, due to the mechanical loads, tends to increase the value of the phase-lag of the temperature gradients. The sixth subfigure represents the distribution against the horizontal distance the distribution takes on the exponential behavior with a smooth increase. When and the distribution of displacement increases sharply in the first range; it takes on exponential propagation behavior until it reaches a minimum value near the zero line. The values of the examined fields grow as the phase-lags of the temperature gradients‘ value decreases; this can be seen from the curves’ behavior.6.4. The Effect of the Phase-Lag of the Heat Flux
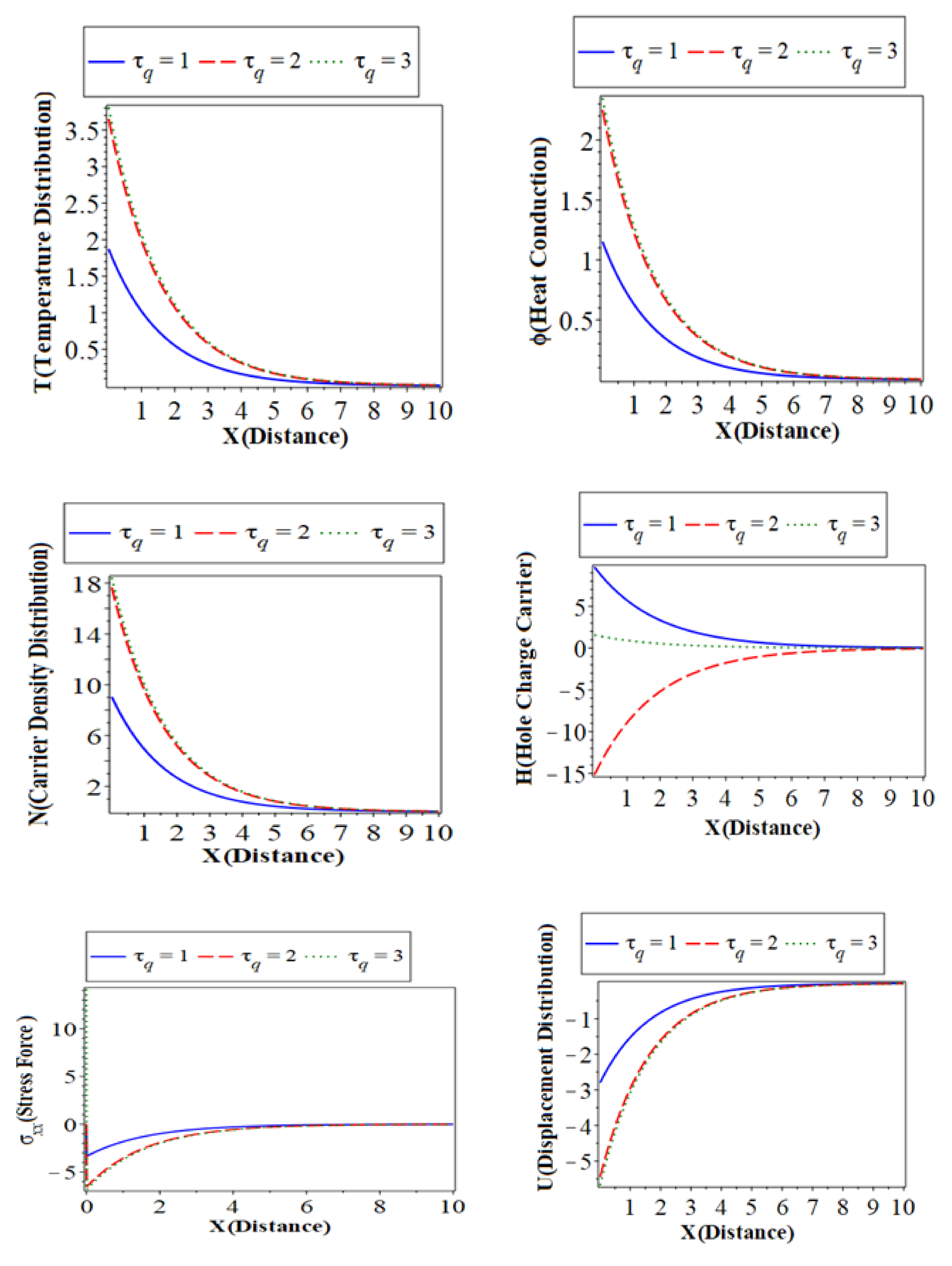
 ) with a blue color curve represent the case when the dashed lines (
) with a blue color curve represent the case when the dashed lines ( ) with red color curve express the case at and the dotted lines (
) with red color curve express the case at and the dotted lines ( ) with a green color curve show the case at . The first, second, and third subfigures are the temperature () distribution, heat conduction, and the carrier density distribution with the distance , which takes on the same behavior as the first category. The fourth subfigure describes the hole charge carrier with the distance. This subfigure shows that the amplitude values of the hole charge carrier distribution increase with the decrease in the values of the thermoelastic. The fifth subfigure shows that the increase of stress force amplitude, due to the mechanical loads, tends to increase the value of the phase-lag of the heat fluxes. The sixth subfigure represents the wave propagation of displacement distribution against the horizontal distance . The displacement distribution starts from the maximum positive value for all three cases. In the case of the distribution takes on the exponential behavior with a smooth decrease. On the other hand, when the distribution of displacement decreases sharply in the first range, and it takes on exponential propagation behavior until it reaches a minimum value near the zero line [31]. The numerical results show that each field of physical quantities is significantly influenced by the phase-lag of the heat flux [32].
) with a green color curve show the case at . The first, second, and third subfigures are the temperature () distribution, heat conduction, and the carrier density distribution with the distance , which takes on the same behavior as the first category. The fourth subfigure describes the hole charge carrier with the distance. This subfigure shows that the amplitude values of the hole charge carrier distribution increase with the decrease in the values of the thermoelastic. The fifth subfigure shows that the increase of stress force amplitude, due to the mechanical loads, tends to increase the value of the phase-lag of the heat fluxes. The sixth subfigure represents the wave propagation of displacement distribution against the horizontal distance . The displacement distribution starts from the maximum positive value for all three cases. In the case of the distribution takes on the exponential behavior with a smooth decrease. On the other hand, when the distribution of displacement decreases sharply in the first range, and it takes on exponential propagation behavior until it reaches a minimum value near the zero line [31]. The numerical results show that each field of physical quantities is significantly influenced by the phase-lag of the heat flux [32].6.5. The Effect of the Hyperbolic Two-Temperature
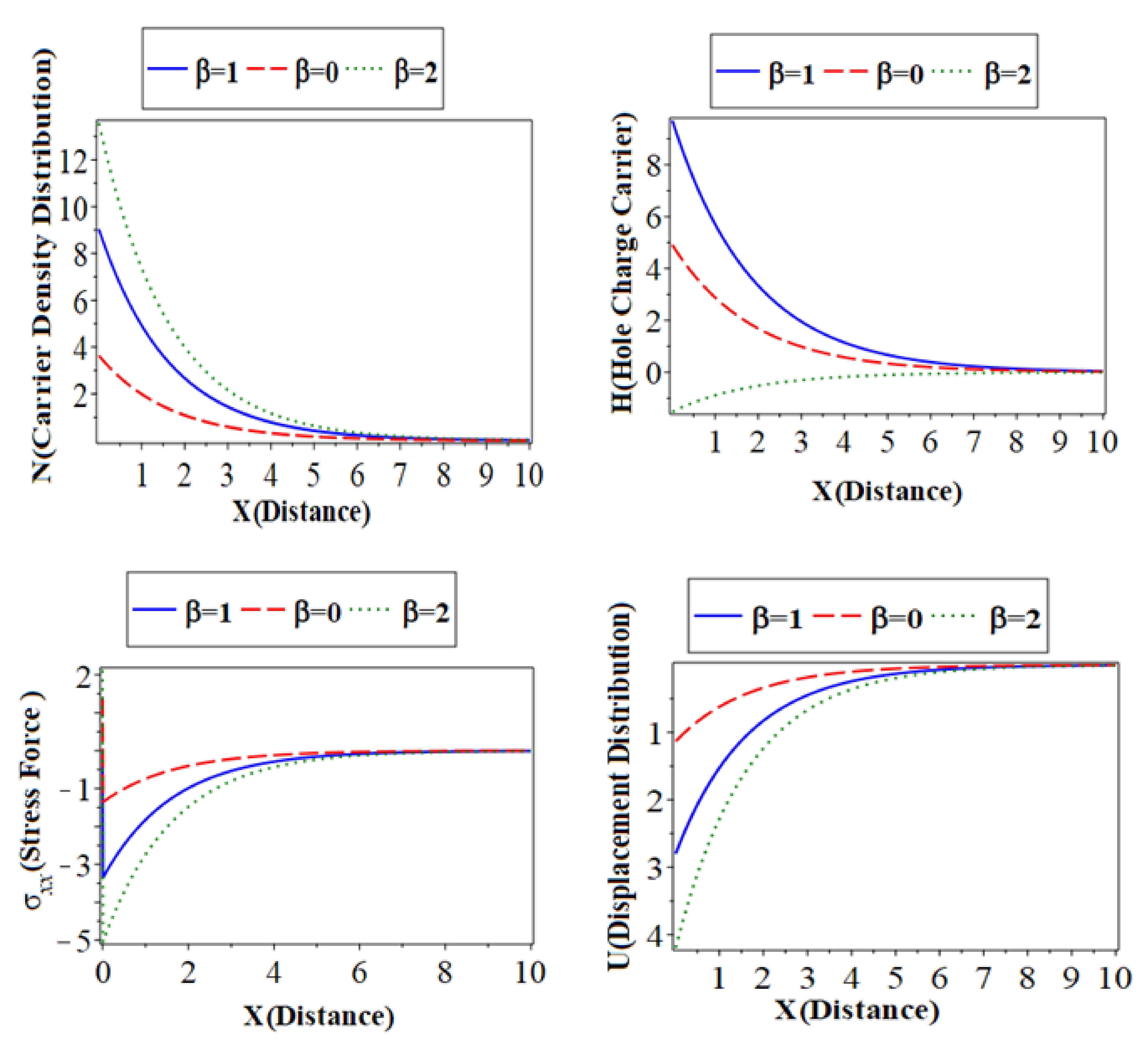
 ) with a blue color curve represent the case when the dashed lines (
) with a blue color curve represent the case when the dashed lines ( ) with red color curve express the case at and the dotted lines (
) with red color curve express the case at and the dotted lines ( ) with a green color curve show the case at . The first subfigure shows temperature () distribution. The second subfigure displays the heat conduction, and the third subfigure displays the carrier density distribution against the distance in variation values of the hyperbolic two-temperature parameters, which take the same behavior in the first category. The fourth subfigure describes the hole charge carrier with the distance. The fifth subfigure displays the increase of stress force amplitude, due to the mechanical loads, that tend to increase the value of the phase-lag of the heat fluxes. The sixth subfigure represents the wave propagation of displacement distribution against the horizontal distance . The displacement distribution starts from the minimum negative value for all three cases. It takes on exponential propagation behavior until it reaches a maximum value near the zero line [33,34]. It is evident that the propagation of the photo-thermal waves within the semiconductor media is reduced by the increase in the hyperbolic two-temperature parameter. Additionally, the significance of the suggested version is demonstrated by contrasting the outcomes of the current framework with those in the case of the hyperbolic two-temperature theory. This is because the issue of heat waves traveling at infinite speeds has been resolved.
) with a green color curve show the case at . The first subfigure shows temperature () distribution. The second subfigure displays the heat conduction, and the third subfigure displays the carrier density distribution against the distance in variation values of the hyperbolic two-temperature parameters, which take the same behavior in the first category. The fourth subfigure describes the hole charge carrier with the distance. The fifth subfigure displays the increase of stress force amplitude, due to the mechanical loads, that tend to increase the value of the phase-lag of the heat fluxes. The sixth subfigure represents the wave propagation of displacement distribution against the horizontal distance . The displacement distribution starts from the minimum negative value for all three cases. It takes on exponential propagation behavior until it reaches a maximum value near the zero line [33,34]. It is evident that the propagation of the photo-thermal waves within the semiconductor media is reduced by the increase in the hyperbolic two-temperature parameter. Additionally, the significance of the suggested version is demonstrated by contrasting the outcomes of the current framework with those in the case of the hyperbolic two-temperature theory. This is because the issue of heat waves traveling at infinite speeds has been resolved.6.6. The Comparison between Si and Ge Materials
7. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rayleigh, L. On waves propagated along the plane surface of an elastic solid. Proc. Lond. Math. Soc. 1885, 1, 4–11. [Google Scholar] [CrossRef]
- Lockett, F.J. Effect of thermal properties of a solid on the velocity of Rayleigh waves. J. Mech. Phys. Solids 1958, 7, 71–75. [Google Scholar] [CrossRef]
- Chandrasekharaiah, D.S. Hyperbolic Thermoelasticity: A review of recent literature. Appl. Mech. Rev. 1998, 51, 705–729. [Google Scholar] [CrossRef]
- Maruszewski, B. Electro-magneto-thermo-elasticity of Extrinsic Semiconductors, Extended Irreversible Thermodynamic Approach. Arch. Mech. 1986, 38, 83–95. [Google Scholar]
- Sharma, J.; Thakur, N. Plane harmonic elasto-thermodiffusive waves in semiconductor materials. J. Mech. Mater. Struct. 2006, 1, 813–835. [Google Scholar] [CrossRef]
- Sharma, J.N.; Thakur, N.; Singh, S. Propagation Characteristics of Elasto-Thermodiffusive Surface Waves in Semiconductor Material Half-Space. J. Therm. Stress. 2007, 30, 357–380. [Google Scholar] [CrossRef]
- Lotfy, K.; El-Bary, A. Elastic-thermal-diffusion model with a mechanical ramp type and variable thermal conductivity of electrons–holes semiconductor interaction. Waves Random Complex Media 2022. [Google Scholar] [CrossRef]
- Aldwoah, K.; Lotfy, K.; Mhemdi, A.; El-Bary, A. A novel magneto-photo-elasto-thermodiffusion electrons-holes model of excited semiconductor. Case Stud. Therm. Eng. 2022, 32, 101877. [Google Scholar] [CrossRef]
- Hobiny, A.; Abbas, I. Generalized Thermo-Diffusion Interaction in an Elastic Medium under Temperature Dependent Diffusivity and Thermal Conductivity. Mathematics 2022, 10, 2773. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Sedighi, H.M.; Shirazi, A.H. The Effect of Excess Carrier on a Semiconducting Semi-Infinite Medium Subject to a Normal Force by Means of Green and Naghdi Approach. Silicon 2021, 14, 4955–4967. [Google Scholar] [CrossRef]
- Awwad, E.; Abouelregal, A.E.; Atta, D.; Sedighi, H.M. Photo-thermoelastic behavior of a functionally graded? Semiconductor medium excited by thermal laser pulses. Phys. Scr. 2022, 97, 030008. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Nemat-Nasser, S. Transient thermoelastic waves in half-space with thermal relaxation. Z. Angew. Math. Phys. 1972, 23, 52–68. [Google Scholar] [CrossRef]
- Chen, P.J.; Gurtin, M.E.; Williams, W.O. On the thermodynamics of non- simple elastic materials with two temperatures. Z. Angew. Math. Phys. 1969, 20, 107–112. [Google Scholar] [CrossRef]
- Chen, J.; Beraun, J.; Tham, C. Ultrafast thermoelasticity for short-pulse laser heating. Int. J. Eng. Sci. 2004, 42, 793–807. [Google Scholar] [CrossRef]
- Quintanilla, T.; Tien, C. Heat transfer mechanism during short-pulse laser heating of metals. ASME J. Heat Transf. 1993, 115, 835–841. [Google Scholar]
- Youssef, H. Theory of two-temperature-generalized thermoelasticity. IMA J. Appl. Math. 2006, 71, 383–390. [Google Scholar] [CrossRef]
- Youssef, H.M. Theory of Two-Temperature Thermoelasticity without Energy Dissipation. J. Therm. Stress. 2011, 34, 138–146. [Google Scholar] [CrossRef]
- Youssef, H.; El-Bary, A. Theory of hyperbolic two-temperature generalized thermoelasticity. Mater. Phys. Mechs. 2018, 40, 158–171. [Google Scholar]
- Lotfy, K.; Elidy, E.S.; Tantawi, R.S. Photothermal Excitation Process during Hyperbolic Two-Temperature Theory for Magneto-Thermo-Elastic Semiconducting Medium. Silicon 2021, 13, 2275–2288. [Google Scholar] [CrossRef]
- Lotfy, K.; Elidy, E.S.; Tantawi, R. Piezo-photothermoelasticity transport process for hyperbolic two temperature theory of semiconductor material. Int. J. Mod. Phys. C 2021, 32, 2150088. [Google Scholar] [CrossRef]
- Christofides, C.; Othonos, A.; Loizidou, E. Influence of temperature and modulation frequency on the thermal activation coupling term in laser photothermal theory. J. Appl. Phys. 2002, 92, 1280–1285. [Google Scholar] [CrossRef]
- Marin, M.; Florea, O. On Temporal Behaviour of Solutions in Thermoelasticity of Porous Micropolar Bodies. An. Univ. Ovidius Constanta 2014, 22, 169–188. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Marin, M. The Size-Dependent Thermoelastic Vibrations of Nanobeams Subjected to Harmonic Excitation and Rectified Sine Wave Heating. Mathematics 2020, 8, 1128. [Google Scholar] [CrossRef]
- Mahdy, A.M.S.; Lotfy, K.; Hassan, W.; El-Bary, A.A. Analytical solution of magneto-photothermal theory during variable thermal conductivity of a semiconductor material due to pulse heat flux and volumetric heat source. Waves Random Complex Media 2020, 31, 2040–2057. [Google Scholar] [CrossRef]
- Honig, G.; Hirdes, U. A method for the numerical inversion of Laplace transforms. J. Comput. Appl. Math. 1984, 10, 113–132. [Google Scholar] [CrossRef]
- Khamis, A.K.; Lotfy, K.; El-Bary, A.A.; Mahdy, A.M.S.; Ahmed, M.H. Thermal-piezoelectric problem of a semiconductor medium during photo-thermal excitation. Waves Random Complex Media 2020, 31, 2499–2513. [Google Scholar] [CrossRef]
- Yadav, A.K. Photothermal plasma wave in the theory of two-temperature with multi-phase-lag thermo-elasticity in the presence of magnetic field in a semiconductor with diffusion. Waves Random Complex Media 2020. [Google Scholar] [CrossRef]
- Mandelis, A.; Nestoros, M.; Christofides, C. Thermoelectronic-wave coupling in laser photothermal theory of semiconductors at elevated temperatures. Opt. Eng. 1997, 36, 459–468. [Google Scholar] [CrossRef]
- Todorović, D.; Nikolić, P.; Bojičić, A. Photoacoustic frequency transmission technique: Electronic deformation mechanism in semiconductors. J. Appl. Phys. 1999, 85, 7716–7726. [Google Scholar] [CrossRef]
- Abbas, I.A.; Alzahrani, F.S.; Elaiw, A. A DPL model of photothermal interaction in a semiconductor material. Waves Random Complex Media 2018, 29, 328–343. [Google Scholar] [CrossRef]
- Liu, J.; Han, M.; Wang, R.; Xu, S.; Wang, X. Photothermal phenomenon: Extended ideas for thermophysical properties characterization. J. Appl. Phys. 2022, 131, 065107. [Google Scholar] [CrossRef]
- Hobinya, A.; Abbas, I. A GN model on photothermal interactions in a two-dimensions semiconductor half space. Result. Phys. 2019, 15, 102588. [Google Scholar] [CrossRef]
- Mahdy, A.; Lotfy, K.; El-Bary, A.; Sarhan, H. Effect of rotation and magnetic field on a numerical-refined heat conduction in a semiconductor medium during photo-excitation processes. Eur. Phys. J. Plus. 2021, 136, 553–560. [Google Scholar] [CrossRef]
- Song, Y.; Todorovic, D.; Cretin, B.; Vairac, P. Study on the generalized thermoelastic vibration of the optically excited semiconducting microcantilevers. Int. J. Solids Struct. 2010, 47, 1871. [Google Scholar] [CrossRef]




| Name (Unit) | Symbol | Si | Ge |
|---|---|---|---|
| Lamé’s constants () | , | , | |
| Density () | |||
| Absolute temperature () | |||
| The photogenerated Carrier lifetime () | |||
| The carrier diffusion coefficient () | |||
| the coefficient of electronic deformation () | |||
| The energy gap () | |||
| The coefficient of linear thermal expansion () | |||
| The thermal conductivity of the sample () | |||
| Specific heat at constant strain () | |||
| The recombination velocities () | |||
| The pulse rise time () | |||
| the radius of the beam () | |||
| the absorption depth of heating energy () | |||
| The absorbed energy () | |||
| the Peltier- Dufour- Seebeck Soret-like constants () | |||
| the diffusion constants of electrons () | |||
| the diffusion constants of holes () | |||
| () thermodiffusive constants of electrons | |||
| () thermodiffusive constants of holes |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raddadi, M.H.; Lotfy, K.; Elidy, E.S.; El-Bary, A.; Tantawi, R.S. A Novel Photo Elasto-Thermodiffusion Waves with Electron-Holes in Semiconductor Materials with Hyperbolic Two Temperature. Crystals 2022, 12, 1458. https://doi.org/10.3390/cryst12101458
Raddadi MH, Lotfy K, Elidy ES, El-Bary A, Tantawi RS. A Novel Photo Elasto-Thermodiffusion Waves with Electron-Holes in Semiconductor Materials with Hyperbolic Two Temperature. Crystals. 2022; 12(10):1458. https://doi.org/10.3390/cryst12101458
Chicago/Turabian StyleRaddadi, Merfat H., Kh. Lotfy, E. S. Elidy, A. El-Bary, and Ramdan. S. Tantawi. 2022. "A Novel Photo Elasto-Thermodiffusion Waves with Electron-Holes in Semiconductor Materials with Hyperbolic Two Temperature" Crystals 12, no. 10: 1458. https://doi.org/10.3390/cryst12101458
APA StyleRaddadi, M. H., Lotfy, K., Elidy, E. S., El-Bary, A., & Tantawi, R. S. (2022). A Novel Photo Elasto-Thermodiffusion Waves with Electron-Holes in Semiconductor Materials with Hyperbolic Two Temperature. Crystals, 12(10), 1458. https://doi.org/10.3390/cryst12101458








