Eshelby Tensors for Two-Dimensional Decagonal Piezoelectric Quasicrystal Composites
Abstract
1. Introduction
2. Mathematical Formulation
3. Problem Statement
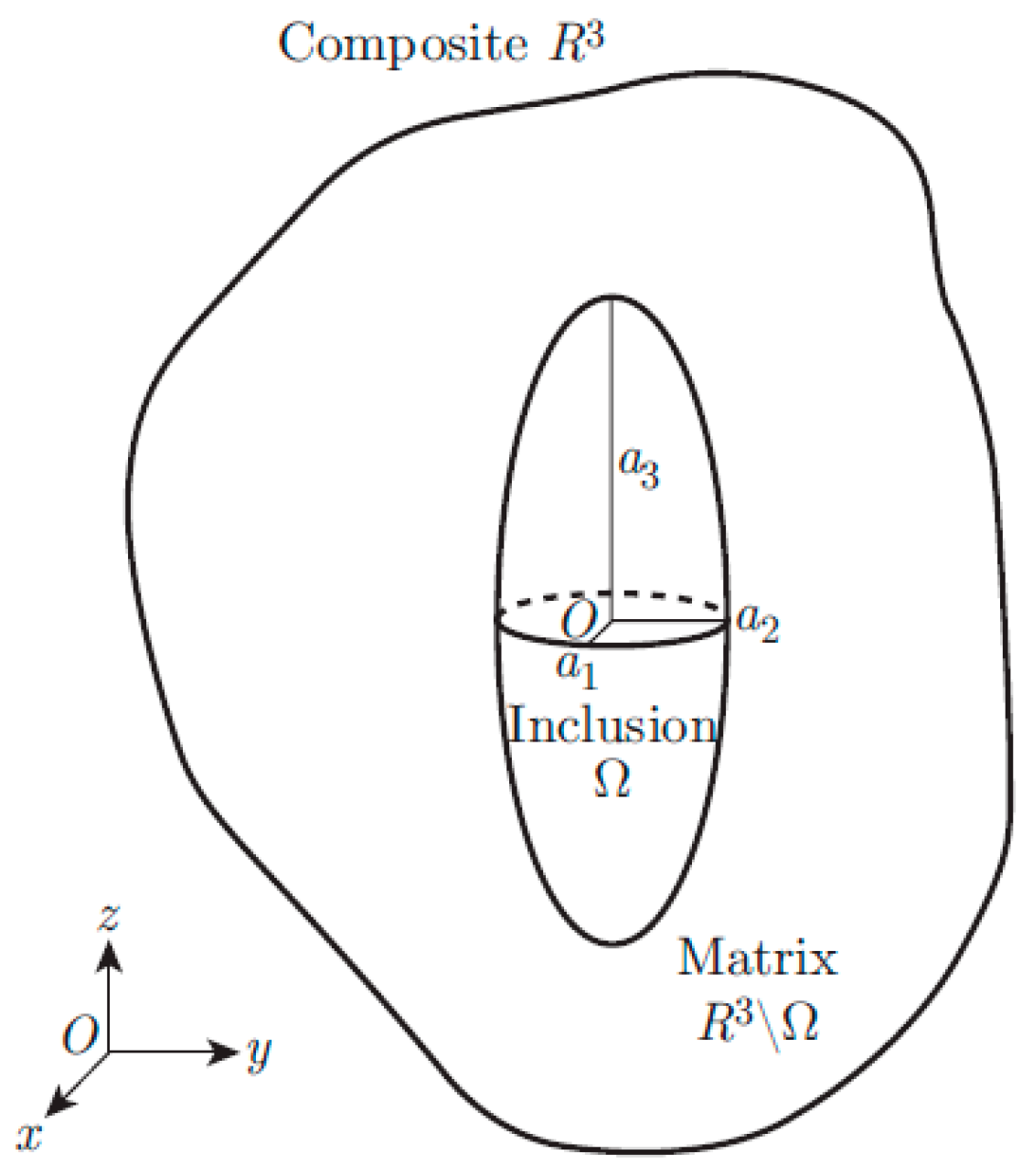
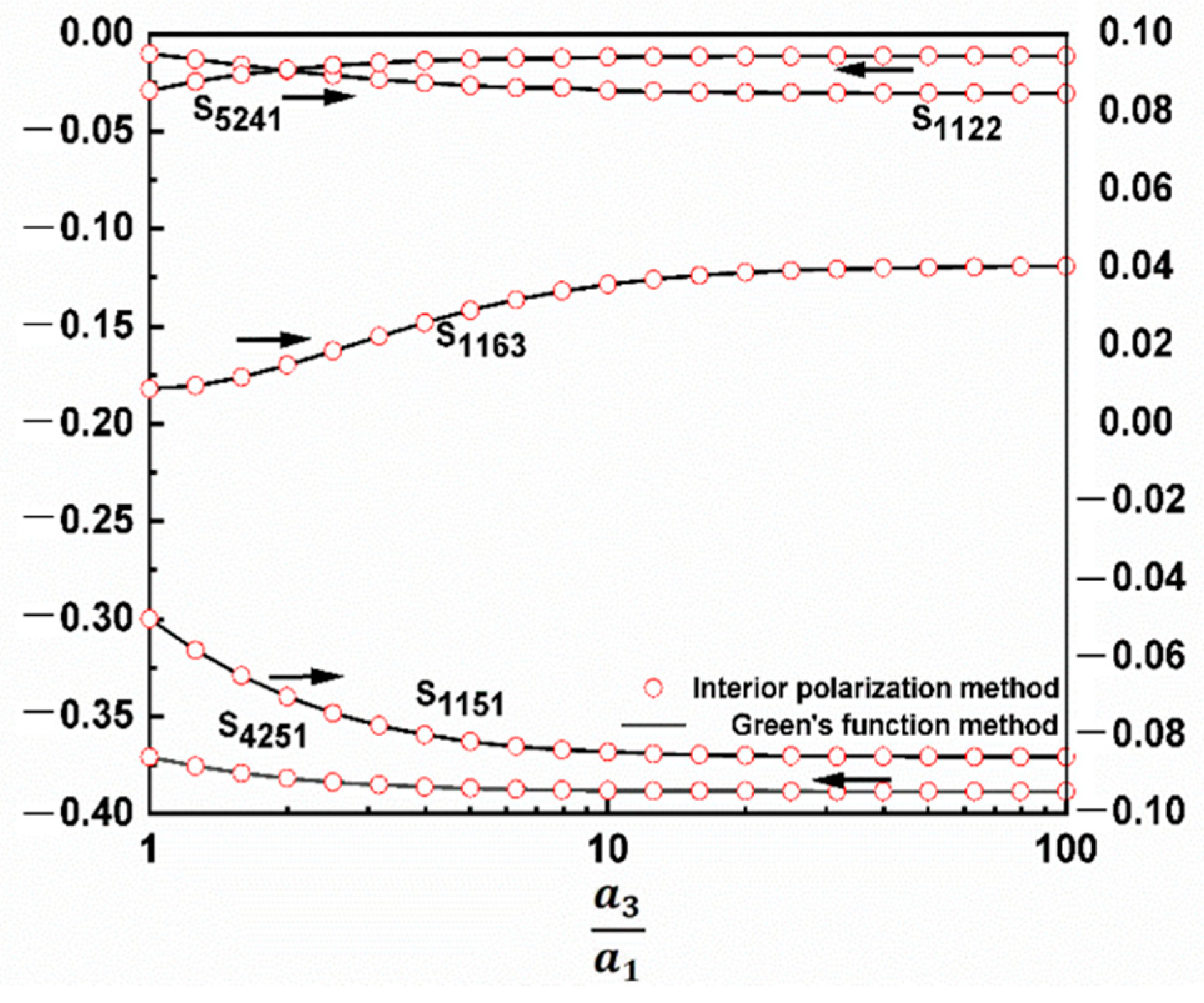
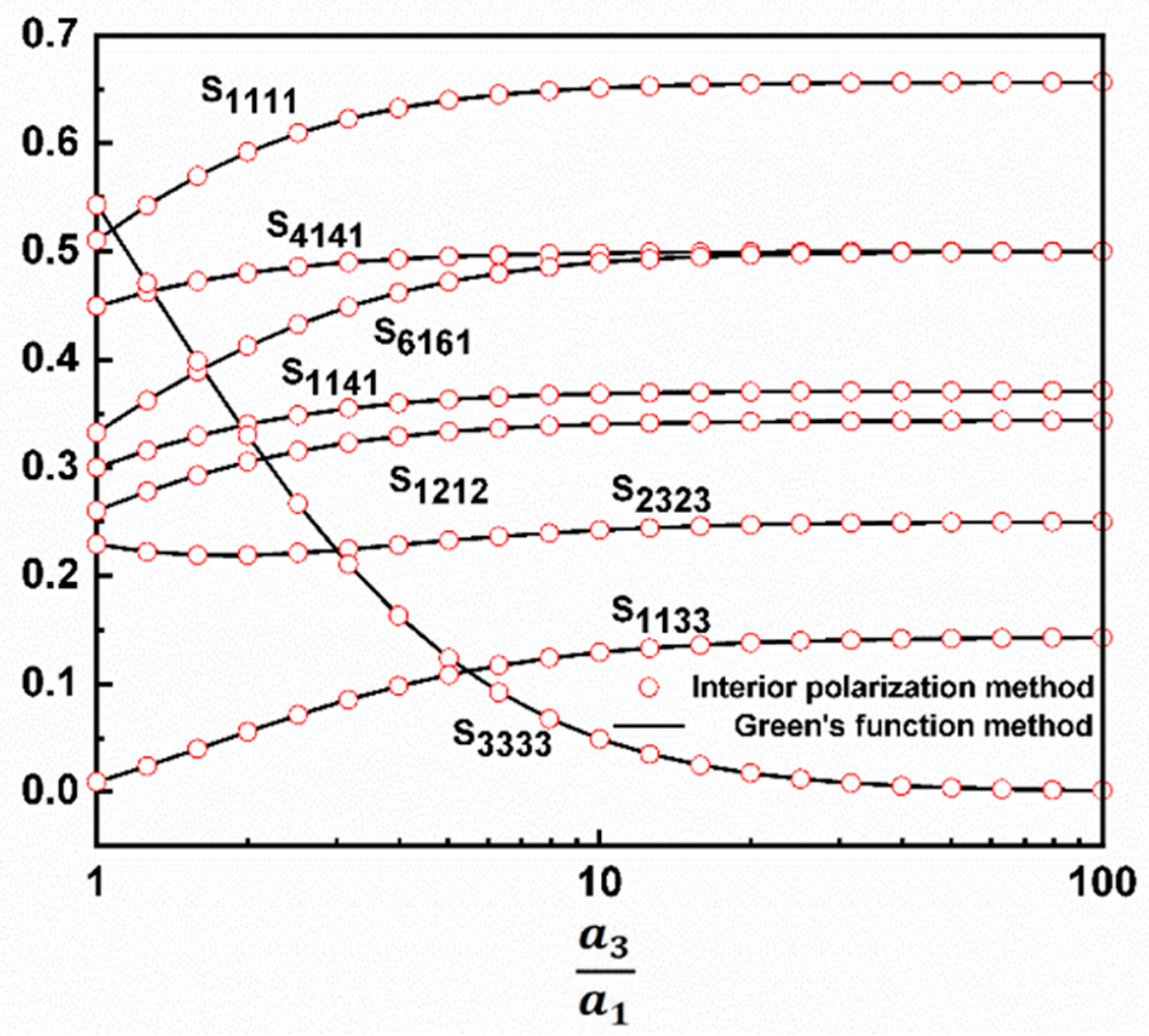
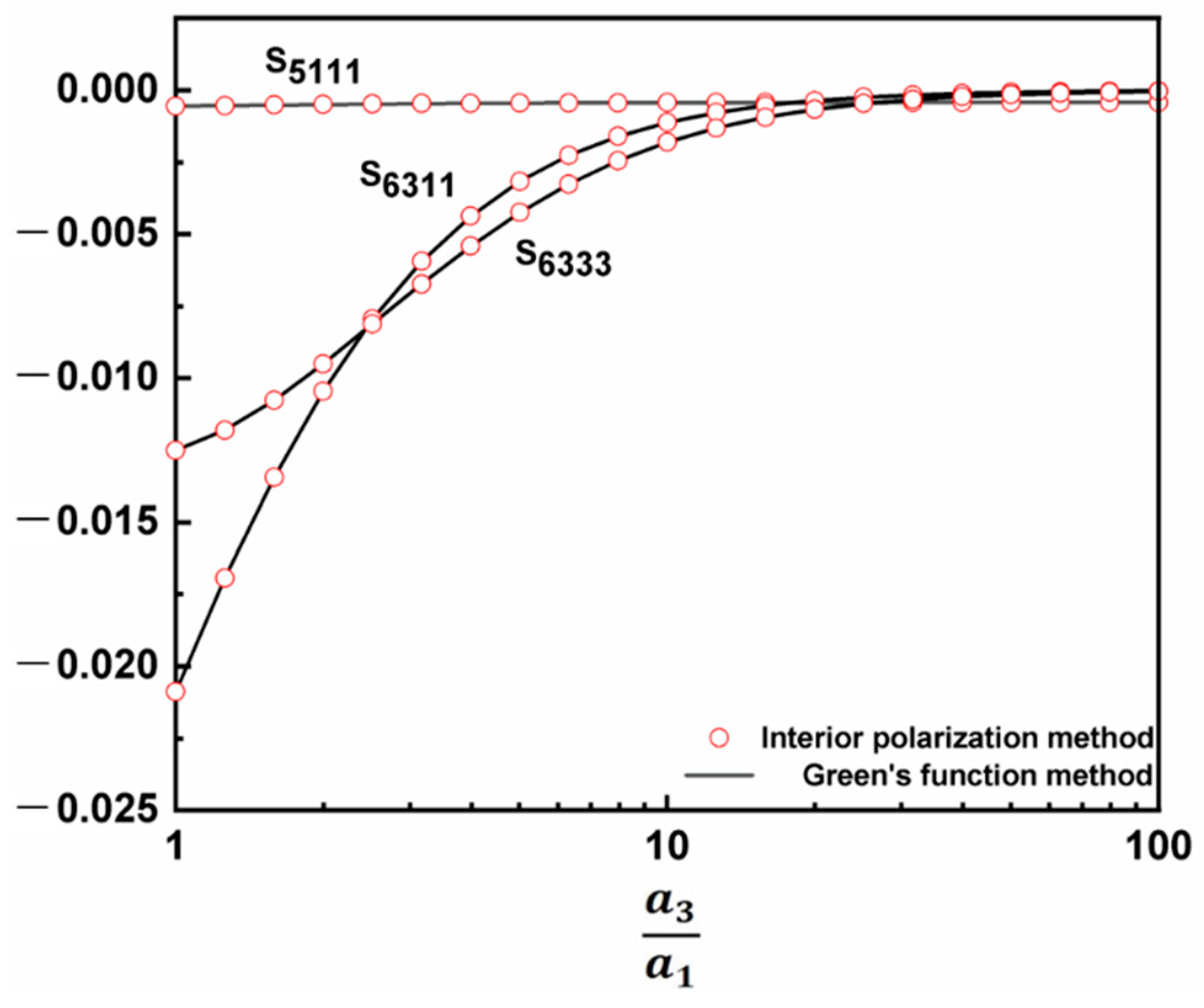
4. Numerical Examples and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- (i)
- Cylindrical inclusions
- (ii)
- Elliptic cylinder
References
- Shechtman, D.; Blech, I.; Gratias, D. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 1984, 53, 1951. [Google Scholar] [CrossRef]
- Dubois, J.M.; Kang, S.S.; Stebut, J.V. Quasicrystalline low-friction coatings. J. Mater. Sci. Lett. 1991, 10, 537–541. [Google Scholar] [CrossRef]
- Dubois, J.M.; Brunet, P.; Costin, W. Friction and fretting on quasicrystals under vacuum. J. Non Cryst. Solids 2004, 334, 475–480. [Google Scholar] [CrossRef]
- Ding, D.; Yang, W.; Hu, C.; Wang, R. Linear elasticity theory of quasicrystals and defects in quasicrystals. Mater. Sci. Forum. 1994, 150, 345–354. [Google Scholar] [CrossRef]
- FAN, T.Y. Mathematical Theory of Elasticity of Quasicrystals and Its Applications; Science Press: Beijing, China, 2011. [Google Scholar]
- Li, X.F.; Xie, Y.L.; Fan, T.Y. Elasticity and dislocations in quasicrystals with 18-fold symmetry. Phys. Lett. A 2014, 377, 2810–2814. [Google Scholar] [CrossRef]
- Wang, X.; Schiavone, P. Elastic field near the tip of an anticrack in a decagonal quasicrystalline material. Appl. Math. Mech.-Engl. 2020, 41, 401–408. [Google Scholar] [CrossRef]
- Rao, K.R.M.; Rao, P.H.; Chaitanya, B.S.K. Piezoelectricity in quasicrystals: A group-theoretical study. Pram. J. Phys. 2007, 68, 481–487. [Google Scholar]
- Altay, G.; Dökmeci, M.C. On the fundamental equations of piezoelasticity of quasicrystal media. J. Solids Struct. 2012, 49, 3255–3262. [Google Scholar] [CrossRef]
- Zhang, L.L.; Zhang, Y.M.; Gao, Y. General solutions of plane elasticity of one-dimensional orthorhombic quasicrystals with piezoelectric effect. Phys. Lett. A 2014, 378, 2768–2776. [Google Scholar] [CrossRef]
- Li, X.Y.; Li, P.D.; Wu, T.H.; Shi, M.X.; Zhu, Z. Three-dimensional fundamental solutions for one-dimensional hexagonal quasicrystal with piezoelectric effect. Phys. Lett. A 2014, 378, 826–834. [Google Scholar] [CrossRef]
- Fan, C.Y.; Li, Y.; Xu, G.T.; Zhao, M. Fundamental solutions and analysis of three-dimensional cracks in one-dimensional hexagonal piezoelectric quasicrystals. Mech. Res. Commun. 2016, 74, 39–44. [Google Scholar] [CrossRef]
- Dang, H.Y.; Lv, S.Y.; Fan, C.Y. Analysis of anti-plane interface cracks in one-dimensional hexagonal quasicrystal coating. Appl. Math. Model. 2020, 81, 641–652. [Google Scholar] [CrossRef]
- Fu, X.Y.; Mu, X.; Zhang, J.M.; Zhang, L.L.; Gao, Y. Green’s functions of two-dimensional piezoelectric quasicrystal in half-space and bimaterials. Appl. Math. Mech.-Engl. 2022, 467, 2622–2642. [Google Scholar]
- Wang, X. Eshelby’s problem of an inclusion of arbitrary shape in a decagonal quasicrystalline plane or half-plane. Int. J. Eng. Sci. 2004, 42, 1911–1930. [Google Scholar] [CrossRef]
- Gao, Y.; Ricoeur, A. Three-dimensional analysis of a spheroidal inclusion in a two-dimensional quasicrystal body. Philos. Mag. 2012, 92, 4334–4353. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, Z.; Xing, Y. Antiplane analysis for an elliptical inclusion in 1D hexagonal piezoelectric quasicrystal composites. Philos. Mag. 2016, 96, 349–369. [Google Scholar] [CrossRef]
- Guo, J.H.; Pan, E. Three-phase cylinder model of one-dimensional hexagonal piezoelectric quasicrystal composites. J. Appl. Mech. 2016, 83, 081007. [Google Scholar] [CrossRef]
- Wang, Y.B.; Guo, J.H. Effective electroelastic constants for three-phase confocal elliptical cylinder model in piezoelectric quasicrystal composites. Appl. Math. Mech.-Engl. 2018, 39, 797–812. [Google Scholar] [CrossRef]
- Zhai, T.; Ma, Y.Y.; Ding, S.H.; Zhao, X.F. Circular inclusion problem of two-dimensional decagonal quasicrystals with interfacial rigid lines under concentrated force. ZAMM-Z. Angew. Math. Mech. 2021, 101, e202100081. [Google Scholar] [CrossRef]
- Hu, C.Z.; Wang, R.H.; Ding, D.H.; Yang, W.G. Piezoelectric effects in quasicrystals. Phys. Rev. B. 1997, 56, 2463. [Google Scholar] [CrossRef]
- Lothe, J.; Barnett, D.M. Integral formalism for surface waves in piezoelectric crystals. Existence considerations. J. Appl. Phys. 1976, 47, 1799–1807. [Google Scholar] [CrossRef]
- Dunn, M.L.; Taya, M. An analysis of piezoelectric composite materials containing ellipsoidal inhomogeneities. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1993, 443, 265–287. [Google Scholar]
- Mura, T. Micromechanics of Defects in Solids, 2nd ed.; Kluwer Ac.; Springer: Cham, Switzerland, 1987. [Google Scholar]
- Deeg, W.F. The Analysis of Dislocation, Crack, and Inclusion Problems in Piezoelectric Solids. Ph.D. Dissertation, Stanford University, Stanford, CA, USA, 1980. [Google Scholar]
- Koutsawa, Y. Overall thermo-magneto-electro-elastic properties of multiferroics composite materials with arbitrary heterogeneities spatial distributions. Compos. Struct. 2015, 133, 764–773. [Google Scholar] [CrossRef]
- Huang, J.H.; Kuo, W.S. Micromechanics determination of the effective properties of piezoelectric composites containing spatially oriented short fibers. Acta Mater. 1996, 44, 4889–4898. [Google Scholar] [CrossRef]
- Lee, J.S.; Jiang, L.Z. Exact electroelastic analysis of piezoelectric laminae via state space approach. Int. J. Solids Struct. 1996, 33, 977–990. [Google Scholar] [CrossRef]
- Fan, T.Y. Mathematical theory and methods of mechanics of quasicrystalline materials. Engineering 2013, 5, 407–448. [Google Scholar] [CrossRef]

| Phonon (GPa) | = 234.33, = 57.41, = 66.63, = 232.22, = 70.19, |
| Phason (GPa) | = 122, = 24, = 12, |
| Phonon-phason coupling (GPa) | = 8.846, = 8.846, |
| piezoelectric coefficient () | = 4.4, = 11.6, = 18.6, |
| dielectric constant () | = 11.2, = 11.2, = 12.6. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Li, L. Eshelby Tensors for Two-Dimensional Decagonal Piezoelectric Quasicrystal Composites. Crystals 2022, 12, 1456. https://doi.org/10.3390/cryst12101456
Li G, Li L. Eshelby Tensors for Two-Dimensional Decagonal Piezoelectric Quasicrystal Composites. Crystals. 2022; 12(10):1456. https://doi.org/10.3390/cryst12101456
Chicago/Turabian StyleLi, Guangfang, and Lianhe Li. 2022. "Eshelby Tensors for Two-Dimensional Decagonal Piezoelectric Quasicrystal Composites" Crystals 12, no. 10: 1456. https://doi.org/10.3390/cryst12101456
APA StyleLi, G., & Li, L. (2022). Eshelby Tensors for Two-Dimensional Decagonal Piezoelectric Quasicrystal Composites. Crystals, 12(10), 1456. https://doi.org/10.3390/cryst12101456






