Investigation of Electronic and Optical Properties of (Cs, Br, Cs-Br) Doped Mono-Layer Hexagonal Boron Nitride Using First Principles
Abstract
1. Introduction
2. Materials and Methods
2.1. Computational Methods
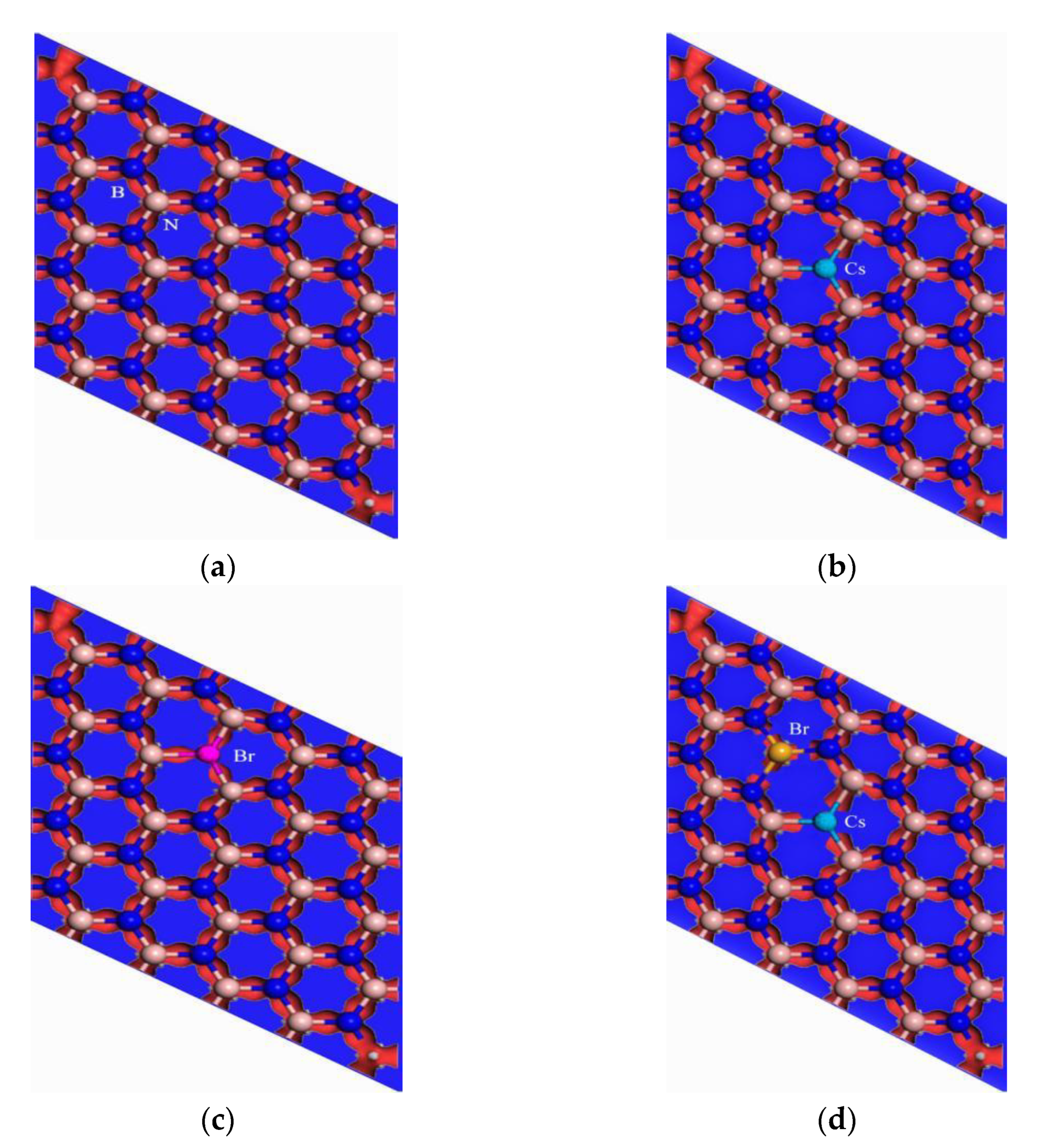
2.2. Computation Models
3. Results
3.1. Geometrical Structures
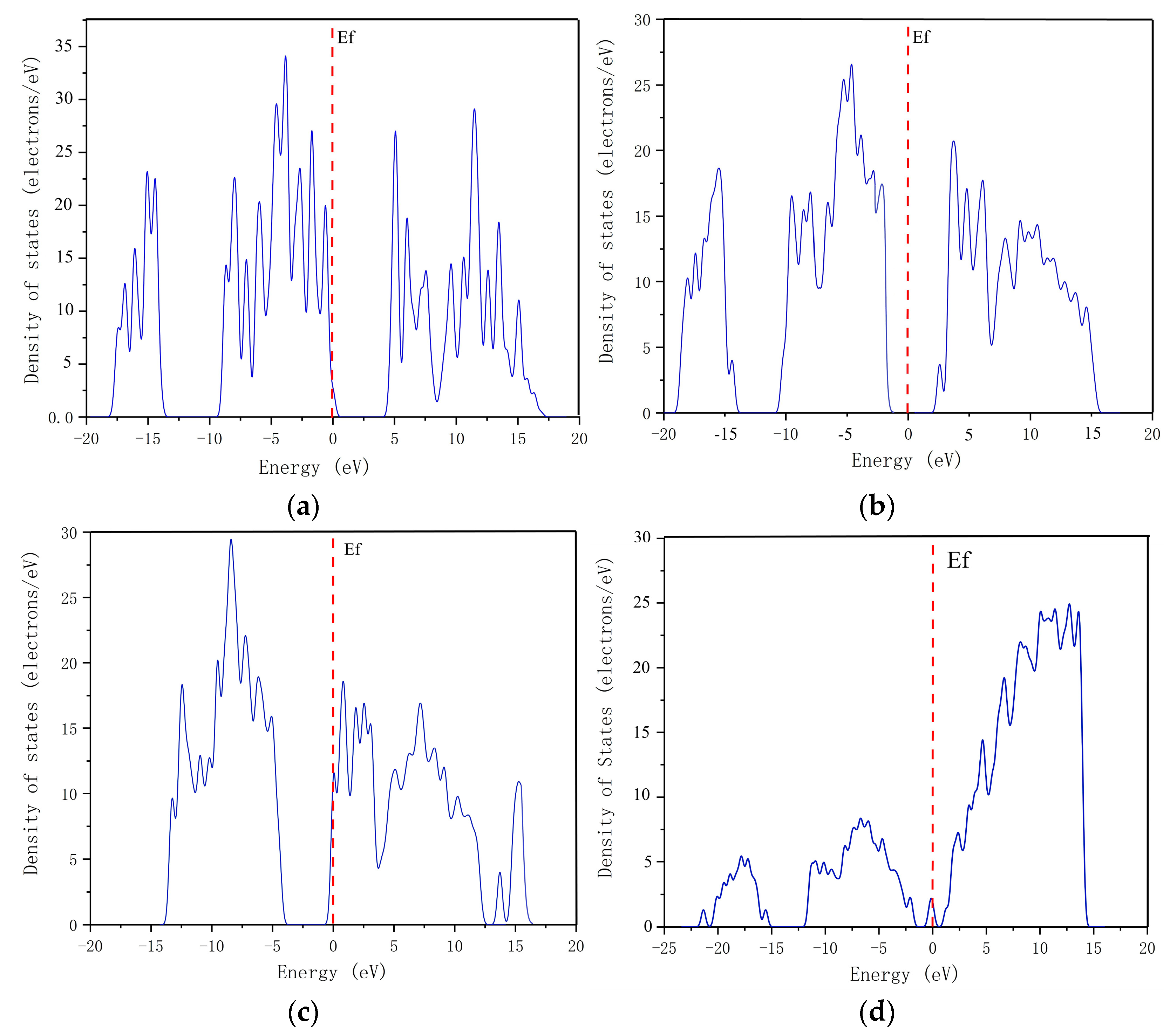
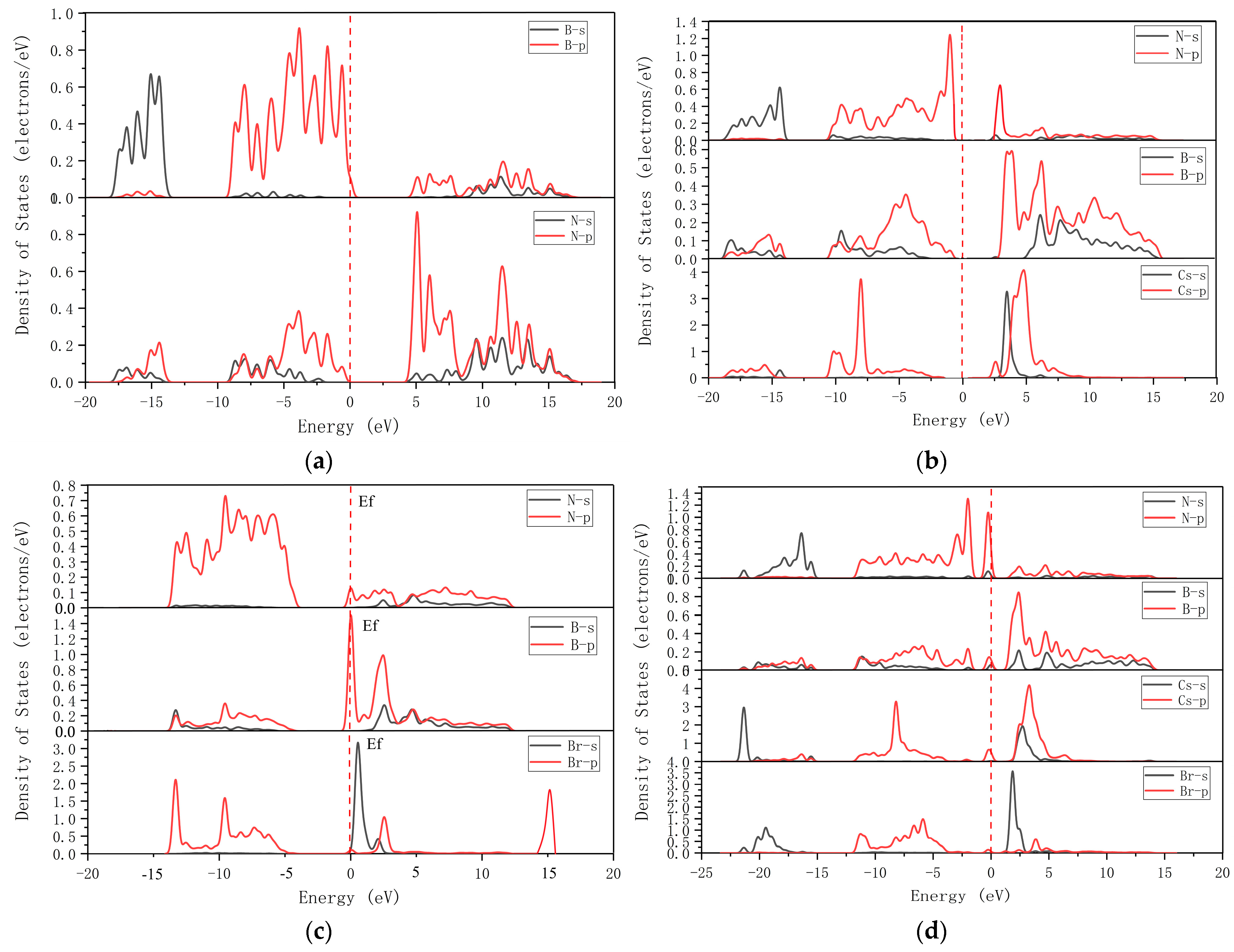
3.1.1. Band Structures and DOS
3.1.2. Electron Density
3.2. Optical Properties
Complex Dielectric Function
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, Y.; Cao, Y.; LI, J.; Qiu, Y.; Qin, W.; Wang, Z. 5 kW fiber coupling diode laser for laserprocessing. Opt. Precis. Eng. 2015, 23, 1279–1287. [Google Scholar]
- Zhang, J. Design and Analysis of High-Temperature Operating 795 nm VCSELs for 87 Rb Based Chip-Scale Atomic Clock; Ciomp-osa Summer Session: Lasers & Their Applications: Changchun, China, 2011. [Google Scholar]
- Xu, H.; Ning, Y.; Zeng, Y.; Zhang, Z.; Qin, L. Design and epitaxial growth of quantum-well for 852 nm laserdiode. Opt. Precis. Eng. 2013, 21, 590–597. [Google Scholar]
- Hirayama, H.; Tohro, Y.; Norimichi, N.; Tomoaki, O. 226-273 nm AlGaN deep violet light-emitting diodesfabricated on multilayer AIN buffers on sapphire. Phys. Statussolidi 2008, 5, 2969–2971. [Google Scholar]
- Ul Ahmad, A.; Liang, H.; Abbas, Q.; Ali, S.; Iqbal, M.; Farid, A.; Abbas, A.; Farooq, Z. A novel mechano-chemical synthesis route for fluorination of hexagonal boron nitride nanosheets. Ceram Int. 2019, 45, 19173–19181. [Google Scholar] [CrossRef]
- Britnell, L.; Ribeiro, R.M.; Eckmann, A.; Jalil, R.; Belle, B.D.; Mishchenko, A.; Kim, Y.J.; Gorbachev, R.V.; Georgiou, T.; Morozov, S.V.; et al. Strong light-matter interactions in heterostructures of atomically thin films. Science 2013, 340, 1311. [Google Scholar] [CrossRef]
- Britnell, L.; Gorbachev, R.V.; Jalil, R.; Belle, B.D.; Schedin, F.; Mishchenko, A.; Georgiou, T.; Katsnelson, M.I.; Eaves, L.; Morozov, S.V.; et al. Field-effect tunneling transistor based on vertical graphene heterostructures. Science 2012, 335, 947. [Google Scholar] [CrossRef]
- Rodriguez-Vega, E.R.M.; Fischer, J.; Das, S.S. Ground state of graphene heterostructures in the presence of random charged impurities. Phys. Rev. Lett. 2014, 90, 035406. [Google Scholar] [CrossRef]
- Govindaraju, N.; Singh, R.N. Chapter 8 Synthesis and Properties of Boron Nitride Nanotubes; EIsevier Inc.: Amsterdam, The Netherlands, 2014; pp. 243–265. [Google Scholar]
- Radhakrishnan, S.; Das, D.; Samanta, A.; de Los Reyes, C.A.; Deng, L.; Alemany, L.B.; Weldeghiorghis, T.K.; Khabashesku, V.N.; Kochat, V.; Jin, Z.; et al. Fluorinated h-BN As a magnetic semiconductor. Sci. Adv. 2017, 3, e1700842. [Google Scholar] [CrossRef]
- Ismach, A.; Chou, H.; Ferrer, D.A.; Wu, Y.P.; McDonnell, S.; Floresca, H.C.; Covacevich, A.; Pope, C.; Piner, R.; Kim, M.J.; et al. Toward the controlled synthesis ofhexagonal boron nitride films. ACS Nano 2012, 6, 6378–6385. [Google Scholar] [CrossRef]
- Van, D.W.; Chris, G.; Catherine, S.; Neugebauer, J. Theory of doping and defects in III-V nitrides. J. Cryst. Growth 1998, 189–190, 505–515. [Google Scholar]
- Qurat, A.A.; Akhtar, H.; Hafiz, M.R.; Muhammad, T. Computational study of Be-doped hexagonal boron nitride (h-BN): Structural and Electronic. Comput. Condens. Matter 2020, 23, e00474. [Google Scholar]
- Lei, L.; Feng, Y.P.; Shen, Z.X. Structural and electronicproperties of h -BN. Phys. Rev. 2003, 10, 185–192. [Google Scholar]
- Tayyab, M.; Hussain, A.; Asif, Q.A.; Adil, W. Band-gap tuning of graphene by Mg doping and adsorption of Br and Be on impurity: A DFT study. Comput. Condens. Matter 2020, 23, e00469. [Google Scholar] [CrossRef]
- Hussain, A.; Ullah, S.; Farhan, M.A. Fine tuning the band-gap of graphene by atomic and molecular doping: A density functional theory study. RSC Adv. 2016, 6, 55990–56003. [Google Scholar] [CrossRef]
- Lei, W.; Zhang, H.; Wu, Y.; Zhang, B.; Liu, D.; Qin, S.; Liu, Z.; Liu, L.; Ma, Y.; Chen, Y. Oxygen-doped boron nitride nanosheets with excellent performance in hydrogen storage. Nano Energy 2014, 6, 219–224. [Google Scholar] [CrossRef]
- Tang, Q.; Zhou, Z.; Chen, Z. Molecular charge transfer: A simple and effective route to engineer the band structures of BN nanosheets and nanoribbons. J. Phys. Chem. C 2011, 115, 18531–18537. [Google Scholar] [CrossRef]
- Xu, J.; Wan, Q.; Anpo, M.; Lin, S. Bandgap opening of graphdiyne monolayer via B, N-codoping for photocatalytic overall water splitting: Design strategy from DFT studies. J. Phys. Chem. C 2020, 124, 6624–6633. [Google Scholar] [CrossRef]
- Jhi, S.H.; Kwon, Y.K. Hydrogen adsorption on boron nitride nanotubes: A path to room-temperature hydrogen storage. Phys. Rev. B Condens. Matter Mater. Phys. 2004, 69, 1–4. [Google Scholar] [CrossRef]
- Liu, Y.J.; Gao, B.; Xu, D.; Wang, H.M.; Zhao, J.X. Theoretical study on Si-doped hexagonal boron nitride (h-BN) sheet: Electronic, magnetic properties, and reactivity. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2014, 378, 2989–2994. [Google Scholar] [CrossRef]
- Tang, C.; Bando, Y.; Huang, Y.; Yue, S.; Gu, C.; Xu, F.; Golberg, D. Fluorination and electrical conductivity of BN nanotubes. J. Am. Chem. Soc. 2005, 127, 6552–6553. [Google Scholar] [CrossRef]
- Xu, M.; Liang, T.; Shi, M.; Chen, H. Graphene-Like Two-Dimensional Materials. Chem. Rev. 2013, 113, 3766–3798. [Google Scholar] [CrossRef] [PubMed]
- Ullah, S.; Hussain, A.; Sato, F. Rectangular and hexagonal doping of graphene with B,N, and O: A DFT study. RSC Adv. 2017, 7, 16064–16068. [Google Scholar] [CrossRef]
- Kochaev, A.; Meftakhutdinov, R.; Sibatov, R.; Katin, K.; Maslov, M.; Efimov, V. Enhanced properties of covalently coupled borophene-graphene layers through fluorination and hydrogenation. Appl. Surf. Sci. 2021, 562, 150150. [Google Scholar] [CrossRef]
- Kochaev, A.; Katin, K.; Maslov, M.; Singh, S. Covalent and van der Waals interactions in a vertical heterostructure composed of boron and carbon. Phys. Rev. B 2022, 105, 235444. [Google Scholar] [CrossRef]
- Kripalani, D.R.; Sun, P.P.; Lin, P.; Xue, M.; Zhou, K. Vacancies and dopants in two-dimensional tin monoxide: An ab initio study. Appl. Surf. Sci. 2020, 538, 147988. [Google Scholar] [CrossRef]
- Kadas, K. Ab initio studies of the (111) and (1-1-1-) surfaces of cubic BN: Structure andenergetics. Phys. Rev. B 1998, 58, 15636–15646. [Google Scholar] [CrossRef]
- Zhou, Y.G.; Wang, Z.G.; Xiao, H.Y.; Gao, F.; Zu, X.T. Electronic and magnetic properties of metal-doped BN sheet: A first-principles study. Phys. Chem. Chem. Phys. 2010, 12, 7588–7592. [Google Scholar] [CrossRef]
- Ambacher, O. Growth and applications of Group III-nitrides. J. Phys. D 1998, 31, 2653–2710. [Google Scholar] [CrossRef]
- Beiranvand, R.; Valedbagi, S. Electronic and optical properties of advance semiconductor materials: BN, Al N and Ga N nanosheets from first principles. Opt.—Int. J. Light Electron Opt. 2016, 127, 1553–1560. [Google Scholar] [CrossRef]
- Jung, W.G.; Jung, S.H.; Kung, P.; Razeghi, M. Fabrication of Ga N nanotubular material using MOCVD with an aluminium oxide membrane. Nanotechnology 2006, 17, 54–59. [Google Scholar] [CrossRef]
- Hussain, A.; Nabi, A.; Tayyab, M.; Rafique, H.M. Computational study of X-doped hexagonal boron nitride (h-BN): Structural and electronic properties (X = P.; S.; O.; F.; Cl). J. Mol. Modeling 2021, 27, 1–15. [Google Scholar]
- Yu, C.; Wang, F.; Liu, Y. First principles study of Zn doped cubic BN crystal. Int. Symp. Next Gener. Electron. (ISNE) 2019, 10, 8896476. [Google Scholar]
- Said, A.; Debbichi, M.; Said, M. Theoretical study of electronicand optical properties of BN, GaN and BxGaxN in zinc blende and wurtzite structures. Opt.—Int. J. Light Opt. 2016, 127, 9212–9221. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Pease, R.S. An X-ray study of boron nitride. Acta Crystallogr. 1952, 5, 356–361. [Google Scholar] [CrossRef]
- Stampfl, C.; Walle, C.G.V.D. Density-functional calculations for III-V nitrides using the local-density approximation and the generalized gradient approximation. Phys. Rev. B Condens. Matter 1999, 59, 5521–5535. [Google Scholar] [CrossRef]
- Milman, V.; Winkler, B.; White, J.A.; Pickard, C.J. Electronic structure.;properties.;and phase stability of inorganic crystals: Apseudopotential plane-wave study. Int. J. Quantum Chem. 2000, 77, 895–910. [Google Scholar] [CrossRef]
- Lu, Q.; Zhao, Q.; Yang, T.; Zhai, C.; Wang, D.; Zhang, M. Preparation of boron nitride nanoparticles with oxygen doping and a study of their room- temperature ferromagnetism. ACS Appl. Mater. Interfaces 2018, 10, 12947–12953. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Krist. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Hamann, D.R.; Schlüter, M.; Chiang, C. Norm-conserving pseudopotentials. Phys. Rev. Lett. 1979, 43, 1494–1497. [Google Scholar]
- Chadi, D.J. Special points for Brillouin-zone integrations. Phys. Rev. B 1977, 16, 1746–1747. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Chernyshev, V.V.; Fetisov, G.V.; Rybakov, V.B.; Petrusha, I.A. Structure analysis of the cubic boron nitridecrystals. J. Phys. Chem. Solids 1990, 51, 1011–1012. [Google Scholar] [CrossRef]
- Yu, S.S.; Zheng, W.T.; Wen, Q.B.; Jiang, Q. First principle calculations of the electronic properties of nitrogen-doped carbon nanoribbons with zigzag edges. Carbon 2008, 46, 537–543. [Google Scholar] [CrossRef]
- Chen, H.X.; OuYang, F.P.; Ma, S.S.; Wu, X.Z.; Xiao, J. First-principles investigation on B/N codoping of metallic carbon nano-tubes. Phys. Lett. A 2010, 374, 4343–4348. [Google Scholar] [CrossRef]
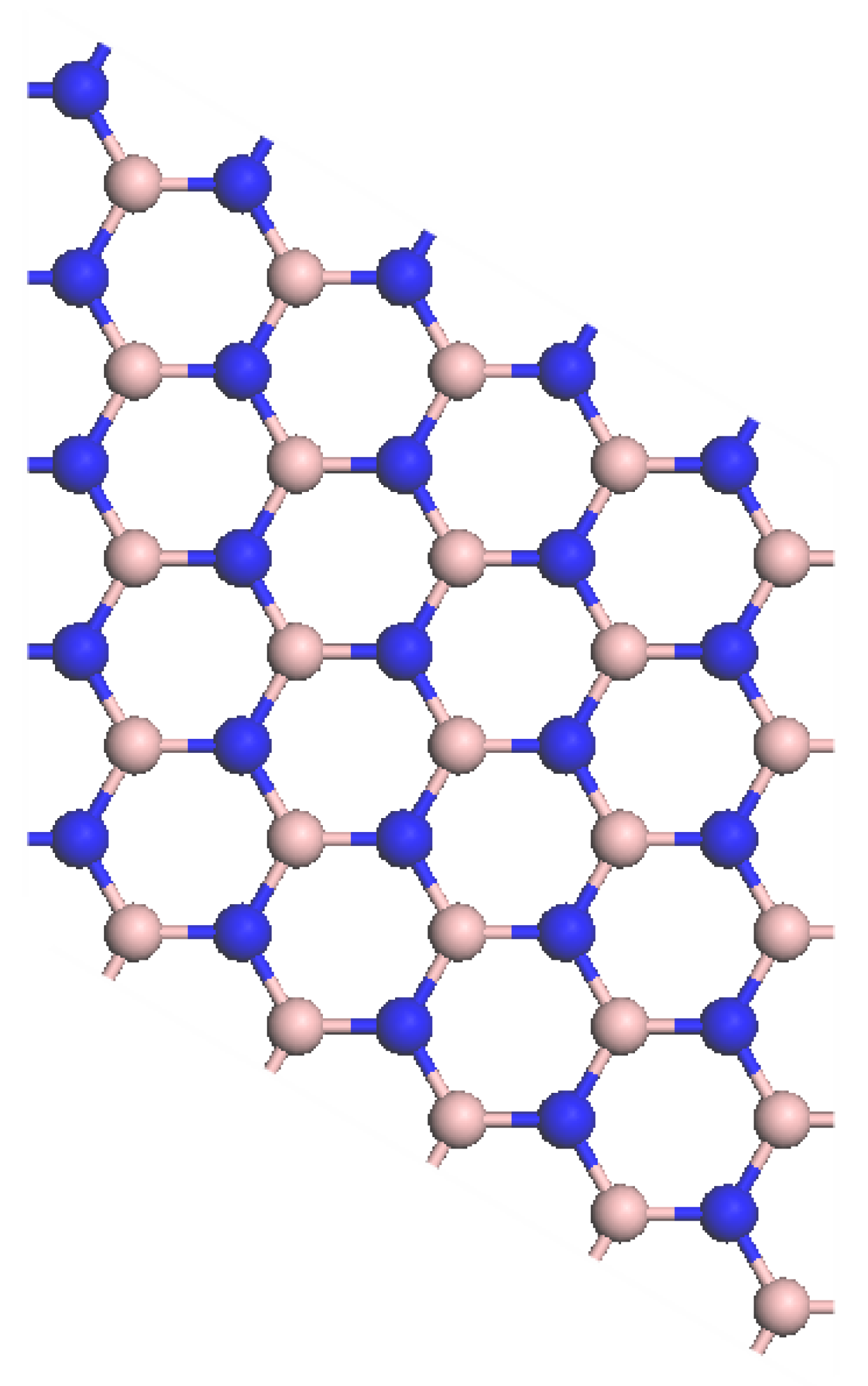
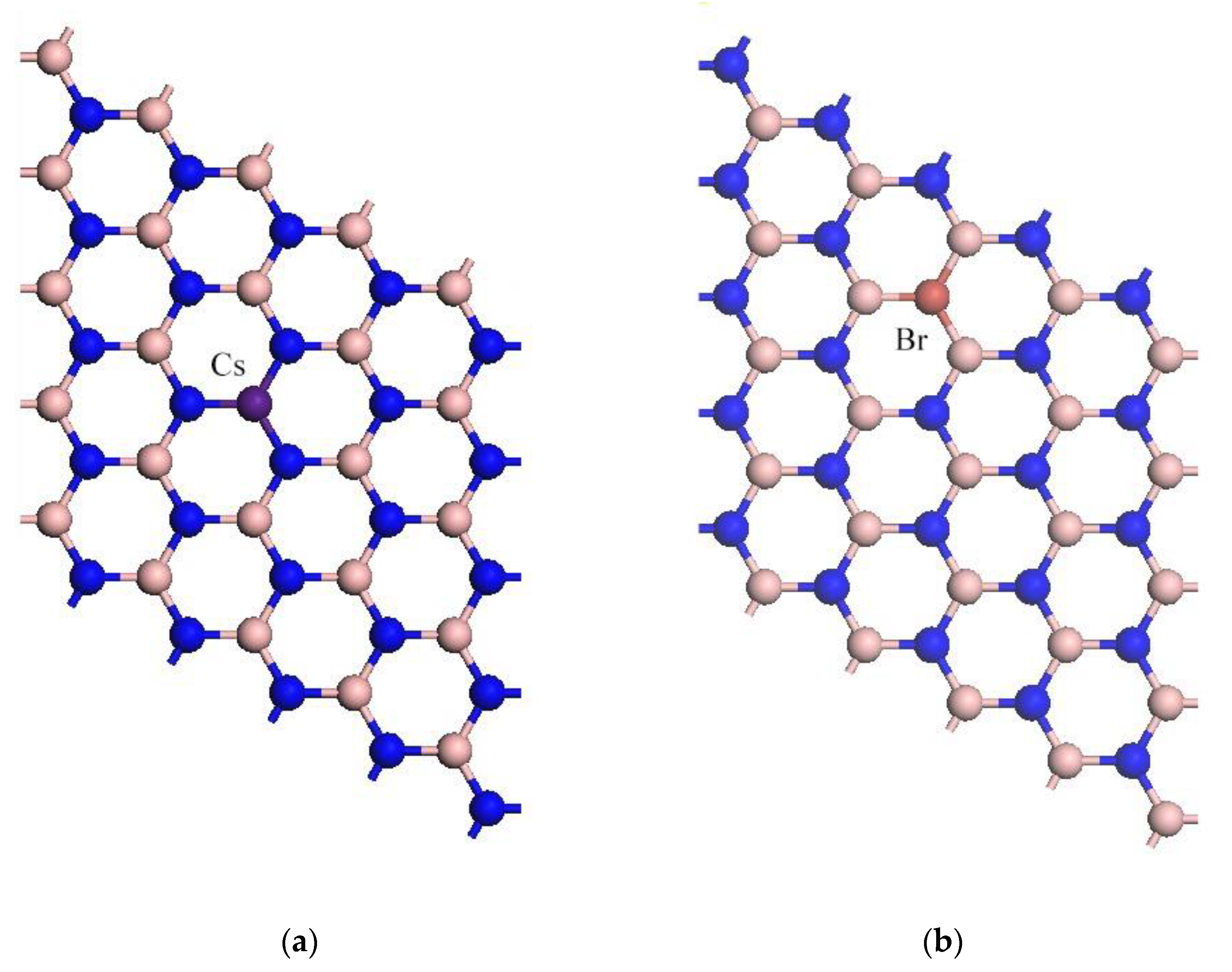
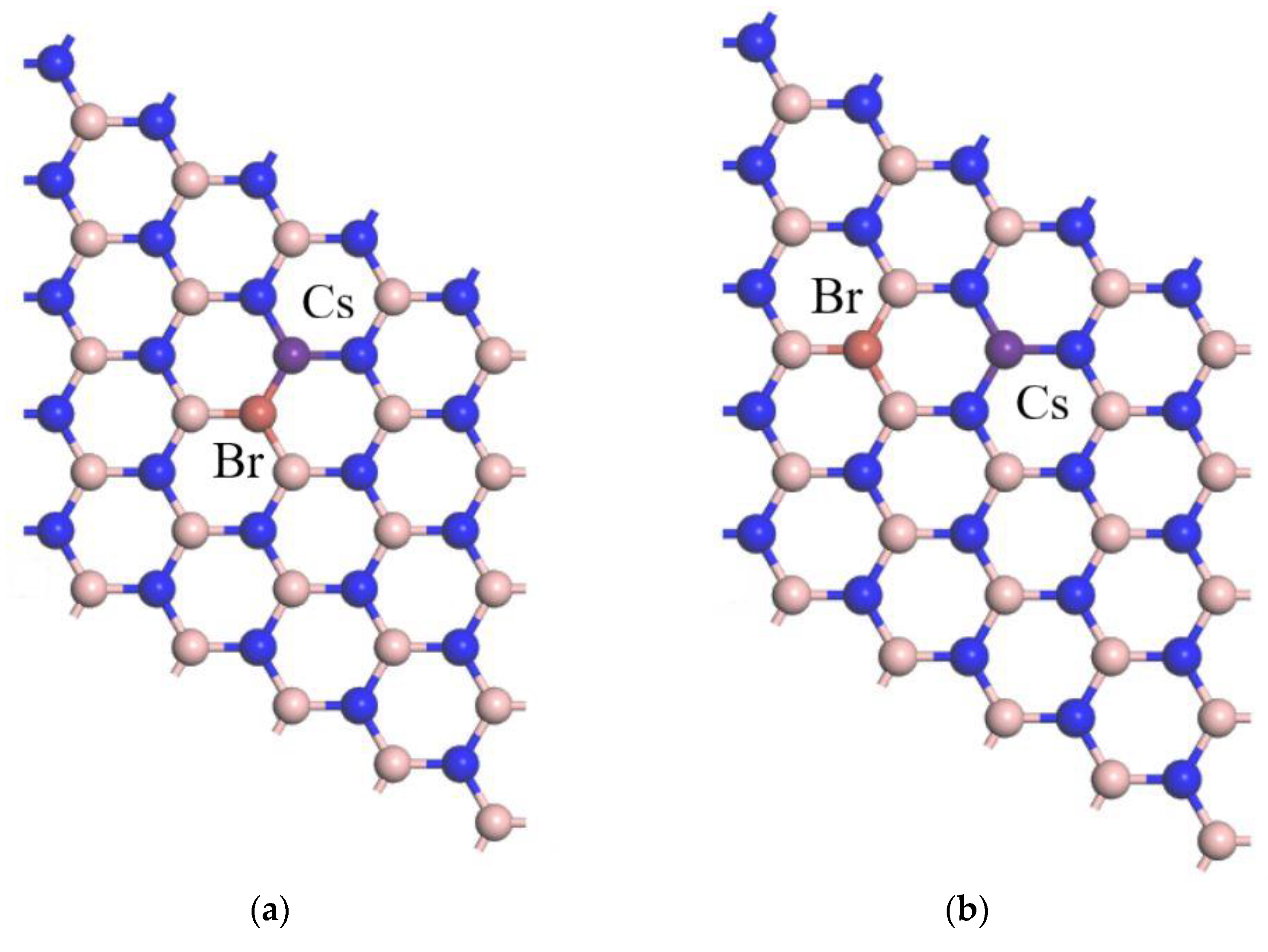


| Models | Bond Type | Bond Length (Å) |
|---|---|---|
| Intrinsic boron nitride | B-N | 1.42 |
| Cs-doped | Cs-N1 | 1.64 |
| Cs-doped | Cs-N2 | 1.64 |
| Br-doped | B1-Br | 1.72 |
| Br-doped | B2-Br | 1.72 |
| Cs-Br co-doped | B-Br | 1.93 |
| Cs-Br co-doped | Cs-N | 1.95 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Y.; Zhang, W.; Fan, Z.; Jiang, H.; Hou, Y.; Luo, Q.; Wang, Y. Investigation of Electronic and Optical Properties of (Cs, Br, Cs-Br) Doped Mono-Layer Hexagonal Boron Nitride Using First Principles. Crystals 2022, 12, 1406. https://doi.org/10.3390/cryst12101406
Fu Y, Zhang W, Fan Z, Jiang H, Hou Y, Luo Q, Wang Y. Investigation of Electronic and Optical Properties of (Cs, Br, Cs-Br) Doped Mono-Layer Hexagonal Boron Nitride Using First Principles. Crystals. 2022; 12(10):1406. https://doi.org/10.3390/cryst12101406
Chicago/Turabian StyleFu, Yangchen, Wenchao Zhang, Zhihua Fan, Hongcheng Jiang, Yuhang Hou, Qiuyu Luo, and Yi Wang. 2022. "Investigation of Electronic and Optical Properties of (Cs, Br, Cs-Br) Doped Mono-Layer Hexagonal Boron Nitride Using First Principles" Crystals 12, no. 10: 1406. https://doi.org/10.3390/cryst12101406
APA StyleFu, Y., Zhang, W., Fan, Z., Jiang, H., Hou, Y., Luo, Q., & Wang, Y. (2022). Investigation of Electronic and Optical Properties of (Cs, Br, Cs-Br) Doped Mono-Layer Hexagonal Boron Nitride Using First Principles. Crystals, 12(10), 1406. https://doi.org/10.3390/cryst12101406





