Shock Properties of One Unsaturated Clay and Its Equation of State Up to 30 GPa
Abstract
:1. Introduction
2. Experimental Measurement of the Hugoniot Parameters
2.1. Subsection
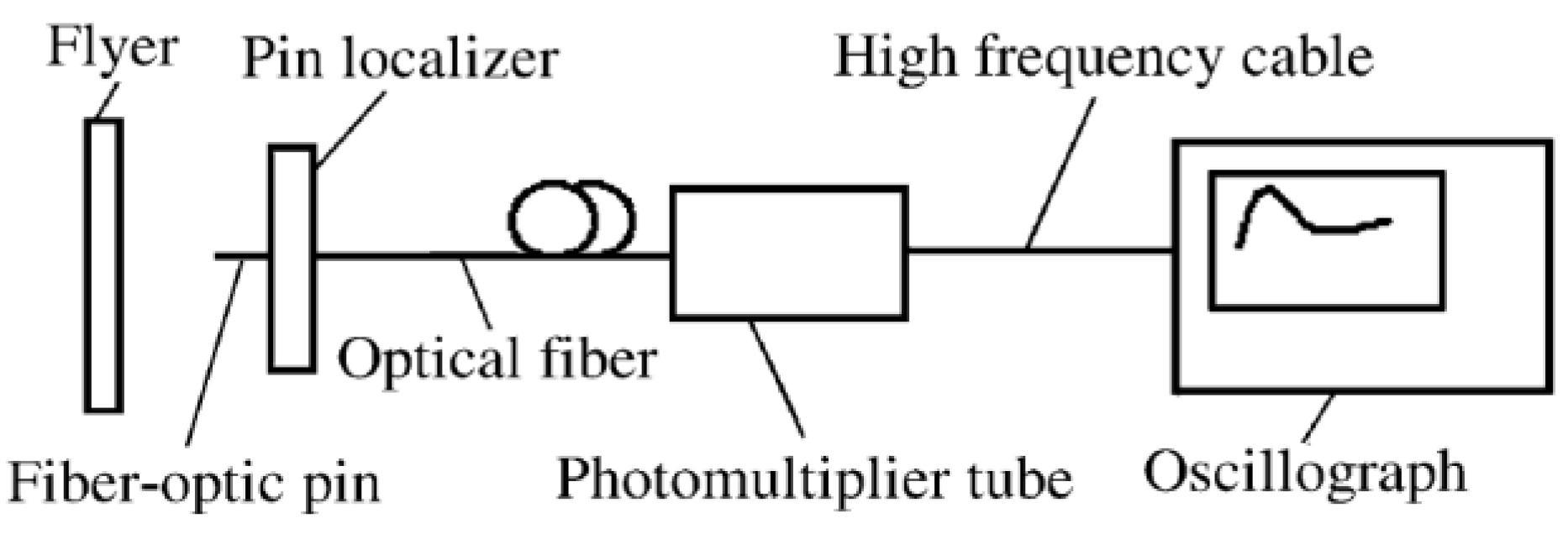
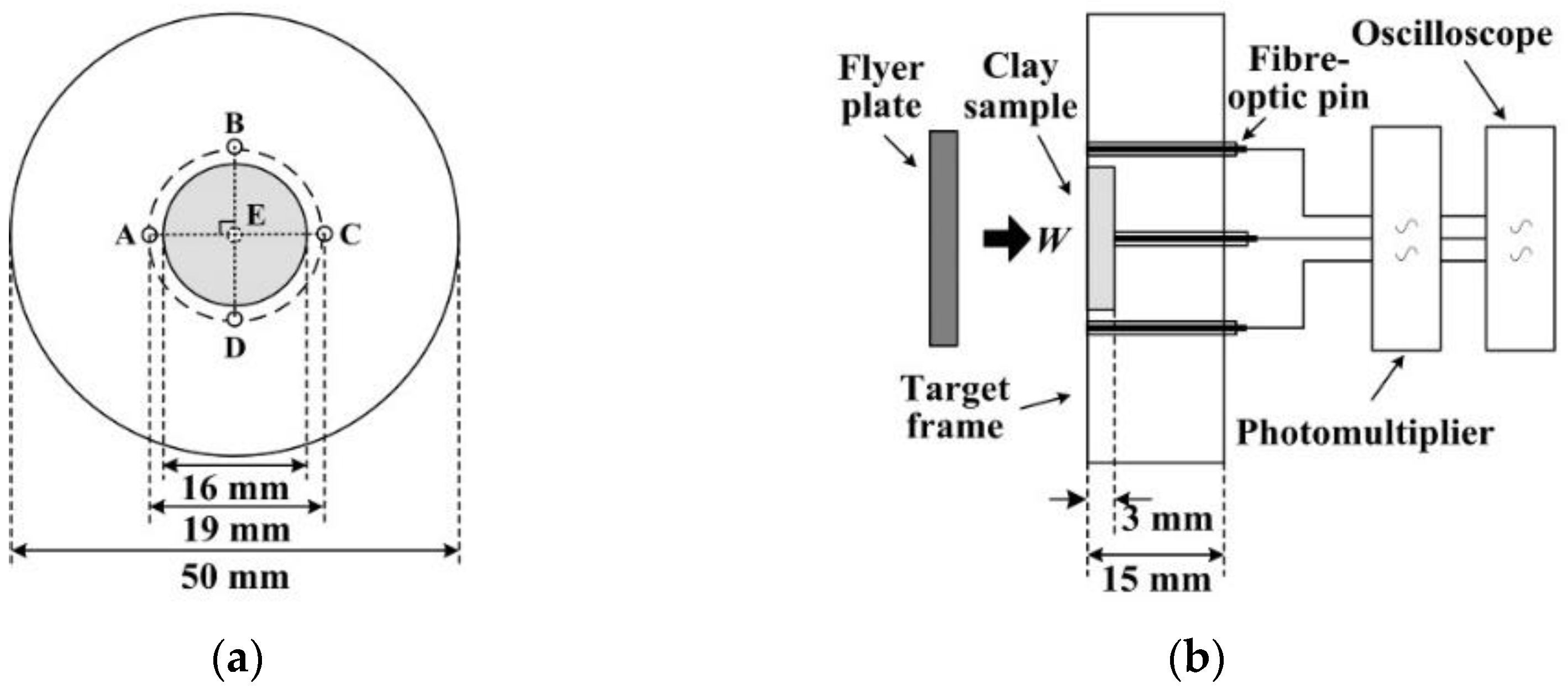
2.2. Experimental Method
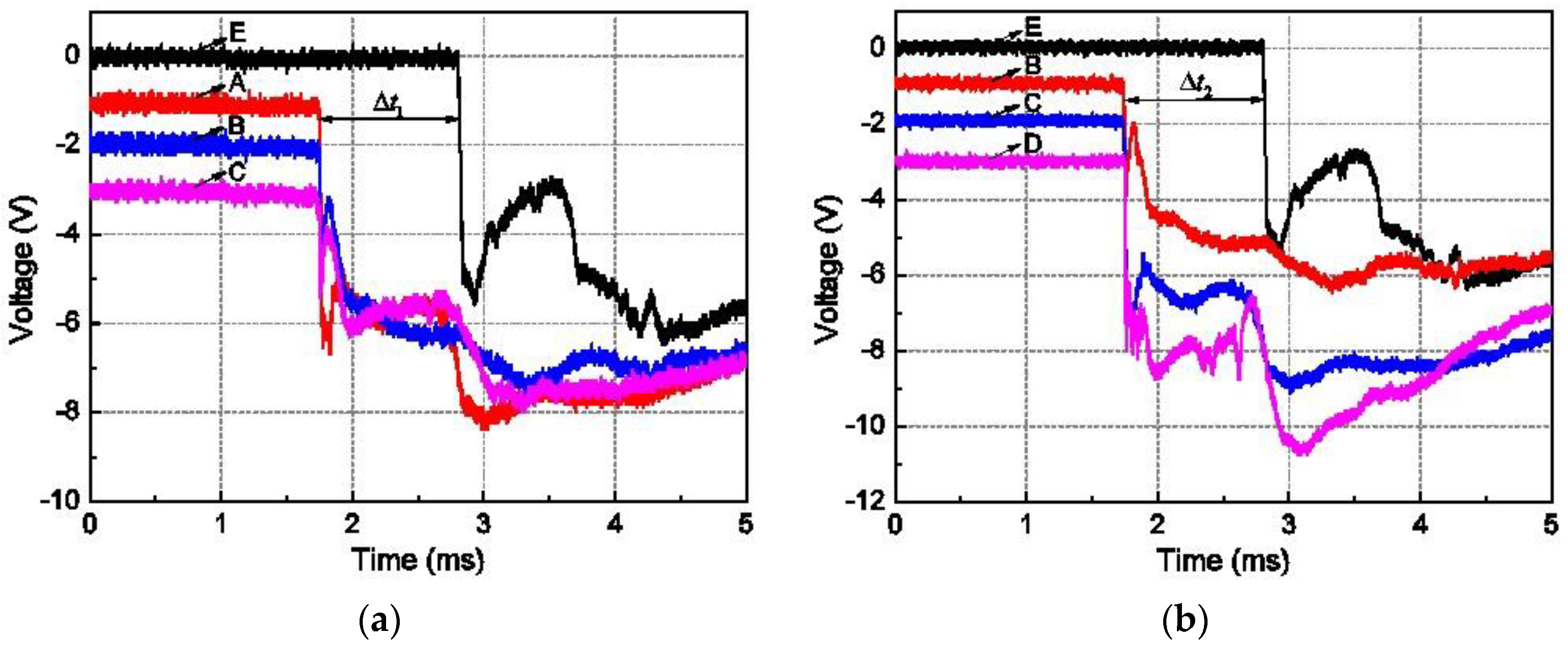
2.3. Data Processing Method
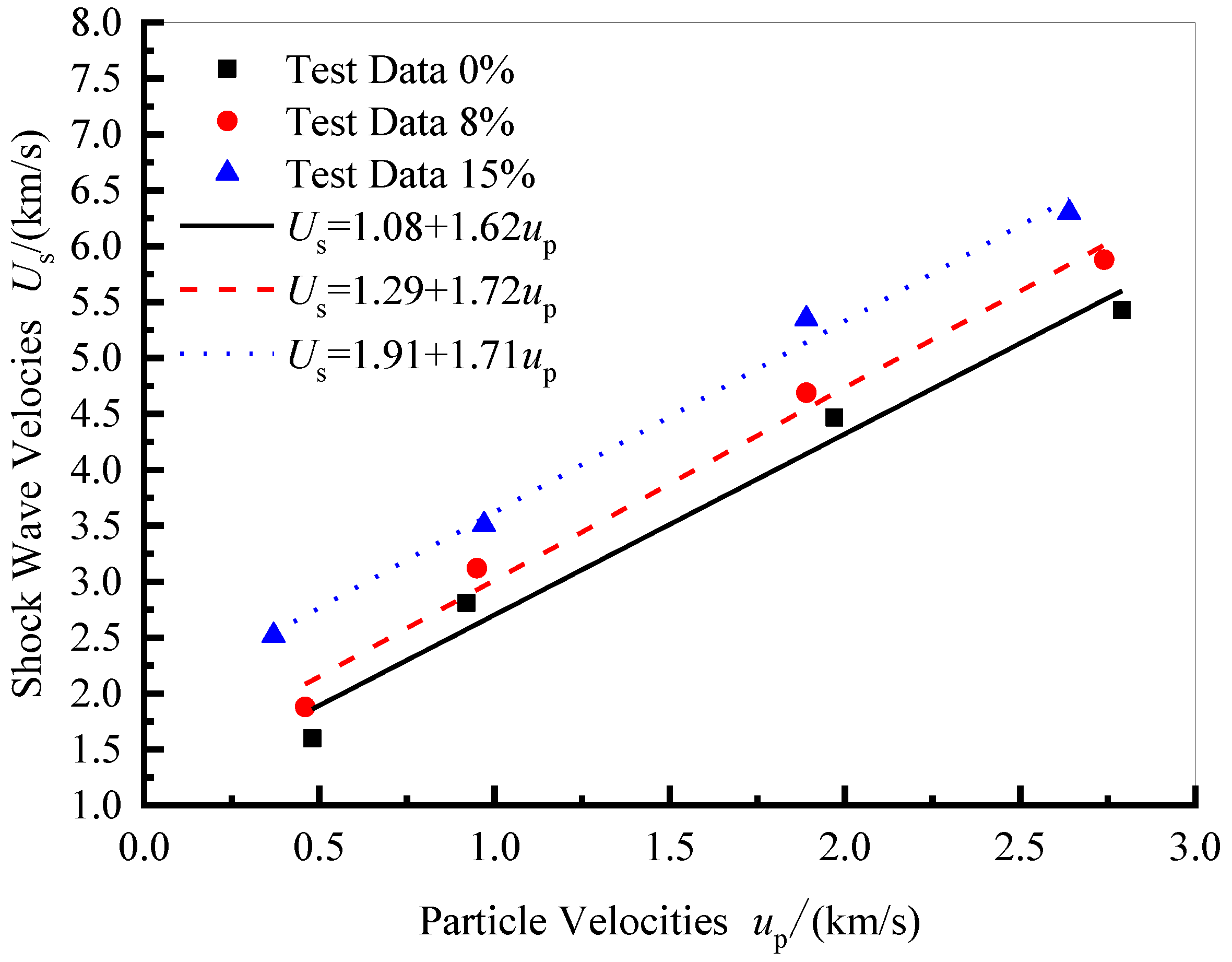
2.4. Experimental Results and Analysis
3. Equation of State of Unsaturated Clay
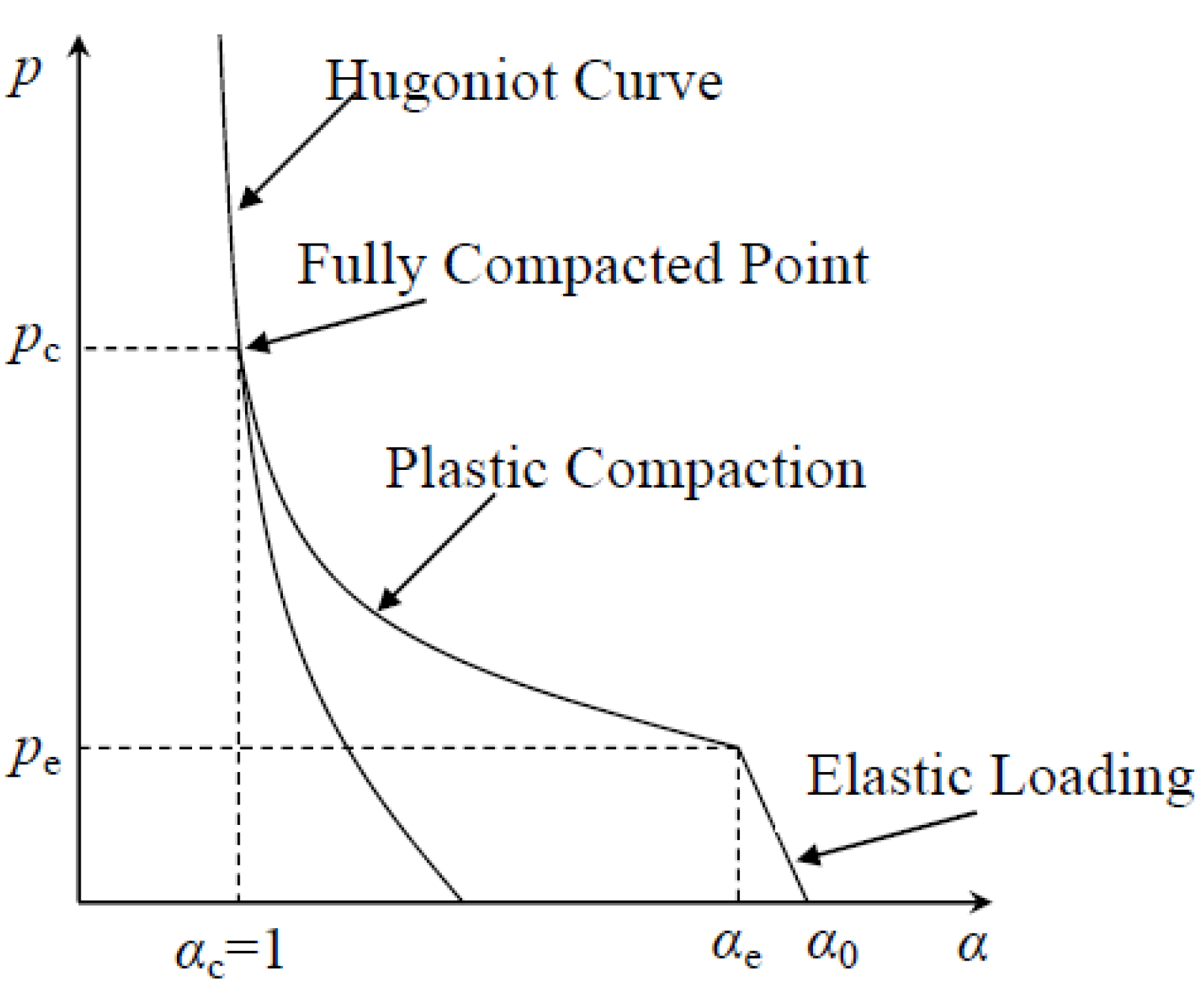
3.1. p-alpha Compaction Model
3.2. p-alpha Compaction Model
4. Discussion
- (1)
- For the unsaturated clay, the EOS could be separated into low-pressure range and high-pressure range by the compacted pressure pc. The p-alpha compacted model could be used in the low-pressure range and the solid-water two-constituent mixed EOS could be applied for the high-pressure range.
- (2)
- With the original clay extracted from the southern suburbs of Luoyang city in China, three unsaturated clays with moisture content 0%, 8%, and 15%, respectively, were remolded. The Hugoniot parameters of three unsaturated clays were determined by means of the plate impact experiment on a one-stage and two-stage light gas gun. The results were: when the moisture content is 0%, ρ0 = 1.70 g/cm3, c0 = 1.08 ± 0.30 km/s, s = 1.62 ± 0.17; when the moisture content is 8%, ρ0 = 1.84 g/cm3, c0 = 1.29 ± 0.24 km/s, s = 1.72 ± 0.14; when the moisture content is 15%, ρ0 = 1.96 g/cm3, c0 = 1.91 ± 0.18 km/s, s = 1.71 ± 0.10.
- (3)
- With the Hugoniot parameters and the model of two-stage EOS presented here, the high-pressure EOS up to 30 GPa was developed for the unsaturated clays of three moisture contents and was consistent with the experimental results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Henrych, J. The Dynamics of Explosion and Its Use; Elsevier Scientific Publishing Company: New York, NY, USA, 1979; pp. 73–84. [Google Scholar]
- Schofield, A.; Wroth, P. Critical State Soil Mechanics; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Van Thiel, M.; Shaner, J.; Salinas, E. Compendium of Shock Wave Data. Introduction. Section A1. Elements; California Univ.: Oakland, CA, USA, 1977. [Google Scholar]
- Kalashnikov, N.G.; Pavlovsky, M.N.; Simakov, G.V.; Trunin, R.F. Dynamic compressibility of calcite-group minerals. Izv. Phys. Solid Earth 1973, 2, 23–29. [Google Scholar]
- Trunin, R.F. Rock compressibility in shock waves. Izv. Earth Phys. 1988, 24, 38–42. [Google Scholar]
- Tsembelis, K.; Proud, W.; Vaughan, B. The behavior of sand under shock wave loading: Experiments and simulations. In Proceedings of the 14th DYMAT Technical Meeting on Behavior of Materials at High Strain Rates: Numerical Modeling, Sevilla, Spain, 1 January 2002. [Google Scholar]
- Chapman, D.; Tsembelis, K.; Proud, W. The behaviour of dry sand under shock loading. In Shock Compression of Condensed Matter; American Institute of Physics: Baltimore, MD, USA, 2005. [Google Scholar]
- Reinhart, W.D.; Thornhill, T.F., III; Chhabildas, L.C.; Vogler, T.J.; Brown, J.L. Shock Response of Dry Sand; Sandia National Laboratories: Albuquerque, NM, USA, 2007. [Google Scholar]
- Resnyansky, A.; Bourne, N. Shock Compression of Dry and Hydrated Sand; AIP Conference Proceedings; American Institute of Physics: Baltimore, MD, USA, 2004; pp. 1474–1477. [Google Scholar]
- Wang, Z.; Lu, Y. Numerical analysis on dynamic deformation mechanism of soils under blast loading. Soil Dyn. Earthq. Eng. 2003, 23, 705–714. [Google Scholar] [CrossRef]
- Wang, Z.; Hao, H.; Lu, Y. A three-phase soil model for simulating stress wave propagation due to blast loading. Int. J. Numer. Anal. Methods Geomech. 2004, 28, 33–56. [Google Scholar] [CrossRef]
- Marsh, S.P. LASL Shock Hugoniot Data; University of California Press: Berkeley, CA, USA, 1980; pp. 57–184. [Google Scholar]
- Shi, S.; Chen, P.; Huang, Y. Velocity measurement of magnet induced system for projectile. Chin. J. High Press. Phys. 1991, 5, 205–214. [Google Scholar]
- Zhao, S.W.; Wang, C.L.; Li, X. Experiment research of fiber probe applied in detonation velocity test. J. Appl. Opt. 2015, 36, 327–331. [Google Scholar]
- Schmitt, D.R.; Ahrens, T.J. Shock temperatures in silica glass: Implications for modes of shock-induced deformation, phase transformation, and melting with pressure. J. Geophys. Res. Solid Earth 1989, 94, 5851–5871. [Google Scholar] [CrossRef] [Green Version]
- Herrmann, W. Constitutive equation for the dynamic compaction of ductile porous materials. J. Appl. Phys. 1969, 40, 2490–2499. [Google Scholar] [CrossRef]
- Borg, J.P.; Chapman, D.J.; Tsembelis, K. Dynamic compaction of porous silica powder. J. Appl. Phys. 2005, 98, 073509. [Google Scholar] [CrossRef]
- Borg, J.P.; Cogar, J.R.; Lloyd, A. Computational simulations of the dynamic compaction of porous media. Int. J. Impact Eng. 2006, 33, 109–118. [Google Scholar] [CrossRef]
- Al’tshuler, L.V.; Pavlovskii, M.N. Response of clay and clay shale to heavy dynamic loading. J. Appl. Mech. Tech. Phys. 1971, 12, 161–165. [Google Scholar] [CrossRef]







| Components | Quartz | Calcite | Chlorite | Montmorillonite | Illite | Feldspar | Kaolinite | Amphibole | Hematite |
|---|---|---|---|---|---|---|---|---|---|
| Mass (%) | 25 | 7 | 15 | 10 | 15 | 18 | 5 | 3 | 2 |
| Sample Number | 1 | 2 | 3 |
|---|---|---|---|
| initial dry density ρd0 (g/cm3) | 1.70 | 1.70 | 1.70 |
| initial wet density ρ0 (g/cm3) | 1.70 | 1.84 | 1.96 |
| sample weight m (g) | 1.03 | 1.11 | 1.18 |
| initial moisture content w (%) | 0 | 8 | 15 |
| initial saturation Sr0 (%) | 0 | 35.8 | 67.4 |
| Material | ρ0 (g/cm3) | c0 (km/s) | s |
|---|---|---|---|
| 2024 aluminum alloy | 2.785 | 5.328 | 1.338 |
| copper | 8.93 | 3.94 | 1.489 |
| tantalum | 16.656 | 3.437 | 1.19 |
| Clay Samples | No. | Flyer Materials | Flyer Velocity (km/s) | Shock Wave Arrival Time (ns) | Sample Thickness (mm) | Particle Velocity (km/s) | Shock Wave Velocity (km/s) | Pressure (GPa) |
|---|---|---|---|---|---|---|---|---|
| Dry Clay | 1 | Aluminum | 0.561 | 1868 | 2.98 | 0.48 | 1.60 | 1.29 |
| 2 | Copper | 1.042 | 1054 | 2.96 | 0.92 | 2.81 | 4.40 | |
| 3 | Copper | 2.340 | 658 | 2.94 | 1.97 | 4.47 | 14.95 | |
| 4 | Tantalum | 3.180 | 556 | 3.02 | 2.79 | 5.43 | 25.71 | |
| Wet clay (moisture content: 8%) | 5 | Aluminum | 0.563 | 1564 | 2.94 | 0.46 | 1.88 | 1.58 |
| 6 | Copper | 1.101 | 956 | 2.98 | 0.95 | 3.12 | 5.46 | |
| 7 | Copper | 2.290 | 640 | 3.00 | 1.89 | 4.69 | 16.26 | |
| 8 | Tantalum | 3.190 | 500 | 2.94 | 2.74 | 5.88 | 29.60 | |
| Wet clay (moisture content: 15%) | 9 | Aluminum | 0.495 | 1192 | 3.00 | 0.37 | 2.52 | 1.84 |
| 10 | Copper | 1.142 | 848 | 2.98 | 0.97 | 3.51 | 6.63 | |
| 11 | Copper | 2.370 | 538 | 2.88 | 1.89 | 5.35 | 19.81 | |
| 12 | Tantalum | 3.130 | 478 | 3.01 | 2.64 | 6.30 | 32.54 |
| EOS | Parameters | Dry Clay | 8% Clay | 15% Clay |
|---|---|---|---|---|
| p-alpha model | Elastic yield strength, pe (GPa) | 0 | 0 | 0 |
| Plastic yield strength, ps (GPa) | 4.97 | 2.15 | 1.38 | |
| Empirical fitting parameter, N | 2 | 2 | 2 | |
| Solid–liquid two-phase model | Fully compacted density, ρc (g/cm3) | 2.73 | 2.42 | 2.23 |
| Water proportion under pc, βwc | 0 | 0.18 | 0.29 | |
| Solid proportion under pc, βsc | 1 | 0.82 | 0.71 | |
| Water phase | ρw0 = 1.0 g/cm3, cw0 = 1500 m/s, kw = 7 | |||
| Solid particle phase | ρs0 = 2.73 g/cm3, cs0 = 4500 m/s, ks = 3 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ran, X.; Zou, X.; Zhou, J.; Tang, W. Shock Properties of One Unsaturated Clay and Its Equation of State Up to 30 GPa. Crystals 2022, 12, 119. https://doi.org/10.3390/cryst12010119
Ran X, Zou X, Zhou J, Tang W. Shock Properties of One Unsaturated Clay and Its Equation of State Up to 30 GPa. Crystals. 2022; 12(1):119. https://doi.org/10.3390/cryst12010119
Chicago/Turabian StyleRan, Xianwen, Xuan Zou, Jingyuan Zhou, and Wenhui Tang. 2022. "Shock Properties of One Unsaturated Clay and Its Equation of State Up to 30 GPa" Crystals 12, no. 1: 119. https://doi.org/10.3390/cryst12010119
APA StyleRan, X., Zou, X., Zhou, J., & Tang, W. (2022). Shock Properties of One Unsaturated Clay and Its Equation of State Up to 30 GPa. Crystals, 12(1), 119. https://doi.org/10.3390/cryst12010119






