Abstract
Rocksalt-type (Pb,Cd)Te belongs to IV–VI semiconductors exhibiting thermoelectric properties. With the aim of understanding of the influence of Cd substitution in PbTe on thermostructural and elastic properties, we studied PbTe and Pb0.884Cd0.116Te (i) at low temperatures (15 to 300 K) and (ii) at high pressures within the stability range of NaCl-type PbTe (up to 4.5 GPa). For crystal structure studies, powder and single crystal X-ray diffraction methods were used. Modeling of the data included the second-order Grüneisen approximation of the unit-cell-volume variation, V(T), the Debye expression describing the mean square atomic displacements (MSDs), <u2>(T), and Birch–Murnaghan equation of state (BMEOS). The fitting of the temperature-dependent diffraction data provided model variations of lattice parameter, the thermal expansion coefficient, and MSDs with temperature. A comparison of the MSD runs simulated for the PbTe and mixed (Pb,Cd)Te crystal leads to the confirmation of recent findings that the cation displacements are little affected by Cd substitution at the Pb site; whereas the Te displacements are markedly higher for the mixed crystal. Moreover, information about static disorder caused by Cd substitution is obtained. The calculations provided two independent ways to determine the values of the overall Debye temperature, θD. The resulting values differ only marginally, by no more than 1 K for PbTe and 7 K for Pb0.884Cd0.116Te crystals. The θD values for the cationic and anionic sublattices were determined. The Grüneisen parameter is found to be nearly independent of temperature. The variations of unit-cell size with rising pressure (the NaCl structure of Pb0.884Cd0.116Te sample was conserved), modeled with the BMEOS, provided the dependencies of the bulk modulus, K, on pressure for both crystals. The K0 value is 45.6(2.5) GPa for PbTe, whereas that for Pb0.884Cd0.116Te is significantly reduced, 33.5(2.8) GPa, showing that the lattice with fractional Cd substitution is less stiff than that of pure PbTe. The obtained experimental values of θD and K0 for Pb0.884Cd0.116Te are in line with the trends described in recently reported theoretical study for (Pb,Cd)Te mixed crystals.
1. Introduction
1.1. General Issues
IV–VI semiconductors of rocksalt-type (space group Fm-3m) are known to exhibit thermoelectric properties. One of the ways to modify the characteristics of such materials is fractional substitution of specific elements at the cationic or anionic sites of the crystal lattice, using a synthesis method allowing for conservation of the rocksalt-type structure. The achievable alloying level for such materials depends on the substituent and preparation method. Such substitution significantly affects the thermoelectric properties and others. We recognized that a determination of thermostructural and elastic properties can contribute to development of these materials, and that detailed studies involving the structure analysis under nonambient pressures and temperatures are lacking for mixed (IV,II)VI semiconductors. This observation gave us motivation to undertake the study for Pb1−xCdxTe, which is one of most studied thermoelectric materials.
Thermostructural properties of a semiconductor are the subject of detailed studies in applied science, because they interfere with electric, optical and magnetic characteristics. Moreover, they are of importance in the design of semiconducting devices, as they affect the crystal and film growth processes and are meaningful for the first response of the material under mechanical or thermal load [1].
The family of thermoelectric materials includes tellurides, selenides, sulfides and some other compounds [2]. The thermoelectric properties of the IV–VI semiconductors of a NaCl structure have been extensively studied, both experimentally and theoretically. One of most important thermoelectrics in the family of Pb and Sn chalcogenides of a rocksalt structure is PbTe (mineral name altaite). Careful choice of the substituent and its amount incorporated into the PbTe lattice can significantly enhance the Seebeck coefficient [3,4]. PbTe exhibits polymorphism, and it is noteworthy that the orthorhombic high-pressure PbTe phase has also been reported to exhibit thermoelectric properties [5].
1.2. Cationic Substitutions
Experimental data on the effect of substitutions on the properties of PbTe have been reported for a number of systems containing various substituents. Scientific research is continuously expanding our knowledge about structural properties of such systems. For PbTe crystals modified by using various substituents, such studies have been performed, e.g., for Ba substituents [6] (experimental study), Cd or Mn [7], rare-earth metals [8], diverse substituents [9], and gold substituents [10] (theoretical studies). The mentioned theoretical study [9] convincingly demonstrates, how the choice of substituent (at the fixed level of 3.1%) incorporated into the PbTe crystal lattice, affects the physical properties and Seebeck coefficient describing the thermoelectric conversion efficiency. According to ref. [9], for most considered substituents incorporated into CdTe lattice, two important characteristics, the Debye temperature and bulk modulus, exhibit apparent decreasing trends. The prediction of the Seebeck coefficient value for tens of diversely substituted PbTe reported in ref. [9] provides a valuable basis and potential support for future work towards improvement of thermoelectrics.
1.3. PbX-CdX (X = Te, Se, S) Solid Solution
Thermoelectric properties of PbTe are improved when the Pb ions are partially replaced by Cd ions [11], forming a metastable Pb1−xCdxTe solid solution of the rocksalt type [12,13,14,15]. Therefore, this material attracts researchers’ attention, being suitable for design of thermoelectric devices. Metastable single-phase NaCl-type crystals have been reported with maximal Cd content depending on the preparation conditions, particularly on applied quenching conditions from high temperature or high pressure or on the annealing method.
The lattice parameter of Pb1−xCdxTe decreases with the CdTe addition, as demonstrated experimentally [16,17,18,19] and theoretically [7]. The behavior is similar for PbSe and PbS matrices with the respective addition of CdSe and CdS. The linearity of lattice parameter variation in these three systems is illustrated in Figure 1, whereas the equations describing the lines are given in Table 1 (on the basis of the above references for PbTe, refs. [20,21,22,23] for PbSe and refs. [24,25,26,27] for PbS. (Some additional information is available in a study of the quaternary system [28].) The lines in Figure 1, representing the Vegard’s rule (linear behavior of lattice parameter) are based on cited studies. The highest reported content, xmax, is shown for each system. Extrapolation to x = 1 gives the lattice parameters of hypothetical cadmium chalcogenides with a NaCl structure. The values of these parameters, of coefficients of Vegard’s equation (in one case, of the equivalent Zen’s equation), and the highest reported Cd content as well as the results of extrapolation are collected in Table 1, including the data from refs. [7,16,18,19,20,21,22,23,25,26,27].
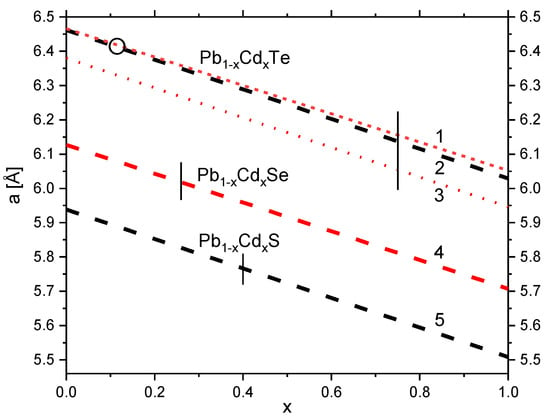
Figure 1.
Reported variations of the metastable-rocksalt-phase lattice parameter of ternary Pb1−xCdxTe, Pb1−xCdxSe and Pb1−xCdxS. The plots present the linear equations reported in ref. [18] (1), ref. [19] (2), ref. [7] (theoretical data) (3), ref. [20] (4), and ref. [25] (5). The highest values of Cd content in quenched samples among the reported ones, xmax (see Table 1), are marked with short vertical solid lines. The variations are extended above the achieved (in quenched crystals) Cd content towards x = 1, in order to indicate the extrapolated lattice parameters of rocksalt structures of the binary Cd chalcogenides. The open circle indicates the composition of the Pb1−xCdxTe sample studied in this work.

Table 1.
Linear equations for a(x) or V(x) (Vegard’s rule and Zen’s rule, respectively) for Pb1−xCdxTe, Pb1−xCdxSe and Pb1−xCdxS solid solutions: equations, maximum reported Cd content, xmax, and extrapolated lattice parameters, aex, for rocksalt type CdTe, CdSe and CdS (at x = 1).
1.4. Knowledge on Thermostructural and Elastic Properties for PbTe and Pb1−xCdxTe
Numerous studies on thermostructural and elastic properties of PbTe have been performed. However, some are not very detailed, and not many of them include the lowest (below 100 K) temperatures. Among the studies, the most detailed work is that of ref. [29], in which neutron powder diffraction was used to determine variations of the lattice parameter, thermal expansion coefficient (TEC), and mean square atomic displacements (MSDs) as a function of temperature. Other experimental studies refer to narrower temperature ranges or describe selected variables only. One of the frequently considered characteristics of thermoelectric materials is the degree of ordering [30]. Some recent studies focus on appearance of the cation disorder in PbTe and related chalcogenides [31,32,33,34]. The introduced disorder can affect the thermal conductivity of the crystal [31]. The substitutional disorder in the (Pb,Cd)Te alloys system has also been recently discussed in ref. [35]. However, the analysis of disorder based on temperature-dependent properties is still lacking for this ternary system.
The basic thermostructural data have been reported as functions of temperature for various temperature ranges:
- the lattice parameter a(T) (experimental ones for PbTe, in refs. [29,31,36,37,38,39,40,41]), for Pb1−xCdxTe in refs. [42,43,44], theoretical ones for PbTe in refs. [45,46,47,48,49,50]) (see Table 2),
 Table 2. Temperature ranges for selected experimental and theoretical studies of the lattice parameter, a(T), of PbTe and Pb1−xCdxTe (x = 0.013, 0.020, 0.056, 0.096, 0.116). In the case of experimental studies, the ranges refer to the lower and upper limit of the experiment.
Table 2. Temperature ranges for selected experimental and theoretical studies of the lattice parameter, a(T), of PbTe and Pb1−xCdxTe (x = 0.013, 0.020, 0.056, 0.096, 0.116). In the case of experimental studies, the ranges refer to the lower and upper limit of the experiment. - thermal expansion α(T) for PbTe (experimental ones in refs. [29,41,51,52] and theoretical ones in refs. [8,45,46,47,53,54] (see Table 3),
 Table 3. Temperature ranges for selected experimental and theoretical studies on the variation of the linear thermal expansion coefficient, α(T), of PbTe and Pb1−xCdxTe (x = 0.116). In the case of the experimental studies, the ranges refer to the lower and upper limit of the experiment.
Table 3. Temperature ranges for selected experimental and theoretical studies on the variation of the linear thermal expansion coefficient, α(T), of PbTe and Pb1−xCdxTe (x = 0.116). In the case of the experimental studies, the ranges refer to the lower and upper limit of the experiment. - atomic displacements for PbTe (experimental ones in refs. [29,31,34,37,38,39,40,41,50,55,56,57] and theoretical ones in refs. [39,49,50,58,59,60] (see Table 4).
 Table 4. Temperature ranges for selected earlier studies of the experimental and theoretical mean square displacements <u2>(T) of PbTe and Pb1−xCdxTe (x = 0.116). In the case of experimental studies, the ranges refer to the lower and upper limit of the experiment.
Table 4. Temperature ranges for selected earlier studies of the experimental and theoretical mean square displacements <u2>(T) of PbTe and Pb1−xCdxTe (x = 0.116). In the case of experimental studies, the ranges refer to the lower and upper limit of the experiment.
As for the properties of PbTe (a) describing the structural behavior under pressure or (b) describing it in the space of both variables, p and T, or (c) describing the variation of compressibility, elastic constants, heat capacity, Debye temperature and the Grüneisen parameter with temperature or pressure, the available data are scarce. For experimental data, see refs. [29,51,52,61,62,63], for theoretical data for PbTe, see refs. [8,45,46,47,53,64,65,66,67,68,69] and for Pb1−xCdxTe, see refs. [66,68] (details are provided in Table 5).

Table 5.
(Completing Table 2, Table 3 and Table 4). Pressure and/or temperature ranges for experimental and theoretical studies of structure-related variables for PbTe and Pb1−xCdxTe (x = 0.116), reported as functions of pressure and/or temperature: volume on pressure dependence, V(p), bulk modulus, K(T), elastic constants, C(T), Debye temperature, θD(p,T) or θD(p), Grüneisen parameter, γ(T) and γ(p), thermal expansion, α(p,T), heat capacity, cp(T) or cp(T). For experimental studies, the ranges refer to the lower and upper limit of the experiment.
1.5. Pb-Te and PbTe-CdTe System
The temperature phase diagram of Pb-Te system shows that the Fm-3m PbTe phase (with the lattice parameter a = 6.460 Å) is stable in the full range, up to Tmax = 1197 K [70] (see refs. [71,72]). The off-stoichiometry range for PbTe is extremely narrow [70,73,74,75,76].
The PbTe–CdTe phase diagram [13] (for theoretical considerations, see ref. [66]) shows that the solubility, with equilibrium conditions at room temperature, of CdTe in PbTe is marginal. This is a consequence of the difference in their crystal structure—a rocksalt type for PbTe and a zinc-blende type for CdTe. However (as mentioned in the Introduction section), the Pb1−xCdxTe solid solution of the rocksalt type can be prepared in a metastable form. A diffraction study on the structure of Pb1−xCdxTe as a function of temperature has shown the decomposition process of metastable Pb1−xCdxTe (x = 0.096) during heating [43]; these results led to evaluation of the maximum achievable Cd content in the metastable solid solution [13]. Some theoretical calculations based on first principles have been presented in ref. [68].
Experimental investigations show that the transition to a high-pressure polymorph occurs at about 6–7 GPa [70,77,78,79,80,81,82,83], (see also theoretical studies [67,84,85]). The space group of this phase is Pnma, the lattice parameters at 7.5 GPa are a = 11.91 Å, b = 4.20 Å, c = 4.51 Å [70]. From about 18 GPa to at least 50 GPa, a CsCl type phase exists [83]. Recently, a topological transition at 4.8 GPa was reported in a density functional theory study [86]. Interestingly, the combination of the features of immiscibility and lattice-parameter similarity of the PbTe and CdTe components leads to the opportunity for the growth of heterostructures (which can be applied in the construction of room-temperature infrared detectors, for example [87]).
1.6. Aim
The purpose of this study is to systematically determine the influence of cadmium substitution on the thermostructural and elastic properties of PbTe. To achieve this goal, these properties (lattice parameter, thermal expansion, atomic displacements, bulk modulus and their variation with temperature or pressure) were studied and compared for two crystals, PbTe and Pb0.884Cd0.116Te. The literature data for PbTe are reviewed and taken into account in the comparative analysis of properties of these two crystals.
2. Materials and Methods
The PbTe and Pb1−xCdxTe single crystals were obtained by the self-selecting vapor growth (SSVG) method described in refs. [88,89]. High purity polycrystalline PbTe and CdTe compounds were used as reaction components. The conditions were similar to those used in earlier work [19]. To produce the PbTe–CdTe solid solution, the synthesis was performed using a mixture of PbTe and CdTe enclosed in a sealed quartz ampoule located in a furnace with a gradient of about 1 deg/cm at a temperature of about 850℃. The process of growth of homogeneous (Pb,Cd)Te crystals lasted two weeks. Further details of the growth procedure can be found in refs. [19,90]. The Cd content, x = 0.116, was derived from the a(T) dependence reported in ref. [19].
Synchrotron-radiation techniques offer valuable experimental approaches for studies of materials; in particular, thermoelectric materials [91]. Here, we focus on the use of synchrotron radiation diffraction to extract the structural information on PbTe and Pb1−xCdxTe. The in-situ low-temperature measurements were performed using synchrotron X-ray powder diffraction [92] at HASYLAB, Hamburg. The Debye–Scherrer geometry with monochromatic radiation (λ = 0.5385 Å) and an image plate detector [93] were applied. The incident beam size was 1 × 15 mm2. The measurements were performed in the 2θ range of 7–58° (corresponding d-spacing range is 4.410–0.555 Å), and for samples mounted in glass capillaries (Hilgenberg) of 0.3 mm diameter, the X-ray powder diffraction patterns were recorded with a 0.004° (2θ) step.
The samples were prepared as a mixture of powdered Pb1−xCdxTe crystals and fine diamond powder (Sigma–Aldrich #48,359-1 synthetic powder), of ~1 μm monocrystalline grain size and purity of 99.9%). Addition of diamond powder served for both, (i) a diluent and (ii) an internal diffraction standard, avoiding the possible influence of wavelength instabilities (the use of such a standard has been proposed in ref. [94]). Low-temperature conditions (temperature range 15–300 K) were ensured by a closed-circuit He-cryostat. For the structural analysis, the Rietveld method [95,96] was applied using the refinement program, Fullprof.2k(v.7) [97]. In calculations, the pseudo-Voigt profile-shape function was assumed. The following parameters were refined: scale factor, lattice parameters, isotropic mean square displacement parameters, peak shape parameters, and systematic line-shift parameter. The background was set manually.
A Merrill-Bassett diamond-anvil cell (DAC) [98] was used in high-pressure experiments. The single-crystal sample was mounted inside the DAC chamber with a MeOH:EtOH:H2O (16:3:1) mixture as the pressure-transmitting medium. The pressure was calibrated with a Photon Control spectrometer by the ruby-fluorescence method [99], assuring a precision of 0.02 GPa. The experiments were conducted at a temperature of 296 K. High-pressure single-crystal X-ray diffraction data were collected at a four-circle KUMA X-ray diffractometer equipped with a graphite monochromator for the applied MoKα radiation. The gasket shadowing method was used for crystal centering and data collection [100]. The size of the diamond culets was 0.7 mm, the size of crystal for PbTe was 0.2 × 0.05 × 0.15 mm3, for Pb0.884Cd0.116Te was 0.23 × 0.05 × 0.17 mm3 (only one crystal was loaded into DAC). UB-matrix determinations and data reductions were performed with the program CrysAlisPro [101]. The structures were solved by direct methods using the program ShelXS and refined by full-matrix least-squares on F2 using the program ShelXT incorporated in Olex2 [102,103]. For high-pressure data analysis, the fitting procedures were conducted with the EoSFit7 program [104,105].
3. Results: Thermostructural and Elastic Properties of PbTe and Pb0.884Cd0.116Te
3.1. Effect of Cd Substitution on Temperature Variation of Unit Cell Size, Thermal Expansion Coefficient and Cationic and Anionic Mean Square Displacements
3.1.1. General Issues
The data provided by powder and single-crystal X-ray diffraction methods allowed the determination of the structural and elastic properties of PbTe and Pb1−xCdxTe (x = 0.116) in the 15–300 K temperature range and separately, in 0.1 MPa–4.5 GPa pressure range. Consequently, the properties measured at the same conditions for each of two crystals could be analyzed, leading to the understanding of the effect of Cd substitution on the crystal characteristics.
For pure PbTe, most of these properties were known in advance, but the information regarding temperatures below 105 K has been mostly based on the results of neutron powder diffraction of ref. [29]. The present study is one of few X-ray diffraction studies of the thermostructural properties of PbTe, covering an extended temperature range, and jointly analyzing all the three a(T), α(T), and <u2>(T) experimental variations, completed by the V(p) study. For the Pb1−xCdxTe system, the detailed investigations at non-ambient temperature and pressure have been almost completely lacking.
Phase analysis showed that the samples were single phase crystals. The analysis of powder diffraction data of PbTe and Pb0.884Cd0.116Te by the Rietveld method yielded direct information on (i) the temperature dependencies of unit-cell size, a(T), and (ii) mean square displacements, <u2>(T), of both, cations and anions. Illustrative examples of structure refinement plots for PbTe and Pb1−xCdxTe at temperatures 15 K and 300 K are given in Appendix A (Figure A1). Subsequent analysis of the a(T) data led to the derivation of the temperature variation of the thermal expansion coefficient, α(T). The modeling of the temperature variations of the studied quantities allowed for independent determination also of other properties, for both the cationic and anionic sublattices of studied crystals.
3.1.2. Variation of Unit Cell Size of PbTe and Pb0.884Cd0.116Te with Temperature
The experimental lattice parameter of PbTe varies in the 15–300 K range in a monotonic way (see Figure 2). The unit-cell volume, V(T), variation was modeled by the second-order Grüneisen approximation, taking into account the Debye internal-energy function [106,107]:
where: Q and b are constants. E(T) in Equation (1), expressed as
represents the Debye energy model of lattice vibrations, n is the number of atoms in the unit cell, kB = Boltzmann constant, θD is the characteristic Debye temperature. The parameters Q, and b are obtained through fitting of experimental V(T) data modeled by Equation (1) (refined parameters are quoted in Appendix C, Table A5). For PbTe, the lattice parameter increases by 0.50% over the whole temperature range. The run of the a(T) (see inset in Figure 2b) is marginally different from the recent experimental data obtained in a wide temperature range (10–500 K) by neutron powder diffraction [29], and in the 105–300 K range by X-ray powder diffraction [31] (Figure 2a).
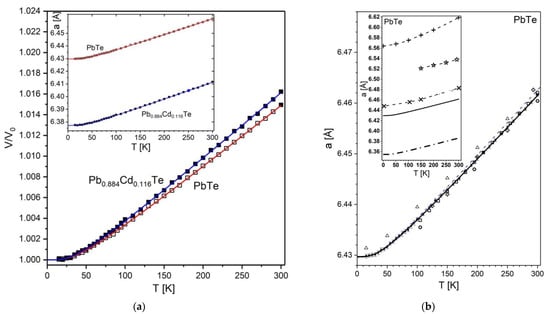
Figure 2.
(a) Experimental variation of normalized unit-cell volume with temperature for PbTe (□) and Pb0.884Cd0.116Te (■) (the main figure). The corresponding dependencies of the absolute values of lattice parameters are shown in the inset. The uncertainties are smaller than the symbol size. The fits of Equation (1) (second-order Grüneisen approximation) are shown in the figure and in the inset using red (PbTe) and blue (Pb0.884Cd0.116Te) solid lines, respectively. (b) Present temperature dependence of the PbTe lattice parameter, compared to selected literature data. Present experimental points (■) and the second-order Grüneisen approximation (thick solid line); experimental data of ref. [38] (△), ref. [31] (  ), ref. [29] (thin dashed line), ref. [39] (◇), ref. [34] (
), ref. [29] (thin dashed line), ref. [39] (◇), ref. [34] (  ). The inset provides a comparison with theoretical data of ref. [45] (+ and dashed line), ref. [46] (
). The inset provides a comparison with theoretical data of ref. [45] (+ and dashed line), ref. [46] (  and dashed line), ref. [39] (
and dashed line), ref. [39] (  and dashed line), and ref. [50,108] (dot-dash line).
and dashed line), and ref. [50,108] (dot-dash line).
 ), ref. [29] (thin dashed line), ref. [39] (◇), ref. [34] (
), ref. [29] (thin dashed line), ref. [39] (◇), ref. [34] (  ). The inset provides a comparison with theoretical data of ref. [45] (+ and dashed line), ref. [46] (
). The inset provides a comparison with theoretical data of ref. [45] (+ and dashed line), ref. [46] ( 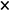 and dashed line), ref. [39] (
and dashed line), ref. [39] ( 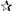 and dashed line), and ref. [50,108] (dot-dash line).
and dashed line), and ref. [50,108] (dot-dash line).
A comparison of both the experimental points and the fitted a(T) curve to literature data is documented in Figure 2b (for refined parameters of all models see Appendix C, Table A5, whereas the numerical a(T) data are quoted in Appendix B). The comparison based on this figure and on the recently reported experimental values near 0 K (data from refs. [29,44] quoted in Table 6) and near 300 K (data from refs. [26,29,31,34,39,41,42,43] quoted in Table 7), shows that the discrepancies between the present and earlier values of lattice parameter are quite small. Namely, near 0 K the discrepancy of the present a value, 6.42972(5) Å (the lattice parameter values given in this work with five decimal places refer to those obtained from fitted Equation (1) in this work and in the cited literature), with recent literature data, 6.42962 Å, is negligible (1 × 10−4 Å). As for the value at 300 K, our result of data fitting is 6.46148(87) Å. It agrees perfectly with the average of the high quality records for PbTe stored in the ICSD database [26] (the quality is based on ICSD-staff evaluation). There are five such records; their a(293 K) values are 6.462(1) Å, 6.459(1) Å, 6.461(1) Å, 6.461(1) Å, and 6.460(1) Å; the average is 6.46060(15) Å. After temperature correction from 293 to 300 K the average increases by 0.00088 Å (based on present a(T) results) leading to the ICSD derived value at 300 K to be 6.46148(15) Å. This value is identical to the above-quoted present one. All these perfect agreements point out both, the high quality of the sample and precision of applied measurement approach, including the instrument calibration. This observation can justify recommendation of the present a(T) run as a reference for the PbTe lattice parameter as a function of temperature; particularly in the near-RT temperatures, through interpolation of the data of Table A2 (Appendix B). The recommended a(300 K) value at 300 K is 6.46148(87) Å (thsi result is quoted together with other ones in Table 7).

Table 6.
Present and recently reported values of experimental lattice parameter, a, near 0 K for PbTe and Pb1−xCdxTe (x = 0.013, 0.056, 0.116). For complete numerical data of a(T) of this work, see Table A1 and Table A2 (Appendix B).

Table 7.
Present and selected recently reported values of the experimental lattice parameter, a, at room temperature for PbTe and Pb1−xCdxTe (x = 0.013, 0.056, 0.116). For complete numerical data of a(T) of this work, see Table A1 and Table A2 (Appendix B).
Also of interest is the compatibility of the experimental and theoretical data. Apparently, the shapes of the present (and other) experimental a(T) variations are generally in line with earlier theoretical ones reported in refs. [39,45,46], whereas the absolute values differ by only 0.3% [46] to 2% [45]. For the best matching data of ref. [46], the increase of the a value across the 15–300 K range is only slightly larger than those experimentally observed (see Figure 2b).
The fitted Equation (1) describing the unit-cell size as a function of temperature perfectly approximates the experimental runs of both crystals, as shown in Figure 2a. The lattice parameter of Pb0.884Cd0.116Te in the whole temperature range is reduced in respect to that of pure PbTe, and the reduction across the whole range is 0.53%, which is apparently larger than the value of 0.50% quoted at the beginning of this section for PbTe.
3.1.3. Variation of Thermal Expansion Coefficient with Temperature
For Pb0.884Cd0.116Te, the lattice parameter, according to the fitted model, increases from 6.37725(6) Å to 6.41133(116) Å. The difference in respect to PbTe in the slope of the cell-size dependence on temperature is visualized in Figure 2a, presenting the temperature variation of the cell volume for both studied crystals. The experimental dependence of the linear-thermal-expansion coefficient on temperature, α(T), was derived from the V(T) Grüneisen approximation (Equation (1)), using the equation:
α(T) = αV(T)/3 = (dV/dT)/(3V(T))
For both materials, the general character of the α(T) variation is typical, with a nearly constant value up to 10 K, and with a pronounced increase observed up to ~100 K; above this temperature, the rise progressively becomes much smaller. In the ~170–300 K range, the variation of α with temperature is weak and nearly linear.
For PbTe, the TEC dependence on temperature obtained in the present work shows a fairly good matching with experimental results based on different earlier exploited techniques: dilatometry [51] and neutron powder diffraction [29] (see Figure 3). In particular, the resulting experimental TEC value of 19.6(6) MK−1 obtained in this work at 300 K matches very well the earlier reported experimental values of 19.80 MK−1 [51] and 19.91 MK−1 [29] (cf. Table 8) (this discrepancy is as low as 1.5%).
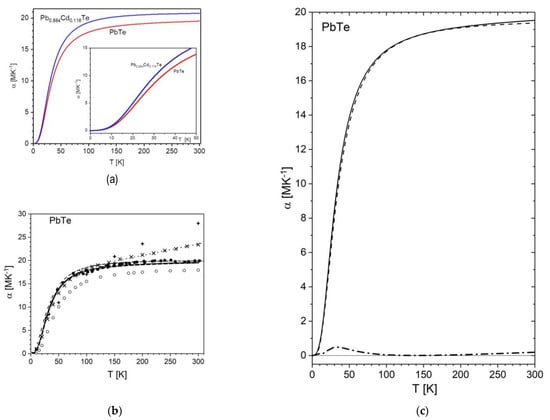
Figure 3.
Variation of thermal expansion with temperature, α(T). (a) The linear thermal expansion coefficient α(T) for PbTe and Pb0.884Cd0.116Te as a function of temperature, was obtained from the experimental-data fitting using a second order Grüneisen approximation (Equation (1)). The inset includes the magnified low-temperature part (0–50 K) of the α(T) run. (b) Comparison of the present data for PbTe (black solid line) with previously reported experimental and theoretical data of PbTe. Selected data from literature (from ref. [51] (●), [29] (black dashed line) (experimental), (from ref. [45] (+); [46] ( 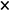 ), from ref. [8] (
), from ref. [8] (  ) (theoretical)) are shown. (c) Comparison of the present experimental data (solid line, also shown as (strongly overlapping) dotted line in (b)), theory [60,108] (dashed line), difference curve (dash-dot line).
) (theoretical)) are shown. (c) Comparison of the present experimental data (solid line, also shown as (strongly overlapping) dotted line in (b)), theory [60,108] (dashed line), difference curve (dash-dot line).
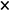 ), from ref. [8] (
), from ref. [8] (  ) (theoretical)) are shown. (c) Comparison of the present experimental data (solid line, also shown as (strongly overlapping) dotted line in (b)), theory [60,108] (dashed line), difference curve (dash-dot line).
) (theoretical)) are shown. (c) Comparison of the present experimental data (solid line, also shown as (strongly overlapping) dotted line in (b)), theory [60,108] (dashed line), difference curve (dash-dot line).

Table 8.
Present and selected literature values of the experimental thermal expansion coefficient, α, at 300 K for PbTe and Pb1−xCdxTe (x = 0.116). For full numerical data of α(T), see Table A2 (Appendix B).
A remarkable agreement of the present experimental thermal expansion data of PbTe is observed with the theory reported in ref. [50,108] (compare to the experimental and theoretical curves in Figure 3c). The agreement is visualized through the difference curve, and it is worth noting that the little bump of 2% height, observed at this curve would be twice as small if the temperature axis of the theoretical curve was shifted by only −0.7 K. The consistency with other theoretical data is not as perfect, but the trends of these results are generally compatible with the experiments described herein and others. In particular, the present data marginally differ from theoretical ones ref. [46] up to 100 K, whereas the discrepancy markedly increases at higher temperatures.
As for Pb0.884Cd0.116Te, the increase of the thermal expansion coefficient, α(T), in the studied temperature range is more pronounced than that observed for PbTe (Figure 3b). At 300 K, the coefficient reaches the value of 20.7(8) MK−1, the increase in respect to PbTe being about 6.5% at this temperature (the rise is comparable at lower temperatures).
3.1.4. Variation of Mean Square Displacements with Temperature
The temperature dependencies of experimental mean square isotropic atomic displacement parameters for cations and anions of PbTe and Pb0.884Cd0.116Te display an apparent monotonically increasing behavior with rising temperature (Figure 4).
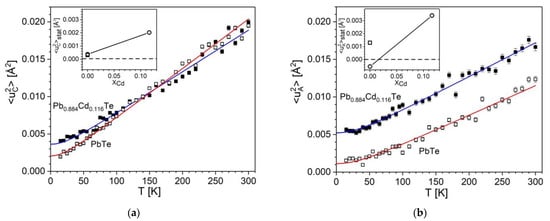
Figure 4.
Temperature dependence of mean square displacements for cations (a) and anions (b), for PbTe (  ) and Pb0.884Cd0.116Te (■). The fitted Debye function is represented by red and blue solid lines, respectively. The insets show the static disorder term <u2>stat as a function of Cd content, xCd (own results (
) and Pb0.884Cd0.116Te (■). The fitted Debye function is represented by red and blue solid lines, respectively. The insets show the static disorder term <u2>stat as a function of Cd content, xCd (own results (  ) with uncertainties smaller than symbol size, and results of ref. [29] (
) with uncertainties smaller than symbol size, and results of ref. [29] (  )).The horizontal dashed line visualizes the zero-disorder level.
)).The horizontal dashed line visualizes the zero-disorder level.
 ) and Pb0.884Cd0.116Te (■). The fitted Debye function is represented by red and blue solid lines, respectively. The insets show the static disorder term <u2>stat as a function of Cd content, xCd (own results (
) and Pb0.884Cd0.116Te (■). The fitted Debye function is represented by red and blue solid lines, respectively. The insets show the static disorder term <u2>stat as a function of Cd content, xCd (own results (  ) with uncertainties smaller than symbol size, and results of ref. [29] (
) with uncertainties smaller than symbol size, and results of ref. [29] (  )).The horizontal dashed line visualizes the zero-disorder level.
)).The horizontal dashed line visualizes the zero-disorder level.
The experimental data were modeled using Equation (4)
where the mean square displacement takes into account the temperature-dependent dynamic disorder term (Debye expression [109]) and the temperature-independent static disorder term <u2>stat in the same way as that used in ref. [110]. The first term at the right side, <u2>dyn(T), is the Debye function based on simplifying the assumption that takes into account the acoustic branches, whereas the optical branches are ignored:
<u2>(T) = <u2>dyn(T) + <u2>stat
In the above expression, T stands for temperature, m for atomic mass, θD for the Debye temperature, kB for the Boltzmann constant, and ħ for the reduced Planck constant. The second term in Equation (4), <u2>stat is an empirical term attributed to the temperature-independent static disorder that can be connected in unsubstituted crystals, e.g., with the presence of point defects [111] (the presence of such defects is known to influence the electrical and other properties of thermoelectric crystals [112]), and in substituted crystals-with the presence of foreign atoms at the cationic or anionic sites.
For both crystals, PbTe and Pb0.884Cd0.116Te, the results of fitting of <u2>(T) defined by Equation (4) correctly describe the run of experimental points (the refined parameters of the model are provided in Table A5). The MSD values referring to temperatures near 0 K and near 300 K are compared with literature data in Table 9 (for values of fitted MSDs see Table A1, Appendix B).

Table 9.
Present and selected reported experimental values of the mean square cationic and anionic displacements, <uC2>(T) and <uA2>(T), respectively, near 0 K and at room temperature for PbTe and Pb1−xCdxTe (x = 0.116). The (independent on temperature) static components, <uC2>stat and <uA2>stat, are provided, where available. For detailed numerical data of the present study, see Table A1 and Table A2, Appendix B.
The run of each <u2>(T) curve shows (i) a characteristic nearly linear dependence at high temperatures, having a specific slope, and with (ii) a curvilinear behavior at low temperatures, characterized by a value of <u2>(T = 0). Each of these features has its own meaning. The given curve representing either the cationic or anionic site has its own characteristics determined by the fixed material parameter m, by the Debye temperature, θD, and by the disorder term, <u2>stat. Basically, <u2>stat and θD are fittable parameters, and m could also be fitted if the composition was not well specified.
Examination of Figure 4 leads to following observations:
- (1)
- The fitted <u2>stat(T) curves for PbTe and Pb0.884Cd0.116Te behave differently. Namely:
- (a)
- The MSDs at 0 K, <u2>(T = 0), increase significantly (by about 0.002–0.004 Å2) with x rising from 0 to 0.116. We attribute this increase to the appearance of the static disorder expressed by the nonzero <u2>stat term resulting from fitting Equation (4) (the values of <u2>stat are quoted in Table 9). This effect is graphically presented in the insets of Figure 4a,b, where the variation of fitted <u2>stat values is displayed. Appearance of marginally small negative fitted value for anionic site in PbTe (instead of zero that represents the lack of disorder) is attributed to be the effect of imperfections of fitted <u2>(T) data points. The quoted values (Table 9) show that the disorder in the anionic sublattice is considerably higher than that at the cationic site. Summarizing, an increase of the static disorder term, <u2>stat, in Equation (4), from approximately zero to a value of the order of 3 × 10−3 Å2 is observed for the mixed crystal in respect to PbTe crystal. Namely, the rise is from 0.38(4) × 10−3 Å2 to 2.03(6) × 10−3 Å2 for cations, and from −0.54(7) × 10−3 Å2 (a value marginally different from zero) to 3.4(1) × 10−3 Å2 for anions.
- (b)
- At higher temperatures, the cationic MSDs are nearly equal for the two crystals, whereas the anionic ones differ markedly in the whole temperature range.
- (c)
- The slope of the cationic <u2>(T) curve decreases with rising x, whereas the anionic one apparently increases. The property of Equation (4) is that the slope of <u2>(T) is governed at high temperatures by the Debye temperature (for high slope the Debye temperature is low and vice versa; the corresponding θD values are discussed in detail in Section 3.3 and Section 4).
- (2)
- The MSDs for the cationic and anionic sites behave differently for x = 0 than for x = 0.116.
- (3)
- Comparison of Figure 4a,b shows that the cationic and anionic MSDs of Pb0.884Cd0.116Te are of comparable values in a broad temperature range. As this effect must depend on x, we expect that for x < 0.116, the <u2> values of anions are lower than those of cations, whereas for x > 0.116 (if the structure is stabilized), the anionic ones are higher.
A comparison of the MSDs for PbTe to literature data shows a similarity of runs with the detailed neutron-scattering based data [29,38] and with some other data based on X-ray diffraction [31,34,37] (see Figure 5). The differences in slopes of the quasilinear parts of experimental <u2>(T) runs can be connected with differences in the defect structure of studied single crystals and polycrystals.
Figure 5.
Temperature dependence of mean square displacements for PbTe for cations (a) and for anions (b). Experimental data: this work (solid line, ■), ref. [55] (◇), ref. [37] (  ), ref. [38] (△), ref. [31] (▽), ref. [57] (□), ref. [34] (●), ref. [29] (dashed line), ref. [39] (+). Theoretical data: ref. [58] (
), ref. [38] (△), ref. [31] (▽), ref. [57] (□), ref. [34] (●), ref. [29] (dashed line), ref. [39] (+). Theoretical data: ref. [58] (  ), and ref. [39] (dotted line).
), and ref. [39] (dotted line).
 ), ref. [38] (△), ref. [31] (▽), ref. [57] (□), ref. [34] (●), ref. [29] (dashed line), ref. [39] (+). Theoretical data: ref. [58] (
), ref. [38] (△), ref. [31] (▽), ref. [57] (□), ref. [34] (●), ref. [29] (dashed line), ref. [39] (+). Theoretical data: ref. [58] (  ), and ref. [39] (dotted line).
), and ref. [39] (dotted line).
Among the theoretical MSD data, a better matching above 50 K with our experiments is found for the most recent molecular-dynamics-based data of ref. [39]. Near 0 K, the present experimental values match well the theoretical data of refs. [58,59], as shown in Figure 5.
3.2. Effect of Substitution of Cd in the PbTe Lattice on Variation of Unit-Cell Size and of Bulk Modulus with Pressure
The in-situ high-pressure X-ray diffraction study was performed under pressures ranging up to 4.5 GPa. The NaCl-type structure found for PbTe and Pb0.884Cd0.116Te single crystals at ambient conditions (T = 295 K and p = 0.1 MPa) was conserved at the applied high-pressure conditions. The structure refinement yielded the lattice parameter monotonically varying with increasing pressure (for values see Table A3 in Appendix B).
In the analysis, the Birch–Murnaghan equation of state [104] was adopted. Its third-order variant is described by the following formula:
where p is the pressure, K0 is the bulk modulus, and K′ is the pressure derivative of the bulk modulus, is the Eulerian strain (V is the volume under pressure p, and V0 is the reference volume). When K′ = 4, Equation (6) is reduced to a simpler, second order equation, applied in the present study (an equation of the second order has also been used in a recently reported experimental diffraction study of PbTe [83]).
The experimental relative unit-cell volume is well approximated for both crystals as a function of pressure by BMESO equation (see Figure 6; numerical data of the model are quoted with 0.5 GPa step in Table A4). The resulting bulk modulus value for PbTe K0 is 45.6(2.5) GPa, which is consistent with previously reported values, in particular with those obtained from X-ray diffraction studies, 38.9 GPa [78,80] and 44(1) GPa [82] as well as with those from early ultrasonic wave velocity measurements of refs. [29,52,63,113], quoted in Table 10.
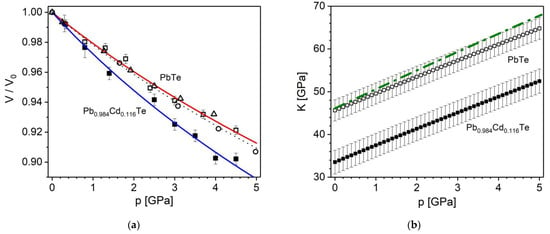
Figure 6.
(a) Relative unit-cell volume as a function of pressure, for PbTe (□), and Pb0.884Cd0.116Te (■). The solid lines correspond to the second-order BMEOS fit. Experimental literature data for PbTe are shown from ref. [83] (data (  ) and fit (dotted line), the theoretical ones from ref. [64] (△ and green dashed line). (b) Bulk modulus, K, dependence on pressure for PbTe (■) and Pb0.884Cd0.116Te (□) crystals (present data). as dash-dot line shows the theoretical data of [64].
) and fit (dotted line), the theoretical ones from ref. [64] (△ and green dashed line). (b) Bulk modulus, K, dependence on pressure for PbTe (■) and Pb0.884Cd0.116Te (□) crystals (present data). as dash-dot line shows the theoretical data of [64].
 ) and fit (dotted line), the theoretical ones from ref. [64] (△ and green dashed line). (b) Bulk modulus, K, dependence on pressure for PbTe (■) and Pb0.884Cd0.116Te (□) crystals (present data). as dash-dot line shows the theoretical data of [64].
) and fit (dotted line), the theoretical ones from ref. [64] (△ and green dashed line). (b) Bulk modulus, K, dependence on pressure for PbTe (■) and Pb0.884Cd0.116Te (□) crystals (present data). as dash-dot line shows the theoretical data of [64].

Table 10.
Fitted parameters of experimental equation of state for PbTe and Pb1−xCdxTe (x = 0.116) at various temperatures.
The bulk modulus values provided by theoretical studies [10,45,46,64,114,115,116,117] based mostly on different approximations of the density functional theory fall into the range from 38.54 GPa to 51.7 GPa (for more details, see Table 10 (experimental data) and Table A6 (theoretical data from refs. [9,10,45,46,47,64,65,66,67,86,114,116,117,118,119,120,121,122,123,124,125]).
The room-temperature bulk modulus of Pb0.884Cd0.116Te is found to be 33.5(2.8) GPa, providing the first experimental evidence that Cd substitution reduces the stiffness of the PbTe matrix. For both crystals, bulk modulus increases with pressure, in the range from 0.1 MPa to 4.5 GPa by about 50% (Figure 6, for numerical data see Table A4). For PbTe, the K(p) dependence is in line with the theoretical one reported in ref. [64].
3.3. Effect of Cd Substitution on Values of Debye Temperature
Modeling three variations, V(T), <u2>(T) and V(p), namely the V(T) variations using the second-order Grüneisen approximation (Equation (1)), the <u2>(T) variation involving the Debye expression (Equation (4)), and the V(p) variations using the BMEOS (Equation (6)) led to determination of the Debye temperature, θD. In general, θD is frequently considered as a quantity depending on temperature, but for PbTe, the reported θD variations are weak and are observed mostly at cryogenic temperatures [53,61]. In most studies, including those based on diffraction, θD is considered a temperature-independent quantity. For compounds of the NaCl structure, different θD values are reported for the cation and anion sublattices. Such distinction is possible thanks to fitting of atomic displacements of the given (cationic or anionic) sublattice using Equation (4). Consequently, from the given experiment, we get a single overall θD value from fitting V(T) and a pair of θD’s from fitting of <uC2>(T) and <uA2>(T) (the corresponding symbols θDV, θDUC, and θDUA are used here, respectively, to highlight the distinction between these three θD definitions), whereas the overall θDU denotes the average of θDUC and θDUA.
The present overall θD values for PbTe (θDV and θDU) are almost identical (135.2(3.8) K and 135.9(7) K; the average is ~135.5 K). The Debye temperature for cation and anion sublattices in PbTe is θDUC = 102.8(3) K and θDUA = 169(1) K. For PbTe, there are a number of articles reporting the Debye temperature values. Selected literature data are collected in Table 11 (experimental X-ray diffraction and neutron diffraction based data from refs. [29,31,41,55,56]). Non-diffraction-based experimental data quoted in Table 12 are taken from refs. [13,52,61,63,126,127,128,129,130,131,132]). For theoretical data, see Table 13 providing the values from refs. [9,29,47,57,133,134]).

Table 11.
Values of experimental Debye temperature θD determined by XRD/ND for PbTe and Pb1−xCdxTe (x = 0.116) and earlier reported experimental values for PbTe: data θDUC and θDUA refer to values determined for cationic and anionic sublattices, respectively.

Table 12.
Experimental Debye temperature, θD, determined by non-diffraction methods for PbTe.

Table 13.
Reported theoretical values of Debye temperature, θD, for PbTe and Pb1−xCdxTe (x = 0.031, 0.116).
The earliest diffraction-based studies of PbTe have reported a relatively low overall Debye temperature of PbTe, about 110 K [55,56]. Our overall θDU and θDV values for the PbTe sublattices are in line with those determined in ref. [29] by both neutron powder and single crystal X-ray diffraction.
The variation of the direction of overall of (small) θD changes appearing with Cd substitution is indicated by θDV reduction by 5.1 K. A small reduction of Debye temperature for Pb0.884Cd0.116Te (θDV = 130.1(4.4) K) in comparison with that for PbTe, θDV = 135.2(3.8) K, is observed.
The present overall θD values are also in line with the trends observed for those obtained by the non-diffraction methods in Table 12 (their average calculated for room-temperature data is 138.1 K, i.e., only 3 K larger than our value. The theoretical methods provided overall values with a higher average (Table 13) of 157.9 K, these data vary in an extended range.
The here-obtained cationic and anionic Debye temperature values are close to those obtained by neutron diffraction θDUC = 99.6(2) K and θDUA = 156.0(5) K [29] (the discrepancy is less than 8%). The results collected in Table 11 (the present one and those reported earlier) document that the cationic values determined in different laboratories are in very good agreement (between 95.5 and 102.8 K), whereas those for anions exhibit a larger scatter between 127 and 169 K. The θDUC and θDUA behave in an opposite way (the former rises, the latter decreases). Interestingly, the contribution of lighter Cd atoms at the Pb sites leads to a reduction of the difference between the cationic and anionic site from 66.2 K for the pure PbTe to 42.9 K in the mixed crystal.
Exploiting the data obtained in this work, the Grüneisen parameter, γ, variation with temperature was evaluated using the formula (see ref. [29] and refs. therein):
where α is the thermal expansion coefficient, K0 is the bulk modulus, and cv describes the isochoric heat capacity. In calculations, the α(T) and Vm(T) based on experimental results obtained in this work were used. The K0(T) variation reported in ref. [29] for PbTe was rescaled to the present K0 at room temperature equal 45.6(2.5) GPa for the PbTe sample and to 33.5(2.8) GPa for the Pb0.884Cd0.116Te sample (for Pb0.884Cd0.116Te we adopted the rescaled K0(T) dependence of PbTe of ref. [29]). For PbTe, the temperature variation of the molar isochoric capacity cv(T) was taken from ref. [29], whereas for the Cd substituted sample the theoretical cv(T) data of Pb0.88Cd0.12Te [68] were used. The dependencies obtained in this way are shown in Figure 7.
γ(T) = α(T)K0(T)Vm(T)/cv(T)
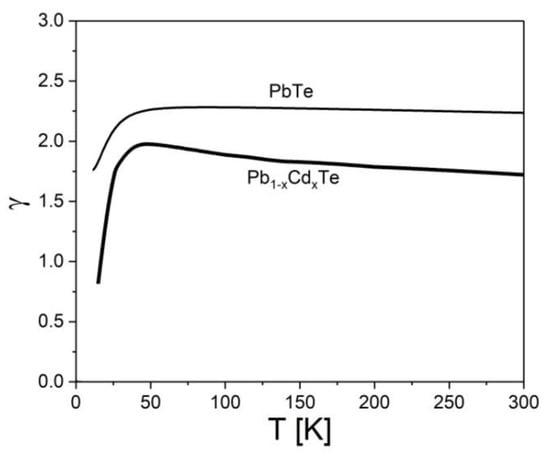
Figure 7.
The temperature variation of the Grüneisen parameter for PbTe and Pb0.884Cd0.116Te in the ranges 10–300 K and 15–300 K, respectively. The thin and the thick lines refer to PbTe and Pb0.884Cd0.116Te, respectively.
The obtained γ(T) dependence for PbTe is comparable with those reported in refs. [51] with value of about 1.5 in the range 30–340 K and ref. [29] with values of about 2.1–2.2 in the range 50–260 K. The parameter γ is frequently considered a constant. Its experimental constant value determined by X-ray diffraction is reported to be 2.03 [29], whereas the sound velocity method has given a result of 0.95 [63] and the ultrasonic wave velocity method, 1.96 [13]. Theoretical values obtained by the density functional theory are 1.96– 2.18 [45], whereas the molecular dynamics yielded γ = 1.66 [117]. Interestingly, the present results and some of those referring to constant γ consistently suggest that its value is close to 2, whereas the roughly evaluated data on the mixed crystal indicate some decrease of gamma due to Cd substitution (see Figure 7).
The reliability of the γ values at the lowest temperatures, as calculated from Equation (7) depends on the accuracy of the very small, divided values of α and cv, therefore the reduction of γ below ~50 K displayed in Figure 7 may be questioned.
4. Discussion
The results on the thermostructural and elastic properties of rocksalt-type crystals, PbTe and Pb0.884Cd0.116Te solid solution, described in Section 3, are derived from X-ray diffraction data through fitting of Equations (1), (4) and (6). Temperature dependencies of the lattice parameter, a(T), the thermal expansion coefficient, α(T), and the mean square displacements, <u2>(T), are determined for both crystals from X-ray diffraction powder diffraction data. These results for PbTe are consistent with recent literature data, in particular with the most detailed ones [29,31]. Moreover, the diffraction study of the equation of state, V(p), provided the value of the PbTe bulk modulus dependence on pressure. The reliability of the present results is verified by the demonstrated close agreement of the a(T), α(T) and <u2>(T) dependencies, as well as of the Debye temperature and bulk modulus variation, for PbTe with earlier experimental and theoretical data. It is also worth noting that the fitted model curves for a(T), <u2>(T) and V(p) dependencies match well the experimental points, therefore we do not expect occurrence of significant systematic errors which could add to the statistical errors quoted in Table A3 and Table A4.
For Pb0.884Cd0.116Te, the obtained results are novel, they describe the thermal characteristics of this crystal and indicate the direction and magnitude of variation of the considered temperature-dependent properties with rising content of Cd at the cationic site. In other words, the earlier unknown effect of sharing the cationic sites by Pb and Cd atoms on thermal properties is revealed.
In Section 3, it is shown that the results on the PbTe lattice parameter, a(T), are of high accuracy, as judged by the perfect agreement of PbTe data with the earlier-reported neutron powder diffraction data of ref. [29]. Moreover, the a value at 300 K is ideally equal to that derived from high-quality ICSD records [26]. Based on the analysis of the literature data, we show that the values of 6.42972(5) Å and 6.46148(87) Å are good candidates for the reference lattice parameter of PbTe at 0 and 300 K, respectively. The Pb0.884Cd0.116Te sample shows a similar behavior with temperature. The a(T) run for Cd-substituted PbTe crystal depends on the amount of substituent (as can be deduced from a comparison with earlier results for lower Cd content [42,43,44]). A related influence of substituent on the a(T) runs is observed for Na and Eu substituted PbTe crystals [41]. In the above-cited results, which refer to temperatures exceeding the room temperature, the deviations from regular behavior indicate the decomposition of a metastable mixed crystal.
The here-obtained thermal expansion data for PbTe match other experimental data, especially those of ref. [29] (the discrepancy does not exceed (3%)). Unexpectedly, we found a surprisingly perfect agreement with data from ref. [50,108] in the whole studied temperature range. This agreement clearly suggests that both the present measurements and cited theory yielded accurate results for temperatures ranging up to 300 K. The fractional substitution of Cd atoms at the Pb site results in a discernible increase of the linear thermal expansion coefficient value. In particular, the value at 300 K is 19.6(6) MK−1 for PbTe and 20.7(8) MK−1 for Pb0.884Cd0.116Te: thus, the expansion rises by 6.2% at this temperature.
The investigation of mean square displacements (independently, the cationic and anionic ones) shows their nearly linear variation with rising temperature, except for the lowest temperatures (see Figure 4 and Figure 5). This finding confirms, for the PbTe sample, the behavior known from earlier neutron diffraction and X-ray diffraction studies such as those described in refs. [29,31]. For Pb0.884Cd0.116Te, the cationic MSDs are comparable to those of PbTe, except in the region of the lowest temperatures. The Cd substitution causes apparent increase of the anionic MSDs. This increase is expected to be proportional to the Cd content.
In fitting the Equation (4), the <u2>stat term describing the static disorder was determined, for both, cationic and anionic sublattices, in the unsubstituted and substituted crystal. As expected, the fitting for PbTe gave <u2>stat a value close to zero, thus indicating that there is no significant disorder in this crystal (small values have also been reported in refs. [29,31]). We believe that the differences between the, values reported for pure PbTe by different groups can probably be attributed to differences in the defects’ kind and density.
The observed increase of the <u2>stat term after incorporating Cd into the PbTe lattice proves that alloying causes appearance of substitutional disorder in the mixed Pb0.884Cd0.116Te. crystal. We observe (see the insets in Figure 4) that the values of cationic and anionic <u2>stat terms describing the static disorder are markedly different in the Pb0.884Cd0.116Te. crystal. Namely, the anionic disorder is significantly larger in this crystal.
The here-reported extraction the information on disorder for both, cationic and anionic sublattices, in a mixed PbTe based crystal, is an important novelty (previously, such calculations have been performed for pure PbTe, only). We notice a significant increase of the static disorder term, showing that information of this kind, extracted from analysis of carefully measured thermostructural properties, can be useful in future studies on IV-VI thermoelectric solid solutions and their application, because the disorder in solid solutions can affect the carrier mobility, electrical conductivity [32,35] and thermal conductivity [31,117] influencing the Seebeck coefficient. We evaluate that the opportunity for detection of disorder can concern low substituent fraction, even much less that x = 0.1 studied in the present work.
For both crystals, the in situ high-pressure single-crystal XRD experiment provided information on the lattice parameter variation for PbTe and Pb0.884Cd0.116Te, at pressures ranging up to 4.5 GPa. The observed pressure variation is in line with a theoretical result reported in ref. [64]. Modeling of the BMEOS led to determination of the bulk modulus and its pressure variation. At 0.1 MPa, the bulk modulus value is 45.6(2.5) for PbTe, well coinciding within error bars with the value 44(1) GPa reported in the most recent diffraction study [83]. The bulk modulus value significantly decreases with rising Cd content; in other words, the Cd substitution leads to a crystal of lower stiffness.
There are a number of theoretical works investigating the bulk modulus changes upon substitution of an element at the cationic site [8,9,123]; most typically, a reduction is predicted. In ref. [9], for 62 elements fractionally substituting Pb in PbTe, the resulting bulk modulus value is calculated; the same calculation is performed for nine substituents at an anionic Te site. For almost all of them, the bulk modulus is reduced; whereas for V, Nb, Ni and Bi, the K0 value is larger than the calculated value of 46.61 GPa [9] for pure PbTe.
In ref. [9], the K0 has been predicted to decrease from 46.61 GPa for PbTe to 46.42 GPa for Pb0.969Cd0.031Te. This leads to 45.90 GPa evaluated through extrapolation for Pb0.884Cd0.116Te. This evaluation differs from the experimental value obtained in the present study (33.5(2.8) GPa), but the direction of changes of K0 with x is clear.
Experimental K0 values for PbTe substituted with any cation are not available, except for the case of Ba substitution, where the mixing effect on K0 consists of a 5% reduction of the PbTe value [6]. The assumption that K0(PbTe) equals 46.61 GPa leads to an evaluation of a (not explicitly reported) experimental value, 44.3 GPa for Pb0.96Ba0.04Te. Extrapolation of the theoretical value of 44.99 GPa for Pb0.969Ba0.031Te quoted in ref. [9] leads to K0 = 44.5 GPa for Pb0.96Ba0.04Te. The excellent agreement between the values of calculated 44.3 GPa and experimental 44.5 GPa points out the reliability of both, the cited experiment and the calculation.
The above-described fittings of V(T) and <u2>(T) models led to the determination of values of Debye temperature, θD, for both crystals. Together with the Cd substitution, a small reduction of the overall Debye temperature, θDU, from 135.2(3.8) K to 130.1(4.4) K (i.e., a reduction of 5.1 K) is observed. Theoretical calculations predict reduction by 2.4 K for the composition of x = 0.031 [9]. Extrapolating this result to the composition of the mixed crystal studied in this work, (x = 0.116) gives a prediction of a 9 K (difference between θD = 187.8 1 K and 178.8 K quoted in Table 13) reduction of the theoretical overall θD. This theoretical result supports the observed trend of reduction of overall Debye temperature by increasing the cadmium content. Interestingly, the θD values reported by different authors for the cationic sublattice are in perfect agreement, whereas those for the anionic one are scattered. The influence of Cd substitution on Debye temperatures of cationic and anionic sublattices, described in Section 3.3, is not uniform; these values differ markedly for PbTe, but the difference is reduced for the Cd substituted crystal.
The observed influence of Cd substitution into PbTe lattice on the thermostructural and elastic properties studied can serve as a basis for evaluation of such features for crystals of different Cd content. They can also be useful in studies of more complex systems, such as those with dual cationic/anionic substitutions. As it is noted in ref. [30], various factors influence the Seebeck coefficient value. One of the ways to optimize this value consists of alloying with a selected element, which means a decrease or increase of the atomic order. It is equally possible to investigate other, more complex systems, for example those with less-conventional doubly substituted cationic systems, such as Na0.03Eu0.03Pb0.94Te [112]. The joint cationic/anionic substitution (Pb,Cu)(Se,Te) system has also been studied, providing another example of a dual system [135]. Mixed bi-cationic–bi-anionic systems such as Na0.03Eu0.03Pb0.94Te0.9Se0.1 [112] are the subject of studies as well. It is noteworthy that upon replacing the Te anion by Se or S, the bond ionicity decreases (for the ionicity scale, see ref. [136]). Along the PbTe, PbSe, PbS series, some of the thermostructural/elastic properties (studied here for PbTe) vary monotonically; for example, the lattice parameter (see Figure 1 at x = 0), bulk modulus [46,85,114] and phase transition pressure [77,85].
5. Conclusions
PbTe of a rocksalt-type structure belongs to a family of thermoelectric materials. A modification of composition, typically by fractional substitution of an element such as Cd, at the Pb cation site, is known to improve the thermoelectric properties. In this work, the combined low-temperature–high-pressure study carried out here describes the effect of sharing the cationic sites by Pb and Cd atoms on the above-mentioned properties. These properties were derived for two samples, PbTe and Pb0.884Cd0.116Te, from X-ray diffraction data collected at varying temperature and pressure.
The dependencies of the lattice parameter, a(T), the thermal expansion coefficient, α(T), and the mean square displacements, <u2>(T), are determined for both crystals. For PbTe, these results and thermal expansion are fully consistent with results of earlier X-ray diffraction, neutron diffraction, dilatometric and other experimental studies, as well as with those of multiple theoretical investigations, and this agreement supports the reliability of the data collected.
The experimental variation of the lattice parameter with temperature was modeled using the Grüneisen-approximation approach whereas the variation of mean square atomic displacements was modeled using the Debye expression. In addition, the equations of state were determined for pressures ranging up to 4.5 GPa, allowing conclusions to be drawn about the value of the bulk modulus and its variations under rising pressure and with varying Cd substitution.
The thermostructural and elastic properties for Pb0.884Cd0.116Te crystal determined in the present study indicate the direction and magnitude of variation of the characteristics of Pb1−xCdxTe system with rising x. The stiffness of the alloy is smaller than that of pure PbTe, the thermal expansion is larger throughout the whole temperature range, and the atomic mean-square displacements change with Cd substitution in a complex way, indicating (i) opposite variations of the Debye temperatures for both sublattices, as well as (ii) the appearance of substitutional disorder in the mixed crystal.
In summary, the study presents detailed quantitative information on the thermostructural and elastic properties of rocksalt-type crystals of PbTe and Pb0.884Cd0.116Te; such data are not yet available for alloys of the Pb1−xCdxTe system. The obtained results show a consistent image of influence of the partial substitution of Pb ions by Cd ions, in the PbTe lattice, on the thermostructural properties. Namely, the obtained results show how the lattice parameter, the thermal expansion coefficient, the atomic mean-square displacements and other thermostructural properties (compressibility, Debye temperature, Grüneisen parameter and others) depend on the cadmium content. In particular it was found, that the Pb0.884Cd0.116Te lattice is less stiff than that of PbTe, whereas thermal expansion of the mixed crystal is discernibly larger. The described extension of the knowledge on the studied properties is expected to be profitable in a further work on the application of the fractionally substituted Cd lead telluride.
Author Contributions
Conceptualization, R.M. and W.P.; methodology, A.K., A.S., F.S., R.M., W.P. and W.S.; software, R.M.; investigation, A.B., A.K., A.S., E.D., F.S., R.M. and W.S.; writing—original draft preparation, R.M. and W.P.; writing—review and editing, R.M. and W.P.; supervision, W.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the National Science Centre (NCN, Poland) under grant UMO-2014/13/B/ST3/04393. The study of R.M. and A.S. has been partially supported by the National Science Centre for Development (Poland) through grant TERMOD No. TECHMATSTRATEG2/408569/5/NCBR/2019.
Acknowledgments
The authors are grateful to José D. Querales-Flores (National Institute, Lee Maltings, Cork, Ireland) for providing the numerical data of ref. [50].
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
| APW | augmented plane-wave |
| BMEOS | Birch-Murnaghan Equation of State |
| CDM | crystal dynamics models |
| CM | calorimetry |
| DFPT | density functional perturbation theory |
| DFT | density functional theory |
| DM | dilatometry |
| DPS | double parton scattering (nuclear inelastic scattering) |
| EC | elastic constants |
| FP | full potential |
| FPBTF | first principles Boltzmann transport framework |
| GGA | generalized gradient approximation |
| GULP | computer program for the symmetry adapted simulation of solids, authored by Julian D. Gale |
| HPM | heat-pulse method |
| HS | hydrostatic conditions |
| HSEsolSOC | revised Heyd-Scuseria-Ernzerhof functional + spin-orbit coupling |
| LAPW | linearized augmented plane-wave |
| LDA | local density approximation |
| LDY | lattice dynamics calculations |
| LEDPXRD | laboratory energy-dispersive X-ray diffraction |
| LKF | Lin-Kleinman formalism |
| LSCXRD | laboratory single-crystal X-ray diffraction |
| MD | molecular dynamics |
| MSD | mean square displacement |
| n.a. | not available |
| ND | neutron diffraction |
| NNI | nearest-neighbor interaction model by Kagan and Maslow |
| NPD | neutron powder diffraction |
| NS | neutron scattering |
| PAW | projector augmented wave method |
| PBE | Perdew-Bucke-Ernzerhof exchange-correlation functional |
| PBEsol | Perdew–Bucke–Ernzerhof exchange-correlation functional revised for solids |
| PM | the paramagnetic resonance. θD estimated by the temperature-dependent hyperfine splitting constant A(T) |
| PTW | plane temperature waves method |
| QHA | quasiharmonic approximation |
| QHS | quasi-hydrostatic conditions |
| RT | room temperature |
| SCXRD | single crystal X-ray diffraction |
| SCXRDS | single crystal X-ray difraction at synchrotron |
| SO | soft-constraint based online |
| SME | slave mode expansion |
| SP | spectroscopy |
| SPXRD | synchrotron powder X-ray diffraction |
| SV | sound velocity method |
| TC | thermal conductivity |
| TEC | thermal expansion coefficient |
| THD | thermodynamic calculations |
| UPE | ultrasonic pulse-echo method |
| UIM | ultrasonic interferometry |
| UWV | ultrasonic wave velocity |
| UWVSC | ultrasonic wave velocity in single crystal |
| XRD/ND/PDF | X-ray diffraction and neutron diffraction, analyzed with pair distribution function (PDF) method |
Appendix A
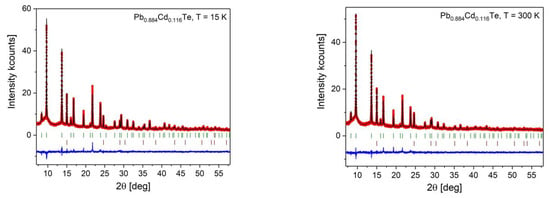
Figure A1.
Rietveld refinement results for PbTe (upper row) and Pb0.884Cd0.116Te (bottom row) at 15 K and 300 K. The experimental points are indicated by dots and the calculated patterns by the solid line. The positions of Bragg reflections of the sample are indicated as short vertical bars at the bottom (upper row), and those of the diamond calibrant (lower row). The difference patterns are displayed at the bottom of each subfigure.
Appendix B

Table A1.
Present a(T) and <u2>(T), obtained from Rietveld refinements for PbTe and Pb0.884Cd0.116Te.
Table A1.
Present a(T) and <u2>(T), obtained from Rietveld refinements for PbTe and Pb0.884Cd0.116Te.
| T [K] | PbTe | Pb0.884Cd0.116Te | ||||
|---|---|---|---|---|---|---|
| a [Å] | <uC2> [Å2] | <uA2> [Å2] | a [Å] | <uC2> [Å2] | <uA2> [Å2] | |
| 15 | 6.4298(4) | 0.0020(1) | 0.0016(2) | 6.3775(5) | 0.0041(2) | 0.0057(3) |
| 20 | 6.4299(3) | 0.0027(1) | 0.0018(2) | 6.3773(4) | 0.0041(2) | 0.0055(3) |
| 25 | 6.4301(3) | 0.0024(1) | 0.0018(2) | 6.3776(5) | 0.0047(2) | 0.0055(3) |
| 30 | 6.4301(4) | 0.0028(1) | 0.0016(2) | 6.3777(5) | 0.0046(2) | 0.0052(3) |
| 35 | 6.4305(4) | 0.0030(1) | 0.0018(2) | 6.3783(5) | 0.0047(2) | 0.0055(3) |
| 40 | 6.4310(4) | 0.0037(1) | 0.0010(2) | 6.3787(7) | 0.0046(2) | 0.0059(3) |
| 45 | 6.4312(3) | 0.0036(1) | 0.0019(2) | 6.3792(6) | 0.0053(2) | 0.0058(3) |
| 50 | 6.4316(3) | 0.0038(1) | 0.0021(2) | 6.3793(6) | 0.0054(2) | 0.0060(3) |
| 55 | 6.4323(3) | 0.0044(1) | 0.0027(2) | 6.3800(7) | 0.0053(2) | 0.0066(3) |
| 60 | 6.4327(3) | 0.0047(1) | 0.0021(2) | 6.3805(5) | 0.0047(2) | 0.0067(3) |
| 65 | 6.4333(3) | 0.0052(1) | 0.0024(2) | 6.3810(7) | 0.0054(2) | 0.0064(3) |
| 70 | 6.4338(3) | 0.0059(1) | 0.0026(2) | 6.3817(6) | 0.0056(2) | 0.0071(3) |
| 75 | 6.4342(5) | 0.0057(2) | 0.0029(2) | 6.3823(5) | 0.0072(2) | 0.0072(3) |
| 80 | 6.4347(5) | 0.0058(2) | 0.0025(2) | 6.3829(6) | 0.0071(2) | 0.0074(3) |
| 85 | 6.4350(3) | 0.0062(1) | 0.0034(2) | 6.3833(5) | 0.0069(2) | 0.0084(3) |
| 90 | 6.4358(4) | 0.0064(2) | 0.0034(2) | 6.3840(4) | 0.0078(2) | 0.0077(3) |
| 95 | 6.4364(5) | 0.0072(2) | 0.0035(3) | 6.3848(4) | 0.0075(2) | 0.0087(3) |
| 100 | 6.4371(4) | 0.0074(2) | 0.0026(3) | 6.3855(4) | 0.0079(2) | 0.0089(3) |
| 110 | 6.4381(3) | 0.0083(2) | 0.0034(2) | 6.3863(5) | 0.0085(2) | 0.0079(4) |
| 120 | 6.4394(3) | 0.0092(2) | 0.0043(3) | 6.3875(4) | 0.0094(2) | 0.0092(4) |
| 130 | 6.4408(4) | 0.0095(2) | 0.0044(3) | 6.3891(4) | 0.0095(2) | 0.0094(3) |
| 140 | 6.4418(4) | 0.0100(2) | 0.0060(3) | 6.3903(4) | 0.0099(2) | 0.0097(4) |
| 150 | 6.4429(3) | 0.0111(2) | 0.0057(3) | 6.3915(4) | 0.0102(2) | 0.0104(4) |
| 160 | 6.4440(3) | 0.0117(2) | 0.0059(3) | 6.3931(5) | 0.0115(2) | 0.0115(4) |
| 170 | 6.4451(3) | 0.0120(2) | 0.0069(3) | 6.3941(5) | 0.0108(2) | 0.0129(4) |
| 180 | 6.4466(3) | 0.0118(2) | 0.0064(3) | 6.3953(5) | 0.0117(2) | 0.0103(4) |
| 190 | 6.4477(3) | 0.0133(2) | 0.0073(3) | 6.3969(5) | 0.0121(2) | 0.0129(4) |
| 200 | 6.4491(4) | 0.0144(2) | 0.0072(3) | 6.3981(5) | 0.0127(2) | 0.0132(4) |
| 210 | 6.4503(3) | 0.0147(2) | 0.0070(3) | 6.3997(4) | 0.0132(2) | 0.0131(4) |
| 220 | 6.4514(4) | 0.0142(2) | 0.0097(3) | 6.4007(5) | 0.0137(3) | 0.0138(4) |
| 230 | 6.4527(3) | 0.0167(2) | 0.0085(3) | 6.4020(4) | 0.0156(3) | 0.0137(4) |
| 240 | 6.4539(3) | 0.0170(3) | 0.0088(3) | 6.4035(3) | 0.0170(3) | 0.0135(4) |
| 250 | 6.4552(3) | 0.0166(2) | 0.0096(3) | 6.4045(3) | 0.0173(3) | 0.0153(4) |
| 260 | 6.4564(3) | 0.0171(2) | 0.0094(3) | 6.4062(3) | 0.0160(3) | 0.0148(4) |
| 270 | 6.4578(3) | 0.0180(3) | 0.0109(4) | 6.4071(3) | 0.0192(3) | 0.0160(5) |
| 280 | 6.4588(3) | 0.0192(3) | 0.0111(4) | 6.4086(4) | 0.0171(3) | 0.0165(5) |
| 290 | 6.4602(3) | 0.0178(3) | 0.0123(4) | 6.4100(4) | 0.0188(3) | 0.0176(5) |
| 300 | 6.4616(3) | 0.0195(3) | 0.0124(4) | 6.4116(4) | 0.0200(3) | 0.0166(5) |

Table A2.
Present values of a(T), α(T) and <u2>(T), modeled by Equations (1) and (2) for PbTe and Pb0.884Cd0.116Te.
Table A2.
Present values of a(T), α(T) and <u2>(T), modeled by Equations (1) and (2) for PbTe and Pb0.884Cd0.116Te.
| T [K] | PbTe | Pb0.884Cd0.116Te | ||||||
|---|---|---|---|---|---|---|---|---|
| a [Å] | α [MK−1] | <uC2> [Å2] | <uA2> [Å2] | a [Å] | α [MK−1] | <uC2> [Å2] | <uA2> [Å2] | |
| 0 | 6.42972(5) | 0 | 0.0021(1) | 0.0011(1) | 6.37725(6) | 0 | 0.0036(1) | 0.0052(1) |
| 10 | 6.42973(5) | 0.70(7) | 0.0022(1) | 0.0012(1) | 6.37726(6) | 0.9(1) | 0.0037(1) | 0.0053(1) |
| 20 | 6.42986(6) | 4.2(3) | 0.0025(1) | 0.0013(1) | 6.37742(7) | 5.0(4) | 0.0040(1) | 0.0054(1) |
| 30 | 6.43026(9) | 8.5(4) | 0.0030(1) | 0.0015(1) | 6.37788(11) | 9.8(6) | 0.0043(1) | 0.0056(1) |
| 40 | 6.43091(12) | 11.7(4) | 0.0035(1) | 0.0017(1) | 6.37861(15) | 13.2(6) | 0.0048(1) | 0.0059(1) |
| 50 | 6.43173(15) | 13.9(4) | 0.0041(1) | 0.0020(1) | 6.37952(18) | 15.4(6) | 0.0052(1) | 0.0062(1) |
| 60 | 6.43266(17) | 15.3(4) | 0.0047(1) | 0.0023(1) | 6.38054(22) | 16.9(5) | 0.0057(1) | 0.0066(1) |
| 70 | 6.43367(20) | 16.2(4) | 0.0053(1) | 0.0027(1) | 6.38165(25) | 17.8(5) | 0.0062(1) | 0.0070(2) |
| 80 | 6.43474(22) | 16.9(4) | 0.0059(1) | 0.0030(1) | 6.38281(28) | 18.5(5) | 0.0068(1) | 0.0074(2) |
| 90 | 6.43584(24) | 17.4(4) | 0.0066(1) | 0.0033(1) | 6.38400(31) | 19.0(5) | 0.0072(2) | 0.0079(2) |
| 100 | 6.43697(27) | 17.8(4) | 0.0072(1) | 0.0037(1) | 6.38523(35) | 19.3(5) | 0.0078(2) | 0.0083(2) |
| 110 | 6.43812(29) | 18.0(4) | 0.0079(1) | 0.0041(1) | 6.38647(38) | 19.6(5) | 0.0084(2) | 0.0087(2) |
| 120 | 6.43929(31) | 18.3(4) | 0.0085(1) | 0.0045(1) | 6.38773(41) | 19.8(5) | 0.0089(2) | 0.0091(2) |
| 130 | 6.44047(34) | 18.5(4) | 0.0092(1) | 0.0049(1) | 6.38900(44) | 20.0(5) | 0.0095(2) | 0.0096(2) |
| 140 | 6.44167(36) | 18.6(4) | 0.0098(1) | 0.0052(2) | 6.39028(47) | 20.1(5) | 0.0100(2) | 0.0100(2) |
| 150 | 6.44287(39) | 18.7(4) | 0.0105(1) | 0.0056(2) | 6.39157(51) | 20.2(5) | 0.0106(2) | 0.0105(2) |
| 160 | 6.44408(41) | 18.8(4) | 0.0111(1) | 0.0060(2) | 6.39287(54) | 20.3(6) | 0.0111(2) | 0.0109(2) |
| 170 | 6.44529(44) | 18.9(4) | 0.0118(1) | 0.0064(2) | 6.39417(58) | 20.4(6) | 0.0117(2) | 0.0113(2) |
| 180 | 6.44652(47) | 19.0(4) | 0.0125(1) | 0.0068(2) | 6.39547(62) | 20.4(6) | 0.0122(3) | 0.0118(2) |
| 190 | 6.44774(50) | 19.1(4) | 0.0131(1) | 0.0072(2) | 6.39678(66) | 20.5(6) | 0.0128(3) | 0.0122(2) |
| 200 | 6.44898(53) | 19.1(5) | 0.0138(1) | 0.0076(2) | 6.39809(70) | 20.5(6) | 0.0133(3) | 0.0127(3) |
| 210 | 6.45021(56) | 19.2(5) | 0.0144(1) | 0.0080(2) | 6.39941(74) | 20.6(6) | 0.0139(3) | 0.0131(3) |
| 220 | 6.45145(59) | 19.3(5) | 0.0151(1) | 0.0084(2) | 6.40073(78) | 20.6(7) | 0.0144(3) | 0.0136(3) |
| 230 | 6.45270(62) | 19.3(5) | 0.0158(1) | 0.0088(2) | 6.40205(82) | 20.6(7) | 0.0150(3) | 0.0140(3) |
| 240 | 6.45394(65) | 19.3(5) | 0.0164(1) | 0.0091(2) | 6.40337(87) | 20.7(7) | 0.0156(3) | 0.0145(3) |
| 250 | 6.45519(69) | 19.4(5) | 0.0171(1) | 0.0095(2) | 6.40469(91) | 20.7(7) | 0.0161(3) | 0.0149(3) |
| 260 | 6.45644(72) | 19.4(5) | 0.0177(1) | 0.0099(2) | 6.40602(96) | 20.7(7) | 0.0167(3) | 0.0154(3) |
| 270 | 6.45770(76) | 19.5(6) | 0.0184(1) | 0.0103(2) | 6.40734(100) | 20.7(8) | 0.0172(4) | 0.0158(3) |
| 280 | 6.45896(79) | 19.5(6) | 0.0191(1) | 0.0107(2) | 6.40867(105) | 20.7(8) | 0.0178(4) | 0.0163(3) |
| 290 | 6.46022(83) | 19.5(6) | 0.0197(2) | 0.0111(2) | 6.41000(110) | 20.7(8) | 0.0183(4) | 0.0167(3) |
| 300 | 6.46148(87) | 19.6(6) | 0.0204(2) | 0.0115(2) | 6.41133(116) | 20.7(8) | 0.0189(4) | 0.0172(3) |

Table A3.
Present high-pressure V(p) data from single-crystal structure refinement for PbTe and Pb0.884Cd0.116Te.
Table A3.
Present high-pressure V(p) data from single-crystal structure refinement for PbTe and Pb0.884Cd0.116Te.
| PbTe | Pb0.884Cd0.116Te | ||
|---|---|---|---|
| p [GPa] | V [Å3] | p [GPa] | V [Å3] |
| 0.33(2) | 271.1(15) | 0.30(2) | 265.40(50) |
| 0.80(2) | 267.9(12) | 0.80(2) | 261.10(80) |
| 1.30(2) | 266.8(15) | 1.40(2) | 256.50(16) |
| 1.80(2) | 264.8(16) | 2.50(2) | 251.78(10) |
| 2.40(2) | 259.5(16) | 3.00(2) | 247.41(12) |
| 3.00(2) | 257.2(15) | 3.50(2) | 245.37(11) |
| 3.70(2) | 254.7(12) | 4.00(2) | 241.37(14) |
| 4.50(2) | 251.8(15) | 4.50(2) | 241.23(14) |

Table A4.
Present unit cell volume and bulk modulus as a function of pressure, modeled using Equation (6) for PbTe and Pb0.884Cd0.116Te.
Table A4.
Present unit cell volume and bulk modulus as a function of pressure, modeled using Equation (6) for PbTe and Pb0.884Cd0.116Te.
| p [GPa] | PbTe | Pb0.884Cd0.116Te | ||
|---|---|---|---|---|
| V [Å3] | K [GPa] | V [Å3] | K [GPa] | |
| 0 | 273.25 | 45.6(2.5) | 273.25 | 33.5(2.8) |
| 0.5 | 270.33 | 47.6(2.5) | 270.33 | 35.5(2.8) |
| 1.0 | 267.57 | 49.6(2.5) | 267.57 | 37.5(2.8) |
| 1.5 | 264.93 | 51.5(2.5) | 264.93 | 39.4(2.8) |
| 2.0 | 262.42 | 53.5(2.5) | 262.42 | 41.3(2.8) |
| 2.5 | 260.02 | 55.4(2.5) | 260.02 | 43.2(2.8) |
| 3.0 | 257.72 | 57.3(2.5) | 257.72 | 45.1(2.8) |
| 3.5 | 255.52 | 59.1(2.5) | 255.52 | 47.0(2.8) |
| 4.0 | 253.41 | 61.1(2.5) | 253.41 | 48.8(2.8) |
| 4.5 | 251.37 | 62.9(2.5) | 251.37 | 50.7(2.8) |
| 5.0 | 249.41 | 64.8(2.5) | 249.41 | 52.5(2.8) |
Appendix C

Table A5.
Fitted values of the parameters of Equations (1), (4) and (6), obtained for PbTe and Pb0.884Cd0.116Te crystals.
Table A5.
Fitted values of the parameters of Equations (1), (4) and (6), obtained for PbTe and Pb0.884Cd0.116Te crystals.
| Function | Fitted Equation | Parameters for PbTe | Parameters for Pb0.884Cd0.116Te |
|---|---|---|---|
| V(T) | Equation (1) | = 265.813(6) Å3, Q = 2.86(3) × 10−18, b = 1.3(6), θD = 135.2(3.9) K | = 259.358(7) Å3, Q = 2.63(4) × 10−18, b = 0.4(7), θD = 130.1(4.4) K |
| <u2>(T), for cationic site | Equation (4) | θD = 102.8(3) K, <u2>stat = 0.00038(4) Å2 | θD = 114.5(5) K, ‰<u2>stat = 0.00203(6) Å2 |
| <u2>(T), for anionic site | Equation (4) | θD = 169.2(1.1) K, <u2>stat = −0.00054(7) Å2 | θD = 158.1(1.3) K, ‰<u2>stat = 0.0034(1) Å2 |
| V(p) | Equation (6) | V0 = 273.3(7) Å3 K0 = 45.6(2.5) GPa K′ = 4 (fixed) | V0 = 267.7(1.5) Å3 K0 = 33.5(2.8) GPa K′ = 4 (fixed) |
Appendix D

Table A6.
Reported theoretical bulk modulus and its derivative for PbTe and Pb1−xCdxTe, x = 0.031, 0.116. In a number of papers (e.g., refs. [10,129]), multiple numerical approaches have been applied, so only selected representative values could be cited here. As a rule (with some exceptions), the experimental values refer to room temperature, whereas in the calculated ones (to 0 K), the temperature is marked if explicitly stated in the given reference.
Table A6.
Reported theoretical bulk modulus and its derivative for PbTe and Pb1−xCdxTe, x = 0.031, 0.116. In a number of papers (e.g., refs. [10,129]), multiple numerical approaches have been applied, so only selected representative values could be cited here. As a rule (with some exceptions), the experimental values refer to room temperature, whereas in the calculated ones (to 0 K), the temperature is marked if explicitly stated in the given reference.
| Compound | K0 [GPa] | K′ | Method | Ref. | Year |
|---|---|---|---|---|---|
| PbTe | 45 | n.a. | LDA | ||
| 48 | n.a. | LDA | (a) | 1983 | |
| 51.7 | 4.52 | LAPW LDA | (b) | 1997 | |
| 51.44 (0 K) 40.30 (0 K) 49.82 (0 K) 39.5 (0 K) | 5.50 4.27 5.76 3.92 | FP-LAPW LDA FP-LAPW GGA FP-LAPW LDA+SO FP-LAPW GGA+SO | (c) | 2000 | |
| 41.4 51.4 | 3.352 4.080 | GGA LDA | (d) | 2002 | |
| 37.5 (0 K) | n.a. | FP-APW PBE | (e) | 2007 | |
| 40.4 (0 K) 50.3 (0 K) 30.7 | n.a. n.a. n.a. | LDA/GGA “ “ | (f) | 2009 | |
| 39.05 | 4.32 | FP-LAPW | (g) | 2011 | |
| 46.0 46.1 | 4.27 4.53 | LDA LDA+SO | (h) | 2012 | |
| 41.0 | n.a. | MD (GULP) | (i) | 2012 | |
| 39.1 | n.a. | PAW PBE | (j) | 2013 | |
| 47 (0 K) | n.a. | FP-LAPW | (k) | 2014 | |
| 38.54 (300 K) ~45.5 (0 K) | n.a. n.a. | PBEsol “ | (l) | 2014 | |
| 34.04 (0 K) | n.a. | LDA, GGA | (m) | 2014 | |
| 46.61 (0 K) | n.a. | PBEsol | (n) | 2015 | |
| 44.1(&) | n.a. | HSEsolSOC | (o) | 2016 | |
| 41.1 | n.a. | FP-LAPW | (p) | 2017 | |
| 36.19 (100 K) 37.52 (300 K) | n.a. n.a. | LDY “ | (q) | 2019 | |
| 48.242 (0 K) | 5.576 (0 K) | LDA | (r) | 2020 | |
| 43.6 | 4.6 | GGA-PBE | (s) | 2020 | |
| Pb0.969Cd0.031Te | 46.42 | n.a. | GGA | (n) | 2015 |
| Pb0.884Cd0.116Te | 45.90 | n.a. | GGA | ($) | 2021 |
References: (a) [118,119], (b) [115], (c) [116], (d) [114], (e) [120], (f) [45], (g) [122], (h) [64], (i) [117], (j) [123], (k) [124], (l) [46], (m) [47], (n) [9], (o) [10], (p) [125], (q) [65], (r) [67], (s) [86]. ($)—extrapolation of ref. [9] data reported for Pb0.969Cd0.031Te. (&)—the authors presented results also for seven other approaches. Abbreviations are explained at the end of this study.
References
- Faber, K.T.; Malloy, K.J. (Eds.) The Mechanical Properties of Semiconductors; Academic Press: Boston, MA, USA, 1992; Volume 37. [Google Scholar]
- Zhang, X.; Zhao, L.D. Thermoelectric materials: Energy conversion between heat and electricity. J. Mater. 2015, 1, 92–105. [Google Scholar] [CrossRef] [Green Version]
- Heremans, J.P.; Jovovic, V.; Toberer, E.S.; Saramat, A.; Kurosaki, K.; Charoenphakdee, A.; Yamanaka, S.; Snyder, G.J. Enhancement of thermoelectric efficiency in PbTe by distortion of the electronic density of states. Science 2008, 321, 554–557. [Google Scholar] [CrossRef] [Green Version]
- Jaworski, C.M.; Wiendlocha, B.; Jovovic, V.; Heremans, J.P. Combining alloy scattering of phonons and resonant electronic levels to reach a high thermoelectric figure of merit in PbTeSe and PbTeS alloys. Energy Environ. Sci. 2011, 4, 4155–4162. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X.; Cui, T.; Niu, Y.; Wang, Y.; Wang, M.; Ma, Y.; Zou, G. Enhanced thermoelectric performance of PbTe within the orthorhombic Pnma phase. Phys. Rev. B 2007, 76, 155127. [Google Scholar] [CrossRef]
- Dynowska, E.; Szuszkiewicz, W.; Szczepanska, A.; Romanowski, P.; Dobrowolski, W.; Lathe, C.; Slynko, E.V. High-Pressure Studies of Bulk Pb1−xBaxTe Mixed Crystals. In Jahresbericht/Hamburger Synchrotronstrahlungslabor HASYLAB am Deutschen Elektronen-Synchrotron DESY= Annual Report; HASYLAB: Hamburg, Germany, 2005; pp. 361–362. [Google Scholar]
- Bukała, M.; Sankowski, P.; Buczko, R.; Kacman, P. Structural and electronic properties of Pb1−xCdxTe and Pb1−xMnxTe ternary alloys. Phys. Rev. B 2012, 86, 085205. [Google Scholar] [CrossRef] [Green Version]
- Joseph, E.; Amouyal, Y. Enhancing thermoelectric performance of PbTe-based compounds by substituting elements: A first principles study. J. Electron. Mater. 2015, 44, 1460–1468. [Google Scholar] [CrossRef]
- Joseph, E.; Amouyal, Y. Towards a predictive route for selection of doping elements for the thermoelectric compound PbTe from first-principles. J. Appl. Phys. 2015, 117, 175102. [Google Scholar] [CrossRef]
- Śpiewak, P.; Kurzydłowski, K.J. Electronic Structure and Transport Properties of Doped Lead Chalcogenides from First Principles. MRS Adv. 2016, 1, 4003–4010. [Google Scholar] [CrossRef]
- Sealy, B.J.; Crocker, A.J. A comparison of phase equilibria in some II-IV-VI compounds based on PbTe. J. Mater. Sci. 1973, 8, 1731–1736. [Google Scholar] [CrossRef]
- Crocker, A.J.; Rogers, L.M. Valence band structure of PbTe. J. Phys. Colloq. 1968, 29, C4-129–C4-132. [Google Scholar] [CrossRef]
- Pei, Y.; LaLonde, A.D.; Heinz, N.A.; Snyder, G.J. High thermoelectric figure of merit in PbTe alloys demonstrated in PbTe–CdTe. Adv. Energy Mater. 2012, 2, 670–675. [Google Scholar] [CrossRef]
- Ahn, K.; Biswas, K.; He, J.; Chung, I.; Dravid, V.; Kanatzidis, M.G. Enhanced thermoelectric properties of p-type nanostructured PbTe–MTe (M = Cd, Hg) materials. Energy Environ. Sci. 2013, 6, 1529–1537. [Google Scholar] [CrossRef]
- Sarkar, S.; Zhang, X.; Hao, S.; Hua, X.; Bailey, T.P.; Uher, C.; Wolverton, C.; Dravid, V.P.; Kanatzidis, M.G. Dual alloying strategy to achieve a high thermoelectric figure of merit and lattice hardening in p-type nanostructured PbTe. ACS Energy Lett. 2018, 3, 2593–2601. [Google Scholar] [CrossRef]
- Rosenberg, A.J.; Woolley, J.C.; Nikolic, P.; Grierson, R. Solid solutions of CdTe and InTe in PbTe and SnTe. I. Crystal chemistry. Trans. Metall. Soc. AIME 1964, 230, 342–349. [Google Scholar]
- Kulvitit, Y.; Rolland, S.; Granger, R.; Pelletier, C.M. Relation entre composition paramètre de maille et bande interdite des composés Pb1−xCdxTe. Rev. Phys. Appliquée 1980, 15, 1501–1504. [Google Scholar] [CrossRef]
- Marx, R.; Range, K.J. Homogene, abschreckbare Hochdruckphasen mit NaCl-Struktur in den systemen CdTe-SnTe und CdTe-PbTe. J. Less Common Met. 1989, 155, 49–59. [Google Scholar] [CrossRef]
- Szot, M.; Szczerbakow, A.; Dybko, K.; Kowalczyk, L.; Smajek, E.; Domukhovski, V.; Łusakowska, E.; Dziawa, P.; Mycielski, A.; Story, T.; et al. Experimental and Theoretical Analysis of PbTe–CdTe Solid Solution Grown by Physical Vapour Transport Method. Acta Phys. Polon. A 2009, 116, 959–961. [Google Scholar] [CrossRef]
- Wald, F.; Rosenberg, A.J. Solid solutions of CdSe and InSe in PbSe. J. Phys. Chem. Solids 1965, 26, 1087–1091. [Google Scholar] [CrossRef]
- Crocker, A.J. Phase equilibria in PbTe/CdTe alloys. J. Mater. Sci. 1968, 3, 534–539. [Google Scholar] [CrossRef]
- Sealy, B.J.; Crocker, A.J. Some physical properties of the systems Pb1−xMgxSe and Pb1−xCdxSe. J. Mater. Sci. 1973, 8, 1247–1252. [Google Scholar] [CrossRef]
- Qian, X.; Wu, H.; Wang, D.; Zhang, Y.; Wang, J.; Wang, G.; Wang, G.; Zheng, L.; Pennycook, S.J.; Zhao, L.D. Synergistically optimizing interdependent thermoelectric parameters of n-type PbSe through alloying CdSe. Energy Environ. Sci. 2019, 12, 1969–1978. [Google Scholar] [CrossRef]
- Bethke, P.M.; Barton, P.B., Jr. Sub-solidus relations in the system PbS-CdS. Am. Mineral. J. Earth Planet. Mater. 1971, 56, 2034–2039. [Google Scholar]
- Tan, G.L.; Liu, L.; Wu, W. Mid-IR band gap engineering of CdxPb1−xS nanocrystals by mechanochemical reaction. AIP Adv. 2014, 4, 067107. [Google Scholar] [CrossRef] [Green Version]
- ICSD Database (FIZ, Karlsruhe), Records 620316, 620315, 620322. Available online: https://icsd.products.fiz-karlsruhe.de/ (accessed on 21 August 2021).
- Bziz, I.; Atmani, E.H.; Fazouan, N.; Aazi, M.; Es-Smairi, A. Ab-initio study of structural, electronic and optical properties of CdS. In Proceedings of the 2019 7th International Renewable and Sustainable Energy Conference (IRSEC), Agadir, Morocco, 27–30 November 2019; 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Kiyosawa, T.; Takahashi, S.; Koguchi, N. Solid solubility range and lattice parameter of semiconducting Pb1−xCdxS1−ySey for mid-infra-red lasers. Phys. Status Solidi A 1989, 111, K21–K25. [Google Scholar] [CrossRef]
- Knight, K.S. Does Altaite Exhibit Emphanitic Behavior? a High Resolution Neutron Powder Diffraction Investigation of the Crystallographic and Thermoelastic Properties of PbTe Between 10 and 500 K. Does Altaite Exhibit Emphanitic Behaviour? Can. Mineral. 2016, 54, 1493–1503. [Google Scholar] [CrossRef]
- Liu, Y.; Ibáñez, M. Tidying up the mess. Science 2021, 371, 678–679. [Google Scholar] [CrossRef] [PubMed]
- Kastbjerg, S.; Bindzus, N.; Søndergaard, M.; Johnsen, S.; Lock, N.; Christensen, M.; Takata, M.; Spackman Brummerstedt, M.A.; Iversen, B. Direct evidence of cation disorder in thermoelectric lead chalcogenides PbTe and PbS. Adv. Funct. Mater. 2013, 23, 5477–5483. [Google Scholar] [CrossRef]
- Wang, H.; LaLonde, A.D.; Pei, Y.; Snyder, G.J. The criteria for beneficial disorder in thermoelectric solid solutions. Adv. Funct. Mater. 2013, 23, 1586–1596. [Google Scholar] [CrossRef]
- Knight, K.S. A high-resolution neutron powder diffraction investigation of galena (PbS) between 10 K and 350 K: No evidence for anomalies in the lattice parameters or atomic displacement parameters in galena or altaite (PbTe) at temperatures corresponding to the saturation of cation disorder. J. Phys. Condens. Matter 2014, 26, 385403. [Google Scholar] [CrossRef]
- Christensen, S.; Bindzus, N.; Sist, M.; Takata, M.; Iversen, B.B. Structural disorder, anisotropic micro-strain and cation vacancies in thermo-electric lead chalcogenides. Phys. Chem. Chem. Phys. 2016, 18, 15874–15883. [Google Scholar] [CrossRef]
- Szot, M.; Pfeffer, P.; Dybko, K.; Szczerbakow, A.; Kowalczyk, L.; Dziawa, P.; Minikayev, R.; Zajarniuk, T.; Piotrowski, P.; Gutowska, M.U.; et al. Two-valence band electron and heat transport in monocrystalline PbTe-CdTe solid solutions with Cd content up to 10 atomic percent. Phys. Rev. Mater. 2020, 4, 044605. [Google Scholar] [CrossRef]
- Tsang, Y.W.; Cohen, M.L. Calculation of the temperature dependence of the energy gaps in PbTe and SnTe. Phys. Rev. B 1971, 3, 1254. [Google Scholar] [CrossRef]
- Noda, Y.; Masumoto, K.; Ohba, S.; Saito, Y.; Toriumi, K.; Iwata, Y.; Shibuya, I. Temperature dependence of atomic thermal parameters of lead chalcogenides, PbS, PbSe and PbTe. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 1987, 43, 1443–1445. [Google Scholar] [CrossRef]
- Božin, E.S.; Malliakas, C.D.; Souvatzis, P.; Proffen, T.; Spaldin, N.A.; Kanatzidis, M.G.; Billinge, S.J. Entropically stabilized local dipole formation in lead chalcogenides. Science 2010, 330, 1660–1663. [Google Scholar] [CrossRef] [PubMed]
- Sangiorgio, B.; Bozin, E.S.; Malliakas, C.D.; Fechner, M.; Simonov, A.; Kanatzidis, M.G.; Billinge, S.J.L.; Spaldin, N.A.; Weber, T. Correlated local dipoles in PbTe. Phys. Rev. Mater. 2018, 2, 085402. [Google Scholar] [CrossRef]
- Holm, K.A.; Roth, N.; Zeuthen, C.M.; Iversen, B.B. Anharmonicity and correlated dynamics of PbTe and PbS studied by single crystal x-ray scattering. Phys. Rev. B 2021, 103, 224302. [Google Scholar] [CrossRef]
- Male, J.P.; Hanus, R.; Snyder, G.J.; Hermann, R.P. Thermal Evolution of Internal Strain in Doped PbTe. Chem. Mater. 2021, 33, 4765–4772. [Google Scholar] [CrossRef]
- Minikayev, E.D.; Dziawa, P.; Kamińska, E.; Szczerbakow, A.; Trots, D.; Szuszkiewicz, W. High-temperature studies of Pb1−xCdxTe solid solution: Structure stability and CdTe solubility limit, Synchrotron Radiation. Nat. Sci. 2009, 8, 8. [Google Scholar]
- Minikayev, R.; Dynowska, E.; Kaminska, E.; Szczerbakow, A.; Trots, D.; Story, T.; Szuszkiewicz, W. Evolution of Pb1− xCdxTe solid solution structure at high temperatures. Acta Phys. Pol. A 2011, 119, 699–701. [Google Scholar] [CrossRef]
- Minikayev, R.; Dynowska, E.; Story, T.; Szczerbakow, A.; Bell, A.; Trots, D.; Szuszkiewicz, W. Low-temperature expansion of metasY Pb(1−x)Cd(x)Te solid solution. In Proceedings of the IX Krajowe Sympozjum Użytkowników Promieniowania Synchrotronowego (KSUPS-9), Warszawa, Polska, 26–27 September 2011. [Google Scholar]
- Zhang, Y.; Ke, X.; Chen, C.; Yang, J.; Kent, P.R.C. Thermodynamic properties of PbTe, PbSe, and PbS: First-principles study. Phys. Rev. B 2009, 80, 024304. [Google Scholar] [CrossRef]
- Skelton, J.M.; Parker, S.C.; Togo, A.; Tanaka, I.; Walsh, A. Thermal physics of the lead chalcogenides PbS, PbSe, and PbTe from first principles. Phys. Rev. B 2014, 89, 205203. [Google Scholar] [CrossRef] [Green Version]
- Boukhris, N.; Meradji, H.; Korba, S.A.; Drablia, S.; Ghemid, S.; Hassan, F.E.H. First principles calculations of structural, electronic and thermal properties of lead chalcogenides PbS, PbSe and PbTe compounds. Bull. Mater. Sci. 2014, 37, 1159–1166. [Google Scholar] [CrossRef]
- Xia, Y. Revisiting lattice thermal transport in PbTe: The crucial role of quartic anharmonicity. Appl. Phys. Lett. 2018, 113, 073901. [Google Scholar] [CrossRef]
- Lu, Y.; Sun, T.; Zhang, D.B. Lattice anharmonicity, phonon dispersion, and thermal conductivity of PbTe studied by the phonon quasiparticle approach. Phys. Rev. B 2018, 97, 174304. [Google Scholar] [CrossRef]
- Querales-Flores, J.D.; Cao, J.; Fahy, S.; Savić, I. Temperature effects on the electronic band structure of PbTe from first principles. Phys. Rev. Mater. 2019, 3, 055405. [Google Scholar] [CrossRef] [Green Version]
- Novikova, S.I.; Abrikosov, N.K. Investigation of the thermal expansion of lead chalcogenides (Иccлeдoвaниe тeплoвoгo pacшиpeния xaлькoгeнидoв cвинцa). Fiz. Tverd. Tela Sov. Phys. Solid State 1963, 5, 1913–1916. [Google Scholar]
- Houston, B.; Strakna, R.E.; Belson, H.S. Elastic constants, thermal expansion, and Debye temperature of lead telluride. J. Appl. Phys. 1968, 39, 3913–3916. [Google Scholar] [CrossRef]
- Cochran, W.; Cowley, R.A.; Dolling, G.; Elcombe, M.M. The crystal dynamics of lead telluride. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1966, 293, 433–451. [Google Scholar] [CrossRef]
- Murphy, A.R. Thermoelectric Properties of PbTe-Based Materials Driven Near the Ferroelectric Phase Transition from First Principles. Ph.D. Thesis, University College Cork, Cork, Irland, 2017; p. 75. [Google Scholar]
- Ghezzi, C. Mean Square Vibrational Amplitudes in PbTe. Phys. Status Solidi 1973, 58, 737–744. [Google Scholar] [CrossRef]
- Bublik, V.T. The mean square atomic displacements and enthalpies of vacancy formation in some semiconductors. Phys. Status Solidi 1978, 45, 543–548. [Google Scholar] [CrossRef]
- Li, C.W.; Ma, J.; Cao, H.B.; May, A.F.; Abernathy, D.L.; Ehlers, G.; Hoffmann, C.; Wang, X.; Hong, T.; Huq, A.; et al. Anharmonicity and atomic distribution of SnTe and PbTe thermoelectrics. Phys. Rev. B 2014, 90, 214303. [Google Scholar] [CrossRef] [Green Version]
- Keffer, C.; Hayes, T.M.; Bienenstock, A. PbTe Debye-Waller factors and band-gap temperature dependence. Phys. Rev. Lett. 1968, 21, 1676–1678. [Google Scholar] [CrossRef]
- Keffer, C.; Hayes, T.M.; Bienenstock, A. Debye-Waller factors and the PbTe band-gap temperature dependence. Phys. Rev. B 1970, 2, 1966–1976. [Google Scholar] [CrossRef]
- Chen, Y.; Ai, X.; Marianetti, C.A. First-principles approach to nonlinear lattice dynamics: Anomalous spectra in PbTe. Phys. Rev. Lett. 2014, 113, 105501. [Google Scholar] [CrossRef] [Green Version]
- Parkinson, D.; Quarrington, J. The Molar Heats of Lead Sulphide, Selenide and Telluride in the Temperature Range 20°K to 260°K. Proc. Phys. Soc. 1954, A67, 569–579. [Google Scholar] [CrossRef]
- El-Sharkawy, A.A.; Abou El-Azm, A.M.; Kenawy, M.I.; Hillal, A.S.; Abu-Basha, H.M. Thermophysical properties of polycrystalline PbS, PbSe, and PbTe in the temperature range 300–700 K. Int. J. Thermophys. 1983, 4, 261–269. [Google Scholar] [CrossRef]
- Jacobsen, M.K.; Liu, W.; Li, B. Sound velocities of PbTe to 14 GPa: Evidence for coupling between acoustic and optic phonons. J. Phys. Condens. Matter 2013, 25, 365402. [Google Scholar] [CrossRef]
- Yang, Y.L. Elastic moduli and band gap of PbTe under pressure: Ab initio study. Mater. Sci. Technol. 2012, 28, 1308–1313. [Google Scholar] [CrossRef]
- Tripathi, S.; Agarwal, R.; Singh, D. Nonlinear elastic, ultrasonic and thermophysical properties of lead telluride. Int. J. Thermophys. 2019, 40, 1–18. [Google Scholar] [CrossRef]
- Naidych, B. Crystal Structure and Thermodynamic Parameters of Thin Film II-VI and IV-VI Alloys (Кpиcтaлічнa cтpуктуpa тa тepмoдинaмічні пapaмeтpи тoнкoплівкoвиx кoндeнcaтів cиcтeм II-VI, IV-VI). Ph.D. Thesis, Vasyl Stefanyk Precarpathian National University, Ivano-Frankivsk, Ukraine, 2019; p. 116. (In Ukrainian). [Google Scholar]
- Öztürk, H.; Arslan, G.G.; Kürkçü, C.; Yamçıçıer, Ç. Structural phase transformation, intermediate states and electronic properties of PbTe under high pressure. J. Electron. Mater. 2020, 49, 3089–3095. [Google Scholar] [CrossRef]
- Naidych, B.; Parashchuk, T.; Yaremiy, I.; Moyseyenko, M.; Kostyuk, O.; Voznyak, O.; Dashevsky, Z.; Nykyruy, L. Structural and thermodynamic properties of Pb-Cd-Te thin films: Experimental study and DFT analysis. J. Electron. Mater. 2021, 50, 580–591. [Google Scholar] [CrossRef]
- Zhang, M.; Tang, G.; Li, Y. Hydrostatic Pressure Tuning of Thermal Conductivity for PbTe and PbSe Considering Pressure-Induced Phase Transitions. ACS Omega 2021, 6, 3980–3990. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.C.; Hsieh, K.C.; Sharma, R.C.; Chang, Y.A. The Pb-Te (lead-tellurium) system. Bull. Alloy Phase Diagr. 1989, 10, 340–347. [Google Scholar] [CrossRef]
- Ngai, T.L.; Marshall, D.; Sharma, R.C.; Chang, Y.A. Thermodynamic properties and phase equilibria of the lead-tellurium binary system. Mon. Für Chem. Chem. Mon. 1987, 118, 277–300. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, L.; Yu, D. Thermodynamic Descriptions for the Cd-Te, Pb-Te, Cd-Pb and Cd-Pb-Te Systems. J. Electron. Mater. 2009, 38, 2033–2045. [Google Scholar] [CrossRef]
- Fujimoto, M.; Sato, Y. P-T-x phase diagram of the lead telluride system. Jpn. J. Appl. Phys. 1966, 5, 128–133. [Google Scholar] [CrossRef]
- Sealy, B.J.; Crocker, A.J. The P-T-x phase diagram of PbTe and PbSe. J. Mater. Sci. 1973, 8, 1737–1743. [Google Scholar] [CrossRef]
- Gierlotka, W.; Łapsa, J.; Jendrzejczyk-Handzlik, D. Thermodynamic description of the Pb–Te system using ionic liquid model. J. Alloy. Compd. 2009, 479, 152–156. [Google Scholar] [CrossRef]
- Peters, M.C.; Doak, J.W.; Zhang, W.W.; Saal, J.E.; Olson, G.B.; Voorhees, P.W. Thermodynamic modeling of the PbX (X = S, Te) phase diagram using a five sub-lattice and two sub-lattice model. Calphad 2017, 58, 17–24. [Google Scholar] [CrossRef] [Green Version]
- Shalvoy, R.B.; Fisher, G.B.; Stiles, P.J. Bond ionicity and structural stability of some average-valence-five materials studied by x-ray photoemission. Phys. Rev. B 1977, 15, 1680–1697. [Google Scholar] [CrossRef]
- Chattopadhyay, T.; Werner, A.; Von Schnering, H.G. Pressure-Induced Phase Transition in IV--VI Compounds. Mat. Res. Soc. Symp. Proc. 1984, 22, 93–96. [Google Scholar] [CrossRef] [Green Version]
- Chattopadhyay, T.; Werner, A.; Von Schnering, H.G.; Pannetier, J. Temperature and pressure induced phase transition in IV-VI compounds. Rev. Phys. Appliquée 1984, 19, 807–813. [Google Scholar] [CrossRef] [Green Version]
- Chattopadhyay, L.; von Schnering, H.G.; Grosshans, W.A.; Holzapfel, W.B. High pressure X-ray diffraction study on the structural phase transitions in PbS, PbSe and PbTe with synchrotron radiation. Phys. B+C 1986, 139–140, 356–360. [Google Scholar] [CrossRef]
- Ves, S.; Pusep, Y.A.; Syassen, K.; Cardona, M. Raman study of high pressure phase transitions in PbTe. Solid State Commun. 1989, 70, 257–260. [Google Scholar] [CrossRef]
- Rousse, G.; Klotz, S.; Saitta, A.M.; Rodriguez-Carvajal, J.; McMahon, M.I.; Couzinet, B.; Mezouar, M. Structure of the intermediate phase of PbTe at high pressure. Phys. Rev. B 2005, 71, 224116. [Google Scholar] [CrossRef]
- Li, Y.; Lin, C.; Li, H.; Liu, X.L.J. Phase transitions in PbTe under quasi-hydrostatic pressure up to 50 GPa. High Press. Res. 2013, 33, 713–719. [Google Scholar] [CrossRef]
- Singh, R.K.; Gupta, D.C. High pressure phase transitions and elastic properties of IV-VI compound semiconductors. Phase Transit. Multinatl. J. 1995, 53, 39–51. [Google Scholar] [CrossRef]
- Ahuja, R. High pressure structural phase transitions in IV–VI semiconductors. Phys. Status Solidi 2003, 235, 341–347. [Google Scholar] [CrossRef]
- Aguado-Puente, P.; Fahy, S.; Grüning, M. GW study of pressure-induced topological insulator transition in group-IV tellurides. Phys. Rev. Res. 2020, 2, 043105. [Google Scholar] [CrossRef]
- Chusnutdinow, S.; Schreyeck, S.; Kret, S.; Kazakov, A.; Karczewski, G. Room temperature infrared detectors made of PbTe/CdTe multilayer composite. Appl. Phys. Lett. 2020, 117, 072102. [Google Scholar] [CrossRef]
- Stöber, D.; Hildmann, B.O.; Böttner, H.; Schelb, S.; Bachem, K.H.; Binnewies, M. Chemical transport reactions during crystal growth of PbTe and PbSe via vapour phase influenced by AgI. J. Cryst. Growth 1992, 121, 656–664. [Google Scholar] [CrossRef]
- Szczerbakow, A. Crystal selection in the Self-selected Vapour Growth (SSVG) of PbSe in a vertical system. Cryst. Res. Technol. 1993, 28, K77–K80. [Google Scholar] [CrossRef]
- Szczerbakow, A.; Durose, K. Self-selecting vapour growth of bulk crystals–Principles and applicability. Prog. Cryst. Growth Character. Mater. 2005, 51, 81–108. [Google Scholar] [CrossRef]
- Xu, W.; Liu, Y.; Marcelli, A.; Shang, P.P.; Liu, W.S. The complexity of thermoelectric materials: Why we need powerful and brilliant synchrotron radiation sources? Mater. Today Phys. 2018, 6, 68–82. [Google Scholar] [CrossRef]
- Knapp, M.; Baehtz, C.; Ehrenberg, H.; Fuess, H. The synchrotron powder diffractometer at beamline B2 at HASYLAB/DESY: Status and capabilities. J. Synchrotron Radiat. 2004, 11, 328–334. [Google Scholar] [CrossRef]
- Knapp, M.; Joco, V.; Baehtz, C.; Brecht, H.H.; Berghaeuser, A.; Ehrenberg, H.; von Seggern, H.; Fuess, H. Position-sensitive detector system OBI for high resolution X-ray powder diffraction using on-site readable image plates. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2004, 521, 565–570. [Google Scholar] [CrossRef]
- Paszkowicz, W.; Knapp, M.; Bähtz, C.; Minikayev, R.; Piszora, P.; Jiang, J.Z.; Bacewicz, R.J. Synchrotron X-ray wavelength calibration using a diamond internal standard: Application to low-temperature thermal-expansion studies. Alloy. Comp. 2004, 382, 107–111. [Google Scholar] [CrossRef]
- Loopstra, B.O.; Rietveld, H.M. The structure of some alkaline–earth metal uranates. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1969, 25, 787–791. [Google Scholar] [CrossRef]
- Rietveld, H. A profile refinement method for nuclear and magnetic structures. J. Appl. Crystallogr. 1969, 2, 65–71. [Google Scholar] [CrossRef]
- Rodríguez-Carvajal, J. Recent developments of the program FULLPROF. Commission on Powder Diffraction (IUCr) Newsletter; 2001; 26; 12–19. Available online: http://journals.iucr.org/iucr-top/comm/cpd/Newsletters/ (accessed on 21 August 2021).
- Merrill, L.; Bassett, W.A. Miniature diamond anvil pressure cell for single crystal X-ray diffraction studies. Rev. Sci. Instrum. 1974, 45, 290–294. [Google Scholar] [CrossRef]
- Mao, H.K.; Xu, J.; Bell, P.M. Calibration of the ruby pressure gauge to 800 kbar under quasi-hydrostatic conditions. J. Geophys. Res. 1986, 91, 4673–4676. [Google Scholar] [CrossRef]
- Budzianowski, A.; Katrusiak, A. High-Pressure Crystallography; Katrusiak, A., McMillan, P.F., Eds.; Kluwer: Dordrecht, The Netherlands, 2004; pp. 101–112. [Google Scholar]
- Xcalibur CCD System. Crys Alis Pro Software System, Version 1.171.33; Oxford Diffraction Ltd.: Wrocław, Poland, 2009. [Google Scholar]
- Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. Sect. A 2008, 64, 112–122. [Google Scholar] [CrossRef] [Green Version]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A Complete Structure Solution, Refinement and Analysis Program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Angel, R.J.; Alvaro, M.; Gonzalez-Platas, J. EosFit7c and a Fortran module (library) for equation of state calculations. Z. Für Krist. Cryst. Mater. 2014, 229, 405–419. [Google Scholar] [CrossRef]
- Gonzalez-Platas, J.; Alvaro, M.; Nestola, F.; Angel, R. EosFit7-GUI. J. Appl. Crystallogr. 2016, 49, 1377–1382. [Google Scholar] [CrossRef]
- Wallace, D.C. Thermodynamics of Crystals; Dover: New York, NY, USA, 1998. [Google Scholar]
- Vočadlo, L.; Knight, K.S.; Price, G.D.; Wood, I.G. Thermal expansion and crystal structure of FeSi between 4 and 1173 K determined by time-of-light neutron powder diffraction. Phys. Chem. Miner. 2002, 29, 132–139. [Google Scholar] [CrossRef]
- Querales-Flores, J.; (Tyndall National Institute, University College Cork, Cork, Ireland). Personal Communication, 2021.
- Willis, B.T.M.; Pryor, A.W. Thermal Vibrations in Crystallography; Cambridge University Press: London, UK, 1975. [Google Scholar]
- Nakatsuka, A.; Shimokawa, M.; Nakayama, N.; Ohtaka, O.; Arima, H.; Okube, M.; Yoshiasa, A. Static disorders of atoms and experimental determination of Debye temperature in pyrope: Low-and high-temperature single-crystal X-ray diffraction study. Am. Mineral. 2011, 96, 1593–1605. [Google Scholar] [CrossRef]
- Inagaki, M.; Sasaki, Y.; Sakai, M. Debye-Waller parameters of lead sulphide powders. J. Mater. Sci. 1987, 22, 1657–1662. [Google Scholar] [CrossRef]
- Zhou, J.; Wu, Y.; Chen, Z.; Nan, P.; Ge, B.; Li, W.; Pei, Y. Manipulation of defects for high-performance thermoelectric PbTe-Based Alloys. Small Struct. 2021, 2, 2100016. [Google Scholar] [CrossRef]
- Miller, A.J.; Saunders, G.A.; Yogurtcu, Y.K. Pressure dependences of the elastic constants of PbTe, SnTe and Ge0.08Sn0.92Te. J. Phys. C Solid State Phys. 1981, 14, 1569–1584. [Google Scholar] [CrossRef]
- Lach-hab, M.; Papaconstantopoulos, D.A.; Meh, M.J. Electronic structure calculations of lead chalocgenides PbS, PbSe, PbTe. J. Phys. Chem. Solids 2002, 63, 833–841. [Google Scholar] [CrossRef]
- Wei, S.H.; Zunger, A. Electronic and structural anomlies in lead chalcogenides. Phys. Rev. B 1997, 55, 13605–13609. [Google Scholar] [CrossRef] [Green Version]
- Albanesi, E.A.; Okoye, C.M.I.; Rodriguez, C.O.; Blanca, E.L.P.; Petukhov, A.G. Electronic structure, structural properties, and dielectric functions of IV-VI semiconductors: PbSe and PbTe. Phys. Rev. B 2000, 61B, 16589. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.; Kaviany, M. Effect of thermal disorder on high figure of merit in PbTe. Phys. Rev. B 2012, 86, 045213. [Google Scholar] [CrossRef] [Green Version]
- Rabe, K.M.; Joannopoulos, J.D. Ab initio relativistic pseudopotential study of the zero-temperature structural properties of SnTe and PbTe. Phys. Rev. B 1985, 32, 2302–2314. [Google Scholar] [CrossRef]
- Rabe, K.M. Ab Initio Statistical Mechanics of Structural Phase Transitions. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1987. [Google Scholar]
- Hummer, K.; Grüneis, A.; Kresse, G. Structural and electronic properties of lead chalcogenides from first principles. Phys. Rev. B 2007, 75, 195211. [Google Scholar] [CrossRef]
- Xu, L.; Zheng, Y.; Zheng, J.C. Thermoelectric transport properties of PbTe under pressure. Phys. Rev. B 2010, 82, 195102. [Google Scholar] [CrossRef]
- Bencherif, Y.; Boukra, A.; Zaoui, A.; Ferhat, M. High-pressure phases of lead chalcogenides. Mater. Chem. Phys. 2011, 126, 707–710. [Google Scholar] [CrossRef]
- Petersen, J.E. First Principles Study of Structural, Electronic, and Mechanical Properties of Lead Selenide and Lead Telluride. Master Thesis, Master Graduate College, Texas State University, San Marcos, TX, USA, 2013. [Google Scholar]
- Gelbstein, Y.; Davidow, J.; Leshem, E.; Pinshow, O.; Moisa, S. Significant lattice thermal conductivity reduction following phase separation of the highly efficient GexPb1–xTe thermoelectric alloys. Phys. Status Solidi 2014, 251, 1431–1437. [Google Scholar] [CrossRef]
- Komisarchik, G.; Gelbstein, Y.; Fuks, D. Solubility of Ti in thermoelectric PbTe compound. Intermetallics 2017, 89, 16–21. [Google Scholar] [CrossRef]
- Inoue, M.; Yagi, H.; Muratani, T.; Tatsukawa, T. EPR studies of Mn2+ in SnTe and PbTe crystals. J. Phys. Soc. Jpn. 1976, 40, 458–462. [Google Scholar] [CrossRef]
- Bevolo, A.J.; Shanks, H.R.; Eckels, D.E. Molar heat capacity of GeTe, SnTe, and PbTe from 0.9 to 60 K. Phys. Rev. B 1976, 13, 3523–3533. [Google Scholar] [CrossRef]
- Finkenrath, H.; Franz, G.; Uhle, N. Reststrahlen spectra of PbSe1−xTex. Phys. Status Solidi 1979, 95, 179–184. [Google Scholar] [CrossRef]
- Lead Telluride (PbTe). Debye Temperature, Heat Capacities, Density, Melting Point, in Non-Tetrahedrally Bonded Elements and Binary Compounds I; Madelung, O., Rössler, U., Schulz, M., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 1–3. [Google Scholar]
- Morelli, D.T.; Slack, G.A. High lattice thermal conductivity solids. In High Thermal Conductivity Materials; Springer: New York, NY, USA, 2006; pp. 37–68. [Google Scholar]
- Wang, H.; Pei, Y.; LaLonde, A.D.; Snyder, G.J. Heavily doped p-type PbSe with high thermoelectric performance: An alternative for PbTe. Adv. Mater. 2011, 23, 1366–1370. [Google Scholar] [CrossRef]
- Bauer Pereira, P.; Sergueev, I.; Gorsse, S.; Dadda, J.; Müller, E.; Hermann, R.P. Lattice dynamics and structure of GeTe, SnTe and PbTe. Phys. Status Solidi 2013, 250, 1300–1307. [Google Scholar] [CrossRef]
- Kemerink, G.J.; Pleiter, F. Recoilless fractions calculated with the nearest-neighbour interaction model by Kagan and Maslow. Hyperfine Interact. 1986, 30, 187–198. [Google Scholar] [CrossRef]
- Kong, F.; Liu, Y.; Wang, B.; Wang, Y.; Wang, L. Lattice dynamics of PbTe polymorphs from first principles. Comput. Mater. Sci. 2012, 56, 18–24. [Google Scholar] [CrossRef]
- Zhou, C.; Yu, Y.; Lee, Y.L.; Ge, B.; Lu, W.; Cojocaru-Mirédin, O.; Im, J.; Cho, S.P.; Wuttig, M.; Shi, Z.; et al. Exceptionally High Average Power Factor and Thermoelectric Figure of Merit in n-type PbSe by the Dual Incorporation of Cu and Te. J. Am. Chem. Soc. 2020, 142, 15172–15186. [Google Scholar] [CrossRef] [PubMed]
- Lucovsky, G.; White, R.M. Effects of resonance bonding on the properties of crystalline and amorphous semiconductors. Phys. Rev. B 1973, 8, 660–667. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).