Abstract
One of the most successful ways to introduce samples in Serial Femtosecond Crystallography has been the use of microscopic capillary liquid jets produced by gas flow focusing, whose length-to-diameter ratio and velocity are essential to fulfill the requirements of the high pulse rates of current XFELs. In this work, we demonstrate the validity of a classical scaling law with two universal constants to calculate that length as a function of the liquid properties and operating conditions. These constants are determined by fitting the scaling law to a large set of experimental and numerical measurements, including previously published data. Both the experimental and numerical jet lengths conform remarkably well to the proposed scaling law. We show that, while a capillary jet is a globally unstable system to linear perturbations above a critical length, its actual and shorter long-term average intact length is determined by the nonlinear perturbations coming from the jet breakup itself. Therefore, this length is determined solely by the properties of the liquid, the average velocity of the liquid and the flow rate expelled. This confirms the very early observations from Smith and Moss 1917, Proc R Soc Lond A Math Phys Eng, 93, 373, to McCarthy and Molloy 1974, Chem Eng J, 7, 1, among others, while it contrasts with the classical conception of temporal stability that attributes the natural breakup length to the jet birth conditions in the ejector or small interactions with the environment.
1. Introduction
The shape, instability, and breakup of capillary jets have attracted scientific curiosity since long ago [1,2]. Capillary jets provide a gentle and reproducible way to transport a liquid without solid contact at distances from a source long compared to the source transverse size [3]. The need for increasingly precise means to deliver tiny liquid samples has grown explosively with the advent of faster and more sensitive detection and analysis procedures. Among these procedures, Serial Femtosecond Crystallography (SFX) has revolutionized the molecular determination of complex biochemical species (from proteins to viruses) through the ability of femtosecond-duration X-ray pulses to overcome exposure limits due to radiation damage [4,5,6,7]. Consequently, using radiation from X-ray free-electron laser pulses, it is possible to obtain high-resolution structural information from small protein crystals without the need for cryogenic cooling, and to do so as a function of time elapsed after triggering a reaction or other structural change [8]. The method has been used to obtain structures from invisibly small crystals [9] and single virus particles [10], follow light-induced ultrafast collective motions in protein structures [11,12], and track conformational changes in RNA and proteins on binding to a ligand [13,14]. Since a single focused X-ray pulse ultimately destroys the sample (shortly after the pulse transits the sample to provide significant X-ray diffraction), fresh crystals or particles must be consistently replenished into the beam focus, matching the arrival rate of the X-ray pulses, to record diffraction patterns on a pulse-by-pulse basis. Thus, SFX has become one of the major applications for microjets: in this regard, maximum jet length combined with jet diameters below 5 m is desirable [4,15].
Despite the numerous studies of jet instabilities [16,17,18,19,20] that provide a highly detailed knowledge of the physics of capillary jets, we are still lacking a general theoretical model for predicting the breakup (intact) length of steadily and freely released capillary jets [21,22,23,24,25,26,27]. The breakup length can be estimated from the classical temporal linear stability analysis of the jet [28,29]. To obtain a useful scaling law [28,30], one may assume that the most unstable (dominant) temporal mode is responsible for the breakup. This mode is supposed to be triggered by a perturbation next to the jet inception region and is convected by the jet, which implies that the residence time in the jet scales as the inverse of the dominant mode growth rate. Rayleigh’s theory for inviscid cylindrical capillary jets [2] and its subsequent refinements to account for different factors allows one to calculate the growth rate of the dominant mode. However, one cannot avoid the presence of a logarithmic dependency on the amplitude of initial perturbations on the scaling law, which has prevented the derivation of a universally valid law, should that law exist: the main motivation of this work. Indeed, the temporal linear stability analysis presents two important drawbacks: (i) the initial perturbation amplitude is a free parameter, which implies that the prefactor of the jet length scaling cannot be predicted; and (ii) the model does not contemplate the energy feedback coming from the jet breakup, as will be described below. Using the temporal stability analysis, Ismail et al. [31] derived two scalings for the breakup length of jets under the action of an axial electric field in the limits of small and large Reynolds numbers. Despite the drawbacks mentioned above, good agreement between those scalings and experimental data was found. The reason lies on their assumptions, reducing the formal logarithmic dependencies mentioned above to constants.
An accurate study of the natural (not externally excited) capillary breakup of jets has been conducted by Umemura [32], who described the breakup mechanism as a “self-destabilizing loop”. In this loop, the energy of the perturbations responsible for the breakup comes exclusively from earlier breakup events. The idea is that the excess of interfacial energy after the interface pinch-off feeds the perturbations that cause the subsequent breakup. In fact, the surface of the drop is, on average, about 20% smaller than that of the jet portion which produces that drop. Although most of the excess of interfacial energy is eventually dissipated in the droplets, a small component of the nonlinear energy spectral density propagates upstream and form imperceptible perturbations. These perturbations grow until causing the next breakup. In this work, we make use of this view of the problem to rationalize our experimental observations.
2. The Breakup Length of Both Ballistic and Flow-Focused Jets
In this work, we aim at showing the universality and determinism of the natural breakup mechanism for capillary jets in the absence of body forces. For this purpose, we consider both ballistic and flow-focused [21] microjets (Figure 1). In a ballistic jet, the pressure applied to the liquid reservoir is essentially transformed into kinetic energy to overcome the resistance offered by surface tension to the jet formation at the orifice exit. In gaseous flow focusing [21], the jet is accelerated driven by both the pressure and viscous forces exerted by a high-speed outer stream in the discharge orifice. This way of focusing the energy necessary for the jet emission allows the reduction of the jet diameter far below that of the discharge orifice D.
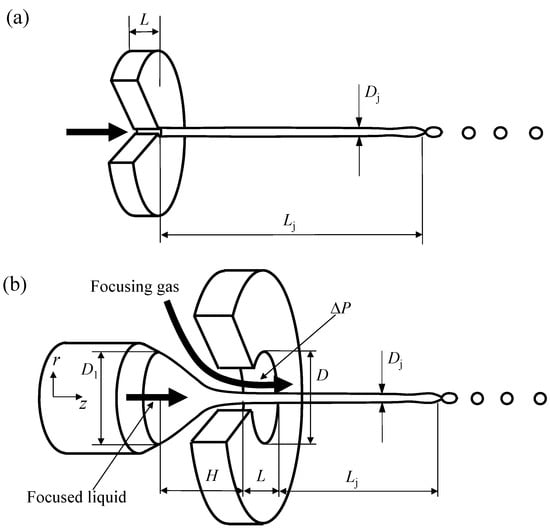
Figure 1.
(a) Ballistic jet issued from an orifice with approximately the same diameter as that of the jet. L represents the axial length of the cylindrical ejector (it may be either the thickness of a plate or the length of a tube). (b) Flow-focused capillary jet emitted from an orifice of diameter D. H is the distance from the front of feeding capillary tube with inner diameter to the inner face of the plate with thickness L where the orifice of diameter D is made. In flow focusing, is the pressure drop along the gas streamlines in the discharge orifice. Note that the diameter is actually not a geometric parameter, since it is obtained from the operating conditions (see text) and cannot be marked in the figure. Despite this, it is assumed equivalent to the diameter of the ejector (either a tube or a plate) in ballistic jets.
The ballistic and flow focusing jet configurations can be characterized in terms of the Weber and Capillary numbers
where and . Both numbers are defined in terms of the liquid density , viscosity and surface tension , as well as both the pressure applied to produce the jet and the emitted flow rate Q. Note that these definitions imply that We is the ratio of inertia to surface tension forces (where is the diameter of a theoretical jet whose kinetic energy comes entirely from ), while Ca is the ratio of viscous to surface tension forces, assuming a characteristic velocity of the liquid equal to . These dimensionless numbers do not involve any geometrical parameter. In the ballistic configuration, since is an indirect parameter that can be obtained from the average axial velocity of the jet assuming , the diameter is thus assumed the same as that of jet, . In flow focusing, due to the viscous diffusion of momentum from the faster gaseous stream to the liquid jet, which increases the jet speed . However, our results show that neither the difference between and (see Figure 2) nor the action of the external environment are significant enough to produce appreciable differences on the eventual breakup mechanism.
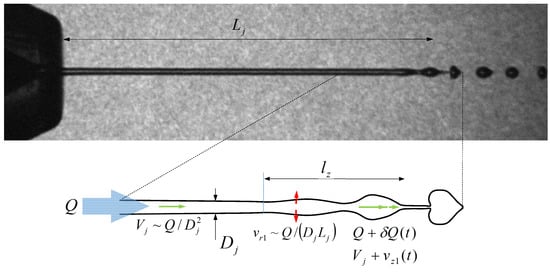
Figure 2.
Scaling of the perturbation in the breakup region.
We focus on the Rayleigh regime in which the jet breaks up axisymmetrically due to surface tension. This regime has technological relevance because it leads to longer jets and more monodisperse collections of droplets. In flow focusing, it is typically obtained for We and , where and are the gaseous environment density and velocity, respectively [3]. In fact, Weber numbers smaller than unity generally lead to dripping, while asymmetric perturbations produce shorter jets and more irregular breakup for We [33]. It means that at high gas flow rates (typically above the point We), jets become shorter and less stable due to the onset of turbulence caused by the rapid nonlinear growth of asymmetric perturbations. On the other hand, ballistic jets break up axisymmetrically for We for analogous reasons. As will be seen, although ballistic and flow-focused jets are emitted in a very different way, the breakup length follows the same scaling law.
Despite significant efforts made in this field [16,17,18,19], it has not as yet been established why the long-term break up of capillary jets spontaneously occurs at a rather deterministic and well-located position for a given set of parameters {We, Ca}, within relatively narrow statistical limits. For the sake of illustration, Figure 3 shows the evolution of the front of a ballistic jet injected at with We = 5 and Ca = from a cylindrical tube into a dynamically negligible environment. The liquid velocity profile is assumed parabolic at the entrance of the computational domain of the tube, which has an axial length equal to the diameter of the tube. The simulation was performed using the free software developed by Popinet [34]. For the user, the numerical convergence of the time averaged jet length has been assessed using levels 10, 11, 12 and 13. No appreciable difference is found between the last two levels. As can be observed, in the long-term evolution the jet spontaneously breaks up at a relatively constant distance from the orifice (the standard deviation is around 13% of the average value).
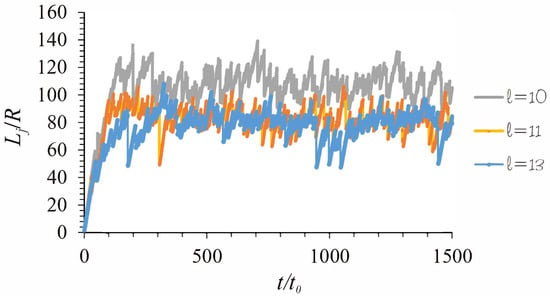
Figure 3.
Distance of the jet front position from the feeding tube exit as a function of time for different levels 10, 11, and 13 of spatial discretization (, [34]). The time is measured in terms of the capillary time , where R is the tube radius. The density and viscosity of the gas environment are 1000 and 100 times smaller than those of the liquid domain, respectively.
Linear Global Instability vs. Nonlinear Breakup Length
We wonder whether both ballistic and flow- focused capillary jets are globally unstable to linear perturbations for a jet length above a critical one. As a fundamental test to assess this, we analyze the global stability of a capillary ballistic jet issuing from a round orifice in the absence of any significant interaction with the environment. The velocity profile at the orifice outlet is assumed parabolic to reflect the experimental conditions, corresponding to a water capillary jet issuing from a long tube with inner diameter mm. Conservation of mass, momentum and surface energy is used to calculate the zeroth-order jet shape, its global linear modes and eigenvalues spectra, according to the numerical method described by Herrada and Montanero [35]. Figure 4 shows the comparison of results from the stability analysis and experiments. To do so, we determine the jet length rendering the capillary jet globally marginally stable for different flow rates Q, which confirms that at least ballistic jets are globally unstable above a critical length. Interestingly, the real jet always exhibits shorter average breakup lengths. Our hypothesis is that the reason for this discrepancy, which increases for increasing We, resides in the finite surface energy excess at breakup and the highly nonlinear perturbation locally exerted by the breakup, which are not contemplated in the global stability analysis. The average breakup lengths measured in the experiments follow the scaling .
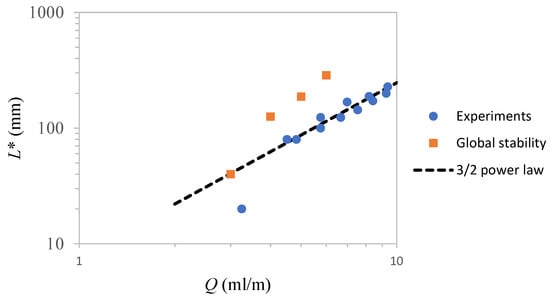
Figure 4.
The critical jet length obtained from the global instability analysis and compared to the average intact jet length L. The results were obtained as a function of the flow rate Q for a water ballistic capillary jet issuing from a PFA tube with inner diameter mm.
The comparison between the linear global instability and nonlinear breakup length gives us the grounds for a simplified analysis leading to a universally valid scaling law for the intact length flow- focused and ballistic capillary jets.
3. Scaling Law
When droplets are formed from the jet breakage, about 80% of the surface energy flowing towards the breakup region leaves the jet in the form of spherical droplets. The excess of surface energy splits into two parts after the breakup: one stays in the drop, provoking oscillations that are eventually dissipated by viscosity, and the other is trapped on the jet side. The latter part propagates in the upstream direction, which is the only route available because the (continuous) jet domain ends at the breakup region. According to Umemura [32], a small amount of this energy is dissipated by viscosity in the jet, while the rest feeds the growth of the perturbation responsible for the next breakup events. This feedback process is akin to a Markov chain which, given the highly nonlinear nature of the breakup, would define its ultimate intrinsically stochastic nature. This approach is currently being investigated and will be published elsewhere.
A Simplified Approach
The liquid incompressibility (i.e., , where v is the liquid velocity vector) implies that the axial distance from the breakup point along which the jet velocity is perturbed (Figure 2) verifies , where and represent the radial and axial perturbation velocities, respectively. Due to the convective character [36] of the jetting regime, the perturbation produced by the breakup travels only a few few jet diameters in the upstream direction, i.e., , which implies that . This is so because is nearly constant around the breakup region. This means that the perturbation radial and axial kinetic energies are commensurate with each other, i.e., , and the radial and axial viscous stresses are also of the same order of magnitude, . These results allow us to retain only the radial kinetic energy and viscous stress in the balance of energy described above.
The production rate of the energy released following the droplet formation scales as . The production rate of the kinetic energy associated with the radial perturbation scales as , while the rate of energy dissipated by viscosity in the jet scales as . Taking into account these scalings, the balance of energy described above leads to the expression
where and are dimensionless constants. This analysis considers the energy balance in the breakup region. Therefore, one may expect the constants and not to depend on the procedure used to emit the jet.
An important element of the present analysis is the scale of the perturbation velocity. As is similarly done in the temporal stability analysis [31], we assume that the residence time in the jet scales as the time for the transverse perturbation to cause the free surface pinching, i.e., . Since and , we get , which implies (i) that the perturbation caused by the breakup can propagate upstream a distance much smaller than the jet length, and (ii) that . This constitutes an essential difference with respect to the scenario assumed in temporal linear stability analysis, in which perturbations grow from the jet inception. The fact that the jet breakup can be regarded as a local phenomenon in terms of the jet length can be considered to be the defining condition of the jetting regime. In fact, if were commensurate with , the growth of the perturbation would be strongly affected by the presence of the discharge orifice, as it is characteristic of the dripping regime.
Taking into account the above scaling for , and absorbing the assumed proportionality constant between and into two new constants and in place of and , Equation (2) becomes
This result can be expressed in dimensionless form as
where and are dimensionless constants proportional to and , respectively. In Equation (4), we have used the Weber and Capillary numbers (1) defined in terms of (instead of ) to avoid experimental errors coming from the measurement of the jet diameter . In this simplification, we have assumed that in ballistic jets, while is the first-order approximation to in flow focusing, as demonstrated by Ganán-Calvo [21]. If , then and . The constant reflects the fraction of the surface energy that feeds the transverse motion in the breakup region, while is an indicator of the ratio of the viscous to the kinetic energies. For low-viscosity jets (), Equation (4) reduces to
where is the Ohnesorge number.
4. Experimental Validation
To validate Equation (4), we make use of: (i) 30 measurements of the length of ballistic jets emanating from the end of a capillary tube with inner diameter of 250 m; (ii) 400 measurements of the length of flow-focused jets using four liquids (see Table 1) and six ejectors (see Table 2); (iii) 10 and 20 measurements conducted by Umemura [32] of the length of ballistic jets emanating from an orifice 0.4 and 1 mm in diameter, respectively; (iv) the length of a nanojet-jet obtained from molecular simulations by Moseler and Landman [37] (the details of the liquid properties and the solid substrate, geometry of the source, and ambient conditions can be found in the original paper); and (v) the lengths calculated in direct numerical simulations of ballistic jets using for the following pairs of (We, Re) numbers: (5,1000), (10,50), (10,100), (10,200), and (15,5000).

Table 1.
Properties of the liquids used in the experiments ofexperiments of flow flow-focused jets.

Table 2.
Micronozzles used in the flow focusing experiments. The third column indicates the dimensions of the discharge orifice. Ejector 6 was described by Beyerlein et al. [38] and Zahoor et al. [27].
In our experiments with ballistic jets, the liquid (Millipore® water) was injected with a precision syringe pump into the air at the atmospheric pressure through an orifice of diameter m. The jet length was determined using a long-time exposure imaging (Canon EOS 2000D) with a telecentric lens (e.g., 0.9× CobaltTL from Edmund Scientific (Barrington, NJ, USA), plus C-Mount adaptor) to avoid spatial distortion. We assumed that the jet ends at the steady position of the sharp transition from the visually undisturbed jet to the larger diameter blurred region (droplets).
In the flow focusing experiments, the liquid jet was focused with helium. The liquid flow rate Q and gas mass flow rate were fixed using a precision syringe pump and a GP1 (Equilibar Inc., Fletcher, NC, USA) gas pressure regulator, respectively. The gas mass flow rate was monitored using a Bronkhorst flow meter. The pressure drop through the orifice, , was calculated by assuming adiabatic flow with a discharge coefficient of (using classical adiabatic quasi-one-dimensional compressible flow calculations). This value was obtained as the average over thousands of measurements with orifice sizes from 20 m to 2 mm. We jetted into both atmospheric pressure and rough vacuum. The jet images were acquired using a Photron FASTCAM SA4 camera (up to 0.5 Mfps) with a Navitar 12× Ultra-Zoom motorized lens and a 10× Mitutoyo objective lens. The jet was illuminated by a laser system (LDX Optronics 250 mW multi-mode fiber coupled 635 nm laser diode powered by a Newport LDP-3830 supply) with a pulse duration between 5 and 500 ns (Figure 5), using a glass diffuser between the laser and the jet chamber to tame the laser speckle effect. The jet length was determined by visually pinpointing the average location of the breakup events during some seconds. We estimate that the magnitude of the breakup length fluctuations is 10–20% of the average value, as also occurs in the simulations (Figure 3).

Figure 5.
(a) A short water microjet emitted with L/min and mg/min. The focused capillary meniscus from whose apex the jet issues can be observed through the translucent plastic nozzle. The jet length is approximately 105 m. (b) A long microjet of a mixture of water/glycerol (20/80 v/v %) emitted with L/min and mg/min. In the two experiments, the jet was emitted with Ejector 4.
We measured jet diameters and lengths for conditions between the onset of dripping and asymmetric breakup. Figure 6 shows the values of We and Ca in our experiments. Two and four orders of magnitude in We and Ca have been explored, respectively. Interestingly, the minimum length occurs for Weber numbers below the classical prediction of Leib and Goldstein [39]. In flow focusing, this is the result of the well-known stabilizing effect of the coflowing gas stream. In both ballistic and flow-focused jets, the boundary layer growing on the inner side of the free surface of low-viscosity jets also delays the convective-to-absolute instability transition [26]. The maximum Weber number for axisymmetric breakup was around 35 for both ballistic and flow-focused jets. This upper limit corresponds to the maximum jet length obtained in the experiments, and it is reached for , where [40].
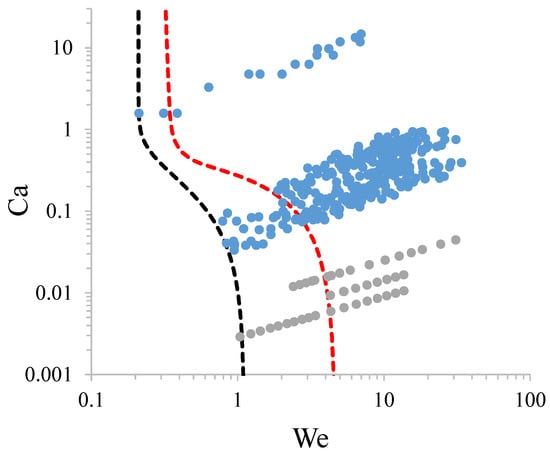
Figure 6.
Values of We and Ca in our experiments. The grey and blue symbols correspond to ballistic and flow-focused jets, respectively. The red line corresponds to the predicted convective-to-absolute instability transition for a cylindrical capillary jet in a vacuum [39]. The black line is a guide to the eye. The upper cloud of points corresponds to the liquid with the highest viscosity.
The best fit of (4) to all the data (experimental and numerical, published and unpublished) considered in this work is represented in Figure 7. To obtain this fit, we calculated the probability density function PDF of the logarithmic error for different values of and . A normal distribution with zero average is fitted to that function (Figure 8). The optimum values of the constants and are those leading to the normal distribution with minimum variance. The minimum variance was obtained for and . The agreement of the resulting scaling law (4) with both experiments and numerical simulations is remarkable. The relatively large value of indicates the relatively small fraction of surface energy necessary to feed the upstream perturbations.
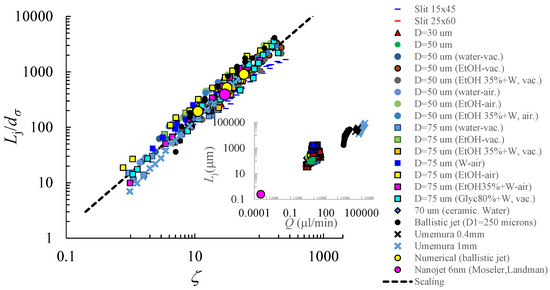
Figure 7.
Breakup length as a function of obtained from both experiments and numerical simulations (symbols) and calculated from (4) (line). The legend indicates the discharge orifice dimensions, the liquid, and the environment (vacuum or air). The legend also indicates the point corresponding to the nanojet [37]. The inset shows as a function of Q. The properties of the liquids used are given in Table 1.
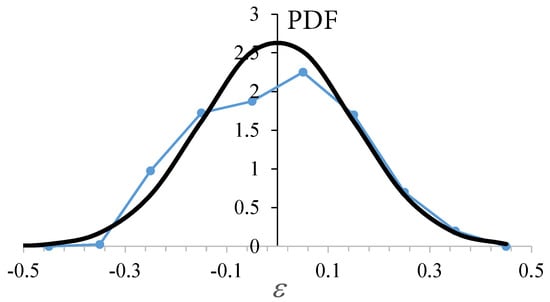
Figure 8.
Probability density function of the logarithmic errors around the scaling law (4) for and (symbols), and the corresponding normal distribution with zero average and variance equal to 0.0225 (line).
Equation (4) exhibits remarkable agreement with experimental and numerical data for optimum values of and within a large parameter space and using different geometries. The result reported by Moseler and Landman [37] is of particular interest since its remarkable agreement with the scaling law provides a strong support to the new physical description and model proposed: its validity is demonstrated from about 200 nm to at least 100 mm in jet length (i.e., a minimum of 6 orders of magnitude) and about 10 orders of magnitude in flow rate. Using this model, one can select the best combination of liquid properties, nozzle outlet area and operating parameters to obtain the desired jet length, diameter and velocity for specific applications. This is remarkably valuable for designing and operating microjet devices in SFX [15,41], where liquid formulations should also be compatible with protein crystals buffer solution.
5. Concluding Remarks
As occurs in the classical temporal stability model, the breakup mechanism assumed in this work relies on the growth of the most unstable capillary mode, which explains the size of the produced droplets and the distance between them. The question is where and how this mode is excited. While the temporal stability approach assumes that the dominant capillary mode is triggered in the jet birth, the model adopted here presumes that the ultimate long-term source of excitation of this mode is the breakup region. In other words, we assume and affirm that the breakup region is the overall long-term source of excitation which determines the average jet breakup length. In effect, in most of the well-controlled experimental realizations, the jet breaks up in a rather deterministic manner in a well-located position. It has not as yet been elucidated why the jet birth could constitute a regular source of perturbation that explains that experimental fact. On the contrary, the jet breakup is a quasi-periodic source of energy which may regularly feed the perturbations leading to each breakup event. On the other hand, the temporal stability approach may suggest that the breakup length should depend on the details of the ejection procedure and geometry, which are expected to play a relevant role in the excitation of the dominant capillary mode. However, the experimental and numerical results presented here, in line with the very early observations of Smith and Moss [30] and later ones [28,29] among others, indicate that the breakup length essentially and solely depends on the liquid properties (, and ) and operating parameters ( and Q), which reinforces the idea that the perturbation origin is in general not located in the ejector. The model adopted here does not exclude the possibility that the temporal stability approach may satisfactorily explain the breakup length measurements under certain experimental conditions. Indeed, certain nozzle configurations producing sufficiently strong local effects (gas turbulence, whistling, mechanical or electrohydrodynamic excitation, etc.) or the presence of ad-hoc elements in the nozzle may overcome the otherwise dominant role of the breakup.
In the absence of these artificial or occasional natural effects, the frequency needed to excite the most dangerous wavelengths for the breakup of our microscopic jets range from hundreds of kHz to MHz in most cases. These frequencies are not likely to be produced by natural or unintended artificial macroscopic mechanical means. Thus, the energy content of the mechanical noise produced in any laboratory within this frequency range is expected to be negligible. In particular, the noise generated by the pumps typically have frequencies at least four or five orders of magnitude lower than those to which the microjets are sensitive.
This work rationalizes experimental observations about the breakup length of steady capillary jets spontaneously breaking in the absence of significant body forces and interaction with the fluid environment. This is remarkably valuable for designing and operating microjet devices in SFX [15,41]. Further investigation on the role played by these forces and interactions on the natural breakup length is still required.
Author Contributions
Conceptualization, A.M.G.-C., S.B.; methodology, A.M.G.-C., S.B. and H.N.C.; software, J.M.L.-H. and M.A.H.; validation, A.M.G.-C. and S.B.; formal analysis, A.M.G.-C., J.M.M. and H.N.C.; investigation, A.M.G.-C., B.G.-R., J.K., M.H., M.O.W., F.C.-M., J.M.L.-H., J.M.M. and M.A.H.; resources, A.M.G.-C. and S.B.; data curation, A.M.G.-C. and S.B.; writing—original draft preparation, A.M.G.-C., J.M.M. and H.N.C.; writing—review and editing, A.M.G.-C., J.M.M., J.M.L.-H., S.B. and H.N.C.; visualization, A.M.G.-C.; supervision, A.M.G.-C., S.B. and H.N.C.; project administration, A.M.G.-C. and S.B.; funding acquisition, A.M.G.-C., S.B. and H.N.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministerio de Economía y Competitividad (Spain) through the projects DPI2016-78887 and PID2019-108278RB. This work is also partly funded by the Cluster of Excellence ‘CUI: Advanced Imaging of Matter’ of the Deutsche Forschungsgemeinschaft (DFG)—EXC 2056—project ID 390715994, and the German Science Foundation (DFG) through the Gottfried Wilhelm Leibniz program.
Acknowledgments
We would like to thank Luigi Adriano (DESY) for technical support. M.H. acknowledges support from the Joachim Herz Foundation through an Add-on Fellowship. F.C.-M. acknowledges support through the project funded by the European Union’s 2020 Research and Innovation Program under the Marie Sklodowska-Curie Grant Agreement No 838997.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Plateau, J. Sur les figures d’equilibre d’une masse liquide sans pesanteur. Mem. Acad. R. Belg. Nouv. Ser. 1849, 23. [Google Scholar]
- Rayleigh, L. On the instability of jets. Proc. Lond. Math. Soc. 1878, s1-10, 4–13. [Google Scholar] [CrossRef] [Green Version]
- Eggers, J.; Villermaux, E. Physics of liquid jets. Rep. Prog. Phys. 2008, 71, 036601. [Google Scholar] [CrossRef]
- Chapman, H.N.; Fromme, P.; Barty, A.; White, T.A.; Kirian, R.A.; Aquila, A.; Hunter, M.S.; Schulz, J.; DePonte, D.P.; Weierstall, U.; et al. Femtosecond X-ray protein nanocrystallography. Nature 2011, 470, 73–79. [Google Scholar] [CrossRef]
- Boutet, S.; Lomb, L.; Williams, G.J.; Barends, T.R.; Aquila, A.; Doak, R.B.; Weierstall, U.; DePonte, D.P.; Steinbrener, J.; Shoeman, R.L.; et al. High-Resolution Protein Structure Determination by Serial Femtosecond Crystallography. Science 2012, 337, 362–364. [Google Scholar] [CrossRef] [Green Version]
- Schlichting, I. Serial femtosecond crystallography: The first five years. IUCrJ 2015, 2, 246–255. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Spence, J.C.H. XFELs for structure and dynamics in biology. IUCrJ 2017, 4, 322–339. [Google Scholar] [CrossRef] [PubMed]
- Aquila, A.; Hunter, M.S.; Doak, R.B.; Kirian, R.A.; Fromme, P.; White, T.A.; Andreasson, J.; Arnlund, D.; Bajt, S.; Barends, T.R.; et al. Time-resolved protein nanocrystallography using an X-ray free-electron laser. Opt. Express 2012, 20, 2706–2716. [Google Scholar] [CrossRef] [PubMed]
- Gati, C.; Oberthuer, D.; Yefanov, O.; Bunker, R.D.; Stellato, F.; Chiu, E.; Yeh, S.M.; Aquila, A.; Basu, S.; Bean, R.; et al. Atomic structure of granulin determined from native nanocrystalline granulovirus using an X-ray free-electron laser. Proc. Natl. Acad. Sci. USA 2017, 114, 2247–2252. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seibert, M.M.; Ekeberg, T.; Maia, F.R.; Svenda, M.; Andreasson, J.; Jönsson, O.; Odić, D.; Iwan, B.; Rocker, A.; Westphal, D.; et al. Single mimivirus particles intercepted and imaged with an X-ray laser. Nature 2011, 470, 78–81. [Google Scholar] [CrossRef] [PubMed]
- Barends, T.R.; Foucar, L.; Ardevol, A.; Nass, K.; Aquila, A.; Botha, S.; Doak, R.B.; Falahati, K.; Hartmann, E.; Hilpert, M.; et al. Direct observation of ultrafast collective motions in CO myoglobin upon ligand dissociation. Science 2015, 350, 445–450. [Google Scholar] [CrossRef]
- Pande, K.; Hutchison, C.D.; Groenhof, G.; Aquila, A.; Robinson, J.S.; Tenboer, J.; Basu, S.; Boutet, S.; DePonte, D.P.; Liang, M.; et al. Femtosecond structural dynamics drives the trans/cis isomerization in photoactive yellow protein. Science 2016, 352, 725–729. [Google Scholar] [CrossRef] [Green Version]
- Stagno, J.R.; Liu, Y.; Bhandari, Y.R.; Conrad, C.E.; Panja, S.; Swain, M.; Fan, L.; Nelson, G.; Li, C.; Wendel, D.R.; et al. Structures of riboswitch RNA reaction states by mix-and-inject XFEL serial crystallography. Nature 2017, 541, 242–246. [Google Scholar] [CrossRef] [PubMed]
- Kupitz, C.; Olmos, J.L., Jr.; Holl, M.; Tremblay, L.; Pande, K.; Pandey, S.; Oberthür, D.; Hunter, M.; Liang, M.; Aquila, A.; et al. Structural enzymology using X-ray free electron lasers. Struct. Dyn. 2017, 4, 044003. [Google Scholar] [CrossRef] [PubMed]
- Wiedorn, M.O.; Awel, S.; Morgan, A.J.; Ayyer, K.; Gevorkov, Y.; Fleckenstein, H.; Roth, N.; Adriano, L.; Bean, R.; Beyerlein, K.R.; et al. Rapid sample delivery for megahertz serial crystallography at X-ray FELs. IUCrJ 2018, 5, 574–584. [Google Scholar] [CrossRef] [Green Version]
- Kalaaji, A.; Lopez, B.; Attane, P.; Soucemarianadin, A. Breakup length of forced liquid jets. Phys. Fluids 2003, 15, 2469–2479. [Google Scholar] [CrossRef]
- Garcia, F.; Gonzalez, H. Normal-mode linear analysis and initial conditions of capillary jets. J. Fluid Mech. 2008, 602, 81–117. [Google Scholar] [CrossRef]
- González, H.; García, F. The measurement of growth rates in capillary jets. J. Fluid Mech. 2009, 619, 179–212. [Google Scholar] [CrossRef]
- García, F.J.; González, H.; Castrejón-Pita, J.R.; Castrejón-Pita, A.A. The breakup length of harmonically stimulated capillary jets. App. Phys. Lett. 2014, 105, 094104. [Google Scholar] [CrossRef]
- Montanero, J.M.; Gañán-Calvo, A.M. Dripping, jetting and tip streaming. Rep. Prog. Phys. 2020, 83, 097001. [Google Scholar] [CrossRef]
- Gañán-Calvo, A.M. Generation of Steady Liquid Microthreads and Micron-Sized Monodisperse Sprays in Gas Streams. Phys. Rev. Lett. 1998, 80, 285–288. [Google Scholar] [CrossRef]
- Gordillo, J.M.; Pérez-Saborid, M.; Gañán-Calvo, A.M. Linear stability of co-flowing liquid-gas jets. J. Fluid Mech. 2001, 448, 23–51. [Google Scholar] [CrossRef]
- DePonte, D.P.; Weierstall, U.; Schmidt, K.; Warner, J.; Starodub, D.; Spence, J.C.H.; Doak, R.B. Gas dynamic virtual nozzle for generation of microscopic droplet streams. J. Phys. D Appl. Phys. 2008, 41, 195505. [Google Scholar] [CrossRef] [Green Version]
- Si, T.; Li, F.; Yin, X.Y.; Yin, X.Z. Modes in flow focusing and instability of coaxial liquid-gas jets. J. Fluid Mech. 2009, 629, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Si, T.; Li, F.; Yin, X.Y.; Yin, X.Z. Spatial instability of coflowing liquid-gas jets in capillary flow focusing. Phys. Fluids 2010, 22, 112105. [Google Scholar] [CrossRef] [Green Version]
- Gañán-Calvo, A.M.; Herrada, M.A.; Montanero, J.M. How does a shear boundary layer affect the stability of a capillary jet? Phys. Fluids 2014, 26, 061701. [Google Scholar] [CrossRef]
- Zahoor, R.; Bajt, S.; Sarler, B. Influence of Gas Dynamic Virtual Nozzle Geometry on Micro-Jet Characteristics. Int. J. Multiph. Flow 2018, 104, 152–165. [Google Scholar] [CrossRef]
- McCarthy, M.J.; Molloy, N.A. Review of Stability of Liquid Jets and the Influence of Nozzle Design. Chem. Eng. J. 1974, 7, 1–20. [Google Scholar] [CrossRef]
- Sterling, A.; Sleicher, C.A. The instability of capillary jets. J. Fluid Mech. 1975, 68, 477–495. [Google Scholar] [CrossRef]
- Smith, S.W.J.; Moss, H. Experiments with mercury jets. Proc. R. Soc. Lond. A Math. Phys. Eng. 1917, 93, 373–393. [Google Scholar]
- Ismail, A.S.; Yao, J.; Xia, H.H.; Stark, J.P.W. Breakup Length of Electrified Liquid Jets: Scaling Laws and Applications. Phys. Rev. Appl. 2018, 10, 064010. [Google Scholar] [CrossRef]
- Umemura, A. Self-destabilising loop of a low-speed water jet emanating from an orifice in microgravity. J. Fluid Mech. 2016, 25, 146–180. [Google Scholar] [CrossRef]
- Rosell-Llompart, J.; Gañán-Calvo, A.M. Turbulence in pneumatic flow focusing and flow blurring regimes. Phys. Rev. E 2008, 77, 036321. [Google Scholar] [CrossRef]
- Popinet, S. Basilisk Flow Solver and PDE Library. Available online: http://basilisk.fr/ (accessed on 23 July 2018).
- Herrada, M.A.; Montanero, J.M. A numerical method to study the dynamics of capillary fluid systems. J. Comput. Phys. 2016, 306, 137–147. [Google Scholar] [CrossRef]
- Huerre, P.; Monkewitz, P.A. Local and Global Instabilites in Spatially Developing Flows. Annu. Rev. Fluid Mech. 1990, 22, 473–537. [Google Scholar] [CrossRef]
- Moseler, M.; Landman, U. Formation, Stability, and Breakup of Nanojets. Science 2000, 289, 1165–1169. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beyerlein, K.R.; Adriano, L.; Heymann, M.; Kirian, R.; Knoska, J.; Wilde, F.; Chapman, H.N.; Bajt, S. Ceramic micro-injection molded nozzles for serial femtosecond crystallography sample delivery. Rev. Sci. Instrum. 2015, 86, 125104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leib, S.J.; Goldstein, M.E. Convective and absolute instability of a viscous liquid jet. Phys. Fluids 1986, 29, 952–954. [Google Scholar] [CrossRef]
- Gañán-Calvo, A.M.; Montanero, J.M. Revision of capillary cone-jet physics: Electrospray and flow focusing. Phys. Rev. E 2009, 79, 066305. [Google Scholar] [CrossRef]
- Wiedorn, M.O.; Oberthür, D.; Bean, R.; Schubert, R.; Werner, N.; Abbey, B.; Aepfelbacher, M.; Adriano, L.; Allahgholi, A.; Al-Qudami, N.; et al. Megahertz serial crystallography. Nat. Commun. 2018, 9, 4025. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).