The simulations include two stages. In the first stage, the transition from the homogeneous state to the spatially periodic state is simulated. In this case, the virtual LC layer with the homogeneous planar alignment is transformed by an electric field to the state with an in-plane periodic texture. In the second stage, the optical properties are evaluated by solving Maxwell equations using the final difference time domain (FDTD) method for the waveguide geometry, when the injected light waves package propagates along the wave vector of the field-induced grating.
The numerical simulations are performed using the author’s LCDTDK and FDTDK software programs, which have had a rather long developing and testing curve (more than 20 years). These software programs allow simulations for both texture (liquid crystal director distribution) and optical problems for LC systems with complicated designs.
Numerical modeling is based on the solution of the complete system of equations of both the continuum theory of liquid crystals with arbitrary boundary conditions and Maxwell’s equations, taking into account a variety of properties that characterize real liquid crystal systems; however, for ease of perception, only the most key equations are presented below, with an indication of the simplifications allowed for our specific system.
2.1. Simulations of the Flexoelectric Instability
The texture calculations are based on solving general equations of the liquid crystal continuum theory for the 3D LC domain.
The governing equations for finding the LC director (
n = (
nx, ny, nz)) distribution are as follows:
where
μ is the Lagrange multiplier, which is due to the constraint
where
is the rotational viscosity of LC and
F is the free energy density, expressed as:
where
K1,
K2 and
K3 are splay, twist and bend elastic coefficients, respectively;
Pf is the flexoelectric polarization;
ε0 ≅ 8.85 × 10
−12 F/m is the vacuum dielectric constant;
E is the electric field vector. The elastic parameters used in this work are variable but close to those of the experimental LC (
K1 = 15 pN,
K2 = 7 pN) [
3,
4]. A value of 0.1 Pa s for the rotational viscosity (
γ) used in dynamics simulations is within the range of quite typical values for nematic LCs (typical range is 0.03–0.2 Pa·s [
31]). The flexoelectricity is of principal significance in this work, and it is assumed that
e1 = 10 pC/m and
e3 = 30 pC/m, so the difference |
e1 −
e3| = 20 pC/m is close to that found in [
3,
4]. As was already mentioned, in the case described here, the low frequency dielectric anisotropy (
εa) is zero, so the dielectric tensor
ε is reduced to a scalar value
ε and no corresponding dielectric torque appears. Our virtual LC is nonchiral and the corresponding term responsible for the natural helix pitch is omitted in (3).
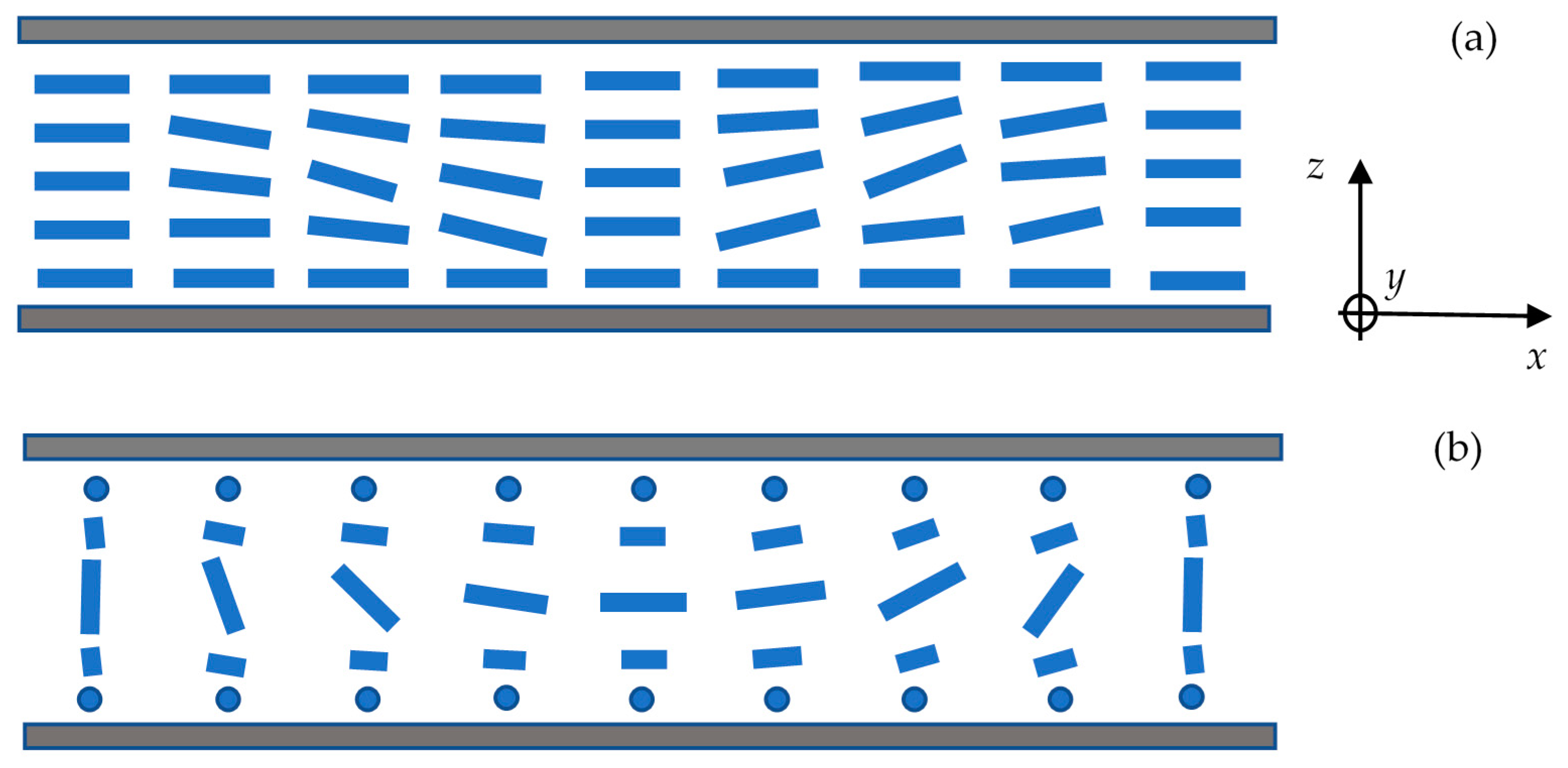
The model boundary conditions are variable, including those close to ones achieved experimentally using the polyimide alignment layer. It should be reiterated that after the rubbing, the polyimide film results in the planar alignment with a small pretilt angle (a value of 2° with respect to the y-axis is used) and strong anchoring (rigid anchoring conditions are used in the model).
Because the director field is not homogeneous, the electric field distribution is also not a homogeneous one. In order to find the electric field distribution, Equation (1) is coupled with the Maxwell equations and ; thus, we assume that the LC is the ideal dielectric with zero free charge density in the bulk.
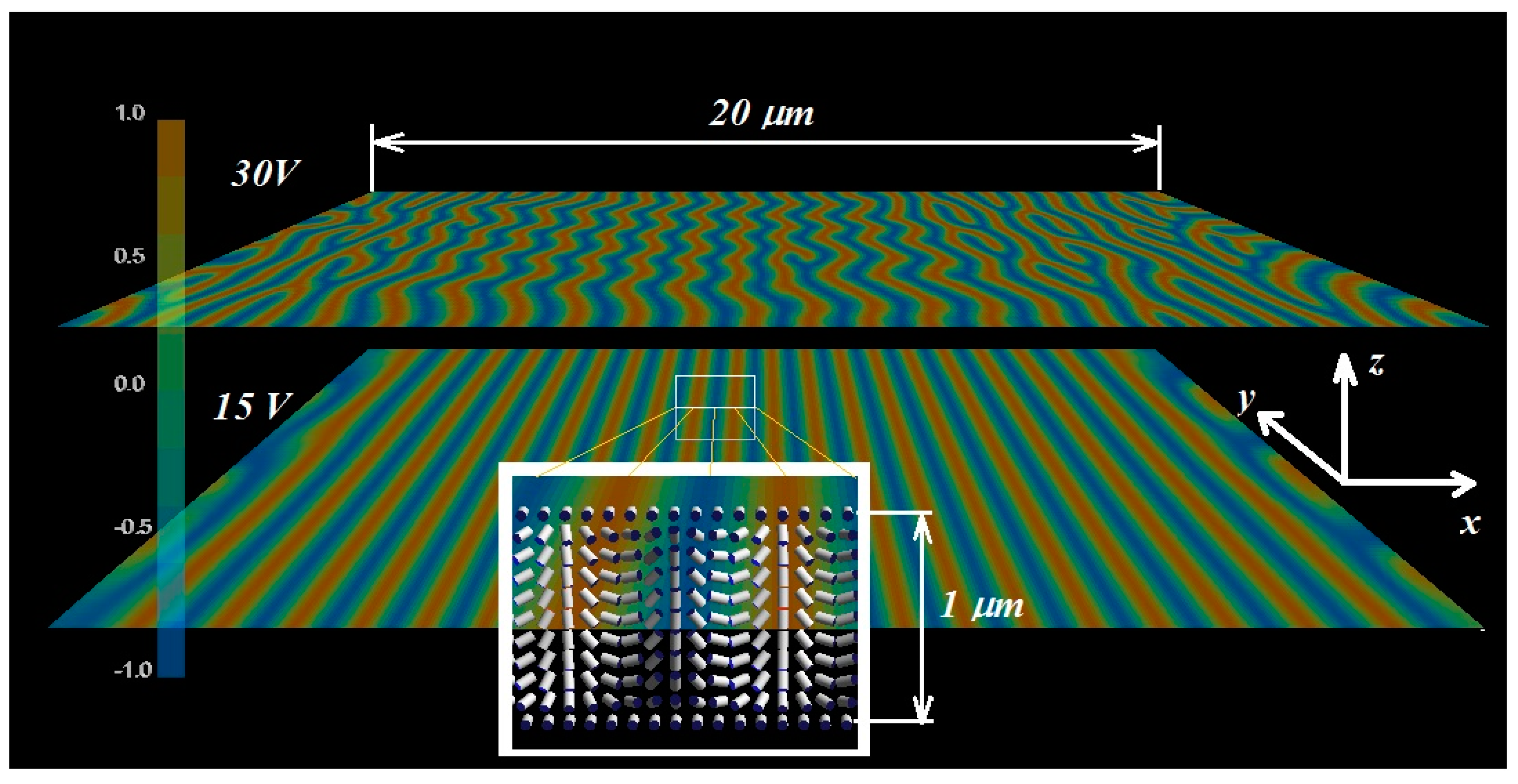
The spatial distribution of the LC director in middle of the layer, which appears as a result of the flexoelectric instability effect, is shown in
Figure 2 at voltages of various magnitudes. Note that at zero voltage, the distribution of the LC director is uniform in all three dimensions. In this case, the orientation plane of the director is parallel to the
yz-plane and the director’s pretilt angle with respect to the
y-axis is 2° (this is a typical value for the pretilt angle achieved in real LC systems). As can be seen, a periodic grating appears in the electric field and the distribution of the director becomes inhomogeneous in both the
z- and
x-directions. The director rotates around the
y-direction as we move along the
x-direction. The distance
p along the
x-direction at which the director makes a full revolution is comparable to the layer thickness. For example, in
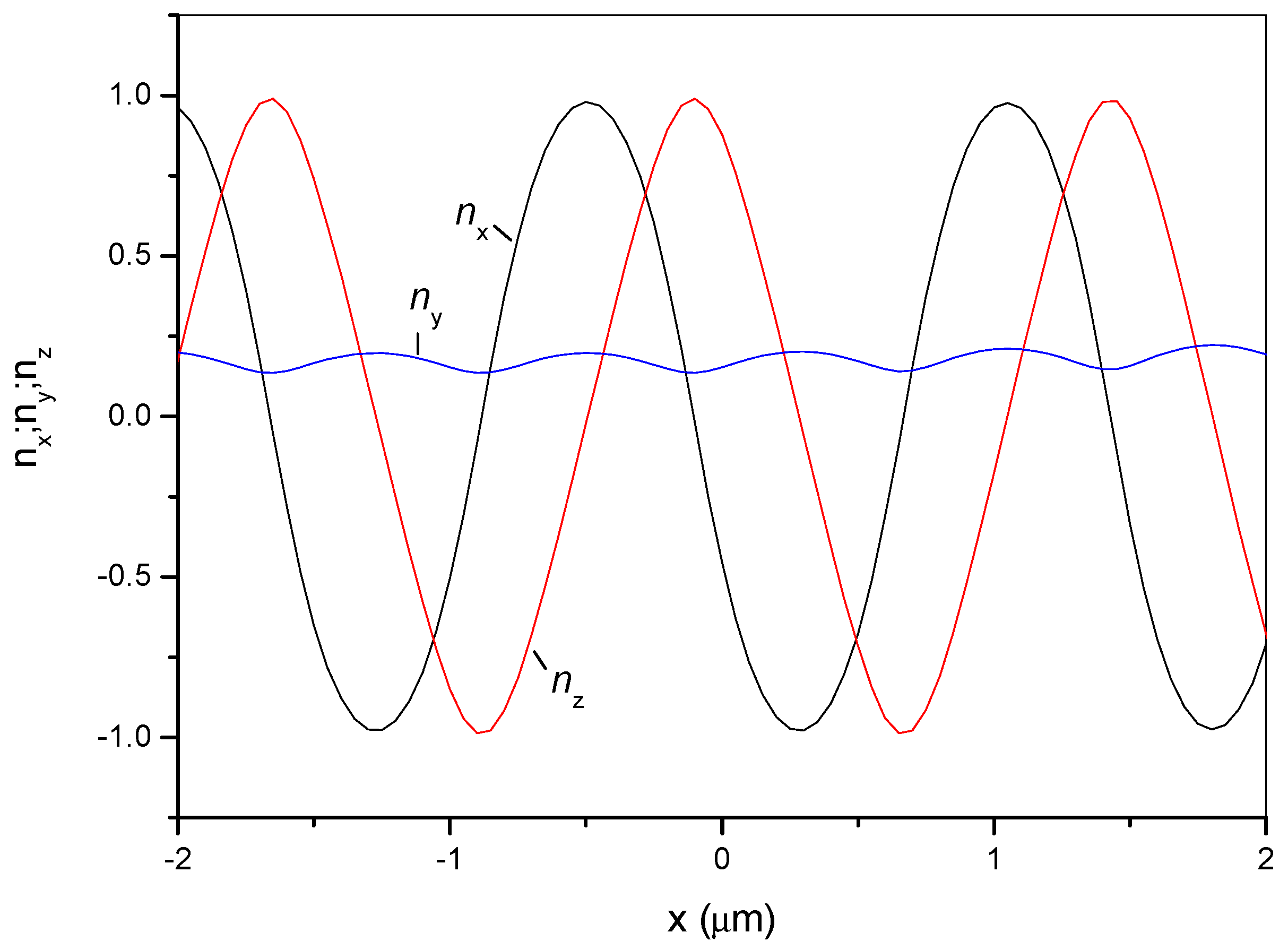
Figure 3, which shows the distribution for a layer with a thickness of 2 μm, the period
p is approximately 1.6 μm. In the center of the layer, the functions describing the
x- and
z-components of the director are close to sinusoids, with a phase shift of 90° even in a sufficiently strong field (10 V/μm). In this case, the
y-component of the director is rather small; that is, the director experiences rotation that is almost in the vertical
xz-plane. The sign of the rotation is defined by the sign of the phase shift between curves for
nx and
nz, which is reversed if we change either direction of the electric field or the sign of the flexoelectric coefficient difference (
e1–
e3).
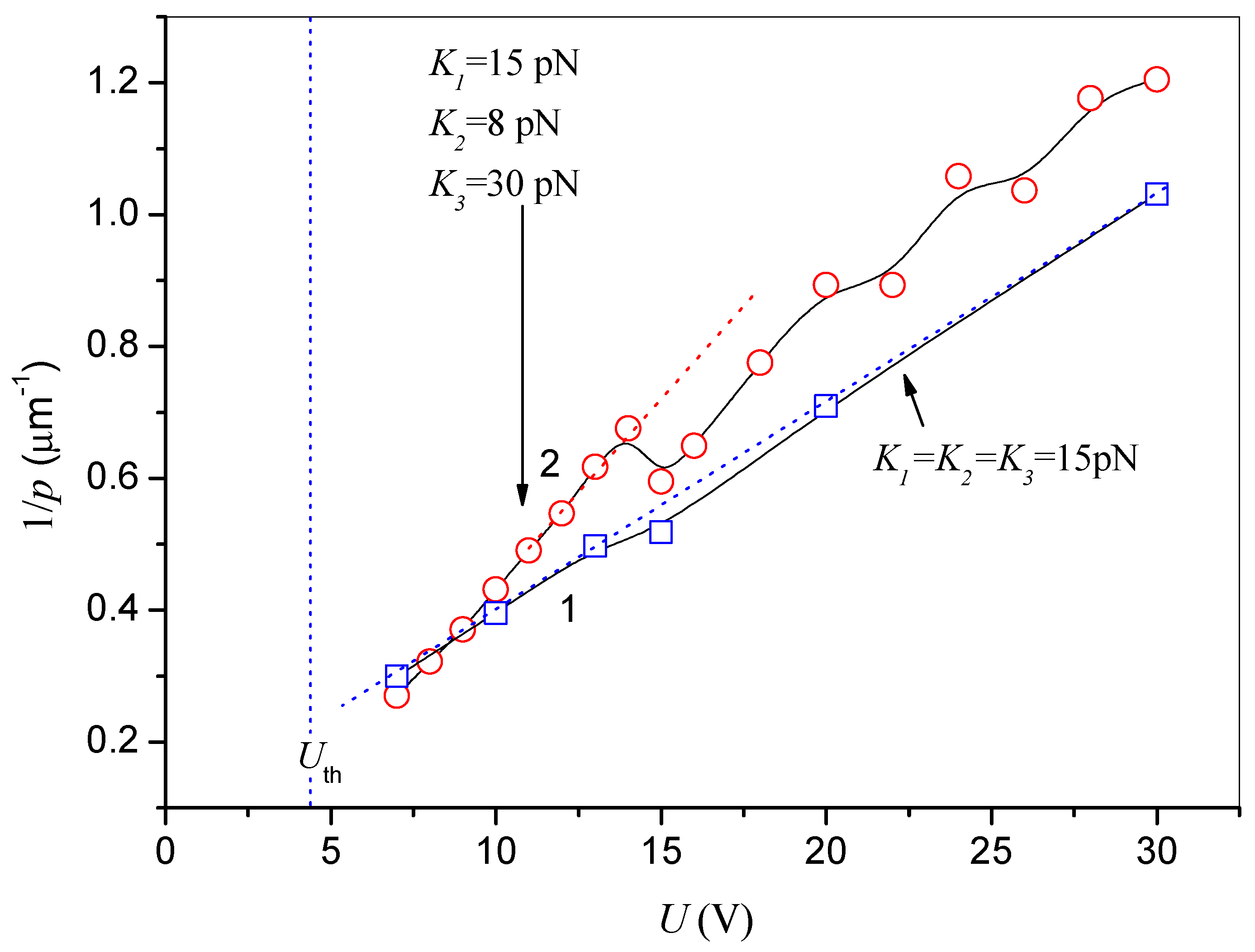
Figure 4 shows the dependence of the spatial frequency (1/
p) on the magnitude of the applied voltage. As can be seen, up to very strong fields, when the director in the center of the layer experiences rotation in an almost vertical plane, these dependences are close to the linear; that is, they can be represented in the following form:
where the value of
a can be defined as the extrapolation frequency at zero voltage
U, when in reality the grating does not exist, since the effect is characterized by the threshold voltage
Uth.
As can be seen in
Figure 4, the rate of change in the spatial frequency as the voltage changes is determined by the coefficient
b, which in turn depends on the ratio between the elastic constants. As follows from the data in
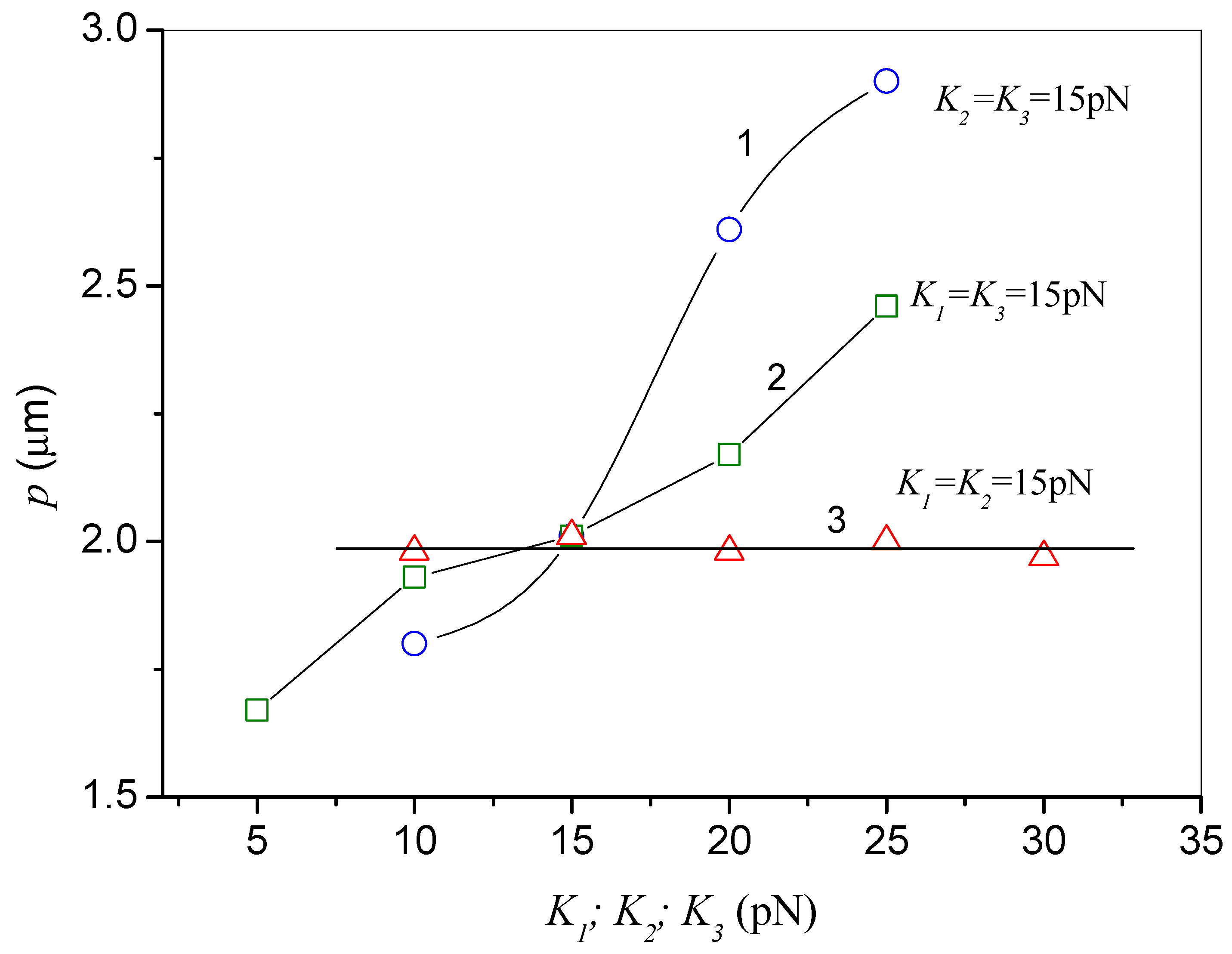
Figure 5, the spatial period depends on the elastic constants
K1 and
K2, but doesn’t depend on
K3. A decrease in
K2 leads to an increase in
b (compare also curves 1 and 2,
Figure 4), and accordingly a greater sensitivity of the spatial frequency to the voltage. In the case of the one-constant approximation, when
K1 = K2 = K3 = K, analytical expressions were obtained in [
1,
2] for both the observed optical period
Wth =
pth/2 of the induced grating and for the threshold voltage
Uth of the appearance of the grating:
where
. Since in our case the dielectric anisotropy
εa = 0, then
μ = 0, and from Equation (5) one can get
Wth =
d = 2 μm and
Uth ≅ 4.5 V, which is in good agreement with the simulations (curve 1,
Figure 4).
At sufficiently high electric fields, the calculated value of the spatial frequency oscillates somewhat as the electric voltage
U increases (see curve 2 in
Figure 4 at
U > 15 V). The analysis shows that these oscillations are caused by edge effects associated with the finite size of the modeled domain, which also defines the
x-size of the induced grating (in our case, this size is 20 μm in the
x-direction,
Figure 2). It can also be found that at high voltages, the distribution can become inhomogeneous in the
y-direction, as shown in
Figure 2 at
U = 30 V.
The dependence of the induced grating period on each of the elasticity constants at two other fixed constants is shown in
Figure 5. As can be seen, the dependences of the grating period on
K1 and
K2 are quite pronounced. For example, an increase in
K1 from 10 pN to 30 pN leads to an increase in the period by about 1.5 times. It is interesting that the period
p does not depend on
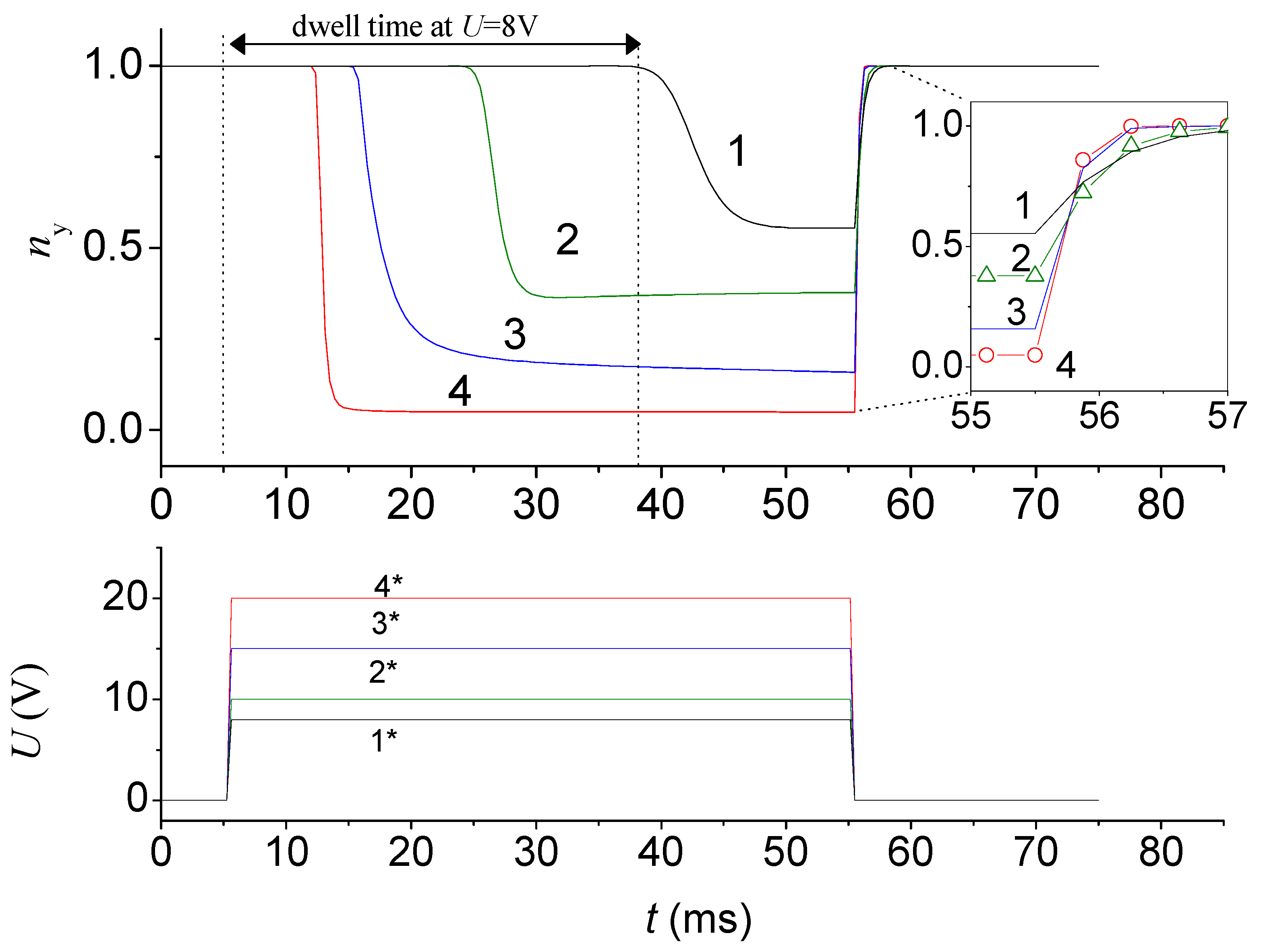
K3. The dynamics of the appearance and relaxation of the grating at different amplitudes of the voltage pulse is illustrated by the data in
Figure 6. These data were obtained for the
x-size of the modeled domain
Lx = 20 μm, which of course coincides with the size of the induced grating. The analysis shows that the dynamics does not depend on the
y-size as long as there are no inhomogeneities in the distribution of the director in the
y-direction (I remind that the
y-direction is for the field-off alignment). To reduce the computation time, as well as to exclude the influence of inhomogeneities in the
y-direction, the data were obtained for a
y-size of 100 nm, which in fact corresponds to the two-dimensional case.
Here, the distribution of the director in the
y-direction is assumed to be uniform. The analysis also shows that after the application of an electric field, deformation occurs at the edges of the modeled domain and propagates at a certain speed to its center. Therefore, to analyze the time response, a spatial point is chosen in the center of the computational domain in
x,
y and in the middle of the layer. In this case, the appearance of the grating is accompanied by decreasing the
y-component of the director, which changes together with other components but experiences the least oscillations (
Figure 3).
Figure 6 shows that the dynamics can be characterized by three characteristic times. First, deformation in the center of the simulated domain begins to appear after a certain dwell time (
td). The second time (
ton) is for the equilibrium state over the entire computational domain, which includes the time
td, and in fact is the time taken to induce an equilibrium grating. After switching off the electric field, very fast relaxation occurs with a characteristic time
toff. As can be seen from the inset in
Figure 6, this time lies in the sub-millisecond range and decreases as the amplitude of the voltage pulse increases; thus, this time can be associated with the period of the induced grating and can be estimated as:
where
K is an effective elastic module and
q = 2π/
p is the voltage-dependent wavenumber of the induced grating. For example, for
K = 15 pN,
γ = 0.1 Pa s and
p = 2 μm, from (6) we obtain
toff ≅ 0.7 ms, which is in good agreement with the numerical data for the lowest voltage in the inset to
Figure 6. Note that the relaxation occurs uniformly over the entire simulated domain, with the exception of small near-boundary regions, where the relaxation time is found to be somewhat longer.
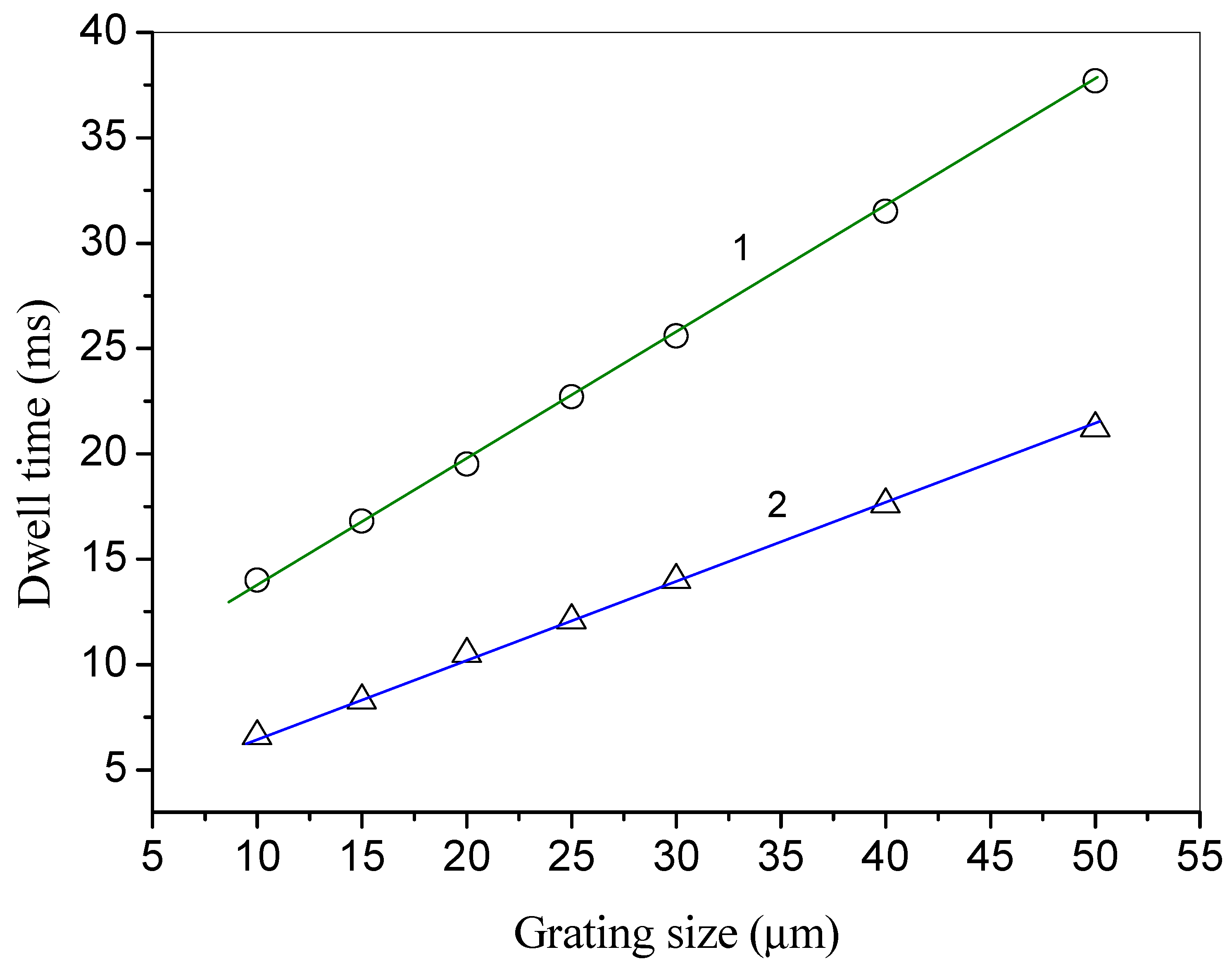
The origin of the dwell time
td is well illustrated by the data in
Figure 7. As can be seen, the dwell time increases linearly with increases in the size of the simulated domain (the size of the induced grating). This is because the dwell time is due to the propagation time of the deformation from the edges of the simulated domain to its center.
The fact that the time (
ton), which includes the dwell time, is determined by its size is very important for understanding the low speed of formation of the periodic texture in the experiments, where static electric fields [
3] had to be used. At the same time, understanding the nature of the dwell time allows us to offer a liquid crystal system with a high response speed. Indeed, the boundaries of the modeled domain are, in fact, the region of nucleation of an elastic deformation wave, which propagates to the central part of the simulated domain; therefore, if on the second boundary of the alignment surface, a periodic structure is created from artificial anchoring “defects”, where the conditions for the vertical alignment of the LC director are achieved at short intervals (
Figure 8,
t = 0), then as a result we can obtain a system for which the total time
ton of the grating induction is determined not by its total size, but the period of modulation of the anchoring conditions. In the example in
Figure 8, the anchoring modulation period at the upper boundary of the LC layer is 10 μm and the corresponding time
ton is about 6 ms, regardless of the overall grating size. Experimentally, the modulation of the anchoring boundary conditions can be carried out using a local focused ion beam treatment [
27] of a rubbed polyimide film, which is usually used for the LC alignment.
2.2. Photonic Properties (FDTD Simulations)
The FDTD method is widely used in modern optical simulations. It is based on a direct solution for the Maxwell equations in the time domain. The basics of the FDTD method are described in numerous sources. I would like to recommend the EMPossible site [
32], where one can find quite detailed and useful lectures explaining different aspects of the method and possible numerical implementations, which can be a good starting point for developing complicated software.
The author’s FDTDK software module used in this work is directly bound to the LC texture module LCDTDK and is briefly described in [
28]. The dielectric properties of materials in FDTDK are defined in terms of the spatial distribution of the dielectric tensor components and by considering their spectral dispersion. The spectral dispersion is considered within framework of the popular, multiple-oscillator Lorentz–Drude model.
It is important to say that in the current study, the spectral dispersion is not taken into account. The virtual LC material is described by frequency-independent values of the principal components of the dielectric tensor (ε|| = 3.06, ε⊥ = 2.31). The last values of the dielectric tensor components correspond to the principal refractive indices n|| = 1.75 and n⊥ = 1.52, which are close to typical for many LC materials (for example, the E7-LC from Merck).
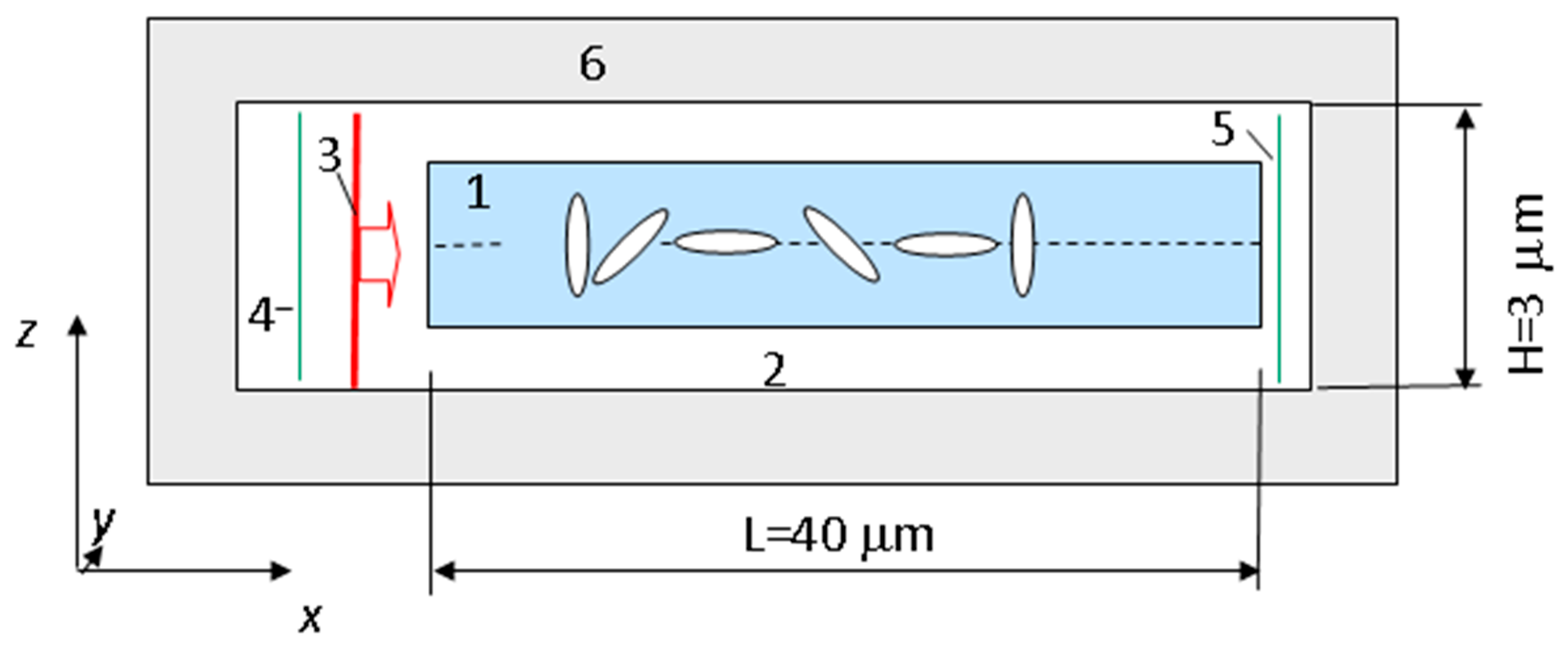
The scheme of the FDTD-simulated space domain is shown in
Figure 9. Because the LC layer is homogeneous along the
y-axis, all of the
d/
dy derivatives vanish and the optical problem is reduced to the 2D problem in the
xz-plane, which allows for significant increases in efficiency of the FDTD simulations. The LC-layer (1) with a thickness of 2 μm and a length
L of 40 μm is placed in a virtual medium (2), with a refractive index of 1.46. Because all principal refractive indices of the LC are higher, the last one allows for a waveguiding regime for the light impinged into the LC layer from the unidirectional light source (3). The virtual sensor (4) is placed in the shadow of the light source (3) and registers only the light reflected by the DLH layer, while the sensor (5) is for the transmitted light. The electrodes used to apply the voltage are neglected in the sense that their refractive indices are set to be the same as for the medium (2). The uniaxial perfectly matched layers (6) prevent reflections from boundaries of the calculated space domain.
The light source (4) generates a pulse of the electromagnetic field propagating along the x-axis. The light has linear polarization in the yz-plane at 45o with respect to the y-axis; thus, both TM- and TE-polarized modes are excited in the LC layer. The magnitude of the pulse is constant in the z-direction. The pulse represents a sine wave (λ = 550 nm) modulated by the Gaussian waveform with a 1/e-height duration of ~1 fs. This results in a rather wide spectrum of generated light, which allows for calculations of the reflectance spectra in a wavelength range of 500 to 4000 nm. The sensor (4) registers across time the components of the electromagnetic field. To obtain the reflectance and transmittance spectra, the ratio of the energy flux in the x-direction (Px) of the electromagnetic field at sensors (4) and (5) to the energy flux irradiated by light source (Pls) is calculated. The values Px and Pls are calculated versus the wavelength by taking the Fourier transform of the field registered by the sensors and finding x-components of the Poynting vector at the sensors and light source (3) positions. Because the x-components of the Poynting vector for the reflected light are negative, the reflectance magnitudes in spectra shown below are also negative. The spectral resolution in the calculated spectra is defined by total registration time for the electromagnetic field. In our calculations, the total registration time is about 2000 fs, which corresponds to resolutions better than 1 nm in the visible spectral range and a few nanometers in the near-infrared range.
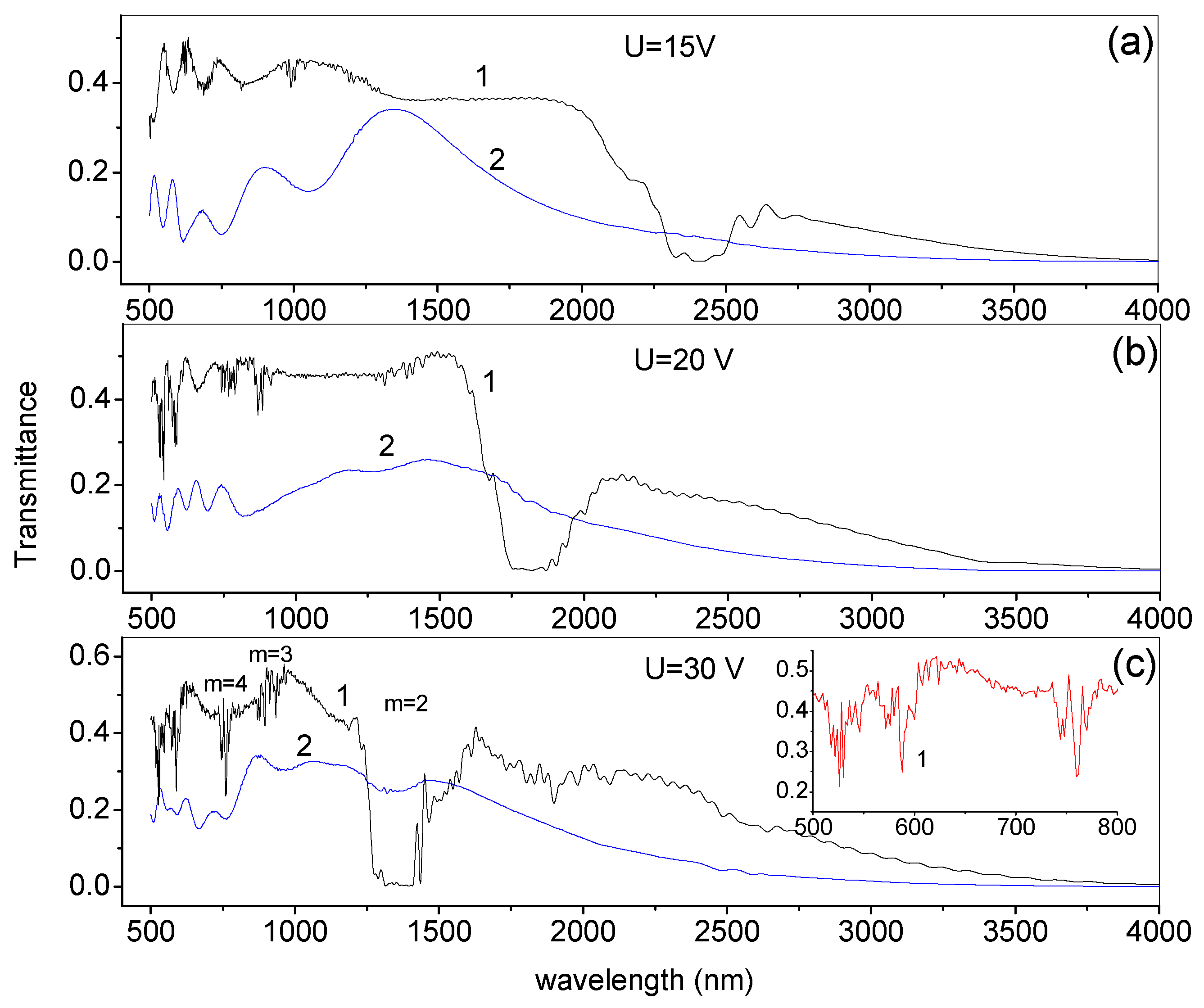
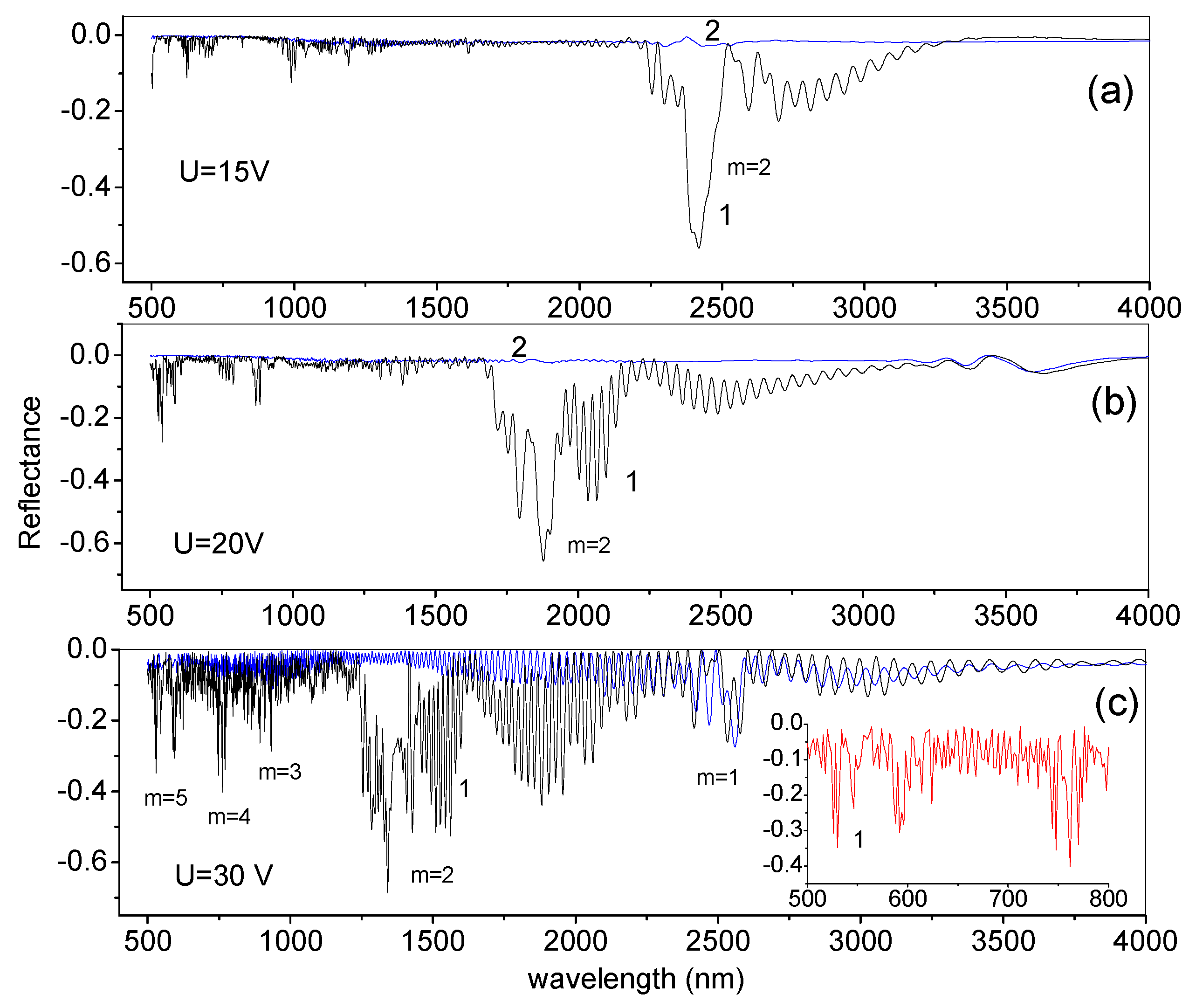
The transmittance and reflectance spectra for
z- and
y-polarized modes are shown in
Figure 10 and
Figure 11. The spectra show pronounced photonic stop bands in the wave intervals of 2200–2700, 1700–2200 and 1200–1600 nm for the applied voltages of 15, 20 and 30 V, respectively. The edge positions (
λ1,
λ2) of these stop bands can be estimated from the Bragg law equation:
where n
⊥ and n
|| are principal refractive indices of the LC material for the diffraction order
m = 2. Actually, at
m = 2, exactly the same situation occurs as in the cholesteric liquid crystals. Nevertheless, there is a principal difference from the cholesteric LCs, which is connected to the tilt of the director in the
yz-plane when the director rotates around the
y-axis (
Figure 3). Because of the tilt, the director state with the maximum positive value of the
nz director component is not equivalent to the state with the minimal negative
nz component. The last property results in that the Bragg reflection is allowed not only for
m = 2, but also for
m = 1. Moreover, the reflections of the higher orders (
m = 3, 4, 5) are very visible, especially in the reflectance spectra at the highest voltage (
Figure 11c).
Photonic stop bands are characteristic only for
z-polarized light. This is due to the peculiarities of modulation of the LC director field, when it is the director projection onto the
xz-plane that undergoes rotation, while the
y-component experiences only insignificant oscillations (
Figure 3). The reflection spectra clearly show not only stop bands associated with modulation of the LC director field, but also fine oscillations caused by the Fabry–Perot effect, showing interference of reflections from the boundaries of a waveguide with a length of 40 μm. These subtle oscillations are present in both the spectra of
z-polarized light and
y-polarized light; however, aside from the Fabry–Perot effect, it is easy to see in the reflection spectra of
z-polarized light that the photonic stop bands are split into several sub-bands. It can be assumed that the nature of this splitting is the same as in the case of a deformed helix in cholesteric LCs [
27,
28]. A sufficiently high reflection in the region of higher-order stop bands (
m = 4, 5; see insets in
Figure 10c and
Figure 11c) makes it possible to use them to excite a laser effect in the visible region of the spectrum in the range of 500–800 nm, as was implemented in [
27].
Finally, one cannot fail to note the extremely wide spectral range of electric tuning for the positions of the stop bands, which for layers with a thickness of one to two microns, can cover both the near-IR and visible ranges.