Magnetism and Thermomechanical Properties in Si Substituted MnCoGe Compounds

Abstract

MnCoGe-based compounds have been increasingly studied due to their possible large magnetocaloric effect correlated to the magnetostructural coupling. In this research, a comprehensive study of structure, magnetic phase transition, magnetocaloric effect and thermomechanical properties for MnCoGe_1−xSi_x is reported. Room temperature X-ray diffraction indicates that the MnCoGe_1−xSi_x (x = 0, 0.05, 0.1, 0.15 and 0.2) alloys have a major phase consisting of an orthorhombic TiNiSi-type structure with increasing lattice parameter b and decreasing others (a and c) with increasing Si concentration. Along with M-T and DSC measurements, it is indicated that the T_c value increased with higher Si concentration and decreased for structural transition temperature T_str. The temperature dependence of the magnetization curves overlaps completely, indicating that there is no thermal hysteresis, and it is shown that the transition is the second-order type. It is also shown that the decreased magnetization on the replacement of Si for Ge decreases the value of −ΔS_M from −ΔS_M~8.36 J kg⁻¹ K⁻¹ at x = 0 to −ΔS_M~5.49 J kg⁻¹ K⁻¹ at x = 0.2 with 5 T applied field. The performed Landau theory has confirmed the second-order transition in this study, which is consistent with the Banerjee criterion. The magnetic measurement and thermomechanical properties revealed the structural transition that takes place with Si substitution of Ge.

1. Introduction

New technology of magnetic refrigeration (MR) that was recently developed has been an alternative to conventional gas compression (CGC). This shows that this new cooling technology is more effective and environmentally friendly. MR is based upon the magnetocaloric effect (MCE), where the adiabatic temperature changes the material upon the application of a magnetic field [1]. Highly advanced industries require materials that come with a large MCE near to room temperature. Hence, immense efforts have been made to meet these rapidly growing requirements for the past few decades. Due to the structural behavior and strong magnetic coupling, it is clear that the magnetostructural transition (MST) of the first order produces a large MCE. A lot of the ongoing studies on magnetic refrigeration are mainly focused on perovskite manganites [2], Gd₅(Si_xGe_1−x)₄ [3], MnFeP_1−xAs_x [4], La(Fe_1−xSi_x)₁₃ [5], NiMn-based Heusler alloys [1], and MM’X alloys (M and M’ denote 3D transition elements and X denotes main group elements) [6,7,8]. The intermetallic MnCoGe-based compound is a typical member of the MM’X family that maintains sufficient physical contents and application prospects that are promising. It has a double crystalline structure, TiNiSi-type orthorhombic structure and Ni₂In-type hexagonal structure [8]. It was previously found that MnCoGe_1−xSi_x offers the best affordable magnetic material compound while still providing a magnetic entropy change and decent refrigeration capacity [9]. This finding is interesting as the compound can provide a pleasing magnetocaloric effect at a lower price for a magnetic refrigeration material.

This work has investigated the thermomechanical properties of MnCoGe_1−xSi_x compounds to understand the essence of the magnetic transition in MnCoGe_1−xSi_x. From the study, the structural change and magnetic phase transition were effectively shifted from a suitable Si concentration into the temperature region of interest. This led to achieving high addition of the GMCE. It is also found that the unit cell volume and lattice parameters of all alloys were found to reduce with the increase in Si content. In addition, the peaks shifted to a higher angle due to a lower atomic radius of Si, ~ 1.32 Å, whereas Ge, ~ 1.37 Å.

2. Experimental Details

In the preparation of a batch of MnCoGe_1−xSi_x compounds (with x = 0–0.2), sufficient amounts of Mn (99.9%), Ge (99.999%) powder, Co (99.9%), and Si (99.999%) chips were arc melted in the vicinity of an argon atmosphere. Approximately 3% of Mn above the stoichiometric amount of the starting materials is needed. This is important for the evaporation that occurs in order to reimburse for the weight lost throughout the melting process. In order to attain a good homogeneity of the samples, the ingots were melted 5 times in a row. They were then closed in a quartz tube and hardened at a temperature of 900 °C for a duration of 120 h. The samples were then characterized by Philips X’Pert PW3040 Powder X-ray Diffractometer (XRD) (Malvern Panalytical, NSW, Australia) (Cu K5-007 radiation, 5-007 = 15,418 Å). They were then analyzed by Rietveld refinement analysis by using the Fullprof program. The phase transition temperatures were analyzed using TA instrument Q100 Differential Calorimeter (DSC) (TA Instruments, New Castle, DE, USA) at room temperature. A Quantum Model P650 14 T Physical Property Measurement System (PPMS) (Quantum Design, San Diego, CA, USA) was used to measure magnetization using the option of a vibrating sample magnetometer. This was achieved in a temperature range of 10–330 K and up to 0.01 T of the applied fields. The thermomechanical measurement was conducted in a Perkin Elmer 8000 dynamic mechanical analyzer (DMA) (Perkin Elmer, Waltham, MA, USA) in the tension mode. The heating rate for the measurement was set at 278 K/min.

3. Results and Discussion

3.1. Structure Properties

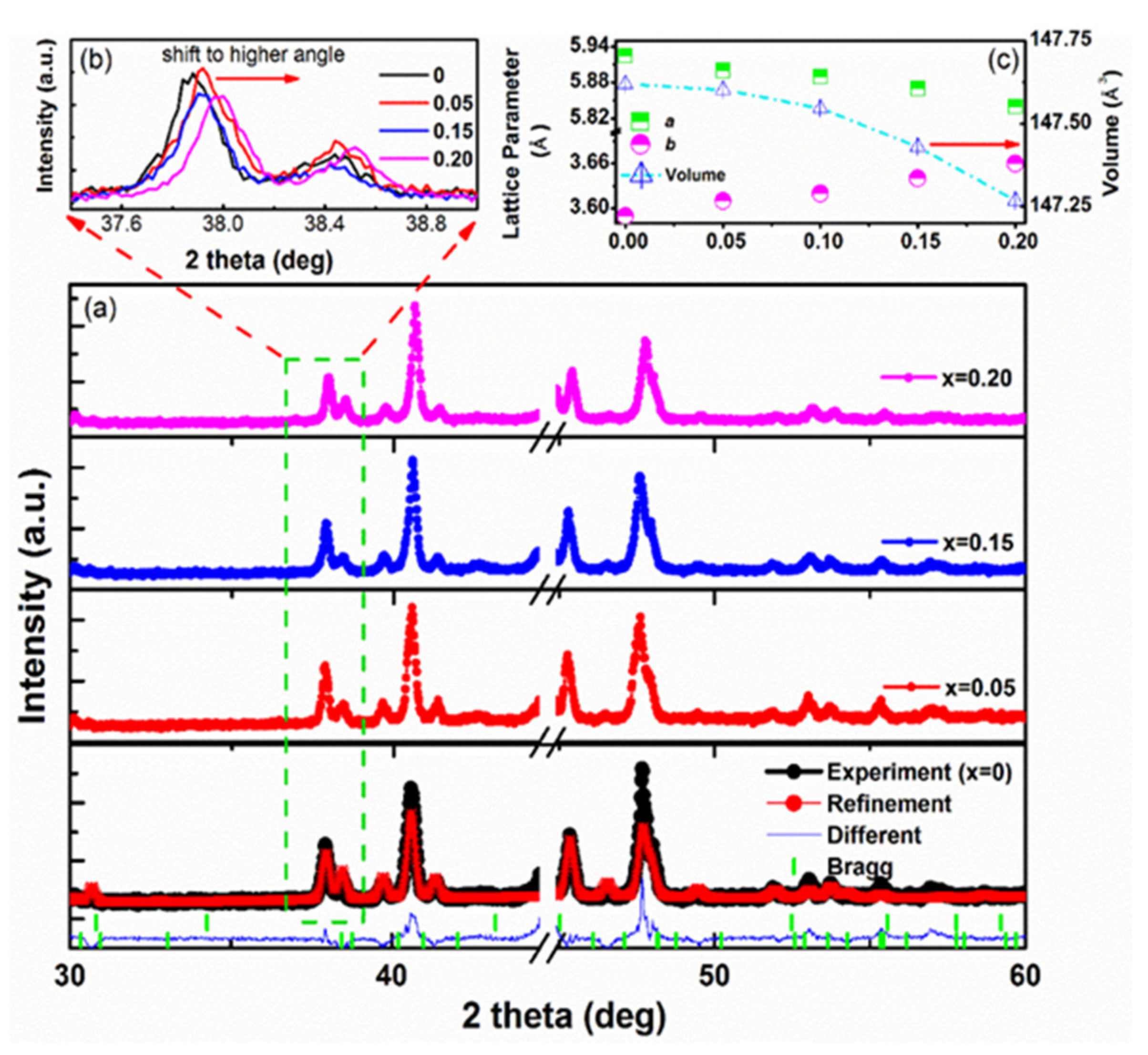
The X-ray diffraction patterns of the MnCoGe_1−xSi_x (x = 0, 0.05, 0.1, 0.15, and 0.2) alloys are shown in Figure 1a. The XRD patterns show that the MnCoGe_1−xSi_x alloy has a major phase comprised of an orthorhombic TiNiSi-type structure with no reflection to a hexagonal Ni₂In-type structure. This is observed with an increase in the Si concentration up to x = 0.2. All diffraction angles (2θ) shifted to the higher angle with the increase in Si concentration. A gradual displacement to the right can be seen for each XRD result (see Figure 1b).

Figure 1. (a) Refined XRD pattern of MnCoGe_1−xSi_x (x = 0.05, 0.10, 0.15, and 0.20) measured at room temperature. (b) The inset shows the patterns for the indicated range of the MnCoGe_1−xSi_x samples, representing that the Bragg peaks shifted to the higher angles. (c) Rietveld refinement analysis indicating the unit cell volumes and lattice parameters.

The Rietveld refinement analysis indicated in Figure 1c showed that the lattice parameter b increases from 3.592 Å at x = 0 to 3.664 Å at x = 0.2. However, the lattice parameters a and c were found to decrease at a (5.925 Å at x = 0 to 5.843 Å at x = 0.2) and c (6.942 Å at x = 0 to 6.891 Å at x = 0.2), which resulted in the unit cell volume of all alloys decreasing at (147.62 ų at x = 0 to 147.27 ų at x = 0.2). As the Si content increases, the peaks seem to be shifted to the higher angle positions related to the lower atomic radius of Si, ~ 1.32 Å, compared to Ge, ~ 1.37 Å. Their unit cell volumes and lattice parameters are correlated by a = a_ortho = c_hex, b = b_ortho = a_hex, c = c_ortho = √3a_hex, and V = V_ortho = 2V_hex [10]. With the increasing Si concentration, the lattice shrinks along the a ortho axis and expands along the b ortho axis, inducing a decrease in volume of the orth. These phenomena are also related to the rule of the valence electron. According to this, the main-group atoms (Si/Ge) occupy the 2c sites. In contrast, the transition-metal atoms with significantly less (Mn) and higher (Ni) valence electrons tend to occupy the 2a and 2d sites, respectively [11].

3.2. Magnetic Phase Transitions

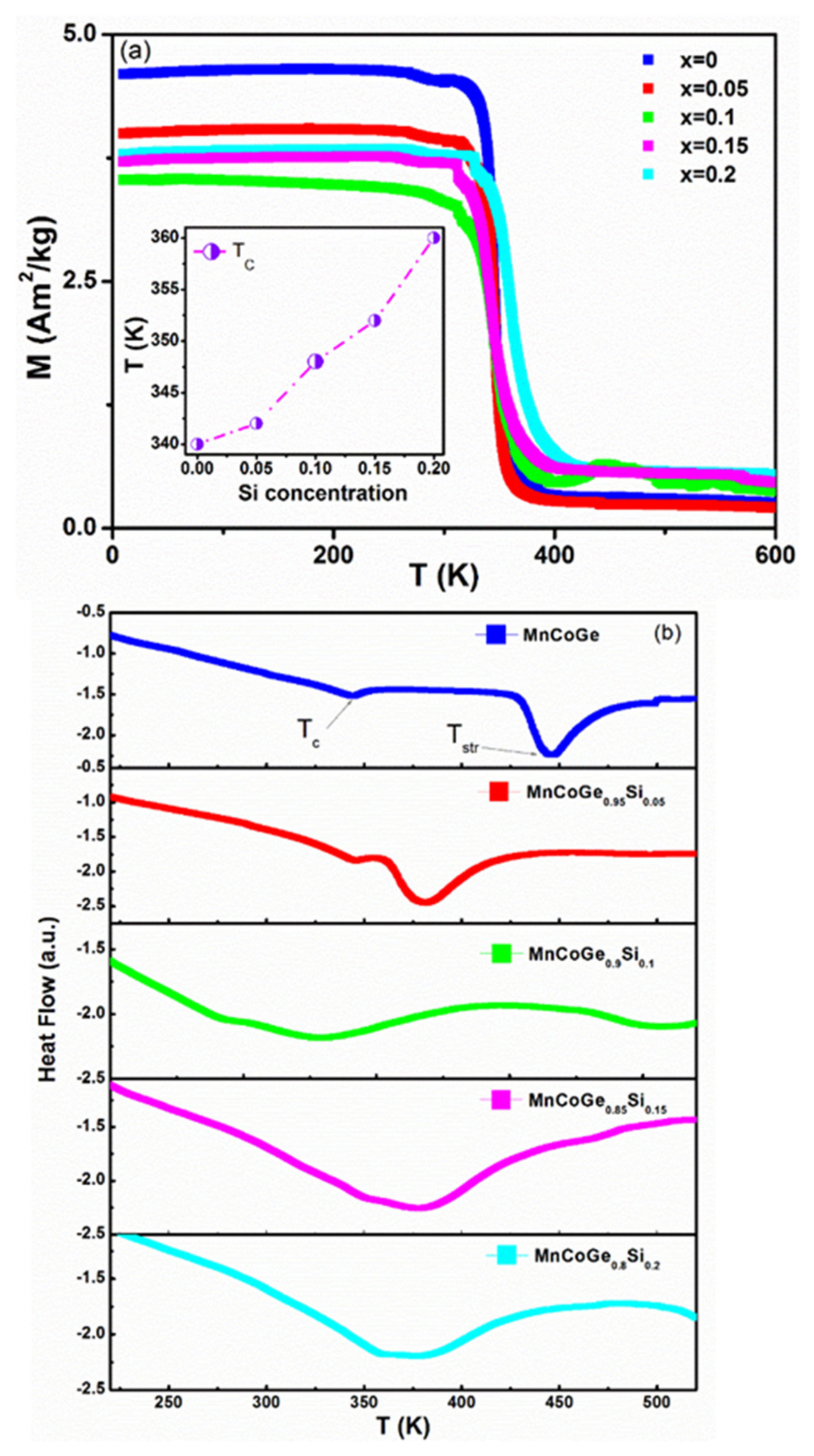
The change in the distance between the magnetic atoms is well known to directly alter the coupling exchange, resulting in a shift in the temperature transition [12]. The Curie temperature increases and decreases in accordance with variations in the lattice parameter b, suggesting that the interaction of the Mn–Mn moments along this axis is significant in defining the Curie temperature. Figure 2a presents the temperature dependence of the magnetization of MnCoGe_1−xSi_x alloys measured in the field of 0.01 T from 10–600 K. In the case of compositions x = 0.00 to 0.2, it was found that the Curie temperature slightly increases (340 K–360 K) with the increase in the Si concentration, as indicated in the inset in Figure 2a. These have shown the same pattern with the previous report on these materials with a different composition, where the maximum Curie temperature reported is T_c = 374 K [9]. In addition, the transition for compounds x > 0.05 was deemed to be incomplete and not reaching the zero moment, as demonstrated by the fact that the structural transition temperatures were higher than 430 K. Consequently, this behavior is thought to be related to the necessity for a lower Si atomic radius in order to change the symmetry of the TiNiSi-type orthorhombic structure to the hexagonal Ni₂In-type structure at a higher temperature.

Figure 2. (a) M–T curves measured for MnCoGe_1−xSi_x (x = 0.05, 0.1, 0.15, and 0.2). The inset shows the pattern of Curie temperature with an increased Si concentration. (b) DSC curves measured ranging from 300 to 500 K. The arrows indicate the Curie temperature structural transition.

In addition, the temperature dependence of the magnetization of MnCoGe_1−xSi_x was measured for heating and cooling in order to determine the thermal hysteresis characteristic of the first-order transition [13,14]. The cooling and heating curves overlap completely, indicating that there is no thermal hysteresis, and it is shown that the transition is the second-order type.

The magnetic moment, structural transition temperature T_str, cell volume, and Curie temperature are all strongly dependent on the concentration of Co vacancy rather than on Ge vacancy [15]. However, Figure 2b shows that the structural transition T_str determined by the DSC measurements decreased from 450 K for x = 0 to 360 K for x = 0.2. This indicates that substituting Ge with a minor percentage of Si (20%) led to a drop in the structural transition temperature and a slight increase in the Curie temperature.

3.3. The Magnetocaloric Effect

Figure 3a,b show the magnetization curves of MnCoGe_0.95Si_0.05 and MnCoGe_0.85Si_0.15 for fields within the range B = 0–5 T near the Curie temperatures with 4 K interval steps. It is apparent that the results are overlapped for increasing and decreasing fields of the compounds. This finding suggests that there are no observable magnetic hysteresis loss effects for the increase in Si content in MnCoGe_1−xSi_x compounds. In addition, Figure 3c,d represent the Arrott plots (M² versus B/M) for MnCoGe_0.95Si_0.05 and MnCoGe_0.85Si_0.15, which were found to exhibit features by the Banerjee criterion of a second-order transition for all samples. Thus, the results show that the ferromagnetic transition at T_C in MnCoGe_1−xSi_x is a second-order transition to the substitution of Si for Ge for Si content up to x = 0.2.

Figure 3. Magnetization curves with an applied field of 0–5 T for the compounds of (a) MnCoGe_0.95Si_0.05 and (b) MnCoGe_0.85Si_0.15. The second-order transition Arrott plot types for both compounds are shown in (c,d).

For the whole range of MnCoGe_1−xSi_x compounds (x = 0–0.2) of their magnetization curves, the magnetic entropy change, −ΔS_M, has been calculated to increase and decrease field values as a function of the temperature and magnetic field (ΔB = 0–5 T). The increase in magnetic entropy was obtained by applying the standard Maxwell relation [16]:

$$-\Delta S_{\mathrm{M}}\left(T,H\right)={{\displaystyle \int }}_0^H{\left(\frac{\partial M}{\partial T}\right)}_H\left(dH\right)$$

(1)

Figure 4a shows that the −ΔSM peak moderately widens towards the higher temperatures with an increase in the magnetic field. As a result, it is observed that the compounds hold a behavior of a field-induced transition from a paramagnetic to a ferromagnetic state. The variations in magnetic entropy for MnCoGe_1−xSi_x alloys (x = 0.05, 0.1, 0.15, and 2.0) around the ferromagnetic temperatures have been presented from increasing and decreasing applied fields (with slightly no hysteresis loss). This is to indicate the feasibility of different experimental and correlated analytical approaches to establish the isothermal entropy change [17]. The values of the entropy at the corresponding Curie temperatures indicated in Figure 4b are slightly decreased, with ΔB = 0–5 T : −ΔS_M~8.36 J kg⁻¹ K⁻¹ at T_C = 340 K at MnCoGe; −ΔS_M ~ 6.92 J kg⁻¹ K⁻¹ at T_C = 342 K at MnCoGe_0.95Si_0.05; −ΔS_M~6.33 J kg⁻¹ K⁻¹ at T_C = 348 K at MnCoGe_0.90Si_0.10; −ΔS_M ~ 6.04 J kg⁻¹ K⁻¹ at T_C = 352 K at MnCoGe_0.85Si_0.15; −ΔS_M~5.49 J kg⁻¹ K⁻¹ at T_C = 360 K at MnCoGe_0.80Si_0.20. The peak |ΔS_M| value of MnCoGe_0.95Si_0.05 is higher than the |ΔS_M| value reported in Mn_0.9Ti_0.1CoGe (−ΔS_M~4.2 J kg⁻¹ K⁻¹) [18] and MnCoGe_0.97Al_0.03 (−ΔS_M~3.5 J kg⁻¹ K⁻¹) [19]. Decreased magnetization on the replacement of Si for Ge similarly decreases the value of −ΔS_M, which is associated with the interaction between Mn–Mn moments.

Figure 4. (a) Temperature dependence of the isothermal magnetic entropy change, −∆S_M, (T, H) for MnCoGe_1−xSi_x compounds (x = 0, 0.05, 0.10, 0.15, 0.20) calculated from magnetization isotherms with 0–5 T field change applied. Increasing fields are denoted by closed symbols, while decreasing fields are denoted by open symbols. (b) The RC and −ΔS_M of MnCoGe_1−xSi_x compounds for 0–5 T.

Moreover, the fundamental requirement for magnetic refrigeration does not only rely on a large magnetic entropy change, but also refrigeration efficiency evaluation such as the refrigeration capacity (RC) also needs to be considered [20]. The RC indicates the amount of heat transmitted during one thermodynamic cycle. Substituting Ge with Si leads to a decrease in RC from 325 at x = 0 to 278 at x−0.2. This behavior related to replacing Si on Ge leads to a change in the interplanar crystal distance. The generated 3D-band can occasionally minimize the electron splitting exchange interactions such that it decreases the value of ΔS_M and RC values.

3.4. Thermomechanical Testing

Figure 5 depicts the behavior of the storage modulus (E′) and the loss modulus (E″), which are the real and imaginary elements of the complex modulus during tension mode testing. The elastic and viscous behavior of a viscoelastic sample is represented by the storage and loss moduli [21]. It was found that the values of E′ for all samples exhibited a gradual decrease. The value of E′ for MnCoGe undergoes a considerable decrease after 437 K. However, in the case of MnCoGe_1−xSi_x (x = 0.05), the values of E′ exhibited this nature after 375 K, which is the point of the magnetostructural transformation of this compound. The transition is due to the glass transition that occurred at the glass transition temperature (Tg). The glass transition temperature is when amorphous polymers transform from a glassy to a rubbery form due to the increased mobility of molecular segments and an increase in the free volume. The values of E″ against T also revealed a similar pattern, with the E″ peak recorded at 462 K at the magnetostructural transition region for MnCoGe. In contrast, the E″ peak is observed at 400 K for the case of MnCoGe_1−xSi_x (x = 0.05).

Figure 5. Storage modulus (E′) and loss modulus (E″) measured for MnCoGe_1−xSi_x (x = 0, 0.05, 0.1, 0.15, and 0.2).

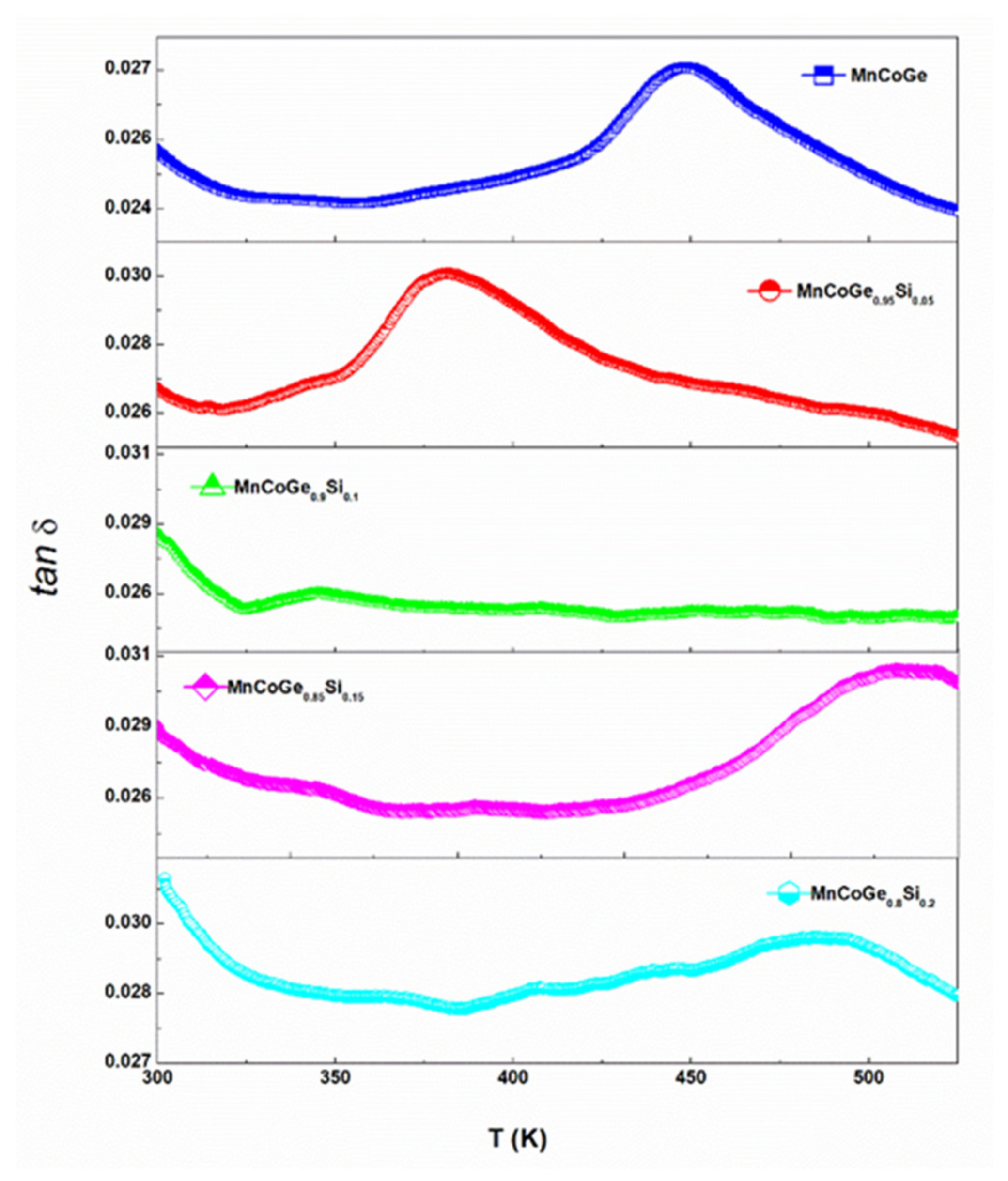
The loss ratio (tangent) tanδ, which quantifies the phase angle between the sample strain and the stress throughout the periodic excitation of the samples, is shown in Figure 6. The values of tanδ are to measure the energy dissipative abilities of a material [22]. It is observed that the values of tanδ gradually increase until ~375 K for MnCoGe_1−xSi_x (x = 0.05) and ~450 K for MnCoGe. These values of tanδ increase to 375 K and 450 K related to the two dissipative mechanisms, which are the dissipative effect due to the twin boundary movement inside the alloy particles and the dissipative effects at the alloy interface. A substantial increase in the value of tan δ for MnCoGe_1−xSi_x (x = 0.05) is visible at a temperature above 375 K. Having stated that the value of tanδ corresponds to the magnetostructural transition, it overcomes the values arising from the glass transition event of the matrix [21]. This behavior also shows the same scenario as DSC curves, where the substitution of Ge with Si leads to a drop in the structural transition temperature.

Figure 6. Tan delta measured for MnCoGe_1−xSi_x (x = 0, 0.05, 0.1, 0.15, and 0.2).

4. Conclusions

To conclude, the Si substitution for Ge atoms in MnCoGe_1−xSi_x compounds demonstrated the major structure as orthorhombic TiNiSi-type with no reflection on the hexagonal Ni2In-type structure with an increase in Si content up to x = 0.2. Furthermore, the Rietveld refinement analysis revealed that the lattice parameters (a and c) and unit cell volume of the compounds were identified to decrease with the increase in Si content, which is related to the small atomic radius of Si compared to Ge.

The magnetization and DSC measurements specified that with the increase in Si content, the T_C value is slightly increased, even though the structural transition temperature, T_str, is reduced. In addition, the structural transition temperatures for all compounds were significantly higher than 430 K, indicating that the transition was incomplete and did not achieve the zero moment.

The magnetic entropy change, −∆S_M, shows decrement behavior with increasing Si concentration up to x = 0.2 (ΔB = 0–5 T: −ΔS_M ~ 8.36 J kg⁻¹ K⁻¹ at MnCoGe; −ΔS_M ~ 6.92 J kg⁻¹ K⁻¹ at MnCoGe_0.95Si_0.05; −ΔS_M ~ 6.33 J kg⁻¹ K⁻¹ at MnCoGe_0.90Si_0.10; −ΔS_M ~ 6.04 J kg⁻¹ K⁻¹ at MnCoGe_0.85Si_0.15; −ΔS_M ~ 5.49 J kg⁻¹ K⁻¹ at MnCoGe_0.80Si_0.20) followed by the absence of any magnetic hysteresis loss, which is a second-order magnetic transition behavior and particularly advantageous to the magnetic refrigerator application. Moreover, substituting Ge with Si leads to a decrease in RC from 325 at x = 0 to 278 at x–0.2 as related to the replacement of Si on Ge, leading to a change in the interplanar crystal distance and the resulting 3d-band minimizing the electron splitting exchange interactions.

On top of that, the thermomechanical measurement shows that the values of tanδ increase to 375 K and 450 K with the increases in Si content related to the two dissipative mechanisms, which are the dissipative effect due to the twin boundary movement inside the alloy particles and the dissipative effects at the alloy interface.