X-ray Natural Circular Dichroism Imaging of Multiferroic Crystals
Abstract
1. Introduction
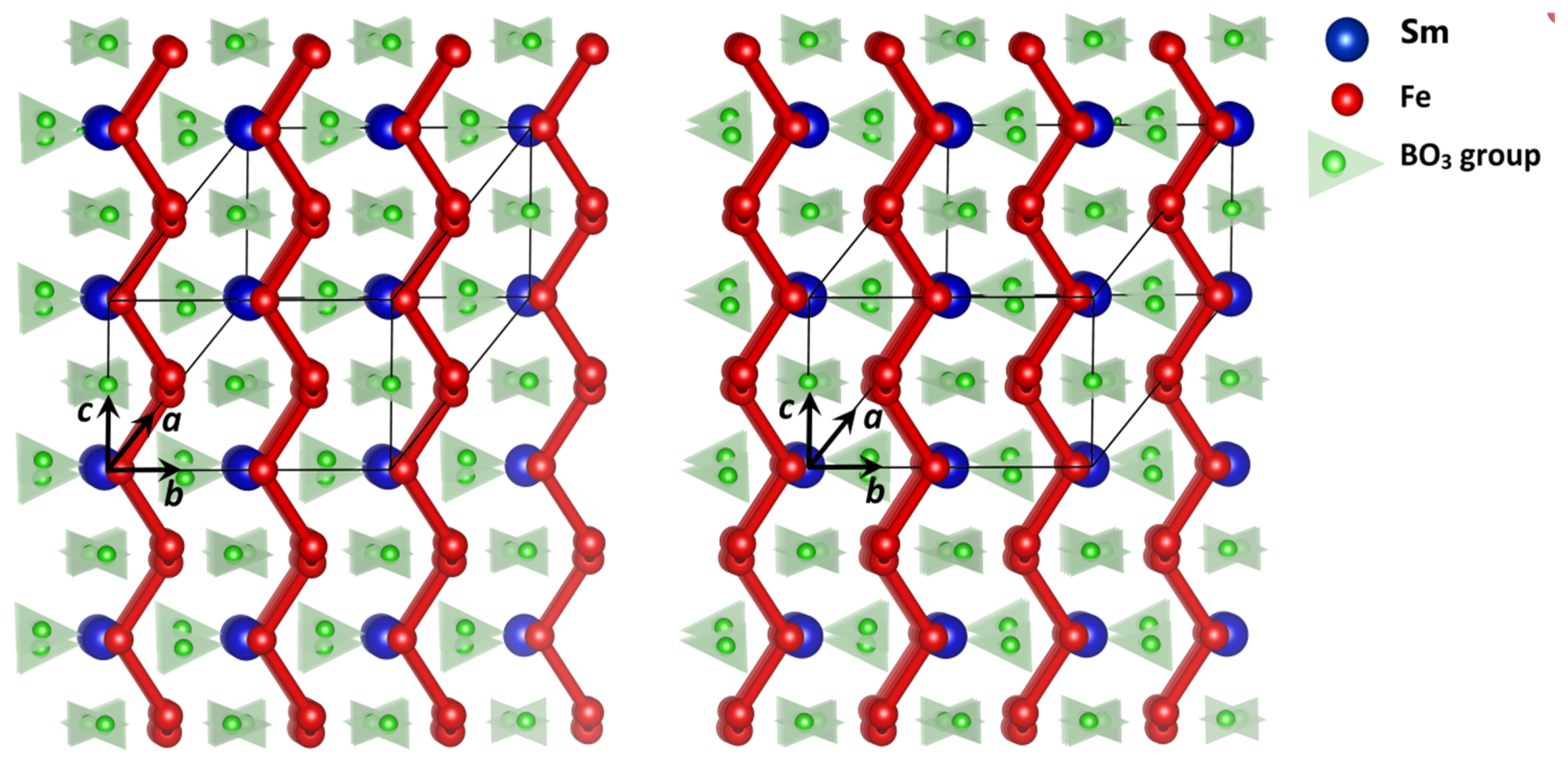
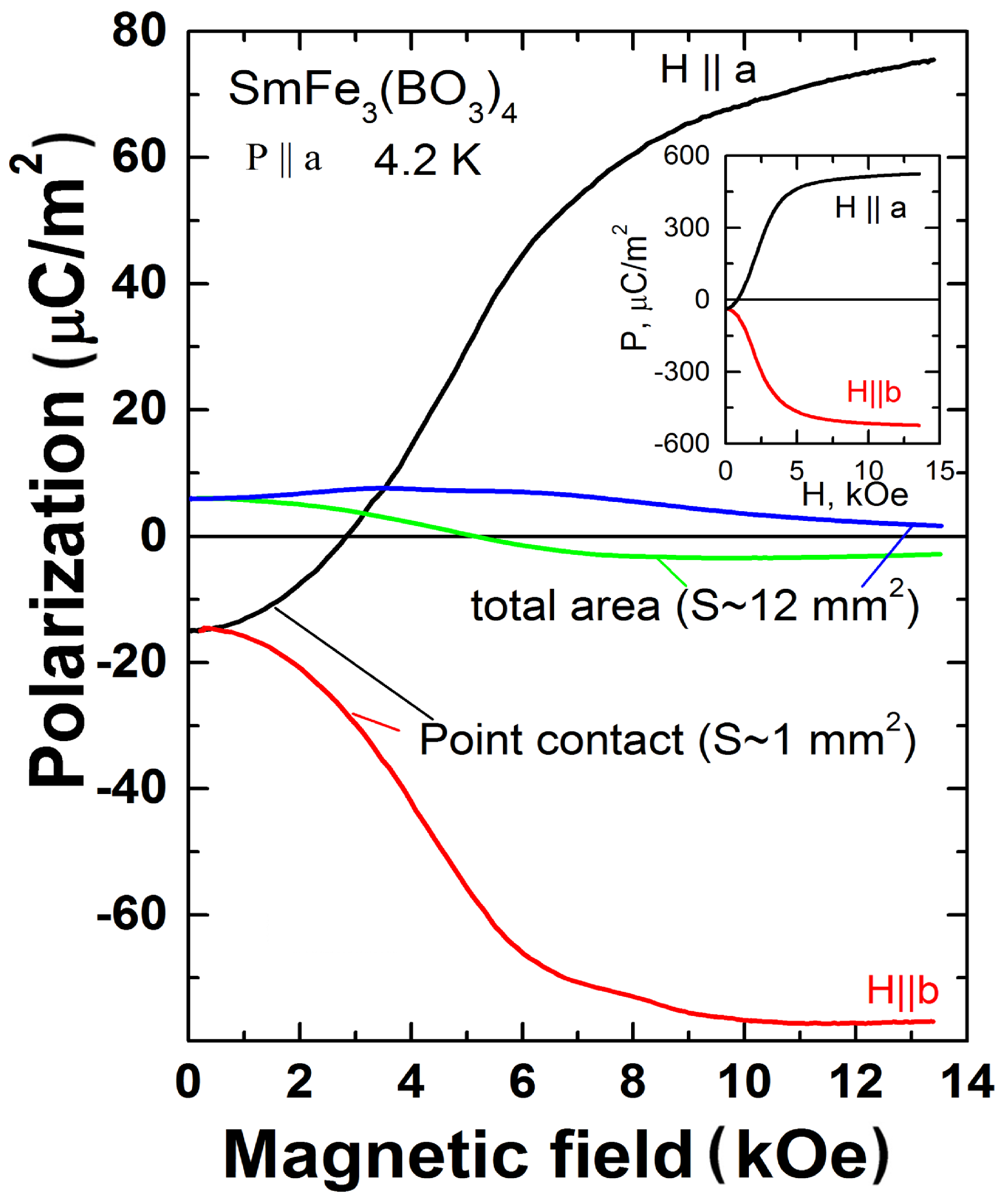
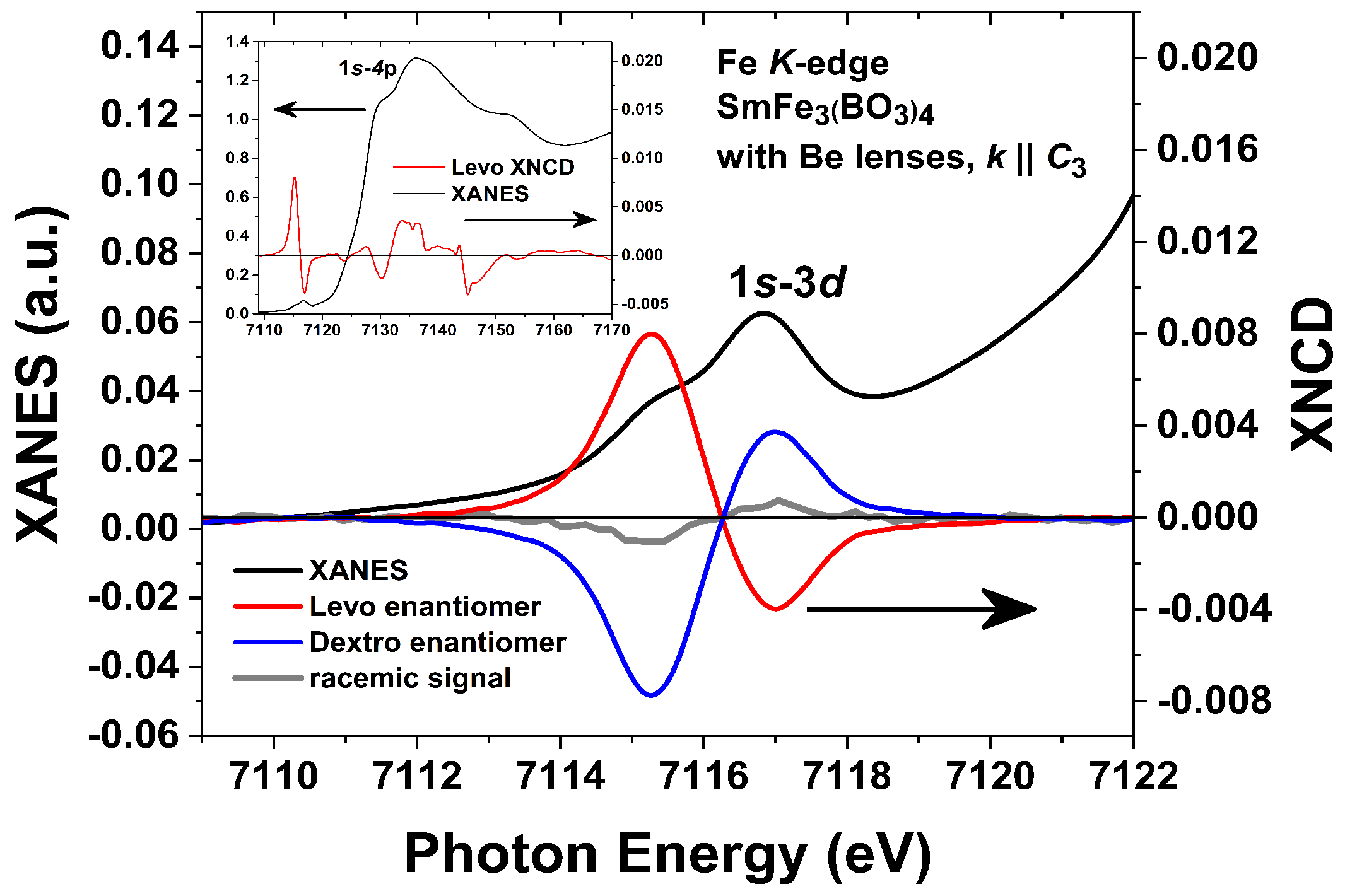
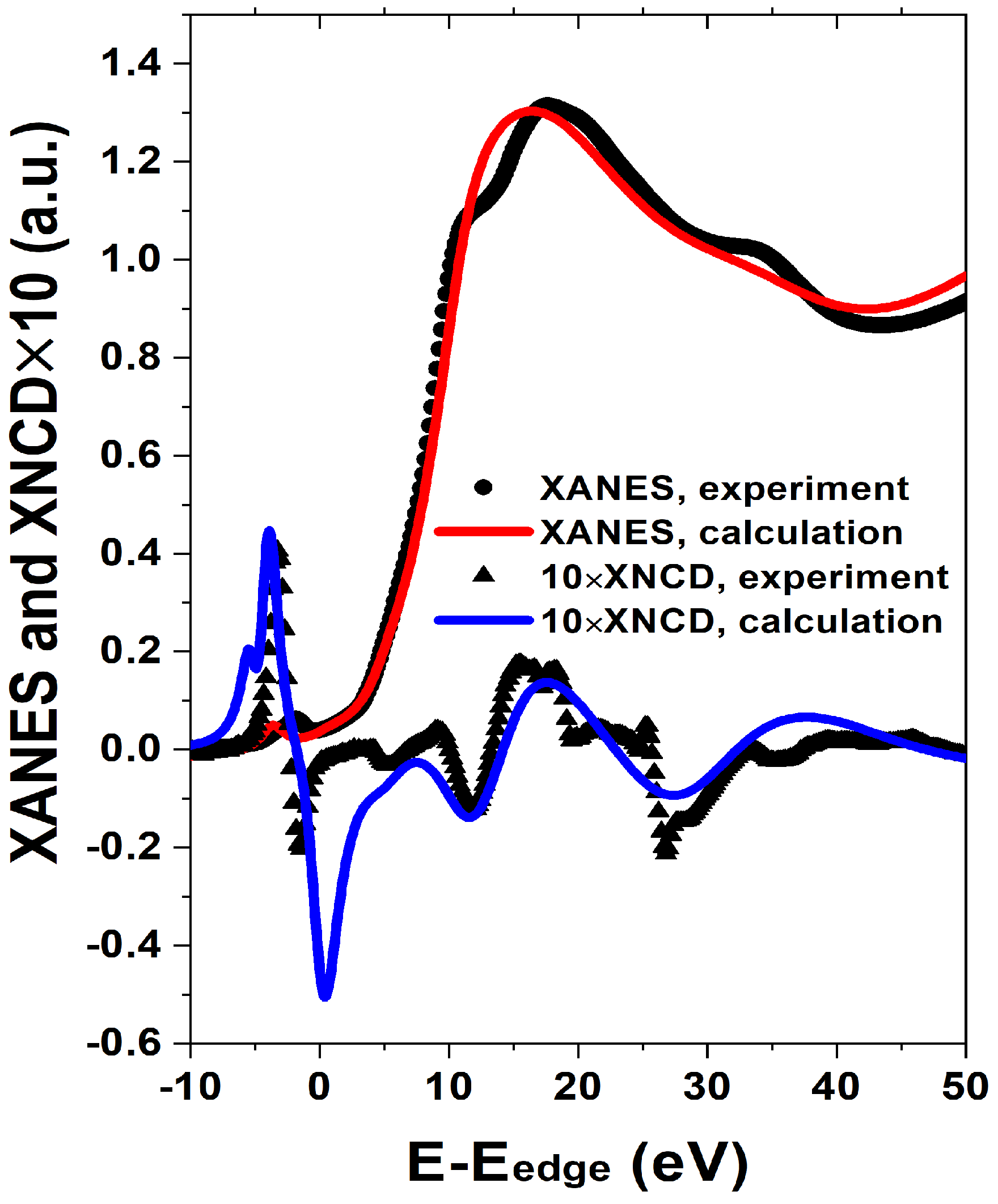
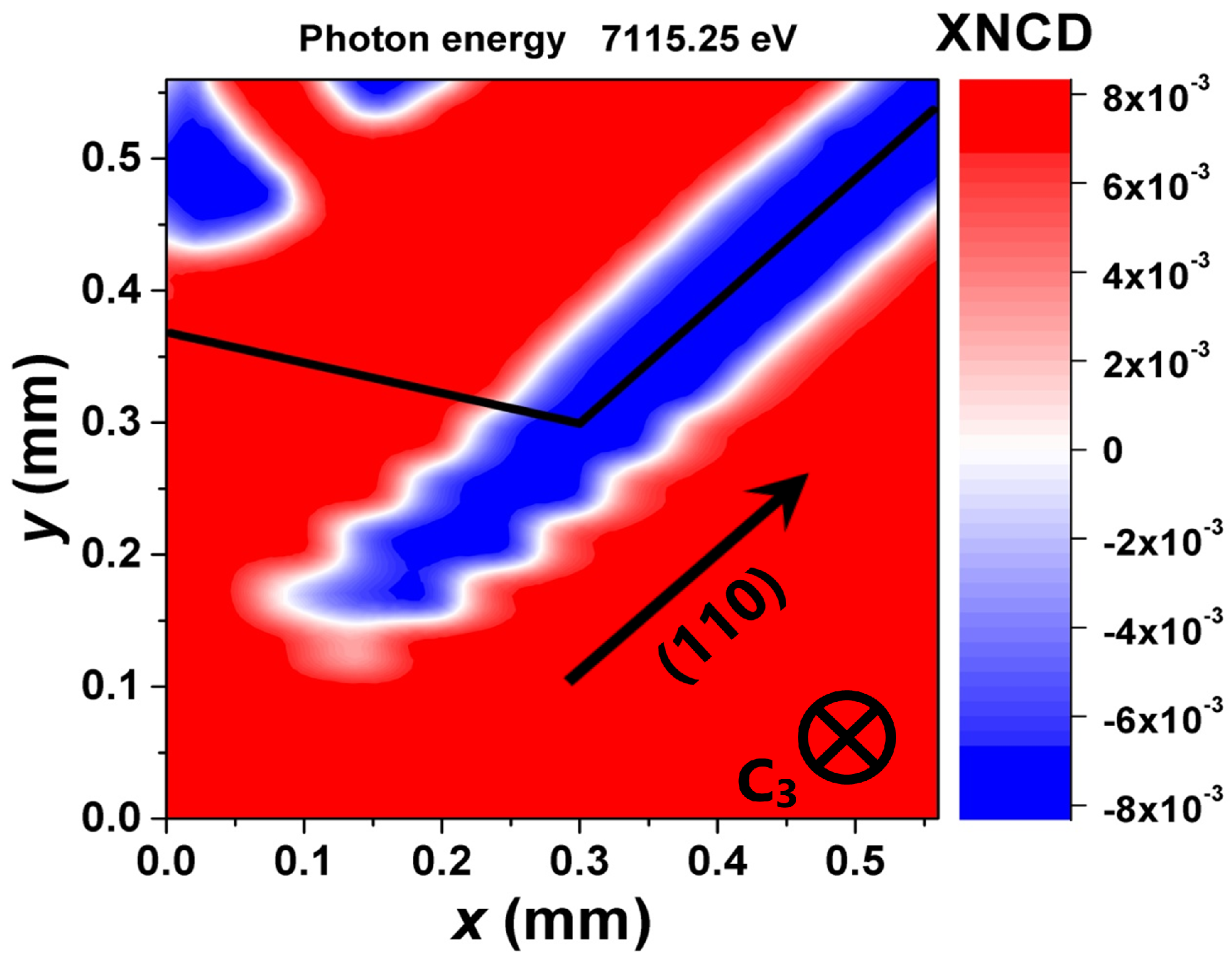
2. Results and Discussions
3. Conclusions
4. Materials and Methods
4.1. Synthesis and Macroscopic Characterization
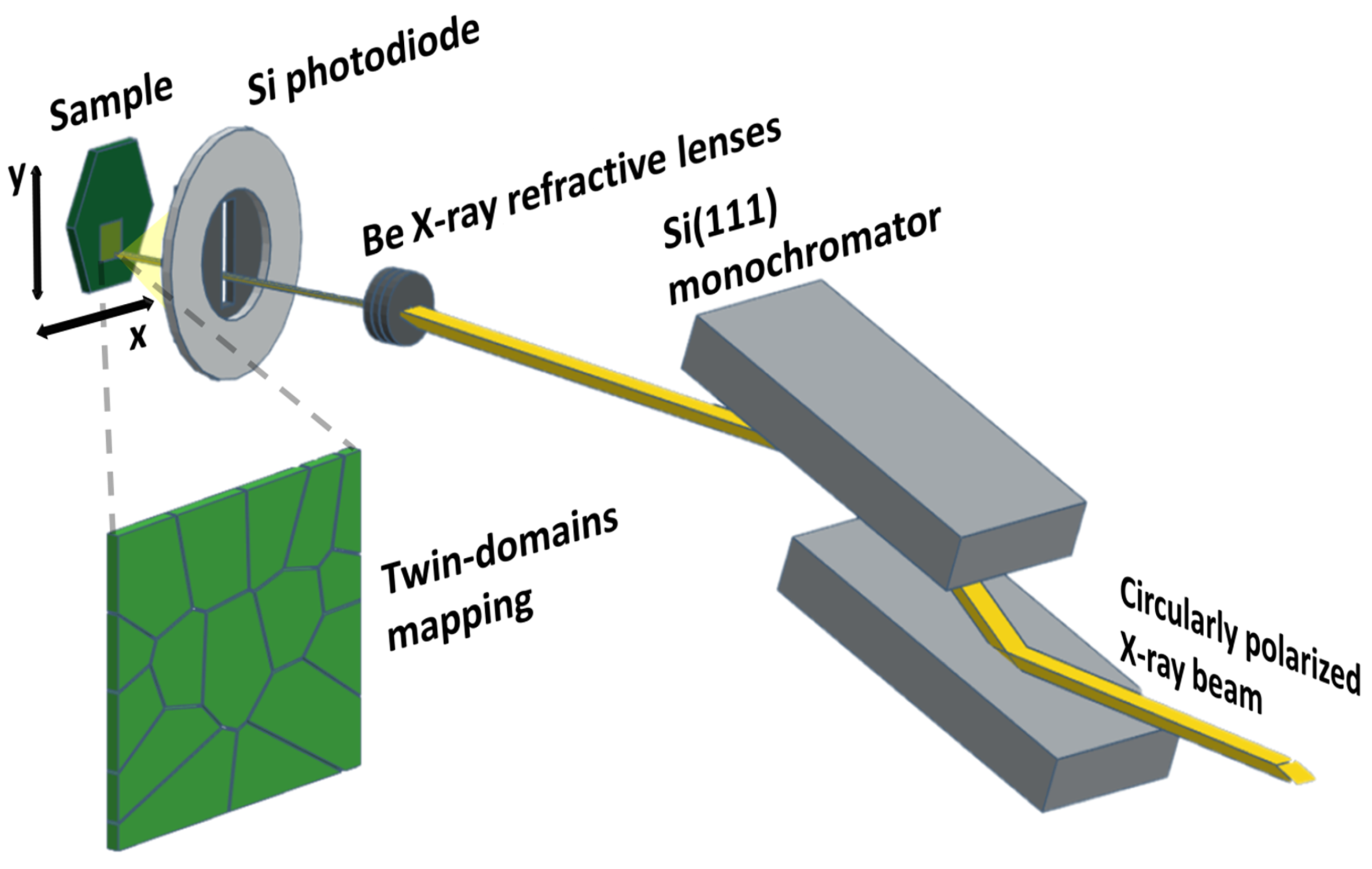
4.2. X-Ray Spectroscopy and Mapping Technique
4.3. XNCD Effect Description
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Spaldin, N.A.; Fiebig, M. The renaissance of magnetoelectric multiferroics. Science 2005, 309, 391–392. [Google Scholar] [CrossRef]
- Eerenstein, W.; Mathur, N.; Scott, J.F. Multiferroic and magnetoelectric materials. Nature 2006, 442, 759–765. [Google Scholar] [CrossRef] [PubMed]
- Zhai, K.; Shang, D.S.; Chai, Y.S.; Li, G.; Cai, J.W.; Shen, B.G.; Sun, Y. Room-Temperature Nonvolatile Memory Based on a Single-Phase Multiferroic Hexaferrite. Adv. Funct. Mater. 2018, 28, 1705771. [Google Scholar] [CrossRef]
- Zhuang, J.; Lu, J.; Zhang, N.; Zhang, J.; Bokov, A.A.; Yang, S.; Ren, W.; Ye, Z.G. Chemically engineered multiferroic morphotropic phase boundary in BiFeO3-based single phase multiferroics. J. Appl. Phys. 2019, 125, 044102. [Google Scholar] [CrossRef]
- Wang, K.; Liu, J.M.; Ren, Z. Multiferroicity: The coupling between magnetic and polarization orders. Adv. Phys. 2009, 58, 321–448. [Google Scholar] [CrossRef]
- Hur, N.; Park, S.; Sharma, P.; Ahn, J.; Guha, S.; Cheong, S.W. Electric polarization reversal and memory in a multiferroic material induced by magnetic fields. Nature 2004, 429, 392–395. [Google Scholar] [CrossRef] [PubMed]
- Kimura, T.; Goto, T.; Shintani, H.; Ishizaka, K.; Arima, T.h.; Tokura, Y. Magnetic control of ferroelectric polarization. Nature 2003, 426, 55–58. [Google Scholar] [CrossRef]
- Jia, T.; Cheng, Z.; Zhao, H.; Kimura, H. Domain switching in single-phase multiferroics. Appl. Phys. Rev. 2018, 5, 021102. [Google Scholar] [CrossRef]
- Sholl, D.S.; Gellman, A.J. Developing chiral surfaces for enantioselective chemical processing. AIChE J. 2009, 55, 2484–2490. [Google Scholar] [CrossRef]
- Zinna, F.; Resta, C.; Gorecki, M.; Pescitelli, G.; Di Bari, L.; Javorfi, T.; Hussain, R.; Siligardi, G. Circular dichroism imaging: Mapping the local supramolecular order in thin films of chiral functional polymers. Macromolecules 2017, 50, 2054–2060. [Google Scholar] [CrossRef]
- Claborn, K.; Puklin-Faucher, E.; Kurimoto, M.; Kaminsky, W.; Kahr, B. Circular dichroism imaging microscopy: Application to enantiomorphous twinning in biaxial crystals of 1, 8-dihydroxyanthraquinone. J. Am. Chem. Soc. 2003, 125, 14825–14831. [Google Scholar] [CrossRef]
- Weissbuch, I.; Kuzmenko, I.; Vaida, M.; Zait, S.; Leiserowitz, L.; Lahav, M. Twinned Crystals of Enantiomorphous Morphology of Racemic Alanine Induced by Optically Resolved. alpha.-Amino Acids; A Stereochemical Probe for the Early Stages of Crystal Nucleation. Chem. Mater. 1994, 6, 1258–1268. [Google Scholar] [CrossRef]
- Ohsumi, H.; Tokuda, A.; Takeshita, S.; Takata, M.; Suzuki, M.; Kawamura, N.; Kousaka, Y.; Akimitsu, J.; Arima, T.H. Three-Dimensional Near-Surface Imaging of Chirality Domains with Circularly Polarized X-rays. Angew. Chem. Int. Ed. 2013, 52, 8718–8721. [Google Scholar] [CrossRef]
- Banerjee-Ghosh, K.; Dor, O.B.; Tassinari, F.; Capua, E.; Yochelis, S.; Capua, A.; Yang, S.H.; Parkin, S.S.; Sarkar, S.; Kronik, L.; et al. Separation of enantiomers by their enantiospecific interaction with achiral magnetic substrates. Science 2018, 360, 1331–1334. [Google Scholar] [CrossRef] [PubMed]
- Buchen, J.; Wesemann, V.; Dehmelt, S.; Gross, A.; Rytz, D. Twins in YAl3(BO3)4 and K2Al2B2O7 Crystals as Revealed by Changes in Optical Activity. Crystals 2019, 9, 8. [Google Scholar] [CrossRef]
- Kaminsky, W.; Claborn, K.; Kahr, B. Polarimetric imaging of crystals. Chem. Soc. Rev. 2004, 33, 514–525. [Google Scholar] [CrossRef] [PubMed]
- Kuroda, R.; Harada, T.; Shindo, Y. A solid-state dedicated circular dichroism spectrophotometer: Development and application. Rev. Sci. Instrum. 2001, 72, 3802–3810. [Google Scholar] [CrossRef]
- Hartshorne, N.H.; Stuart, A. Practical Optical Crystallography; Edward Arnold: London, UK, 1964. [Google Scholar]
- Yariv, A.; Yeh, P. Optical Waves in Crystals; Wiley: New York, NY, USA, 1984; Volume 5. [Google Scholar]
- Palmer, B.A.; Edwards-Gau, G.R.; Kariuki, B.M.; Harris, K.D.; Dolbnya, I.P.; Collins, S.P. X-ray birefringence imaging. Science 2014, 344, 1013–1016. [Google Scholar] [CrossRef]
- Hu, X.; Jiang, S.; Huang, X.; Liu, W.; Ge, C.; Wang, J.; Pan, H.; Ferrari, C.; Gennari, S. X-ray topographic study of twins in NdxY1−xAl3(BO3)4 crystal. Nuovo C. D 1997, 19, 175–180. [Google Scholar] [CrossRef]
- Usui, T.; Tanaka, Y.; Nakajima, H.; Taguchi, M.; Chainani, A.; Oura, M.; Shin, S.; Katayama, N.; Sawa, H.; Wakabayashi, Y.; et al. Observation of quadrupole helix chirality and its domain structure in DyFe3(BO3)4. Nat. Mater. 2014, 13, 611–618. [Google Scholar] [CrossRef] [PubMed]
- Di Gregorio, M.C.; Shimon, L.J.; Brumfeld, V.; Houben, L.; Lahav, M.; van der Boom, M.E. Emergence of chirality and structural complexity in single crystals at the molecular and morphological levels. Nat. Commun. 2020, 11, 1–9. [Google Scholar]
- Thomas, S.P.; Grosjean, A.; Flematti, G.R.; Karton, A.; Sobolev, A.N.; Edwards, A.J.; Piltz, R.O.; Iversen, B.B.; Koutsantonis, G.A.; Spackman, M.A. Investigation of an unusual crystal habit of hydrochlorothiazide reveals large polar enantiopure domains and a possible crystal nucleation mechanism. Angew. Chem. 2019, 131, 10361–10365. [Google Scholar] [CrossRef]
- Bijvoet, J.; Peerdeman, A.; Van Bommel, A. Determination of the absolute configuration of optically active compounds by means of X-rays. Nature 1951, 168, 271–272. [Google Scholar] [CrossRef]
- Flack, H. On enantiomorph-polarity estimation. Acta Crystallogr. Sect. Found. Crystallogr. 1983, 39, 876–881. [Google Scholar] [CrossRef]
- Hooft, R.W.; Straver, L.H.; Spek, A.L. Determination of absolute structure using Bayesian statistics on Bijvoet differences. J. Appl. Crystallogr. 2008, 41, 96–103. [Google Scholar] [CrossRef]
- Rogalev, A.; Goulon, J.; Wilhelm, F. X-ray detected optical activity. Comptes Rendus Phys. 2008, 9, 642–656. [Google Scholar] [CrossRef]
- Snigirev, A.; Kohn, V.; Snigireva, I.; Lengeler, B. A compound refractive lens for focusing high-energy X-rays. Nature 1996, 384, 49–51. [Google Scholar] [CrossRef]
- Hinatsu, Y.; Doi, Y.; Ito, K.; Wakeshima, M.; Alemi, A. Magnetic and calorimetric studies on rare-earth iron borates LnFe3(BO3)4 (Ln= Y, La–Nd, Sm–Ho). J. Solid State Chem. 2003, 172, 438–445. [Google Scholar] [CrossRef]
- Zvezdin, A.K.; Krotov, S.S.; Kadomtseva, A.M.; Vorob’ev, G.P.; Popov, Y.F.; Pyatakov, A.P.; Bezmaternykh, L.N.; Popova, E. Magnetoelectric effects in gadolinium iron borate GdFe3(BO3)4. J. Exp. Theor. Phys. Lett. 2005, 81, 272–276. [Google Scholar] [CrossRef]
- Zvezdin, A.K.; Vorob’ev, G.P.; Kadomtseva, A.M.; Popov, Y.F.; Pyatakov, A.P.; Bezmaternykh, L.N.; Kuvardin, A.; Popova, E. Magnetoelectric and magnetoelastic interactions in NdFe3(BO3)4 multiferroics. JETP Lett. 2006, 83, 509–514. [Google Scholar] [CrossRef]
- Vasil’ev, A.; Popova, E. Rare-earth ferroborates RFe3(BO3)4. Fiz. Nizk. Temp. 2006, 32, 968–984. [Google Scholar] [CrossRef]
- Chaudhury, R.P.; Yen, F.; Lorenz, B.; Sun, Y.; Bezmaternykh, L.N.; Temerov, V.L.; Chu, C.W. Magnetoelectric effect and spontaneous polarization in HoFe3(BO3)4 and Ho0.5Nd0.5Fe3(BO3)4. Phys. Rev. B 2009, 80, 104424. [Google Scholar] [CrossRef]
- Kadomtseva, A.; Popov, Y.F.; Vorob’ev, G.; Pyatakov, A.; Krotov, S.; Kamilov, K.; Ivanov, V.Y.; Mukhin, A.; Zvezdin, A.; Kuz’menko, A.; et al. Magnetoelectric and magnetoelastic properties of rare-earth ferroborates. Low Temp. Phys. 2010, 36, 511–521. [Google Scholar] [CrossRef]
- Popova, M.N. Spectroscopy of compounds from the family of rare-earth orthoborates. J. Rare Earths 2009, 27, 607–611. [Google Scholar] [CrossRef]
- Popova, M.; Chukalina, E.; Stanislavchuk, T.; Malkin, B.; Zakirov, A.; Antic-Fidancev, E.; Popova, E.; Bezmaternykh, L.; Temerov, V. Optical spectra, crystal-field parameters, and magnetic susceptibility of multiferroic NdFe3(BO3)4. Phys. Rev. B 2007, 75, 224435. [Google Scholar] [CrossRef]
- Popov, Y.F.; Pyatakov, A.; Kadomtseva, A.; Vorob’ev, G.; Zvezdin, A.; Mukhin, A.; Ivanov, V.Y.; Gudim, I. Peculiarities in the magnetic, magnetoelectric, and magnetoelastic properties of SmFe3(BO3)4 multiferroic. J. Exp. Theor. Phys. 2010, 111, 199–203. [Google Scholar] [CrossRef]
- Mukhin, A.A.; Vorob’ev, G.P.; Ivanov, V.Y.; Kadomtseva, A.M.; Narizhnaya, A.; Kuz’menko, A.; Popov, Y.F.; Bezmaternykh, L.N.; Gudim, I. Colossal magnetodielectric effect in SmFe3(BO3)4 multiferroic. JETP Lett. 2011, 93, 275–281. [Google Scholar] [CrossRef]
- Platunov, M.; Kazak, N.; Dudnikov, V.; Temerov, V.; Gudim, I.; Knyazev, Y.; Gavrilkin, S.; Dyadkin, V.; Dovgaliuk, I.; Chernyshov, D.; et al. Element selective magnetism in Ho0.5Nd0.5Fe3(BO3)4 single crystal probed with hard X-ray magnetic circular dichroism. J. Magn. Magn. Mater. 2019, 479, 312–316. [Google Scholar] [CrossRef]
- Freydman, A.; Erofeev, D.; Temerov, V.; Gudim, I. The magnetoelectric MEE-effect in the SmFe3(BO3)4 multiferroic in dc and ac electric fields. J. Appl. Phys. 2018, 124, 134101. [Google Scholar] [CrossRef]
- Chukalina, E.; Popova, M.; Bezmaternykh, L.; Gudim, I. Spectroscopic study of the magnetic ordering in SmFe3(BO3)4. Phys. Lett. A 2010, 374, 1790–1792. [Google Scholar] [CrossRef]
- Ritter, C.; Pankrats, A.; Gudim, I.; Vorotynov, A. Determination of the magnetic structure of SmFe3(BO3)4 by neutron diffraction: Comparison with other RFe3(BO3)4 iron borates. J. Phys. Condens. Matter 2012, 24, 386002. [Google Scholar] [CrossRef] [PubMed]
- Popov, A.; Plokhov, D.; Zvezdin, A. Quantum theory of magnetoelectricity in rare-earth multiferroics: Nd, Sm, and Eu ferroborates. Phys. Rev. B 2013, 87, 024413. [Google Scholar] [CrossRef]
- Campa, J.; Cascales, C.; Gutierrez-Puebla, E.; Monge, M.; Rasines, I.; Ruiz-Valero, C. Crystal structure, magnetic order, and vibrational behavior in iron rare-earth borates. Chem. Mater. 1997, 9, 237–240. [Google Scholar] [CrossRef]
- Kuzmenko, A.; Szaller, D.; Kain, T.; Dziom, V.; Weymann, L.; Shuvaev, A.; Pimenov, A.; Mukhin, A.; Ivanov, V.Y.; Gudim, I.; et al. Switching of magnons by electric and magnetic fields in multiferroic borates. Phys. Rev. Lett. 2018, 120, 027203. [Google Scholar] [CrossRef] [PubMed]
- Moshkina, E.; Krylov, A.; Sofronova, S.; Gudim, I.; Temerov, V. Crystal Growth and Raman Spectroscopy Study of Sm1−xLaxFe3(BO3)4 Ferroborates. Cryst. Growth Des. 2016, 16, 6915–6921. [Google Scholar] [CrossRef]
- Klimin, S.; Fausti, D.; Meetsma, A.; Bezmaternykh, L.; Van Loosdrecht, P.; Palstra, T. Evidence for differentiation in the iron-helicoidal chain in GdFe3(BO3)4. Acta Crystallogr. Sect. Struct. Sci. 2005, 61, 481–485. [Google Scholar] [CrossRef]
- Goulon, J.; Rogalev, A.; Gauthier, C.; Goulon-Ginet, C.; Signorato, R.; Neumann, C.; Varga, L.; Malgrange, C. Instrumentation developments for X-ray linear and circular dichroism at the ESRF beamline ID12A. J. Synchrotron Radiat. 1998, 5, 232–238. [Google Scholar] [CrossRef]
- Goulon, J.; Goulon-Ginet, C.; Rogalev, A.; Benayoun, G.; Brouder, C.; Natoli, C.R. X-ray natural circular dichroism and chiral-EXAFS in gyrotropic crystals. J. Synchrotron Radiat. 2000, 7, 182–188. [Google Scholar] [CrossRef]
- Goulon, J.; Goulon-Ginet, C.; Rogalev, A.; Gotte, V.; Malgrange, C.; Brouder, C.; Natoli, C.R. X-ray natural circular dichroism in a uniaxial gyrotropic single crystal of LiIO3. J. Chem. Phys. 1998, 108, 6394–6403. [Google Scholar] [CrossRef]
- Alagna, L.; Prosperi, T.; Turchini, S.; Goulon, J.; Rogalev, A.; Goulon-Ginet, C.; Natoli, C.R.; Peacock, R.D.; Stewart, B. X-ray natural circular dichroism. Phys. Rev. Lett. 1998, 80, 4799. [Google Scholar] [CrossRef]
- Goulon, J.; Goulon-Ginet, C.; Rogalev, A.; Gotte, V.; Malgrange, C.; Brouder, C. X-ray natural circular dichroism of gyrotropic crystals. J. Synchrotron Radiat. 1999, 6, 673–675. [Google Scholar] [CrossRef]
- Stewart, B.; Peacock, R.D.; Alagna, L.; Prosperi, T.; Turchini, S.; Goulon, J.; Rogalev, A.; Goulon-Ginet, C. Circular Dichroism at the Edge: Large X-ray Natural CD in the 1s–3d Pre-Edge Feature of 2[Co(en)3Cl3] NaCl 6H2O. J. Am. Chem. Soc. 1999, 121, 10233–10234. [Google Scholar] [CrossRef]
- Rogalev, A.; Goulon, J.; Wilhelm, F.; Bosak, A. X-Ray Detected Optical Activity. In Magnetism and Synchrotron Radiation; Springer: Berlin/Heisenberg, Germany, 2010; pp. 169–190. [Google Scholar]
- Natoli, C.; Brouder, C.; Sainctavit, P.; Goulon, J.; Goulon-Ginet, C.; Rogalev, A. Calculation of X-ray natural circular dichroism. Eur. Phys. J. Condens. Matter Complex Syst. 1998, 4, 1–11. [Google Scholar] [CrossRef]
- Peacock, R.D.; Stewart, B. Natural circular dichroism in X-ray spectroscopy. J. Phys. Chem. B 2001, 105, 351–360. [Google Scholar] [CrossRef]
- Goulon, J.; Rogalev, A.; Wilhelm, F.; Goulon-Ginet, C.; Carra, P.; Marri, I.; Brouder, C. X-ray optical activity: Applications of sum rules. J. Exp. Theor. Phys. 2003, 97, 402–431. [Google Scholar] [CrossRef]
- Cortijo, M.; Valentín-Pérez, Á.; Rogalev, A.; Wilhelm, F.; Sainctavit, P.; Rosa, P.; Hillard, E.A. Rapid Discrimination of Crystal Handedness by X-ray Natural Circular Dichroism (XNCD) Mapping. Chem. Eur. J. 2020, 26, 13363–13366. [Google Scholar] [CrossRef]
- Buerger, M. The genesis of twin crystals. Am. Mineral. J. Earth Planet. Mater. 1945, 30, 469–482. [Google Scholar]
- Kohn, V.; Folomeshkin, M. Feasibility of X-ray beam nanofocusing with compound refractive lenses. J. Synchrotron Radiat. 2021, 28, 419–428. [Google Scholar] [CrossRef] [PubMed]
- Joly, Y. X-ray absorption near-edge structure calculations beyond the muffin-tin approximation. Phys. Rev. B 2001, 63, 125120. [Google Scholar] [CrossRef]
- Bunău, O.; Joly, Y. Self-consistent aspects of X-ray absorption calculations. J. Phys. Condens. Matter 2009, 21, 345501. [Google Scholar] [CrossRef] [PubMed]
- Giacovazzo, C.; Monaco, H.; Viterbo, F.; Scordari, G.; Gilli, G.; Zanotti, G.; Catti, M. Fundamentals of crystallography. IUCr texts on crystallography no. 2. Acta Crystallogr. Found. Crystallogr 1993, 49, 373–374. [Google Scholar]
- Hahn, T.; Klapper, H. Twinning of crystals. Int. Tables Crystallogr. 2006, 500, 413–483. [Google Scholar]
- Ilas, S. Elaboration et Caractérisation de Matériaux non Linéaires pour la Conception de Dispositifs Laser Émettant dans L’ultraviolet. Ph.D. Thesis, Université Pierre et Marie Curie-Paris VI, Paris, France, 2014. [Google Scholar]
- Okutani, M.; Jo, T.; Carra, P. Tight-binding approach to natural circular dichroism in the X-ray region. J. Phys. Soc. Jpn. 1999, 68, 3191–3194. [Google Scholar] [CrossRef]
- Goulon, J.; Rogalev, A.; Wilhelm, F.; Jaouen, N.; Goulon-Ginet, C.; Brouder, C. Optical activity probed with X-rays. J. Phys. Condens. Matter 2003, 15, S633. [Google Scholar] [CrossRef]
- Jerphagnon, J.; Chemla, D. Optical activity of crystals. J. Chem. Phys. 1976, 65, 1522–1529. [Google Scholar] [CrossRef]
- Sirotin, Y.I.; Shaskol’skaia, M.P. Fundamentals of Crystal Physics; MIR Publishers: Moscow, Russia, 1982. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Platunov, M.S.; Gudim, I.A.; Ovchinnikova, E.N.; Kozlovskaya, K.A.; Wilhelm, F.; Rogalev, A.; Hen, A.; Ivanov, V.Y.; Mukhin, A.A.; Dmitrienko, V.E. X-ray Natural Circular Dichroism Imaging of Multiferroic Crystals. Crystals 2021, 11, 531. https://doi.org/10.3390/cryst11050531
Platunov MS, Gudim IA, Ovchinnikova EN, Kozlovskaya KA, Wilhelm F, Rogalev A, Hen A, Ivanov VY, Mukhin AA, Dmitrienko VE. X-ray Natural Circular Dichroism Imaging of Multiferroic Crystals. Crystals. 2021; 11(5):531. https://doi.org/10.3390/cryst11050531
Chicago/Turabian StylePlatunov, Mikhail S., Irina A. Gudim, Elena N. Ovchinnikova, Ksenia A. Kozlovskaya, Fabrice Wilhelm, Andrei Rogalev, Amir Hen, Vsevolod Y. Ivanov, Alexander A. Mukhin, and Vladimir E. Dmitrienko. 2021. "X-ray Natural Circular Dichroism Imaging of Multiferroic Crystals" Crystals 11, no. 5: 531. https://doi.org/10.3390/cryst11050531
APA StylePlatunov, M. S., Gudim, I. A., Ovchinnikova, E. N., Kozlovskaya, K. A., Wilhelm, F., Rogalev, A., Hen, A., Ivanov, V. Y., Mukhin, A. A., & Dmitrienko, V. E. (2021). X-ray Natural Circular Dichroism Imaging of Multiferroic Crystals. Crystals, 11(5), 531. https://doi.org/10.3390/cryst11050531







