Numerical Simulation of Microstructure Evolution in Solidification Process of Ferritic Stainless Steel with Cellular Automaton
Abstract
1. Introduction
2. Model Description
2.1. Nucleation Model
2.2. Solute Field Calculation
2.3. Interface Growth Kinetics
2.4. Calculation of the SL Interface Curvature and the Capture Rules
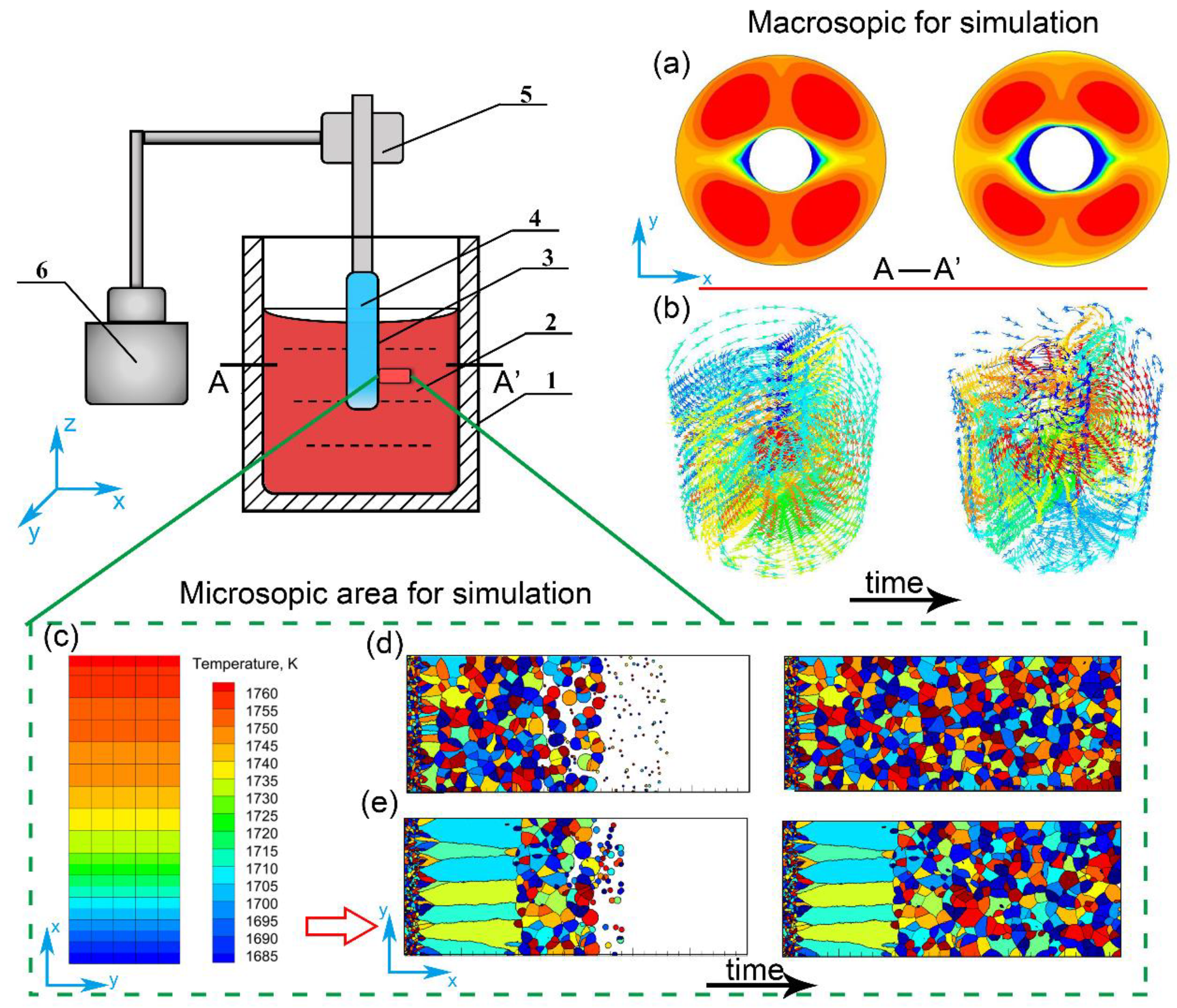
2.5. The Simulation Principle of Technique
3. Results and Discussion
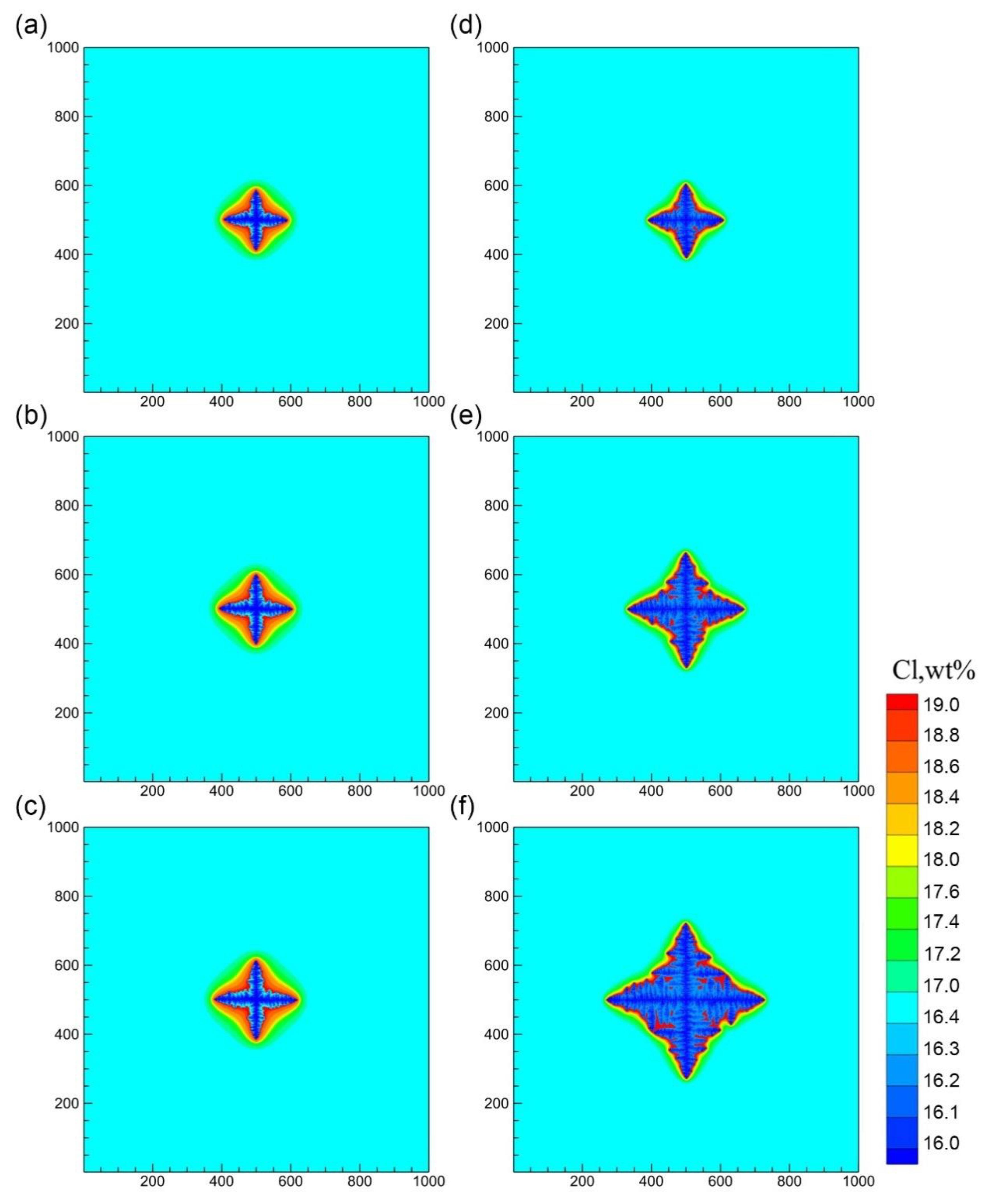
3.1. Equiaxed Dendritic Growth in Undercooled Melt
3.2. The Evolution of Microstructure
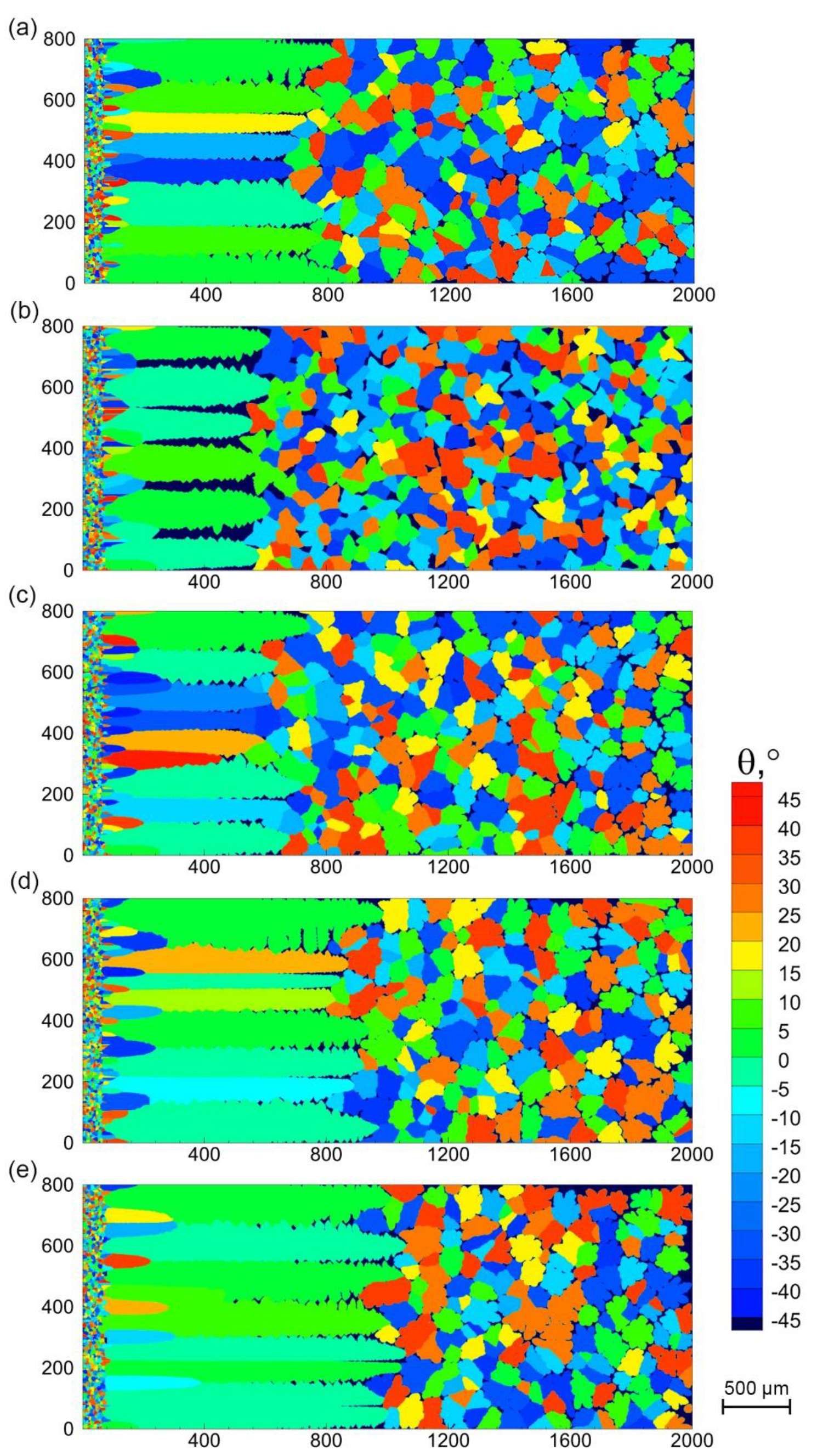
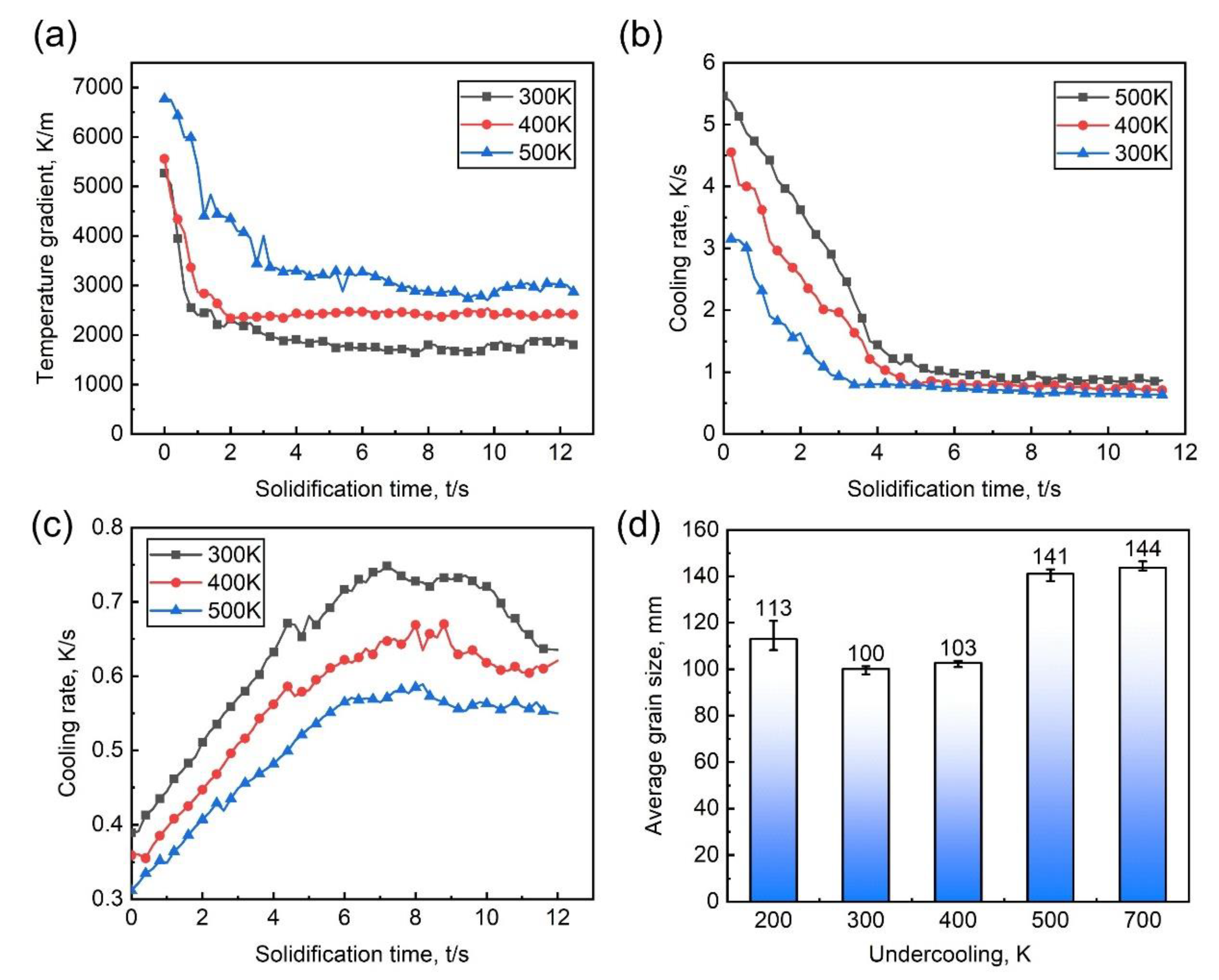
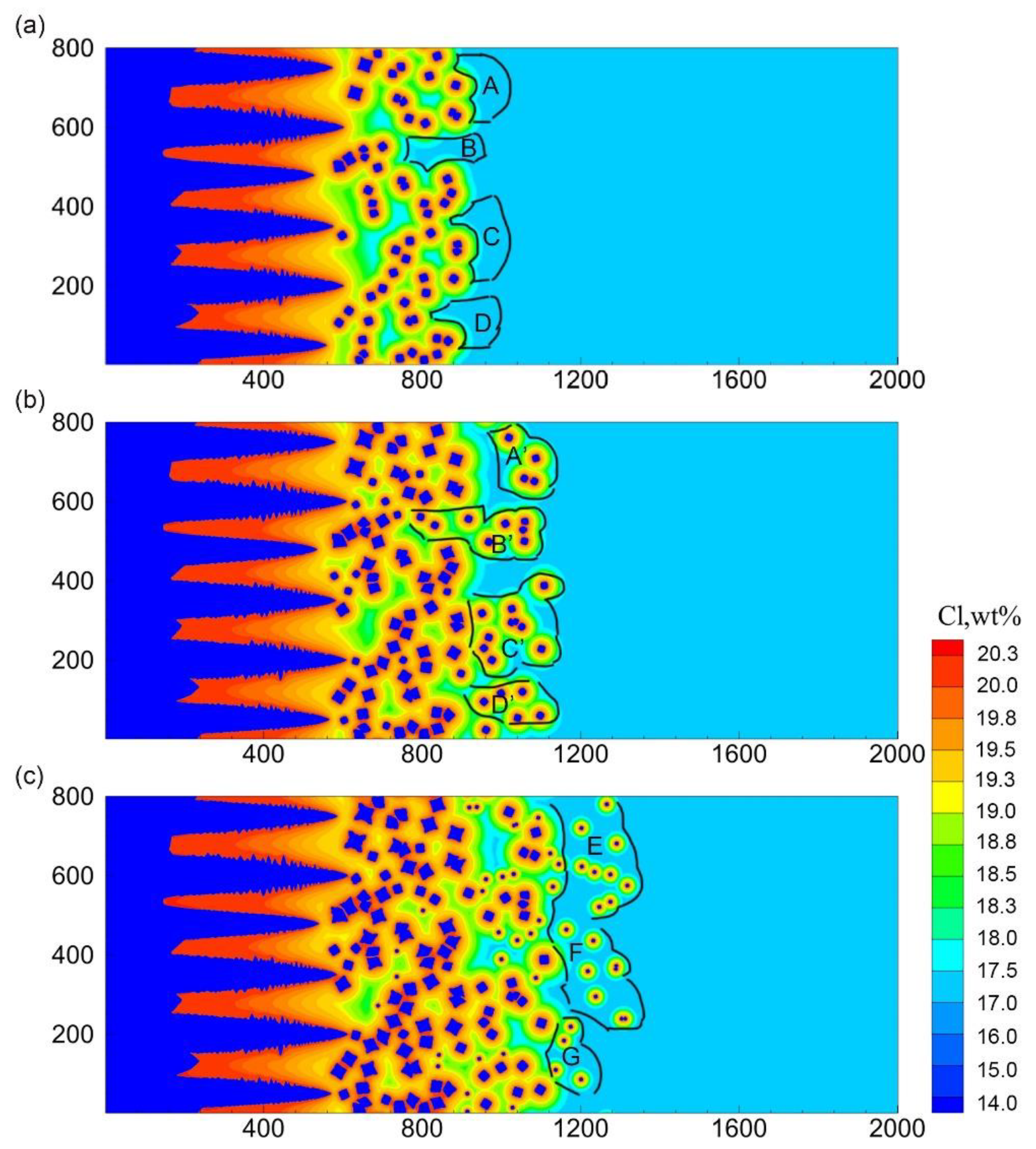
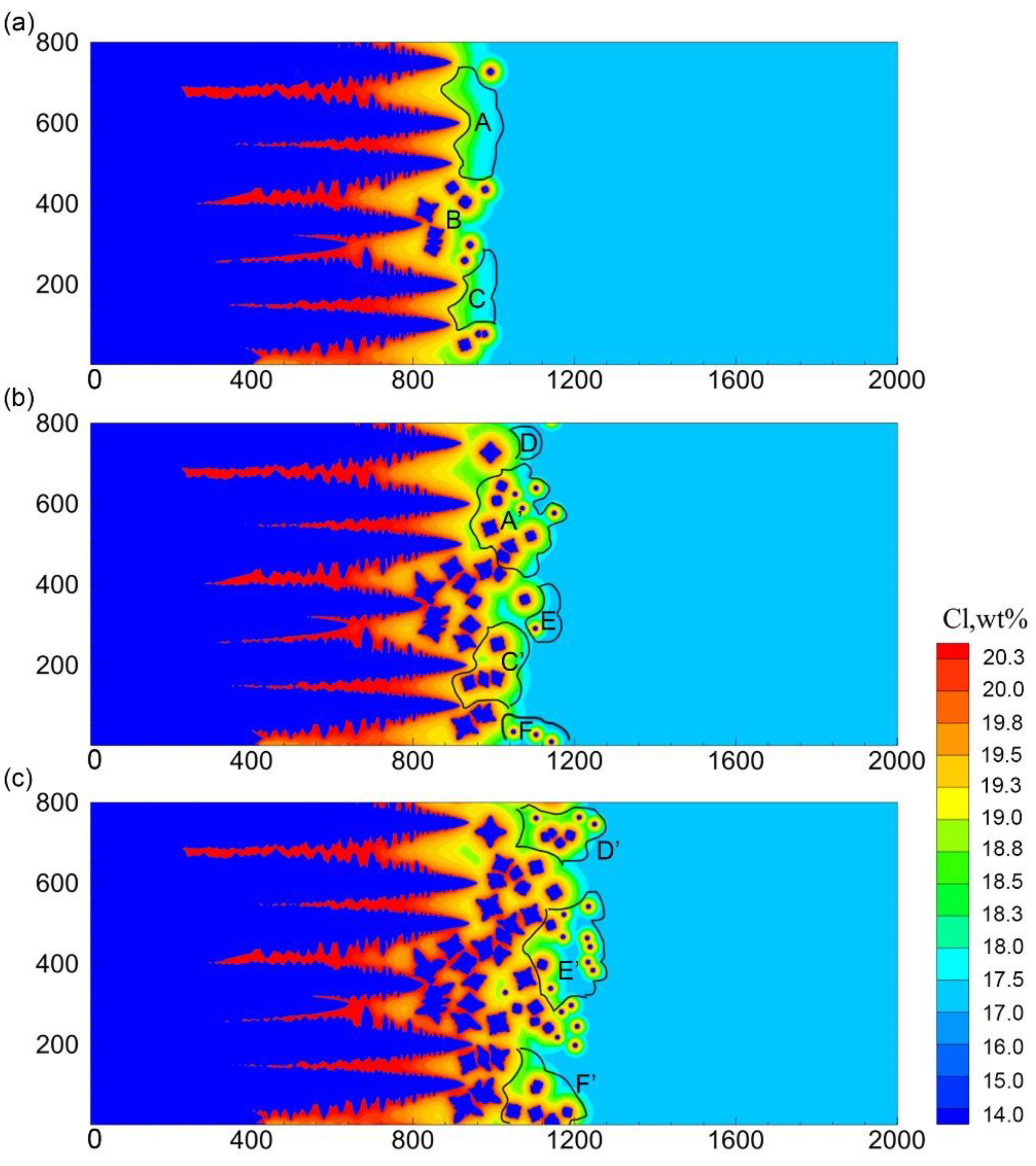
3.3. Influence of the Surface Undercooling Degree
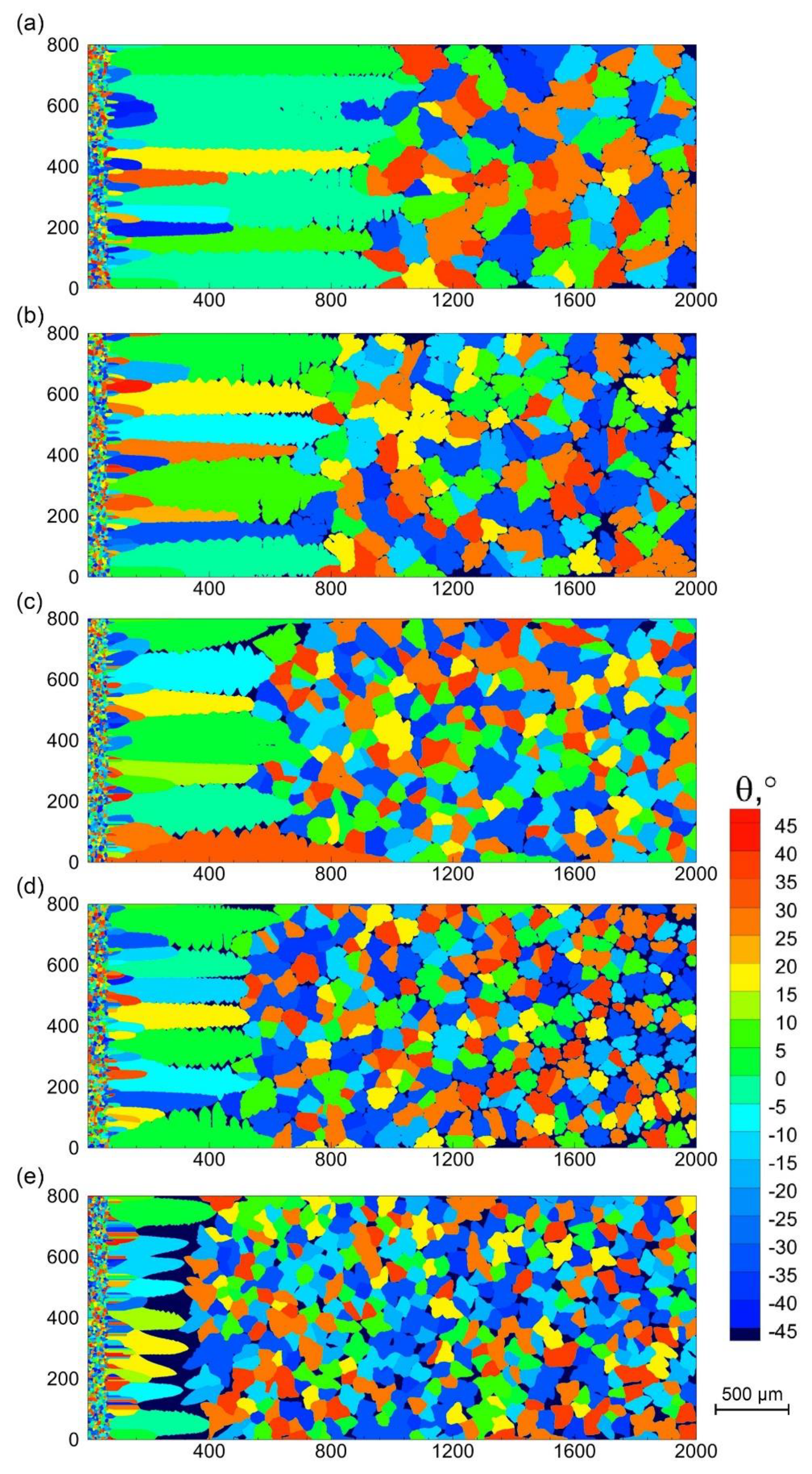
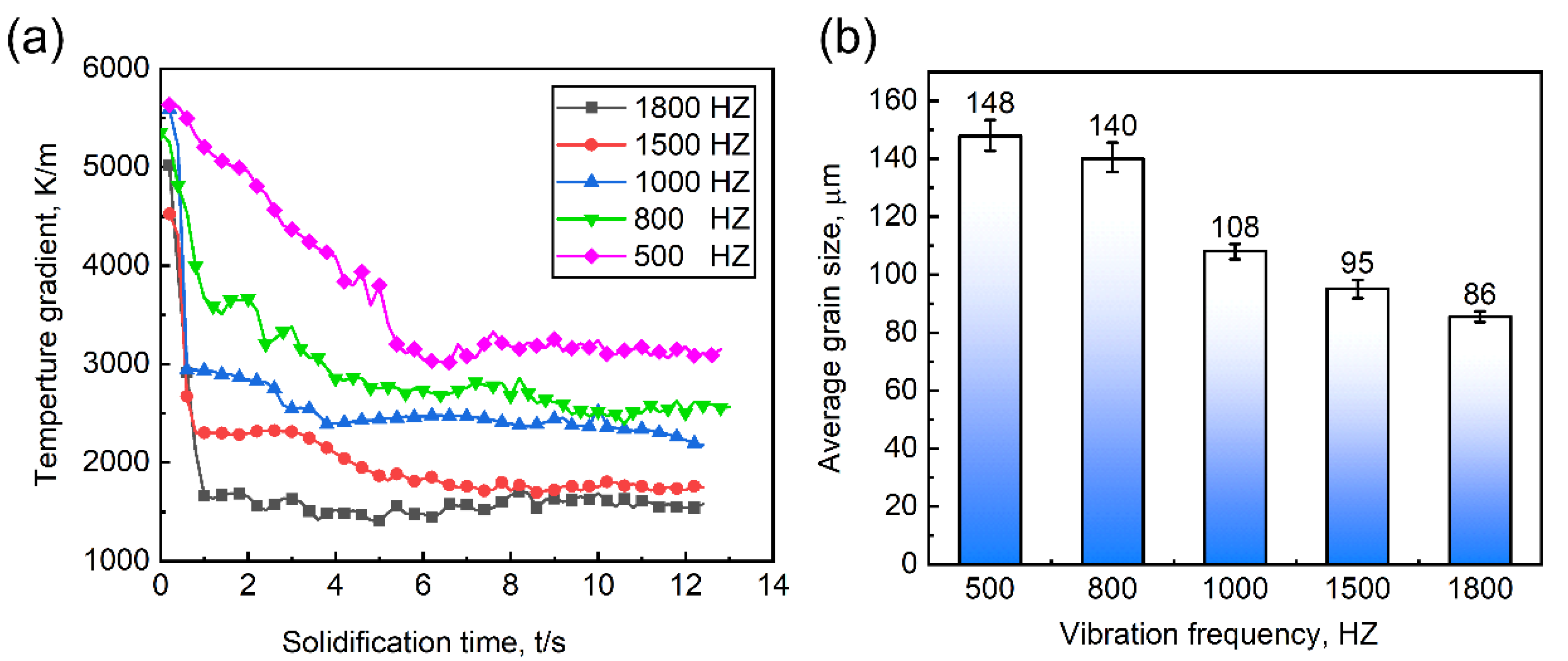
3.4. Influence of the External Vibration Effect
4. Conclusions
- With the increase of surface undercooling on the crystal nucleus generator, the columnar dendrites regions are more developed, and the equiaxed dendrites regions decrease visibly, the number of new-born equiaxed dendrites decreases, and the average grain size increases. The quantitative analysis of the temperature field distribution in the melt shows that the temperature gradient at the columnar crystal front played a critical role in the nucleation and growth of the center equiaxed grain;
- With the vibration frequency increases, the area of the equiaxed dendrites regions is obviously extended, and the refined grains and homogenized microstructure are achieved. With the vibration intensified, the possibility of dendrite fragmentation is increased by increasing the probability of nucleation in the melt; the convection stirring ability of the melt is improved, resulting in uniform temperature gradient distribution and making a large area in the melt to reach the critical nucleation undercooling.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Huh, M.Y.; Engler, O. Effect of intermediate annealing on texture, formability and ridging of 17%Cr ferritic stainless steel sheet. Mater. Sci. Eng. A. 2001, 308, 74–87. [Google Scholar] [CrossRef]
- Park, S.; Kim, K.; Lee, Y.; Park, C. Evolution of microstructure and texture associated with ridging in ferritic stainless steels. ISIJ Int. 2002, 408, 1335–1340. [Google Scholar] [CrossRef]
- Gan, Y.; Zhao, P.; Wang, M.; Zhang, H. Physical analogue of liquid metal original position nucleation stirred by vibration. J. Iron Steel Res. 2006, 8, 9–13. [Google Scholar] [CrossRef]
- Zhang, H.; Tao, H.; Li, F.; Wang, M.; Huang, W. Research on mechanism of nucleation in liquid metal excited by vibration. Iron Steel 2008, 8, 20–24. [Google Scholar] [CrossRef]
- Wang, W.; Chang, X.; Xu, R. Effect of wetting angle on crystal grains nucleation and detachment of vibration chilling surface. Foundry Technol. 2013, 34, 1682–1685. [Google Scholar]
- Asta, M.; Beckermann, C.; Karma, A.; Kurz, W.; Napolitano, R.; Plapp, M.; Purdy, G.; Rappaz, M.; Trivedi, R. Solidification microstructures and solid-state parallels: Recent developments, future directions. Acta Mater. 2009, 57, 941–971. [Google Scholar] [CrossRef]
- Liu, B.C.; Xu, Q.Y.; Jing, T.; Shen, H.F.; Han, Z.Q. Advances in multi-scale modeling of solidification and casting processes. JOM 2011, 63, 19–25. [Google Scholar] [CrossRef]
- Nakajima, K.; Zhang, H.W.; Oikawa, K.; Ohno, M.; Jönsson, P. Methodological progress for computer simulation of solidification and casting. ISIJ Int. 2010, 50, 1724–1734. [Google Scholar] [CrossRef]
- Reuther, K.; Rettenmayr, M. Perspectives for cellular automata for the simulation of dendritic solidification-A review. Comput. Mater. Sci. 2014, 95, 213–220. [Google Scholar] [CrossRef]
- Stefanescu, D.M. Microstructure evolution during the solidification of steel. ISIJ Int. 2006, 46, 786–794. [Google Scholar] [CrossRef]
- Stefanescu, D.M. 30 years of modeling of microstructure evolution during casting solidification. Adv. Mater. Res. 2007, 23, 9–16. [Google Scholar] [CrossRef]
- Zhu, M.F.; Pan, S.Y.; Sun, D.K.; Zhao, H.L. Numerical simulation of microstructure evolution during alloy solidification by using cellular automaton method. ISIJ Int. 2010, 50, 1851–1858. [Google Scholar] [CrossRef]
- Smolin, A.Y.; Shilko, E.V.; Astafurov, S.V.; Konovalenko, I.S.; Buyakova, S.P.; Psakhie, S.G. Modeling mechanical behaviors of composites with various ratios ofmatrixeinclusion properties using movable cellular automaton method. Def. Technol. 2015, 11, 18–34. [Google Scholar] [CrossRef]
- Psakhie, S.G.; Shilko, E.V.; Popov, M.V.; Popov, V.L. Key role of elastic vortices in the initiation of intersonic shear cracks. Phys. Rev. E 2015, 91, 063302. [Google Scholar] [CrossRef] [PubMed]
- Zhu, M.F.; Hong, C.P. A modified cellular automaton model for the simulation of dendritic growth in solidification of alloys. ISIJ Int. 2001, 41, 436–445. [Google Scholar] [CrossRef]
- Zhu, M.F.; Kim, J.M.; Hong, C.P. Modeling of globular and dendritic structure evolution in solidification of an Al-7mass%Si alloy. ISIJ Int. 2001, 41, 992–998. [Google Scholar] [CrossRef]
- Kurz, W.; Fisher, D.J. Dendrite growth at the limit of stability: Tip radius and spacing. Acta Metall. 1981, 29, 11–20. [Google Scholar] [CrossRef]
- Kurz, W.; Giovanola, B.; Trivedi, R. Theory of microstructural development during rapid solidification. Acta Metall. 1986, 34, 823–830. [Google Scholar] [CrossRef]
- Zhu, M.F.; Dai, T.; Lee, S.Y.; Hong, C.P. Modeling of solutal dendritic growth with melt convection. Comput. Math. Appl. 2008, 55, 1620–1628. [Google Scholar] [CrossRef]
- Zhu, M.F.; Lee, S.Y.; Hong, C.P. Modified cellular automaton model for the prediction of dendritic growth with melt convection. Phys. Rev. E 2004, 69, 061610. [Google Scholar] [CrossRef]
- Zhu, M.F.; Stefanescu, D.M. Virtual front tracking model for the quantitative modeling of dendritic growth in solidification of alloys. Acta Mater. 2007, 55, 1741–1755. [Google Scholar] [CrossRef]
- Pan, S.Y.; Zhu, M.F. A three-dimensional sharp interface model for the quantitative simulation of solutal dendritic growth. Acta Mater. 2010, 58, 340–352. [Google Scholar] [CrossRef]
- Zhu, M.F.; Li, Z.Y.; An, D.; Zhang, Q.Y.; Dai, T. Cellular automaton modeling of microporosity formation during solidification of aluminum alloys. ISIJ Int. 2014, 54, 384–391. [Google Scholar] [CrossRef]
- Yin, H.; Felicelli, S.D. Dendrite growth simulation during solidification in the LENS process. Acta Mater. 2010, 58, 1455–1465. [Google Scholar] [CrossRef]
- Han, R.; Dong, W.; Lu, S.; Li, D.; Li, Y. Modeling of morphological evolution of columnar dendritic grains in the molten pool of gas tungsten arc welding. Comput. Mater. Sci. 2014, 95, 351–361. [Google Scholar] [CrossRef]
- Han, R.; Lu, S.; Dong, W.; Li, D.; Li, Y. The morphological evolution of the axial structure and the curved columnar grain in the weld. J. Cryst. Growth 2015, 431, 49–59. [Google Scholar] [CrossRef]
- Ao, X.; Xia, H.; Liu, J.; He, Q. Simulations of microstructure coupling with moving molten pool by selective laser melting using a cellular automaton. Mater. Des. 2020, 185, 108230. [Google Scholar] [CrossRef]
- Liu, S.; Shin, Y.C. Integrated 2D cellular automata-phase field modeling of solidification and microstructure evolution during additive manufacturing of Ti6Al4V. Comput. Mater. Sci. 2020, 183, 109889. [Google Scholar] [CrossRef]
- Rai, A.; Markl, M.; Körner, C. A coupled cellular automaton-lattice boltzmann model for grain structure simulation during additive manufacturing. Comput. Mater. Sci. 2016, 124, 37–48. [Google Scholar] [CrossRef]
- Beltran-Sanchez, L.; Stefanescu, D.M. Growth of solutal dendrites: A cellular automaton model and its quantitative capabilities. Metall. Mater. Trans. A 2003, 34, 367–382. [Google Scholar] [CrossRef]
- Beltran-Sanchez, L.; Stefanescu, D.M. A quantitative dendrite growth model and analysis of stability concepts. Metall. Mater. Trans. A 2004, 35, 2471–2485. [Google Scholar] [CrossRef]
- Dong, H.B.; Lee, P.D. Simulation of the columnar-to-equiaxed transition in directionally solidified Al–Cu alloys. Acta Mater. 2005, 53, 659–668. [Google Scholar] [CrossRef]
- Luo, S.; Zhu, M.Y. A two-dimensional model for the quantitative simulation of the dendritic growth with cellular automaton method. Comput. Mater. Sci. 2013, 71, 10–18. [Google Scholar] [CrossRef]
- Wang, W.; Lee, P.D.; McLean, M. A model of solidification microstructures in nickel-based superalloys: Predicting primary dendrite spacing selection. Acta Mater. 2003, 51, 2971–2987. [Google Scholar] [CrossRef]
- Wang, W.L.; Luo, S.; Zhu, M.Y. Development of a CA-FVM model with weakened mesh anisotropy and application to Fe-C alloy. Crystal 2016, 6, 147. [Google Scholar] [CrossRef]
- Lin, X.; Wei, L.; Wang, M.; Huang, W.D. A cellular automaton model with the lower mesh-induced anisotropy for dendritic solidification of pure substance. Mater. Sci. Forum 2010, 654–656, 1528–1531. [Google Scholar] [CrossRef]
- Wei, L.; Lin, X.; Wang, M.; Huang, W.D. A cellular automaton model for the solidification of a pure substance. Appl. Phys. A Mater. 2011, 103, 123–133. [Google Scholar] [CrossRef]
- Wei, L.; Lin, X.; Wang, M.; Huang, W.D. Orientation selection of equiaxed dendritic growth by three-dimensional cellular automaton model. Physica B 2012, 407, 2471–2475. [Google Scholar] [CrossRef]
- Wei, L.; Cao, Y.Q.; Lin, X.; Wang, M.; Huang, W.D. Quantitative cellular automaton model and simulations of dendritic and anomalous eutectic growth. Comput. Mater. Sci. 2019, 156, 157–166. [Google Scholar] [CrossRef]
- Reuther, K.; Rettenmayr, M. A comparison of methods for the calculation of interface curvature in two-dimensional cellular automata solidification models. Comput. Mater. Sci. 2019, 166, 143–149. [Google Scholar] [CrossRef]
- Wei, L.; Cao, Y.Q.; Lin, X.; Chang, K.; Huang, W.D. Globular to lamellar transition during anomalous eutectic growth. Model. Simul. Mater. Sci. Eng. 2020, 28, 065014. [Google Scholar] [CrossRef]
- Wang, W.L.; Chen, J.; Li, M.M.; Wang, A.L.; Su, M.Y. Numerical simulation of temperature and fluid fields in solidification process of ferritic stainless steel under vibration conditions. Crystals 2019, 9, 174. [Google Scholar] [CrossRef]
- Thévoz, P.; Desbiolles, J.L.; Rappaz, M. Modeling of equiaxed microstructure formation in casting. Metall. Mater. Trans. A 1989, 20, 311–322. [Google Scholar] [CrossRef]
- Wei, L.; Lin, X.; Wang, M.; Huang, W.D. Low artificial anisotropy cellular automaton model and its applications to the cell-to-dendrite transition in directional solidification. Mater. Discov. 2016, 3, 17–28. [Google Scholar] [CrossRef]
- Gueyffier, D.; Li, J.; Nadim, A.; Scardovelli, R.; Zaleski, S. Volume-of-fluid interface tracking with smoothed surface stress methods for three-dimensional flows. J. Comput. Phys. 1999, 152, 423–456. [Google Scholar] [CrossRef]
- Sergei, N.; Vladimir, S.; Sergey, K.; Alexey, G.; Victor, G. Formation mechanism of micro- and nanocrystalline surface layers in titanium and aluminum alloys in electron beam irradiation. Metals 2020, 10, 1399. [Google Scholar] [CrossRef]
- Mizukami, H.; Suzuki, T.; Umeda, T.; Kurz, W. Initial stage of rapid solidification of 18-8 stainless steel. Mat. Sci. Eng. A 1993, 173, 361–364. [Google Scholar] [CrossRef]
- Yang, M.B.; Pan, F.S. Analysis about forming mechanism of equiaxed crystal zone for 1Cr18Ni9Ti stainless steel twin-roll thin strip. J. Mater. Process. Tech. 2009, 209, 2203–2211. [Google Scholar] [CrossRef]



| Definition and Symbols | Values |
|---|---|
| Liquidus temperature, (K) | 1781 |
| Solute composition, (wt.%) | 17.0 |
| Partition coefficient, | 0.83 |
| Liquidus slope, (K∙wt%−1) | −2.27 |
| Gibbs–Thomson coefficient, (K∙m) | 3.0 × 10−7 |
| Liquid diffusion coefficient, (m2·s−1) | 5.0 × 10−9 |
| Solid diffusion coefficient, (m2·s−1) | 3.0 × 10−13 |
| Maximum density of nuclei, (m−3) | 5.5 × 109 |
| Mean nucleation undercooling, (K) | 7.0 |
| Standard deviation of undercooling, (K) | 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Shi, Q.; Zhu, X.; Liu, Y. Numerical Simulation of Microstructure Evolution in Solidification Process of Ferritic Stainless Steel with Cellular Automaton. Crystals 2021, 11, 309. https://doi.org/10.3390/cryst11030309
Wang W, Shi Q, Zhu X, Liu Y. Numerical Simulation of Microstructure Evolution in Solidification Process of Ferritic Stainless Steel with Cellular Automaton. Crystals. 2021; 11(3):309. https://doi.org/10.3390/cryst11030309
Chicago/Turabian StyleWang, Wenli, Qin Shi, Xu Zhu, and Yinhua Liu. 2021. "Numerical Simulation of Microstructure Evolution in Solidification Process of Ferritic Stainless Steel with Cellular Automaton" Crystals 11, no. 3: 309. https://doi.org/10.3390/cryst11030309
APA StyleWang, W., Shi, Q., Zhu, X., & Liu, Y. (2021). Numerical Simulation of Microstructure Evolution in Solidification Process of Ferritic Stainless Steel with Cellular Automaton. Crystals, 11(3), 309. https://doi.org/10.3390/cryst11030309





