Role of Hydrodynamics, Li+ Addition and Transformation Kinetics on the Formation of Plate-Like {001} Calcite Crystals
Abstract
1. Introduction
2. Materials and Methods
2.1. Preparation of Plate-Like Crystal Seed
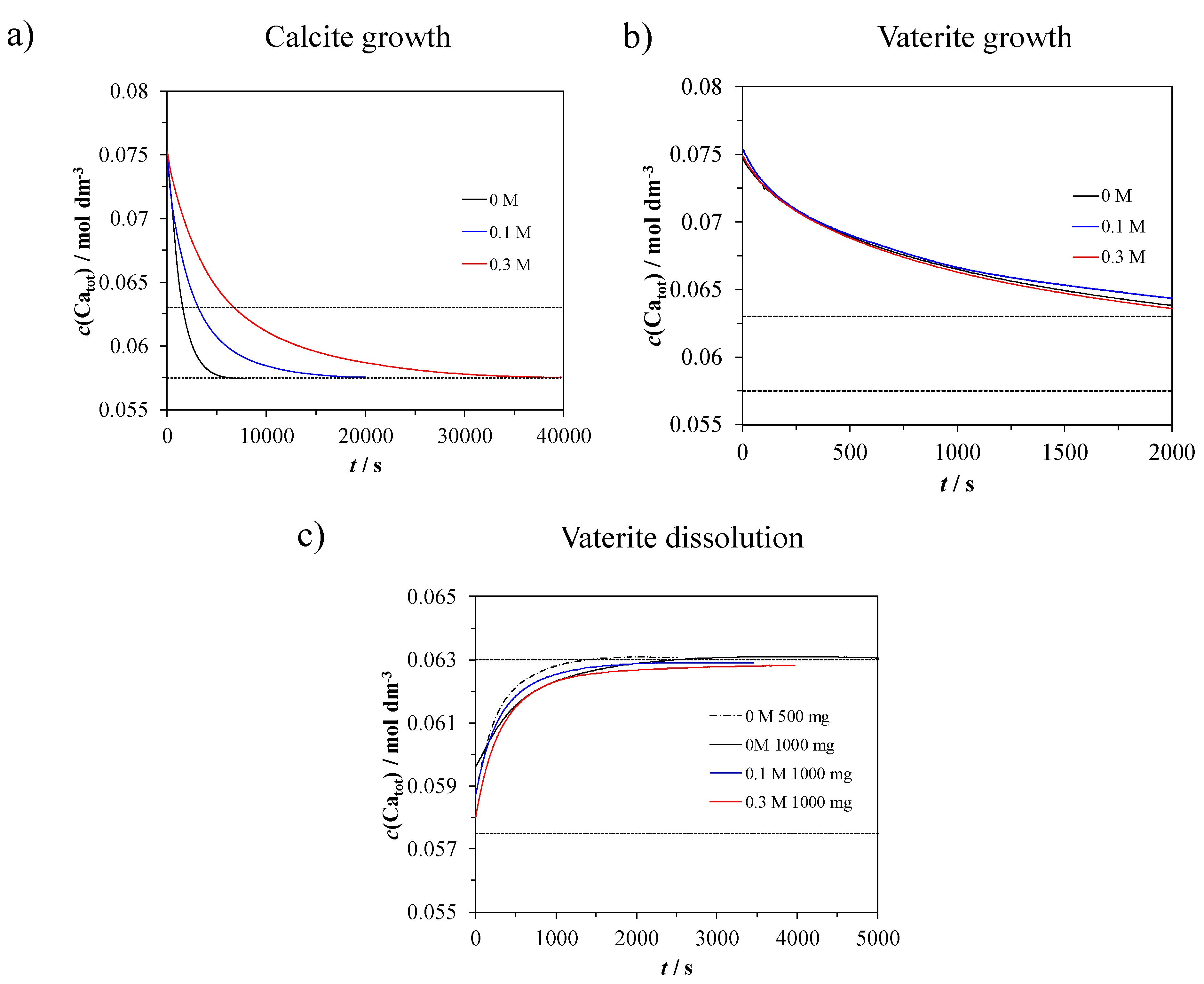
2.2. Precipitation Kinetic (Transformation, Crystal Growth and Dissolution)
2.3. Treatment of Data
exp(−Ke/ln(c/cS))
3. Results and Discussion
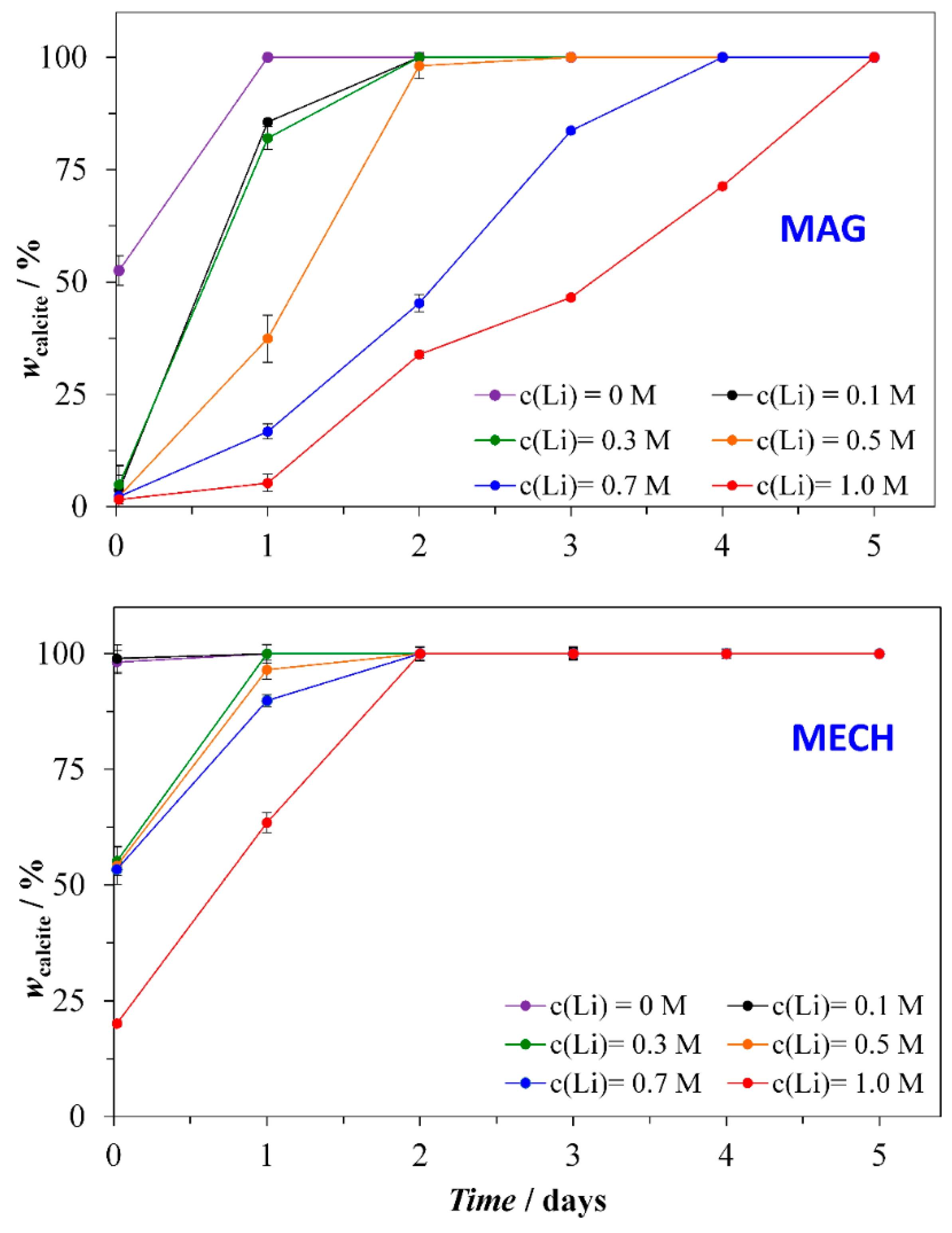
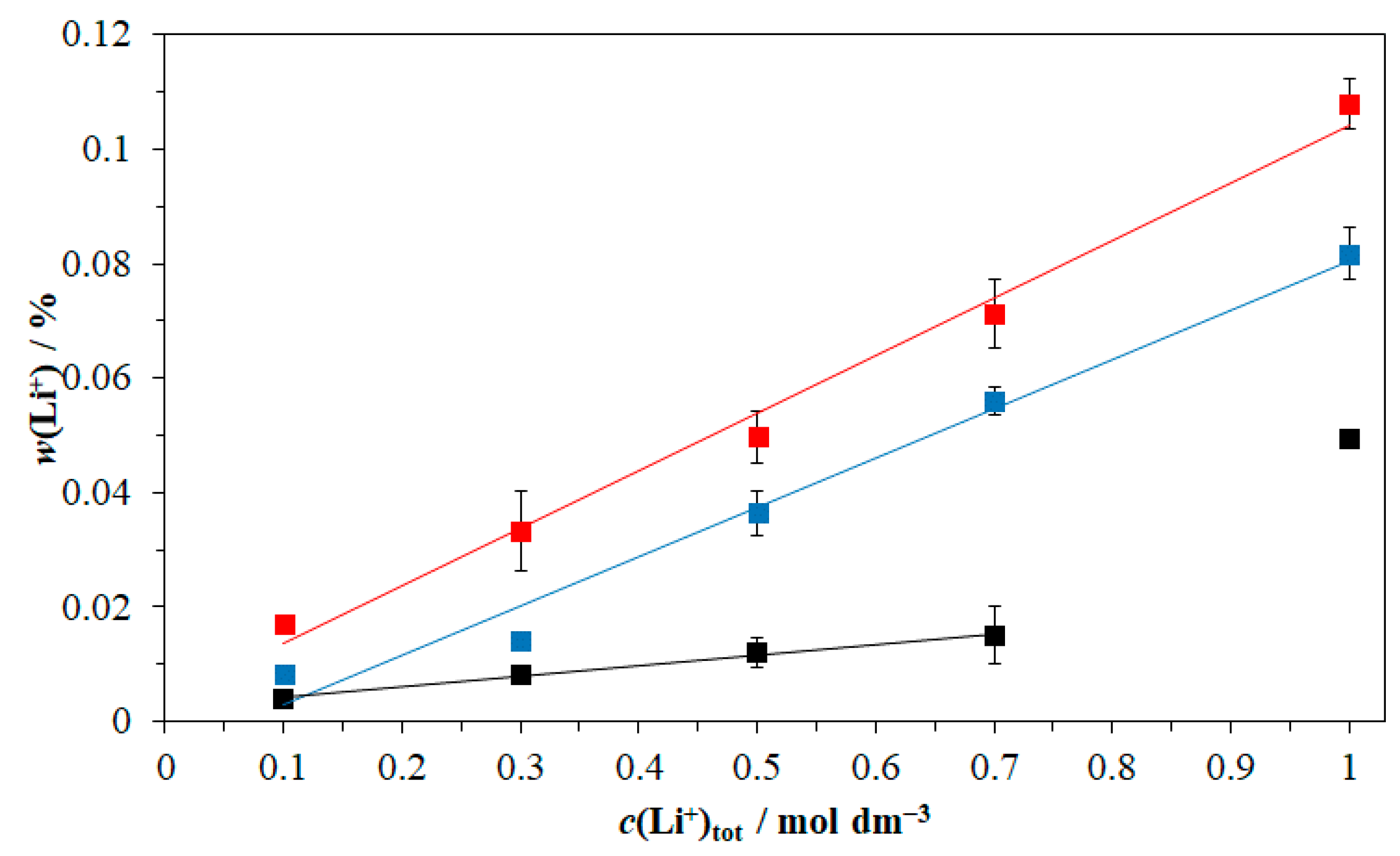
3.1. Structural Analysis
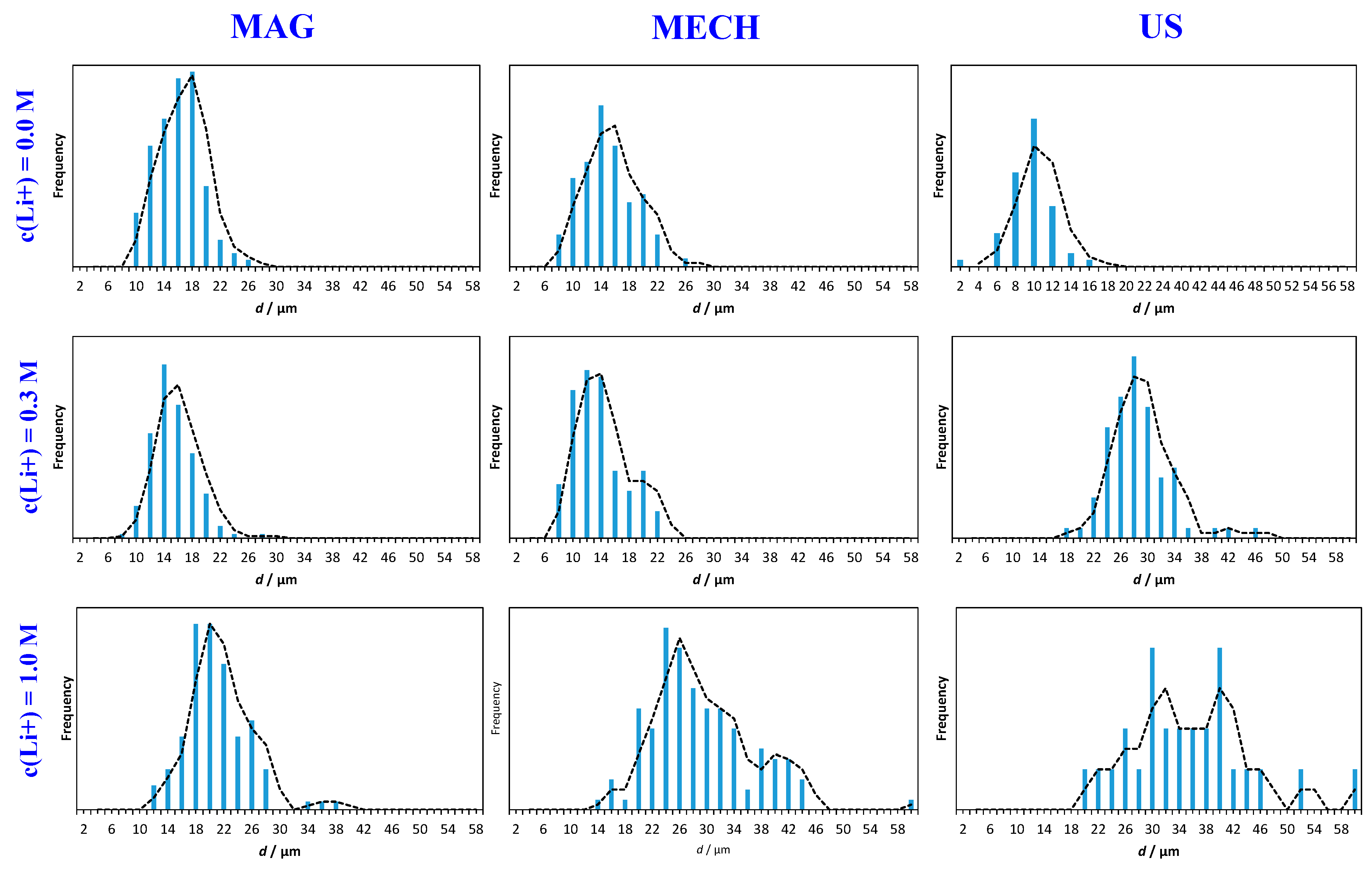
3.2. Particle Size Distribution
3.3. Morphology
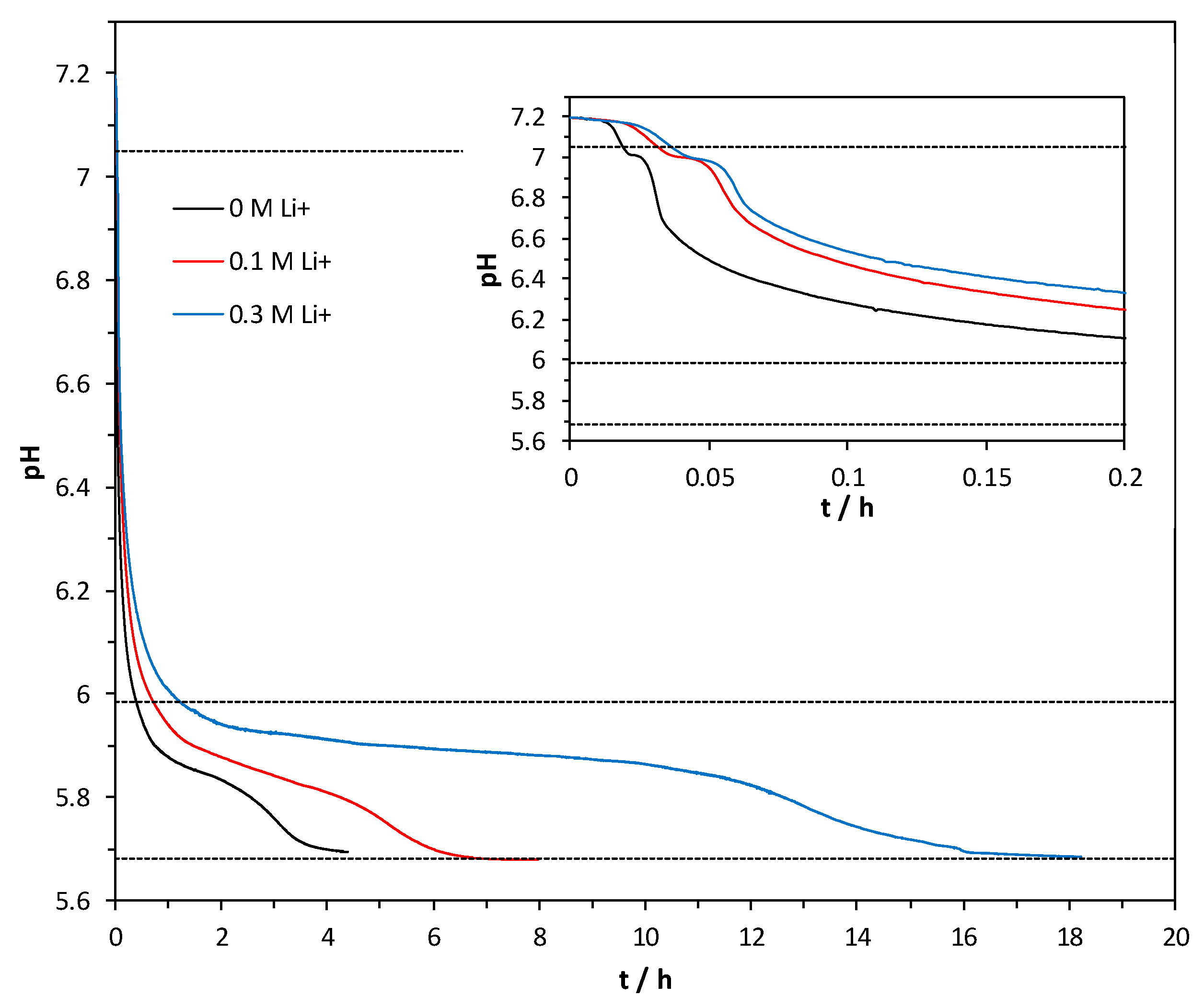
3.4. Precipitation Kinetics
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Matijaković, N.; Magnabosco, G.; Scarpino, F.; Fermani, S.; Falini, G.; Kralj, D. Synthesis and Adsorbing Properties of Tabular {001} Calcite Crystals. Crystals 2019, 9, 16. [Google Scholar] [CrossRef]
- Ukrainczyk, M.; Kontrec, J.; Kralj, D. Precipitation of different calcite crystal morphologies in the presence of sodium stearate. J. Colloid Interface Sci. 2009, 329, 89–96. [Google Scholar] [CrossRef]
- Stepić, R.; Jurković, L.; Klementyeva, K.; Ukrainczyk, M.; Gredičak, M.; Smith, D.M.; Kralj, D.; Smith, A.S. Adsorption of Aspartate Derivatives to Calcite Surfaces in Aqueous Environment. Cryst. Growth Des. 2020, 20, 2853–2859. [Google Scholar] [CrossRef]
- Orme, C.A.; Noy, A.; Wierzbicki, A.; Mcbride, M.T.; Grantham, M.; Teng, H.H.; Dove, P.M.; Deyoreo, J.J. Formation of chiral morphologies through selective binding of amino acids to calcite surface steps. Nature 2001, 411, 775–779. [Google Scholar] [CrossRef]
- Davis, K.J.; Dove, P.M.; De Yoreo, J.J. The role of Mg2+ as an impurity in calcite growth. Science 2000, 290, 1134–1137. [Google Scholar] [CrossRef] [PubMed]
- De Yoreo, J.J.; Vekilov, P.G. Principles of Crystal Nucleation and Growth. Rev. Mineral. Geochem. 2003, 54, 57–93. [Google Scholar] [CrossRef]
- Mann, S. Biomineralization: Principles and Concepts in Bioinorganic Materials Chemistry; Oxford University Press on Demand: New York, NY, USA, 2001; ISBN 0198508824. [Google Scholar]
- Mann, S. Molecular recognition in biomineralization. Nature 1988, 332, 119–124. [Google Scholar] [CrossRef]
- Rani, R.S.; Saharay, M. Molecular dynamics simulation of protein-mediated biomineralization of amorphous calcium carbonate. RSC Adv. 2019, 9, 1653–1663. [Google Scholar] [CrossRef]
- Chen, T.; Shi, P.; Li, Y.; Duan, T.; Yu, Y.; Li, X.; Zhu, W. Biomineralization of varied calcium carbonate crystals by the synergistic effect of silk fibroin/magnesium ions in a microbial system. CrystEngComm 2018, 20, 2366–2373. [Google Scholar] [CrossRef]
- de Carvalho, R.T.; Salgado, L.T.; Amado Filho, G.M.; Leal, R.N.; Werckmann, J.; Rossi, A.L.; Campos, A.P.C.; Karez, C.S.; Farina, M. Biomineralization of calcium carbonate in the cell wall of Lithothamnion crispatum (Hapalidiales, Rhodophyta): Correlation between the organic matrix and the mineral phase. J. Phycol. 2017, 53, 642–651. [Google Scholar] [CrossRef] [PubMed]
- Njegić-Džakula, B.; Brečević, L.; Falini, G.; Kralj, D. Kinetic Approach to Biomineralization: Interactions of Synthetic Polypeptides with Calcium Carbonate Polymorphs. Croat. Chem. Acta 2011, 84, 301–314. [Google Scholar] [CrossRef]
- Addadi, L.; Weiner, S. Interactions between acidic proteins and crystals: Stereochemical requirements in biomineralization. Proc. Natl. Acad. Sci. USA 1985, 82, 4110–4114. [Google Scholar] [CrossRef] [PubMed]
- Falini, G.; Fermani, S.; Goffredo, S. Coral biomineralization: A focus on intra-skeletal organic matrix and calcification. Semin. Cell Dev. Biol. 2015, 46, 17–26. [Google Scholar] [CrossRef]
- Yang, M.; Stipp, S.L.S.; Harding, J. Biological control on calcite crystallization by polysaccharides. Cryst. Growth Des. 2008, 8, 4066–4074. [Google Scholar] [CrossRef]
- Freeman, C.L.; Harding, J.H.; Quigley, D.; Rodger, P.M. Simulations of ovocleidin-17 binding to calcite surfaces and its implications for eggshell formation. J. Phys. Chem. C 2011, 115, 8175–8183. [Google Scholar] [CrossRef]
- Aizenberg, J.; Hendler, G. Designing efficient microlens arrays: Lessons from Nature. J. Mater. Chem. 2004, 14, 2066–2072. [Google Scholar] [CrossRef]
- Ye, X.; Zhang, F.; Ma, Y.; Qi, L. Brittlestar-inspired microlens arrays made of calcite single crystals. Small 2015, 11, 1677–1682. [Google Scholar] [CrossRef]
- Rajam, S.; Mann, S. Selective stabilization of the (001) face of calcite in the presence of lithium. J. Chem. Soc. Chem. Commun. 1990, 1789–1791. [Google Scholar] [CrossRef]
- Pastero, L.; Aquilano, D.; Costa, E.; Rubbo, M. 2D epitaxy of lithium carbonate inducing growth mechanism transitions on {0 0 0 1}-K and {0 1 1 8}-S forms of calcite crystals. J. Cryst. Growth 2005, 275, 1625–1630. [Google Scholar] [CrossRef]
- Pastero, L.; Aquilano, D. CaCO3 (Calcite)/Li2CO3 (zabuyelite) anomalous mixed crystals. Sector zoning and growth mechanisms. Cryst. Growth Des. 2008, 8, 3451–3460. [Google Scholar] [CrossRef]
- Kitano, Y. The Behavior of Various Inorganic Ions in the Separation of Calcium Carbonate from a Bicarbonate Solution. Bull. Chem. Soc. Jpn. 1962, 35, 1973–1980. [Google Scholar] [CrossRef]
- Titiloye, J.O.; Parker, S.C.; Osguthorpe, D.J.; Mann, S. Predicting the influence of growth additives on the morphology of ionic crystals. J. Chem. Soc. Chem. Commun. 1991, 1494–1496. [Google Scholar] [CrossRef]
- Pastero, L.; Costa, E.; Bruno, M.; Rubbo, M.; Sgualdino, G.; Aquilano, D. Morphology of calcite (CaCO3) crystals growing from aqueous solutions in the presence of Li+ ions. Surface behavior of the {0001} form. Cryst. Growth Des. 2004, 4, 485–490. [Google Scholar] [CrossRef]
- Bruno, M.; Massaro, F.R.; Prencipe, M.; Aquilano, D. Surface reconstructions and relaxation effects in a centre-symmetrical crystal: The {00.1} form of calcite (CaCO3). CrystEngComm 2010, 12, 3626–3633. [Google Scholar] [CrossRef]
- Song, R.Q.; Cölfen, H. Additive controlled crystallization. CrystEngComm 2011, 13, 1249–1276. [Google Scholar] [CrossRef]
- Titiloye, J.O.; Parker, S.C.; Mann, S. Atomistic simulation of calcite surfaces and the influence of growth additives on their morphology. J. Cryst. Growth 1993, 131, 533–545. [Google Scholar] [CrossRef]
- Ukrainczyk, M.; Stelling, J.; Vučak, M.; Neumann, T. Influence of etidronic acid and tartaric acid on the growth of different calcite morphologies. J. Cryst. Growth 2013, 369, 21–31. [Google Scholar] [CrossRef]
- Enomoto, N.; Sung, T.-H.; Nakagawa, Z.-E.; Lee, S.-C. Effect of ultrasonic waves on crystallization from a supersaturated solution of alum. J. Mater. Sci. 1992, 27, 5239–5243. [Google Scholar] [CrossRef]
- Choi, H.L.; Enomoto, N.; Nakagawa, Z.E. Effect of ultrasonic irradiation on precipitation of lead oxalate from aqueous solution. J. Mater. Sci. 1994, 29, 3239–3242. [Google Scholar] [CrossRef]
- Boyjoo, Y.; Pareek, V.K.; Liu, J. Synthesis of micro and nano-sized calcium carbonate particles and their applications. J. Mater. Chem. A 2014, 2, 14270–14288. [Google Scholar] [CrossRef]
- Štajner, L.; Kontrec, J.; Njegić Džakula, B.; Maltar-Strmečki, N.; Plodinec, M.; Lyons, D.M.; Kralj, D. The effect of different amino acids on spontaneous precipitation of calcium carbonate polymorphs. J. Cryst. Growth 2018, 486, 71–81. [Google Scholar] [CrossRef]
- Njegić-Džakula, B.; Falini, G.; Brečević, L.; Skoko, Ž.; Kralj, D. Effects of initial supersaturation on spontaneous precipitation of calcium carbonate in the presence of charged poly-l-amino acids. J. Colloid Interface Sci. 2010, 343, 553–563. [Google Scholar] [CrossRef] [PubMed]
- Kralj, D.; Brečević, L.; Kontrec, J. Vaterite growth and dissolution in aqueous solution II. Kinetics of transformation. J. Cryst. Growth 1997, 177, 248–257. [Google Scholar] [CrossRef]
- Fermani, S.; Njegić-Džakula, B.; Reggi, M.; Falini, G.; Kralj, D. Magnesium and temperature control on aragonite crystal aggregation and morphology. CrystEngComm 2017, 19, 2451–2455. [Google Scholar] [CrossRef]
- Kelly, D.R.; Harrison, S.J.; Jones, S.; Masood, M.A.; Morgan, J.J.G. Rapid crystallisation using ultrasonic irradiation—sonocrystallisation. Tetrahedron Lett. 1993, 34, 2689–2690. [Google Scholar] [CrossRef]
- Dalas, E. The effect of ultrasonic field on calcium carbonate scale formation. J. Cryst. Growth 2001, 222, 287–292. [Google Scholar] [CrossRef]
- Njegić Džakula, B.; Kontrec, J.; Ukrainczyk, M.; Sviben, S.; Kralj, D. Polymorphic composition and morphology of calcium carbonate as a function of ultrasonic irradiation. Cryst. Res. Technol. 2014, 49, 244–256. [Google Scholar] [CrossRef]
- Rasband, W. Image J Image Processing and Analysis in Java. Available online: https://ui.adsabs.harvard.edu/abs/2012ascl.soft06013R/abstract (accessed on 26 February 2021).
- Ukrainczyk, M.; Kontrec, J.; Babić-Ivančić, V.; Brečević, L.; Kralj, D. Experimental design approach to calcium carbonate precipitation in a semicontinuous process. Powder Technol. 2007, 171, 192–199. [Google Scholar] [CrossRef]
- Kralj, D.; Brečević, L.; Nielsen, A.E. Vaterite Growth and Dissolution in Aqueous Solution II. Kinetics of disolution. J. Cryst. Growth 1994, 143, 269–276. [Google Scholar] [CrossRef]
- Kralj, D.; Brečević, L.; Nielsen, A.E. Vaterite growth and dissolutionin aqueous solution I. Kinetics of crystal growth. J. Cryst. Growth 1990, 104, 793–800. [Google Scholar] [CrossRef]
- Brečević, L.; Kralj, D. Kinetics and Mechanisms of Crystal Growth in Aqueous Systems; Kallay, N., Ed.; Marcel Dekker, Inc.: New York, NY, USA, 2000. [Google Scholar]
- Aquilano, D.; Pastero, L. Anomalous mixed crystals: A peculiar case of adsorption/absorption. Cryst. Res. Technol. 2013, 48, 819–839. [Google Scholar] [CrossRef]
- Brečević, L.; Kralj, D.; Garside, J. Factors influencing the distibution of hydrates in calcium oxalate precipitation. J. Cryst. Growth 1989, 97, 460–468. [Google Scholar] [CrossRef]
- Stanković, A.; Kontrec, J.; Džakula, B.N.; Kovačević, D.; Marković, B.; Kralj, D. Preparation and characterization of calcium oxalate dihydrate seeds suitable for crystal growth kinetic analyses. J. Cryst. Growth 2018, 500, 91–97. [Google Scholar] [CrossRef]
- Hem, S.L. The effect of ultrasonic vibrations on crystallization processes. Ultrasonics 1967, 5, 202–207. [Google Scholar] [CrossRef]
- Luque De Castro, M.D.; Priego-Capote, F. Ultrasound-assisted crystallization (sonocrystallization). Ultrason. Sonochem. 2007, 14, 717–724. [Google Scholar] [CrossRef] [PubMed]
- Patel, M.A.; Bhanvase, B.A.; Sonawane, S.H. Production of Cerium Zinc Molybdate Nano Pigment by Innovative Ultrasound-Assisted Approach. Ultrason. Sonochem. 2013, 20, 906–913. [Google Scholar] [CrossRef]
- Beck, R.; Andreassen, J.P. Spherulitic growth of calcium carbonate. Cryst. Growth Des. 2010, 10, 2934–2947. [Google Scholar] [CrossRef]
- Andreassen, J.P. Formation mechanism and morphology in precipitation of vaterite—Nano-aggregation or crystal growth? J. Cryst. Growth 2005, 274, 256–264. [Google Scholar] [CrossRef]


| c(Li+)/mol dm−3 | Calcite Growth | Vaterite Growth | Vaterite Dissolution |
|---|---|---|---|
| kln/μm s−1 | kln/μm s−1 | D/m2 s−1 | |
| 0.00 | 20.4 | 37.9 | 3.4 × 10−9 |
| 0.10 | 9.0 | 32.1 | 3.3 × 10−9 |
| 0.30 | 4.8 | 32.1 | 2.9 × 10−9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matijaković Mlinarić, N.; Kontrec, J.; Njegić Džakula, B.; Falini, G.; Kralj, D. Role of Hydrodynamics, Li+ Addition and Transformation Kinetics on the Formation of Plate-Like {001} Calcite Crystals. Crystals 2021, 11, 250. https://doi.org/10.3390/cryst11030250
Matijaković Mlinarić N, Kontrec J, Njegić Džakula B, Falini G, Kralj D. Role of Hydrodynamics, Li+ Addition and Transformation Kinetics on the Formation of Plate-Like {001} Calcite Crystals. Crystals. 2021; 11(3):250. https://doi.org/10.3390/cryst11030250
Chicago/Turabian StyleMatijaković Mlinarić, Nives, Jasminka Kontrec, Branka Njegić Džakula, Giuseppe Falini, and Damir Kralj. 2021. "Role of Hydrodynamics, Li+ Addition and Transformation Kinetics on the Formation of Plate-Like {001} Calcite Crystals" Crystals 11, no. 3: 250. https://doi.org/10.3390/cryst11030250
APA StyleMatijaković Mlinarić, N., Kontrec, J., Njegić Džakula, B., Falini, G., & Kralj, D. (2021). Role of Hydrodynamics, Li+ Addition and Transformation Kinetics on the Formation of Plate-Like {001} Calcite Crystals. Crystals, 11(3), 250. https://doi.org/10.3390/cryst11030250










