Study on Tunable Band Gap of Flexural Vibration in a Phononic Crystals Beam with PBT

Abstract

Low-frequency flexural vibration plays a significant role in beam vibration control. To efficiently attenuate the propagation of flexural vibration at a low-frequency range, this paper proposes a new type of a phononic crystals beam with an adjustable band gap. The governing equations of flexural vibration in a periodic beam are established based on the Euler theory and Timoshenko theory. The band structures are calculated by the plane wave expansion method, the attenuation properties and transmission response curves with a finite periodic beam are calculated by the spectral element method and finite element method. The effects of the elastic foundation and axial stress on band gaps are discussed in detail, and the regulation of the temperature field on the band gap is emphatically studied. The theoretical and numerical results show that the elastic foundation and axial stress have significant influence on the band gap, and the location and width of the band gaps can be adjusted effectively when the Young’s modulus of PBT is changed by a varying temperature. The results are very useful for understanding and optimizing the design for composite vibration isolation beams.

1. Introduction

As the main load-bearing component, a beam is the primary bearer and transmitter of vibration, and its vibration control has attracted much attention. The vibration propagating in the beam mainly includes longitudinal vibration, torsional vibration and flexural vibration. As the main source of structural vibration, the amplitude of flexural vibration is much larger than the other vibrations. Therefore, the control of flexural vibration in beams is of great importance.

The appearance of phononic crystals (PCs) has provided a new idea for the control of flexural vibration in beams. PCs, as a kind of periodic artificial structure, have been widely studied with regard to their unique frequency characteristic called a band gap, in which the elastic/acoustic waves cannot propagate [1,2]. This unique property makes PCs show potential applications such as acoustic and mechanical wave filters, acoustic barriers, vibration control, etc. [3,4,5,6,7]. At present, some researchers have introduced PCs into civil engineering to control vibration [8,9,10,11,12], especially in beams [13,14,15,16,17,18,19,20,21,22].

The band gap characteristics of flexural vibration in a two-dimensional periodic frame structure composed of locally resonant composite beams were studied by Zhang et al. [20]. Guo et al. [21] revealed the flexural vibration attenuation performance of traditional periodic constraint layer damping in a sandwich beam, and pointed out that flexural vibration can be attenuated by both the Bragg scattering effect and damping effect, where the attenuation level is mainly dominated by Bragg scattering in the band gaps and by damping in the pass bands. Tang et al. [22] discussed flexural vibration propagation and attenuation through a Timoshenko beam coupled with periodic resonators by the method of a reverberation–ray matrix, their numerical results showing that the coupling between the beam and the resonators results in a local resonant attenuation band and multiple non-local resonant attenuation bands. These researches show that a lot of hard work has been devoted to designing periodic beams for isolate vibration. However, most of those beams are complex and it is not easy to obtain a low-frequency band gap to isolate the vibration caused by human activities, which is usually within the range of 1-100 Hz [23,24,25]. In addition, once the material and geometric parameters are determined, the periodic beam operates at fixed frequency ranges, which, inevitably, limits their applications in practical engineering. Therefore, it is of great significance to design periodic beams with a simple configuration, low-frequency and tunable band gaps for isolating vibration.

The introduction of polybutylene terephthalate (PBT) into periodic structures makes it possible to regulate the band structure [26,27]. As a smart composite material, PBT is a kind of composite material with a unique temperature dependence. The mechanical properties of PBT (such as young’s modulus) vary with temperature. This property offers the possibility of the band gap modulation of periodic beams.

As we all known, beams, plates and other components cannot be separated from interacting with the outside world. They are subject to external forces, and are bound by other objects. At present, some works have been conducted to discuss the influence of an elastic foundation and axial stress on band gaps [28,29]. However, no work appears in the open literature studying the regulation of temperature on the band gap of flexural vibration in a periodic beam with PBT, discussing the influence of axial stress and elastic foundation on band gap simultaneously. Hence, in this paper, a PC periodic beam considering the effects of foundation stiffness and axial stress is proposed. We assume this periodic beam is composed of PBT, steel and concrete to obtain tunable band gaps in a low-frequency range for vibration control in complex civil engineering environments. The governing equation of flexural vibration in the periodic beam is established based on Euler and Timoshenko’s theory. Numerical examples are performed to show the dispersion curves of flexural vibration in a periodic beam. The effects of foundation stiffness and axial stress on band structures are analyzed. The regulation of the temperature field on the band gap is studied. The methods and results in this paper can provide a solid theoretical basis for the design of periodic beams in civil engineering.

2. Formulation of the Problem

A periodic beam with a variable cross-section is shown as Figure 1. In order to obtain a higher bearing capacity, material A was assumed as steel, material B was PBT and material C was concrete. The lattice constant a = a₁ + a₂, and the filling ratio of each part were defined as f₁ = a₁/a, f₂ = a₂/a. The width of 1-1 and 2-2 cross-section are b and b₁, b₂ and b₃ are the width of the steel cross-section. h and h₁ are the height of 1-1 and 2-2 cross-section, h₂ and h₃ are the height of the steel cross-section. The width and height of each part are shown in Figure 1b–d, respectively.

In order to study the flexural vibration characteristics of the periodic beam, the plane wave expansion method (PWE) was used to calculate the dispersion curves. The Euler beam model and Timoshenko beam model are discussed, respectively. Considering the influence of the elastic foundation and axial stress on flexural vibration, the governing equation based on the Euler beam model could be expressed as:

$$\frac{{\partial }^2}{\partial x^2}\left(EI\frac{{\partial }^{2}w\left(x,t\right)}{\partial x^2}\right)+\rho S\frac{{\partial }^{2}w\left(x,t\right)}{\partial t^2}+cbw\left(x,t\right)-\frac{\partial }{\partial x}\left(N\frac{\partial w\left(x,t\right)}{\partial x}\right)=0$$

(1)

where $w$, $\rho$, S, E and I are the displacement, density, cross-sectional area, Young’s modulus and the moment of inertia; c and b are the foundation stiffness and width of the cross-section; $N=\sigma S$ is the axial force; $\sigma$ is the axial stress.

Compared with the Euler beam model, the Timoshenko beam model incorporates rotational inertia and shear effects, so the flexural vibration equation could be expressed as:

$$\begin{array}{c}\frac{{\partial }^2}{\partial x^2}\left(EI\frac{{\partial }^{2}w\left(x,t\right)}{\partial x^2}\right)+\rho S\frac{{\partial }^{2}w\left(x,t\right)}{\partial t^2}-\frac{{\partial }^2}{\partial t^2}\left[\frac{\partial }{\partial x}\left(\left(1+\frac{E}{k^{\prime }\mu }\right)\rho I\frac{\partial w\left(x,t\right)}{\partial x}\right)\right]+\frac{{\rho }^{2}I}{k^{\prime }\mu }\frac{{\partial }^{4}w\left(x,t\right)}{\partial t^4}\\ -\frac{\partial }{\partial x}\left(\frac{EIcb}{k^{\prime }S\mu }\frac{\partial w\left(x,t\right)}{\partial x}\right)+\frac{\rho Icb}{k^{\prime }S\mu }\frac{{\partial }^{2}w\left(x,t\right)}{\partial t^2}+cbw\left(x,t\right)-\frac{\partial }{\partial x}\left(N\frac{\partial w\left(x,t\right)}{\partial x}\right)\\ +\frac{{\partial }^2}{\partial x^2}\left(\frac{EIN}{k^{\prime }S\mu }\frac{{\partial }^{2}w\left(x,t\right)}{\partial x^2}\right)-\frac{{\partial }^2}{\partial t^2}\left[\frac{\partial }{\partial x}\left(\frac{\rho IN}{k^{\prime }S\mu }\frac{\partial w\left(x,t\right)}{\partial x}\right)\right]=0\end{array}$$

(2)

where $\mu$ is the shear modulus, $k^{\prime }=5/6$ is the shear coefficient.

Let $m_1=EI,$ $m_2=\rho S,$ $m_3=\left(1+\frac{E}{k^{\prime }\mu }\right)\rho I,$ $m_4=\frac{{\rho }^{2}I}{k^{\prime }\mu }$, $m_5=\frac{EI{K}_f}{k^{\prime }S\mu }$, $m_6=\frac{\rho I{K}_f}{k^{\prime }S\mu }$, $m_7=cb$, $m_8=N$, $m_9=\frac{EIN}{k^{\prime }S\mu }$, $m_{10}=\frac{\rho IN}{k^{\prime }S\mu }$; then, Equations (1) and (2) could be simplified as:

$$\frac{{\partial }^2}{\partial x^2}\left(m_1\frac{{\partial }^{2}w\left(x,t\right)}{\partial x^2}\right)+m_2\frac{{\partial }^{2}w\left(x,t\right)}{\partial t^2}+m_{7}w\left(x,t\right)-\frac{\partial }{\partial x}\left(m_8\frac{\partial w\left(x,t\right)}{\partial x}\right)=0$$

(3)

$$\begin{array}{c}\frac{{\partial }^2}{\partial x^2}\left(m_1\frac{{\partial }^{2}w\left(x,t\right)}{\partial x^2}\right)+m_2\frac{{\partial }^{2}w\left(x,t\right)}{\partial t^2}-\frac{{\partial }^2}{\partial t^2}\left[\frac{\partial }{\partial x}\left(m_3\frac{\partial w\left(x,t\right)}{\partial x}\right)\right]+m_4\frac{{\partial }^{4}w\left(x,t\right)}{\partial t^4}\\ -\frac{\partial }{\partial x}\left(m_5\frac{\partial w\left(x,t\right)}{\partial x}\right)+m_6\frac{{\partial }^{2}w\left(x,t\right)}{\partial t^2}+m_{7}w\left(x,t\right)-\frac{\partial }{\partial x}\left(m_8\frac{\partial w\left(x,t\right)}{\partial x}\right)\\ +\frac{{\partial }^2}{\partial x^2}\left(m_9\frac{{\partial }^{2}w\left(x,t\right)}{\partial x^2}\right)-\frac{{\partial }^2}{\partial t^2}\left[\frac{\partial }{\partial x}\left(m_{10}\frac{\partial w\left(x,t\right)}{\partial x}\right)\right]=0\end{array}$$

(4)

Due to the spatial periodicity, the material constants $m_i\left(i=1,2,3\cdots 10\right)$ could be expanded in the Fourier series as follows:

$$m_i\left(x\right)={\displaystyle \sum }_G{m}_i\left(G\right)e^{iGx}$$

(5)

where $G$ is the reciprocal vector.

Utilizing the Bloch theorem and expanding the displacement vector in Fourier series, we obtained:

$$w\left(x,t\right)=e^{i\left(kx-\omega t\right)}{w}_k\left(x\right)$$

(6)

where $k$ is the reduced wave vector, $\omega$ is the circular frequency and $w_k\left(x\right)$ could be written as:

$$w_k\left(x\right)={\displaystyle \sum }_{G_0}{e}^{i{G}_{0}x}{w}_k\left(G_0\right)$$

(7)

where $G_0$ is the reciprocal vector.

Substituting Equations (5)–(7) into Equations (3) and (4), Equations (3) and (4) could be simplified as:

$${\displaystyle \sum }_{G_0}\left[{\left(k+G_0\right)}^2{\left(k+G^{\prime }\right)}^2{m}_1\left(G^{\prime }-G_0\right)+m_7\left(G^{\prime }-G_0\right)+\left(k+G_0\right)\left(k+G^{\prime }\right)m_8\left(G^{\prime }-G_0\right)\right]w_k\left(G_0\right)-{\omega }^2{\displaystyle \sum }_{G_0}\left[m_2\left(G^{\prime }-G_0\right)\right]w_k\left(G_0\right)=0$$

(8)

$$\begin{array}{c}{\displaystyle {\displaystyle \sum }_{G_0}}[{\left(k+G_0\right)}^2{\left(k+G^{\prime }\right)}^2{m}_1\left(G^{\prime }-G_0\right)+\left(k+G_0\right)\left(k+G^{\prime }\right)m_5\left(G^{\prime }-G_0\right)+m_7\left(G^{\prime }-G_0\right)+\left(k+G_0\right)\left(k+G^{\prime }\right)m_8\left(G^{\prime }-G_0\right)+{\left(k+G_0\right)}^2{\left(k+G^{\prime }\right)}^2{m}_9\left(G^{\prime }-G_0\right)]w_k\left(G_0\right)\\ -{\omega }^2{\displaystyle {\displaystyle \sum }_{G_0}}[m_2\left(G^{\prime }-G_0\right)+\left(k+G_0\right)\left(k+G^{\prime }\right)m_3\left(G^{\prime }-G_0\right)+m_6\left(G^{\prime }-G_0\right)+\left(k+G_0\right)\left(k+G^{\prime }\right)m_{10}\left(G^{\prime }-G_0\right)]w_k\left(G_0\right)+{\omega }^4{\displaystyle {\displaystyle \sum }_{G_0}}{m}_4\left(G^{\prime }-G_0\right)w_k\left(G_0\right)=0\end{array}$$

(9)

where $G_0$, $G$ and $G^{\prime }$ are reciprocal vectors with the relation $G^{\prime }=G+G_0$.

Equation (9) could be further simplified as follows:

$${\lambda }^{2}AY+\lambda BY+CY=0$$

(10)

where $\lambda ={\omega }^2$, $A=[m_4\left(G^{\prime }-G_0\right)]$, $B=-\left[m_2\left(G^{\prime }-G_0\right)+\left(k+G_0\right)\left(k+G^{\prime }\right)m_3\left(G^{\prime }-G_0\right)+m_6\left(G^{\prime }-G_0\right)+\left(k+G_0\right)\left(k+G^{\prime }\right)m_{10}\left(G^{\prime }-G_0\right)\right]$, $C=\left[{\left(k+G_0\right)}^2{\left(k+G^{\prime }\right)}^2{m}_1\left(G^{\prime }-G_0\right)+\left(k+G_0\right)\left(k+G^{\prime }\right)m_5\left(G^{\prime }-G_0\right)+m_7\left(G^{\prime }-G_0\right)+\left(k+G_0\right)\left(k+G^{\prime }\right)m_8\left(G^{\prime }-G_0\right)+{\left(k+G_0\right)}^2{\left(k+G^{\prime }\right)}^2{m}_9\left(G^{\prime }-G_0\right)\right]$, $Y=\left[w_k\left(G_0\right)\right]$.

Let $X=\lambda Y$; then, Equation (10) could be transformed into a standard eigenvalue problem:

$$\left[\begin{array}{cc}0& I\\ -A^{-1}C& -A^{-1}B\end{array}\right]\left[\begin{array}{c}Y\\ X\end{array}\right]=\lambda \left[\begin{array}{c}Y\\ X\end{array}\right]$$

(11)

By solving Equations (8) and (11), we could obtain the dispersion relationship of the Euler beam and Timoshenko beam, respectively.

3. Numerical Results

In order to illustrate the accuracy of the results, we compared the results calculated in this study with Reference [30] by PWE. The computational model, materials and geometric parameters were the same as the reference. Figure 2 shows the results. The solid lines represent the results of this paper, and the circles represent the results of the reference. We found that these two results were in good agreement, which testified that the derivation and program used in this study were valid.

Unless otherwise specified, the material and geometric parameters of the periodic beam are shown in

Table 1. Material parameters.

Material	$\mathit{E} \left(\mathbf{G}\mathbf{P}\mathbf{a}\right)$	$\mathit{\upsilon }$	$\mathit{\rho } \left(\mathbf{k}\mathbf{g}/{\mathbf{m}}^3\right)$
Concrete	30	0.2	2500
Steel	210.6	0.3	7780

and

Table 2. Geometric parameters.

a1 (m)	b (m)	b1 (m)	b2 (m)	b3 (m)
1.4	0.4	0.2	0.1	0.05
a2 (m)	h (m)	h1 (m)	h2 (m)	h3 (m)
0.6	0.6	0.3	0.1	0.05

.

Material B was assumed to be the temperature sensitive material—PBT—, as mentioned earlier, for regulating the band gap. The young’s modulus of PBT depends strongly on the temperature, and relevant experiments showed that its young’s modulus was 12.9 Gpa at 20$℃$, 12 Gpa at 30$℃$, 10.4 Gpa at 40$℃$, 6.7 Gpa at 50$℃$, 1 Gpa at 60$℃$, 62.6 Mpa at 65$℃$, 50 Mpa at 70$℃$ and 10 Mpa at 80$℃$ [26]. From these data, we found that when the temperature changed from 20$℃$ to 80$℃$, the young’s modulus of PBT could experience a change of three orders of magnitude. However, the PBT maintained an elastic solid state even at a significant reduction in Young’s modulus during the varied temperature [27]. The Poisson ratio (0.3) and mass density (1180 kg/m³) of PBT were independent of the temperature. Unless stated otherwise, we assumed the young’s modulus of PBT was 12.9 Gpa.

3.1. Influence of Foundation Stiffness on Band Gaps

The ground beams were subjected to the action of the elastic foundation. The influence of the foundation stiffness on flexural vibration was not negligible. Figure 3 shows the dispersion curve of the periodic beam with or without an elastic foundation. The blue-shaded area represents the band gap of the Euler beam, and the yellow-shaded area represents the band gap of the Timoshenko beam. We found that when the foundation stiffness $c=0 \mathrm{N}/{\mathrm{m}}^3$, there was only one band gap from 80.4 Hz to 163.7 Hz in the Euler beam and 66.2~163.8 Hz in the Timoshenko beam. However, when $c=3\times {10}^6 \mathrm{N}/{\mathrm{m}}^3$, in addition to the original band gap, a new band gap from 0 to 24.3 Hz emerged.

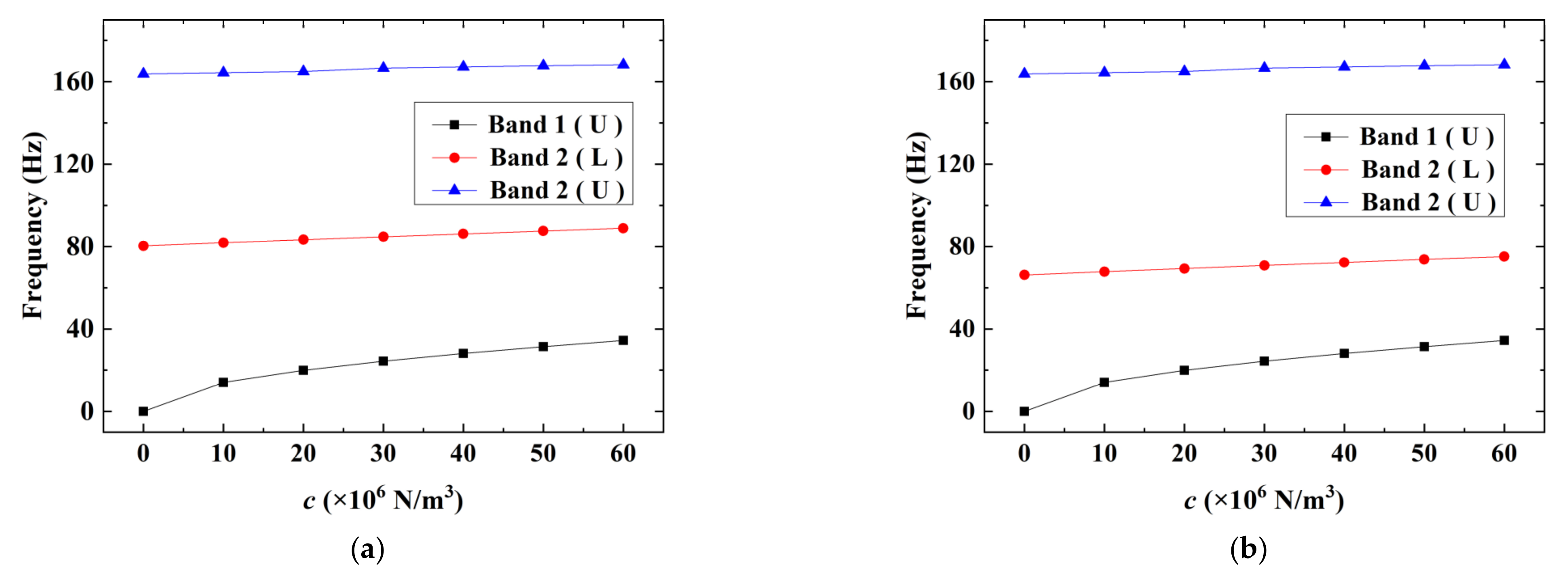
In order to show the effect of the elastic foundation on the band gap more clearly, we presented the lower and upper boundary of these two band gaps in Figure 4. L and U refer to the lower and upper boundary of the band gap, respectively. Due to the lower boundary of the first band gap always starting from 0 Hz, unless otherwise specified, the lower boundary of the first band gap was not shown. From Figure 4, we found that, with the increase in c, the first band gap and the second band gap increased gradually. Compared with the first band gap, the elastic foundation had less effect on the second band gap.

In addition, from Figure 3b and Figure 4, it was found that the upper boundary of the first band gap of the Timoshenko beam was the same as that of the Euler beam when c was equal, while the lower boundary of the second band gap of the Timoshenko beam was smaller than that of the Euler beam. The reason for this phenomenon was that the influence of shear deformation was taken into account in the Timoshenko beam, which was equivalent to reducing constraints and stiffness; meanwhile, the rotational inertia amplified the influence of mass. Hence, the lower boundary of the second band gap of the Timoshenko beam was lower than that of the Euler beam. To a periodic beam based on an elastic foundation, the upper boundary of the first band gap is a crucial frequency [31], which was define as

$$f_0=\frac{1}{2\pi }\sqrt{\frac{c{b}_1{a}_1+c{b}_2{a}_2}{{\rho }_1{S}_1{a}_1+{\rho }_2{S}_2{a}_2}}$$

(12)

Therefore, when the geometric and material parameters remained unchanged, the upper boundary depended on c. In order to further verify the correctness of the results, Figure 5 gives a comparison between the result obtained by the PWE and by Equation (12). It can be seen from Figure 5 that the two results were in good agreement, which testified that the analysis of the paper was correct.

3.2. Influence of Axial Stress on Band Gaps

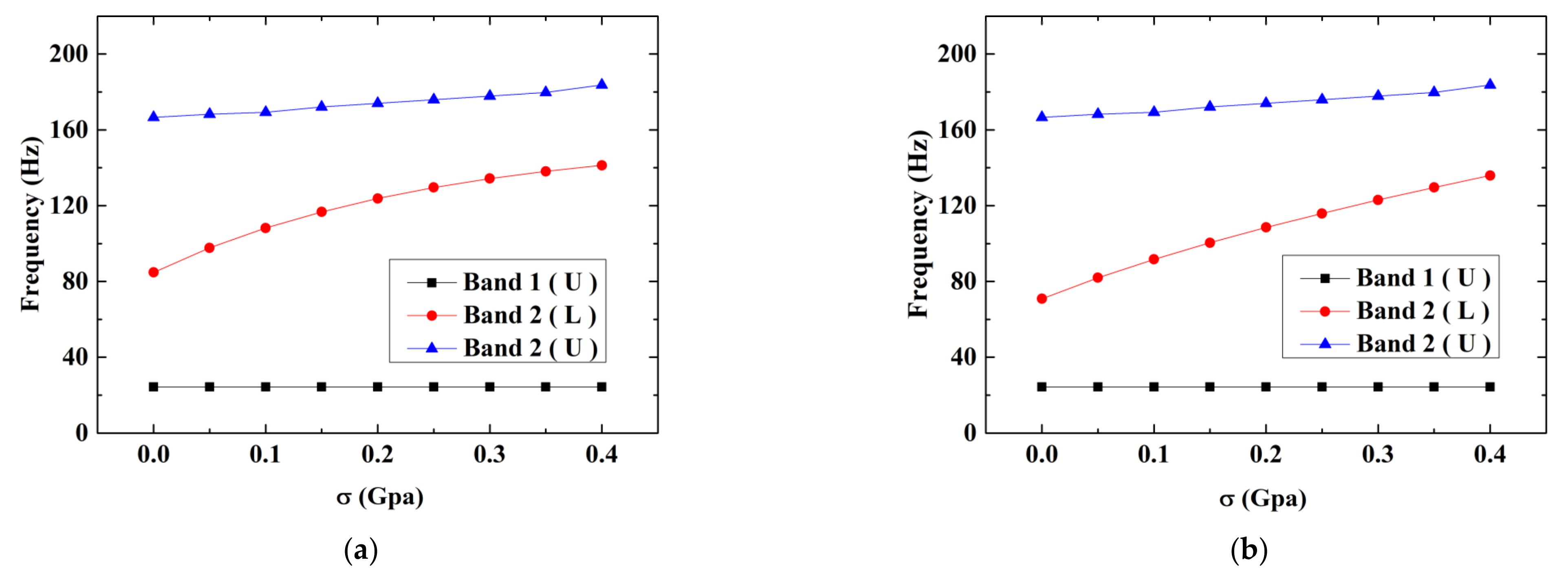
As previously mentioned, axial stress may affect the band gap. Assuming $c=3\times {10}^6 \mathrm{N}/{\mathrm{m}}^3$, the influence of axial tensile stress on the band gap is presented in Figure 6. It can be seen that the axial tensile stress had a significant effect on the band gap. Although the first band gap, which depended on c, did not change with the increase in axial tensile stress, the second band gap increased with the increase in axial tensile stress. When the axial tensile stress increased from 0 Gpa to 0.4 Gpa, the second band gap of the Euler beam increased from 84.7~166.6 Hz to 141.3~183.7 Hz, and the second band gap of the Timoshenko beam increased from 70.8~166.6 Hz to 135.9~183.7 Hz. The reason for this phenomenon was that when axial tensile stress was applied, it was equivalent to increasing the stiffness of the beam, so the frequency of the second band gap increased.

Figure 7 displays the influence of axial compressive stress on the band gap. Both for the Euler beam or the Timoshenko beam, the influence of axial compressive stress on the band gap was similar. We found that when the axial compressive stress increased from 0 Gpa to 0.4 Gpa, the lower boundary of the second band gap of the Euler beam decreased drastically from 84.8 Hz to 24.3 Hz, while the upper boundary only decreased 6.5 Hz, from 166.6 Hz to 160.1 Hz. The scenario was similar to the Timoshenko beam, with which we found that the second band gap decreased from 70.9~166.6 Hz to 24.3~156.6 Hz. In addition, when the axial compressive stress reached 0.15 Gpa, the lower boundary of the second band gap of both the Euler beam and the Timoshenko beam decreased to 24.3 Hz; then, they remained unchanged. Thus, if one wanted to obtain a low and broadband gap, applying appropriate axial compressive stress is an effective approach. From Figure 7, we also found that the upper boundary of the first band gap decreased with the increase in axial compressive stress in the beginning; then, they tended to be stable. In order to show the change of the upper boundary of the first band gap more clearly, we presented the first band structure of the dispersion curve in Figure 8 when the axial compressive stress was 0 Gpa, −0.05 Gpa, −0.1 Gpa and −0.15 Gpa, respectively.

From Figure 8, it can be seen that, with the increase in axial compressive stress, the first band structure changed, (0, 24.3) was no longer the minimum point, and c no longer played a decisive role in the first band gap. Therefore, when axial compressive stress was applied, the first band gap would change. As the application of axial compressive stress was equivalent to reducing the stiffness of the beam, the upper boundary of the first band gap would decrease.

3.3. Influence of Temperature on Band Gaps

As shown in the aforementioned, PBT is a kind of material with a strong temperature dependence, which suggests that temperature can be used to tune the band gap of a periodic beam when it uses PBT as one of its materials. Figure 9 shows the influence of temperature on the band gap when $c=3\times {10}^6 \mathrm{N}/{\mathrm{m}}^3$. As can be seen, with the increase in temperature, the first band gap remained unchanged, while the lower boundary and upper boundary of the second band gap both decreased whether it was the Euler beam or Timoshenko beam. When the temperature increased from 20$℃$ to 80$℃$, the second band gap of Euler beam decreases from 84.7~166.2 Hz to 43.4~89.5 Hz, and it decreased from 70.9~166.2 Hz to 39.3~89.5 Hz in the Timoshenko beam. This result showed that temperature could regulate the second band gap effectively, while it had no influence on the first band gap.

3.4. Influence of Period Number n on Attenuation Properties

In order to verify the correctness of the previous calculation and analysis, we calculated the attenuation properties and transmission response curves by the spectral element method (SEM). In view of there being no infinite periodic structure in the actual engineering, we took a finite period in the calculation.

Figure 10 shows the transmission response curves when the period number n was 4, 6 and 8, respectively. The influence of the elastic foundation was ignored, that is to say $c=0 \mathrm{N}/{\mathrm{m}}^3$. From Figure 10, it can be seen that there were sharp drops both in the transmission response curves of the Euler beam and Timoshenko beam. The attenuation domain of the Euler beam and Timoshenko beam was 77~170 Hz and 68~174 Hz, respectively, when the periods number n = 8. Comparing Figure 10 with the dispersion curve of the infinite period in Figure 3a, we found that these two results were in good agreement. In addition, from Figure 10, we found, apparently, that the attenuation coefficient and amplitude increased as the period number n increased. These results indicated that vibration decayed quickly when the period number increased.

In general, such as the experimental method to obtain the transmission energy loss, the calculation results by FEM could simulate the damping effect of the periodic beam in an actual vibration environment. Therefore, we used COMSOL Multiphysics to calculate the transmission response curve. The computational model is shown in Figure 11, in which the unit cell was the same as in Figure 1. The excitor was on the left, and the receiver was on the right. The excitation was assumed as a vertical displacement. In addition, the external boundaries were surrounded by perfect match layers (PML), which simulated the infinite region by suppressing any reflection.

Figure 12 shows the transmission curves when the period number n = 8. The blue dash line and red dash line represent the results of the Euler beam and Timoshenko beam, which were calculated by SEM. The black solid line represents the FEM result regardless of the beam model. From Figure 12, we can see that the attenuation domain of the FEM result was 62~156 Hz. This result was close to the result based on the Timoshenko beam model. That is to say, using the Timoshenko beam model to calculate the band gap of flexural vibration was more coincident with real situations.

4. Conclusions

In this paper, we investigated the propagation of flexural vibration in a periodic beam composed of PBT, concrete and steel. By using the plane wave expansion method, the dispersion relation of flexural vibration was obtained. The transmission responses were calculated by the spectral element method and finite element method. Numerical results were presented to illustrate the band structures and vibration propagation characteristics of the periodic beam with an elastic foundation.

Based on the numerical results, we found that the foundation stiffness and axial stress had a significant effect on the band gap. The band gap of flexural vibration could be effectively modulated by applying a temperature field. PBT played a significant role in the regulation of the band gap. Moreover, the effect of the period number on the attenuation was very obvious. The proposed periodic beam was demonstrated to possess a large band gap in the low-frequency range, resulting in the low-frequency broadband flexural vibration attenuation and vibration suppression. The study opens a new possibility to broaden band gaps of periodic beams at a lower frequency, and the results can potentially be used to reduce low-frequency vibration in actual civil engineering.