Abstract
In this paper, a new magneto-electro-elastic functionally graded Timoshenko microbeam model is developed by using the variational formulation. The new model incorporates the extended modified couple stress theory in order to describe the microstructure effect. The power-law variation through the thickness direction of the two-phase microbeams is considered. By the direct application of the derived general formulation, the static bending and free vibration behavior of the newly developed functionally graded material microbeams are analytically determined. Parametric studies qualitatively demonstrate the microstructural effect as well as the magneto-electro-elastic multi-field coupling effect. The proposed model and its classic counterpart produce significant differences for thin graded magneto-electro-elastic Timoshenko microbeams. The thinner the microbeam is, the larger the difference becomes.
1. Introduction
Currently, magneto-electro-elastic (MEE) materials have attracted more and more attention. MEE materials can realize the mutual conversion between magnetic, electrical, and mechanical energies. Such characteristics have found important applications in stability controlling, actuating, health monitoring, medical ultrasonic, and some smart structure technologies [1,2,3]. In addition, functionally graded materials (FGMs) are characterized by continuous changes in material properties [4,5,6]. The mechanical properties of MEE materials synthesized from functionally graded materials are of great significance in both research and industrial fields [7,8]. In recent years, the research on investigating magneto-electro-elastic functionally graded materials (MEE-FGMs) on thin beams and plates has become a major trend. Bhangale and Ganesan [9] studied the free vibration behavior of anisotropic and linear MEE-FGM plates. Sladek et al. [10] proposed a meshless method for the bend analysis of circular MEE-FGM plates. Vinyas et al. [11] studied the effectiveness of utilizing MEE-FGM plates in precise frequency responses control. Mahesh and Harursampath [12] and Mahesh [13] evaluated nonlinear deflections of MEE-FGM porous flat panels and shells subjected to mechanical, electrical, and magnetic loads, respectively. However, numerous experiments [14,15] have proved that thin beams and plates usually exhibit size effects, (i.e., the thinner, the stiffer). Such size effects arise from non-local interactions of material particles at a very small scale, which cannot be described by classical theories at the micron or nanometer level due to a lack of any material length scale parameters. Therefore, it is necessary to develop thin MEE-FGM structure models based on non-classical theories.
In order to predict the size effects, numerous theories have been proposed with additional material parameters, such as non-local theories [16], couple stress theories [17,18,19], strain gradient theories [20,21,22], and a series of simpler versions [23,24,25,26,27,28]. These theories were successfully applied to develop size-dependent structure models for very small scales. For example, based on nonlocal theories, a number of MEE/MEE-FGM beam and plate models have been developed to capture non-local size effects [29,30,31,32], in which a non-local medium, including long-range material interactions, is adopted. Lim et al. [33] proposed a non-local strain gradient theory to include both non-local and strain gradient effects, and the bending, buckling, and free variation problems of FGM beams have been solved [34,35]. In addition, the modified couple stress theory (MCST) [24,25] contains only one additional parameter for isotropic materials. This MCST and its extended versions only consider the symmetrical part of the curvature tensor, which leads to fewer material parameters than their classical counterparts. In view of the great difficulties for determining additional parameters and interpreting the relevant microstructures, these modified theories have been applied to build micro/nano-beam and periodic composite pipe models [36,37,38,39,40,41], from which a microstructure-dependent stiffness is revealed. Recently, three such models have been proposed for MEE Timoshenko homogeneous beams [39] and MEE homogeneous plates [42,43] based on the extended modified couple stress theory. However, to the best of our knowledge, the extended modified couple stress theory is not applicable to MEE-FGM microbeams, which are inhomogeneous and might be helpful for smart devices miniaturization [44,45,46,47,48]. This motivated the present work.
The present work uses the extended modified couple stress theory to develop a MEE-FGM Timoshenko microbeam model for the first time and analytically solves the static bending and free vibration problems of the new model.
2. Materials and Methods
Consider a two-phase FGM microbeam with length L, width b and thickness h under the combined electric, magnetic, and mechanical loadings, as shown in Figure 1. The effective material properties P(z) (i.e., elastic stiffness, couple stress stiffness, piezoelectric constant, piezomagnetic constant, dielectric constant, magnetic permeability constant, magneto-dielectric constant and density) of the current microbeam change continuously in the thickness direction based on a power-law distribution [36], where P1 and P2 are the material properties of material I and II, respectively. The functionally graded power-law index n determines the material distribution across the thickness.
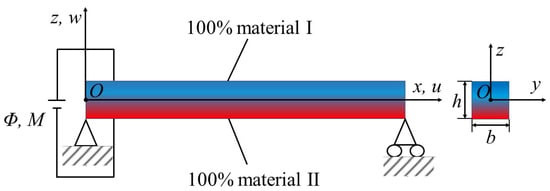
Figure 1.
Functionally graded microbeam configuration.
Based on the extended modified couple stress theory [42,49], the constitutive equations for transversely isotropic magneto-electro-elastic materials are given by [39,42,50,51].
where σij, mij, Di, Bi are the Cauchy stress tensor, the deviatoric part of the couple stress tensor, the electric displacements, and the magnetic fluxes, respectively. Cαβ (α, β = 1, 2, …, 6) is the elastic stiffness tensor, Aαβ (α, β = 1, 2, …, 6) is the couple stress stiffness tensor, eiα and qiα are the piezoelectric and piezomagnetic tensors, sij and μij are the dielectric and magnetic permeability tensors, dij is the magneto-dielectric tensor, and εij and χij are, respectively, the infinitesimal strain and the symmetric curvature tensors, which are defined by
with ui being the displacement, and εijk is the Levi-Civita symbol. In addition, Ek and Hk are, respectively, the electric field intensity and magnetic field intensity read
where Φ and M are the electric and magnetic potentials.
For a MEE Timoshenko beam with a uniform cross-section shown in Figure 1, the displacement field and electric and magnetic potentials can be given by [52,53,54,55]
where u and w are the beam extension and deflection, φ represents the rotation angle, γ and ζ are the spatial variations of the electric and magnetic potentials along the x-direction, respectively. γ0 and ζ0 are, respectively, the external electric and magnetic potentials.
By substituting Equations (9) and (10) into Equations (6)–(8) yields
Based on Equations (11)–(14), the constitutive equations in Equations (2)–(5) can be obtained as
From Equations (11)–(18), the first variation of the total strain energy in the current beam satisfying the extended modified couple stress theory over the time span [0, T] takes the form [39,42]
where A is the cross-sectional area.
The first variation of the kinetic energy of the Timoshenko beam over the time interval [0, T] is given by [53]
where ρ is the mass density.
Furthermore, the virtual work performed by the applied forces acting on the current Timoshenko beam over the time span [0, T] can be written as [55,56]
where f and q are, respectively, the x- and z-components of the body force per unit length along the x-axis.
According to Hamilton’s principle [53,56],
Substituting Equations (19)–(21) into Equation (22), applying the fundamental lemma of the calculus of variations [57], and considering the arbitrariness of δu, δw, and δφ yield
as the equation of motion, and
as boundary conditions, where the overbar denotes the prescribed value. Note that the stress, electric, magnetic resultants, and mass inertias can be expressed as
where ks denotes the shape correction factor [58,59], and
Based on Equations (23)–(55), it is found that the current MEE-FGM beam model can additionally capture the effects of couple stress, piezomagnetism, piezoelectricity, and MEE coupling, when compared to the classical FGM Timoshenko beam model.
3. Analytical Solution
This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.
In order to illustrate the newly developed model in Section 2, the static bending and free vibration problems of the current beam are solved in this section.
According to Equations (28)–(33), the relevant boundary conditions of a simply supported beam can be identified as
It should be noted that the boundary of the electric and magnetic conditions given in Equations (60) and (61) are for an open circuit.
3.1. Static Bending
Consider Fourier solutions for u(x), φ(x), w(x), γ(x), and ζ(x):
where Uk, Φk, Wk, Гk, and Zk are the Fourier coefficients to be determined. It can be shown that the Fourier solutions in Equations (62)–(66) satisfy the boundary conditions in Equations (56)–(61). In addition, the body force f is equal to zero, and the uniform load q(x) can also be expanded in Fourier series as:
where Qk is a Fourier coefficient calculated by q(x) = p0 in the current case as
According to the Equations (23)–(27), (62)–(66) and (67), the equilibrium equations of static bending problems can be written as
Substituting Equations (62)–(66) into Equations (69)–(73) results in
where
According to Equation (74), the Fourier coefficients Uk, Φk, Wk, Гk, and Zk will be solved. The solutions of u(x), φ(x), w(x), γ(x), and ζ(x) for the current simple supported beam can also be given by inserting these results into Equations (62)–(66).
3.2. Free Vibration
In the free vibration problem of the current beam, both the external forces are vanished (i.e., f = q = 0). Consider the following Fourier series expansions for u(x, t), φ(x, t), w(x, t), γ(x, t), and ζ(x, t):
where ωk is the kth vibration frequency, , , and are Fourier coefficients. It should be noted that the Fourier series expansions in Equations (76)–(80) satisfy the boundary conditions in Equations (56)–(61). Based on Equations (76)–(80) and Equations (23)–(27), the equations of motion can be expressed as
Using Equations (76)–(80) in Equations (81)–(85), yields
Therefore, the first natural frequency ω1 of the current beam can be solved from the smallest positive root of ωk2 (k = 1) of the Equation (86).
4. Numerical Results
The 50%-50% BaTiO3-CoFe2O4 is adopted for material I [39,42,60,61,62], and the material II is taken to be epoxy [63], as listed in Table 1. Note that the couple stress constants A11 and A12 are estimates based on the formula provided in [14,39]. The magnitude of the uniform load p0 is equal to 1/2000h N/m, the shear correction factor ks is 0.81/2, and the cross-sectional shape is kept at b = 2h and L = 20h.

Table 1.
Material properties of the BaTiO3-CoFe2O4 [39] and epoxy [63].
In order to verify the correctness of the current model, a comparative study of the deflection of a simply supported microbeam subjected to uniform load between the current model (with Gradient index n = 0) and the model provided by Zhang et al. [39] are plotted in Figure 2. The beam parameters are adopted from Zhang et al. [39].

Figure 2.
Comparison of the deflection of the simply supported microbeam subjected to a uniform load.
From Figure 2, it is obvious that the results of the classical and current model are the same as those in Zhang et al. [39]. In addition, this validates the current model and shows that the microstructure effect will always cause the deflection to decrease, as expected.
4.1. Static Bending
Figure 3 shows the distributions of the deformation, axial normal stress, and the electric and magnetic potentials of the current beam. In order to facilitate the observation of the deformation trend of the current beam, the x-component of the displacement vector u of a point (x, y, z) on the beam cross-section has been enlarged by 10 times. In addition, the thickness h is 20 μm, and the gradient index n is 5.
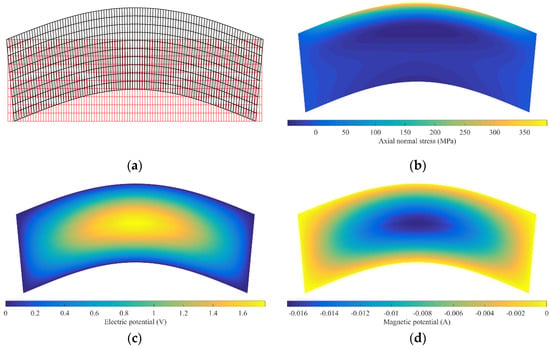
Figure 3.
Distribution of (a) deformation, (b) axial normal stress, (c) electric potential, and (d) magnetic potential (Gradient index n = 5).
From Figure 3b, it can be observed that the axial normal stress in the middle of the current beam is relatively small, and the axial normal stress at the top of the beam is relatively large. From Figure 3c,d, it is clear that the distributions of electric and magnetic potentials in the current beam are center-symmetrical, and the maximum magnitudes both appear at the center of the beam.
Figure 4 and Figure 5 show the deflections and rotation angles with different thicknesses predicted by current and classical models. The gradient index n is 5. The numerical results for the current model (solid lines) incorporating the couple stress effect (with A11 ≠ 0 and A12 ≠ 0) are directly calculated from Equations (62), (63) and (74), while those for the classical model (dashed lines) are obtained using the same equations but with A11 = A12 = 0.

Figure 4.
Deflection of the MEE-FGM simply supported beam (Gradient index n = 5).
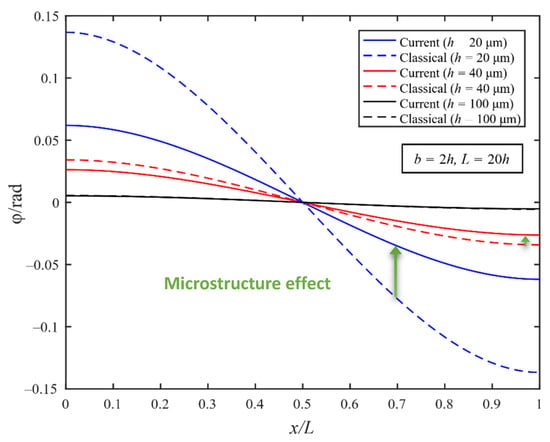
Figure 5.
Rotation of the MEE-FGM simply supported beam (Gradient index n = 5).
From Figure 4 and Figure 5, it can be found that the deflections and rotation angles of the current model are always smaller than those of the classical model in all cases. The difference between the results of the current and classical models is obvious when the beam thickness h is small, as expected.
Figure 6 shows the axial normal stress at the beam center (x = L/2) along the thickness direction of the current and classical models. From Figure 6, it is clear that the magnitude of the axial normal stress of the current model is always smaller than that of the classical model. The differences between the axial normal stress predicted by the two models also become smaller with the increase in the thickness h.
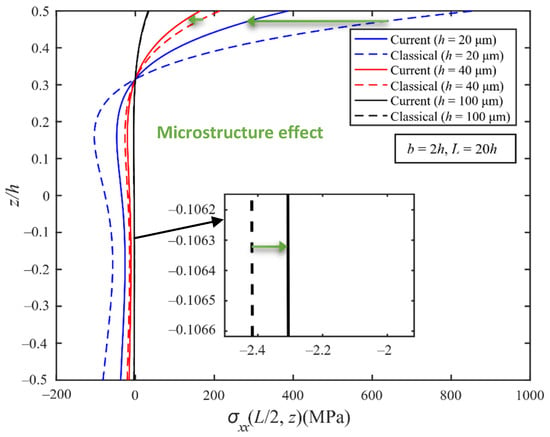
Figure 6.
Axial normal stress of the MEE-FGM simply supported beam (Gradient index n = 5).
Figure 7 and Figure 8 display the electric and magnetic potentials of the FGM simply supported beam with different thickness of the current and classical models. From Figure 7 and Figure 8, it can be observed that the values of electric and magnetic potentials of the current model are always smaller than those of the classical model. When the beam thickness h is small, the differences between the two sets of results are very large. However, the differences become small when the beam thickness increases. This phenomenon also indicates that the microstructure effect is significant for very thin beams.

Figure 7.
Electric potential of the MEE-FGM simply supported beam (Gradient index n = 5).

Figure 8.
Magnetic potential of the MEE-FGM simply supported beam (Gradient index n = 5).
To illustrate the material inhomogeneity, Figure 9 shows the variation of the maximum deflections wmax (x = L/2) of the MEE-FGM beam with the different gradient index n for h = 20 μm and 20 mm, respectively. From Figure 9a, it can be seen that the maximum deflections wmax increases with the increase of the gradient index—for both current and classical models—and the deflection of the classical model is always larger than that of the current model. From Figure 9b, it is found that when the thickness of the beam is large enough, there is almost no difference in the prediction results of the maximum deflections predicted by the two models, which further confirms that the microstructure effect is only important for very thin beams. In addition, from Figure 9a,b, it is shown that the gradient index n does have a significant effect on the static bending response for all length scales.
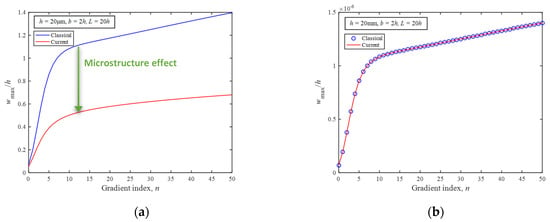
Figure 9.
Maximum deflections of the MEE-FGM beam for different gradient index with (a) h = 20 μm, (b) h = 20 mm.
Figure 10 shows the variation of the axial normal stress σxx(L/2, z) of the current MEE-FGM beam through the thickness for different gradient index n. From Figure 10, it can be found that the axial normal distribution of current MEE-FGM beam is different from that of a homogeneous beam for both h = 20 μm and 20 mm cases. In addition, the axial normal stress of homogenous beams on the geometric central axial (z = 0) is zero, but the zero-valued stresses positions of the current FGM beam are varying with the n. Furthermore, the axial normal stress of a homogeneous beam is linear, while those of current MEE-FGM beam are nonlinear at all length scales.

Figure 10.
Axial normal stress of the current MEE-FGM beam through the thickness with (a) h = 20 μm, (b) h = 20 mm.
4.2. Free Vibration
Figure 11 shows the variation of natural frequency (with k = 1) of the MEE-FGM beam of the current and classical models with different beam thickness. From Figure 11, it is obvious that the natural frequencies of both the current and classical models decrease with the thickness increases. The results also show that the current model incorporating the couple stress effect always increases the value of the natural frequency (and thus increased the beam stiffness). When the beam thickness is small enough, the couple stress effect is significant.

Figure 11.
Natural frequency with different MEE-FGM beam thickness (Gradient index n = 5).
Figure 12 shows the variation of the natural frequency ω1 (k = 1) of the current and classical models with different gradient index n for h = 20 μm and 20 mm. From Figure 12a, it is clear that when the thickness of the beam is small (micro scale), the prediction results of the two models are very different. However, from Figure 12b, when the thickness is big enough (macro scale), the prediction results of the two models are almost the same. In addition, the effect of the gradient index is found to be important for all length scales.

Figure 12.
Natural frequency of the MEE-FGM beam for different gradient index with (a) h = 20 μm, (b) h = 20 mm.
5. Conclusions
Based on the extended modified couple stress theory, a new graded magneto-electro-elastic Timoshenko microbeam model is developed. The new model considers the effects of both three-field coupling and couple stress. The equations of motion and complete boundary conditions of the new microbeam model are determined through a variational approach.
As two direct applications of the new model, the static bending and free vibration properties of a simply supported microbeam subjected to uniformly distributed loads are analytically obtained. For the static bending problem, parametric studies demonstrate that the deflections, rotations, axial normal stresses, electric and magnetic potentials predicted by the current model are all smaller than those of the classical theory. The differences decrease with the increase in the microbeam thickness. For the problem of free vibration, the natural frequency obtained from the current model is found to be higher than that of the classical model. The difference increases as the thickness of the beam decreases. Such a behavior also indicates that the microstructure effect tends to make the graded magneto-electro-elastic microbeam stiffer, and the current model can predict the size effect for magneto-electro-elastic functionally graded microbeam. In addition, it was demonstrated that changing the gradient index significantly affects both the static and vibrational properties of the graded magneto-electro-elastic microbeam at all length scales. These findings are helpful in guiding the engineering design and optimization of graded magneto-electro-elastic materials in MEMS and NEMS devices.
Author Contributions
Conceptualization, C.M. and G.Z.; methodology, J.H., S.W.; writing—original draft preparation, J.H. and S.W. All authors have read and agreed to the published version of the manuscript.
Funding
The work reported here is funded by the National Key R&D Program of China (grant number 2018YFD1100401) and the National Natural Science Foundation of China [grant numbers 12002086, 11872149 and 11772091].
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| L, b, h | Length, width and thickness of beam |
| P(z), P1, P2 | Material properties of the current beam, material I and II |
| n | Functionally graded power-law index |
| σij | The components of Cauchy stress tensor |
| mij | The components of the couple stress tensor |
| Di | Electric displacements |
| Bi | Magnetic fluxes |
| Cαβ | The components of elastic stiffness tensor |
| Aαβ | The components of couple stress stiffness tensor |
| eiα | The components of piezoelectric tensor |
| qiα | The components of piezomagnetic tensor |
| sij | The components of dielectric tensor |
| μij | The components of magnetic permeability tensor |
| dij | The components of magneto-dielectric tensor |
| εij | The components of infinitesimal strain tensor |
| χij | The components of the symmetric curvature tensor |
| ui | Displacement components |
| εijk | Levi-Civita symbol |
| Ek, Hk | Electric field intensity and magnetic field intensity |
| Φ, M | Electric potential and magnetic potential |
| u, w | Beam extension and deflection |
| φ | Rotation angle |
| γ, ζ | The electric potential and magnetic potentials |
| γ0, ζ0 | External electric potential, external magnetic potential |
| A | Cross-sectional area |
| ρ | Mass density |
| f, q | The x- and z-components of the body force per unit length |
| ks | Shape correction factor |
| Uk, Φk, Wk, Гk, Zk, Qk | Fourier coefficients |
| ωk | The kth vibration frequency |
| , , , | Fourier coefficients |
References
- Sahmani, S.; Aghdam, M.M. Nonlocal Strain Gradient Shell Model for Axial Buckling and Postbuckling Analysis of Magneto-Electro-Elastic Composite Nanoshells. Compos. Part B Eng. 2018, 132, 258–274. [Google Scholar] [CrossRef]
- Farajpour, M.R.; Shahidi, A.R.; Hadi, A.; Farajpour, A. Influence of Initial Edge Displacement on the Nonlinear Vibration, Electrical and Magnetic Instabilities of Magneto-Electro-Elastic Nanofilms. Mech. Adv. Mater. Struct. 2019, 26, 1469–1481. [Google Scholar] [CrossRef]
- Yakhno, V.G. An Explicit Formula for Modeling Wave Propagation in Magneto-Electro-Elastic Materials. J. Electromagn. Waves Appl. 2018, 32, 899–912. [Google Scholar] [CrossRef]
- Chen, W.; Yan, Z.; Wang, L. On Mechanics of Functionally Graded Hard-Magnetic Soft Beams. Int. J. Eng. Sci. 2020, 157, 103391. [Google Scholar] [CrossRef]
- Taati, E. On Buckling and Post-Buckling Behavior of Functionally Graded Micro-Beams in Thermal Environment. Int. J. Eng. Sci. 2018, 128, 63–78. [Google Scholar] [CrossRef]
- Yang, Z.; Xu, J.; Lu, H.; Lv, J.; Liu, A.; Fu, J. Multiple Equilibria and Buckling of Functionally Graded Graphene Nanoplatelet-Reinforced Composite Arches with Pinned-Fixed End. Crystals 2020, 10, 1003. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Alici, G. Size-Dependent Performance of Microgyroscopes. Int. J. Eng. Sci. 2016, 100, 99–111. [Google Scholar] [CrossRef]
- Tang, Y.; Ma, Z.S.; Ding, Q.; Wang, T. Dynamic Interaction between Bi-Directional Functionally Graded Materials and Magneto-Electro-Elastic Fields: A Nano-Structure Analysis. Compos. Struct. 2021, 264, 113746. [Google Scholar] [CrossRef]
- Bhangale, R.K.; Ganesan, N. Free Vibration of Simply Supported Functionally Graded and Layered Magneto-Electro-Elastic Plates by Finite Element Method. J. Sound Vib. 2006, 294, 1016–1038. [Google Scholar] [CrossRef]
- Sladek, J.; Sladek, V.; Krahulec, S.; Chen, C.S.; Young, D.L. Analyses of Circular Magnetoelectroelastic Plates with Functionally Graded Material Properties. Mech. Adv. Mater. Struct. 2015, 22, 479–489. [Google Scholar] [CrossRef]
- Vinyas, M.; Harursampath, D.A.; Nguyen-Thoi, T. Influence of Active Constrained Layer Damping on the Coupled Vibration Response of Functionally Graded Magneto-Electro-Elastic Plates with Skewed Edges. Def. Technol. 2020, 16, 1019–1038. [Google Scholar] [CrossRef]
- Mahesh, V.; Harursampath, D. Large Deflection Analysis of Functionally Graded Magneto-Electro-Elastic Porous Flat Panels. Eng. Comput. 2021, 1–20. [Google Scholar] [CrossRef]
- Mahesh, V. Porosity Effect on the Nonlinear Deflection of Functionally Graded Magneto-Electro-Elastic Smart Shells under Combined Loading. Mech. Adv. Mater. Struct. 2021, 1–27. [Google Scholar] [CrossRef]
- Lam, D.C.C.; Yang, F.; Chong, A.C.M.; Wang, J.; Tong, P. Experiments and Theory in Strain Gradient Elasticity. J. Mech. Phys. Solids 2003, 51, 1477–1508. [Google Scholar] [CrossRef]
- McFarland, A.W.; Colton, J.S. Role of Material Microstructure in Plate Stiffness with Relevance to Microcantilever Sensors. J. Micromech. Microeng. 2005, 15, 1060. [Google Scholar] [CrossRef]
- Eringen, A.C. On Differential Equations of Nonlocal Elasticity and Solutions of Screw Dislocation and Surface Waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Toupin, R.A. Elastic Materials with Couple-Stresses. Arch. Ration. Mech. Anal. 1962, 11, 385–414. [Google Scholar] [CrossRef] [Green Version]
- Mindlin, R.D. Influence of Couple-Stresses on Stress Concentrations. Exp. Mech. 1963, 3, 1–7. [Google Scholar] [CrossRef]
- Kolter, W.T. Couple Stresses in the Theory of Elasticity: I and II. Proc. K. Ned. Akad. Wet. B 1964, 67, 17–44. [Google Scholar]
- Mindlin, R.D. Micro-Structure in Linear Elasticity. Arch. Ration. Mech. Anal. 1964, 16, 51–78. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Eshel, N.N. On First Strain-Gradient Theories in Linear Elasticity. Int. J. Solids Struct. 1968, 4, 109–124. [Google Scholar] [CrossRef]
- Polizzotto, C. A Hierarchy of Simplified Constitutive Models within Isotropic Strain Gradient Elasticity. Eur. J. Mech. A Solids 2017, 61, 92–109. [Google Scholar] [CrossRef]
- Altan, B.S.; Aifantis, E.C. On Some Aspects in the Special Theory of Gradient Elasticity. J. Mech. Behav. Mater. 1997, 8, 231–282. [Google Scholar] [CrossRef]
- Yang, F.; Chong, A.C.M.; Lam, D.C.C.; Tong, P. Couple Stress Based Strain Gradient Theory for Elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Park, S.K.; Gao, X.-L. Variational Formulation of a Modified Couple Stress Theory and Its Application to a Simple Shear Problem. Z. Angew. Math. Phys. 2008, 59, 904–917. [Google Scholar] [CrossRef]
- Zhang, G.Y.; Gao, X.L. A New Bernoulli–Euler Beam Model Based on a Reformulated Strain Gradient Elasticity Theory. Math. Mech. Solids 2020, 25, 630–643. [Google Scholar] [CrossRef]
- Qu, Y.L.; Zhang, G.Y.; Fan, Y.M.; Jin, F. A Non-Classical Theory of Elastic Dielectrics Incorporating Couple Stress and Quadrupole Effects: Part I—Reconsideration of Curvature-Based Flexoelectricity Theory. Math. Mech. Solids 2021. [Google Scholar] [CrossRef]
- Zhang, G.Y.; Gao, X.L.; Zheng, C.Y.; Mi, C.W. A Non-Classical Bernoulli-Euler Beam Model Based on a Simplified Micromorphic Elasticity Theory. Mech. Mater. 2021, 161, 103967. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R. Vibration Analysis of Embedded Biaxially Loaded Magneto-Electrically Actuated Inhomogeneous Nanoscale Plates. J. Vib. Control 2018, 24, 3587–3607. [Google Scholar] [CrossRef]
- Kiani, A.; Sheikhkhoshkar, M.; Jamalpoor, A.; Khanzadi, M. Free Vibration Problem of Embedded Magneto-Electro-Thermo-Elastic Nanoplate Made of Functionally Graded Materials via Nonlocal Third-Order Shear Deformation Theory. J. Intell. Mater. Syst. 2018, 29, 741–763. [Google Scholar] [CrossRef]
- Liu, H.; Lv, Z. Vibration Performance Evaluation of Smart Magneto-Electro-Elastic Nanobeam with Consideration of Nanomaterial Uncertainties. J. Intell. Mater. Syst. Struct. 2019, 30, 2932–2952. [Google Scholar] [CrossRef]
- Xiao, W.S.; Gao, Y.; Zhu, H. Buckling and Post-Buckling of Magneto-Electro-Thermo-Elastic Functionally Graded Porous Nanobeams. Microsyst. Technol. 2019, 25, 2451–2470. [Google Scholar] [CrossRef]
- Lim, C.W.; Zhang, G.; Reddy, J.N. A Higher-Order Nonlocal Elasticity and Strain Gradient Theory and Its Applications in Wave Propagation. J. Mech. Phys. Solids 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Şimşek, M. Nonlinear Free Vibration of a Functionally Graded Nanobeam Using Nonlocal Strain Gradient Theory and a Novel Hamiltonian Approach. Int. J. Eng. Sci. 2016, 105, 12–27. [Google Scholar] [CrossRef]
- Li, X.; Li, L.; Hu, Y.; Ding, Z.; Deng, W. Bending, Buckling and Vibration of Axially Functionally Graded Beams Based on Nonlocal Strain Gradient Theory. Compos. Struct. 2017, 165, 250–265. [Google Scholar] [CrossRef]
- Reddy, J.N. Microstructure-Dependent Couple Stress Theories of Functionally Graded Beams. J. Mech. Phys. Solids 2011, 59, 2382–2399. [Google Scholar] [CrossRef]
- Gao, X.-L.; Zhang, G.Y. A Microstructure-and Surface Energy-Dependent Third-Order Shear Deformation Beam Model. Z. Angew. Math. Phys. 2015, 66, 1871–1894. [Google Scholar] [CrossRef]
- Yu, T.; Hu, H.; Zhang, J.; Bui, T.Q. Isogeometric Analysis of Size-Dependent Effects for Functionally Graded Microbeams by a Non-Classical Quasi-3D Theory. Thin-Walled Struct. 2019, 138, 1–14. [Google Scholar] [CrossRef]
- Zhang, G.Y.; Qu, Y.L.; Gao, X.L.; Jin, F. A Transversely Isotropic Magneto-Electro-Elastic Timoshenko Beam Model Incorporating Microstructure and Foundation Effects. Mech. Mater. 2020, 149, 103412. [Google Scholar] [CrossRef]
- Hong, J.; He, Z.Z.; Zhang, G.Y.; Mi, C.W. Tunable Bandgaps in Phononic Crystal Microbeams Based on Microstructure, Piezo and Temperature Effects. Crystals 2021, 11, 1029. [Google Scholar] [CrossRef]
- Hong, J.; He, Z.Z.; Zhang, G.Y.; Mi, C.W. Size and Temperature Effects on Band Gaps in Periodic Fluid-Filled Micropipes. Appl. Math. Mech. 2021, 42, 1219–1232. [Google Scholar] [CrossRef]
- Qu, Y.L.; Li, P.; Zhang, G.Y.; Jin, F.; Gao, X.L. A Microstructure-Dependent Anisotropic Magneto-Electro-Elastic Mindlin Plate Model Based on an Extended Modified Couple Stress Theory. Acta Mech. 2020, 231, 4323–4350. [Google Scholar] [CrossRef]
- Shen, W.; Zhang, G.; Gu, S.; Cong, Y. A Transversely Isotropic Magneto-electro-elastic Circular Kirchhoff Plate Model Incorporating Microstructure Effect. Acta Mech. Solida Sin. 2021, 1–13. [Google Scholar] [CrossRef]
- Qu, Y.L.; Jin, F.; Yang, J.S. Magnetically induced charge motion in the bending of a beam with flexoelectric semiconductor and piezomagnetic dielectric layers. J. Appl. Phys. 2021, 127, 064503. [Google Scholar] [CrossRef]
- Zhu, F.; Ji, S.; Zhu, J.; Qian, Z.; Yang, J. Study on the Influence of Semiconductive Property for the Improvement of Nanogenerator by Wave Mode Approach. Nano Energy 2018, 52, 474–484. [Google Scholar] [CrossRef]
- Shingare, K.B.; Kundalwal, S.I. Static and Dynamic Response of Graphene Nanocomposite Plates with Flexoelectric Effect. Mech. Mater. 2019, 134, 69–84. [Google Scholar] [CrossRef]
- Wang, L.; Liu, S.; Feng, X.; Zhang, C.; Zhu, L.; Zhai, J.; Qin, Y.; Wang, Z.L. Flexoelectronics of Centrosymmetric Semiconductors. Nat. Nanotechnol. 2020, 15, 661–667. [Google Scholar] [CrossRef]
- Sharma, S.; Kumar, A.; Kumar, R.; Talha, M.; Vaish, R. Geometry Independent Direct and Converse Flexoelectric Effects in Functionally Graded Dielectrics: An Isogeometric Analysis. Mech. Mater. 2020, 148, 103456. [Google Scholar] [CrossRef]
- Zhang, G.Y.; Gao, X.L.; Guo, Z.Y. A Non-Classical Model for an Orthotropic Kirchhoff Plate Embedded in a Viscoelastic Medium. Acta Mech. 2017, 228, 3811–3825. [Google Scholar] [CrossRef]
- Han, X.; Pan, E. Fields Produced by Three-Dimensional Dislocation Loops in Anisotropic Magneto-Electro-Elastic Materials. Mech. Mater. 2013, 59, 110–125. [Google Scholar] [CrossRef]
- Kumar, D.; Sarangi, S.; Saxena, P. Universal Relations in Coupled Electro-Magneto-Elasticity. Mech. Mater. 2020, 143, 103308. [Google Scholar] [CrossRef]
- Wang, Q. On Buckling of Column Structures with a Pair of Piezoelectric Layers. Eng. Struct. 2002, 24, 199–205. [Google Scholar] [CrossRef]
- Ma, H.M.; Gao, X.L.; Reddy, J.N. A Microstructure-Dependent Timoshenko Beam Model Based on a Modified Couple Stress Theory. J. Mech. Phys. Solids 2008, 56, 3379–3391. [Google Scholar] [CrossRef]
- Ansari, R.; Gholami, R.; Rouhi, H. Size-Dependent Nonlinear Forced Vibration Analysis of Magneto-Electro-Thermo-Elastic Timoshenko Nanobeams Based upon the Nonlocal Elasticity Theory. Compos. Struct. 2015, 126, 216–226. [Google Scholar] [CrossRef]
- Hong, J.; Wang, S.P.; Zhang, G.Y.; Mi, C.W. Bending, Buckling and Vibration Analysis of Complete Microstructure-Dependent Functionally Graded Material Microbeams. Int. J. Appl. Mech. 2021, 13, 2150057. [Google Scholar] [CrossRef]
- Reddy, J.N. Energy Principles and Variational Methods in Applied Mechanics, 2nd ed.; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Gao, X.-L.; Mall, S. Variational Solution for a Cracked Mosaic Model of Woven Fabric Composites. Int. J. Solids Struct. 2001, 38, 855–874. [Google Scholar] [CrossRef]
- Yang, J. An Introduction to the Theory of Piezoelectricity; Springer: New York, NY, USA, 2005. [Google Scholar] [CrossRef]
- Yang, J. The Mechanics of Piezoelectric Structures; World Scientific: Singapore, 2006. [Google Scholar] [CrossRef]
- Li, J.Y. Magnetoelectroelastic Multi-Inclusion and Inhomogeneity Problems and Their Applications in Composite Materials. Int. J. Eng. Sci. 2000, 38, 1993–2011. [Google Scholar] [CrossRef]
- Sih, G.C.; Song, Z.F. Magnetic and Electric Poling Effects Associated with Crack Growth in BaTiO3–CoFe2O4 Composite. Theor. Appl. Fract. Mech. 2003, 39, 209–227. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, R.; Ding, H. Axisymmetric Bending of Functionally Graded Circular Magneto-Electro-Elastic Plates. Eur. J. Mech. A Solids 2011, 30, 999–1011. [Google Scholar] [CrossRef]
- Zhang, G.Y.; Gao, X.L. Elastic Wave Propagation in 3-D Periodic Composites: Band Gaps Incorporating Microstructure Effects. Compos. Struct. 2018, 204, 920–932. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).