Magnetic Field and Dilution Effects on the Phase Diagrams of Simple Statistical Models for Nematic Biaxial Systems
Abstract
1. Introduction
2. The SVD Model
3. Effects of a Magnetic Field
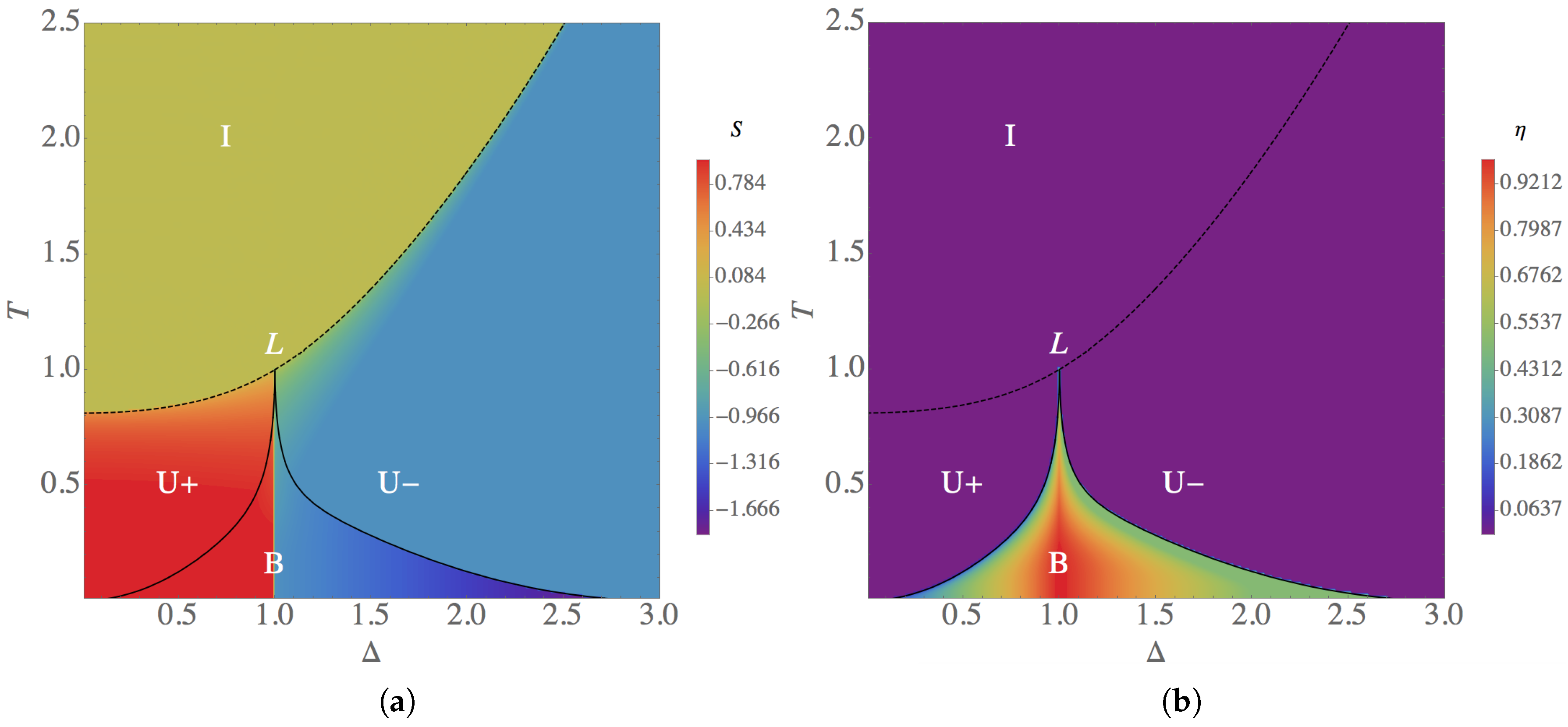
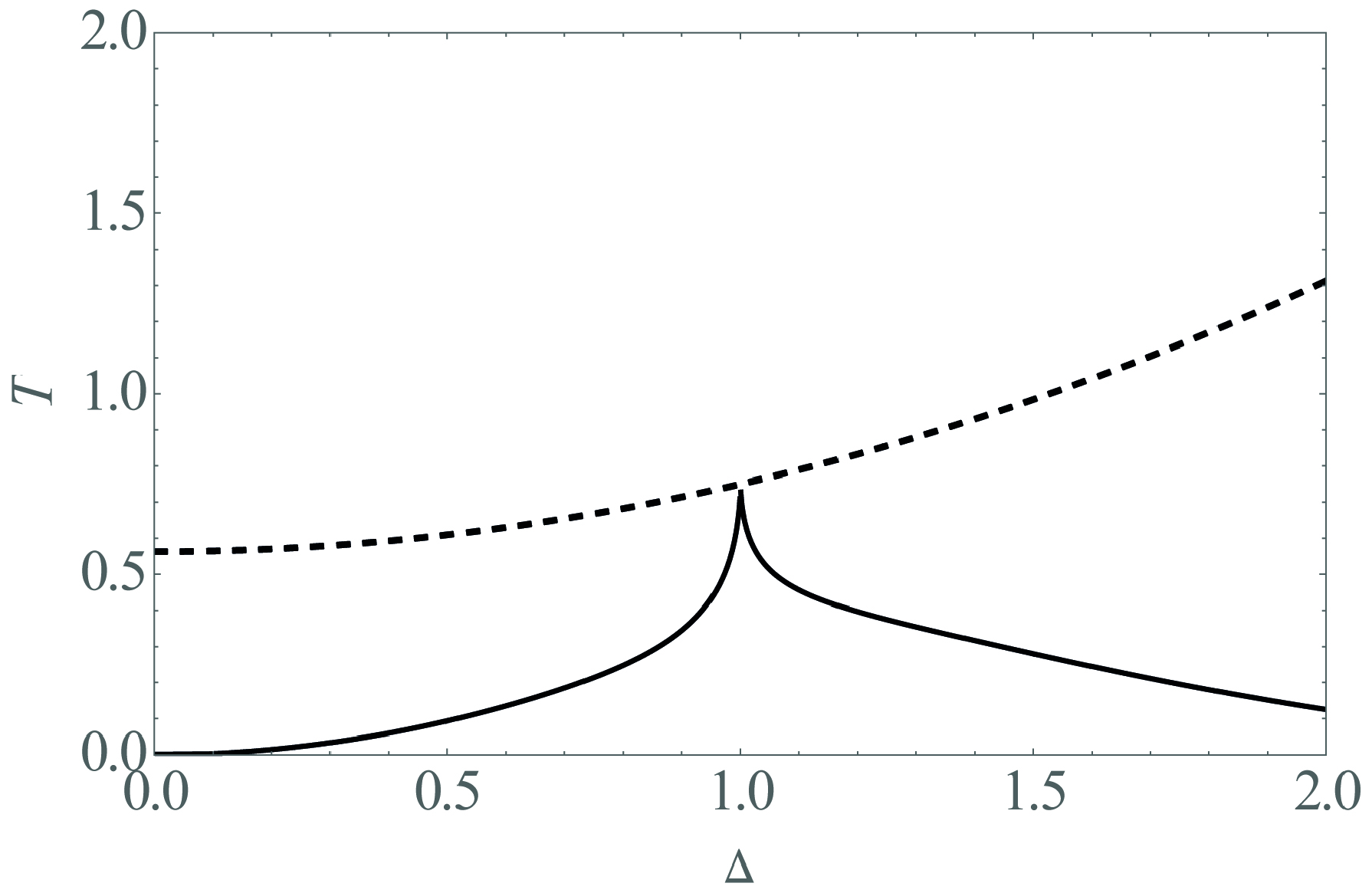
3.1. Behavior at Zero Field
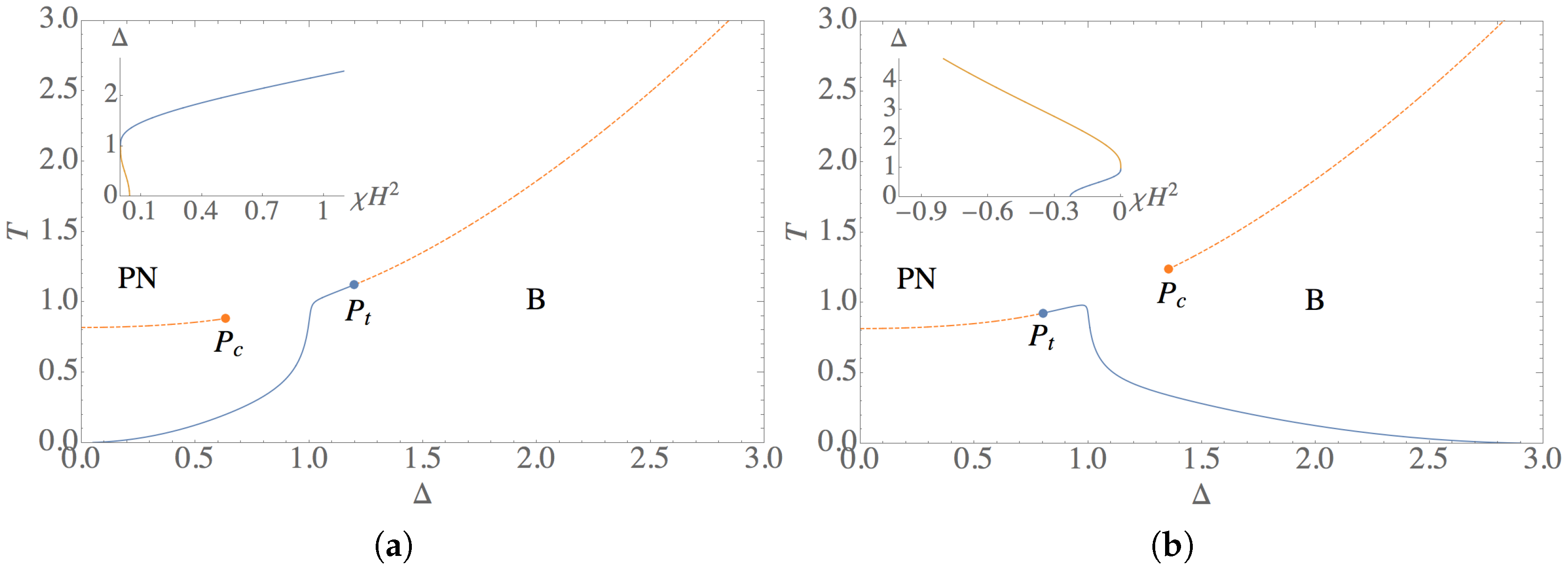
3.2. Phase Diagrams in a Field
4. Introducing Dilution
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- do Carmo, E.; Liarte, D.B.; Salinas, S.R. Statistical models of mixtures with a biaxial nematic phase. Phys. Rev. E 2010, 81, 062701. [Google Scholar] [CrossRef] [PubMed]
- do Carmo, E.; Vieira, A.P.; Salinas, S.R. Phase diagram of a model for a binary mixture of nematic molecules on a Bethe lattice. Phys. Rev. E 2011, 83, 011701. [Google Scholar] [CrossRef] [PubMed]
- Liarte, D.B.; Salinas, S.R. Enhancement of Nematic Order and Global Phase Diagram of a Lattice Model for Coupled Nematic Systems. Braz. J. Phys. 2012, 42, 261. [Google Scholar] [CrossRef]
- Nascimento, E.S.; Henriques, E.F.; Vieira, A.P.; Salinas, S.R. Maier-Saupe model for a mixture of uniaxial and biaxial molecules. Phys. Rev. E 2015, 92, 062503. [Google Scholar] [CrossRef] [PubMed]
- Nascimento, E.S.; Vieira, A.P.; Salinas, S.R. Lattice Statistical Models for the Nematic Transitions in Liquid-Crystalline Systems. Braz. J. Phys. 2016, 46, 664. [Google Scholar] [CrossRef]
- Petri, A.; Salinas, S.R. Field-induced uniaxial and biaxial nematic phases in the Maier–Saupe–Zwanzig (MSZ) lattice model. Liquid Cryst. 2018, 45, 980–992. [Google Scholar] [CrossRef]
- Yu, L.J.; Saupe, A. Observation of a Biaxial Nematic Phase in Potassium Laurate-1-Decanol-Water Mixtures. Phys. Rev. Lett. 1980, 45, 1000–1003. [Google Scholar] [CrossRef]
- Melnik, G.; Photinos, P.; Saupe, A. Landau point on a nematic-isotropic transition line. Phys. Rev. A 1989, 39, 1597–1600. [Google Scholar] [CrossRef]
- Lemaire, B.J.; Davidson, P.; Ferré, J.; Jamet, J.P.; Panine, P.; Dozov, I.; Jolivet, J.P. Outstanding Magnetic Properties of Nematic Suspensions of Goethite (α-FeOOH) Nanorods. Phys. Rev. Lett. 2002, 88, 125507. [Google Scholar] [CrossRef]
- van den Pol, E.; Lupascu, A.; Diaconeasa, M.A.; Petukhov, A.V.; Byelov, D.V.; Vroege, G.J. Onsager Revisited: Magnetic Field Induced Nematic–Nematic Phase Separation in Dispersions of Goethite Nanorods. J. Phys. Chem. Lett. 2010, 1, 2174–2178. [Google Scholar] [CrossRef]
- Ostapenko, T.; Wiant, D.B.; Sprunt, S.N.; Jákli, A.; Gleeson, J.T. Magnetic-Field Induced Isotropic to Nematic Liquid Crystal Phase Transition. Phys. Rev. Lett. 2008, 101, 247801. [Google Scholar] [CrossRef] [PubMed]
- To, T.B.T.; Sluckin, T.J.; Luckhurst, G.R. Biaxiality-induced magnetic field effects in bent-core nematics: Molecular-field and Landau theory. Phys. Rev. E 2013, 88, 062506. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, P.K.; Rahman, M. Isotropic to biaxial nematic phase transition in an external magnetic field. Chem. Phys. 2013, 423, 178. [Google Scholar] [CrossRef]
- Aliev, M.; Ugolkova, E.; Kuzminyh, N. Effect of an external magnetic field on the phase behavior of the thermotropic melt of V-shaped molecules. J. Mol. Liquids 2019, 292, 111395. [Google Scholar] [CrossRef]
- Matsuyama, A.; Arikawa, S.; Wada, M.; Fukutomi, N. Uniaxial and biaxial nematic phases of banana-shaped molecules and the effects of an external field. Liquid Cryst. 2019, 46, 1672. [Google Scholar] [CrossRef]
- Mukherjee, P.K.; De, A.K.; Mandal, A. Mean-field theory of isotropic-uniaxial nematic-biaxial nematic phase transitions in an external field. Phys. Scr. 2019, 94, 025702. [Google Scholar] [CrossRef]
- Sonnet, A.M.; Virga, E.G.; Durand, G.E. Dielectric shape dispersion and biaxial transitions in nematic liquid crystals. Phys. Rev. E 2003, 67, 061701. [Google Scholar] [CrossRef]
- de Oliveira, M.J.; Figueiredo Neto, A.M. Reentrant isotropic-nematic transition in lyotropic liquid crystals. Phys. Rev. A 1986, 34, 3481. [Google Scholar] [CrossRef]
- Sauerwein, R.A.; de Oliveira, M.J. Lattice model for biaxial and uniaxial nematic liquid crystals. J. Chem. Phys. 2016, 144, 194904. [Google Scholar] [CrossRef]
- Luckhurst, G.R.; Zannoni, C.; Nordio, P.L.; Segre, U. A molecular field theory for uniaxial nematic liquid crystals formed by non-cylindrically symmetric molecules. Mol. Phys. 1975, 30, 1345. [Google Scholar] [CrossRef]
- Luckhurst, G.R.; Naemura, S.; Sluckin, T.J.; Thomas, K.S.; Turzi, S.S. Molecular-field-theory approach to the Landau theory of liquid crystals: Uniaxial and biaxial nematics. Phys. Rev. E 2012, 85, 031705. [Google Scholar] [CrossRef] [PubMed]
- Dussi, S.; Tasios, N.; Drwenski, T.; van Roij, R.; Dijkstra, M. Hard Competition: Stabilizing the Elusive Biaxial Nematic Phase in Suspensions of Colloidal Particles with Extreme Lengths. Phys. Rev. Lett. 2018, 120, 177801. [Google Scholar] [CrossRef] [PubMed]
- Photinos, D.J. Alignment of biaxial nematics. In Biaxial Nematic Liquid Crystals: Theory, Simulation, and Experiment; Luckhurst, G.R., Sluckin, T.J., Eds.; Wiley: West Sussex, UK, 2015; p. 205. [Google Scholar]
- Boccara, N.; Mejdani, R.; De Seze, L. Solvable model exhibiting a first-order phase transition. J. Phys. France 1977, 38, 149. [Google Scholar] [CrossRef]
- Camp, P.J.; Allen, M.P. Phase diagram of the hard biaxial ellipsoid fluid. J. Chem. Phys. 1997, 106, 6681–6688. [Google Scholar] [CrossRef]
- Figueiredo Neto, A.M.; Galerne, Y.; Levelut, A.M.; Liebert, L. Pseudo-lamellar ordering in uniaxial and biaxial lyotropic nematics: A synchrotron X-ray diffraction experiment. J. Phys. Lett. 1985, 46, 499. [Google Scholar] [CrossRef]
- Galerne, Y.; Figueiredo Neto, A.M.; Liébert, L. Microscopical structure of the uniaxial and biaxial lyotropic nematics. J. Chem. Phys. 1987, 87, 1851–1856. [Google Scholar] [CrossRef]
- Oliveira, E.A.; Liebert, L.; Neto, A.M.F. A new soap/detergent/water lyotropic liquid crystal with a biaxial nematic phase. Liquid Cryst. 1989, 5, 1669–1675. [Google Scholar] [CrossRef]
- Akpinar, E.; Reis, D.; Figueiredo Neto, A.M. Effect of alkyl chain length of alcohols on nematic uniaxial-to-biaxial phase transitions in a potassium laurate/alcohol/K2SO4/water lyotropic mixture. Liquid Cryst. 2012, 39, 881–888. [Google Scholar] [CrossRef]
- Varga, S.; Kronome, G.; Szalai, I. External field induced tricritical phenomenon in the isotropicnematic phase transition of hard non-spherical particle systems. Mol. Phys. 2000, 98, 911–915. [Google Scholar] [CrossRef]
- Vause, C.A. Connection between the isotropic-nematic Landau point and the paranematic-nematic critical point. Phys. Lett. A 1986, 114, 485–490. [Google Scholar] [CrossRef]
- Varga, S.; Jackson, G.; Szalai, I. External field induced paranematic–nematic phase transitions in rod-like systems. Mol. Phys. 1998, 93, 377–387. [Google Scholar]
- Lelidis, I.; Durand, G. Electric-field-induced isotropic-nematic phase transition. Phys. Rev. E 1993, 48, 3822–3824. [Google Scholar] [CrossRef] [PubMed]

| k | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 0 | 0 | ||||
| 2 | 1 | 0 | 1 | 0 | 0 | ||||
| 3 | 1 | 0 | 0 | 0 | 1 | ||||
| 4 | 1 | 0 | 0 | 1 | 0 | ||||
| 5 | 1 | 0 | 0 | 0 | 1 | ||||
| 6 | 1 | 0 | 0 | 1 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodrigues, D.D.; Vieira, A.P.; Salinas, S.R. Magnetic Field and Dilution Effects on the Phase Diagrams of Simple Statistical Models for Nematic Biaxial Systems. Crystals 2020, 10, 632. https://doi.org/10.3390/cryst10080632
Rodrigues DD, Vieira AP, Salinas SR. Magnetic Field and Dilution Effects on the Phase Diagrams of Simple Statistical Models for Nematic Biaxial Systems. Crystals. 2020; 10(8):632. https://doi.org/10.3390/cryst10080632
Chicago/Turabian StyleRodrigues, Daniel D., André P. Vieira, and Silvio R. Salinas. 2020. "Magnetic Field and Dilution Effects on the Phase Diagrams of Simple Statistical Models for Nematic Biaxial Systems" Crystals 10, no. 8: 632. https://doi.org/10.3390/cryst10080632
APA StyleRodrigues, D. D., Vieira, A. P., & Salinas, S. R. (2020). Magnetic Field and Dilution Effects on the Phase Diagrams of Simple Statistical Models for Nematic Biaxial Systems. Crystals, 10(8), 632. https://doi.org/10.3390/cryst10080632





