Infrared Optical Conductivity of Bulk Bi2Te2Se
Abstract
1. Introduction
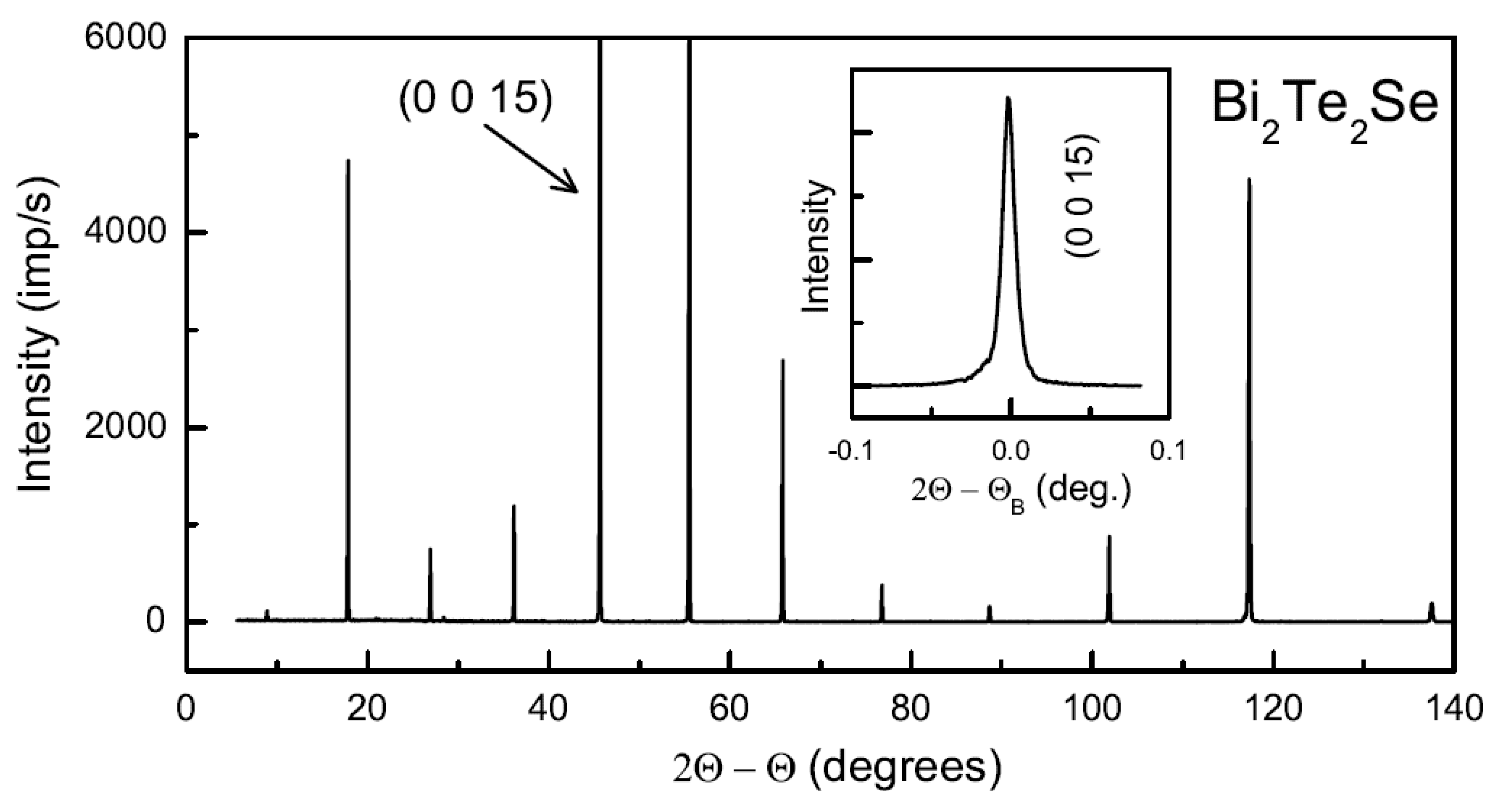
2. Materials and Methods
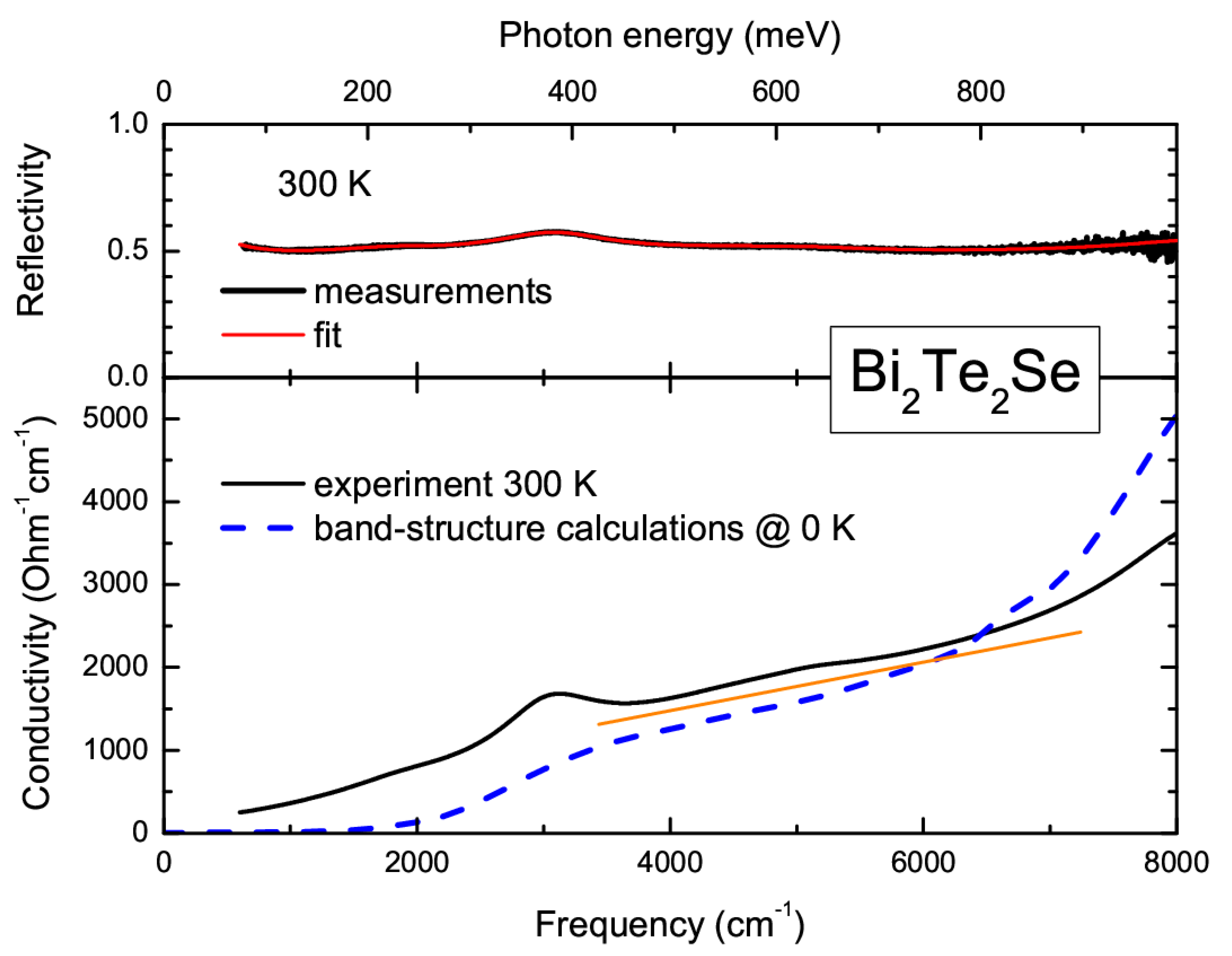
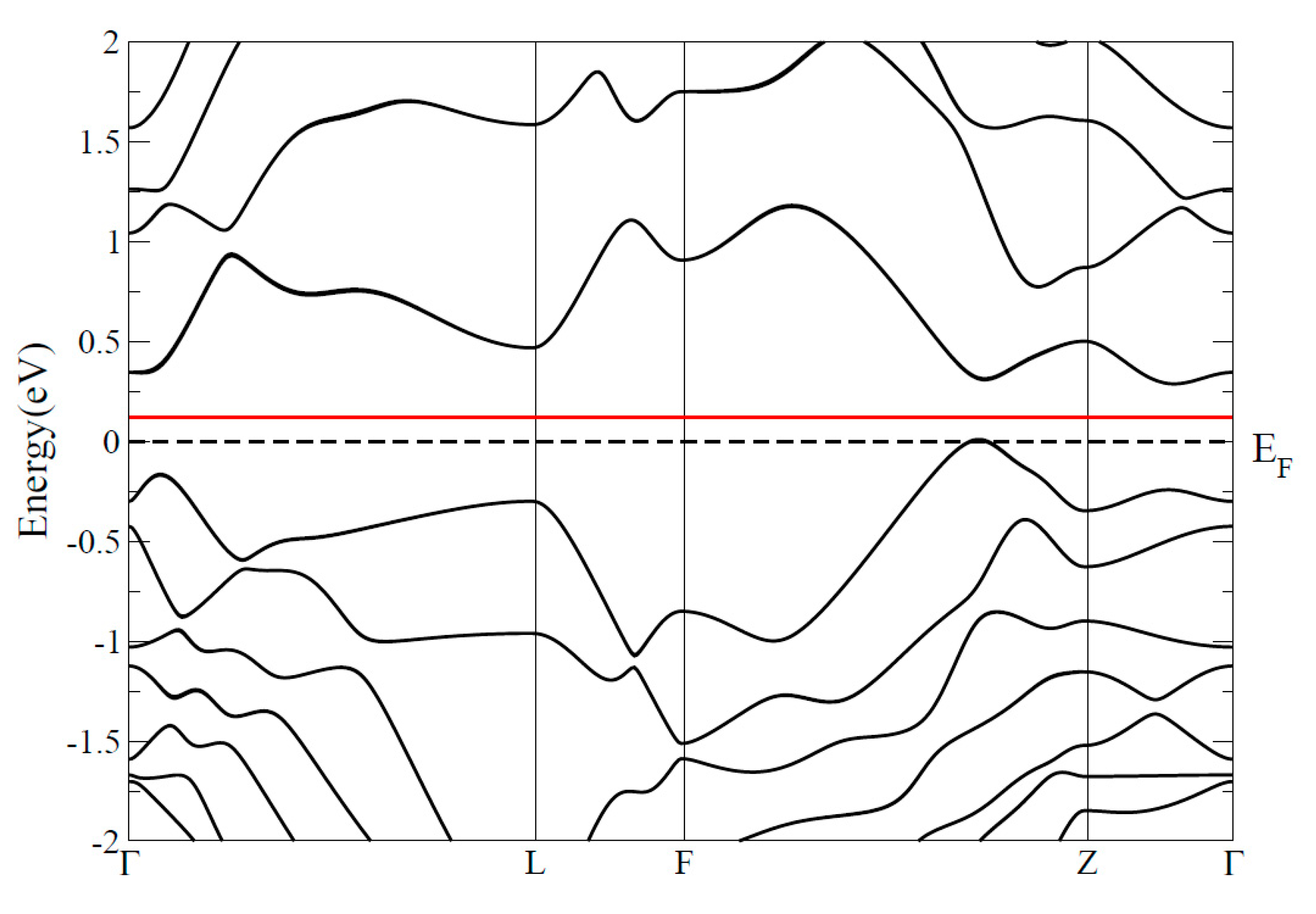
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Neto, A.C.; Guinea, F.; Peres, N.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef]
- Qi, X.L.; Zhang, S.C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057. [Google Scholar] [CrossRef]
- Wehling, T.O.; Black-Schaffer, A.M.; Balatsky, A.V. Dirac materials. Adv. Phys. 2014, 63, 1. [Google Scholar] [CrossRef]
- Armitage, N.P.; Mele, E.J.; Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 2018, 90, 015001. [Google Scholar] [CrossRef]
- Hosur, P.; Parameswaran, S.A.; Vishwanath, A. Charge transport in Weyl semimetals. Phys. Rev. Lett. 2012, 108, 046602. [Google Scholar] [CrossRef] [PubMed]
- Bacsi, A.; Virosztek, A. Low-frequency optical conductivity in graphene and in other scale-invariant two-band systems. Phys. Rev. B 2013, 87, 125425. [Google Scholar] [CrossRef]
- Kuzmenko, A.B.; van Heumen, E.; Carbone, F.; van der Marel, D. Universal Optical conductance of graphite. Phys. Rev. Lett. 2008, 100, 117401. [Google Scholar] [CrossRef]
- Mak, K.F.; Sfeir, M.Y.; Wu, Y.; Lui, C.H.; Misewich, J.A.; Heinz, T.F. Measurement of the Optical conductivity of graphene. Phys. Rev. Lett. 2008, 101, 196405. [Google Scholar] [CrossRef]
- Schilling, M.B.; Schoop, L.M.; Lotsch, B.V.; Dressel, M.; Pronin, A.V. Flat Optical Conductivity in ZrSiS due to two-dimensional Dirac bands. Phys. Rev. Lett. 2017, 119, 187401. [Google Scholar] [CrossRef]
- Chen, R.Y.; Zhang, S.J.; Schneeloch, J.A.; Zhang, C.; Li, Q.; Gu, G.D.; Wang, N.L. Optical spectroscopy study of the three-dimensional Dirac semimetal ZrTe5. Phys. Rev. B 2015, 92, 075107. [Google Scholar] [CrossRef]
- Neubauer, D.; Carbotte, J.P.; Nateprov, A.A.; Löhle, A.; Dressel, M.; Pronin, A.V. Interband optical conductivity of the [001]-oriented Dirac semimetal Cd3As2. Phys. Rev. B 2016, 93, 121202. [Google Scholar] [CrossRef]
- Xu, B.; Dai, Y.M.; Zhao, L.X.; Wang, K.; Yang, R.; Zhang, W.; Liu, J.Y.; Xiao, H.; Chen, G.F.; Taylor, A.J.; et al. Optical spectroscopy of the Weyl semimetal TaAs. Phys. Rev. B 2016, 93, 121110. [Google Scholar] [CrossRef]
- Timusk, T.; Carbotte, J.P.; Homes, C.C.; Basov, D.N.; Sharapov, S.G. Three-dimensional Dirac fermions in quasicrystals as seen via optical conductivity. Phys. Rev. B 2013, 87, 235121. [Google Scholar] [CrossRef]
- Xu, S.-Y.; Xia, Y.; Wray, L.A.; Jia, S.; Meier, F.; Dil, J.H.; Osterwalder, J.; Slomski, B.; Bansil, A.; Lin, H.; et al. Topological phase transition and texture inversion in a tunable topological insulator. Science 2011, 332, 560. [Google Scholar] [CrossRef]
- Aleshchenko, Y.A.; Muratov, A.V.; Pavlova, V.V.; Selivanov, Y.G.; Chizhevskii, E.G. Infrared spectroscopy of Bi2Te2Se. JETP Lett. 2014, 99, 187. [Google Scholar] [CrossRef]
- Jia, S.; Ji, H.; Climent-Pascual, E.; Fuccillo, M.K.; Charles, M.E.; Xiong, J.; Ong, N.P.; Cava, R.J. Low-carrier-concentration crystals of the topological insulator Bi2Te2Se. Phys. Rev. B 2011, 84, 235206. [Google Scholar] [CrossRef]
- Dressel, M.; Grüner, G. Electrodynamics of Solids; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Kuzmenko, A.B. Kramers–Kronig constrained variational analysis of optical spectra. Rev. Sci. Instrum. 2005, 76, 083108. [Google Scholar] [CrossRef]
- Chanda, G.; Lobo, R.P.S.M.; Schachinger, E.; Wosnitza, J.; Naito, M.; Pronin, A.V. Optical study of superconducting Pr2CuOx with x≃4. Phys. Rev. B 2014, 90, 024503. [Google Scholar] [CrossRef]
- Xu, S.-Y.; Wray, L.A.; Xia, Y.; Shankar, R.; Petersen, A.; Fedorov, A.; Lin, H.; Bansil, A.; Hor, Y.S.; Grauer, D.; et al. Discovery of several large families of topological insulator classes with backscattering-suppressed spin-polarized single-Dirac-cone on the surface. arXiv 2010, arXiv:1007.5111. [Google Scholar]
- Ren, Z.; Taskin, A.A.; Sasaki, S.; Segawa, K.; Ando, Y. Large bulk resistivity and surface quantum oscillations in the topological insulator Bi2Te2Se. Phys. Rev. B 2010, 82, 241306. [Google Scholar] [CrossRef]
- Xiong, J.; Petersen, A.C.; Qu, D.; Hor, Y.S.; Cava, R.J.; Ong, N.P. Quantum oscillations in a topological insulator Bi2Te2Se with large bulk resistivity (6 Ωcm). Physica E 2012, 44, 917. [Google Scholar] [CrossRef]
- Li, Z.; Chen, T.; Pan, H.; Song, F.; Wang, B.; Han, J.; Qin, Y.; Wang, X.; Zhang, R.; Wan, J.; et al. Two-dimensional universal conductance fluctuations and the electron-phonon interaction of surface states in Bi2Te2Se microflakes. Sci. Rep. 2012, 2, 595. [Google Scholar] [CrossRef] [PubMed]
- Tian, J.; Miotkowski, I.; Hong, S.; Chen, Y.P. Electrical injection and detection of spin-polarized currents in topological insulator Bi2Te2Se. Sci. Rep. 2015, 5, 14293. [Google Scholar] [CrossRef]
- Arakane, T.; Sato, T.; Souma, S.; Kosaka, K.; Nakayama, K.; Komatsu, M.; Takahashi, T.; Ren, Z.; Segawa, K.; Ando, Y. Tunable Dirac cone in the topological insulator Bi2-xSbxTe3-ySey. Nat. Commun. 2011, 3, 636. [Google Scholar] [CrossRef]
- Neupane, M.; Xu, S.-Y.; Wray, L.A.; Petersen, A.; Shankar, R.; Alidoust, N.; Liu, C.; Fedorov, A.; Ji, H.; Allred, J.M.; et al. Topological surface states and Dirac point tuning in ternary topological insulators. Phys. Rev. B 2012, 85, 235406. [Google Scholar] [CrossRef]
- di Pietro, P.; Vitucci, F.M.; Nicoletti, D.; Baldassarre, L.; Calvani, P.; Cava, R.; Hor, Y.S.; Schade, U.; Lupi, S. Ab initio studying of topological insulator Bi2Se3 under the stress. Phys. Rev. B 2012, 86, 045439. [Google Scholar] [CrossRef]
- Akrap, A.; Tran, M.; Ubaldini, A.; Teyssier, J.; Giannini, E.; van der Marel, D.; Lerch, P.; Homes, C.C. Optical properties of Bi2Te2Se at ambient and high pressures. Phys. Rev. B 2012, 86, 235207. [Google Scholar] [CrossRef]
- Reijnders, A.A.; Tian, Y.; Sandilands, L.J.; Pohl, G.; Kivlichan, I.D.; Zhao, S.Y.F.; Jia, S.; Charles, M.E.; Cava, R.J.; Alidoust, N.; et al. Optical evidence of surface state suppression in Bi-based topological insulators. Phys. Rev. B 2014, 89, 075138. [Google Scholar] [CrossRef]
- LaForge, A.D.; Frenzel, A.; Pursley, B.C.; Lin, T.; Liu, X.; Shi, J.; Basov, D.N. Optical characterization of Bi2Se3 in a magnetic field: Infrared evidence for magnetoelectric coupling in a topological insulator material. Phys. Rev. B 2010, 81, 125120. [Google Scholar] [CrossRef]
- Sushkov, A.B.; Jenkins, G.S.; Schmadel, D.C.; Butch, N.P.; Paglione, J.; Drew, H.D. Far-infrared cyclotron resonance and Faraday effect in Bi2Se3. Phys. Rev. B 2010, 82, 125110. [Google Scholar] [CrossRef]
- Dordevic, S.V.; Wolf, M.S.; Stojilovic, N.; Lei, H.; Petrovic, C. Signatures of charge inhomogeneities in the infrared spectra of topological insulators Bi2Se3, Bi2Te3 and Sb2Te3. J. Phys. Condens. Matter 2013, 25, 075501. [Google Scholar] [CrossRef] [PubMed]
- Chapler, B.C.; Post, K.W.; Richardella, A.R.; Lee, J.S.; Tao, J.; Samarth, N.; Basov, D.N. Infrared electrodynamics and ferromagnetism in the topological semiconductors Bi2Te3 and Mn-doped Bi2Te3. Phys. Rev. B 2014, 89, 235308. [Google Scholar] [CrossRef]
- Post, K.W.; Lee, Y.S.; Chapler, B.C.; Schafgans, A.A.; Novak, M.; Taskin, A.A.; Segawa, K.; Goldflam, M.D.; Stinson, H.T.; Ando, Y.; et al. Infrared probe of the bulk insulating response in Bi2−xSbxTe3−ySey topological insulator alloys. Phys. Rev. B 2015, 91, 165202. [Google Scholar] [CrossRef]
- Wang, L.-L.; Johnson, D.D. Ternary tetradymite compounds as topological insulators. Phys. Rev. B 2011, 83, 241309. [Google Scholar] [CrossRef]
- Available online: http://www.wien2k.at (accessed on 6 June 2020).
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Frenzel, A.J.; Homes, C.C.; Gibson, Q.D.; Shao, Y.M.; Post, K.W.; Charnukha, A.; Cava, R.J.; Basov, D.N. Anisotropic electrodynamics of type-II Weyl semimetal candidate WTe2. Phys. Rev. B 2017, 95, 245140. [Google Scholar] [CrossRef]
- Neubauer, D.; Yaresko, A.; Li, W.; Löhle, A.; Hübner, R.; Schilling, M.B.; Shekhar, C.; Felser, C.; Dressel, M.; Pronin, A.V. Optical conductivity of the Weyl semimetal NbP. Phys. Rev. B 2018, 98, 195203. [Google Scholar] [CrossRef]
- Santos-Cottin, D.; Klein, Y.; Werner, P.; Miyake, T.; Medici, L.d.; Gauzzi, A.; Lobo, R.P.S.M.; Casula, M. Linear behavior of the optical conductivity and incoherent charge transport in BaCoS2. Phys. Rev. Materials 2018, 2, 105001. [Google Scholar] [CrossRef]
- Hütt, F.; Yaresko, A.; Schilling, M.B.; Shekhar, C.; Felser, C.; Dressel, M.; Pronin, A.V. Linear-in-frequency optical conductivity in GdPtBi due to transitions near the triple points. Phys. Rev. Lett. 2018, 121, 176601. [Google Scholar] [CrossRef]
| Lateral Dimensions | Thickness | Bulk electron Density | Mobility | Lattice Constant |
|---|---|---|---|---|
| 5 × 5 mm2 | 350 μm | 1.0 × 1018 cm−3 | 330 cm2/Vs | 29.766 A |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhukova, E.S.; Zhang, H.; Martovitskiy, V.P.; Selivanov, Y.G.; Gorshunov, B.P.; Dressel, M. Infrared Optical Conductivity of Bulk Bi2Te2Se. Crystals 2020, 10, 553. https://doi.org/10.3390/cryst10070553
Zhukova ES, Zhang H, Martovitskiy VP, Selivanov YG, Gorshunov BP, Dressel M. Infrared Optical Conductivity of Bulk Bi2Te2Se. Crystals. 2020; 10(7):553. https://doi.org/10.3390/cryst10070553
Chicago/Turabian StyleZhukova, Elena S., Hongbin Zhang, Victor P. Martovitskiy, Yurii G. Selivanov, Boris P. Gorshunov, and Martin Dressel. 2020. "Infrared Optical Conductivity of Bulk Bi2Te2Se" Crystals 10, no. 7: 553. https://doi.org/10.3390/cryst10070553
APA StyleZhukova, E. S., Zhang, H., Martovitskiy, V. P., Selivanov, Y. G., Gorshunov, B. P., & Dressel, M. (2020). Infrared Optical Conductivity of Bulk Bi2Te2Se. Crystals, 10(7), 553. https://doi.org/10.3390/cryst10070553






