1. Introduction
One of the main disadvantages of concrete for structure design is its low tensile strength. For this reason, research has focused on improving and developing a new composition and reinforcement that can eliminate this major disadvantage [
1,
2]. Scattered reinforcement has local tensile effects and affects the spatial stress in the concrete structure. As a result of the use of scattered reinforcement, both the tensile strength and the load–displacement diagram itself are significantly affected. There are many variants of fiber-reinforced concrete, which differ mainly in the material and shape properties of the fibers used [
3]. The shape of the fibers affects the mechanical properties [
4]. The resulting mechanical properties of fiber-reinforced concrete are further influenced by the recipe of the plain concrete, fiber volume fraction, and processing of the fiber-reinforced concrete (e.g., degree of compaction). The effects include the development of micro-cracks, resistance to temperature changes, shrinkage, and impact strength. The wider development and application of fiber-reinforced concrete have been prevented primarily by the difficultly of correct technological and static assessment. The price of fibers also increases the overall cost of concrete production. On the other hand, the complexity of the work due to the laying of steel bar-reinforced concrete is eliminated. In selected cases of structural design, fiber-reinforced concrete can also replace classical reinforcement. In terms of the technological process, it is especially necessary to ensure that the resulting composite has a homogeneous structure [
5]. This is especially true in the case of a higher volume of the fiber fraction, for which processing is difficult [
6].
A very important property that is sometimes largely neglected is the density of concrete/fiber-reinforced concrete. We distinguish several types of densities. These are the density of the fresh concrete mixture, the density of the sample in natural storage, the density of the dried sample, and the density of the sample stored in water. The difference between the individual densities can be in the order of a few percent. The density is primarily determined by the concrete recipe, i.e., the type of aggregate used, cement content, and water content (respectively water–cement ratio). In the case of fiber-reinforced concrete, the density is further affected by the volume of the fiber fraction. Another factor that can strongly affect the density is the degree of compaction and the number of pores. In the case of fiber-reinforced concrete, the degree of compaction is greatly influenced by the fibers themselves. It is true that the larger the number of fibers in the concrete, the more difficult it is to perform thorough compaction. The density can also further affect the resulting mechanical properties (compressive strength, tensile strength, and others), the permeability of the concrete, or the resistance to chlorine.
Structural parts suitable for fiber-reinforced concrete include slabs and floors [
7,
8,
9] or beams without shear reinforcement [
10]. The main limitation of fiber-reinforced concrete, however, is that even with very good mechanical properties of compression and tensility, the full replacement of classical reinforcement cannot be expected. However, the ductility and the safety level of a typical reinforced concrete beam and slab remain significantly higher. The optimal solution is to use fiber-reinforced concrete in combination with classical reinforcement. These are mainly lightweight sections without shear reinforcement in the variant with classical or prestressed reinforcement. The design and use of fiber-reinforced concrete must be approached qualitatively because it is a different material to conventional concrete. The fibers affect the mechanical properties [
11,
12] and fracture properties [
13,
14], i.e., the deformability and ductility. The biggest difference is in the mentioned tensile strength. However, it is necessary to use a load–displacement diagram to describe tensile strength [
15]. This is because it is necessary to differentiate between the phases of behavior before crack formation and during crack formation and fiber activation. We also distinguish the nature of the behavior of the concrete matrix and fibers in crack propagation, namely, whether the matrix cracks, the fibers break, or the fibers are pulled out of the matrix. For practical reasons, these phenomena are described with the help of the residual tensile strength [
16] or elastic properties of the material [
17]. For concrete of lower compressive and tensile strengths, steel fibers are typically rapidly activated. Furthermore, the crack width increases, and the fibers are pulled out (not broken). The cohesion of concrete with fibers is lower.
On the other hand, in the case of high-strength concrete, the effect of the fibers on the tensile strength is typically less, the fibers are fully activated, and the fibers break when the crack increases. The specific problem in using fiber-reinforced concrete is the recipe design [
6,
18]. Typically, the volume of the steel fiber fraction is no more than 3–4%. However, the workability of concrete beyond a fiber volume fraction of 2% is very difficult. The presented research deals with fiber volume fractions of 0, 0.51, 0.96, and 1.40%, which correspond to fiber dosages of 0, 40, 75, and 110 kg/m
3, respectively. The fibers also affect the microstructure of the concrete and change the nature of the bonding between the aggregate and the cement. As a result, it is advisable to adjust the composition of the concrete recipe by increasing the fiber volume fraction. A fiber volume fraction above 1%, given the same recipe, can, in some cases, also negatively reduce its compressive strength. Current directions for fiber-reinforced concrete include the use of hybrid fiber-reinforced concrete [
19,
20,
21], fiber-reinforced self-compacting concrete [
22,
23], or high-strength concrete [
24].
Research into fiber-reinforced concrete and its mechanical properties has led to several recommendations and standards [
25,
26,
27]. The most important ones are the Model Code 2010 [
28], the RILEM recommendations [
29], and the German DAfStb standard [
30]. In addition to the basic mechanical properties of fiber-reinforced concrete required for the design of structures, it is also important to address durability, which also includes research on chloride in concrete [
22].
2. Load–Displacement Diagram and Fracture Energy
For concrete and concrete structures, it is also very important to evaluate fracture-mechanical parameters [
31], such as absorbed fracture energy and fracture energy. The fracture parameters need to be determined for both plain concrete and concrete with dispersed reinforcement, where it is necessary to determine the brittleness of this material. These fracture-mechanical parameters also serve very well to predict crack formation [
32]. The size of the fracture energy tells us how much energy contributes to the formation of cracks. Fracture tests in a three-point bend of a notched beam are usually used to determine these parameters. The determination of fracture-mechanical properties is also important for the assessment of concrete structures and numerical modeling [
33].
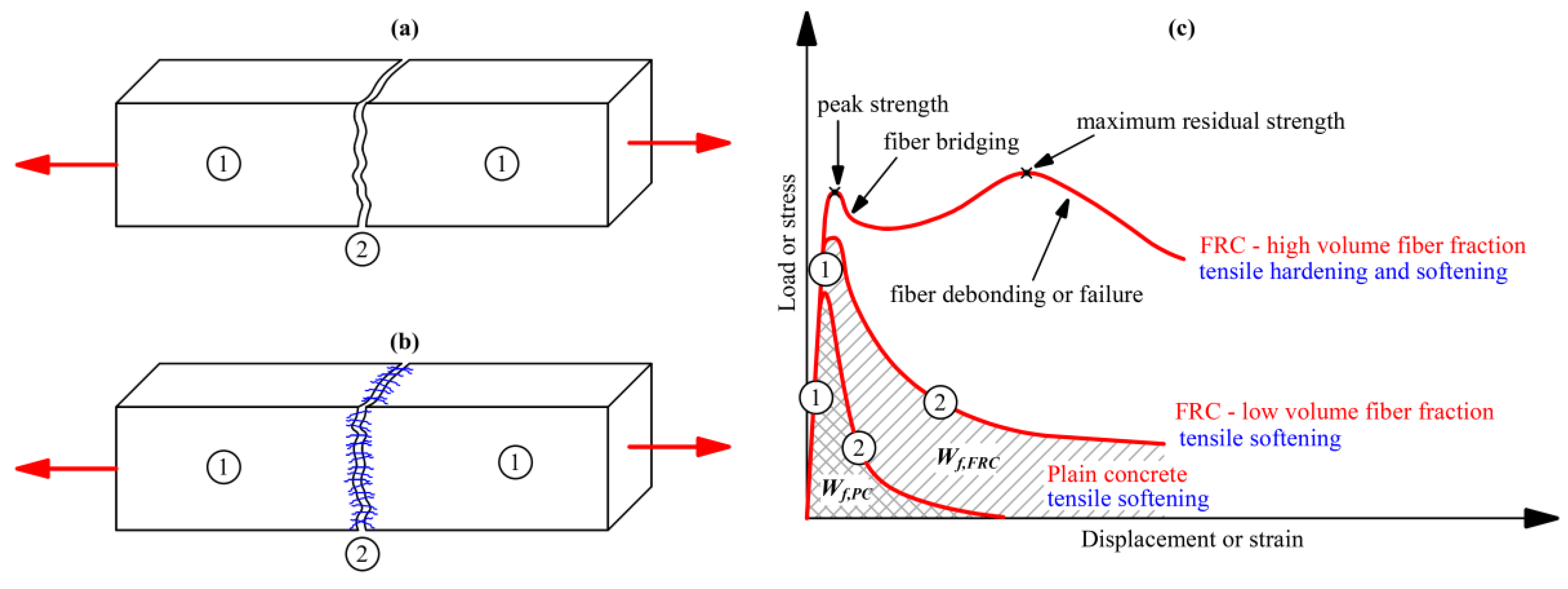
Figure 1 describes the difference in the behavior of plain concrete and fiber-reinforced concrete. In the case of plain concrete, the load–displacement diagram after peak strength has been reached can be characterized as an exponential curve. When the tensile strength of plain concrete is reached, the element suddenly breaks. Therefore, this tensile strength is not applied in practice. Adding fibers to the concrete changes the behavior of the element and substantially changes the shape of the load–displacement diagram [
34,
35]. After reaching the concrete strength (peak strength), there is a macro-crack, which quickly opens and lengthens. At this point, the fibers in the concrete are activated, and the tensile stress transfers these fibers. Tensile behavior can be defined in two ways, i.e., tensile softening [
36] and tensile hardening. Whether tensile softening or tensile hardening occurs is influenced mainly by the number of fibers but certainly also by the recipe of the concrete and the processing of the fiber-reinforced concrete. In that case, another peak appears in the load–displacement diagram, which we call the residual tensile strength. When this limit is reached, the tensile capacity is exhausted. The tensile strength of the matrix or the tensile strength of the matrix with fibers is exceeded, and a tensile softening is applied, which is typical for plain concrete or fiber-reinforced concrete with a low fiber volume fraction.
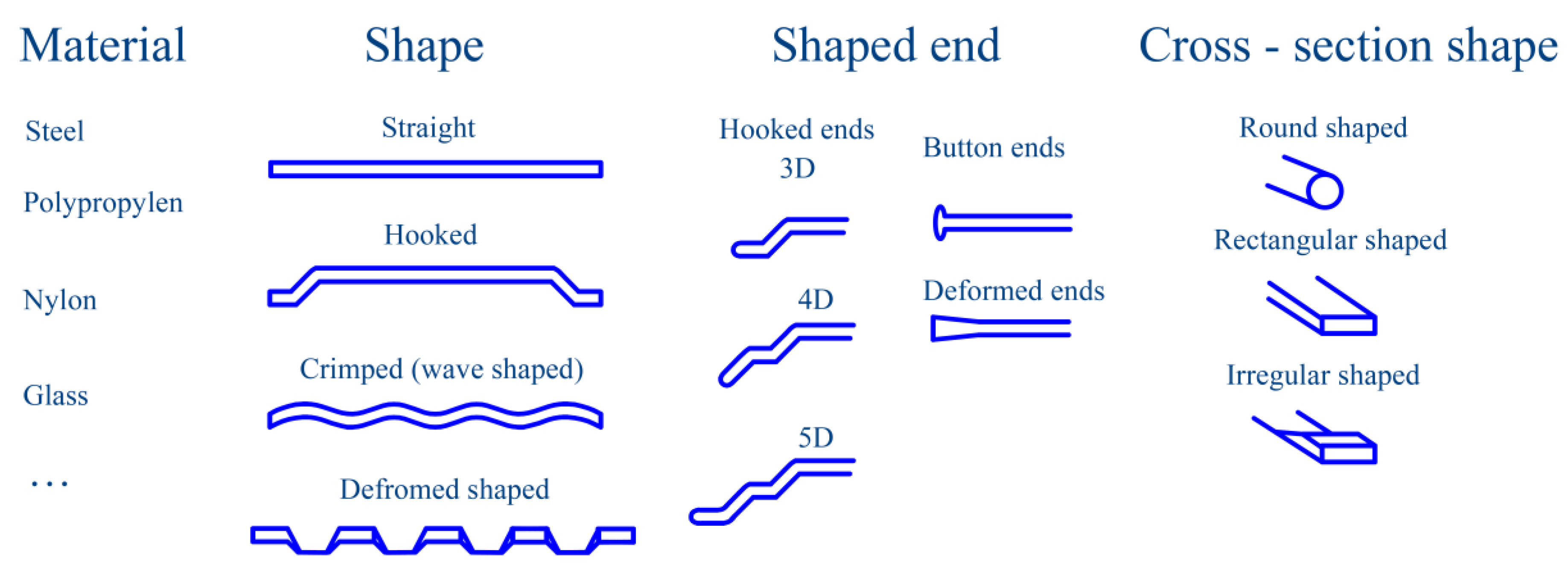
The shape of the load–displacement diagram varies depending on the fiber volume fraction in the concrete, as well as the type of fibers used. There is a wide range of fibers on the market, which differ mainly in material, shape, shaped end, and the surface treatment of the fibers. Some of the types of fibers are shown in
Figure 2.
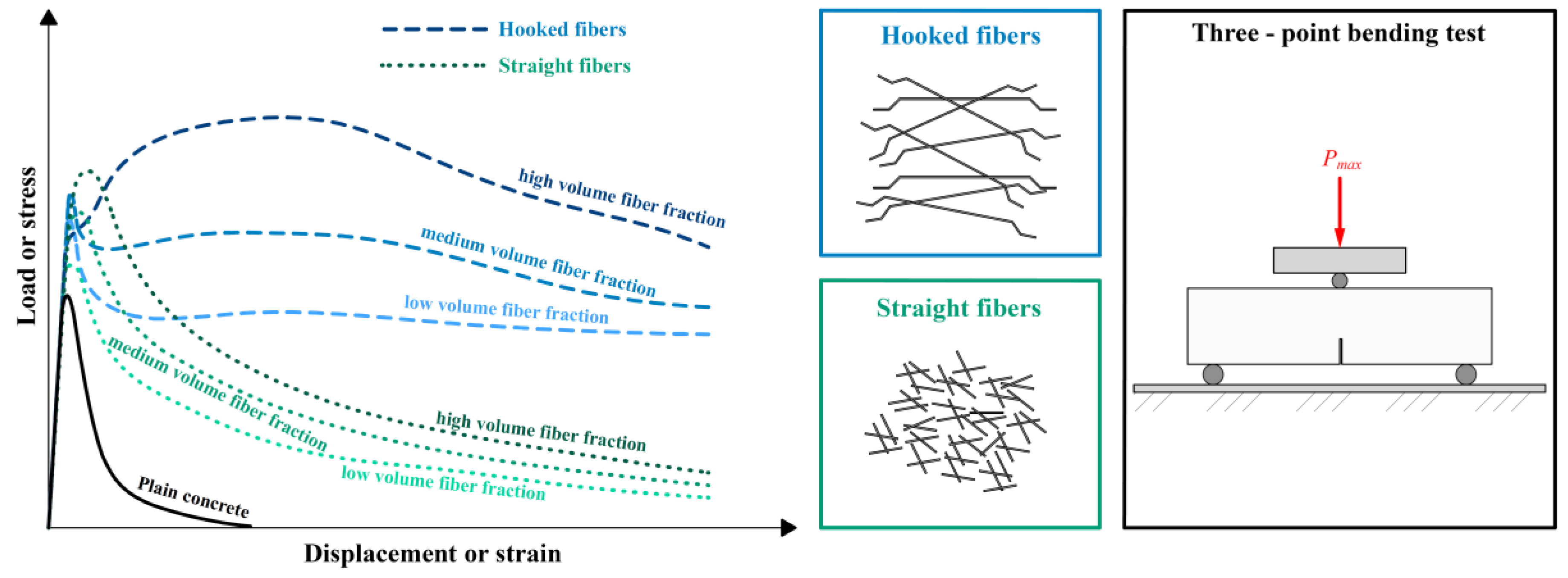
Most often, hooked fibers, straight fibers, or their combinations are used. The shape of the load–displacement diagrams (
fc < 50 MPa) for fibers with hooked fibers for different fiber dosages is shown in
Figure 3 (blue lines). The figure shows the effect of the fiber volume fraction. By increasing the fiber volume fraction in the concrete, the absorbed fracture energy/fracture energy and tensile strength are increased.
Straight fibers are most often used to prevent shrinkage cracks. They can also be used in combination with other fibers that significantly increase the fracture energy and residual strength. In this case, this type of composite is called hybrid fiber-reinforced concrete.
Figure 3 (green lines) shows load–displacement diagrams for typical fiber-reinforced concrete (
fc < 50 MPa) with straight fibers for different fiber dosages. The figure shows the effect of fibers on the tensile strength of the fiber-reinforced concrete and the effect on fracture energy. However, straight fibers are usually used for high-strength concrete, for which the load–displacement diagram may be more similar in shape to that of a load–displacement diagram for fiber-reinforced concrete with hooked fibers. For straight fibers, the quality of cohesion between the fiber and the concrete matrix is important, and in the case of high-strength concrete, this cohesion is significantly better. From a basic comparison of the load–displacement diagrams in
Figure 3, it can be argued that hooked fibers usually have a greater influence on the tensile strength, residual tensile strength, and fracture energy increase. The fracture energy determined according to Formula (2) can be many times greater compared to that fiber-reinforced concrete with straight fibers.
3. Experimental Program
3.1. Recipe for Fiber Reinforcement Concrete
In the laboratory of the Faculty of Civil Engineering, VSB-Technical University of Ostrava, Czech Republic specimens with the following concrete recipe were tested: Min. cement content = 320 kg (CEM II/A-S 42.5); aggregate 0/2 = 525 kg; aggregate 0/4 = 420 kg; aggregate 4/8 = 150 kg; aggregate 8/16 = 820 kg; water = 200 l; and water/cement ratio (
w/
c) = 0.625. Parts of the laboratory program were samples that differed in the type of fibers. The hooked fibers Dramix
® 3D 55/30 BG (
Figure 4a) and straight fibers Dramix
® OL13/.20 (
Figure 4b) [
38] with dosages of 40, 75, and 110 kg/m
3 were added to the concrete. The basic characteristics of the fibers specified by the producer Bekaert are shown in
Table 1 [
38]. For the classification of the concrete and the determination of the initial reference characteristics, test samples of plain concrete were also made, i.e., the fiber dosage was 0 kg/m
3. In total, seven test series were made (3× fiber-reinforced concrete with hooked fibers, 3× fiber-reinforced concrete with straight fibers, 1× plain concrete), which differed mainly in the type and dosage of fibers. Research on fiber-reinforced concrete followed.
3.2. Determination of Mechanical Properties of Fiber-Reinforced Concrete
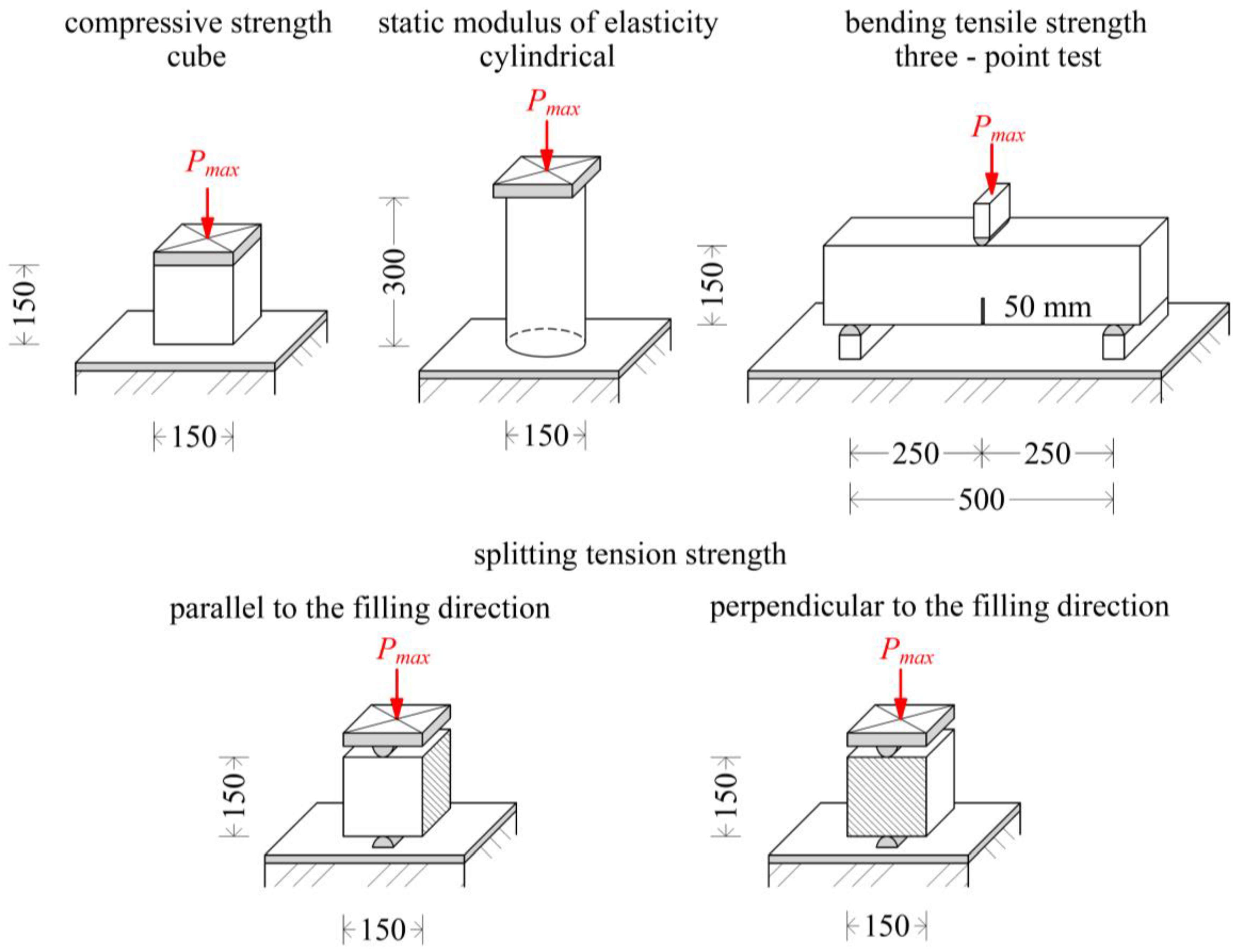
The mechanical properties of fiber-reinforced concrete/plain concrete were determined according to CSN EN 12390-3 [
39], CSN EN 12390-5 [
40], CSN EN 12390-6 [
41], and CSN ISO 1920-10 [
42]. The experimental program included the following examinations:
The density, ρ: 3× 150 mm × 150 mm × 150 mm cube;
3-day compressive strength, fc,cube,28: 3× 150 mm × 150 mm × 150 mm cube;
28-day compressive strength, fc,cube,3: 3× 150 mm × 150 mm × 150 mm cube;
Splitting tensile strength, perpendicular to the direction of filling, fct,sp,⊥: 3× 150 × 150 × 150 mm cube;
Splitting tensile strength, parallel to the direction of filling, fct,sp,‖: 2× 150 mm × 150 mm × 150 mm cube;
Bending tensile strength, fct,fl: 3× 150 mm × 150 mm × 600 mm beam with a notch in the middle of the span. The notch was 50 mm high and 3 mm wide. The load transfer device from the testing machine to the beam is composed of a support roller and one load roller. The support rollers were placed at a distance of 50 mm from the edge of the beam. The load was applied using a loading roller by displacement The load was applied using a loading roller by displacement increasing.
The test scheme is shown in
Figure 5 according to [
34,
39,
40,
41,
42]. Additionally, plain concrete tests were carried out for the static modulus of elasticity,
Ec, for a cylindrical diameter of 150 mm and a height of 300 mm.
The formulas used to calculate the basic mechanical properties were those recommended by Model Code 2010 [
28]. For bending tensile strength, the formula is
where
Pmax is the maximum load achieved in the test press,
L is the span,
b and
h are the transverse dimensions of the sample, and
a0 is the notch size.
The fracture energy
Gf can be calculated from the load–displacement diagram and fracture plane. The fracture energy is defined by the relation
where
Wf is absorbed fracture energy,
b is the width of the sample,
h is the height of the sample, and
a0 is the depth of the notch.
4. Results of Laboratory Tests
The mechanical properties, derived from the laboratory experiment program, of fiber-reinforced concrete for individual dosages and individual types of fibers are summarized in
Table 2 and
Table 3.
Table 2 and
Table 3 also give the resulting mechanical properties of plain concrete. The average modulus of elasticity of plain concrete of 26.53 GPa was also determined. Two types of splitting tensile tests were performed to verify the homogeneity of the fiber-reinforced concrete, i.e., the even spatial distribution/orientation of the fibers in the concrete. This was a splitting tensile test perpendicular to the filling direction and parallel to the filling direction. The location of the test specimen in the press for the filling direction is shown in
Figure 5.
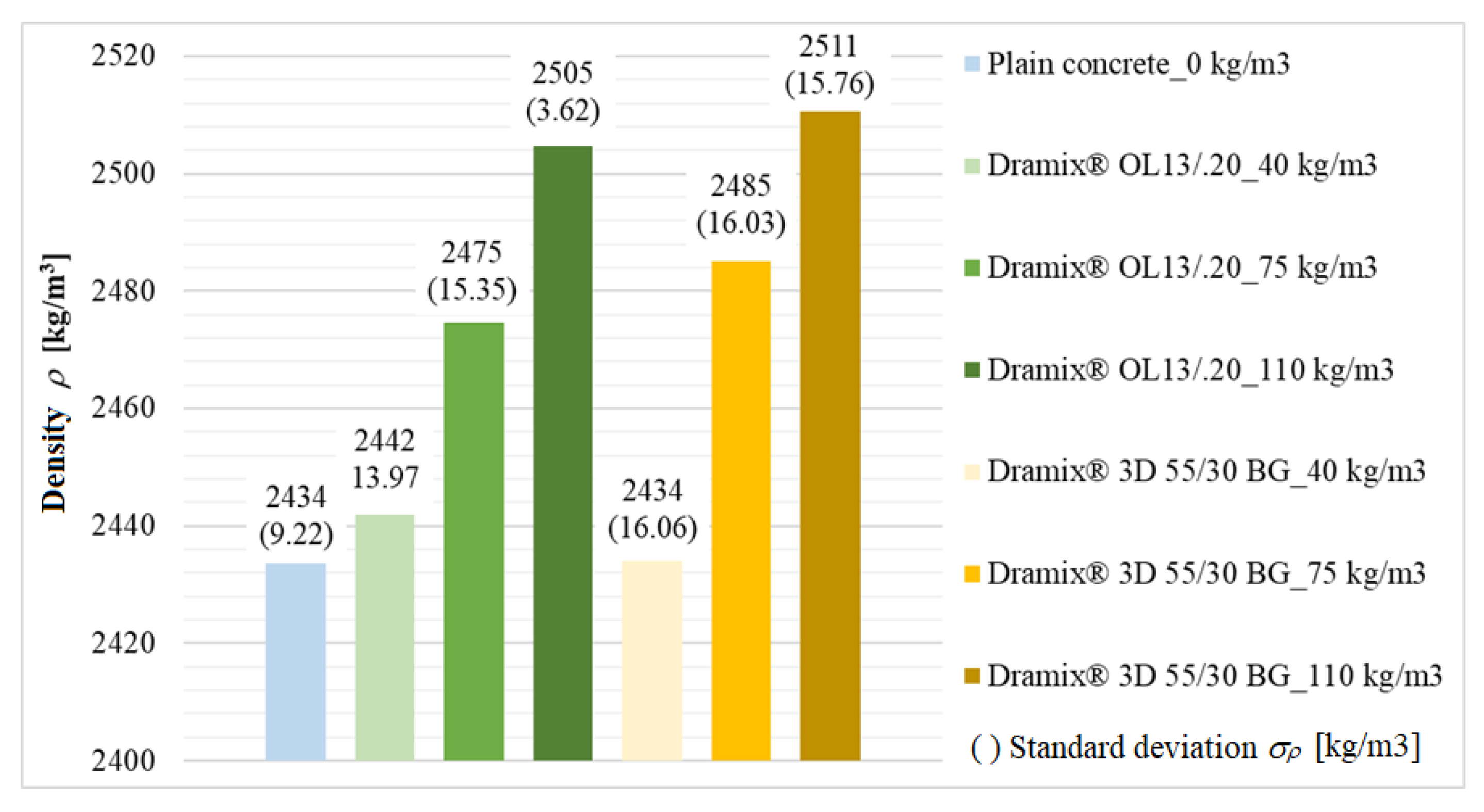
The average densities of the plain concrete and fiber-reinforced concrete are shown in the form of a bar graph in
Figure 6. In each series (a total of seven test series), three samples were evaluated.
Figure 6 also shows the standard deviations of the determined densities. The density was determined after 3 days of curing the samples stored in water. The initial density of the plain concrete was 2434 kg/m
3. In the case of the fiber-reinforced concrete, there was a gradual increase in densities with fiber dosing.
The 28-day compressive strength of the plain concrete was 33.80 MPa. There was an increase in compressive strength when increasing the dosage of the fibers. The increase in compressive strength compared with that of the plain concrete was up to 21% (fiber dosage of 75 kg/m
3) for fiber-reinforced concrete with hooked fibers and 27% (fiber dosage of 110 kg/m
3) for fiber-reinforced concrete with straight fibers. The values of the 28-day compressive strength are also specified in more detail in
Table 2.
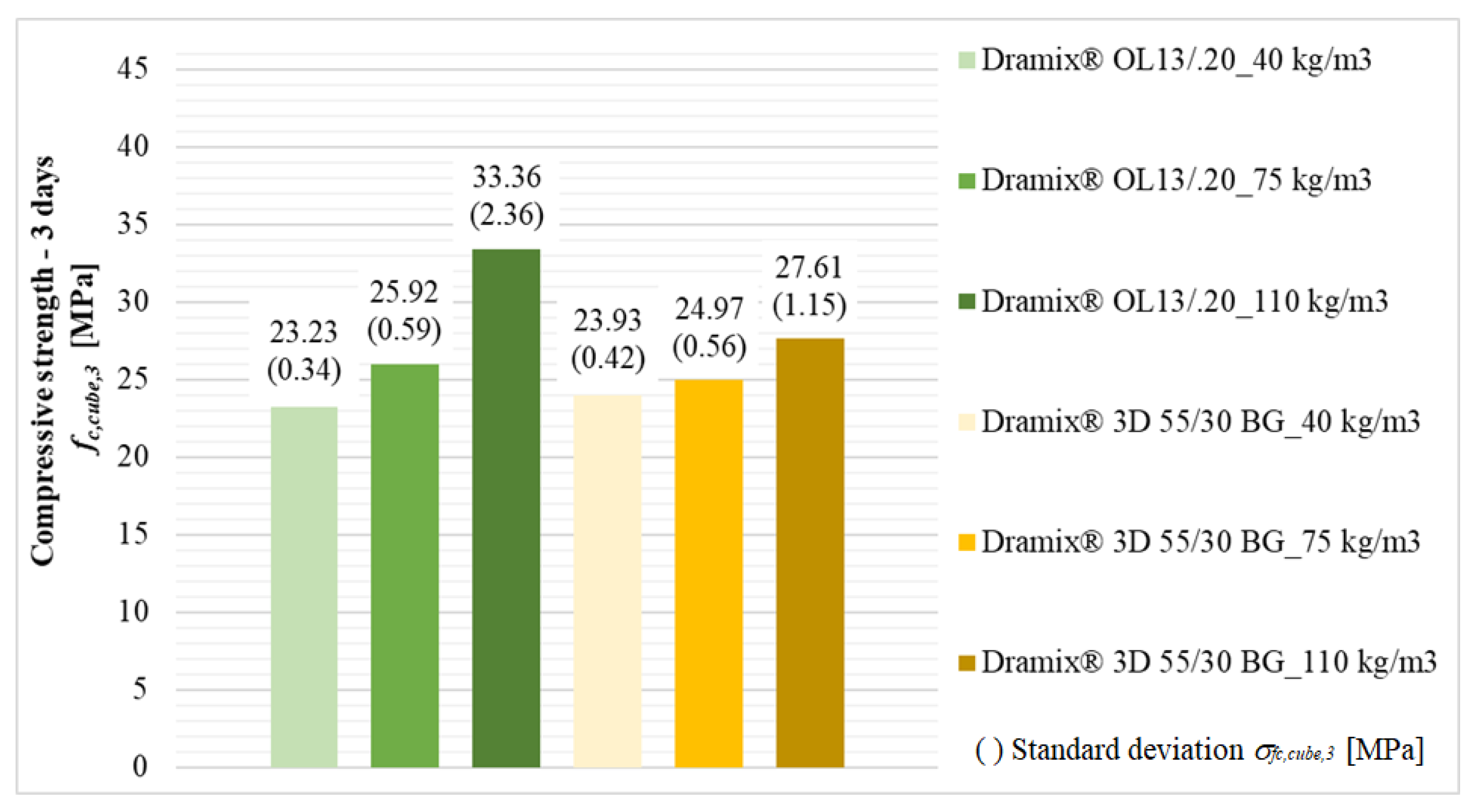
The initial increase in the compressive strength of the fiber-reinforced concrete was also observed. Specifically, the 3-day compressive strength of the fiber-reinforced concrete was monitored. These compressive strength values are shown in the form of a bar graph in
Figure 7.
Table 2 and
Figure 7 show a difference between the average 3-day compressive strength and the average 28-day compressive strength of the fiber-reinforced concrete. In the case of the fiber-reinforced concrete with hooked fibers, the 3-day compressive strength was about 61–69% of the 28-day compressive strength, and for the fiber-reinforced concrete with straight fibers, it was 60–78% of the 28-day compressive strength.
Figure 7 also shows, in parentheses, the standard deviations of the average values the 3-day compressive strength.
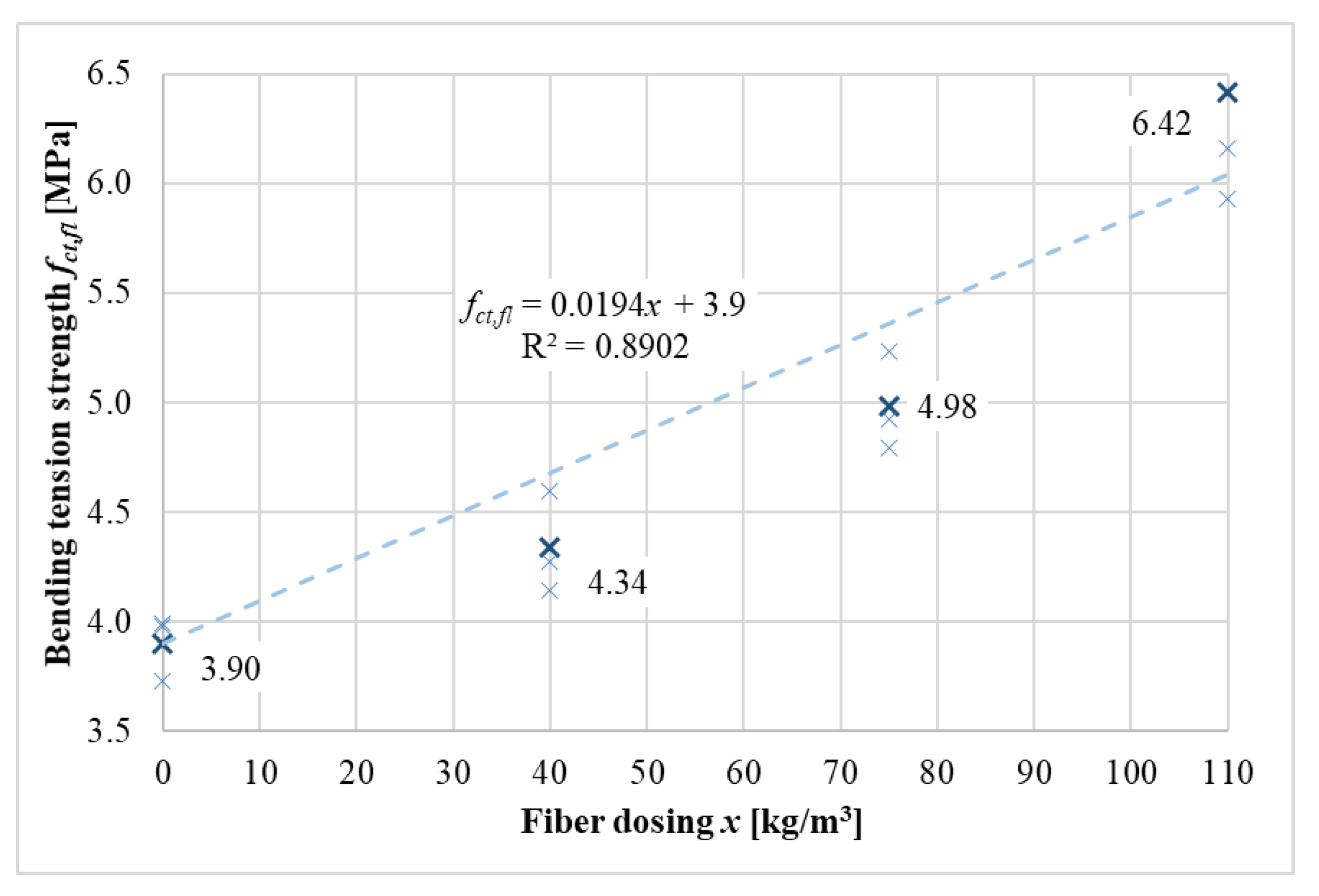
Table 3 shows the tensile strengths and their standard deviations. The increase in tensile strength was much greater for the fiber-reinforced concrete with hooked fibers. A comparison with the plain concrete revealed that the splitting tensile strength perpendicular to the filling direction increased from 2.64 to 4.75 MPa for the fiber-reinforced concrete with hooked fibers (fiber dosage of 110 kg/m
3), which is about 80%. The bending tensile strength increased from 3.90 to 6.42 MPa (fiber dosage of 110 kg/m
3), which is about 65%.
In this case, the fiber-reinforced concrete with straight fibers also had increased tensile strength, but the increase in strength was not as pronounced as that the fiber-reinforced concrete with hooked fibers. In comparison with the plain concrete, the splitting tensile strength perpendicular to the filling direction increased from 2.64 to 3.08 MPa for the fiber-reinforced concrete with straight fibers (fiber dosage of 110 kg/m3), which is about 17%. The bending tensile strength increased from 3.90 to 4.98 MPa (fiber dosage of 75 kg/m3), which is about 28%.
In comparison with the plain concrete, the splitting tensile strength parallel to the filling direction increased from 2.34 to 2.70 MPa for the fiber-reinforced concrete with straight fibers (fiber dosage of 40 kg/m3), which is about 15%. In the case of the fiber-reinforced concrete with hooked fibers, the increase was from 2.34 to 2.91 MPa (fiber dosage of 110 kg/m3), which is about 24%. The tensile strength (perpendicular and parallel to the filling direction) and the bending tensile strength of the fiber-reinforced concrete with straight fibers did not increase further with higher fiber dosages. In some cases, the tensile strength was even reduced with an increase in the fiber dosage.
The homogeneity of the concrete was verified by the ratio of the splitting tensile strength perpendicular and parallel to the filling direction. The splitting tensile strength ratios are shown by the bar graph in
Figure 8. The graph shows a smaller difference between these strengths in the case of straight fibers, which is due to the better spatial orientation of these fibers.
5. Evaluation of Mechanical Properties for Fiber-Reinforced Concrete
The data from the laboratory tests on the fiber-reinforced concrete with hooked fibers were evaluated using regression analysis. The functional dependence of the compressive strength (cube)
fc,cube, the splitting tensile strength perpendicular to the filling direction
fct,sp,⊥, the splitting tensile strength parallel to the filling direction
fct,sp,‖, and the bending tensile strength
fct,fl with respect to hooked fiber dosing can be expressed according to the following relations:
where
x is the fiber dosage. On the basis of the coefficient of determination, R
2, the dependence of the mechanical properties of fiber-reinforced concrete on the fiber dosage,
x, can be classified as very significant. Linear regression models fit the initial values of the mechanical properties of the plain concrete.
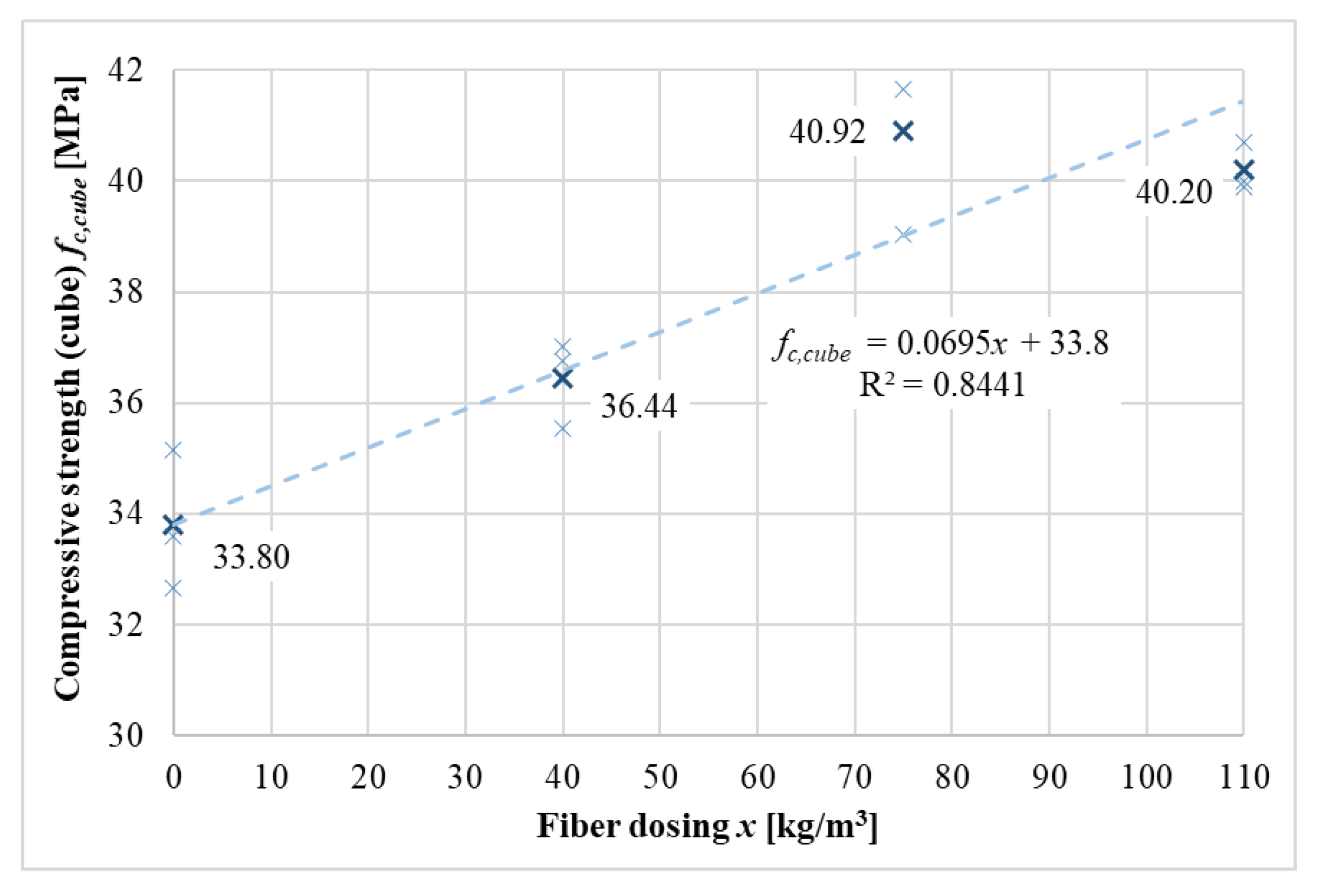
Graphically, the functional dependence of the compressive strength on the fiber dosing is shown in
Figure 9. From the linear regression model, good agreement (84%) with the compressive strength data is evident. From Equation (3), it is possible to determine an estimate of the intermediate values of compressive strength. It is evident from the regression model that the increase in fiber dosing increased the compressive strength up to a fiber dosage of 75 kg/m
3. After this, there was a slight decline in this compressive strength (fiber dosage of 110 kg/m
3).
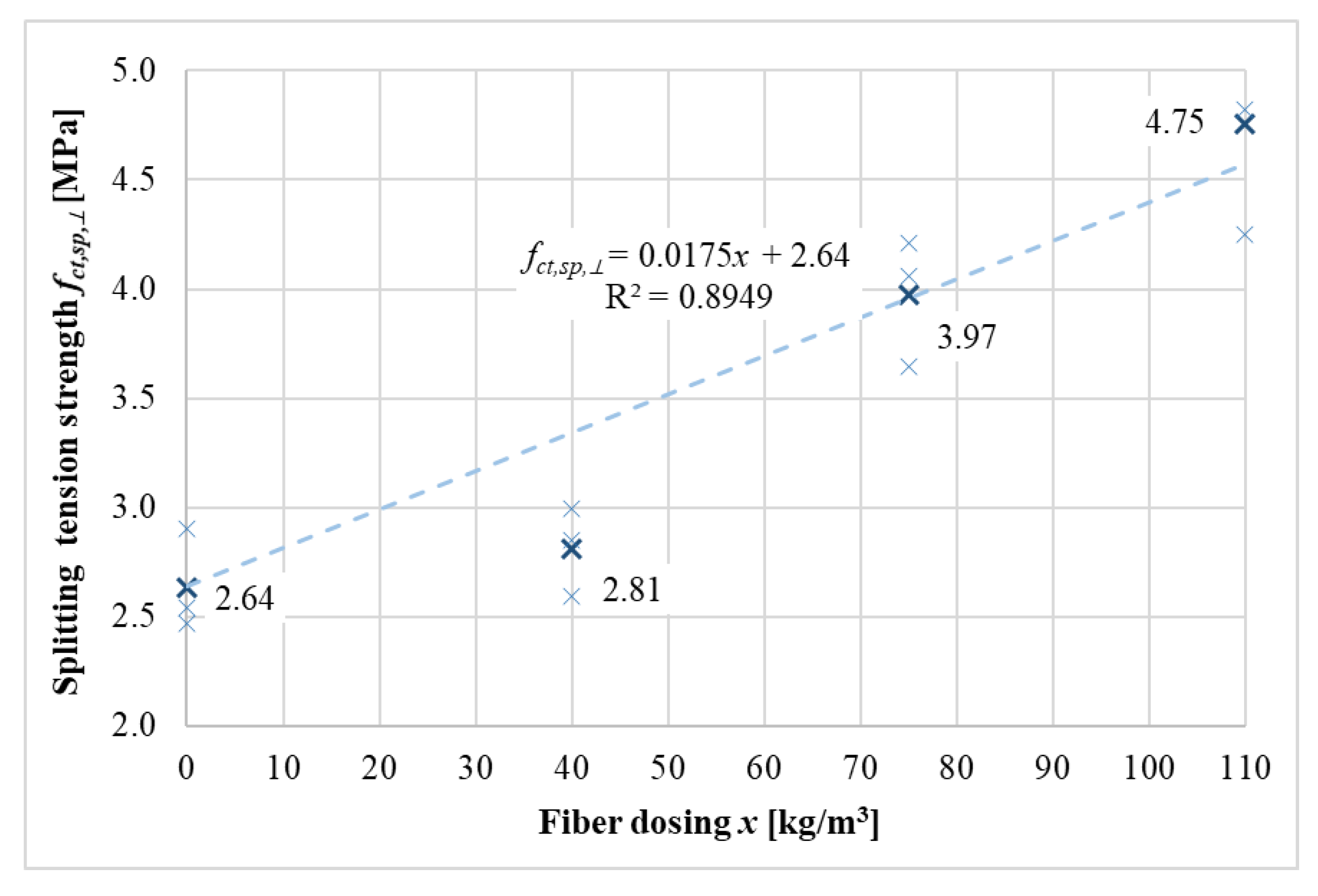
Figure 10 shows the functional dependence of the splitting tensile strength perpendicular to the filling direction on the fiber dosage.
Figure 10 shows a continuous increase in the splitting tensile strength perpendicular to the filling direction. The regression model shows good agreement, which is 89%. The estimation of the intermediate values of the splitting tensile strengths perpendicular to the filling direction can be performed using Equation (4). It is clear that the tensile strength perpendicular to the filling direction increased by up to 2.11 MPa.
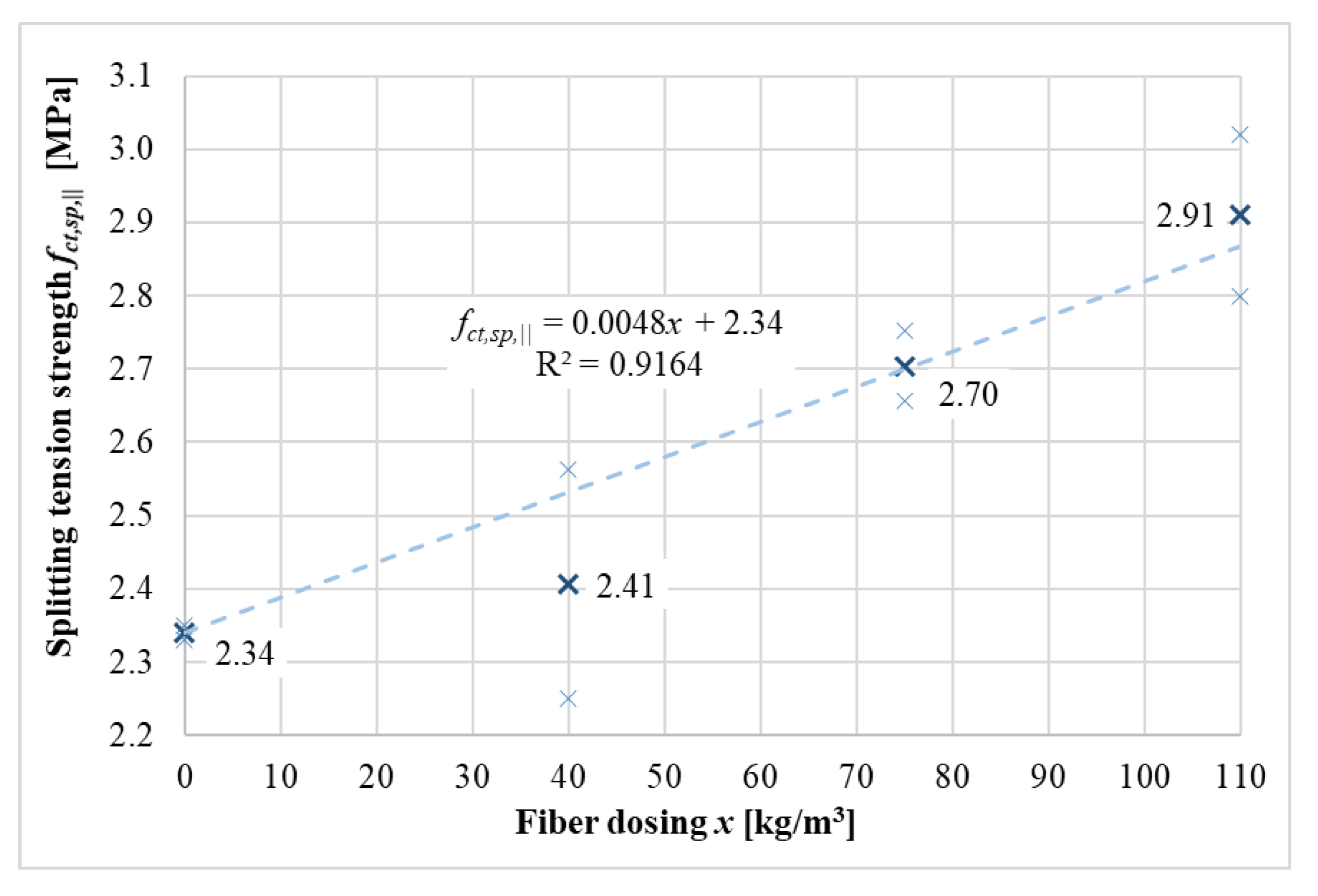
Figure 11 shows the functional dependence of the splitting tensile strength parallel to the filling direction on the fiber dosage. Again, there was a gradual increase in this strength. This corresponds to the good agreement of the regression model, which is 92%. Intermediate values of the splitting tensile strength parallel to the filling direction can be estimated using Equation (5). Again, there was an increase in tensile strength, but it was not very significant.
The functional dependence of the bending tensile strength on the fiber dosage is shown in
Figure 12. It is possible to observe a gradual increase in strength with increased fiber dosages. Intermediate values of the bending tensile strength can be determined using Formula (6) with good agreement (about 92%).
For all the tensile strength tests, the regression analysis was in good agreement and was around 90%.
6. Comparison and Evaluation of Load–Displacement Diagrams
From the three-point bending test, load–displacement diagrams were evaluated.
Figure 13,
Figure 14 and
Figure 15 show the load–displacement diagrams for the plain concrete and fiber-reinforced concrete with hooked fibers and straight fibers, which differ in fiber dosage (40, 75, and 110 kg/m
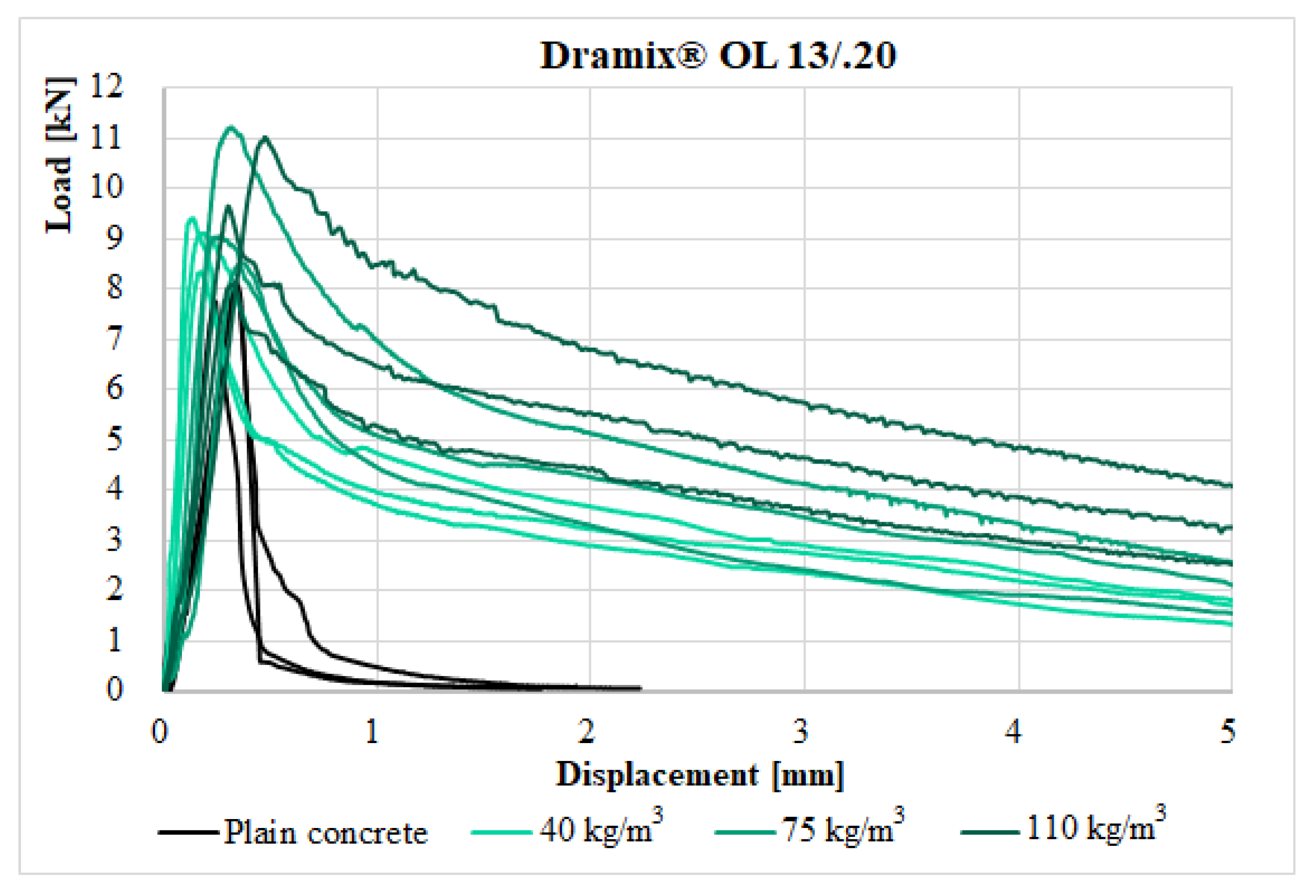
3). The black curves show the load–displacement diagrams of the plain concrete, the blue curves are those of the fiber-reinforced concrete with hooked fibers, and the green curves are those of the fiber-reinforced concrete with straight fibers.
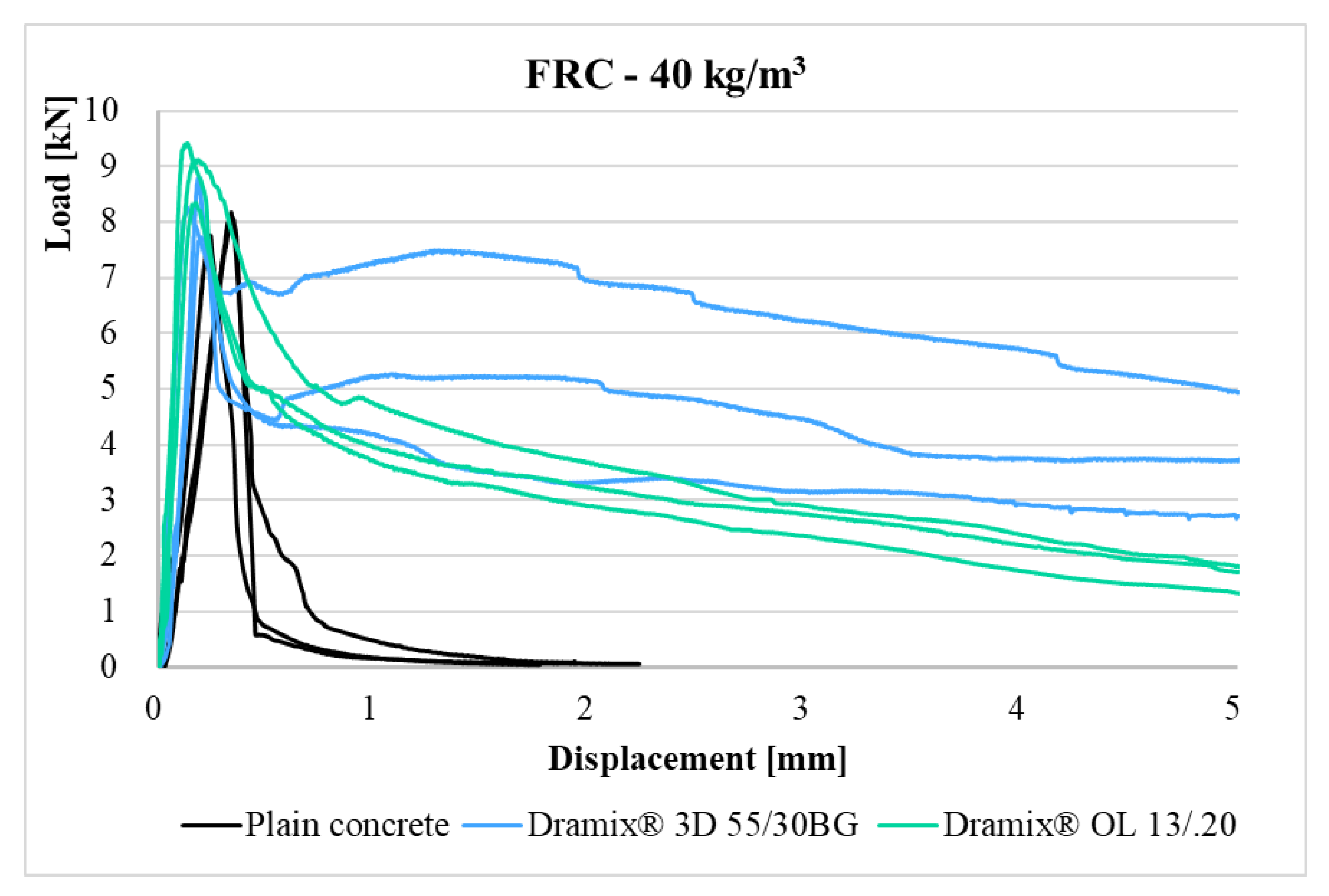
Figure 13 shows the curves of the load–displacement diagrams for the fiber-reinforced concrete with a fiber dosage of 40 kg/m
3 and plain concrete. At first glance, it can be seen that the maximum load/peak strength at which the crack was located is slightly higher in the case of straight fibers. On the other hand, a different course of load–displacement curves for straight fibers and hooked fibers can be observed. The course of the load–displacement diagrams for the concrete with hooked fibers is more favorable. In the case of the fiber-reinforced concrete with straight fibers, tensile softening only occurs after the crossing of the point at which the crack was located (maximum load/peak strength). At first glance, the size of the absorbed fracture energy (area under the curve) involved in crack formation is also evident. In the case of the fiber-reinforced concrete with hooked fibers, this absorbed fracture energy is significantly greater. Furthermore, the residual strength is much higher for the fiber-reinforced concrete with hooked fibers. In the case of the fiber-reinforced concrete with hooked fibers, there is also tensile hardening and the formation of a second peak in the curve. This is the limit at which the fibers that bridge the crack were activated. However, the magnitude of the load of the second peak is smaller than the magnitude of the load at the first point, where the crack was located.
Figure 14 shows load–displacement diagrams for the fiber-reinforced concrete with a fiber dosage of 75 kg/m
3 and plain concrete. The course of the curve for the fiber-reinforced concrete with straight fibers is very similar to the course of the curve for the fiber dosage of 40 kg/m
3. Again, there is only tensile softening after the localization of the crack (first peak/peak strength). The course of the curve for the fiber-reinforced concrete with hooked fibers is very different. It can be observed that by increasing the fiber dosage, a more significant tensile hardening is induced. In two cases, the value of the load of the second peak on the curve exceeds the value of the load at the crack location (first peak).
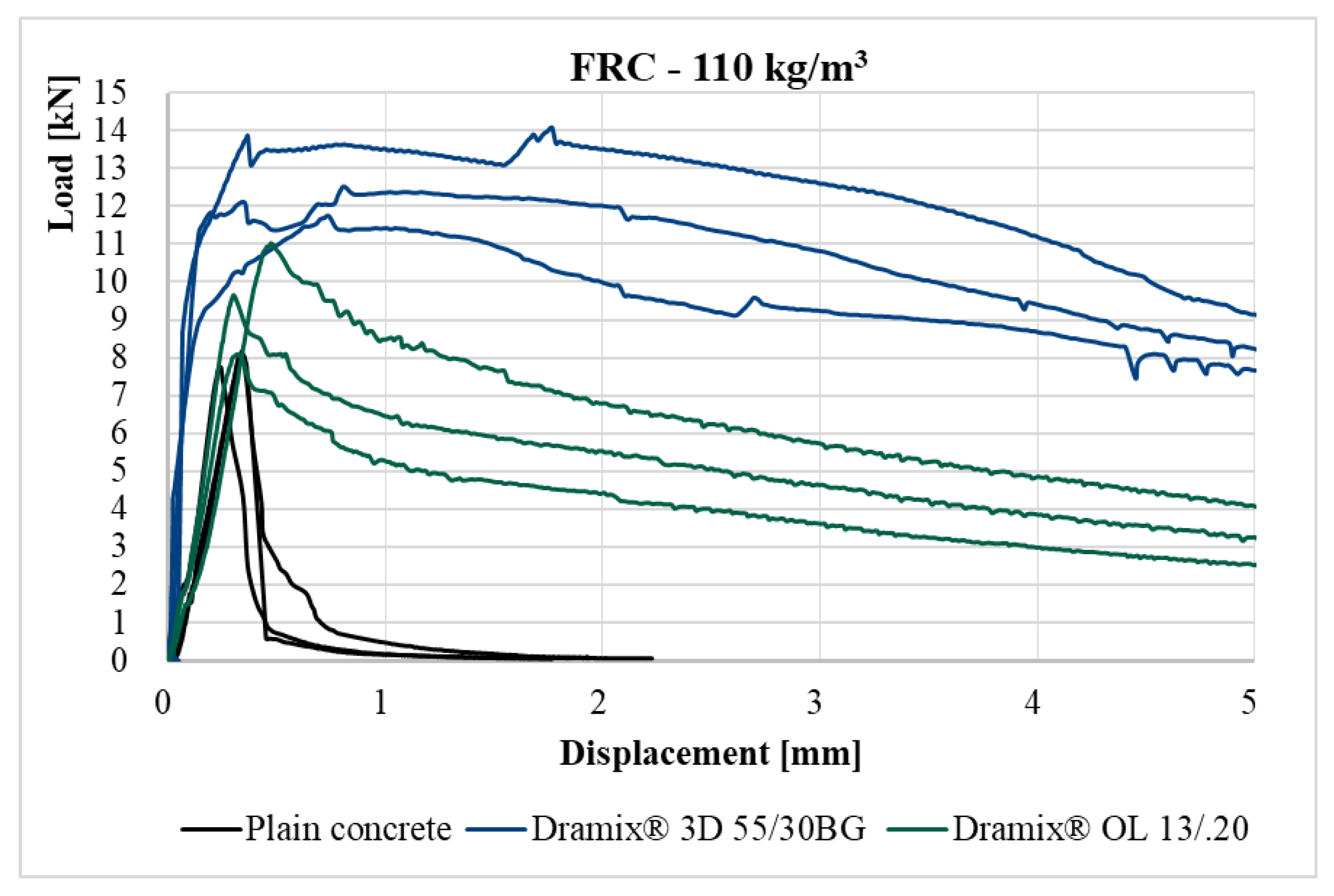
Figure 15 shows load–displacement diagrams for the fiber-reinforced concrete with a fiber dosage of 110 kg/m
3 and plain concrete. The most significant difference can again be observed from the curves for the fiber-reinforced concrete with hooked fibers. The first peak, where the crack is located, is not very pronounced. There is a transition to the second peak without the presence of tensile softening. This course of the curve is also typical of high-strength concrete with straight fibers, which are added to the concrete to reduce shrinkage cracks.
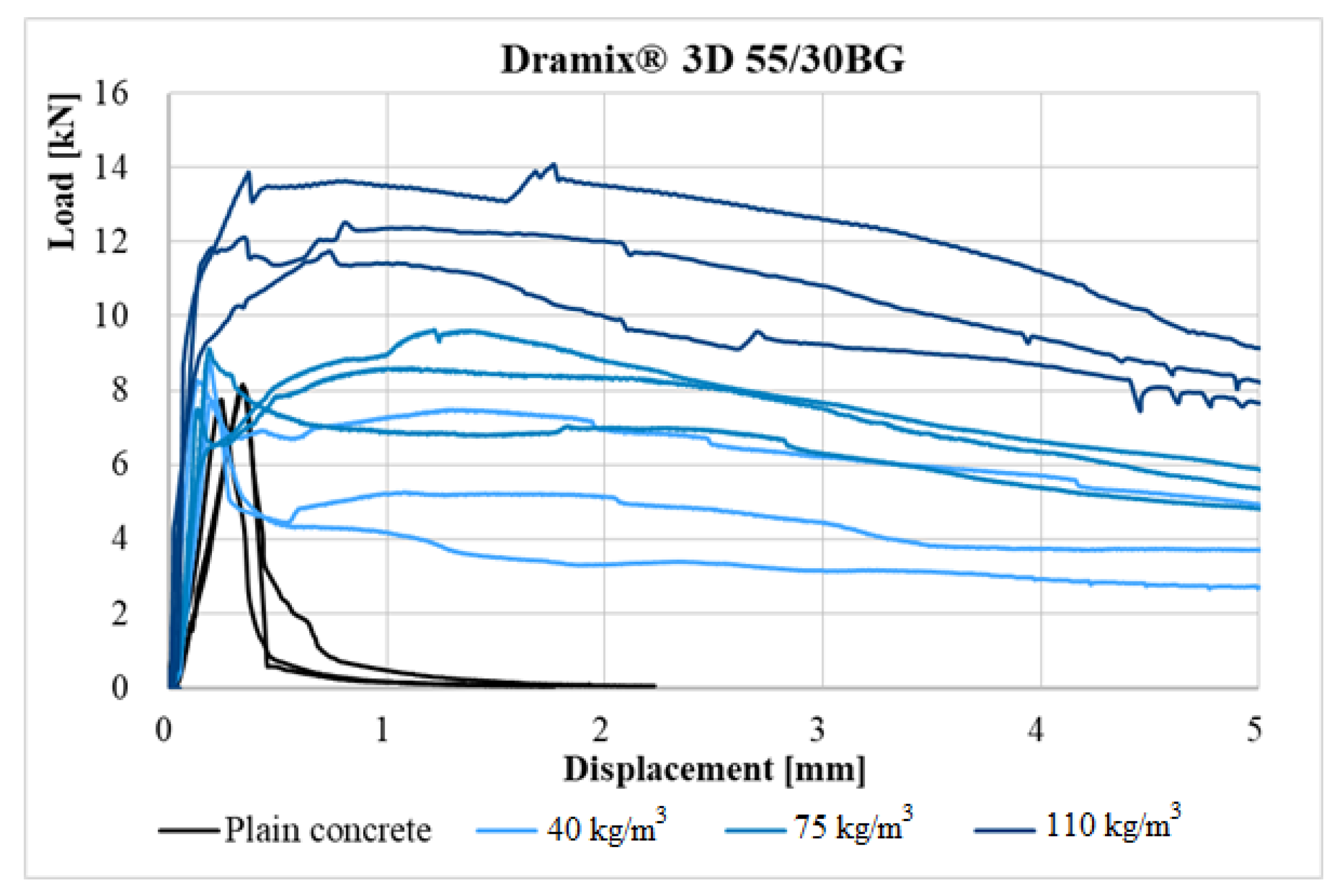
Figure 16 and
Figure 17 show the load–displacement diagrams for the plain concrete and fiber-reinforced concrete with hooked fibers and straight fibers, which differ in fiber dosage (40, 75, and 110 kg/m
3).
It can be seen from
Figure 16 and
Figure 17 that with an increasing fiber dosage, the tensile strength and residual tensile strength increase, but in comparison with fiber-reinforced concrete with hooked fibers, the increase is smaller for fiber-reinforced concrete with straight fibers.
Figure 16 shows that with increasing fibre dosage, a significant change in the shape of the load–displacement diagrams can be observed. For the case of dosages of 40 and 75 kg/m
3, two sharp peaks occur (the first peak is crack location, and the second peak is maximum fiber activation). Between the start of loading and the first peak, only the concrete matrix cracks. After the crossing of the first peak, tensile softening occurs, when the fibers are still not fully activated. Tensile hardening continues to occur when the fibers are fully activated, which prevents further displacement until the second peak. After this peak, tensile softening occurs again, where the fibers break or are ripped out of the matrix. For the case of a dosage of 110 kg/m
3, the transition from the first peak to the second peak is smooth, and only tensile hardening occurs. The smooth transition is due to the greater dosage and cohesiveness between the fibers and the matrix. First, matrix cracks occur, and then, the fibers are rapidly activated.
Additionally, the effect of straight fibers was verified, as shown in
Figure 17, which suggests that the fibers mainly prevent shrinkage cracks and do not have a big influence on the bearing capacity of the element/tensile strength. The residual strength of the fiber-reinforced concrete with straight fibers is small compared with that of the fiber-reinforced concrete with hooked fibers, and there is no second peak in the diagram. In this case, only tensile softening of the fiber-reinforced concrete occurs.
The average fracture energies corresponding to 5 mm displacement were also evaluated. The values are shown in
Table 4. The table shows an increase in fracture energy with increasing fiber dosage in the concrete. For the fiber-reinforced concrete with hooked fibers, the increase is much more significant. When comparing the fracture energy of the fiber-reinforced concrete with hooked fibers, the increase between values of individual fiber dosages is an average of 49%. In the case of the fiber-reinforced concrete with straight fibers, the increase in the fracture energy between individual dosage values is an average of 23%.
7. Determination of Shear Resistance of a Reinforced Concrete Beam without Shear Reinforcement
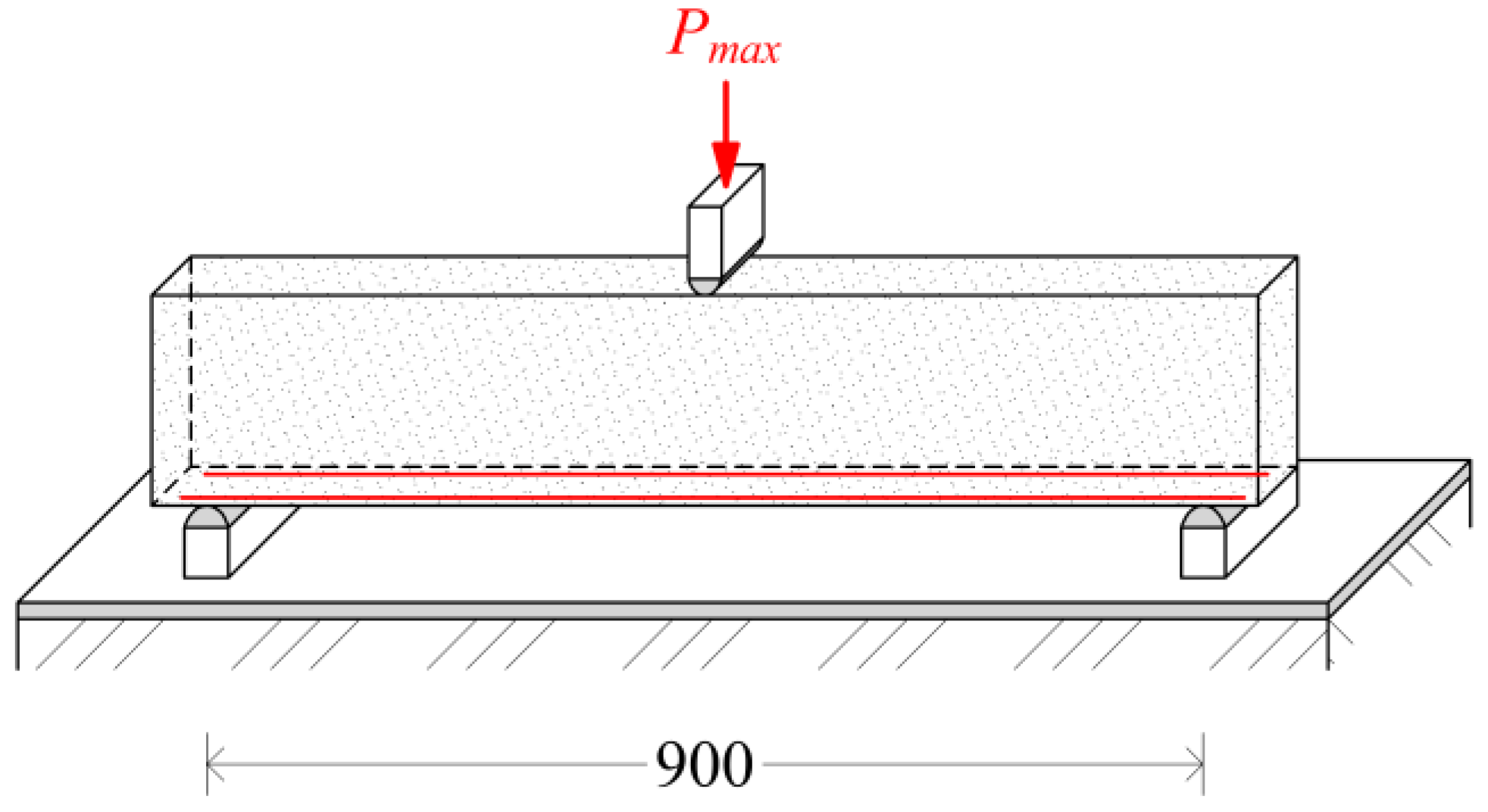
Based on laboratory tests for the structural verification of shear resistance, fiber-reinforced concrete with hooked fibers (Dramix
® 3D 55/30 BG) was selected. The structural element was a reinforced concrete beam without shear reinforcement with dimensions of 190 mm × 100 mm × 1000 mm. This test was performed using a three-point bending test. The beam was provided with a reinforcement of 10 mm in diameter at the bottom surface. The coverage of the reinforcement was 20 mm. The test scheme of the beam is shown in
Figure 18.
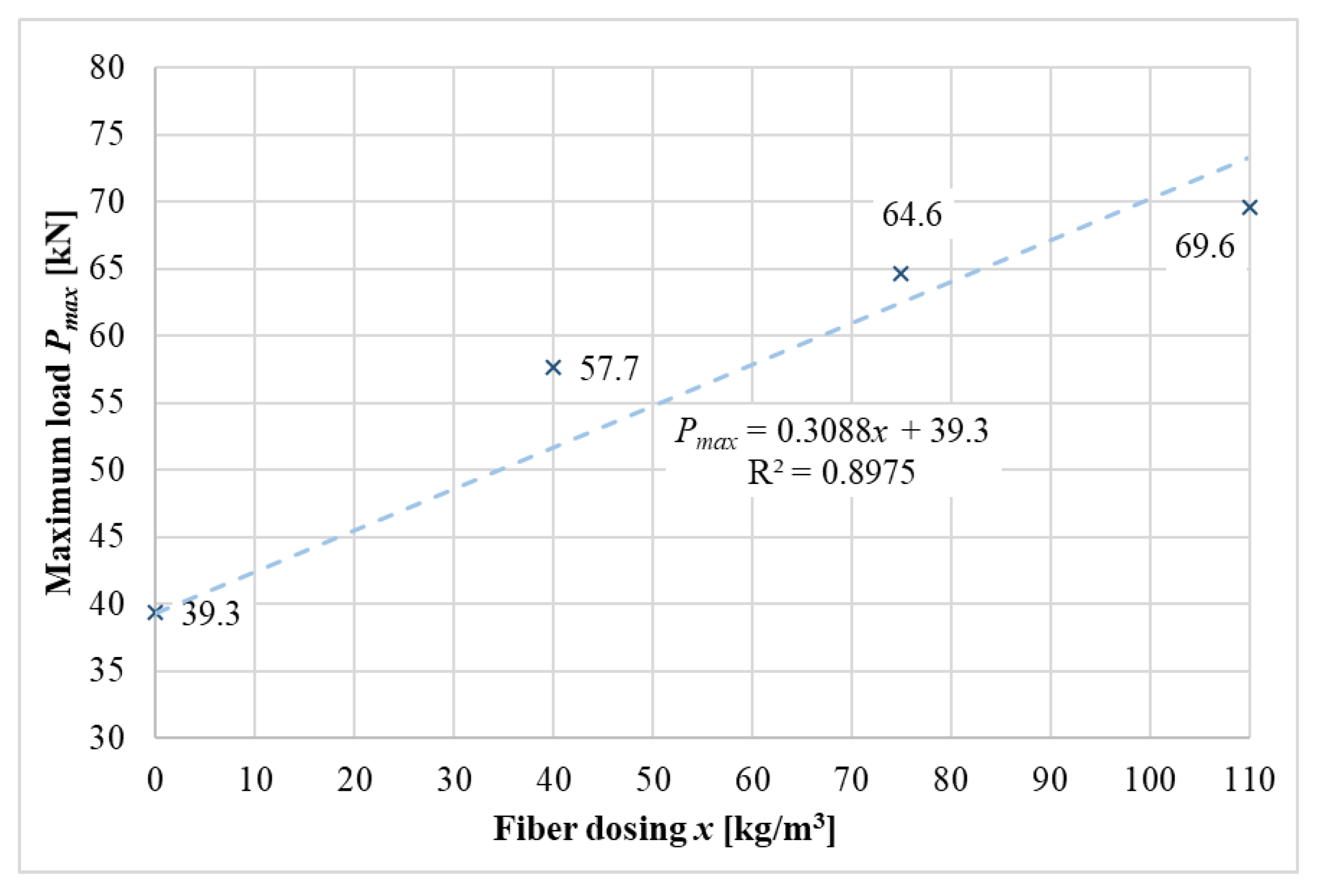
Using regression analysis (
Figure 19), the dependence of the maximum load
Pmax (at which the rays failed) on the fiber dosage was determined. It is possible to observe a gradual increase in the maximum load at which the failure occurred with increasing fiber dosage. Intermediate load values at which the failure occurred can be determined according to Equation (7). The model also shows very good data agreement, which is about 90%. The maximum achieved load for the plain concrete was 39.3 kN. Compared with the fiber-reinforced concrete, the maximum load increased by 47% (57.7 kN) for a fiber dosage of 40 kg/m
3, by 64% (64.6 kN) for a fiber dosage of 75 kg/m
3, and by 77% (69.6 kN) for a fiber dosage of 110 kg/m
3. The functional dependence of the maximal load
Pmax on the fiber dosage
x can be expressed according to the following relation:
where
x is fiber dosage. On the basis of the coefficient of determination, R
2, the dependence of the resistance of the fiber-reinforced concrete (maximum load
Pmax) on the fiber dosage
x can be considered very significant. Linear regression models fit the initial values (
Pmax) of the plain concrete.
In
Figure 20, it is possible to see the beams after a three-point bending test with a shear crack. The detail of the shear failure is shown in
Figure 21. In all the fiber dosing cases, the nature of the failure was the same. It was a diagonal crack that widened from the lower edge to the upper edge of the beam during the three-point bending test.
8. Discussion
The positive effect of both types of fibers was confirmed by the evaluation of the compressive strength, which increased by up to 21% for the fiber-reinforced concrete with hooked fibers and up to 27% for the fiber-reinforced concrete with straight fibers. A more significant increase in compressive strength was observed for the fiber-reinforced concrete with straight fibers. On the other hand, a larger standard deviation for the compressive strength was found. As for straight fibers, it should be noted that their optimal use is in high-strength concrete, in which better cohesion between the fibers and concrete is ensured. Tensile tests allowed for more detailed comparisons. In the case of straight fibers, differences in the increase in splitting tensile strength and bending tensile strength were small for higher fiber dosages.
However, the standard deviation was greater for larger fiber dosages. The standard deviations of the compressive strength and tensile strength for the fiber-reinforced concrete with straight fibers were greater than those for the fiber-reinforced concrete with hooked fibers. Significant differences—an increase in the splitting tensile strength and bending tensile strength for higher fiber dosages—are evident for the fiber-reinforced concrete with hooked fibers. For all tensile tests, a regression function could be determined depending on the dosage, with a reliability minimum of 89%. For the 28-day compressive strength, the reliability of the regression function was 84%.
The verification of the homogeneity and spatial orientation of the fibers was an important area of this research. Splitting tensile tests were carried out for two variants: perpendicular to the filling direction and parallel to the filling direction. Control tests for the plain concrete showed the smallest differences between these tensile strengths. These small differences can be explained by the good compaction of the concrete layers. In the case of the fiber-reinforced concrete, the situation is further complicated:the homogeneity/fiber orientation must be taken into account when determining the splitting tensile strength. In the case of the splitting strength test perpendicular to the filling direction, the load was applied through the load roller to all the concrete layers that had formed in the samples as a result of the alternating placement of layers of concrete and compaction until the formwork was filled. When testing the splitting strength parallel to the filling direction, the load (load roller) during the test is situated in the place of the middle compacted layer of the concrete. Here, the influences of the size and shape of the fibers are introduced. In the case of the fiber-reinforced concrete with straight fibers, the maximum difference in the splitting tensile strength ratio was 1.2. The difference with plain concrete is small. Furthermore, a detailed visual study of the samples used confirmed that the fibers were spatially oriented in all directions. Greater differences were found for the fiber-reinforced concrete with hooked fibers. The maximum ratio of the splitting tensile strengths was as high as 1.6. With higher fiber dosages, the difference increased. A visual study of the damaged specimens also showed that when the fiber-reinforced concrete was compacted, fibers settled in the lower layers and were oriented horizontally. This particular problem can also be affected by the weight of the fibers.
Tests were also performed to determine the density. From the evaluated tests, a gradual increase in the density of the fiber-reinforced concrete relative to that of the plain concrete can be observed. The increase is due to the added fibers and also fiber dosing. The initial density of the plain concrete was 2434 kg/m3. The density of the fiber-reinforced concrete is a very specific property, where large deviations in the determination can occur. The density is affected by many factors, especially the processing of the concrete and compaction. In the case of a higher fiber dosage, thorough compaction cannot be achieved because of the fibers. The rate of compaction also depends on the percentage of coarse aggregate contained in the concrete. In the case of a higher fiber dosage, it is more appropriate to modify the concrete recipe so that better workability of the concrete is achieved. The resulting density is also affected by the storage of the samples, i.e., the density of the natural storage, the density of the dried sample, the density of the sample stored in water, and the density of the fresh concrete mixture. The values of the stated the densities can vary by up to several percent.
A comparison of the 3-day compressive strength and 28-day compressive strength for fiber-reinforced concrete was also performed. In the case of the fiber-reinforced concrete with hooked fibers, the 3-day compressive strength was as high as 69% of the 28-day compressive strength, and for the fiber-reinforced concrete with straight fibers, it was as high as 78% of the 28-day compressive strength.
For a more detailed evaluation of the mechanical properties of fiber-reinforced concrete, bending tests are important. These tests also allow the post-peak behavior of fiber-reinforced concrete to be monitored. These are mainly residual tensile strength or fracture energy calculations. The resulting differences are very well distinguishable for different fiber dosages. In the case of straight fibers, the fracture energy increased significantly compared with the tensile strength. However, because of the poor cohesion of the concrete with the fibers, there was no tensile hardening. The load–displacement diagrams for the fiber-reinforced concrete with straight fibers were characterized by exponential curves. In the case of the fiber-reinforced concrete with hooked fibers and fiber dosages starting from 75 kg/m3, there was also tensile hardening, and there were two peaks in the load–displacement diagram. For both types of fibers, all the specimens were compact after the test, even if they were considerably damaged (respectively deformed).
The shear resistance of the reinforced concrete beams with hooked fibers without shear reinforcement was also verified. Compared with plain concrete, there was a significant increase in shear resistance, and at a fiber dosage of 40 kg/m3, there was an increase of 47%.
9. Conclusions
This article deals with the determination of the mechanical properties of two types of fiber-reinforced concrete with different fibers. These are hooked fibers and straight fibers. In total, three test series of samples were made for each type of fiber-reinforced concrete, which differed in fiber dosage (40, 75, and 110 kg/m3). A series of plain concrete samples were also concreted and evaluated to determine the initial characteristics of the concrete. The laboratory tests also included the determination of the bending tensile strength and load–displacement diagrams. The splitting tensile strength (perpendicular to the filling direction) of the fiber-reinforced concrete with hooked fibers increased with an increase in the fiber dosage. In the case of the fiber-reinforced concrete with straight fibers, this strength did not increase at larger dosages; it remained unchanged. The uniformity of the distribution of the fibers in the test samples was also verified using the splitting tensile test. The uniformity of the fiber distribution was taken into account by the position of the sample, i.e., perpendicular and parallel to the filling direction. The splitting tensile strength perpendicular to the filling direction was, in some cases, as high as 1.5 times the splitting tensile strength parallel to the filling direction. The difference between these two strengths was larger with higher fiber dosages. The fiber-reinforced concrete with straight fibers allowed for the better spatial orientation of the fibers in the samples.
The results of the three-point bending test were also evaluated. From the load–displacement diagram, it is possible to determine the effect of different types of fibers (respectively dosage of fibers) on the resulting fracture energy and the shape of this diagram. In the case of hooked fibers, the increase in fracture energy was more pronounced: in some cases, it was as high as two times greater than that with straight fibers. The bending tensile strength increased with the dosage of hooked fibers. In the case of fiber-reinforced concrete with straight fibers, this strength did not show a significant increase.
The experimental testing also included a three-point bending test of a reinforced concrete beam without shear reinforcement and with hooked fibers to determine shear resistance. In the case of this test, the maximum load in the case of beam failure was monitored. By adding hooked fibers to the concrete, it was possible to increase the shear resistance by up to 77%.
The conclusions of the article are as follows:
Reinforced concrete with straight fibers shows a better spatial orientation of the fibers in the concrete.
The effect of fibers on the compressive strength is relatively small compared with that on the tensile strength.
The density of fiber-reinforced concrete increases relative to that of plain concrete.
To verify the homogeneity of the fiber-reinforced concrete, it is possible to use the splitting tensile test for the different directions of filling. The tensile strength is typically about 20% greater in the perpendicular direction to the filling direction than that in the parallel filling direction.
Fibers in concrete always positively influence the tensile strength.
For fiber-reinforced concrete with straight fibers, it is typical that with higher fiber dosages, the tensile strength increases very little, but the fracture energy significantly increases.
For fiber-reinforced concrete with hooked fibers, it is typical that with higher fiber dosages, the tensile strength increases, and the fracture energy also significantly increases. Hooked fibers also have a significant positive effect on shear resistance.