Ordering Phase Transition with Symmetry-Breaking from Disorder over Non-Equivalent Sites: Calorimetric and Crystallographic Study of Crystalline d-Sorbose
Abstract
1. Introduction
2. Materials and Methods
2.1. Material
2.2. Adiabatic Calorimetry
2.3. X-ray Crystallography
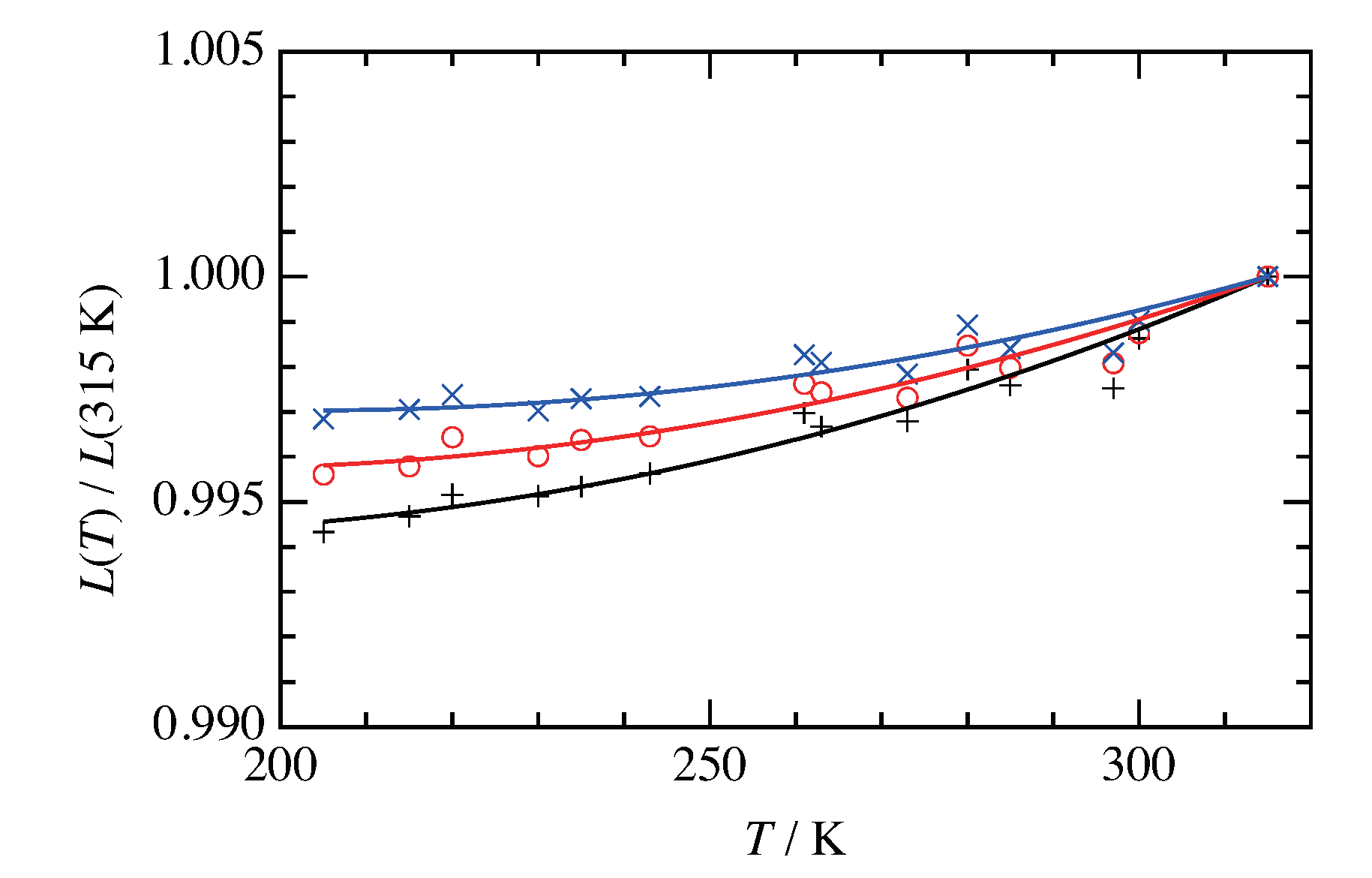
3. Results and Discussion
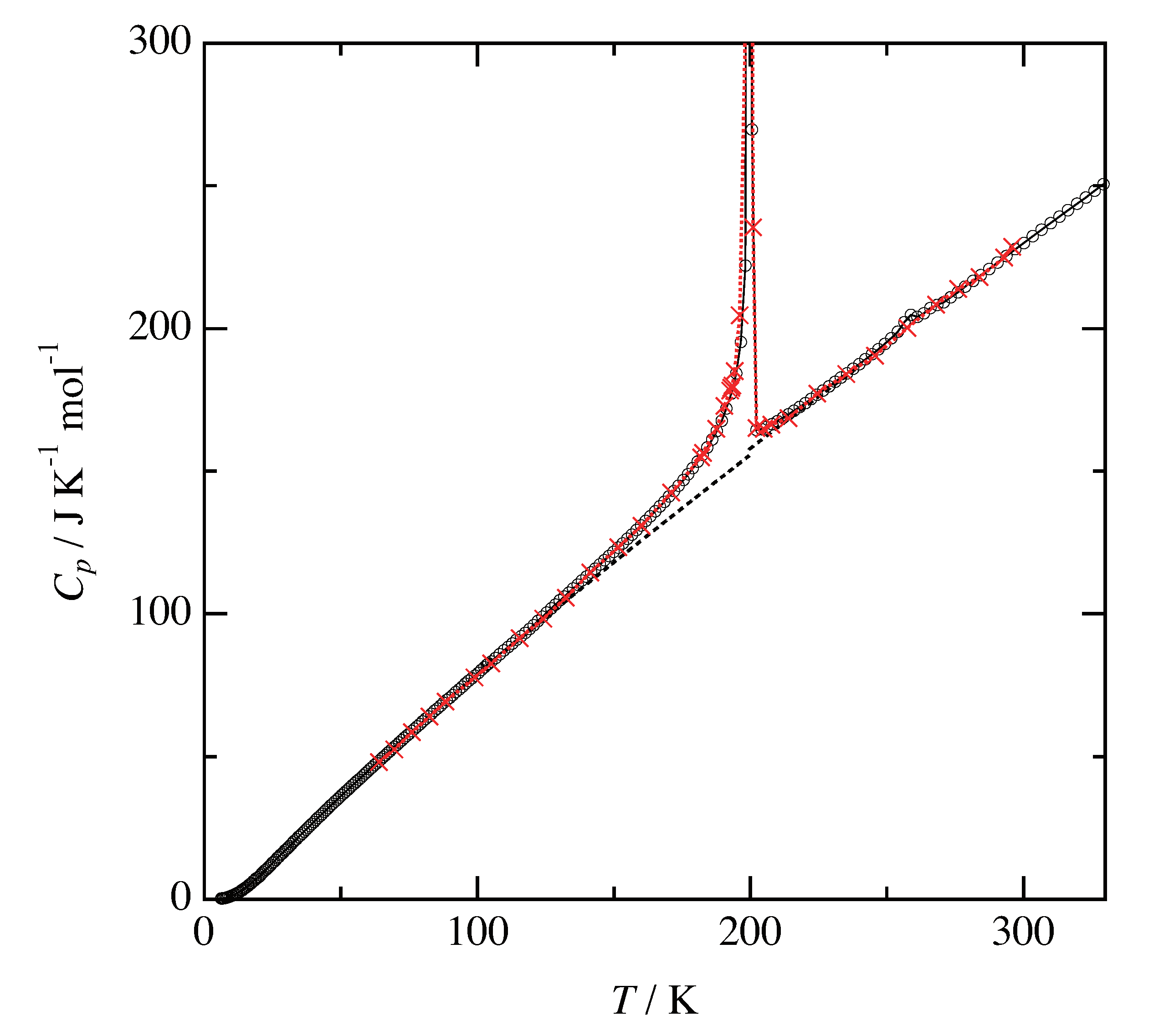
3.1. Heat Capacity and Phase Sequence
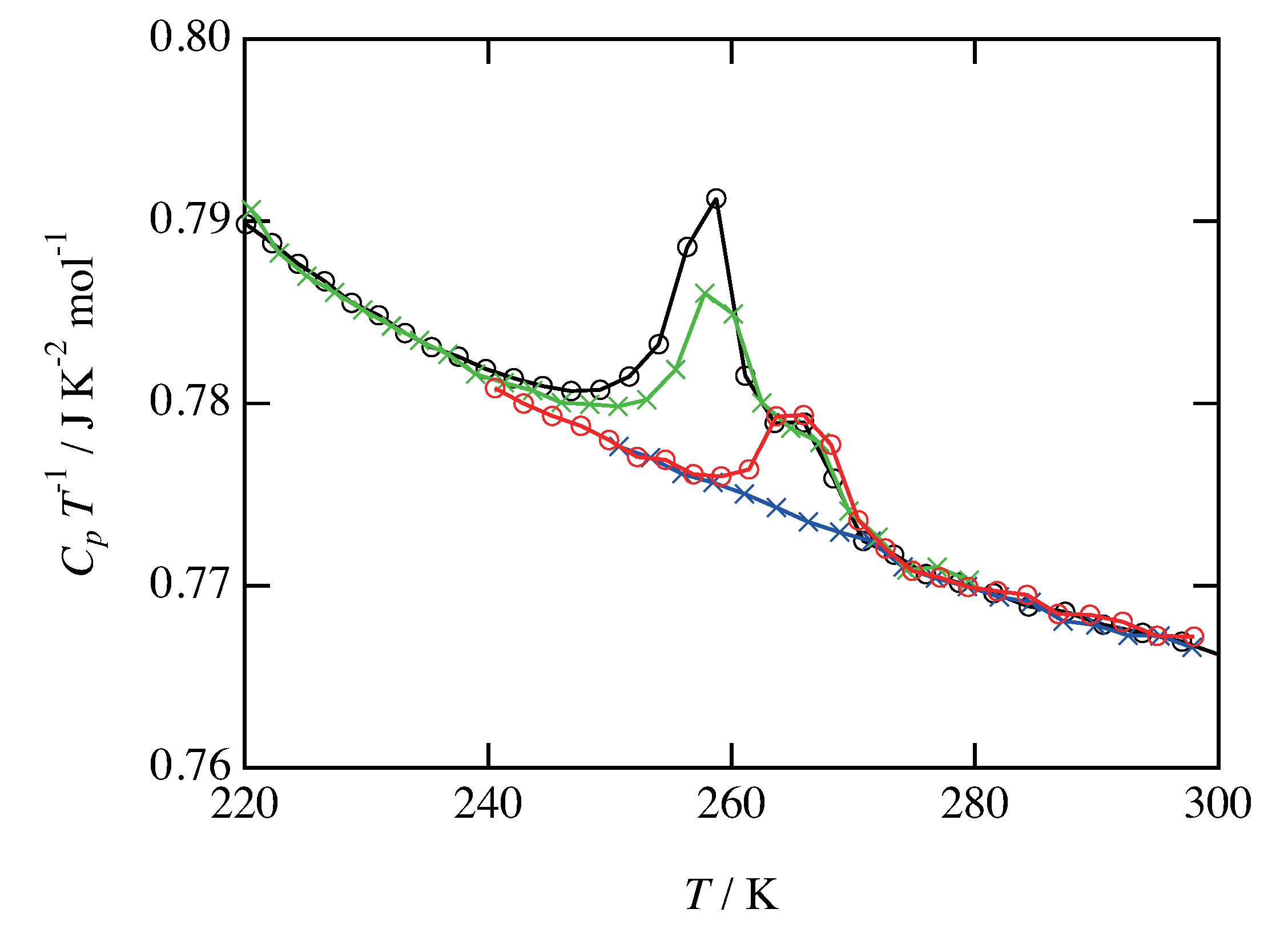
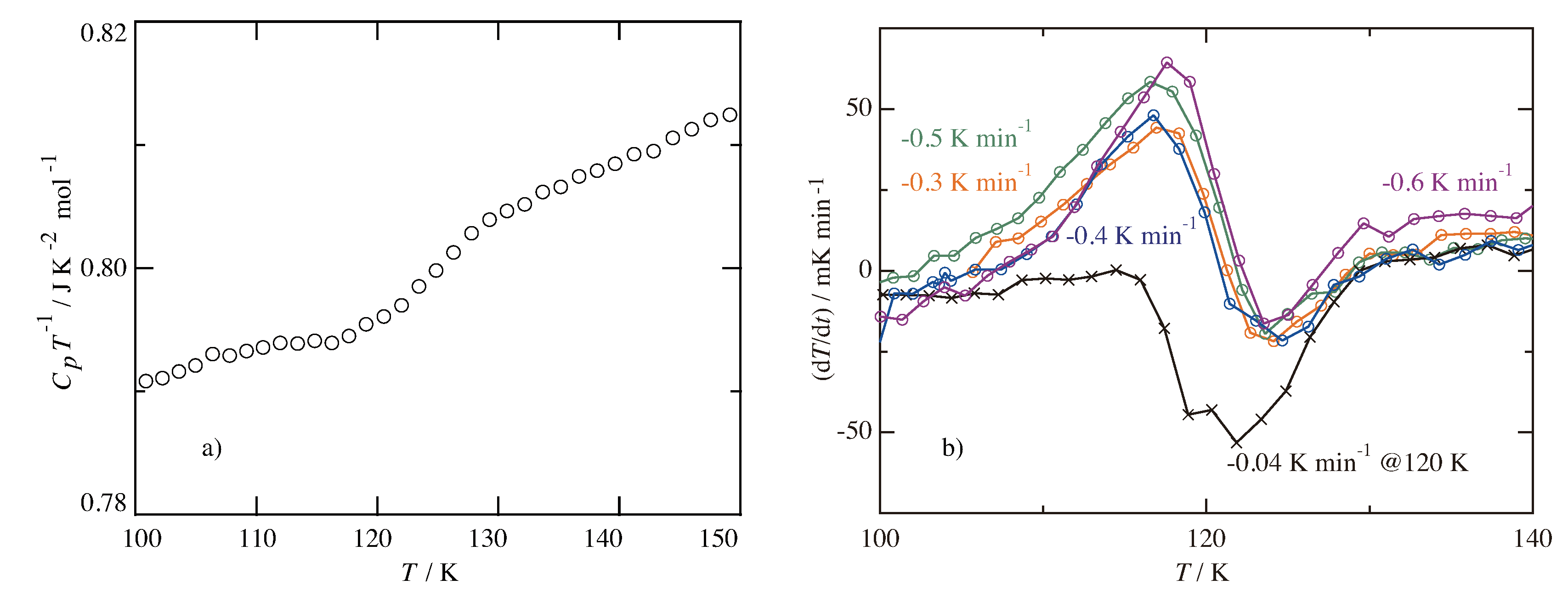
3.2. Glass Transition
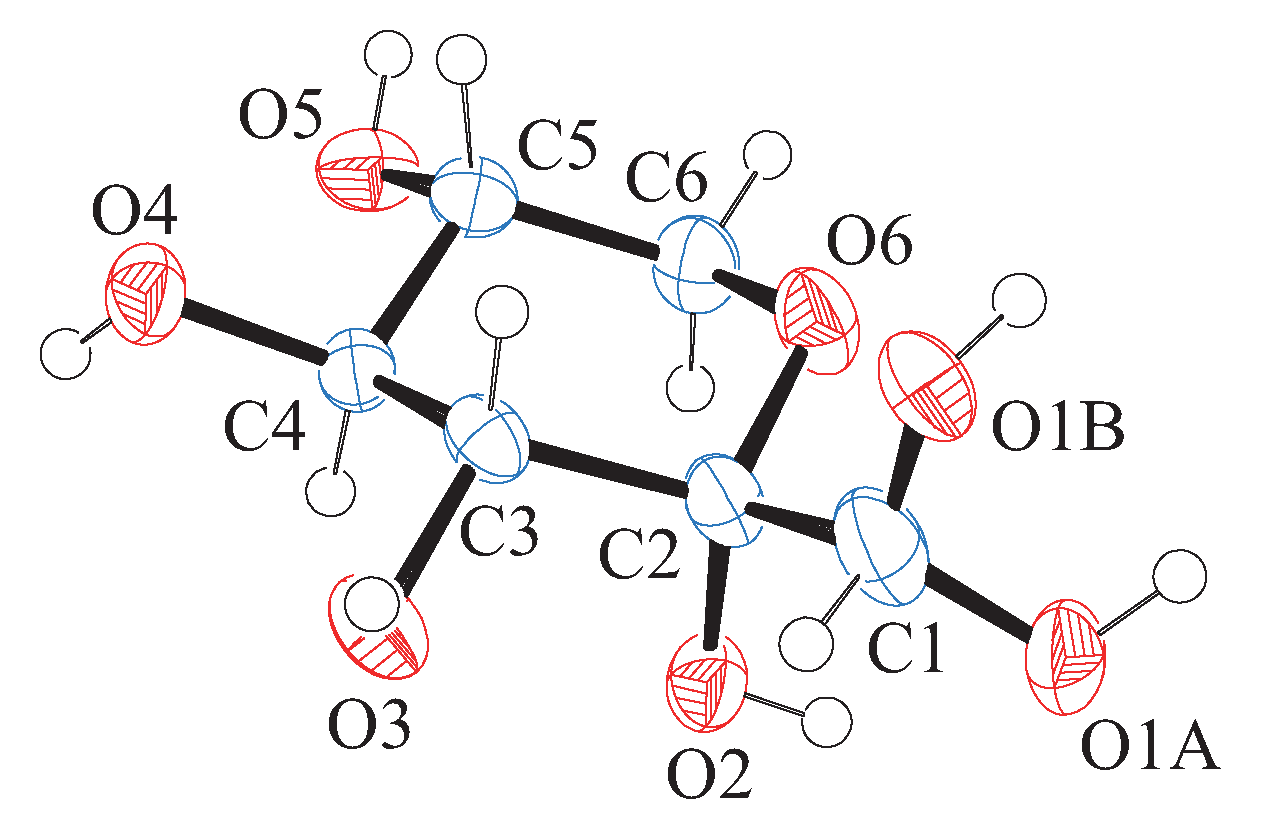
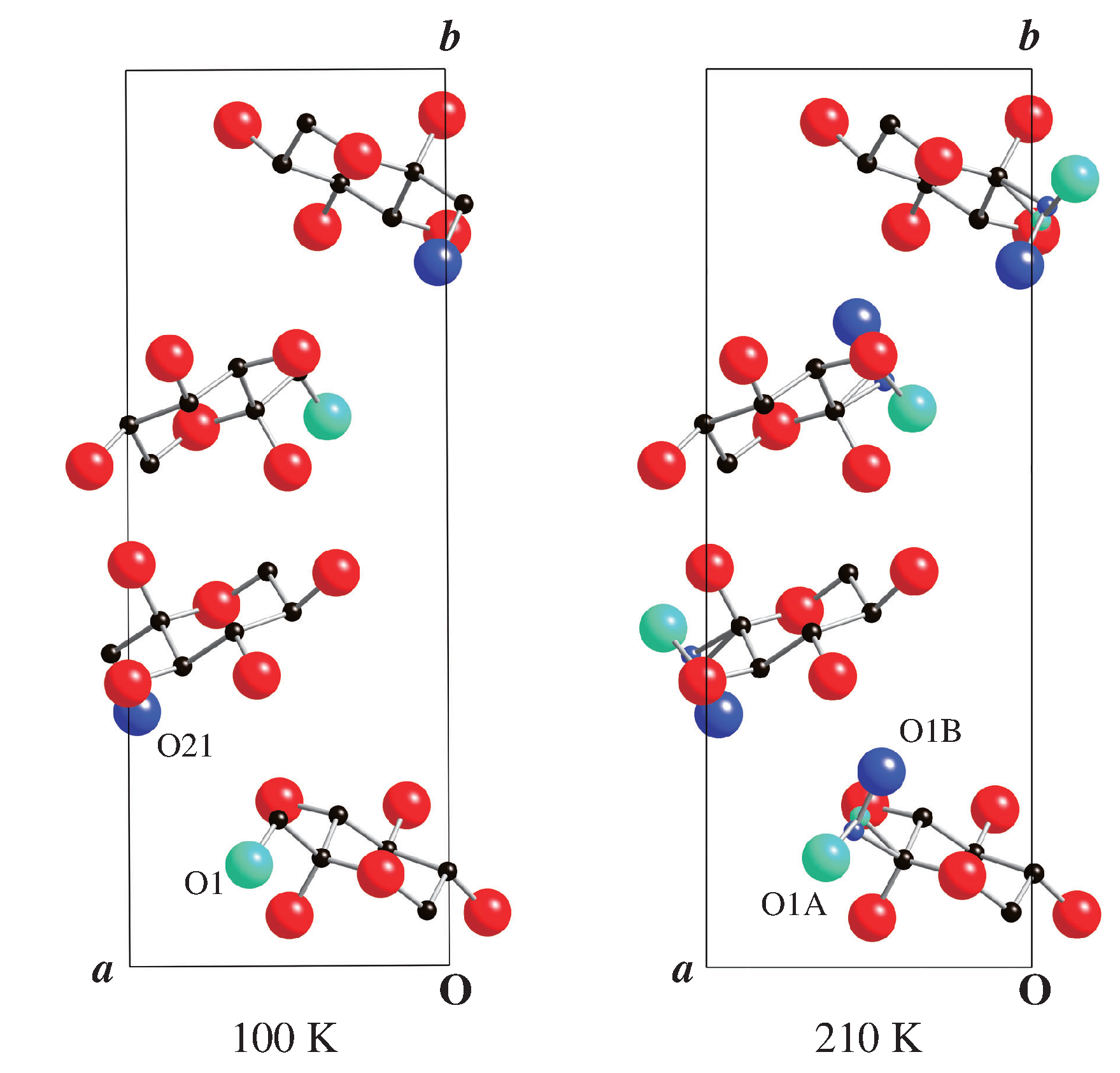
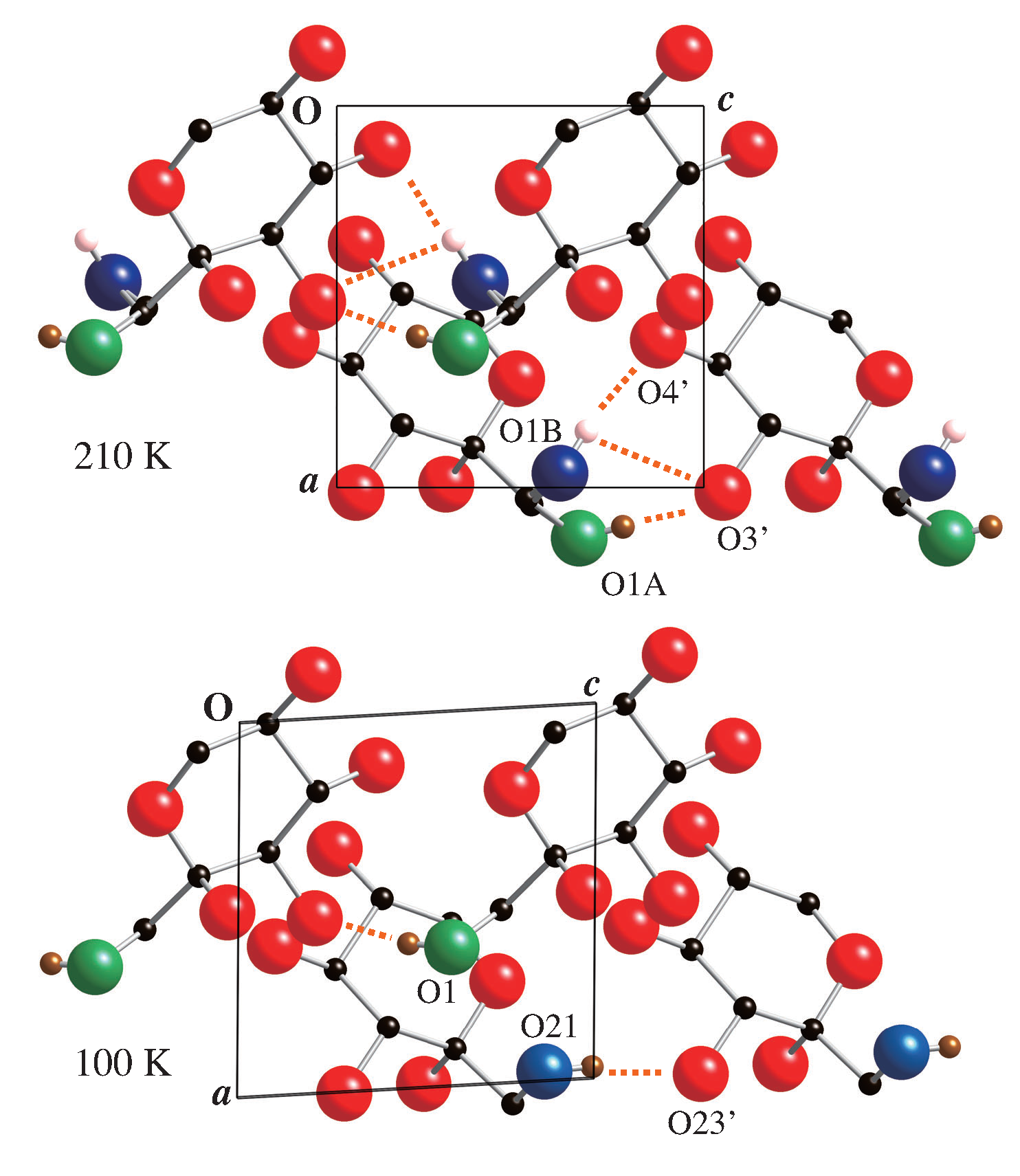
3.3. Structure of Room Temperature Phase
3.4. Structure of Low Temperature Phase
3.5. Symmetry Breaking in the Main Transition of Crystalline Sorbose
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Stanley, H.E. Introduction to Phase Transitions and Critical Phenomena; Oxford University Press: New York, NY, USA, 1987. [Google Scholar]
- Nishimori, H.; Ortiz, G. Elements of Phase Transitions and Critical Phenomena; Oxford University Press: New York, NY, USA, 2010. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 1980. [Google Scholar]
- Sherwood, J.N. Plastically Crystalline State: Orientationally-Disordered Crystals; John Wiley & Sons Ltd.: Chichester, UK, 1979. [Google Scholar]
- Nambu, Y.; Jona-Lasinio, G. Dynamical model of elementary particles based on an analogy with superconductivity. I. Phys. Rev. 1961, 122, 345–358. [Google Scholar] [CrossRef]
- Nakazawa, Y.; Tamura, M.; Shirakawa, N.; Shiomi, D.; Takahashi, M.; Kinoshita, M.; Ishikawa, M. Low-temperature magnetic properties of the ferromagnetic organic radical, p-nitrophenyl nitronyl nitroxide. Phys. Rev. B 1992, 46, 8906–8914. [Google Scholar] [CrossRef] [PubMed]
- Jack, G.W.; Stegeman, G. The heat capacities and entropies of two monosaccharides. J. Am. Chem. Soc. 1941, 63, 2121–2123. [Google Scholar] [CrossRef]
- Kim, S.H.; Rosenstein, R.D. The crystal structure of α-L-sorbose. Acta Cryst. 1967, 22, 648–656. [Google Scholar] [CrossRef] [PubMed]
- Nordenson, S.; Takagi, S.; Jefferey, G.A. α-L-Sorbopyranose: A neutron diffraction refinement. Acta Cryst. B 1979, 35, 1005–1007. [Google Scholar] [CrossRef]
- Boerio-Goates, J. Heat-capacity measurements and thermodynamic functions of crystalline α-D-glucose at temperatures from 10 K to 340 K. J. Chem. Thermodyn. 1991, 23, 403–409. [Google Scholar] [CrossRef]
- Yamamura, Y.; Iwagaki, S.; Hishida, M.; Nagatomo, S.; Fukada, K.; Saito, K. Heat capacity and standard thermodynamic functions of three ketohexoses in monosaccharides including rare sugars: d-fructose, d-psicose, and d-tagatose. J. Chem. Thermodyn. 2019, 131, 420–430. [Google Scholar] [CrossRef]
- Izumori, K. Bioproduction strategies for rare hexose sugars. Naturwissenschaften 2002, 89, 120–124. [Google Scholar] [CrossRef]
- Granström, T.B.; Takata, G.; Tokuda, M.; Izumori, K. Izumoring: A novel and complete strategy for bioproduction of rare sugars. J. Biosci. Bioeng. 2004, 97, 89–94. [Google Scholar] [CrossRef]
- Izumori, K. Izumoring: A strategy for bioproduction of all hexoses. J. Biotechnol. 2006, 124, 717–722. [Google Scholar] [CrossRef]
- Yamamura, Y.; Saito, K.; Saitoh, H.; Matsuyama, H.; Kikuchi, K.; Ikemoto, I. Heat capacity measurements and phase transition of crystalline 4,4″-difluoro-p-terphenyl. J. Phys. Chem. Solids 1995, 56, 107–115. [Google Scholar] [CrossRef]
- Preston-Thomas, H. The International Temperature Scale of 1990 (ITS-90). Metrologia 1990, 27, 3–10. [Google Scholar] [CrossRef]
- SAINT Version 8.34A 2013; Bruker AXS: Madison, WI, USA, 2013.
- Sheldrick, G.M. SADABS; University of Göttingen: Göttingen, Germany, 1996. [Google Scholar]
- Sheldrick, G.M. TWINABS 2012/1; Bruker: Madison, WI, USA, 2012. [Google Scholar]
- Sheldrick, G.M. SHELXS-97. Acta Cryst. A 2008, 64, 112–122. [Google Scholar] [CrossRef] [PubMed]
- Sheldrick, G.M. SHELXL-2014. Acta Cryst. C 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Deposition Numbers 1990266 (at 295 K), 1990267 (at 210 K), and 1990268 (at 100 K), Copies of the Data Can Be Obtained Free of Charge. Available online: https://www.ccdc.cam.ac.uk/structures/ (accessed on 24 April 2020).
- Suga, H.; Seki, S. Thermodynamic investigation on glassy states of pure simple compounds. J. Non-Cryst. Solids 1974, 16, 171–194. [Google Scholar] [CrossRef]
- Stokes, H.T.; Hatck, D.M. Isotropy Subgroups of the 230 Crystallographic Space Groups; World Scientific: Singapore, 1988. [Google Scholar]
- Alexander, S.; McTague, J. Should all crystals be bcc? Landau theory of solidification and crystal nucleation. Phys. Rev. Lett. 1978, 41, 702–705. [Google Scholar] [CrossRef]
- Saito, K.; Yamamura, Y.; Kutsumizu, S. Possible formation of multicontinuous structures by rodlike particles. J. Phys. Soc. Jpn. 2008, 77, 093601. [Google Scholar] [CrossRef]
- Onodera, Y. Dynamic susceptibility of classical anharmonic oscillator: A unified oscillator model for order-disorder and displacive ferroelectrics. Prog. Theor. Phys. 1970, 44, 1477–1499. [Google Scholar] [CrossRef]
- Saito, K.; Yamamura, Y.; Saitoh, H.; Matsuyama, H.; Kikuchi, K.; Ikemoto, I. Phase transition associated with molecular twisting in crystalline 4,4″-difluoro-p-terphenyl: Displacive or order-disorder transition? Solid State Commun. 1993, 87, 903–906. [Google Scholar] [CrossRef]
- Saito, K.; Yamamura, Y.; Saitoh, H.; Matsuyama, H.; Kikuchi, K.; Ikemoto, I. Phase transition in crystalline p-polyphenyls: Heat capacity of 4,4‴-difluoro-p-quaterphenyl. Solid State Commun. 1994, 92, 495–499. [Google Scholar] [CrossRef]
- Yamamura, Y.; Saito, K.; Ikemoto, I.; Sorai, M. Entropic evidence of the order-disorder nature of the phase transition in p-terphenyl crystal. J. Phys. Cond. Matter 1998, 10, 3359–3366. [Google Scholar] [CrossRef]
- Yamamura, Y.; Saito, K.; Sorai, M.; Ikemoto, I. Disappearance of a displacive phase transition in crystalline biphenyl by a small amount of impurity. J. Phys. Soc. Jpn. 1998, 67, 1649–1654. [Google Scholar] [CrossRef]
- Yamamura, Y.; Saitoh, H.; Sumita, M.; Saito, K. One-dimensional correlation in the dipolar Ising crystal tricyclohexylmethanol: Crystal structure revisited and heat capacity. J. Phys. Cond. Matter 2007, 19, 176219. [Google Scholar] [CrossRef]
- Saito, K.; Ikeda, T.; Yamamura, Y.; Saitoh, H.; Hishida, M.; Kobayashi, Y.; Fujita, T.; Ichikawa, J. Cell-quintupling: Structural phase transition in a molecular crystal, bis(trans-4–butylcyclohexyl)methanol. J. Chem. Phys. 2017, 146, 074503. [Google Scholar] [CrossRef] [PubMed]

| (K) | |||
| Order of transition | 1 | 1 | 1 |
| (J mol) | |||
| (J K mol) | |||
| Note | main transition |
| Empirical formula | CHO | |||
| Formula weight | 180.16 | |||
| Molecular form | d | d | d | l |
| Radiation | X-ray | X-ray | X-ray | neutron |
| T (K) | 100 | 210 | 295 | RT [9] |
| Crystal system | monoclinic | orthorhombic | orthorhombic | orthorhombic |
| Space group | P | P | P | P |
| a (Å) | 6.4999 (7) | 6.5258 (2) | 6.5372 (1) | 6.545 (2) |
| b (Å) | 18.1977 (20) | 18.0150 (6) | 18.0528 (3) | 18.062 (7) |
| c (Å) | 6.1935 (7) | 6.2922 (2) | 6.3059 (1) | 6.310 (2) |
| () | 93.562 (5) | 90 | 90 | 90 |
| V (Å) | 731.18 (14) | 739.73 (4) | 744.19 (2) | 745.94 |
| Z | 4 | 4 | 4 | 4 |
| 0.0279 | 0.0286 | 0.0302 | 0.044 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iwagaki, S.; Kakuta, H.; Yamamura, Y.; Saitoh, H.; Hishida, M.; Fukada, K.; Saito, K. Ordering Phase Transition with Symmetry-Breaking from Disorder over Non-Equivalent Sites: Calorimetric and Crystallographic Study of Crystalline d-Sorbose. Crystals 2020, 10, 361. https://doi.org/10.3390/cryst10050361
Iwagaki S, Kakuta H, Yamamura Y, Saitoh H, Hishida M, Fukada K, Saito K. Ordering Phase Transition with Symmetry-Breaking from Disorder over Non-Equivalent Sites: Calorimetric and Crystallographic Study of Crystalline d-Sorbose. Crystals. 2020; 10(5):361. https://doi.org/10.3390/cryst10050361
Chicago/Turabian StyleIwagaki, Sakiko, Hiroki Kakuta, Yasuhisa Yamamura, Hideki Saitoh, Mafumi Hishida, Kazuhiro Fukada, and Kazuya Saito. 2020. "Ordering Phase Transition with Symmetry-Breaking from Disorder over Non-Equivalent Sites: Calorimetric and Crystallographic Study of Crystalline d-Sorbose" Crystals 10, no. 5: 361. https://doi.org/10.3390/cryst10050361
APA StyleIwagaki, S., Kakuta, H., Yamamura, Y., Saitoh, H., Hishida, M., Fukada, K., & Saito, K. (2020). Ordering Phase Transition with Symmetry-Breaking from Disorder over Non-Equivalent Sites: Calorimetric and Crystallographic Study of Crystalline d-Sorbose. Crystals, 10(5), 361. https://doi.org/10.3390/cryst10050361






