Mechanisms-Based Transitional Viscoplasticity
Abstract
1. Introduction
2. Mechanism of Plastic Flow
3. Thermal Activation
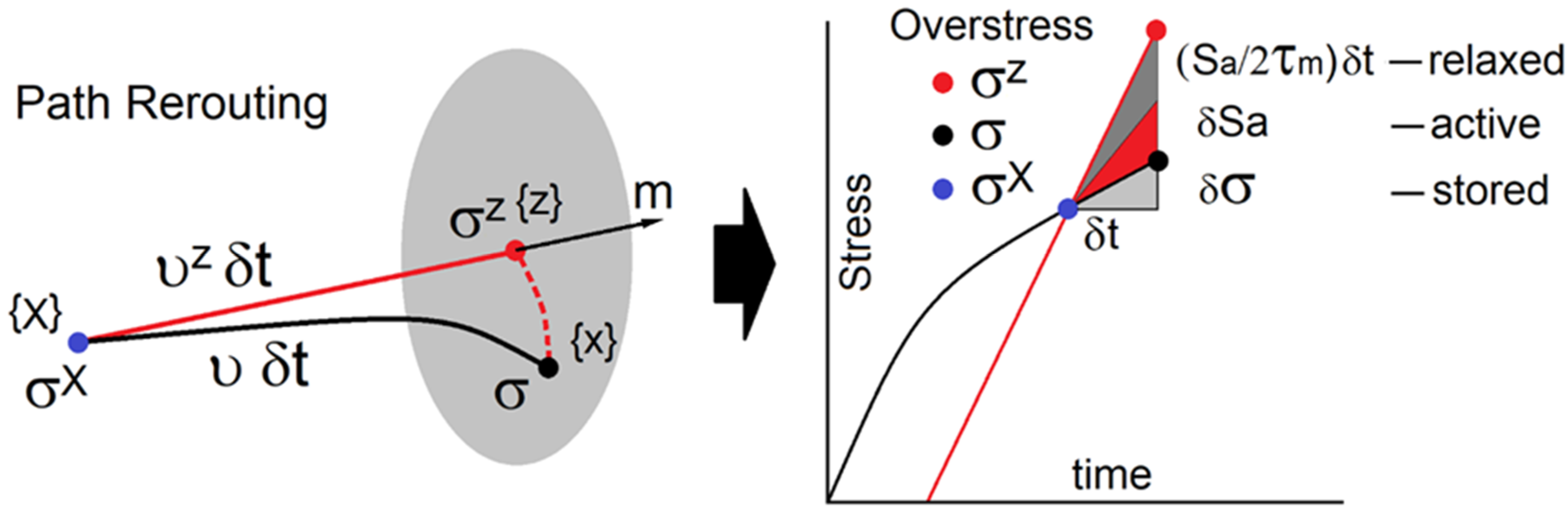
4. Rerouting of Plastic Flow and Consequences
5. Dynamic Overstress
6. Plasticity-Induced Heating
7. Hall–Petch Relation
7.1. Energy-Based Hall–Petch Relation
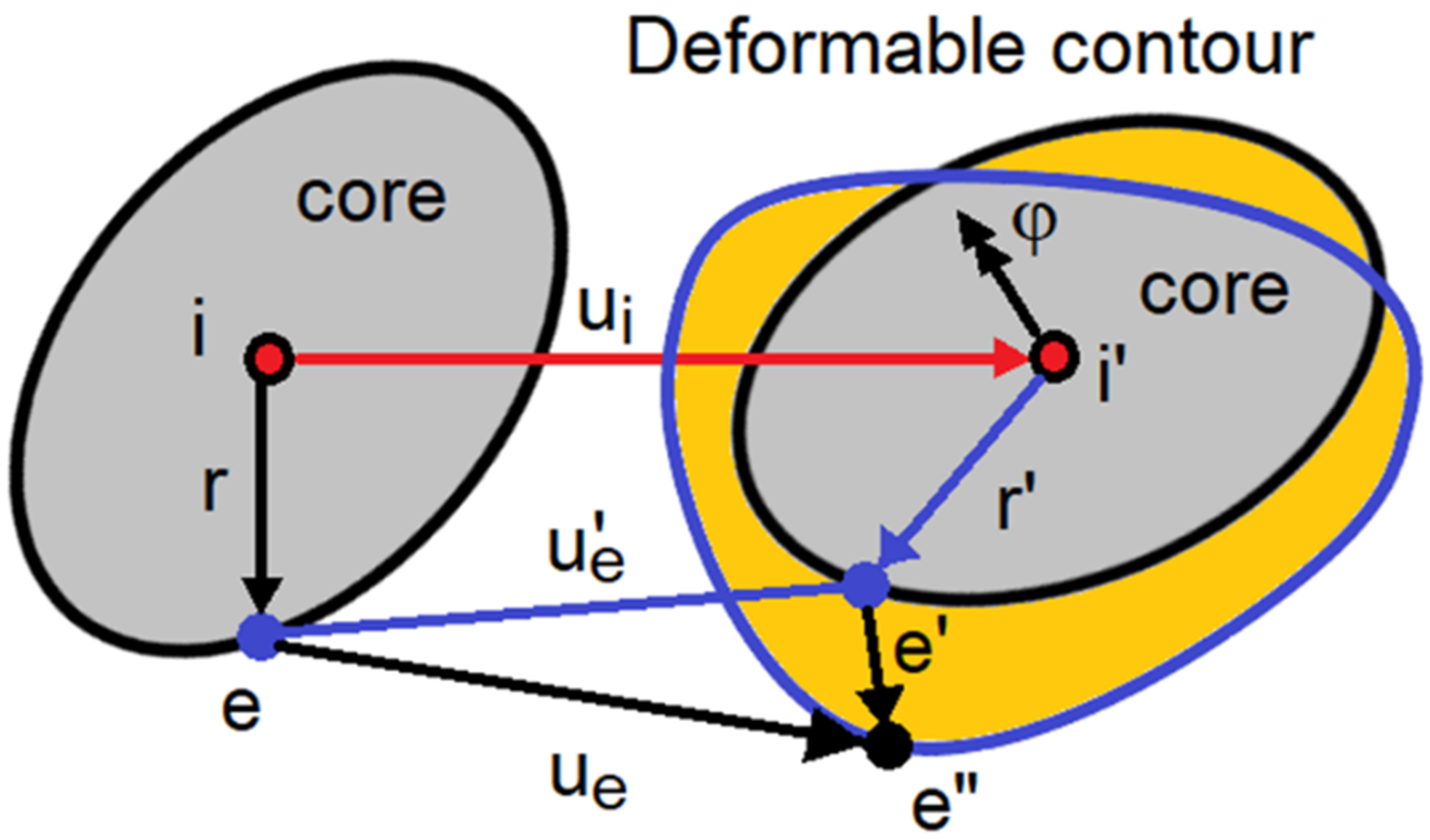
7.2. Kinematics-Based Construction of Hall–Petch Relation
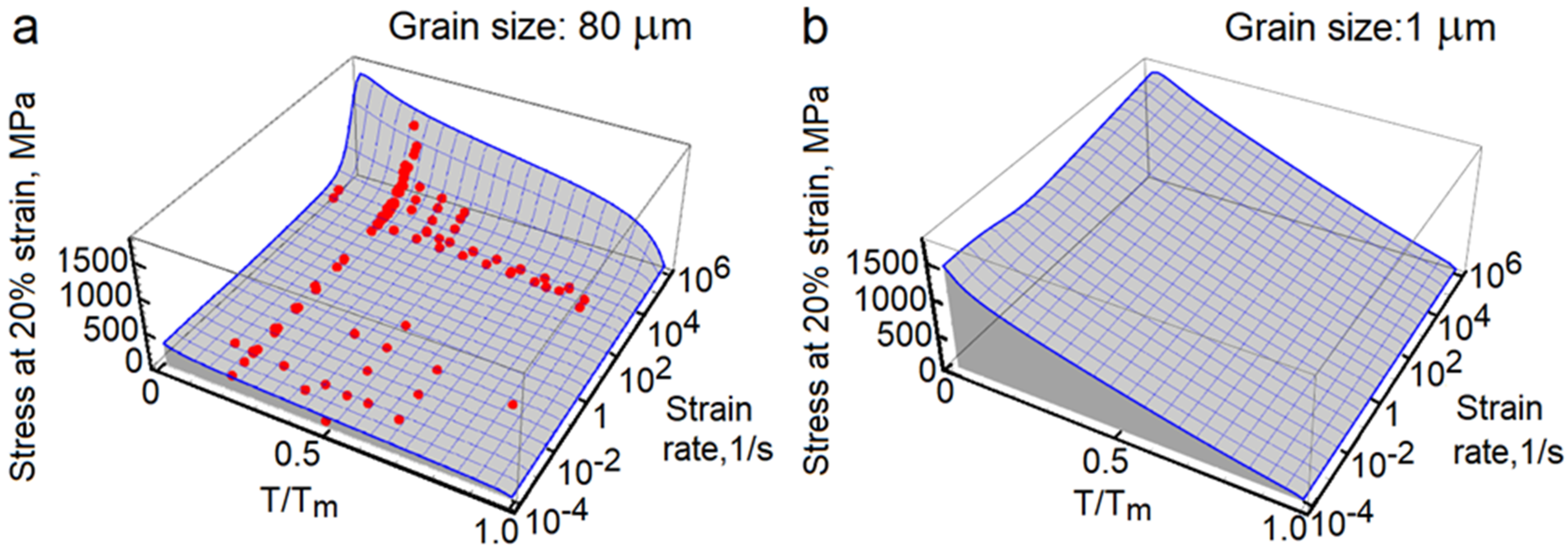
8. Transitional Viscoplasticity
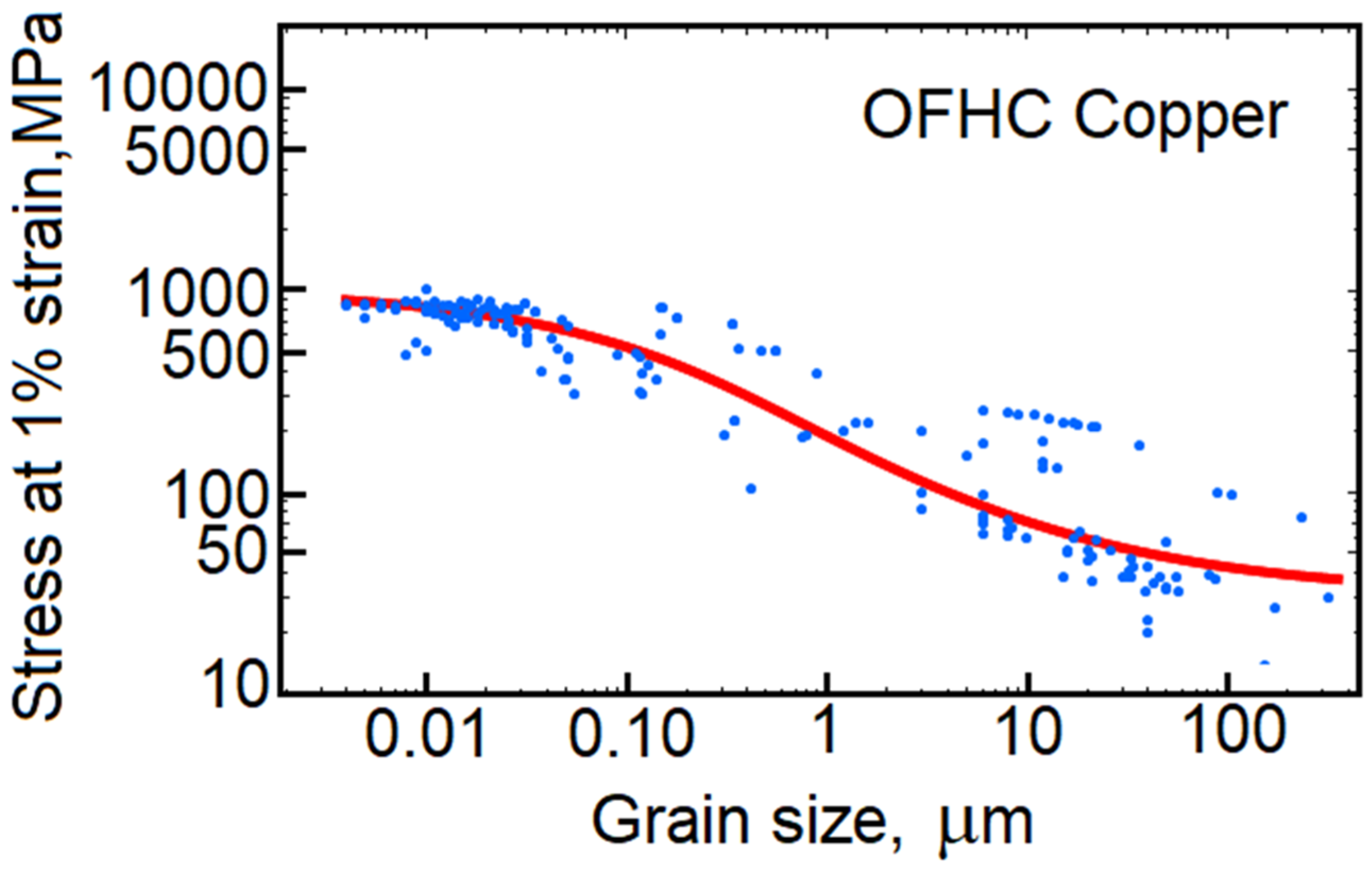
9. OFHC Copper
10. Plate Impact Problem
11. Conclusions
- The macroscopic plastic flow results from plastic slippages and slip reorganizations. The description is constructed on the basis of the tensor representation concept. It is my conviction that tensor representations derived for generic dyads represent useful tools in the hands of a modeler.
- In the proposed model, thermally activated processes are considered stochastic. The concept explains the transition of flow mechanisms from power-law creep to high strain rate dislocation glide.
- The proposed description of plasticity-induced heating is based on the hypothesis that plasticity-induced heating quantifies the efficiency of the plastic flow process, while plastic work aids in configurational entropy (suppleness) of the material.
- Drag on dislocations is activated by dynamic excitations. As shown, the excitations result from the kinematically-necessary readjustments of flow pathways.
- The stress–strain relations are constructed in the framework of transitional viscoplasticity. The power-law relations enable a smooth elastic-plastic transition during loading and unloading processes.
- I developed an energy-based Hall–Petch relation, where the commonly known stress-based relation is replaced by its kinematics-based counterpart. The proposed Hall–Petch concept was born out of extensive discussions with Ron Armstrong, who walked me through the sixty years of Hall–Petch interpretations, for which I am grateful.
- The model is calibrated for OFHC copper, implemented to a deformable discrete element code (my Ph.D. thesis) and validated in simulations of a plate impact problem. The method itself describes a semi-Cosserat medium, where grain translations and rotations are accounted for.
Funding
Acknowledgments
Conflicts of Interest
Appendix A. A Short Note on Deformable Discrete Element Method
References
- Meyers, M.S.; Jarmakani, H.; Bringa, E.M.; Remington, B.A. Dislocations in shock compression and release. In Dislocations in Solids; Hirth, J.P., Kubin, L., Eds.; North-Holland: Amsterdam, The Netherland, 2009; Volume 15, pp. 91–197. [Google Scholar]
- Follansbee, P.S. High-strain-rate deformation of FCC metals and alloys. In Proceedings of the EXPLOMET ’85—International Conference on Metallurgical Applications of Shock Wave and High Strain-Rate Phenomena, Portland, OR, USA, 28 July 1985. [Google Scholar]
- Kumar, A.; Kumble, R.G. Viscous drag on dislocations at high strain rates in copper. J. Appl. Phys. 1969, 40, 3475–3480. [Google Scholar] [CrossRef]
- Regazzoni, G.; Kocks, U.F.; Follansbee, P.S. Dislocation kinetics at high strain rates. Acta Metall. 1987, 35, 2865–2875. [Google Scholar] [CrossRef]
- Bragov, A.; Igumnov, L.; Konstantinov, A.; Lomunov, A.; Rusin, E. Effects of high strain rate on plastic deformation of metal materials under fast compression loading. J. Dyn. Behav. Mater. 2019, 5, 309–319. [Google Scholar] [CrossRef]
- Dodd, B.; Bai, Y. Adiabatic Shear Localization: Frontiers and Advances, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2012; pp. 2–18. [Google Scholar]
- Bever, M.B.; Holt, D.L.; Titchener, A.L. The stored energy of cold work. Prog. Mater Sci. 1973, 17, 5–177. [Google Scholar] [CrossRef]
- Farren, W.S.; Taylor, G.I. The heat developed during plastic extension of metals. Proc. R. Soc. A 1952, 5, 398–451. [Google Scholar]
- Taylor, G.I.; Quinney, H. The latent energy remaining in a metal after cold working. Proc. R. Soc. A 1934, 143, 307–326. [Google Scholar]
- Hall, E.O. The deformation and aging of mild steel. Proc. Phys. Soc. Lond. 1951, 64, 747–753. [Google Scholar] [CrossRef]
- Petch, N.J. The cleavage strength of polycrystals. J. Iron Steel Inst. 1953, 174, 25–28. [Google Scholar]
- Armstrong, R.W. On size effect in polycrystal plasticity. J. Mech. Phys. Solids 1961, 9, 196–199. [Google Scholar] [CrossRef]
- Armstrong, R.W.; Codd, L.; Douthwaite, R.M.; Petch, N.J. The plastic deformation of polycrystalline aggregates. Philos. Mag. 1962, 7, 45–58. [Google Scholar] [CrossRef]
- Park, H.-S.; Rudd, R.E.; Cavallo, R.M.; Barton, N.R.; Arsenlis, A.; Belof, J.L.; Blobaum, K.J.M.; El-Dasher, B.S.; Florando, J.N.; Huntington, C.M.; et al. Grain-size-independent plastic flow at ultrahigh pressures and strain rates. Phys. Rev. Lett. 2015, 114, 065502. [Google Scholar] [CrossRef]
- Mao, Z.N.; An, X.H.; Liao, X.Z.; Wang, J.T. Opposite grain size dependence of strain rate sensitivity of copper at low vs high strain rates. Mater. Sci. Eng. A 2018, 738, 430–438. [Google Scholar] [CrossRef]
- Arzt, E. Size effects in materials due to microstructural and dimensional constraints: A comparative review. Acta Mater. 1998, 46, 5611–5626. [Google Scholar] [CrossRef]
- Pande, C.S.; Cooper, K.P. Nanomechanics of Hall-Petch relationship in nanocrystalline materials. Prog. Mater. Sci. 2009, 54, 689–706. [Google Scholar] [CrossRef]
- Zerilli, F.J.; Armstrong, R.W. Dislocation-mechanics-based constitutive relations for material dynamics calculations. J. Appl. Phys. 1987, 61, 1816–1825. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. A constitutive model and data for metals subjected to large strains, high strain rates and high. In Proceedings of the 7th International Symposium, Ballistics, The Hague, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Follansbee, P.S.; Kocks, U.F. A constitutive description of the deformation of copper based on the use of the mechanical threshold. Acta Metall. 1988, 36, 81–93. [Google Scholar] [CrossRef]
- Preston, D.L.; Tonks, D.L.; Wallace, D.C. Model of plastic deformation for extreme loading conditions. J. Appl. Phys. 2003, 93, 211–220. [Google Scholar] [CrossRef]
- Salvado, F.C.; Teixeira-Dias, F.; Walley, S.M.; Lea, L.J.; Cardoso, J.B. A review on the strain rate dependency of the dynamic viscoplastic response of fcc metals. Prog. Mater. Sci. 2017, 88, 186–231. [Google Scholar] [CrossRef]
- Gurrutxanga-Lerma, B. A stochastic study of the collective effect of random distribution of dislocations. J. Mech. Phys. Solids 2019, 124, 10–34. [Google Scholar] [CrossRef]
- Langer, J.S. Statistical thermodynamics of crystal plasticity. J. Stat. Phys. 2019, 175, 531–541. [Google Scholar] [CrossRef]
- Brown, L.M. Power laws in dislocation plasticity. Philos. Mag. 2016, 96, 2696–2713. [Google Scholar] [CrossRef]
- Richeton, T.; Weiss, J.; Louchet, F. Dislocation avalanches: Role of temperature, grain size and strain hardening. Acta Mater. 2005, 53, 4463–4471. [Google Scholar] [CrossRef]
- Zaiser, M.; Nikitas, N. Slip avalanches in crystal plasticity: Scaling of avalanche cutoff. J. Stat. Mech. Theory Exp. 2007, 2007, P04013. [Google Scholar] [CrossRef]
- Pantheon, W. Distribution in dislocation structures: Formation and spatial correlation. J. Mater. Res. 2002, 17, 2433–2441. [Google Scholar] [CrossRef]
- Zubelewicz, A. Micromechanical study of ductile polycrystalline materials. J. Mech. Phys. Solids 1993, 41, 1711–1722. [Google Scholar] [CrossRef]
- Zubelewicz, A. Tensor Representations in Application to Mechanisms-Based Constitutive Modeling; Technical Report ARA-2; Alek & Research Associates, LLC: Los Alamos, NM, USA, 2015. [Google Scholar] [CrossRef]
- Zubelewicz, A. Overall stress and strain rates for crystalline and frictional materials. Int. J. Non Linear Mech. 1991, 25, 389–393. [Google Scholar] [CrossRef]
- Zubelewicz, A. Metal behavior at extreme loading rates. Mech. Mat. 2009, 41, 969–974. [Google Scholar] [CrossRef]
- Armstrong, R.W.; Walley, S.M. High strain rate properties of metals and alloys. Int. Mater. Rev. 2008, 53, 105–128. [Google Scholar] [CrossRef]
- Ryu, S.; Kang, K.; Cai, W. Entropic effect on the rate of dislocation nucleation. Proc. Natl. Acad. Sci. USA 2011, 108, 5174–5178. [Google Scholar] [CrossRef]
- Kubin, L.P. Dislocation patterns: Experiment, theory and simulations. In Stability of Materials; Plenum Press: New York, NY, USA, 1996; pp. 99–135. [Google Scholar]
- Gray, G.T.; Chen, S.R.; Wright, W.; Lopez, M.F. Constitutive Equations for Annealed Metals under Compression at High Strain Rates and High Temperature; IS-4 Report, LA-12669-MS; Los Alamos National Laboratory: Los Alamos, NM, USA, 1994.
- Gray, G.T., III. High strain rate deformation: Mechanical behavior and deformation substructures induced. Annu. Rev. Mater. Res. 2012, 42, 285–303. [Google Scholar] [CrossRef]
- Gao, C.Y.; Zhang, L.C. Constitutive modelling of plasticity of fcc metals under extremely high strain rates. Int. J. Plast. 2012, 32–33, 121–133. [Google Scholar] [CrossRef]
- Huang, S.H.; Clifton, R.J. Macro and Micro-Mechanics of High Velocity Deformation and Fracture; Kawata, K., Shioiki, J., Eds.; IUTAM: Tokyo, Japan, 1985; pp. 63–74. [Google Scholar]
- Tong, W.; Clifton, R.J.; Huang, S.H. Pressure-shear impact investigation of strain rate history effects in oxygen-free high-conductivity copper. J. Mech. Phys. Solids 1992, 40, 1251–1294. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Li, Y. Flow stress of fcc polycrystals with application to OFHC Cu. Acta Mater. 1988, 46, 565–577. [Google Scholar] [CrossRef]
- Tanner, A.B.; McGinty, R.D.; McDowell, D.L. Modeling temperature and strain rate history effects in OFHC Cu. Int. J. Plast. 1999, 15, 575–603. [Google Scholar] [CrossRef]
- Baig, M.; Khan, A.S.; Choi, S.-H.; Jeong, A. Shear and multiaxial responses of oxygen free high conductivity (OFHC) copper over wide range of strain-rates and temperatures and constitutive modeling. Int. J. Plast. 2013, 40, 65–80. [Google Scholar] [CrossRef]
- Jordan, L.J.; Siviour, C.R.; Sunny, G.; Bramlette, C.; Spowart, J.E. Strain rate-dependent mechanical properties of OFHC copper. J. Mater. Sci. 2013, 48, 7134–7141. [Google Scholar] [CrossRef]
- Rittel, D.; Zhang, L.H.; Osovski, S. The dependence of the Taylor-Quinney coefficient on the dynamic loading mode. J. Mech. Phys. Solids 2017, 107, 96–114. [Google Scholar] [CrossRef]
- Nieto-Fuentes, J.C.; Rittel, D.; Osovski, S. On a dislocation-based constitutive model and dynamic thermomechanical considerations. Int. J. Plast. 2018, 108, 55–69. [Google Scholar] [CrossRef]
- Armstrong, R.W. Size effect on material yield strength/deformation/fracturing properties. J. Mater. Res. 2019, 34. [Google Scholar] [CrossRef]
- Ashby, M.F. The deformation of plasticity non-homogeneous materials. Philos. Mag. 1970, 21, 399–424. [Google Scholar] [CrossRef]
- Guo, Y.; Collins, D.M.; Tarleton, E.; Hofmann, F.; Tischler, J.; Liu, W.; Xu, R.; Wilkinson, A.J.; Britton, T.B. Measurements of stress fields near a grain boundary: Exploring blocked arrays of dislocations in 3D. Acta Mater. 2015, 96, 229–236. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Zhang, C. The mechanical behavior during nanoindentation near the grain boundary in a bicrystal fcc metal. Mater. Sci. Eng. A 2015, 621, 218–228. [Google Scholar] [CrossRef]
- Udler, D.; Seidman, D.N. Grain boundary and surface energies of fcc metals. Phys. Rev. B 1996, 54, 133–136. [Google Scholar] [CrossRef]
- Cordero, Z.C.; Knight, B.E.; Schuh, C.A. Six decades of the Hall-Petch effect—A survey of grain-size strengthening studies on pure metals. Int. Mater. Rev. 2016, 61, 495–512. [Google Scholar] [CrossRef]
- Van Vlack, L.H. Elements of Materials Science and Engineering, 6th ed.; Addison Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Keller, C.; Hug, E.; Retoux, R.; Feaugas, X. TEM study of dislocation patterns in near-surface and core regions of deformed nickel polycrystals with few grains across the cross section. Mech. Mater. 2010, 42, 44–54. [Google Scholar] [CrossRef]
- Zubelewicz, A. Metal behavior in the extremes of dynamics. Sci. Rep. 2018, 8, 5162. [Google Scholar] [CrossRef]
- Zubelewicz, A. Century-long Taylor-Quinney interpretation of plasticity-induced heating reexamined. Sci. Rep. 2019, 9, 9088. [Google Scholar] [CrossRef]
- Ravi Chandran, K.S. A new exponential function to represent the effect of grain size on the strength of pure iron over multiple length scales. J. Mater. Res. 2019, 34, 2315–2324. [Google Scholar] [CrossRef]
- Zubelewicz, A.; Addessio, F.L.; Cady, C. Constitutive model for uranium-niobium alloy. J. Appl. Phys. 2006, 100, 013523. [Google Scholar] [CrossRef]
- Zubelewicz, A.; Zurek, A.K.; Potocki, M.L. Dynamic behavior of copper under extreme loading rates. J. Phys. IV 2006, 134, 23–27. [Google Scholar] [CrossRef]
- Chen, S.R.; Kocks, U.F. On the strain rate dependence of dynamic recrystallization in copper polycrystals. In Proceedings of the International Conference Recrystallization 92, San Sebastian, Spain, 31 August–4 September 1992. [Google Scholar]
- Freed, A.D.; Walker, K.P. High temperature constitutive modeling: Theory and applications. In Proceedings of the Winter Annual Meeting of the American Society of Mechanical Engineers, Atlanta, GA, USA, 1–6 December 1991. [Google Scholar]
- Banerjee, B. An evaluation of plastic flow stress models for the simulation of high-temperature and high-strain-rate deformation of metals. arXiv 2005, arXiv:cond-mat/0512466. [Google Scholar] [CrossRef]
- Selyutina, N.S.; Borodin, E.N.; Petrov, Y.V. Structural-temporal peculiarities of dynamic deformation of nanostructured and nanoscaled metals. Phys. Solid State 2018, 60, 1813–1820. [Google Scholar] [CrossRef]
- Thomas, S.A.; Veeser, L.R.; Turley, W.D.; Hixson, R.S. Comparison of CTH simulations with measured wave profiles for simple flyer plate experiments. J. Dyn. Behav. Mater. 2016, 2, 365–371. [Google Scholar] [CrossRef]
- Zubelewicz, A. Iterative method of finite elements. In Proceedings of the 2nd Conference on Computational Methods in Mechanics of Structures, Gdansk, Poland, 24–26 November 1975. [Google Scholar]
- Zubelewicz, A. A Certain Version of Finite Element Method. Ph.D. Thesis, Warsaw University of Technology, Warsaw, Poland, 1979. [Google Scholar]






| Bulk Modulus | Shear Modulus | Mass Density | Yield Stress, 298 K | Burgers Vector | Melting Point | Specific Heat, 298 K |
|---|---|---|---|---|---|---|
| 385 |
| Strain Rate Exponent | Stress Exponent | Heat Coefficient | Crystallographic Constant | Schmid Factor | Transition Temperature | Overstress Exponent |
|---|---|---|---|---|---|---|
| 0.5 |
| Activation Energy Factor | Thermal Activation | Stress Pre-Factor | Critical Energy | Schmid Factor | Ductility | Damage Strain |
|---|---|---|---|---|---|---|
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zubelewicz, A. Mechanisms-Based Transitional Viscoplasticity. Crystals 2020, 10, 212. https://doi.org/10.3390/cryst10030212
Zubelewicz A. Mechanisms-Based Transitional Viscoplasticity. Crystals. 2020; 10(3):212. https://doi.org/10.3390/cryst10030212
Chicago/Turabian StyleZubelewicz, Aleksander. 2020. "Mechanisms-Based Transitional Viscoplasticity" Crystals 10, no. 3: 212. https://doi.org/10.3390/cryst10030212
APA StyleZubelewicz, A. (2020). Mechanisms-Based Transitional Viscoplasticity. Crystals, 10(3), 212. https://doi.org/10.3390/cryst10030212




