Next Article in Journal
Stable and Metastable Patterns in Chromonic Nematic Liquid Crystal Droplets Forced with Static and Dynamic Magnetic Fields
Next Article in Special Issue
Does Chlorine in CH3Cl Behave as a Genuine Halogen Bond Donor?
Previous Article in Journal
Comparison of Hafnium Dioxide and Zirconium Dioxide Grown by Plasma-Enhanced Atomic Layer Deposition for the Application of Electronic Materials
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 10
Issue 2
10.3390/cryst10020137
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Regium Bonds between Silver(I) Pyrazolates Dinuclear Complexes and Lewis Bases (N2, OH2, NCH, SH2, NH3, PH3, CO and CNH)

by
Ibon Alkorta
1,*,
Cristina Trujillo
2,
Goar Sánchez-Sanz
3,4 and
José Elguero
1
1
Instituto de Química Médica, CSIC, Juan de la Cierva, 3, E-28006 Madrid, Spain
2
School of Chemistry, Trinity Biomedical Sciences Institute, Trinity College, Dublin, 152–160 Pearse St, Dublin 2, Ireland
3
Irish Centre of High-End Computing, Grand Canal Quay, Dublin 2, Ireland
4
School of Chemistry, University College Dublin, Belfield, Dublin 4, Ireland
*
Author to whom correspondence should be addressed.
Crystals 2020, 10(2), 137; https://doi.org/10.3390/cryst10020137
Submission received: 28 January 2020 / Revised: 18 February 2020 / Accepted: 19 February 2020 / Published: 24 February 2020
(This article belongs to the Special Issue σ- and π-Hole Interactions)
Browse Figures
Versions Notes

Abstract

:
A theoretical study and Cambridge Structural Database (CSD) search of dinuclear Ag(I) pyrazolates interactions with Lewis bases were carried out and the effect of the substituents and ligands on the structure and on the aromaticity were analyzed. A relationship between the intramolecular Ag–Ag distance and stability was found in the unsubstituted system, which indicates a destabilization at longer distances compensated by ligands upon complexation. It was also observed that the asymmetrical interaction with phosphines as ligands increases the Ag–Ag distance. This increase is dramatically higher when two simultaneous PH3 ligands are taken into account. The calculated 109Ag chemical shielding shows variation up to 1200 ppm due to the complexation. Calculations showed that six-membered rings possessed non-aromatic character while pyrazole rings do not change their aromatic character significantly upon complexation.

1. Introduction

Non-covalent interactions (NCIs) are present in complexes formed between two or more Lewis acids and Lewis bases. In fact, those interactions are commonly named by the Lewis acid [1]. On the one hand, a Lewis base (LB) or a LB motif is associated with a region of space where there exists an excess of negative charge (i.e., electron density) in the proximity of an atom or atoms within a molecule. This is predominant in anions and in some neutral molecules such as those that exhibit lone pairs (LP: carbenes, amines, phosphines, N-oxides, etc.), multiple bonds (olefins, acetylenes, benzenes and other aromatic molecules), single bonds (alkanes, dihydrogen, etc.), radicals, metals (rarely), etc. On the other hand, a Lewis acid (LA) is associated with a region of space where there is an excess of positive charge (in other words a deficit of negative charge or electron deficiency) in the proximity of an atom or atoms in a molecule. This can be found in cations, molecules or atoms exhibiting σ- and π-holes and metals (frequently). The concept of a σ-hole was introduced by Politzer et al. [2,3,4,5] to describe regions of positive potential along the vector of a covalent bond. It was latter extended to other situations, for example, the π-hole [6,7,8,9,10,11] (positive electrostatic potential perpendicular to an atom of a molecular framework) and lone pair hole (similar to σ-hole but along the atom–lone pair direction) [12,13,14]. The maximum value of the molecular electrostatic potential within a given molecular density isosurface surface, VS,max, has also been classified based on the nature of the orbitals (s-, p- and d- orbitals) and it is associated with the corresponding deficiencies (σs-, σp- and σd-holes) [15].
There is a wide variety of non-covalent interactions due to most groups of the periodic table being associated with a certain type of NCI: starting from the archetypical hydrogen bond (HB) there are “alkali bonds” (group 1) [16,17], “alkaline earth bonds” (group 2) [18,19,20], “regium bonds” (groups 10 and 11) [21,22,23], “triel bonds” (group 13) [24], “tetrel bonds” (group 14) [25,26,27,28], “pnictogen (also called pnicogen) bonds” (group 15) [29,30,31], “chalcogen bonds” (group 16) [32,33,34,35], “halogen bonds” (group 17) [36,37], and “aerogen bonds” (group 18) [38]. Regium (or coinage-metal bonds) bonds involve mainly coinage metals, Cu, Ag and Au. These weak interactions are particularly interesting since they are associated with organometallic chemistry. However, it is necessary to clearly differentiate between clusters (e.g., Au2 or Ag11) [22,39] and molecules (e.g., AuX) [40,41]. Recent published works show an increased interest in regium bonds, some example of which are discussed here [42,43,44,45].
In this article, the dinuclear silver(I) pyrazolates (Scheme 1) have been considered following a previous paper on trinuclear silver(I) pyrazolates [46]. The effect of the ligands on the silver atom and the substituents on the pyrazole rings on the structure, energetic, electronic and magnetic properties have been analyzed.

2. Materials and Methods

2.1. Cambridge Structural Database Search

The Cambridge Structural Database (CSD) [47] version 5.40 with updates from November 2018, May 2019, and August 2019 was searched for systems with cyclic (Pz-Ag)2 structure. The geometrical characteristics of these systems have been analysed.

2.2. Ab Initio Calculations

The geometry of the systems have been fully optimized using the MP2 computational method [48,49,50,51] and the jul-cc-pVDZ basis set [52,53,54] for all the atoms except for the silver atoms, of which the aug-cc-pVDZ-PP effective core potential basis set [55] has been used. Frequency calculations have been carried out at the same computational level to verify that the obtained structures correspond to energetic minima. Dissociation energies have been obtained as the difference between the sum of the energies of the isolated monomers in their optimized geometry and the energy of the complex. These calculations have been carried out with the Gaussian-16 program [56].
The molecular electrostatic potential on the 0.001 au electron density isosurface (MESP) was calculated with the Gaussian16 program, analyzed with the Multiwfn program [57] and represented with the JMol program [58].
The topological analysis of the electron density was carried out by means of the quantum theory of atoms in molecules (QTAIM) method [59,60,61,62] using the AIMAll program [63]. This method identifies the points of space where the gradient of the electron density vanishes (critical points) and based on the number of positive curvatures characterizes them as nuclear attractors (3, −3), bond critical points (3, −1), ring critical points (3, +1) or cage critical points (3, +3). By connecting the bond critical points with the nuclear attractor, following the minimum gradient path, the molecular graph is obtained.
The natural bond orbital (NBO) method [64] was employed using the NBO-3 program to evaluate atomic charges, and to analyze charge-transfer interactions between occupied and unoccupied orbitals.
The TOPMOD program [65] has been used to analyze the areas of electron concentration in terms of the electron localization function (ELF) [66]. For the three-dimensional plots, a convenient ELF value of 0.7 was used [67].
Relativistic-corrected NMR chemical shielding values for the geometries optimized at MP2 level were obtained using the relativistic ZORA spin–orbit Hamiltonian [68,69], the BP86 functional [70,71,72], and the full electron QZ4P basis [73]. In addition, the nuclear-independent chemical shift (NICS) [74] at the centre and 1 Å above the centre of the ring formed by the two Ag atoms and the pyrazole moieties were calculated to study the aromaticity of all systems. In addition, a scan of the NICS values from 0 to 2 Å in steps of 0.25 Å for (PzAg)2 was calculated [75,76]. These calculations have been performed with the ADF-2017 program [77].

3. Results and Discussion

In this paper we will report the study of nineteen compounds corresponding to the general formula depicted in Scheme 1 and named by a simple code that allows to easy identification: (R-pzAg)2(L)n. Firstly, the substituents (R) on the pyrazole ring are indicated: Pz, 4NO2pz, DMepz and 4Clpz for the unsubstituted (H), 4-nitro, 3,5-dimethyl, and 4-chloro derivatives, respectively. Secondly, the ligands (L) interacting with the silver atoms are indicated. Thus, for instance, (4NO2pzAg)2(PH3)4 corresponds to the (4-nitropyrazole:Ag)2 cyclic structure with four phosphines interacting with the silver atoms (two phosphines per each silver atom).

3.1. CSD Search

A search in the Cambridge Structural Database has been carried out and the resulting compounds with the structure represented in Scheme 1 were summarized and reported in Table 1 ordered by increasing Ag–Ag intramolecular distance. Two simplified views of these structures can be found in Table S1 of the Supplementary Materials. Structures with dinuclear silver(I) pyrazolates without ligands were not found within the CSD search.
As observed by the crystallographic data, the Ag–Ag distance ranges between 4.305 Å (ZIGSEQ) and 3.392 Å (FINWOR). The shortest distances correspond to complexes with only two ligands present concomitantly with the 3,5-bis-CF3 substituent on the pyrazole. It is also clear that the larger the number of ligands, the longer the intramolecular Ag–Ag distance. Moreover, it is noteworthy that, in structures with four phosphines ligands, the Ag–Ag distance increases as the substitutes of the pyrazole are H < 4-Cl < 4-NO2. These results will be compared against our theoretical calculations in the following sections.
Concerning the conformation of the six-membered rings in the crystal structures (similar to those of 1,4-cyclo-hexadiene, 9,10-dihydroanthracenes, phenothiazines, etc.), very little energy differences between those conformations in the crystals were found, in agreement what was proposed by Rasika Dias [78]. Regarding the tetrahedral configuration of Ag(I) atom, we have used Houser’s τ4 index [79] as recommended by Raptis [80]. This index is defined as:
τ4 = [360 − (α + β)]/141
where, α and β correspond to the two largest angles of the six angles around the tetrahedral silver atom. The values of τ4 range from 1 (perfect tetrahedral geometry, i.e., τ4 = [360 − (109.5 + 109.5)]/141 = 1) to 0 (perfect square planar geometry). The τ4 values obtained for three substituents, 0.9 (RATFEX and ZIGSIU) are very similar to those for 4 substituents (ZIGROZ and ZIGSEQ, 0.89 and 0.88 respectively) with both identical Ag atoms. The two lowest values (0.78) correspond to a substituent that differs from PPh3 (see notes (a) and (b) of Table 1).

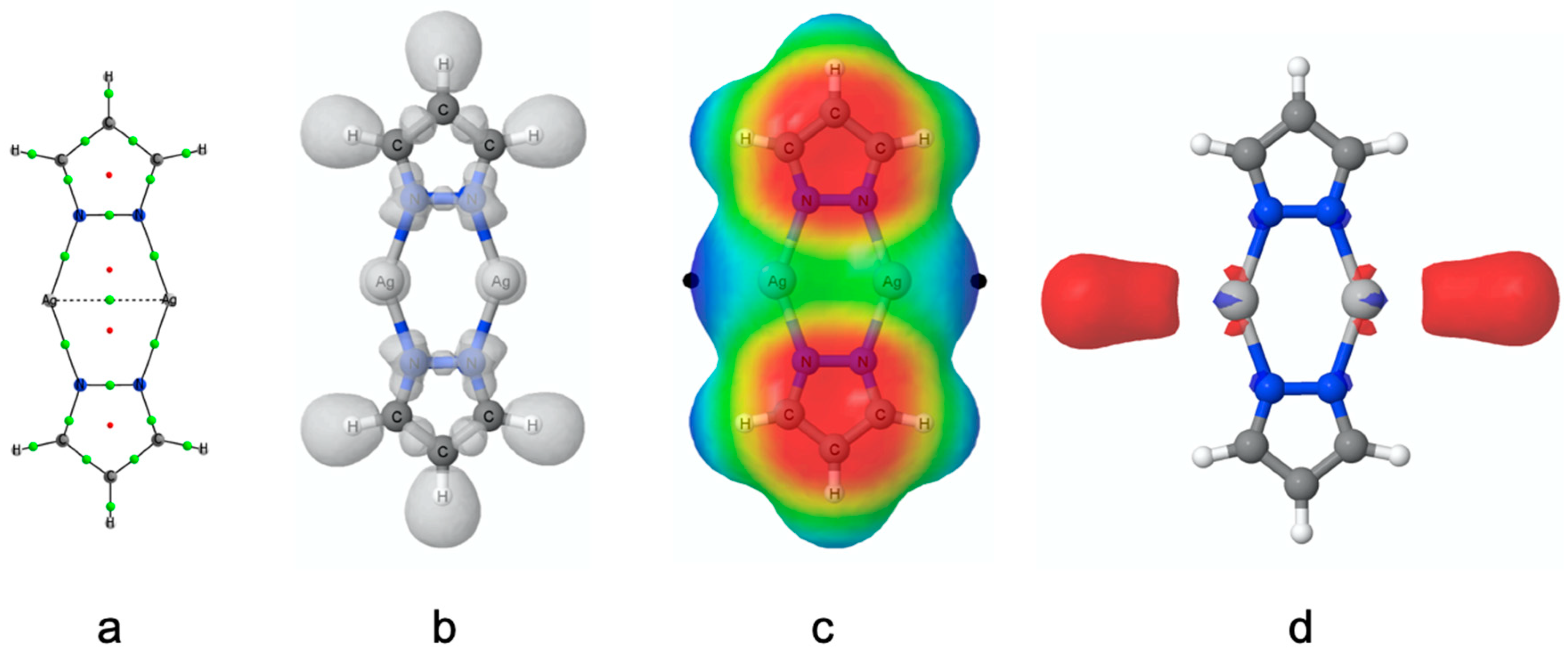
3.2. Electronic Properties of the Isolated (PzAg)2 System

The isolated (PzAg)2 system calculated at MP2 level presents a planar structure with D2h symmetry, where the silver atoms are equidistant to the pyrazole rings with an intramolecular Ag–Ag distance of 2.801 Å (Table S2). This intramolecular distance is slightly larger than that of the Ag2 cluster (2.514 Å) calculated at the same computational level. In fact, its molecular graph (Figure 1a) shows the presence of an Ag–Ag bond with the corresponding bond critical point. However, other electronic analysis carried out: ELF (Figure 1b) and NBO, do not indicate the presence of such bonds between the silver atoms due to the absence of the corresponding basin concomitantly with the Wiberg bond index of the Ag–Ag contact in (PzAg)2—being 0.01, while that of Ag2 is 0.92.
The molecular electrostatic potential on the 0.001 au electron density isosurface (MESP) of the (PzAg)2 system (Figure 1c) shows negative values above and below the pyrazole ring while the MESP in the extension of the CH and Ag–Ag bonds are positive. Moreover, the calculated maximum value on the MESP, VS,max, in the vicinity of the silver atoms is +0.03 a.u. (marked with black dots) being the most positive value in the whole isosurface. Interestingly the LUMO orbital (Figure 1d) is solely associated to the Ag atoms and located in a region that coincides with the location of the VS,max. Thus, the silver atoms of this molecule should act as a Lewis acid using both the electrostatic and orbital criteria.

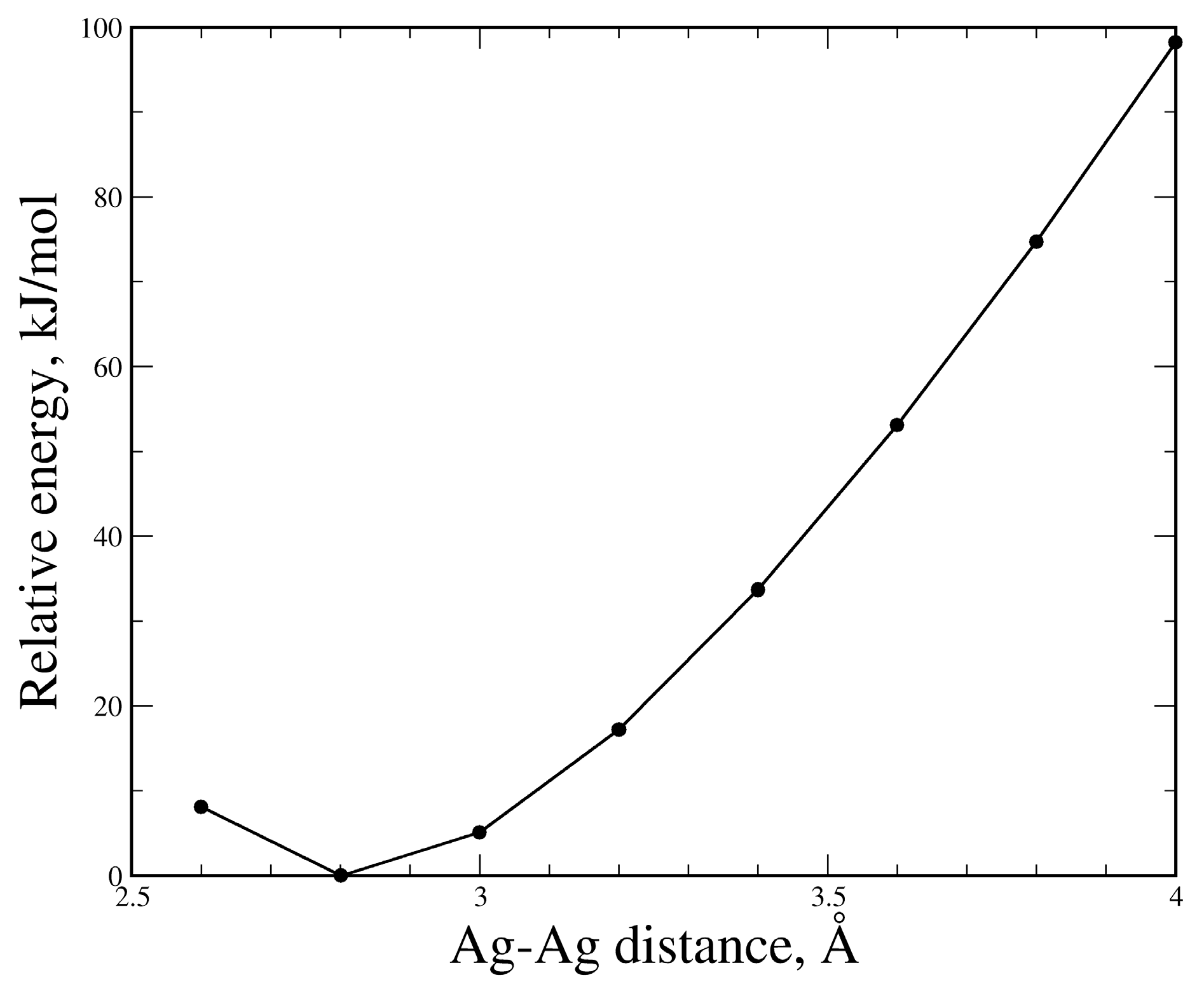
3.3. The (PzAg)2 Free Complex and the Effect of the Ag–Ag Distance on its Stability

The complex without ligands, (PzAg)2, has in its minimum energy structure a distance between both silver atoms of 2.801 Å (Table S2) which is considerably shorter than any of the Ag–Ag distances found in the CSD. As we have already indicated in the CSD search, this distance is very sensitive to the environment (substituents of the pyrazole and ligands of the silver atoms) and can vary almost 1.0 Å from the shortest to the longest distance (3.392 and 4.305 Å, respectively). In order to explore the energetic penalty due to the elongation of the intramolecular Ag–Ag distance, the (PzAg)2 system has been optimized while keeping fixed the Ag–Ag distance from 2.6 to 4.0 Å in steps of 0.2 Å (Table S2 and Figure 2). The energetic results indicate that lengthening the distance 1 Å, up to 3.8 Å, considerably decreases the stability of the system by 75 kJ·mol−1 which should be compensated by the interactions with the ligands.

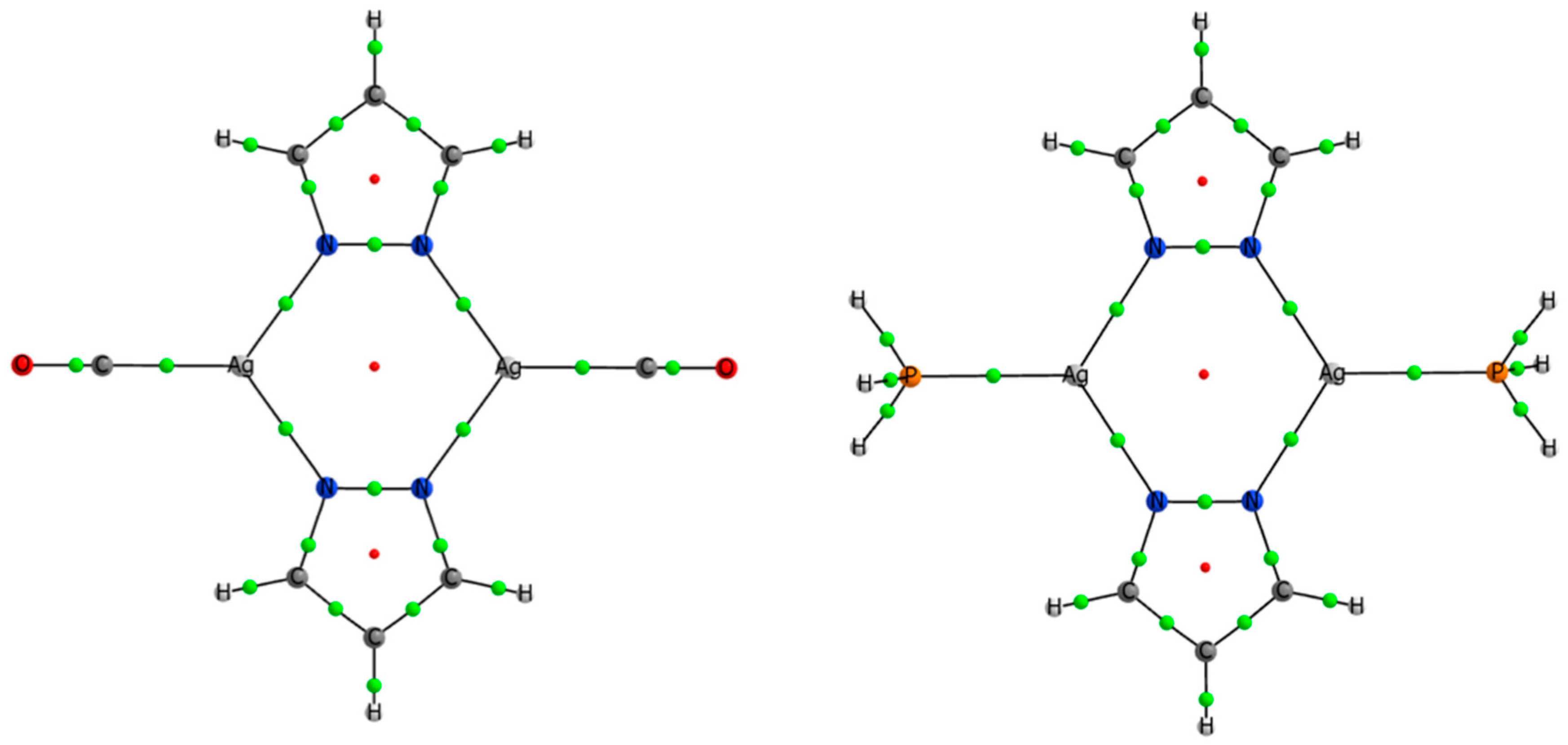
3.4. Effect of the Ligands and Substituents on the Structure and Dissociation Energy (De)

After studying the free (PzAg)2 system, the complexes with two ligands simultaneously interacting with the (PzAg)2 system have been optimized, i.e., each silver atom interacts with a single ligand. The minimum structures obtained show that the interacting atom of the ligand is coplanar with the plane defined by the (PzAg)2 system. The molecular graphs of two illustrative examples are shown in Figure 3 and the Cartesian coordinates of all of them were summarized in Table S3.
The complexation with ligands produces an elongation of the Ag–Ag distance up to 1.1 Å (Table 2) in agreement with the large variety of structures and the range of Ag–Ag distances found in the CSD search. For example, the crystal structure RATPAT (L = (PPh3)2) shows an Ag–Ag distance of 3.870 Å while in the calculated (PzAg)2(PH3)2 complex this value is 3.689 Å. It is known that ligands coordinated by O, C or P atoms are strong, while those ligands coordinated by N atoms are weak. In the cases of CNH and HCN ligands are both -donors and -acceptors but the former is coordinated by the C atom while the latter is coordinated by the N atom. This results in larger dissociation energies for the (PzAg)2(CNH)2 complex in comparison with (PzAg)2(NCH)2. Similarly, this happens with CO and NH3 ligands (both -donors), but while CO is a good -acceptor NH3 is not, resulting in smaller values of De. In the case of the PH3 ligand, it is both a -donor and -acceptor ligand, which is in agreement with the (PzAg)2(PH3)2 complex, showing the second largest De. Chalcogen ligands, OH2 (-donor) and SH2 (-donor) present similar trends. In addition, it is also observed that the distance between both pyrazole rings decreases with the elongation of the Ag–Ag distance.
But, does this have any impact on the dissociation energy? Or, in other words, is there any relationship between the Ag–Ag intramolecular distance and the dissociation energy? The dissociation energy values corresponding to the (PzAg)2L2 complexes range between 23 kJ mol−1 for L = N2 to 137 kJ mol−1 for L = CNH (Table 2). In general, despite observing a trend between the dissociation energy and the elongation of the Ag–Ag distance (Figure S1), no good fitting has been found (logarithmic fitting, R2 = 0.73). The only outlier corresponds to the (PzAg)2(CO)2 complex, and when this point is neglected the fitting is more evident (R2 = 0.90). A better exponential relationship has been found for the distance between the pyrazole rings vs. De (De = 5.55·e−0.114Pz-Pz, R2 = 0.92) which may suggest that the repulsion between pyrazole groups is partially responsible for the increase of the De energy but somehow compensated by the Ag–Ligand interaction.
The effect of the substituents (pyrazole ring) within the Ag–Ag distance and dissociation energies have been explored by considering four different pyrazole derivatives, R = H, 3,5-di(CH3), 4-Cl and 4-NO2. These isolated (R-pzAg)2 systems have been fully optimized as well as in the presence of two phosphine molecules ligands with the results gathered in Table 3.
In relation to the Ag–Ag distance in the isolated (R-pzAg)2 systems, it increases in the following order: 3,5-di(CH3) < H < 4-Cl < 4-NO2 with a variation of 0.05 Å between both extremes. The same order was found within the (R-pzAg)2(PH3)2 complexes but with a slightly larger range of 0.12 Å. This evolution was also found in the CSD search for complexes with three PPh3 ligands: RATFEX (R = H) (3.706 Å) < ZIGRUF (R = 4-Cl) (3.707 Å) < ZIGSIU (R = 4-NO2) (3.827 Å), and for complexes with four PPh3 ligands: KIRVIX (R = H) (3.900 Å) < ZIGROG (R = 4-Cl) (4.209 Å) < ZIGSEQ (R = 4-NO2) (4.305 Å).
The dissociation energies for the (R-pzAg)2(PH3)2 complexes increase following the same trend of Ag–Ag distances (Table 3 and Figure S2). Furthermore, linear correlation with R2 value of 0.97 was obtained between Ag–Ag distances and the De.
So far, only the systems with no ligands, (R-pzAg)2, and complexes with two identical ligands, (R-pzAg)2L2, have been studied. In Table 4, the results corresponding to the complexes with 0, 1, 2 and 4 phosphine ligands bonded to (PzAg)2 and (4NO2pzAg)2 systems are shown. In both series, the intramolecular Ag–Ag distance increases with the number of phosphine ligands bonded. When one PH3 is bonded the increase in the Ag–Ag distance with respect to the isolated system is 0.286 and 0.311 Å for (PzAg)2 and (4NO2pzAg)2 systems respectively. However, the change is two times larger when moving from 1 to 2 simultaneous ligands. Finally, the change is again moderate when 4 PH3 ligands interacting with each Ag are considered. The CDS search also shows an increase of the Ag–Ag distance with the number of ligands. For example in the unsubstituted complexes (R=H) the Ag–Ag distance in RATFET (L = 3) is 3.706 Å and increases to 3.900 Å with four ligands (KIRXIV). This is also observed for substituted complexes with R=4-Cl: ZIGRUF (L = 3) 3.707 Å to ZIGROZ (L = 4) 4.209 Å and for R = 4NO2: ZIGSIU (L = 3) 3.827 Å) to ZIGSEQ (L = 4) 4.305 Å. In addition, it is interesting to notice that in complexes with four phosphines, the (R-PzAg)2 system adopts a chair conformation (Figure 4) vs. the planar one observed with one or two ligands. The experimental Ag–Ag distances are longer than the calculated ones; this could be due to the fact that the ligand found in the crystals are bulkier (for instance PPh3 vs. PH3). This can be also related with the ratio of σ-donor/π-acceptor capacity in phosphorus ligands. In principle P(CH3)3 is a better σ-donor than PH3, while the latter is a better π-acceptor [81]. However, the σ-donor/π-acceptor ratio indicates that the P(CH3)3 is a stronger ligand than PH3. The same can be expected for PPh3 and therefore the Ag–Ag distance will be larger for complexes that are PPh3-coordinated compared with those for PH3 ones.
Regarding the τ4 index for (PzAg)2(PH3)4 and (4NO2pzAg)2(PH3)4: the values for both Ag are 0.81 and 0.83 respectively, in between of those found for ZIGSAM (0.78) and ZIGROZ (0.89) crystal structures.
The values of De show an anticooperativity effect as the number of phosphines increases, thus the De’s of the systems with two phosphines are smaller than twice the corresponding ones with one phosphine and the same happens when the results between the systems with two and four phosphines are compared. Looking at the values shown in Table 4, (PzAg)2(PH3) complex yields a De of 64.2 kJ·mol−1, whereas (PzAg)2(PH3)2 complex’s is 122.9 kJ·mol−1, 5.5 kJ·mol−1 smaller than twice the corresponding value for (PzAg)2(PH3). This is an indication of an anti-cooperativity effect, which is more evident when (PzAg)2(PH3)4 complex is taken into account (~42 kJ·mol−1 less than four times the De of (PzAg)2(PH3)). This is also observed for (4NO2pzAg)2 and the corresponding complexes, but the differences, i.e., the anti-cooperativity, is rather smaller (4.0 kJ·mol−1) for (4NO2pzAg)2(PH3)2 and slightly larger for (4NO2pzAg)2(PH3)4 (57.9 kJ·mol−1).

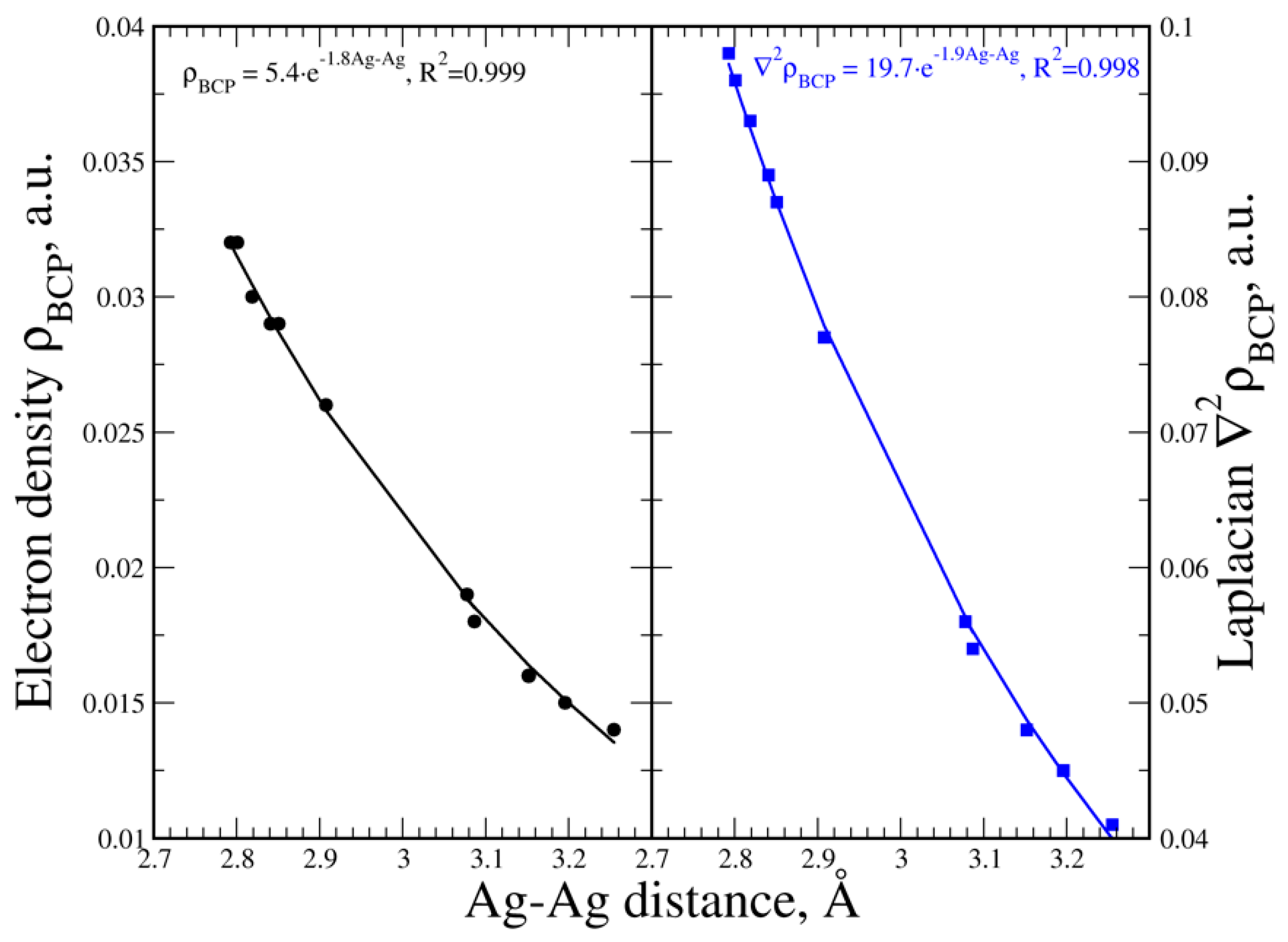
3.5. Electron Density

The critical points of the electron density of all systems have been characterized using the quantum theory of atoms in molecules (QTAIM) method. As aforementioned, a bond critical point (BCP) is obtained for the (PzAg)2 system in between both Ag atoms. A similar feature has been obtained for all the systems with Ag–Ag distances shorter than 3.3 Å. The electron density values, ρBCP, of this BCP (Table S4) range between 0.032 and 0.014 a.u., with positive values of the Laplacian, ∇2ρ (between 0.098 and 0.041 a.u.) and negative values of the total energy density, HBCP, except for the system with the largest Ag–Ag bond in this set ((PzAg)2(NH3)2). Excellent exponential relationships are obtained between the ρBCP and ∇2ρBCP and the interatomic distance in agreement with previous reports (Figure 5) [82,83].
Concering the Ag–L bonds, the corresponding bond critical points between the silver atom and the different ligands have been gathered in Table S5. In all the cases, the interactions exhibit positive values of the ∇2ρBCP and negative values of HBCP, which indicates a partial covalent character of the bond formed [84,85]. The only exception corresponds to the weakest complex, (PzAg)2(N2)2, which shows a small positive HBCP value. The 14 unique Ag–P contacts found in this set show similar relationships between ρBCP and ∇2ρBCP vs. the Ag–P distance to those previously mentioned for Ag–Ag BCPs.

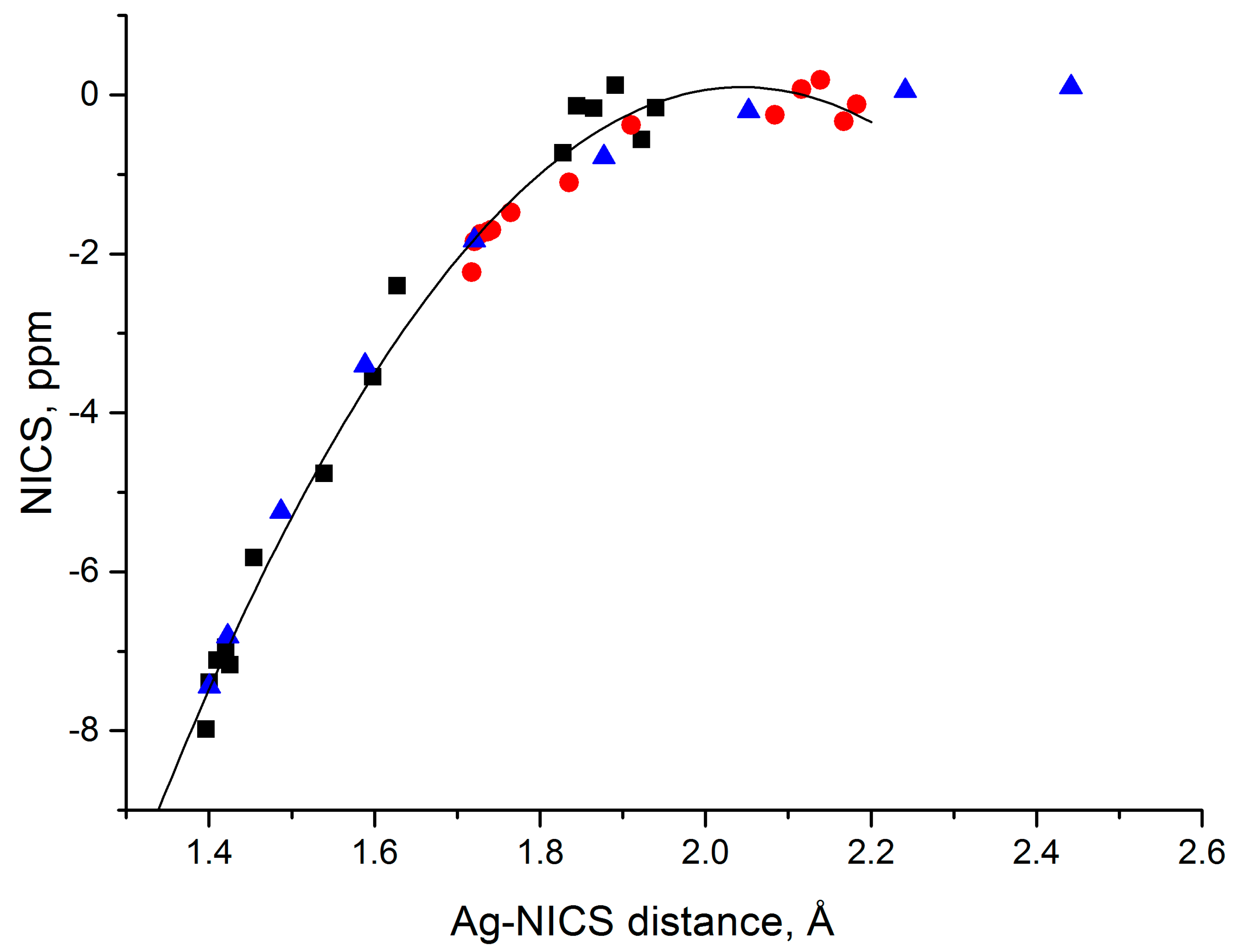
3.6. Magnetic Properties and Aromaticity

Among the different nuclei suitable for NMR spectra present in these systems (1H, 13C and 15N), 109Ag is the one with the largest range of chemical shifts. The calculated 109Ag chemical shielding for all the systems studied in this article are listed in Table 5. It is worth noting that upon complexation 109Ag can change its chemical shielding by more than 1200 ppm to lower field, from 3765 ppm ((PzAg)2) to 2550.48 ppm ((PzAg)2(PH3)4). Furthermore, a good relationship between the chemical shielding and the intramolecular Ag–Ag distance (only for complexes with two ligands) was found (Figure S3). Unfortunatelly, there are no experimental data on (PzAg)2 compounds but a recent report on (PzAg)3 derivatives show that the methodology used here provides δ109Ag values within 10 ppm of the experimental ones [46].
In order to explore the potential aromaticity of the six membered ring formed by the nitrogen atoms of the pyrazoles and the two silver atoms, the NICS(0) and NICS(1) have been calculated (Table 5). Despite NICS isotropic values being widely used and well established, there is still a controversy about the reliability of NICS values for assessment of the aromaticity of certain molecules [86,87]. Nevertheless, and following our previous experience, the isotropic values have in several cases been shown to present an accurate description of the aromatic behaviour in poly-aromatic systems [88,89,90].
Despite almost all the systems studied presenting negative NICS(0) values in the six-membered ring, only those with short Ag–Ag distances (2.8−3.0 Å) present very negative values close to the benzene molecule (−8 ppm) [91], and, also, those NICS(0) values decrease in absolute value as the Ag–Ag distance increases. NICS(1) are smaller, in absolute value, than NICS(0), but follow the same trend as the latter. Also, NICS(1) are very small compared with benzene ones (−10.2 ppm) [91] which suggest non-aromatic character. But, those values should be taken carefully, since the two silver atoms are very close and the proximity of the nuclei may affect the NICS(0) measure. To provide a further insight on this, Figure 6 clearly shows that there is a unique dependence between the NICS(0) and NICS(1), the distance between the location where the NICS is measured and the silver atom. The scan of the NICS values for (PzAg)2 from 0 to 2.0 Å above the centre of the six-membered ring (Table S6) have also been plotted in Figure 6 showing a similar evolution to the NICS(0) and NICS(1) of the rest of the molecules. This indicates that, as aforementioned, this ring is not aromatic but the NICS values obtained are somehow affected by the proximity of the silver atom.
In contrast the NICS(0) and NICS(1) values of the pyrazole rings are negative and large in all cases and very close to the ones obtained by Kusakiewicz-Dawid (−13.5 and −11.4 ppm respectively) [92].
On the other hand, the substituents on the pyrazole ring have a greater effect on the NICS values than the different ligands on the (PzAg)2L2 complexes, most likely due to changes in the electron density on the ring current electrons. For instance the NICS(0) in the (Rpz-Ag)2 systems ranges between −10.5 and −13.1 ppm while in the (PzAg)2L2 complexes it is between −12.3 and −13.1 ppm.

4. Conclusions

A theoretical study and CSD search of the different effects provoked by substituents and ligands upon complexation with dinuclear Ag(I) pyrazolates has been carried out and the structural, energetic, electron density and magnetic features analyzed.
The CSD search shows a great variability of the Ag–Ag distance in the crystal structures. These results have been rationalized based on the number of ligand interactions with the Ag atoms and the substituents of the pyrazole ring.
In the isolated (PzAg)2 system, it was observed that for Ag–Ag the longer the distance, the lesser the stability of the unsubstituted complex with no ligands. This decrease in the stability is somehow compensated by the ligands upon complexation.
Furthermore, complexation with ligands through the Ag atoms increases the intramolecular distance Ag–Ag. In fact, considering the PH3 ligand, the increase of the Ag–Ag distance was found moderate when going from no ligand to one ligand. However, when two simultaneous PH3 are interacting, the Ag–Ag distance increases dramatically. Nevertheless, when four PH3 are considered, the increase is again moderate.
In terms of the QTAIM analysis, it is noteworthy the presence of a BCP between both Ag atoms among all the systems with Ag–Ag distances shorter than 3.3 Å.
Finally, regarding the aromatic/non-aromatic properties, six-membered rings containing the Ag–Ag motif show negative NICS values but those reveal a non-aromatic character mainly affected by the proximity of the Ag nuclei. This was confirmed by the relationship found between the NICS values and the Ag–NICS distance. On the other hand, pyrazole rings maintain their aromatic behaviour with slight changes.

Supplementary Materials

The following are available online at https://www.mdpi.com/2073-4352/10/2/137/s1, Table S1: Two simplified views of the structures found in the CSD search, Table S2. Effect of the Ag(I)–Ag(I) distance (Å) on the relative energy (kJ·mol−1) of the (PzAg)2 system, Table S3: Cartesian coordinates (Å) of the optimized systems at MP2/jul-cc-pVDZ/jul-cc-pVDZ-PP level, Figure S1: Relative energy vs. Ag–Ag distance in the (PzAg)2 system, Figure. S2: De (kJ·mol−1) vs. Ag–Ag dist. (Å) in the (PzAg)2L2 complexes, Figure S3: De (kJ·mol−1) vs. Ag–Ag dist. (Å) in the (R-pzAg)2(PH3)2 complexes, Table S4: Distance (Å) and electron density properties (au) of the Ag–Ag BCPs, Table S5: Distance (Å) and electron density properties (au) of the Ag–L BCPs, Figure S4: 109Ag chemical shielding vs. Ag–Ag distance in the (PzAg)2L2 complexes. Table S6. NICS values (ppm) from 0.0 to 2.0 Å of the center of the 6-membered ring in (PzAg)2.

Author Contributions

Conceptualization and project design, I.A., J.E.; resources, I.A., C.T., G.S.-S, data curation, I.A, J.E, C.T., G.S.-S., writing—original draft preparation, I.A, J.E, C.T., G.S.-S.; writing—review and editing, I.A, J.E, C.T., G.S.-S.; funding acquisition, I.A. C.T.; All authors have read and agreed to the published version of the manuscript.

Funding

This work was carried out with financial support from the Spanish Ministerio de Ciencia, Innovación y Universidades (Projects PGC2018-094644-B-C2) and Dirección General de Investigación e Innovación de la Comunidad de Madrid (PS2018/EMT-4329 AIRTEC-CM), and Science Foundation of Ireland (SFI), grant number 18/SIRG/5517.

Acknowledgments

We are grateful to the Irish Centre for High-End Computing (ICHEC) and CTI(CSIC) for the provision of computational facilities. We are also grateful to Dr Lee O’Riordan for his continuous support and help.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Cavallo, G.; Metrangolo, P.; Pilati, T.; Resnati, G.; Terraneo, G. Naming Interactions from the Electrophilic Site. Cryst. Growth Des. 2014, 14, 2697–2702. [Google Scholar] [CrossRef]
  2. Politzer, P.; Murray, J.S. An Overview of σ-Hole Bonding, an Important and Widely-Occurring Noncovalent Interaction Practical Aspects of Computational Chemistry; Leszczynski, J., Shukla, M.K., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 149–163. [Google Scholar]
  3. Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding: An electrostatically-driven highly directional noncovalent interaction. PCCP 2010, 12, 7748–7757. [Google Scholar] [CrossRef] [PubMed]
  4. Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding and other [sigma]-hole interactions: A perspective. PCCP 2013, 15, 11178–11189. [Google Scholar] [CrossRef] [PubMed]
  5. Bauzá, A.; Mooibroek, T.J.; Frontera, A. The Bright Future of Unconventional σ/π-Hole Interactions. ChemPhysChem 2015, 16, 2496–2517. [Google Scholar] [CrossRef] [PubMed]
  6. Murray, J.; Lane, P.; Clark, T.; Riley, K.; Politzer, P. σ-Holes, π-holes and electrostatically-driven interactions. J. Mol. Model. 2012, 18, 541–548. [Google Scholar] [CrossRef] [PubMed]
  7. Solimannejad, M.; Ramezani, V.; Trujillo, C.; Alkorta, I.; Sánchez-Sanz, G.; Elguero, J. Competition and Interplay between σ-Hole and π-Hole Interactions: A Computational Study of 1:1 and 1:2 Complexes of Nitryl Halides (O2NX) with Ammonia. J. Phys. Chem. A 2012, 116, 5199–5206. [Google Scholar] [CrossRef]
  8. Grabowski, S.J. Hydrogen bonds, and σ-hole and π-hole bonds—Mechanisms protecting doublet and octet electron structures. PCCP 2017, 19, 29742–29759. [Google Scholar] [CrossRef]
  9. Bauzá, A.; Mooibroek, T.J.; Frontera, A. Directionality of π-holes in nitro compounds. Chem. Commun. 2015, 51, 1491–1493. [Google Scholar] [CrossRef] [Green Version]
  10. Zierkiewicz, W.; Michalczyk, M.; Wysokiński, R.; Scheiner, S. On the ability of pnicogen atoms to engage in both σ and π-hole complexes. Heterodimers of ZF2C6H5 (Z = P, As, Sb, Bi) and NH3. J. Mol. Model. 2019, 25, 152. [Google Scholar] [CrossRef] [Green Version]
  11. Azofra, L.; Alkorta, I.; Scheiner, S. Noncovalent interactions in dimers and trimers of SO3 and CO. Theor. Chem. Acc. 2014, 133, 1–8. [Google Scholar] [CrossRef]
  12. Blanco, F.; Alkorta, I.; Rozas, I.; Solimannejad, M.; Elguero, J. A theoretical study of the interactions of NF3 with neutral ambidentate electron donor and acceptor molecules. PCCP 2011, 13, 674–683. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  13. Alkorta, I.; Elguero, J.; Del Bene, J.E. Exploring the PX3:NCH and PX3:NH3 potential surfaces, with X=F, Cl, and Br. Chem. Phys. Lett. 2015, 641, 84–89. [Google Scholar] [CrossRef]
  14. Bauzá, A.; Mooibroek, T.J.; Frontera, A. σ-Hole Opposite to a Lone Pair: Unconventional Pnicogen Bonding Interactions between ZF3 (Z=N, P, As, and Sb) Compounds and Several Donors. ChemPhysChem 2016, 17, 1608–1614. [Google Scholar] [CrossRef] [PubMed]
  15. Stenlid, J.H.; Brinck, T. Extending the σ-Hole Concept to Metals: An Electrostatic Interpretation of the Effects of Nanostructure in Gold and Platinum Catalysis. JACS 2017, 139, 11012–11015. [Google Scholar] [CrossRef]
  16. Shahi, A.; Arunan, E. Hydrogen bonding, halogen bonding and lithium bonding: An atoms in molecules and natural bond orbital perspective towards conservation of total bond order, inter- and intra-molecular bonding. PCCP 2014, 16, 22935–22952. [Google Scholar] [CrossRef]
  17. Solimannejad, M.; Rabbani, M.; Ahmadi, A.; Esrafili, M.D. Cooperative and diminutive interplay between the sodium bonding with hydrogen and dihydrogen bondings in ternary complexes of NaC3N with HMgH and HCN (HNC). Mol. Phys. 2014, 112, 2017–2022. [Google Scholar] [CrossRef]
  18. Yáñez, M.; Sanz, P.; Mó, O.; Alkorta, I.; Elguero, J. Beryllium Bonds, Do They Exist? J. Chem. Theor. Comput. 2009, 5, 2763–2771. [Google Scholar] [CrossRef]
  19. Alkorta, I.; Legon, A.C. Non-Covalent Interactions Involving Alkaline-Earth Atoms and Lewis Bases B: An ab Initio Investigation of Beryllium and Magnesium Bonds, B·MR2 (M = Be or Mg, and R = H, F or CH3). Inorganics 2019, 7, 35. [Google Scholar] [CrossRef] [Green Version]
  20. Montero-Campillo, M.M.; Mó, O.; Yáñez, M.; Alkorta, I.; Elguero, J. Chapter Three—The beryllium bond. In Advances in Inorganic Chemistry; van Eldik, R., Puchta, R., Eds.; Academic Press: Cambridge, MA, USA, 2019; Volume 73, pp. 73–121. [Google Scholar]
  21. Frontera, A.; Bauzá, A. Regium–π bonds: An Unexplored Link between Noble Metal Nanoparticles and Aromatic Surfaces. Chem. Eur. J. 2018, 24, 7228–7234. [Google Scholar] [CrossRef]
  22. Zierkiewicz, W.; Michalczyk, M.; Scheiner, S. Regium bonds between Mn clusters (M = Cu, Ag, Au and n = 2–6) and nucleophiles NH3 and HCN. PCCP 2018, 20, 22498–22509. [Google Scholar] [CrossRef] [Green Version]
  23. Legon, A.C.; Walker, N.R. What’s in a name? ‘Coinage-metal’ non-covalent bonds and their definition. PCCP 2018, 20, 19332–19338. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  24. Grabowski, S.J. Triel Bonds, π-Hole-π-Electrons Interactions in Complexes of Boron and Aluminium Trihalides and Trihydrides with Acetylene and Ethylene. Molecules 2015, 20, 11297–11316. [Google Scholar] [CrossRef] [PubMed]
  25. Alkorta, I.; Rozas, I.; Elguero, J. Molecular Complexes between Silicon Derivatives and Electron-Rich Groups. J. Phys. Chem. A 2001, 105, 743–749. [Google Scholar] [CrossRef]
  26. Alkorta, I.; Blanco, F.; Elguero, J.; Dobado, J.A.; Ferrer, S.M.; Vidal, I. Carbon·Carbon Weak Interactions. J. Phys. Chem. A 2009, 113, 8387–8393. [Google Scholar] [CrossRef] [PubMed]
  27. Bauzá, A.; Mooibroek, T.J.; Frontera, A. Tetrel-Bonding Interaction: Rediscovered Supramolecular Force? Angew. Chem. Int. Ed. 2013, 52, 12317–12321. [Google Scholar] [CrossRef] [PubMed]
  28. Grabowski, S.J. Tetrel bond-[sigma]-hole bond as a preliminary stage of the SN2 reaction. Phys. Chem. Chem. Phys. 2014, 16, 1824–1834. [Google Scholar] [CrossRef]
  29. Del Bene, J.E.; Alkorta, I.; Elguero, J. The Pnicogen Bond in Review: Structures, Binding Energies, Bonding Properties, and Spin-Spin Coupling Constants of Complexes Stabilized by Pnicogen Bonds. In Noncovalent Forces; Scheiner, S., Ed.; Springer International Publishing: Cham, Switzerland, 2015; pp. 191–263. [Google Scholar] [CrossRef]
  30. Zahn, S.; Frank, R.; Hey-Hawkins, E.; Kirchner, B. Pnicogen Bonds: A New Molecular Linker? Chem. Eur. J. 2011, 17, 6034–6038. [Google Scholar] [CrossRef]
  31. Scheiner, S. The Pnicogen Bond: Its Relation to Hydrogen, Halogen, and Other Noncovalent Bonds. Acc. Chem. Res. 2013, 46, 280–288. [Google Scholar] [CrossRef]
  32. Minyaev, R.M.; Minkin, V.I. Theoretical study of O- > X (S, Se, Te) coordination in organic compounds. Can. J. Chem. 1998, 76, 776–788. [Google Scholar] [CrossRef]
  33. Wang, W.; Ji, B.; Zhang, Y. Chalcogen Bond: A Sister Noncovalent Bond to Halogen Bond. J. Phys. Chem. A 2009, 113, 8132–8135. [Google Scholar] [CrossRef]
  34. Sanz, P.; Yáñez, M.; Mó, O. Competition between X···H···Y Intramolecular Hydrogen Bonds and X····Y (X = O, S, and Y = Se, Te) Chalcogen−Chalcogen Interactions. J. Phys. Chem. A 2002, 106, 4661–4668. [Google Scholar] [CrossRef]
  35. Azofra, L.M.; Alkorta, I.; Scheiner, S. Strongly bound noncovalent (SO3)n:H2CO complexes (n = 1, 2). Phys. Chem. Chem. Phys. 2014, 16, 18974–18981. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  36. Legon, A.C. Prereactive Complexes of Dihalogens XY with Lewis Bases B in the Gas Phase: A Systematic Case for the Halogen Analogue B⋅⋅⋅XY of the Hydrogen Bond B⋅⋅⋅HX. Angew. Chem. Int. Ed. 1999, 38, 2686–2714. [Google Scholar] [CrossRef]
  37. Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The Halogen Bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  38. Bauzá, A.; Frontera, A. Aerogen Bonding Interaction: A New Supramolecular Force? Angew. Chem. Int. Ed. 2015, 54, 7340–7343. [Google Scholar] [CrossRef] [PubMed]
  39. Halldin Stenlid, J.; Johansson, A.J.; Brinck, T. σ-Holes and σ-lumps direct the Lewis basic and acidic interactions of noble metal nanoparticles: Introducing regium bonds. PCCP 2018, 20, 2676–2692. [Google Scholar] [CrossRef] [Green Version]
  40. Li, Q.; Li, H.; Li, R.; Jing, B.; Liu, Z.; Li, W.; Luan, F.; Cheng, J.; Gong, B.; Sun, J. Influence of Hybridization and Cooperativity on the Properties of Au-Bonding Interaction: Comparison with Hydrogen Bonds. J. Phys. Chem. A 2011, 115, 2853–2858. [Google Scholar] [CrossRef]
  41. Sánchez-Sanz, G.; Alkorta, I.; Elguero, J.; Yáñez, M.; Mó, O. Strong interactions between copper halides and unsaturated systems: New metallocycles? Or the importance of deformation. PCCP 2012, 14, 11468–11477. [Google Scholar] [CrossRef] [Green Version]
  42. Zhang, J.; Wang, Z.; Liu, S.; Cheng, J.; Li, W.; Li, Q. Synergistic and diminutive effects between triel bond and regium bond: Attractive interactions between π-hole and σ-hole. Appl. Organomet. Chem. 2019, 33, e4806. [Google Scholar] [CrossRef]
  43. Sánchez-Sanz, G.; Trujillo, C.; Alkorta, I.; Elguero, J. Understanding Regium Bonds and their Competition with Hydrogen Bonds in Au2:HX Complexes. ChemPhysChem 2019, 20, 1572–1580. [Google Scholar] [CrossRef]
  44. Wang, R.; Yang, S.; Li, Q. Coinage-Metal Bond between [1.1.1]Propellane and M2/MCl/MCH3 (M = Cu, Ag, and Au): Cooperativity and Substituents. Molecules 2019, 24, 2601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  45. Zheng, B.; Liu, Y.; Wang, Z.; Zhou, F.; Liu, Y.; Ding, X.; Lu, T. Regium bonds formed by MX (M = Cu, Ag, Au; X = F, Cl, Br) with phosphine-oxide/phosphinous acid: Comparisons between oxygen-shared and phosphine-shared complexes. Mol. Phys. 2019, 117, 2443–2455. [Google Scholar] [CrossRef]
  46. Alkorta, I.; Elguero, J.; Dias, H.V.R.; Parasar, D.; Martín-Pastor, M. An experimental and computational NMR study of organometallic nine-membered rings: Trinuclear silver(I) complexes of pyrazolate ligands. Magn. Reson. Chem. 2020. [Google Scholar] [CrossRef] [PubMed]
  47. Allen, F. The Cambridge Structural Database: A quarter of a million crystal structures and rising. Acta Crystallogr. Sect. B Struct. Sci. 2002, 58, 380–388. [Google Scholar] [CrossRef]
  48. Pople, J.A.; Binkley, J.S.; Seeger, R. Theoretical models incorporating electron correlation. Int. J. Quantum Chem. 1976, 10, 1–19. [Google Scholar] [CrossRef]
  49. Krishnan, R.; Pople, J.A. Approximate fourth-order perturbation theory of the electron correlation energy. Int. J. Quantum Chem. 1978, 14, 91–100. [Google Scholar] [CrossRef]
  50. Bartlett, R.J.; Silver, D.M. Many-body perturbation theory applied to electron pair correlation energies. I. Closed-shell first-row diatomic hydrides. J. Chem. Phys. 1975, 62, 3258–3268. [Google Scholar] [CrossRef]
  51. Bartlett, R.J.; Purvis, G.D. Many-body perturbation theory, coupled-pair many-electron theory, and the importance of quadruple excitations for the correlation problem. Int. J. Quantum Chem. 1978, 14, 561–581. [Google Scholar] [CrossRef]
  52. Del Bene, J.E. Proton affinities of ammonia, water, and hydrogen fluoride and their anions: A quest for the basis-set limit using the Dunning augmented correlation-consistent basis sets. J. Phys. Chem. 1993, 97, 107–110. [Google Scholar] [CrossRef]
  53. Dunning, T.H. Gaussian-Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
  54. Woon, D.E.; Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. V. Core-valence basis sets for boron through neon. J. Chem. Phys. 1995, 103, 4572–4585. [Google Scholar] [CrossRef] [Green Version]
  55. Peterson, A.K.; Puzzarini, C. Systematically convergent basis sets for transition metals. II. Pseudopotential-based correlation consistent basis sets for the group 11 (Cu, Ag, Au) and 12 (Zn, Cd, Hg) elements. Theor. Chem. Acc. 2005, 114, 283–296. [Google Scholar] [CrossRef]
  56. Frisch, M.J.T.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; Li, X.; et al. Gaussian 16, Revision A.03; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  57. Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
  58. Jmol: An Open-Source Java Viewer for Chemical Structures in 3D. Available online: http://www.jmol.org/ (accessed on 24 February 2020).
  59. Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
  60. Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
  61. Popelier, P.L.A. Atoms in Molecules An Introduction; Prentice Hall: Harlow, UK, 2000. [Google Scholar]
  62. Matta, C.F.; Boyd, R.J. The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design; Wiley-VCH: Weinheim, Germany, 2007. [Google Scholar]
  63. Keith, T.A. AIMAll, 17.11.14 B; Version 17.11.14 B; TK Gristmill Software: Overland Park, KS, USA, 2017. [Google Scholar]
  64. Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular Interactions from a Natural Bond Orbital, Donor-Acceptor Viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
  65. Noury, S.; Krokidis, X.; Fuster, F.; Silvi, B. TopMod Package; Universite Pierre et Marie Curie: Paris, France, 1997. [Google Scholar]
  66. Silvi, B.; Savin, A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 1994, 371, 683–686. [Google Scholar] [CrossRef]
  67. Savin, A.; Silvi, B.; Coionna, F. Topological analysis of the electron localization function applied to delocalized bonds. Can. J. Chem. 1996, 74, 1088–1096. [Google Scholar] [CrossRef]
  68. Schreckenbach, G.; Ziegler, T. Calculation of NMR Shielding Tensors Using Gauge-Including Atomic Orbitals and Modern Density Functional Theory. J. Phys. Chem. 1995, 99, 606–611. [Google Scholar] [CrossRef]
  69. Lenthe, E.V.; Baerends, E.J.; Snijders, J.G. Relativistic regular two-component Hamiltonians. J. Chem. Phys. 1993, 99, 4597–4610. [Google Scholar] [CrossRef]
  70. Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef] [Green Version]
  71. Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
  72. Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar] [CrossRef] [PubMed]
  73. Van Lenthe, E.; Baerends, E.J. Optimized Slater-type basis sets for the elements 1–118. J. Comput. Chem. 2003, 24, 1142–1156. [Google Scholar] [CrossRef] [PubMed]
  74. Schleyer, P.V.; Maerker, C.; Dransfeld, A.; Jiao, H.J.; Hommes, N.J.R.V. Nucleus-independent chemical shifts: A simple and efficient aromaticity probe. JACS 1996, 118, 6317–6318. [Google Scholar] [CrossRef]
  75. Stanger, A. Nucleus-Independent Chemical Shifts (NICS): Distance Dependence and Revised Criteria for Aromaticity and Antiaromaticity. J. Org. Chem. 2006, 71, 883–893. [Google Scholar] [CrossRef]
  76. Gershoni-Poranne, R.; Stanger, A. Magnetic criteria of aromaticity. Chem. Soc. Rev. 2015, 44, 6597–6615. [Google Scholar] [CrossRef]
  77. Te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
  78. Omary, M.A.; Rawashdeh-Omary, M.A.; Diyabalanage, H.V.K.; Dias, H.V.R. Blue Phosphors of Dinuclear and Mononuclear Copper(I) and Silver(I) Complexes of 3,5-Bis(trifluoromethyl)pyrazolate and the Related Bis(pyrazolyl)borate. Inorg. Chem. 2003, 42, 8612–8614. [Google Scholar] [CrossRef]
  79. Yang, L.; Powell, D.R.; Houser, R.P. Structural variation in copper(i) complexes with pyridylmethylamide ligands: Structural analysis with a new four-coordinate geometry index, τ4. Dalton Trans. 2007, 955–964. [Google Scholar] [CrossRef]
  80. Kandel, S.; Stenger-Smith, J.; Chakraborty, I.; Raptis, R.G. Syntheses and X-ray crystal structures of a family of dinuclear silver(I)pyrazolates: Assessment of their antibacterial efficacy against P. aeruginosa with a soft tissue and skin infection model. Polyhedron 2018, 154, 390–397. [Google Scholar] [CrossRef]
  81. Mitoraj, M.P.; Michalak, A. σ-Donor and π-Acceptor Properties of Phosphorus Ligands: An Insight from the Natural Orbitals for Chemical Valence. Inorg. Chem. 2010, 49, 578–582. [Google Scholar] [CrossRef] [PubMed]
  82. Mata, I.; Alkorta, I.; Molins, E.; Espinosa, E. Universal Features of the Electron Density Distribution in Hydrogen-Bonding Regions: A Comprehensive Study Involving H⋅⋅⋅X (X=H, C, N, O, F, S, Cl, π) Interactions. Chem. Eur. J. 2010, 16, 2442–2452. [Google Scholar] [CrossRef] [PubMed]
  83. Alkorta, I.; Solimannejad, M.; Provasi, P.; Elguero, J. Theoretical Study of Complexes and Fluoride Cation Transfer between N2F+ and Electron Donors. J. Phys. Chem. A 2007, 111, 7154–7161. [Google Scholar] [CrossRef] [PubMed]
  84. Cremer, D.; Kraka, E. A description of the chemical bond in terms of local properties of electron density and energy. Croat. Chem. Acta 1984, 57, 1259–1281. [Google Scholar]
  85. Rozas, I.; Alkorta, I.; Elguero, J. Behavior of ylides containing N, O, and C atoms as hydrogen bond accepters. J. Am. Chem. Soc. 2000, 122, 11154–11161. [Google Scholar] [CrossRef]
  86. Poater, J.; Solà, M.; Viglione, R.G.; Zanasi, R. Local Aromaticity of the Six-Membered Rings in Pyracylene. A Difficult Case for the NICS Indicator of Aromaticity. J. Org. Chem. 2004, 69, 7537–7542. [Google Scholar] [CrossRef]
  87. Poater, J.; Bofill, J.M.; Alemany, P.; Solà, M. Role of Electron Density and Magnetic Couplings on the Nucleus-Independent Chemical Shift (NICS) Profiles of [2.2]Paracyclophane and Related Species. J. Org. Chem. 2006, 71, 1700–1702. [Google Scholar] [CrossRef]
  88. Sánchez-Sanz, G. Aromatic behaviour of benzene and naphthalene upon pnicogen substitution. Tetrahedron 2015, 71, 826–839. [Google Scholar] [CrossRef]
  89. Sánchez-Sanz, G.; Trujillo, C.; Rozas, I.; Alkorta, I. Influence of fluoro and cyano substituents in the aromatic and antiaromatic characteristics of cyclooctatetraene. Phys. Chem. Chem. Phys. 2015, 17, 14961–14971. [Google Scholar] [CrossRef] [Green Version]
  90. Trujillo, C.; Sánchez-Sanz, G. A Study of π–π Stacking Interactions and Aromaticity in Polycyclic Aromatic Hydrocarbon/Nucleobase Complexes. ChemPhysChem 2016, 17, 395–405. [Google Scholar] [CrossRef]
  91. Sánchez-Sanz, G.; Alkorta, I.; Trujillo, C.; Elguero, J. A theoretical NMR study of the structure of benzynes and some of their carbocyclic and heterocyclic analogs. Tetrahedron 2012, 68, 6548–6556. [Google Scholar] [CrossRef]
  92. Kusakiewicz-Dawid, A.; Porada, M.; Dziuk, B.; Siodlak, D. Annular Tautomerism of 3(5)-Disubstituted-1H-pyrazoles with Ester and Amide Groups. Molecules 2019, 24, 2632. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Crystals 10 00137 sch001 550
Scheme 1. General structure of the complexes under study and their corresponding names.
Scheme 1. General structure of the complexes under study and their corresponding names.
Crystals 10 00137 sch001
Crystals 10 00137 g001 550
Figure 1. (a) Molecular graph, (b) electron localization function (ELF) at 0.7 isosurface value, (c) molecular electrostatic potential on the 0.001 au electron density isosurface (MESP) and (d) LUMO orbital of the (PzAg)2 system. The green and red dots in the molecular graph indicate the location of the bond and ring critical points. The range of colors used in the MESP are red (MESP < –0.02 a.u.) and blue (MESP > 0.03 a.u.). The locations of the VS,max in the MESP are indicated with black dots.
Figure 1. (a) Molecular graph, (b) electron localization function (ELF) at 0.7 isosurface value, (c) molecular electrostatic potential on the 0.001 au electron density isosurface (MESP) and (d) LUMO orbital of the (PzAg)2 system. The green and red dots in the molecular graph indicate the location of the bond and ring critical points. The range of colors used in the MESP are red (MESP < –0.02 a.u.) and blue (MESP > 0.03 a.u.). The locations of the VS,max in the MESP are indicated with black dots.
Crystals 10 00137 g001
Crystals 10 00137 g002 550
Figure 2. Relative energy vs. Ag–Ag distance in the (PzAg)2 system.
Figure 2. Relative energy vs. Ag–Ag distance in the (PzAg)2 system.
Crystals 10 00137 g002
Crystals 10 00137 g003 550
Figure 3. Molecular graph of the (PzAg)2(CO)2 and (PzAg)2(PH3)2 complexes. The green and red dots indicate the location of the bond and ring critical points, respectively.
Figure 3. Molecular graph of the (PzAg)2(CO)2 and (PzAg)2(PH3)2 complexes. The green and red dots indicate the location of the bond and ring critical points, respectively.
Crystals 10 00137 g003
Crystals 10 00137 g004 550
Figure 4. Two orthogonal views of the molecular graph of the (4NO2pzAg)2(PH3)4 complex.
Figure 4. Two orthogonal views of the molecular graph of the (4NO2pzAg)2(PH3)4 complex.
Crystals 10 00137 g004
Crystals 10 00137 g005 550
Figure 5. Electron density, ρBCP, and Laplacian, ∇2ρBCP, vs. the Ag–Ag distance (Å). The fitted exponential relationships are shown.
Figure 5. Electron density, ρBCP, and Laplacian, ∇2ρBCP, vs. the Ag–Ag distance (Å). The fitted exponential relationships are shown.
Crystals 10 00137 g005
Crystals 10 00137 g006 550
Figure 6. NICS(0), black squares, and NICS(1) values, red dots, of the six-membered ring versus the distance between the silver atom and the location where the NICS were measured (Ag–NICS distance). The blue triangles representes the NICS values for the (PzAg)2 scan between 0.0 and 2.0 Å. The second order polynomial equation fitting the values of the NICS(0) and NICS(1) has an R2 value of 0.989.
Figure 6. NICS(0), black squares, and NICS(1) values, red dots, of the six-membered ring versus the distance between the silver atom and the location where the NICS were measured (Ag–NICS distance). The blue triangles representes the NICS values for the (PzAg)2 scan between 0.0 and 2.0 Å. The second order polynomial equation fitting the values of the NICS(0) and NICS(1) has an R2 value of 0.989.
Crystals 10 00137 g006
Table
Table 1. Results of the Cambridge Structural Database (CSD) search. Abbreviations: nature of the pyrazolate anion, nature of the ligand (L), number of ligands; Ag(I)–Ag(I) distance in Å, silver–ligand distance in Å, conformation of the six-membered ring and tetrahedral configuration of the Ag (τ4 index).
Table 1. Results of the Cambridge Structural Database (CSD) search. Abbreviations: nature of the pyrazolate anion, nature of the ligand (L), number of ligands; Ag(I)–Ag(I) distance in Å, silver–ligand distance in Å, conformation of the six-membered ring and tetrahedral configuration of the Ag (τ4 index).
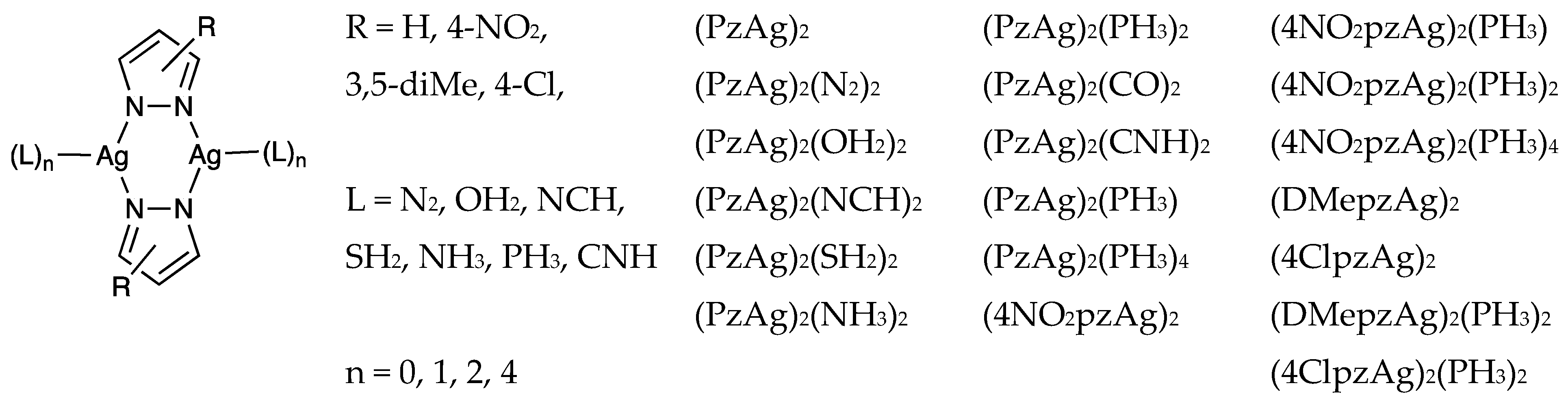
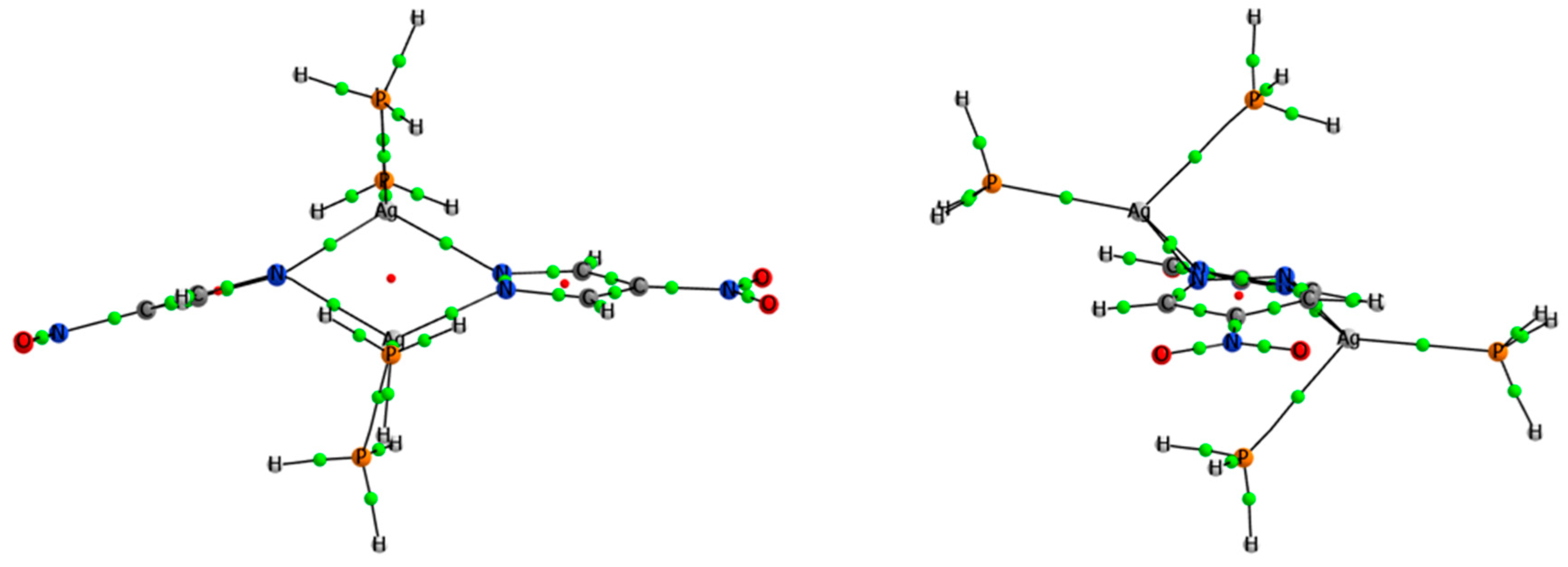
RefcodePyrazolateLigand (L)Nº of LsAg–AgAg–LConformationτ4 index
FINWOR3,5-bis-CF33,5-bis-CF3-pyrazole-Ag23.3922.250Nearly planar----
PIRCUR3,5-bis-CF3PPh323.4252.343Boat----
PIRCUR3,5-bis-CF3PPh323.4252.414Boat----
FINWIL3,5-bis-CF3PPh323.4792.366Twisted boat----
IPIGOD3,5-bis-CF32,4,6-collidine23.4992.277Boat + flattened chair----
IPIGOD3,5-bis-CF32,4,6-collidine23.4992.254Boat + lattened chair----
IPIGOD3,5-bis-CF32,4,6-collidine23.5022.269Boat + flattened chair----
IPIGOD013,5-bis-CF32,4,6-collidine23.5622.253Half boat----
IPIGOD013,5-bis-CF32,4,6-collidine23.5622.253Half boat----
SOJCIG3,5-bis-CF33,5-bis-CF3-pyrazole-Ag23.6323.218Chair----
SOJCIG3,5-bis-CF3pyrazole-Ag23.6322.258Chair----
RATFEXParentPPh333.7062.370Flattened chair0.90
RATFEXParentPPh333.7062.484Flattened chair
RATFEXParentPPh333.7062.461Flattened chair
ZIGRUF4-ClPPh333.7072.374Flattened boat0.83
ZIGRUF4-ClPPh333.7072.475Flattened boat
ZIGRUF4-ClPPh333.7072.485Flattened boat
ZIGSIU4-NO2PPh333.8272.379Boat0.90
ZIGSIU4-NO2PPh333.8272.495Boat
ZIGSIU4-NO2PPh333.8272.469Boat
RATFATParentPPh323.8702.376Planar----
KIRXIVParent(a)2 (4)3.9002.532Planar0.78
KIRXIVParentPPh343.9002.539Planar
ZIGSAM4-Cl(b): PR344.2052.460Twisted0.78
ZIGSAM4-ClPR3 4.2052.534Twisted
ZIGROZ4-ClPPh344.2092.484Twisted0.89
ZIGROZ4-ClPPh344.2092.500Twisted
ZIGSEQ4-NO2PPh344.3052.502Twisted0.88
ZIGSEQ4-NO2PPh344.3052.487Twisted
max-------- 4.3053.218--------
min-------- 3.3922.250--------
Crystals 10 00137 i001
Table
Table 2. Geometries and dissociation energy of (PzAg)2 and (PzAg)2L2 systems.
Table 2. Geometries and dissociation energy of (PzAg)2 and (PzAg)2L2 systems.
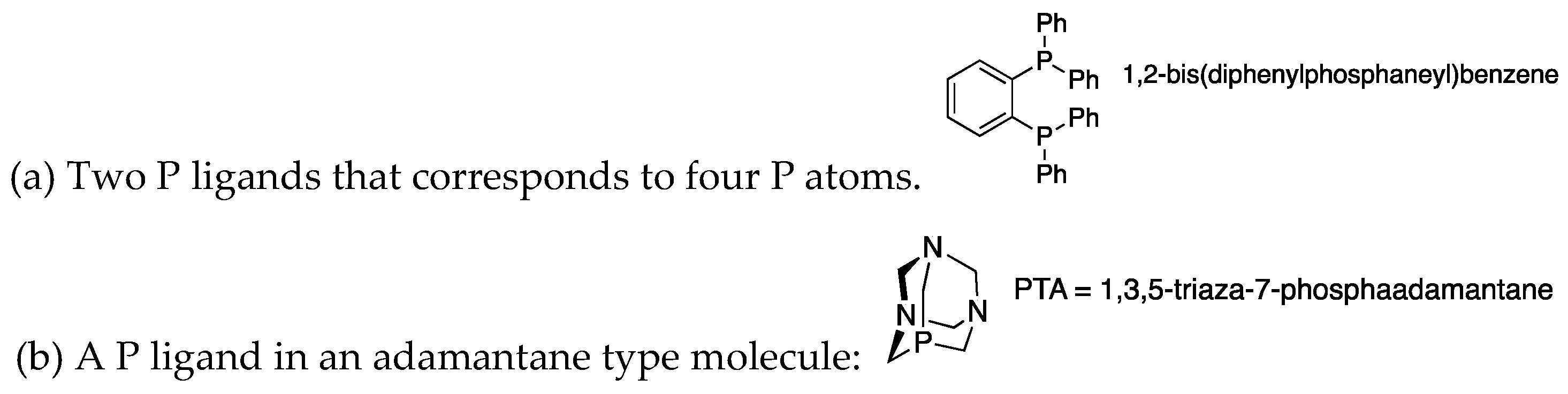
CompoundAg–Ag dist. (Å)Pz-Pz dist. (Å) aAg-Z dist. (Å) bDe (kJ·mol−1)
(PzAg)22.8013.968—0.0
(PzAg)2(N2)22.8513.9682.83722.7
(PzAg)2(OH2)22.9083.9942.63054.5
(PzAg)2(NCH)23.0783.9332.42556.3
(PzAg)2(SH2)23.1963.8892.63171.2
(PzAg)2(NH3)23.2553.9052.35891.7
(PzAg)2(PH3)23.6893.6572.373122.9
(PzAg)2(CO)23.8453.5191.99890.0
(PzAg)2(CNH)23.8803.5342.018136.6
a Measured as the distance between the smallest N–N distance in two pyrazole rings. b Z is the atom of L directly interacting with the silver atoms.
Table
Table 3. Effect of the 3,5-dimethyl, 4-chloro and 4-nitro substituents (pyrazole ring) within the Ag–Ag distance and on the dissociation energy, De.
Table 3. Effect of the 3,5-dimethyl, 4-chloro and 4-nitro substituents (pyrazole ring) within the Ag–Ag distance and on the dissociation energy, De.
CompoundAg–Ag dist. (Å)De (kJ·mol−1)
(DMepzAg)22.793----
(PzAg)22.801----
(4ClpzAg)22.819----
(4NO2pzAg)22.841----
(DMepzAg)2(PH3)23.656120.0
(PzAg)2(PH3)23.689122.9
(4ClpzAg)2(PH3)23.730135.1
(4NO2pzAg)2(PH3)23.782150.8
Table
Table 4. Effect of the number of ligands.
Table 4. Effect of the number of ligands.
CompoundNumber of LsAg–Ag dist. (Å)De (kJ·mol−1)τ4 index
(PzAg)202.8010.0----
(PzAg)2(PH3)13.08764.2----
(PzAg)2(PH3)223.689122.9----
(PzAg)2(PH3)443.798214.50.81 & 0.83
(4NO2pzAg)202.8410.0----
(4NO2pzAg)2(PH3)13.15277.4
(4NO2pzAg)2(PH3)223.782150.8----
(4NO2pzAg)2(PH3)443.870251.70.80 & 0.81
Table
Table 5. 109Ag absolute chemical shielding (σ, ppm) and nuclear-independent chemical shift (NICS) values (ppm) of the six-membered and pyrazole rings.
Table 5. 109Ag absolute chemical shielding (σ, ppm) and nuclear-independent chemical shift (NICS) values (ppm) of the six-membered and pyrazole rings.
Systemσ109Ag (ppm)6-Membered RingPz Ring
NICS(0)NICS(1)NICS(0)NICS(1)
(PzAg)23765.7−7.39−1.84−13.06−10.97
(PzAg)2(N2)23648.3−7.17−1.70−12.70−10.95
(PzAg)2(OH2)23752.8−5.82−1.48−12.88−11.22
(PzAg)2(NCH)23515.5−4.76−1.10−12.67−11.03
(PzAg)2(SH2)23288.3−3.55−0.65−12.75−11.04
(PzAg)2(NH3)23511.9−2.40−0.38−12.74−11.12
(PzAg)2(PH3)22900.9−0.140.12−12.27−11.11
(PzAg)2(CO)22706.9−0.56−0.33−12.37−11.13
(PzAg)2(CNH)22825.4−0.16−0.12−12.29−11.16
(DMepzAg)23720.4−7.98−2.23−10.50−9.34
(4ClpzAg)23815.9−7.11−1.75−12.62−9.98
(4NO2pzAg)23835.5−6.95−1.72−11.98−9.50
(DMepzAg)2(PH3)22893.1−0.73−0.25−9.32−9.29
(4ClpzAg)2(PH3)22954.4−0.170.07−11.74−10.09
(4NO2pzAg)2(PH3)23010.20.120.19−10.81−9.41
(PzAg)2(PH3)42561.6
2550.5
(4NO2pzAg)2(PH3)42619.5
2627.7

Share and Cite

MDPI and ACS Style

Alkorta, I.; Trujillo, C.; Sánchez-Sanz, G.; Elguero, J. Regium Bonds between Silver(I) Pyrazolates Dinuclear Complexes and Lewis Bases (N2, OH2, NCH, SH2, NH3, PH3, CO and CNH). Crystals 2020, 10, 137. https://doi.org/10.3390/cryst10020137

AMA Style

Alkorta I, Trujillo C, Sánchez-Sanz G, Elguero J. Regium Bonds between Silver(I) Pyrazolates Dinuclear Complexes and Lewis Bases (N2, OH2, NCH, SH2, NH3, PH3, CO and CNH). Crystals. 2020; 10(2):137. https://doi.org/10.3390/cryst10020137

Chicago/Turabian Style

Alkorta, Ibon, Cristina Trujillo, Goar Sánchez-Sanz, and José Elguero. 2020. "Regium Bonds between Silver(I) Pyrazolates Dinuclear Complexes and Lewis Bases (N2, OH2, NCH, SH2, NH3, PH3, CO and CNH)" Crystals 10, no. 2: 137. https://doi.org/10.3390/cryst10020137

APA Style

Alkorta, I., Trujillo, C., Sánchez-Sanz, G., & Elguero, J. (2020). Regium Bonds between Silver(I) Pyrazolates Dinuclear Complexes and Lewis Bases (N2, OH2, NCH, SH2, NH3, PH3, CO and CNH). Crystals, 10(2), 137. https://doi.org/10.3390/cryst10020137

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop